ELSEVIER Information Processing Letters 52 (1994) 317-322
Information
Processing
Letters
The path-partition problem in block graphs
’Jing-Ho Yan, Gerard J. Chang *
Department of Applied Mathematics, National Chiao Tung University, Hsinchu 30050, Taiwan Communicated by D. Gries; received 3 December 1993; wised 12 August 1994
Abstract
We present a linear-time algorithm for the path-partition problem in block graphs. Keywords: Algorithms; Graph theory; Path-partition
1. Introduction
A path partition of a graph G is a collection of vertex-disjoint paths that cover all vertices of the graph. The path-partition problem is to find the path-partition number p(G): the minimum size of a path partition of G. Note that G has a Hamiltonian path iff p(G) = 1. Since the Hamiltonian path problem is NP-complete for planar graphs, bipartite graphs, and chordal graphs (see [ 61)) so is the path-partition problem. Bonucelli and Bovet [ 41 and Arikati and Pandu Rangan [ 21 gave linear-time algorithms for the path-partition problem in interval graphs, Skupien [ 81 gave a polynomial-time algorithm for forests, and Chang and Kuo [ 31 gave a linear-time algorithm for cographs, and Srikant et al. [9] gave linear-time algorithms for bipartite permutation graphs and block graphs.
Srikant et al. [9] did not prove the correctness of their algorithm for block graphs. In fact, as discussed in Section 4, it does not work for all block graphs. The purpose of this paper is to give a linear-time algorithm for the path-partition problem for all block graphs and prove its correctness. For technical reasons, we also consider the following variant problem, which is the path-partition problem with a side condition. For a fixed vertex u in G, a v-path-partition of G is a path partition in which v is an end-vertex of a path in the partition. The u-path-partition problem is to find the u-path-partition number pU (G) : the minimum size of a u-path-partition of G.
We now review block graphs. A vertex x is a cut-vertex if deleting x and all edges incident to it increases the number of connected components. A block is a maximal connected subgraph without a cut-vertex. The intersection of two distinct blocks contains at most one vertex, and a vertex is a cut-vertex iff it is the intersection of two or more blocks. Consequently, a graph with one or more cut-vertices has at least two blocks. A block graph is a graph whose blocks are complete graphs.
* Corresponding author. Email: gjchang@math.nctu.edu.tw.
’ Supported in part by the National Science Council under grant NSC83-0208-M009-050.
0020.0190/94/$07.00 @ 1994 Elsevier Science B.V. All rights reserved .SSDIOO20-0190(94)00158-8
318 J.-H. Yan, G.J. Chang/lnformation Processing Letters 52 (1994) 317-322
Suppose Gt , G2, . . . , G, are disjoint graphs and Ui E V( Gi) for 1 < i 6 t. The composition of Gt , G2, . . . , G, is the graph G = (YE) obtained from the union of these graphs by making
{ut ,
~2,. . . , vt} a clique, i.e.V = u V(Gi) and E = ( U E(Gi)) U {uiuj ) 1 < i < j < t}.
l<i<t 1 (i<r
On the other hand, suppose B is a block of t vertices in a connected block graph G. Deleting all edges in B results in t connected block graphs whose composition is G. Repeatedly applying this inverse operation of composition to a connected block graph give trivial graphs. In other words, a connected block graph can be obtained from trivial graphs by a series of compositions.
2. Path partition in block graphs
We establish some basic theorems to be used later. Suppose P is a path partition of graph G. For any induced subgraph H of G, PH denotes the path partition of H resulting from P when each vertex in G - H is deleted from the path containing it in P.
Lemma 1. The following relations hold. (4 p(G - u) + 1 b p”(G).
(b) p,(G) >p(G).
(c) p(G - 0) + 1 b p,(G) 2 p(G - u).
proof. p ( G - U) + 1 3 p”(G) , since a path partition of G - u together with the path u forms a u-path-partition of G. pu (G) 2 p(G) , since a u-path-partition is a path partition. pu (G) > p (G -
v) , since the deletion of u
from a path of a u-path-partition results in a path partition of G - U. 0Lemma 2. p(G) > p(G - u) ifsp(G - v) + 1 =p,(G) =p(G).
Proof. The lemma follows immediately from (a) and (b) of Lemma 1. •i
Suppose Gt , G2, . . . , G, are disjoint graphs and Ui E V( Gi) for 1 < i < t. Define I={il 1 <i< t andp(Gi-ui) +l=p,(Gi) =p(Gi)},
J = {i 1 1 6 i 6 t and p(Gi - Ui) =pu,(Gi) =p(Gi)}. By Lemma l(c),
ZUJ={i(l<i<tandp,,,(Gi)=p(Gi)}.
Theorem 3. If G is the composition of G1 , G2,. . . , Gt, then ifI#@andJ=@,
otherwise.
Proof. For each 1 < i < t, let Pi be an optimal path partition of Gi. For i E Z (respectively, i E J), we may assume that Ui is a path in Pi (respectively, there is a path qi with an end-vertex ui in Pi). For
J.-H. Yan, G.J. Chang/lnformation Processing Letters 52 (1994) 317-322 319
the case of Z + 0 and J =
0,
P = (lJIGiGtS) - <U,,,{u~}> U {q} is a path partition of G, where q is the path formed by all vertices ui with i E I. Hence p(G) < xi=, p(Gi) - )I[ + 1. For the other cases, p = (tJl<i<rPi) - (U&ui}) - (UiEJ(4i)) u {rl~rZ~~~~~r~~J~/2~} is a path partition of G, where each ri except ri is the catenation of two qi’s and 11 is formed by the remaining one or two qi’s together with all Ui’s with i E I. HenceP(G)
G
kP(Gi)
-
III - IJI + [IJ1/21
=
&p(Gi)
-
11)
- l)Jl/2J.
i=l i=I
On the other hand, suppose P is an optimal path partition of G. A path in P is called mixed if it contains vertices in at least two different Gi’s. We may assume that P is chosen to contain the fewest vertices in all mixed paths. Note that any mixed path q is of the form q’q”q”‘, where q’ or q”’ is 0 or a nontrivial path in some Gi with Ui as an end vertex and q” is a sequence of some Ui’s. It follows that the deletion of any vertex x in q” is still a path, which we denote by q - x. Let
I’ = {i ) Ui is the only vertex of Gi that is in some mixed path q },
J’ = {i 1 Gi contains a nonempty q[ or q[11 of a mixed path qi }. Note that I’ n J’ = 8. We claim that I’ & Z and J’ & Z U J.
Suppose i E I’ - 1. Let Ui be the only vertex of Gi that is in a mixed path q. Assume Pi is an optimal path partition of Gi. Consider the path partition P’ = P - PG,-~, - {q} U Pi U {q - Ui}. Then
IP’l = IPI - IPc,-uiI + IPi1 G
lpi
U implies
IFI
IpG,I
+
c
IPG,-~:I +
c
IPG,-v(~;,I
+
miftl’UJ’ iEI’ GJ’
2
iezJ
P(Gi) +
CP(Gi - ui>
+
C(pu(G,) -
1) +
mI %I’ iEJ’
= Cp(Gi) - 11'1 -
IJ’I +
m.i=l
Note that the last equality follows from p(Gi - Ui) + 1 = p(Gi) for i E I’ c Z and p”(Gi) = p(Gi) for
iE J’CZUJ.ForthecaseofZ# 0andJ=0,Z’UJ’~Z.Ifm=O,thenZ’=J’=Q),so-jZ’l-IJ’I+m=O3
320 J.-H. Yan. G.J. Chang/lnformtion Processing Letters 52 (1994) 317-322
since each mixed path contains vertices in at most two Gi’s with i E J’, -(I’1 - 1 .I’\ + m 2 -11’1 - 11 J/1/2] >
-11’1 - IJ’ n II - [IJ’ I-? 4/2] > -III - [I.4/2]. H ence P(G) Z Xi=, p(Gi) - IZI - LlZl/2J. 0
An argument similar to that used above gives the solution to pu (G) for v = v,. For this purpose, use I’ = Z II {i I i # t} and J*=Jn{ili # t}.
Theorem 4. Zf G is the composition of GI , G2, . ..,Gtandv=v,andG’isthecompositionofG~,G2,...,Gr_~, then
I p(G’) + P,(G,) ifs, =p(Gt -v,),
p,(G) =
I
‘-’
Cp(Gi)
+~u,(Gr)-
II*1 - [IJ*l/21
ifp,(Gr)
>
p(Gr -v,>.i=l
Proof. Suppose P is an optimal v-path-partition of G in which q is a path ending at v.
For the case pu,(G,) = p(G, - vl), we may assume that q is in G, and hence p,(G) = p(G’) +p,(G,). Otherwise, suppose q is not in Gt, i.e. q intersects G,, only at 0,. Let Pl be an optimal v,-path-partition of Gr. Then P’ = P - {q} - PC,_“, U {q - vt} U P, is another v,-path-partition with
Ip’l = IpI - /PC,-o,\ + lptl < IpI -p(Gr - ut) +p,(G,) = IpI.
So P’ is another optimal u-path-partition in which the only path ending at v, is in G,.
For the case po, (G,) > p(G, - v,), we may assume that q intersects G,,, only at u,. Otherwise, PG, is a q-path-partition of Gt. Then we can replace PG, by vt together with an optimal partition of G, - U, to obtain an optimal v,-path-partition in which q intersects G,, only at vf. So p,,(G) = p,(G*) +p(G, - v,), where G* = G - (G, - v,). Let G** be the graph obtained from G* by adding a new vertex U’ adjacent to u only. Then
p,(G*) = pvf (G**) = p(G**), since a v-path-partition of G* corresponds to a v’-path-partition of G** and a path partition of G** is a u’-path-partition of G**. However, G** is the composition of Gt , G2, . . . , G,_l , K2. So we may apply Theorem 3 to G** by considering I* to be Z and J* U {t} to be J. Note that .Z* U {t} # 8 gives
t-1 t-1
p(G**) = 1 + Cp(Gi) - lZ*l - [(lJ*l + 1)/2J = Cp(Gi) - [Z*l - [IJ*1/21 + 1.
i=l i=l
Also, by Lemma 1, p (G, - v,) + 1 = pu (G,) . Hence the theorem holds. 0
Theorem 5. Zf G is the composition of G,, G2,. . . , G, and v = v, and G’ is the composition of G1, G2, . . . , G,_l , thenp(G-v)=p(G’)+p(Gt-vr).
Proof. The theorem follows from the fact that G - v is the disjoint union of G’ and Gt - vt. 0
3. Algorithm
We are ready to give a linear-time algorithm for the path-partition problem in block graphs. We may consider only connected block graphs G. Our algorithm iteratively processes a block B = {VI, ~2, . . . , vt} with exactly one cut-vertex vt of the current graph G’. Let Gi - Ui be the graph that has been deleted from the original graph G so far and let Gi connect to G only at vi. Then the composition of Gt , G2, . . . , G, connects to G’ - { ~1, u:! . . . , v,-1) only at uI. Theorems 3-5 can be used to compute p and pu for this composition. After computing p and pu,
J.-H. Yan, G.J. Chang/Information Processing Letters 52 (1994) 317-322 321
Algorithm PPN
Find the path-partition number p(C) of a connected block graph G: for all ui E V(G): pl(v;) := 1; /* for p(Gi) */
PI(Q) := 1; /* for p”,(Gi) */ p3(Ui) := 0; /* for p(Gi - ui) */ while G contains more than one vertex do
choose a block B = {ut, ~2,. , II,} with exactly one cut-vertex U, or with no cut-vertex;
I := {i 1 1 < i < t and P~(zJ;) + 1 =p2(Ui) = pt(Ui)}; J := (i ) 1 < i < t and p3(Ui) = pl(ui) = pt(Ui)}; I*:=ln{i~l<i<t-l};
J*=Jfl{i~1<~<f--1};
ifI#OandJ=e)
then pi := xi=, pl(ui) - 111 + 1 eke m(ur) := Cf=, Pl(4) - III - LIJ1/2J;
if I* # 0 and .I* = 0
then pi := c:i’ pl (ui) - [I*1 + 1
else pi := CiG’pl(Vi) - II*1 - [/J1/2];
ifp2Cut) = ~3(ut)
then p2(ut) := pi + p2Cu1)
else pz(or) := C:i’Pl(ui) +p2(ut) - II*) - ~15*1/21; P3CUr) := P; + p3(e);
G:=G-{LJ,,cJ:! ,..., u,-,} end while;
let v be the only vertex in G;
output p,(v).
Fig. 1. Algorithm PPN
delete ~1, ~2, . . . , ut-1 from G’ and continue the same process until G’ has only one vertex. The algorithm is shown in Fig. 1.
Theorem 6. Algorithm PPN computes the path-partition number of a connected block graph in linear time. Proof. The correctness of the algorithm follows from Theorems 3-5. The algorithm takes only linear time since depth-first search can be used to find end blocks and each iteration of the while loop requires only O( IBI ) operations. 0
4. Discussion
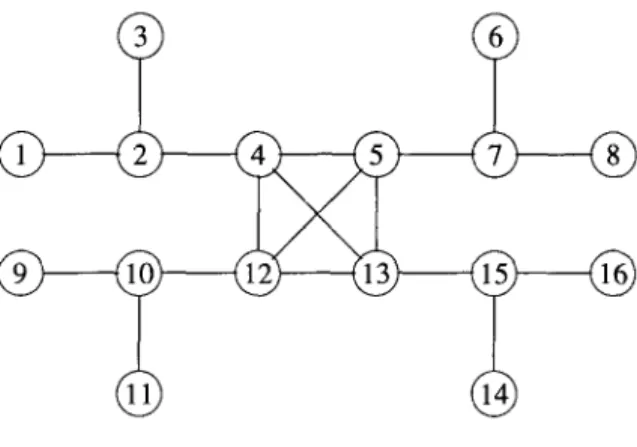
Srikant et al.‘s [9] algorithm for the path-partition problem in block graphs is similar to ours except that it solves only the case when I = 0 in all iterations (see the definition of I after Lemma 2). If I # 8 at some iterations, their algorithm does not provide a correct answer. For instance, consider the block graph G in Fig. 2. The correct value of p(G) is 5 with a path partition {PI, P2, P3, P4, Ps U Ph}, while their algorithm gives 6 with a path partition { 9, &, P3, P4, Ps, Ph}, where
9 = (1,2,3), P2 = (6,7,8), P3 = (9,10, ll),
322 J.-H. Yan, G.J. Chang/lnformation Processing Letters 52 (1994) 317-322
Fig. 2. A block graph G.
We explain why the two algorithms give different solutions. At some iteration, the subgraphs rooted at 4,5,12,13, respectively, have optimal solutions {Pi,4}, {Pz,~}, {Ps, 12}, {Pd, 13). Algorithm PPN merges 4,5,12,13 to make a new path, since they are in a block. But their algorithm merges 4 and 5 to get P5 and merges 12 and 13 to get PG. In the case of there are many paths of single vertices in a block, these two methods give answers with a big gap.
Acknowledgments
The authors thank the referee and Professor David Gries for many constructive suggestions for the revision of this paper. References 111 121 131 141 [51 [ol 171 [gl [91
A. Aho, J. Hopcroft and J.D. Ullman, The Design and Analysis of Computer Algorithms (Addison-Wesley, Reading, MA, 1974). S.R. Arikati and C. Pandu Rangan, Linear algorithm for optimal path cover problem on interval graphs, Inform. Process, Lett. 35 (1990) 149-153.
G.J. Chang and D. Kuo, The L(2, I)-labeling problem on graphs, SIAM Discrete Math., to appear.
M.A. Bonuccelli and D.P. Bovet, Minimum node disjoint path covering for circular-arc graphs, Inform. Process. L&t. 8 (1979) 159-161.
J.S. Deogun and G. Steiner, Hamiltonian cycle is polynomial on cocomparability graphs, Discrete Appl. Math. 39 ( 1992) 165-172. M.C. Golumbic, Algorithmic Graph Theory and Perfect Graphs (Academic Press, New York, 1980).
W.L. Hsu, An 0(n2 logn) algorithm for the Hamiltonian cycle problem on circular-arc graphs, SIAM J. Comput. 21 ( 1992) 1026-1046. Z. Skupien, Path partitions of vertices and hamiltonity of graphs, in: Proc. 2nd Czechoslovakian Symp. on Graph Theory, Prague, 1974.
R. Srikant, Ravi Sundaram, Karan Sher Singh and C. Pandu Rangan, Optimal path cover problem on block graphs and bipartite permutation graphs, Theoret. Comput. Sci. 115 (1993) 351-357.