Interfacial operator approach to computing modes of surface plasmon polaritons for periodic structures

Institute of Applied Mechanics, National Taiwan University, Taipei 106, Taiwan, Republic of China

3_{Department of System Engineering and Naval Architecture, National Taiwan Ocean University,}

Keelung 202, Taiwan, Republic of China

共Received 3 August 2005; published 9 November 2005兲

It has been difficult to compute the band structures for photonic crystals with metallic components included in the periodic units. The existence of modes of surface plasmon polariton presents the major difficulty not only because of the localized nature of the modes but also of the apparent necessity of handling a nonlinear eigenvalue problem. Here we show that by introducing an interfacial operator within the finite-difference framework, we are able to formulate the problem for computing modes of surface plasmon polariton in the format of standard eigenvalue problems. Results are uncovered by applying the method to periodic structures with corrugated interfaces between metals and dielectric materials, as well as other classes of interfaces. DOI:10.1103/PhysRevB.72.205112 PACS number共s兲: 42.70.Qs, 02.70.Bf, 78.20.Bh

I. INTRODUCTION

The optical properties of a photonic crystal are dependent upon the comprising materials. Most previous studies in this area of research are concerned with the optical properties of a periodic structure comprising two or more dielectric mate-rials. Recently, we have seen a steadily growing interest in considering the effects of including metallic components in photonic crystals. In particular, the interaction of light with metals in a periodic structure excites the modes of surface plasmon polariton1,2 _{and causes possible band gaps in the} dispersion relations.3,4_{This enables us to explore plasmonic} crystals or plasmonic band gap materials made of metallic materials in a similar way to photonic crystals or photonic band gap materials made of dielectric materials.

In considering the real metal effects for a photonic crystal, such as the free-electron model␧m共␻兲=1−␻p

2_/␻2_{, where␻} p denotes the bulk plasma frequency, the dielectric function is frequency dependent, and therefore for a given wave vector the solution of the dispersion relation or band structure ap-parently poses a nonlinear eigenvalue problem as the eigen-frequency itself appears in the solution operator.5_{It is known} that surface plasmon polaritons are evanescent TE modes, living in the neighborhood of the interface of the metallic inclusion and the surrounding dielectric material. This is only possible if␻⬍␻p, that is, when the dielectric function of the metallic components is in the opposite sign to that of the surrounding dielectric material. The latter means that in mathematical terms, the equation would change type as one crosses the interface from the dielectric to the metal, and vice versa. The localized nature of surface plasmon polaritons requires fine resolution near the interface, and the change of type of the equation makes the problem nondefinite that causes numerical difficulties for many solvers such as the method of conjugate gradient.6_{Nevertheless, a few methods} have been applied for this frequency-dependent nonlinear eigenvalue problem. The method of multiple multipole

expansion7_{is another choice in which a careful definition of} cost function is required for detecting resonant frequencies. The method of solution for eigenfrequencies by detecting resonance peaks is also applicable to the finite-difference time-domain method.8_{A theory of complex resonances was} introduced for the general absorptive periodic dielectric structures; the resonances define the eigenfrequencies.9–11 Along this line, a specific perturbation theory was also de-veloped with mathematical rigor to study the spectral prop-erties of absorptive photonic crystals.12 _{Also, we have seen} the method of vectorial eigenmode expansion applied to study phonon-polariton excitation in photonic crystals.13

In this study, we present a direct method for obtaining the modes of surface plasmon polariton as well as other branches of modes. This is achieved by considering

Max-well’s equations for the metallic and dielectric regions sepa-rately and treating the interface by an interfacial operator that passes information between both sides of the interface. In particular, within the finite-difference framework, we are able to formulate the problem for computing modes of sur-face plasmon polaritons in the format of standard eigenvalue problems. The method will first be illustrated for a one-dimensional periodic array of alternating layers of metals and dielectrics, as shown in Fig. 1, and then we show how the method can be extended to problems in two space dimen-sions. Perturbation analysis is also included to consider the effect of Drude damping.

II. INTERFACIAL OPERATOR

For linear isotropic and nonmagnetic dielectric materials, the equation for time-harmonic TM modes in two dimen-sions can be written as

−1 ␧ⵜ2E =

冉

␻ c

冊

2 E, 共1兲

where ␧=␧共r兲 is the dielectric function. Let ␧=␧d in the dielectric, and␧=␧min the metal. Consider the free-electron 1098-0121/2005/72共20兲/205112共12兲/$23.00 205112-1 ©2005 The American Physical Society

model␧m= 1 −␻p 2

/␻2. In the metal, Eq.共1兲 becomes −ⵜ2E =

冋

冉

␻ c

冊

2 −

冉

␻p c

冊

2

册

E, 共2兲 or, equivalently,

冋

−ⵜ2+

冉

␻p c

冊

2

册

E =

冉

␻ c

冊

2 E. 共3兲

The present authors developed a fast inverse method with multigrid acceleration14_{to solve Eq.共3兲. However, this} can-not be done for TE modes

−ⵜ ·

冉

1 ␧ⵜ H

冊

=

冉

␻ c

冊

2 H. 共4兲

But in the strict insides of the dielectric and the metal, we can move 1 /␧ outside the operator −ⵜ, and still obtain

− 1 ␧d ⵜ2_{H =}

冉

␻ c

冊

2 H, 共5兲 and

冋

−ⵜ2+

冉

␻p c

冊

2

册

H =

冉

␻ c

冊

2 H. 共6兲

First of all, let us discretize Eqs.共5兲 and 共6兲 in the strict insides of the dielectrics and metal by a central finite differ-ence with the interface point Hi as the boundary value. The lattice with lattice constant a is partitioned into n equal seg-ments with n independent variables, as shown in Fig. 1, be-cause the共n+1兲th variable is related to the first variable by Bloch’s condition

Hn+1= eikaH1. 共7兲

We obtain a system of linear equations with⌳=共␻/ c兲2,

ing equation is needed. This is provided by applying Eq.共4兲 at the interface to relate the normal derivatives on both sides as 1 ␧+

冏

⳵H ⳵n

冏

₊= 1 ␧−

冏

⳵H ⳵n

冏

₋. 共9兲

Then, we have, with␧₊=␧d and␧−= 1 −␻p 2_/␻2

冏

⳵H ⳵n

冏

₊= ␻2 ␻p 2

冏

冉

冏

⳵H ⳵n

冏

₊−␧d ⳵H ⳵n

冏

₋

冊

. 共10兲

Nevertheless, Eqs. 共6兲 and 共10兲 do not constitute an easy eigenvalue problem because the variable in Eq. 共6兲 is H, while the one in Eq.共10兲 would be⳵H /⳵n兩₊−␧d⳵H /⳵n兩−.

The crucial step taken here is to introduce an interfacial variable into the discretized form of Eq. (10), and reformu-late the eigensystem in terms of the H field in the strict in-sides along with this new variable. Applying one-sided finite

difference to Eq.共10兲 at the interface point i, we have, with ⌳p=共␻p/ c兲2 ⌳p

冉

Hi− Hi−1 h

冊

=⌳

冋

− Hi−1+共1 + ␧d兲Hi−␧dHi+1 h

册

. 共11兲 This suggests that we introduce an interfacial variable

Ri⬅ − Hi−1+共1 + ␧d兲Hi−␧dHi+1 共12兲 or, reversely, Hi= − Hi−1+ Ri− Hi+1 1 +␧d 共13兲 so that Eq.共11兲 can be recast into the form

FIG. 1.共Color online兲 Discretization points of one unit cell for a one-dimensional periodic array of alternating layers of metals and dielectrics, where␤ is the off-line wave number.

FIG. 2.共Color online兲 Interfacial and neighboring points for the square lattice of square metal cylinders with lattice constant a and half width w / a = 0.25.

⌳p 1 +␧d

共− ␧dHi−1+ Ri+␧dHi+1兲 = ⌳Ri. 共14兲

Meanwhile, we rewrite the matrix Eq.共8兲 by using Eq. 共13兲 to replace each Hiat the interface. The resultant matrix sys-tem supplemented by Eq.共14兲 constitutes an eigensystem of standard format

An_⫻nHn=⌳Hn, 共15兲 where Hn=关H1 ¯ Hi−1RiHi+1 ¯ Hn兴T. Then, more ex-plicitly, we have the entries of the rows corresponding to

Hi−1, Ri, and Hi+1

A = 1 h2

冤

¯ ¯ − 1 1 + 2␧d 1 +␧d − 1 1 +␧d − ␧d 1 +␧d −␧d⌳ph 2 1 +␧d ⌳ph2 1 +␧d ␧d⌳ph2 1 +␧d − 1 1 +␧d − 1 1 +␧d 2 +␧d 1 +␧d +⌳ph2 − 1 ¯ ¯

冥

. 共16兲 III. EXTENSION TO TWO DIMENSIONS

Next, we illustrate how the above method can be applied to two-dimensional problems. Consider a square region of FIG. 3. 共Color online兲 Disper-sion relations at k = 0 for the one-dimensional photonic crystal with

d₂/ a = 0.2. Solid lines denote com-puted results by the interfacial op-erator approach and dots denote analytical solutions of Eq.共35兲 by Newton-Ralphson’s method.

FIG. 4. 共Color online兲 Disper-sion relations at ka / 2␲=0.1 for the one-dimensional photonic crystal with d2/ a = 0.2.

metal surrounded by dielectrics as shown in Fig. 2. The in-terface condition共10兲 is applied in horizontal, vertical, and oblique directions. Therefore, in two dimensions there are two types of interface points: side and corner. At the interfa-cial point S1 共side兲, now denoted as 共i, j兲, discretization of the interfacial operator is along N1L− S1− N1R,

⌳p

冉

Hi,j− Hi−1,j

h

冊

=⌳

冋

− Hi−1,j+共1 + ␧d兲Hi,j−␧dHi+1,j

h

册

,

共17兲 and we define the interfacial variable as

Ri,j⬅ − Hi−1,j+共1 + ␧d兲Hi,j−␧dHi+1,j, 共18兲 or, reversely,

Hi,j=

Hi−1,j+ Ri,j+␧dHi+1,j 1 +␧d

. 共19兲

Then, the interface condition共10兲 for the interfacial point S1 is

⌳p 1 +␧d

共− ␧dHi−1,j+ Ri,j+␧dHi+1,j兲 = ⌳Ri,j. 共20兲

Ri,j is defined similarly at the other interfacial points S2, S3, and S4. At the interfacial point C1 共corner兲, now denoted as 共i, j兲, discretization of the interfacial operator is along

A1− C1− N13

FIG. 5. 共Color online兲 Eigen-frequencies at point ⌫ for TE modes computed with different grid resolutions for the square lat-tice of square metallic cylinders with w / a = 0.3.

FIG. 6. 共Color online兲 Band structures for the square lattice of square cylinders with half width

⌳p

冉

H_i,j− H_i−1,j−1

冑

2h

冊

=⌳

冋

− Hi−1,j−1+共1 + ␧

_冑

d兲Hi,j−␧dHi+1,j+1

2h

册

, 共21兲

and the interfacial variable is defined as

Ri,j⬅ − Hi−1,j−1+共1 + ␧d兲Hi,j−␧dHi+1,j+1, 共22兲 or, reversely,

Hi,j=

Hi−1,j−1+ Ri,j+␧dHi+1,j+1 1 +␧d

. 共23兲

Then, the interface condition共10兲 for the interfacial point C1 is

⌳p 1 +␧d

共− ␧dHi−1,j−1+ Ri,j+␧dHi+1,j+1兲 = ⌳Ri,j. 共24兲

Ri,jis defined similarly at the other interfacial points C2, C3, and C₄. The finite-difference equations for the points next to the interface are obtained by replacing each Hijat the

inter-face points with Rijthrough Eqs.共19兲 and 共23兲, and the like equations. For example, for point N1L, central finite differ-ence applied to Eq.共5兲 gives

1 ␧dh2

共− Hi−1,j− Hi,j−1+ 4Hi,j− Hi+1,j− Hi,j+1兲 = ⌳Hi. 共25兲 Using Eq.共19兲 for 共i+1, j兲 to replace Hi+1,j with Ri+1,j, we obtain 1 ␧dh2

冋

冉

4 − 1 1 +␧d

冊

Hi,j− Hi−1,j− 1 1 +␧d Ri+1,j − ␧d 1 +␧d

H_i+2,j− H_i,j−1− H_i,j+1

册

=⌳H_i,j. 共26兲 Also, for point N5L, using Eq. 共23兲 for 共i+1, j兲 to replace

H_i+1,jwith R_i+1,j, we obtain

FIG. 7. 共Color online兲 First to third TE modes in magnitude at point ⌫ for the square lattice of square cylinders with half width

1 ␧dh2

冋

4H_i,j− H_i−1,j− 1 1 +␧d R_i+1,j− ␧d 1 +␧d H_i+2,j+1 −

冉

1 + 1 1 +␧d

冊

Hi,j−1− Hi,j+1

册

=⌳Hi,j, 共27兲 and, for point N₁₃, central finite difference applied to Eq.共6兲 gives

1

h2关− Hi−1,j− Hi,j−1+共4 + ⌳ph

2_兲H

i,j− Hi+1,j− Hi,j+1兴 = ⌳Hi. 共28兲 Using similar equations for共i−1, j兲 and 共i, j−1兲 to replace

Hi−1,jand Hi,j−1with Ri−1,jand Ri,j−1, we obtain 1 h2

冋

冉

4 − 2␧d 1 +␧d +⌳p

冊

Hi,j− 1 1 +␧d Hi−2,j− 1 1 +␧d Ri−1,j − H_i+1,j− 1 1 +␧d H_i,j−2− 1 1 +␧d

R_i,j−1− H_i,j+1

册

=⌳H_i,j. 共29兲

The other neighboring points can be obtained in a similar manner. Along with the modifications for the neighboring points described above, the resultant matrix is then obtained by replacing Hi,jat all interface points with Ri,jthrough Eqs. 共20兲 and 共24兲, and the like equations.

IV. RESULTS AND DISCUSSION

In order to justify the present approach, we report the results in one-dimensional photonic crystals, which analyti-cal solutions of band structures are available. Consider a photonic crystal with lattice constant a. The widths of the dielectric and the metal are d₁ and d₂, respectively. Then, according to Eqs.共5兲 and 共6兲, we have the equations for the

H fields in the dielectric共denoted as H+兲 and the metal 共de-noted as H−兲, respectively, as

再

H₊

⬙

+ k₁2H+= 0, 0艋 x 艋 d1,

H₋

⬙

+ k₂2H₋= 0, d₁艋 x 艋 a,

冎

共30兲 where k₁2=共␻/ c兲2␧d−␤2 and k2

2

=共␻/ c兲2␧m−␤2 are the in-plane wave numbers in the dielectric and the metal, respec-FIG. 8. 共Color online兲 Fourth to sixth TE modes in magnitude at point ⌫ for the square lattice of square cylinders with half width

tively, and␤is the off-plane wave number. Assume the so-lutions have the form

再

H+共x兲 = Aeik1x+ Be−ik1x, 0艋 x 艋 d1,

H−共x兲 = Ceik2x+ De−ik2x, d1艋 x 艋 a,

冎

共31兲 where A, B, C, and D are the weighting coefficients to be determined by using the continuity conditions at the interface

再

H+共d1兲 = H−共d1兲, ␧mH+

⬘

共d1兲 = ␧dH−

⬘

共d1兲,

冎

共32兲 and the Bloch conditions at the domain boundary

再

H₊共0兲 = e−ikdH₋共a兲,

␧mH+

⬘

共0兲 = ␧de−ikdH−

⬘

共a兲.

冎

共33兲 In order to obtain a nontrivial solution, the determinant of the 4⫻4 matrix has to be zero

冨

1 1 − ei共k2−k兲a _{− e}−i共k2+k兲a

k1 ␧d − k1 ␧d − k2 ␧m ei共k2−k兲a k2 ␧m e−i共k2+k兲a eik1d1 _e−ik1d1 _{− e}ik2d1 _{− e}−ik2d1 k1 ␧d eik1d1 ₋k1 ␧d e−ik1d1 ₋ k2 ␧m eik2d1 k2 ␧m e−ik2d1

冨

= 0, 共34兲 which can be rearranged to obtain the analytical formula15

cos共ka兲 = cos共k1d1兲cos共k2d2兲 −1 2

冉

␧mk1 ␧dk2 + ␧dk2 ␧mk1

冊

sin共k1d1兲sin共k2d2兲. 共35兲 Next, we present the results in two dimensions. In the following discussion, we take␧d= 1共air兲. Let␻spdenote the surface plasma frequency for a single flat interface between the metal and the air共␻_sp=␻p/

冑

2兲, and here the normalized

␻pa / 2␲c is taken to be unity. In particular, we are interested in the dependence of the modes of surface plasmon polariton on the off-line wave number␤at the zone center k = 0. Fig-ure 3 shows the computed results by the interfacial operator FIG. 9. 共Color online兲 Seventh to ninth TE modes in magnitude at point ⌫ for the square lattice of square cylinders with half width

formulation, which are in very close agreement with the ones obtained by applying the Newton-Ralphson method6 _{to the} analytical formula共35兲. In addition to the lower branch of surface plasmon polariton, there is an upper branch that also converges to the surface plasma frequency␻spin the large␤ limit. In the case of thin metallic components, interaction of surface plasmon polaritons on both sides leads to mode split-ting: one lower frequency with odd symmetry and one higher frequency with even symmetry. In the case of thick metallic components, the upper branch corresponds to collective os-cillations of electrons in the metal; this can be observed by increasing the thickness of the metal layer 共small air gap兲 that the upper branch at k = 0 shifts to a higher frequency, and eventually to the plasma frequency␻p. Figure 4 is a similar plot at k⫽0. The difference between Figs. 3 and 4 is that at small off-line wave-number ␤, the first mode is symmetric for k = 0 and is antisymmetric for k⫽0. Both of the first two TE bands tend to have the surface plasma frequency

␻spa / 2␲c = 1 /

冑

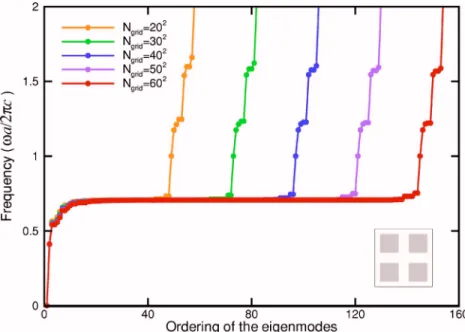
2. However, it is known that at large off-line wave-number␤, the lower frequency mode has odd symme-try, while the higher frequency has even symmetry.16 There-fore, there is a crossing for k = 0 共Fig. 3兲, while we would expect the anticrosssing scheme for k⫽0. Moreover, the pe-riodic array of metals can be considered as metal gratings

that cause crossing of the light line by the second TE band.17 Next, we turn to the square lattice with square metallic components as in Fig. 2 with half width w / a = 0.3. It has been suggested that the number of modes of surface plasmon polariton is infinite.8 _{To test this hypothesis, we solve the} eigenvalue problem 共15兲 with a different number of grid points, which can also help check the dependence of modes on the grid resolution. Figure 5 presents the results that 共i兲 for the mode with a frequency lower or greater than the surface plasma frequency␻sp, the mode is little dependent on the grid resolution as long as the number of grid points is not less then 30⫻30 and 共ii兲 there is an increasing number of stationary 共dispersionless兲 modes near the resonant fre-quency ␻sp with increasing the grid resolution. Figure 5 seems to indicate that the number of stationary modes in-creases with a rate proportional to the linear resolution of the grid, i.e., with N, if the number of grid points is N⫻N.

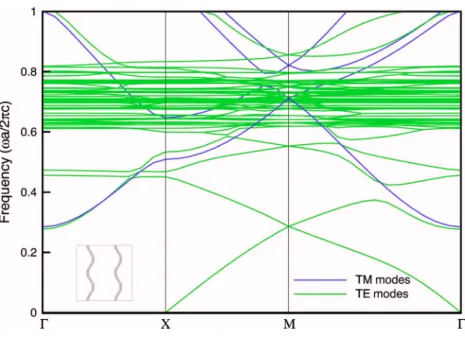
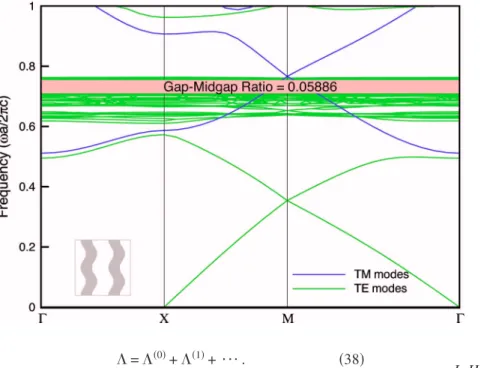
Figure 6 shows the band structures computed by the in-terfacial operator approach. Unlike TE modes, the lowest branch of TM modes has a cut-off frequency even at small filling ratios of the metal, and the cut-off frequency shifts further upward with increasing the filling ratio, leaving a large full photonic band gap that is solely determined by the TE modes. From the fourth branch of modes, the dispersion FIG. 10. 共Color online兲 Tenth to twelfth TE modes in magnitude at point ⌫ for the square lattice of square cylinders with half width

relation for the TE modes is each a quite flat one, denoting standing modes for frequencies up to the surface plasma fre-quency␻sp. A small band gap is observed to exist between

these flat bands, and is qualified for the name of plasmonic band gap. The gap is larger at even larger filling ratios.

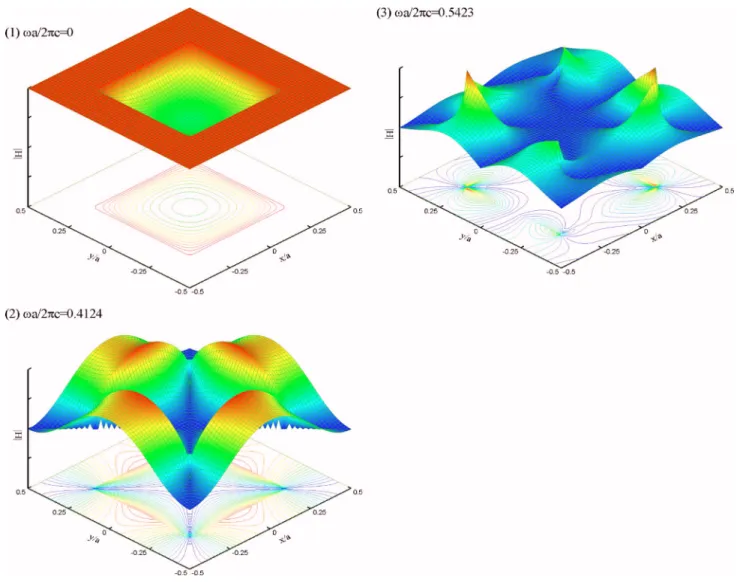
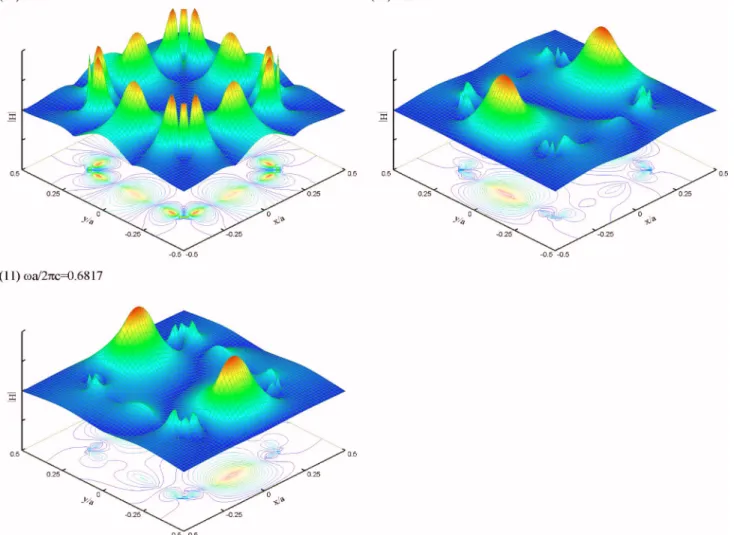
Fig-ures 7–10 show the first 12 TE modes for the square lattice in Fig. 2 at the point⌫. All these modes have a frequency lower than the surface plasma frequency␻sp, but as we can see, each mode concentrates more or less on the neighborhood of the interface between the metal and the dielectric. It is noted that some of these modes are degenerate, e.g., the third and the fourth modes, the seventh and eightth modes, and the eleventh and twelfth modes. Figure 11 shows an example of highly localized nature of surface plasmon polariton共at␻_sp兲, living in a close neighborhood of the interface. As the fre-quency exceeds the plasma frefre-quency ␻p, the typical TE mode is highly oscillatory共Fig. 12兲.

As a final example, we examine the effect of 共regular兲 roughness on the modes of surface plasmon polariton. Figure 13 shows the band structures for the square lattice with thin-ner wavy metallic components with amplitude r / a = 0.1 and thickness t / a = 0.1. The most significant feature is widely spread flat bands of stationary modes with frequencies well exceeding the surface plasma frequency. This flat-band

broadening was not observed for the square lattice with square or circular metallic components. The physical origin

of this broadening could be explained as effective mode in-teraction due to the geometry of the interface. The modes of surface plasmon polariton interact with each other from both the normal and the lateral directions, further lifting the

de-generacy. The broadening of the flat bands may be particu-larly useful for those applications which exploit modes of surface plasmon polarition such as surface enhanced Raman scattering,18_{and conceivably solar cells.}4_{As we increase the} thickness of the metallic components, the broadening be-comes less significant with most flat-band frequencies below the surface plasma frequency ␻sp 共Fig. 14兲. Nevertheless,

densely distributed bands exist with frequencies substantially above the surface plasma frequency␻sp, leaving a significant

plasmonic band gap.

The present method can be extended in order to take into account the Drude damping in the dielectric function, which comes from the collisions of the electrons. For this purpose, we introduce the Drude model

␧共␻兲 = 1 − ␻p 2

␻2_{+ i␥␻}, 共36兲

where␥ is the collision frequency of free electrons. If the damping is small such that␥Ⰶ␻, then the damped solutions can be regarded as perturbations to the undamped solutions for␥= 0共the free-electron model兲. First, the operator L of the eigensystem Lu =⌳u is split into two terms

L = L₀+ L₁, 共37兲

where L0 is the operator of the undamped eigensystem. Let ⌳共0兲_{denote the eigenvalue of L}

0, and assume the solution for the operator L is expanded as

FIG. 11.共Color online兲 One of the highly localized TE modes near the frequency␻spfor the square lattice of square cylinders with half width w / a = 0.3.

FIG. 12. 共Color online兲 One of the highly oscillatory TE modes above the frequency␻spfor the square lattice of square cylinders with half width w / a = 0.3.

FIG. 13. 共Color online兲 Band structures for the square lattice of wavy structure with thickness t / a = 0.1 and amplitude r / a = 0.1.

⌳ = ⌳共0兲_+⌳共1兲_{+ ¯ . 共38兲} Based on the interfacial operator within the finite-difference framework, we have LHi= 1 ␧dh2 共− Hi−1+ 2Hi− Hi+1兲, L0Hi= 1 ␧dh2 共− Hi−1+ 2Hi− Hi+1兲, L₁= 0, 共39兲

for points in the dielectric

LHi= 1 h2

冋

− Hi−1+

冉

2 + ⌳ph2 1 + i␥/␻

冊

Hi− Hi+1

册

, L0Hi= 1 h2关− Hi−1+共2 + ⌳ph2兲Hi− Hi+1兴, L1Hi= −⌳p

冉

i␥ ␻+ i␥

冊

Hi, 共40兲

for points in the metal, and

LRi=

冉

− ␧d⌳p 1 +␧d Hi−1+

冉

⌳p 1 +␧d − i␥␻

冊

Ri+ ␧d⌳p 1 +␧d Hi+1

冊

, L0Ri=

冉

− ␧d⌳p 1 +␧d Hi−1+ ⌳p 1 +␧d Ri+ ␧d⌳p 1 +␧d Hi+1

冊

, L₁Ri= − i␥␻Ri, 共41兲 for points at the interface. With this operator splitting, we can refer to standard perturbation theory11–14 _{to obtain the} first-FIG. 14. 共Color online兲 Band structures for the square lattice of wavy structure with thickness

t / a = 0.4 and amplitude r / a = 0.1.

FIG. 15.共Color online兲 Imagi-nary part of ␻共1兲 for first few bands of the one-dimensional pho-tonic crystal with d₂/ a = 0.2 and ␥/␻p= 0.01.

bands for a one-dimensional photonic crystal with d₂/ a = 0.2 and␥/␻p= 0.01. It is noted that even bands have larger dissipations at the zone center, while odd bands have larger dissipations at the band edges. Besides, the dissipation be-comes smaller for higher bands.

V. CONCLUDING REMARKS

In conclusion, the present approach presents a direct ei-genvalue problem for computing the modes of surface plas-mon polariton as well as the higher frequency modes. In particular, we have considered the free-electron model and the model of Drude damping for the metal. Several

interest-interband transitions is not negligible.19,20 _{This proposes a} further challenge for the present methodology because the contribution of the interband transitions lacks a simple func-tional form in frequency. The issue is currently under inves-tigation.

ACKNOWLEDGMENTS

This work was supported in part by National Science Council of the Republic of China under Contract No. NSC 91-2212-E-002-072, and the Ministry of Economic Affairs of the Republic of China under Contract No. MOEA 93-EC-17-A-08-S1-0006.

*Electronic address: mechang@gate.sinica.edu.tw 1_{R. H. Ritchie, Phys. Rev. 106, 874共1957兲.}

2_{J. B. Pendry, L. Martin-Moreno, and F. J. Garcia-Vidal, Science} 305, 847共2004兲.

3_{S. C. Kitson, W. L. Barnes, and J. R. Sambles, Phys. Rev. Lett.} 77, 2670共1996兲.

4_{W. L. Barnes, A. Dereux, and T. W. Ebbesen, Nature共London兲} 424, 824共2003兲.

5_{O. Toader and S. John, Phys. Rev. E 70, 046605共2004兲.} 6_{D. Kincaid and W. Cheney, Numerical Analysis, 2nd ed.共Brooks/}

Cole, Pacific Grove, 1996兲.

7_{E. Moreno, D. Erni, and C. Hafner, Phys. Rev. B 65, 155120} 共2002兲.

8_{T. Ito and K. Sakoda, Phys. Rev. B 64, 045117共2001兲.} 9_{A. Tip, A. Moroz, and J. M. Combes, J. Phys. A 33, 6223共2000兲.} 10_{A. Moroz, A. Tip, and J. M. Combes, Synth. Met. 116, 481}

共2001兲.

11_{H. van der Lem, A. Tip, and A. Moroz, J. Opt. Soc. Am. B 20,}

1334共2003兲.

12_{J. M. Combes, B. Gralak, and A. Tip, Contemp. Math. 339, 1} 共2003兲.

13_{K. C. Huang, P. Bienstman, J. D. Joannopoulos, K. A. Nelson,} and S. Fan, Phys. Rev. Lett. 90, 196402共2003兲.

14_{C. C. Chang, J. Y. Chi, R. L. Chern, C. C. Chang, C. H. Lin, and} C. O. Chang, Phys. Rev. B 70, 075108共2004兲.

15_{P. Yeh, Optical Waves in Layered Media 共Wiley, New York,} 1988兲.

16_{B. E. Sernelius, Surface Modes in Physics 共Wiley, New York,} 2001兲, p. 125.

17_{W.-C. Tan, T. W. Preist, J. R. Sambles, and N. P. Wanstall, Phys.} Rev. B 59, 12661共1999兲.

18_{M. Fleischmann, P. J. Hendra, and A. J. McQuillan, Chem. Phys.} Lett. 26, 163共1974兲.

19_{P. B. Johnson and R. W. Christy, Phys. Rev. B 6, 4370共1972兲.} 20_{A. Pinchuk, U. Kreibig, and A. Hilger, Surf. Sci. 557, 269}