Artificial Intelligence Approach to Evaluate Students' Answerscripts Based on the Similarity Measure between Vague Sets

Wang, H.-Y., & Chen, S. M. (2007). Artificial Intelligence Approach to Evaluate Students’ Answerscripts Based on the Similarity Measure between Vague Sets. Educational Technology & Society, 10 (4), 224-241.

224

ISSN 1436-4522 (online) and 1176-3647 (print). © International Forum of Educational Technology & Society (IFETS). The authors and the forum jointly retain the

Artificial Intelligence Approach to Evaluate Students’ Answerscripts Based on

the Similarity Measure between Vague Sets

Hui-Yu Wang

Department of Education, National Chengchi University, Taiwan // 94152514@@nccu.edu.tw

Shyi-Ming Chen

Department of Computer Science and Information Engineering, National Taiwan University of Science and Technology, Taiwan // Tel: +886-2-27376417 // smchen@mail.ntust.edu.tw

ABSTRACT

In this paper, we present two new methods for evaluating students’ answerscripts based on the similarity measure between vague sets. The vague marks awarded to the answers in the students’ answerscripts are represented by vague sets, where each element ui in the universe of discourse U belonging to a vague set is

represented by a vague value. The grade of membership of ui in the vague set à is bounded by a subinterval

[tÃ(ui), 1 – fà (ui)] of [0, 1]. It indicates that the exact grade of membership μÃ(ui) of ui belonging the vague set

à is bounded by tÃ(ui) ≤ μÃ(ui) ≤ 1 – fÃ(ui), where tÃ(ui) is a lower bound of the grade of membership of ui

derived from the evidence for ui, fÃ(ui) is a lower bound of the negation of ui derived from the evidence against

ui, tÃ(ui) + fÃ(ui) ≤ 1, and ui

∈

U. An index of optimism λ determined by the evaluator is used to indicate the

degree of optimism of the evaluator, where λ

∈

[0, 1]. Because the proposed methods use vague sets to evaluate students’ answerscripts rather than fuzzy sets, they can evaluate students’ answerscripts in a more flexible and more intelligent manner. Especially, they are particularly useful when the assessment involves subjective evaluation. The proposed methods can evaluate students’ answerscripts more stable than Biswas’s methods (1995).

Keywords

Similarity functions, Students’ answerscripts, Vague grade sheets, Vague membership values, Vague sets, Index of optimism

Introduction

In recent years, some methods have been presented for students’ evaluation (Biswas, 1995; Chang & Sun, 1993; Chen & Lee, 1999; Cheng & Yang, 1998; Chiang and Lin, 1994; Frair, 1995; Echauz & Vachtsevanos, 1995; Hwang, Lin, & Lin, 2006; Kaburlasos, Marinagi, & Tsoukalas, 2004; Law, 1996; Ma & Zhou, 2000; Liu, 2005; McMartin, Mckenna, & Youssefi, 2000; Nykanen, 2006; Pears, Daniels, Berglund, & Erickson, 2001; Wang & Chen 2006a; Wang & Chen, 2006b; Wang & Chen, 2006c; Wang & Chen, 2006d; Weon & Kim, 2001; Wu, 2003). Chang and Sun (1993) presented a method for fuzzy assessment of learning performance of junior high school students. Chen and Lee (1999) presented two methods for evaluating students’ answerscripts using fuzzy sets. Cheng and Yang (1998) presented a method for using fuzzy sets in education grading systems. Chiang and Lin (1994) presented a method for applying the fuzzy set theory to teaching assessment. Frair (1995) presented a method for student peer evaluations using the analytic hierarchy process method. Echauz and Vachtsevanos (1995) presented a fuzzy grading system to translate a set of scores into letter grades. Hwang, Lin and Lin, (2006) presented an approach for test-sheet composition with large-scale item banks. Kaburlasos, Marinagi, and Tsoukalas (2004) presented a software tool, called PARES, for computer-based testing and evaluation used in the Greek higher education system. Law (1996) presented a method for applying fuzzy numbers in education grading systems. Liu (2005) presented a method for using mutual information for adaptive item comparison and student assessment. Ma and Zhou (2000) presented a fuzzy set approach for the assessment of student-centered learning. McMartin, Mckenna and Youssefi (2000) used scenario assignments as assessment tools for undergraduate engineering education. Nykanen (2006) presented inducing fuzzy models for student classification. Pears, Daniels, Berglund, and Erickson (2001) presented a method for student evaluation in an international collaborative project course. Wang and Chen (2006a) presented two methods for students’ answerscripts evaluations using fuzzy sets. Wang and Chen (2006b) presented two methods for evaluating students’ answerscripts using fuzzy numbers associated with degrees of confidence. Wang and Chen (2006c) presented two methods for students’ answerscripts evaluation using vague sets. Weon and Kim (2001) presented a leaning achievement evaluation strategy in student’s learning procedure using fuzzy membership

functions. Wu (2003) presented a method for applying the fuzzy set theory and the item response theory to evaluate learning performance.

Biswas (1995) pointed out that the chief aim of education institutions is to provide students with the evaluation reports regarding their test/examination as sufficient as possible and with the unavoidable error as small as possible. Therefore, Biswas (1995) presented a fuzzy evaluation method (fem) for applying fuzzy sets in students’ answerscripts evaluation. He also generalized the fuzzy evaluation method to propose a generalized fuzzy evaluation method (gfem) for students’ answerscripts evaluation. In (Biswas, 1995), the fuzzy marks awarded to answers in the students’ answerscripts are represented by fuzzy sets (Zadeh, 1965). In a fuzzy set, the grade of membership of an element ui in the universe of discourse U belonging to a fuzzy set is represented by a real value between zero and

one, However, Gau and Buehrer (1993) pointed out that this single value between zero and one combines the evidence for ui

∈

U and the evidence against ui

∈

U. They pointed out that it does not indicate the evidence for ui

∈

U

and the evidence against ui

∈

U, respectively, and it does not indicate how much there is of each. Gau and Buehrer

(1993) also pointed out that the single value between zero and one tells us nothing about its accuracy. Thus, they proposed the theory of vague sets, where each element in the universe of discourse belonging to a vague set is represented by a vague value. Therefore, if we can allow the marks awarded to the questions of the students’ answerscripts to be represented by vague sets, then there is room for more flexibility.

In this paper, we present two new methods for evaluating students’ answerscripts based on the similarity measure between vague sets. The vague marks awarded to the answers in the students’ answerscripts are represented by vague sets, where each element belonging to a vague set is represented by a vague value. An index of optimismλ(Cheng and Yang, 1998) determined by the evaluator is used to indicate the degree of optimism of the evaluator, whereλ

∈

[0, 1]. If 0 ≤λ< 0.5, then the evaluator is a pessimistic evaluator. Ifλ= 0.5, then the evaluator is a normal evaluator. If 0.5 <λ≤ 1.0, then the evaluator is an optimistic evaluator. Because the proposed methods use vague sets to evaluate students’ answerscripts rather than fuzzy sets, they can evaluate students’ answerscripts in a more flexible and more intelligent manner. Especially, they are particularly useful when the assessment involves subjective evaluation. The proposed methods can evaluate students’ answerscripts more stable than Biswas’ methods (1995). In this paper, we present two new methods for students’ answerscripts evaluation based on the similarity measure between vague sets. The vague marks awarded to the answers in the students’ answerscripts are represented by vague sets. An index of optimismλ(Cheng and Yang, 1998) determined by the evaluator is used to indicate the degree of optimism of the evaluator, whereλ

∈

[0, 1]. If 0 ≤λ< 0.5, then the evaluator is a pessimistic evaluator. If λ= 0.5, then the evaluator is a normal evaluator. If 0.5 <λ≤ 1.0, then the evaluator is an optimistic evaluator. The proposed methods can evaluate students’ answerscripts in a more flexible and more intelligent manner. Especially, they are particularly useful when the assessment involves subjective evaluation. The proposed methods can evaluate students’ answerscripts more stable than Biswas’s methods (1995).

Basic Concepts of the Vague Set Theory

Gau and Buehrer (1993) presented the theory of vague sets. Chen (1995a) presented the arithmetic operations between vague sets. In (Chen, 1995b) and (Chen, 1997), Chen presented similarity measures between vague sets. A vague set à in the universe of discourse U is characterized by a truth-membership function tà and a false-membership

function fÃ, where tÃ: U → [0, 1], fÃ: U → [0, 1], tÃ(ui) is a lower bound of the grade of membership of ui derived

from the evidence for ui, fÃ(ui) is a lower bound of the negation of ui derived from the evidence against ui, tÃ(ui) +

fÃ(ui) ≤ 1, and ui

∈

U. The grade of membership of ui in the vague set à is bounded by a subinterval [tÃ(ui), 1 – fà (ui)]

of [0, 1]. The vague value [tÃ(ui), 1 – fÃ(ui)] indicates that the exact grade of membership μÃ(ui) of ui is bounded by

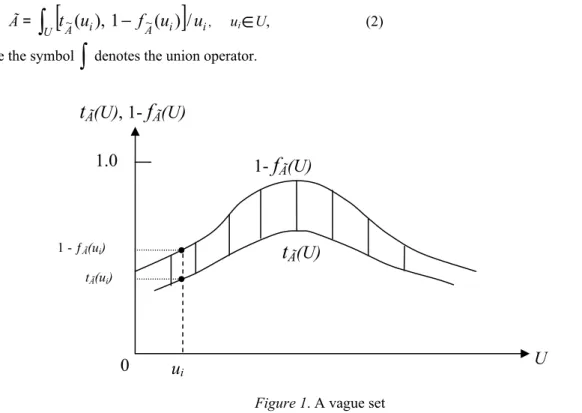
tÃ(ui) ≤ μÃ(ui) ≤ 1 – fÃ(ui), where tÃ(ui) + fÃ(ui) ≤ 1. An example of a vague set à in the universe of discourse U is

shown in Fig. 1.

If the universe of discourse U is a finite set, then a vague set à of the universe of discourse U can be represented as follows:

à =

n

[

]

_i i A i A i

u

u

f

u

t

(

),

1

(

)

/

1 ~ ~

∑

=

−

. (1)

If the universe of discourse U is an infinite set, then a vague set à of the universe of discourse can be represented as à =

[

~

(

),

1

~

(

)

]

/

_i,

U

t

A

u

i

f

A

u

i

u

∫

−

ui

∈

U, (2)

where the symbol

∫

denotes the union operator.

Figure 1. A vague set

Definition 1: Let à be a vague set of the universe of discourse U with the truth-membership function tà and the

false-membership function fÃ, respectively. The vague set à is convex if and only if for all u1, u2 in U,

tÃ(λ u1 + (1 –λ )u2) ≥Min(tÃ(u1), tÃ(u2)), (3)

1 – fà (λ u1 + (1 –λ ) u2) ≥Min(1 – fÃ(u1), 1 – fÃ(u2)), (4)

whereλ

_∈

[0, 1].

Definition 2: A vague set à of the universe of discourse U is called a normal vague set if

∃

ui

∈

U, such that 1 –

fÃ(ui) = 1. That is, fÃ(ui) = 0.

Definition 3: A vague number is a vague subset in the universe of discourse U that is both convex and normal.

Chen (1995b) presented a similarity measure between vague values. Let X = [tx, 1 – fx] be a vague value, where

tx

∈

[0, 1], fx

∈

[0, 1] and tx + fx ≤ 1. The score of the vague value X can be evaluated by the score function S shown as

follows:

S(X) = tx – fx, (5)

where S(X)

∈

[-1, 1]. Let X and Y be two vague values, where X = [tx, 1 – fx], Y = [ty, 1 – fy], tx

∈

[0, 1], fx

∈

[0, 1], tx +

fx ≤ 1, ty

∈

[0, 1], fy

∈

[0, 1], and ty + fy ≤ 1. The degree of similarity M(X, Y) between the vague values X and Y can be

evaluated by the function M,

2

)

(

)

(

1

)

,

(

X

Y

S

X

S

Y

M

=

−

−

, (6)

where S(X) = t – f and S(Y) = t – f. The larger the value of M(X, Y), the higher the degree of similarity between the

0

_u

_i

U

t

Ã

(U), 1-

f

Ã

(U)

1.0

1 - ƒÃ(ui)

t

_Ã

(U)

1-

f

Ã

(U)

tÃ(ui)

vague values X and Y. It is obvious that if X and Y are identical vague values (i.e., X = Y), then S(X) = S(Y). By applying Eq. (6), we can see that M(X, Y) = 1, i.e., the degree of similarity between the vague values X and Y is equal to 1.

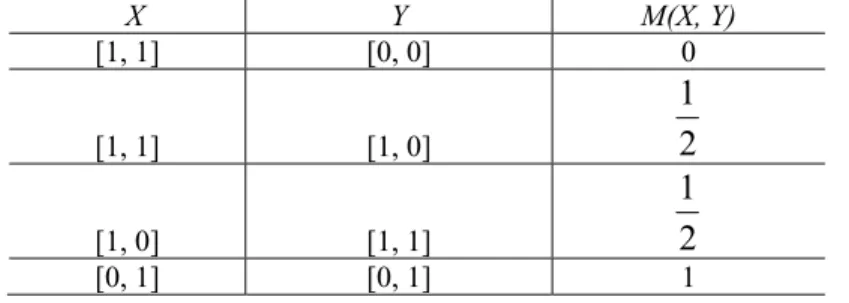
Table 1 shows some examples of the degree of similarity M(X, Y) between X and Y.

Table 1. Some examples of the degree of similarity M(X, Y) between the vague values X and Y

X Y M(X, Y) [1, 1] [0, 0] 0 [1, 1] [1, 0]

2

1

[1, 0] [1, 1]

2

1

[0, 1] [0, 1] 1

Let X and Y be two vague values, where X = [tx, 1 – fx], Y = [ty, 1 – fy], tx

∈

[0, 1], fx

∈

[0, 1], tx + fx ≤ 1, ty

∈

[0, 1],

fy

∈

[0, 1], and ty + fy ≤ 1. The proposed similarity measure between vague values has the following properties:

Property 1: Two vague values X and Y are identical if and only if M(X, Y) = 1. Proof:

(i) If X and Y are identical, then tx = ty and 1 – fx = 1 – fy (i.e., fx = fy). Because S(X) = tx – fx and S(Y) = ty – fy = tx – fx,

the degree of similarity between the vague values X and Y is calculated as follows:

2

)

(

)

(

1

)

,

(

X

Y

S

X

S

Y

M

=

−

−

=

2

)

(

)

(

1

−

t

x

−

f

x

−

t

y

−

f

y =

2

)

(

)

(

1

₋

t

x

−

f

x

−

t

x

−

f

x = 1. (ii) If M(X, Y) = 1, then

2

)

(

)

(

1

)

,

(

X

Y

S

X

S

Y

M

=

−

−

=

2

)

(

)

(

1

−

t

x

−

f

x

−

t

y

−

f

y = 1.

It implies that tx = fx and ty = fy (i.e., 1 –ty = 1 – fy). Therefore, the vague values X and Y are identical. Q. E. D.

Property 2: M(X, Y) = M(Y, X). Proof: Because

,

2

)

(

)

(

1

)

,

(

X

Y

S

X

S

Y

M

=

−

−

,

2

)

(

)

(

1

)

,

(

X

Y

S

Y

S

X

M

=

−

−

and

,

2

)

(

)

(

2

)

(

)

(

X

S

Y

S

Y

S

X

S

−

₌

−

we can see that

2

)

(

)

(

1

2

)

(

)

(

1

−

S

X

−

S

Y

=

−

S

Y

−

S

Y

and M(X, Y) = M(Y, X). Q. E. D.

Let à and

B

~

be two vague sets in the universe of discourse U, U = {u1, u2, …, un}, where

à =

[

t

~

(

u

₁

),

1

f

~

(

u

₁

)]

A A

−

/ u1 +

[

t

A~

(

u

2

),

1

−

f

A~

(

u

2

)]

/ u2 + … +

[

t

A~

(

u

n

),

1

−

f

A~

(

u

n

)]

/ un, and

B

~

=

[

t

~

(

u

₁

),

1

f

_~

(

u

₁

)]

B B

−

/ u1 +

[

t

B~

(

u

2

),

1

−

f

B~

(

u

2

)]

/ u2 + … +

[

t

B~

(

u

n

),

1

−

f

B~

(

u

n

)]

/ un. Let _{~ i}( ) A u V = [ ~

(

_i

)

A

u

t

, 1 – ~

(

_i

)

A

u

f

] be the vague membership value of ui in the vague set Ã, and let

V

_B~

(

u

_i

)

=

[

t

_B~

(

u

_i

)

, 1 –

f

_B~

(

u

i

)

] be the vague membership value of ui in the vague set

B

~

. By applying Eq. (5), we can see

that the score

S

(

V

~_A

(

u

_i

))

of the vague membership value V_{~ iA}(u) can be evaluated as follows:

))

(

(

~ _i A

u

V

S

= ~

(

_i

)

A

u

t

– ~

(

_i

)

A

u

f

,

and the score

S

(

V

_B~

(

u

_i

))

of the vague membership value

V

_B~

(

u

_i

)

can be evaluated as follows:

))

(

(

V

_B~

u

_i

S

=

t

_B~

(

u

_i

)

–

f

_B~

(

u

_i

),

where 1 ≤ i ≤ n. Then, the degree of similarity H(Ã,

B

~

) between the vague sets à and

B

~

can be evaluated by the function H,

∑

=

=

n i A i B i

u

V

u

V

M

n

B

A

H

1 ~ ~

(

),

(

))

(

1

)

~

,

~

(

,

2

))

(

(

))

(

(

1

1

1 ~ ~

∑

=

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

₋

−

=

n i i B i A

u

S

V

u

V

S

n

(7)

where H(Ã, B)

∈

[0, 1]. The larger the value of H(Ã,

B

~

), the higher the similarity between the vague sets à and

B

~

. Let à and

B

~

be two vague sets in the universe of discourse U, U = {u1, u2, …, un}, where

à =

[

t

~

(

u

₁

),

1

f

~

(

u

₁

)]

A A

−

/ u1 +

[

t

A~

(

u

2

),

1

−

f

A~

(

u

2

)]

/ u2 + … +

[

t

A~

(

u

n

),

1

−

f

A~

(

u

n

)]

/ un, and

B

~

=

[

t

~

(

u

₁

),

1

f

_~

(

u

₁

)]

B B

−

/ u1 +

[

t

B~

(

u

2

),

1

−

f

B~

(

u

2

)]

/ u2 + … +

[

t

B~

(

u

n

),

1

−

f

B~

(

u

n

)]

/ un. The proposed similarity measure between vague sets has the following properties:

Property 3: Two vague sets à and

B

~

are identical if and only if H(Ã,

B

~

) = 1.

Proof:

)]

(

1

),

(

[

~ ~ _i A i A

u

f

u

t

−

=

[

~

(

),

1

_~

(

_i

)],

B i B

u

f

u

t

−

where 1 ≤ i ≤ n.

That is,

t

_A~

(

u

_i

)

=

t

_B~

(

u

_i

)

,

f

_A~

(

u

_i

)

=

f

_B~

(

u

_i

),

and 1 ≤ i ≤ n. Because

))

(

(

V

_A~

u

_i

S

=

t

~_A

(

u

_i

)

–

f

~_A

(

u

i

)

and

S

(

V

_B~

(

u

_i

))

=

t

_B~

(

u

_i

)

–

f

_B~

(

u

i

)

=

t

_A~

(

u

_i

)

–

f

_A~

(

u

i

)

=

S

(

V

~_A

(

u

i

)).

Therefore, we can see that

H(Ã,

B

~

)

∑

=

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

−

−

=

n i i B i A

u

S

V

u

V

S

n

1 ~ ~

2

))

(

(

))

(

(

1

1

=

∑

=

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

−

−

n i i A i A

u

S

V

u

V

S

n

1 ~ ~

2

))

(

(

))

(

(

1

1

= 1. (ii) If H(Ã,

B

~

) = 1, then H(Ã,

B

~

)

∑

=

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

−

−

=

n i i B i A

u

S

V

u

V

S

n

1 ~ ~

2

))

(

(

))

(

(

1

1

= 1.

It implies that

S

(

V

_A~

(

u

_i

))

=

S

(

V

_B~

(

u

_i

)),

where 1 ≤ i ≤ n. Because

S

(

V

_A~

(

u

_i

))

=

))

(

(

V

_B~

u

_i

S

and

S

(

V

_B~

(

u

_i

))

=

t

_B~

(

u

_i

)

–

f

_B~

(

u

_i

),

where 1 ≤ i ≤ n, we can see that

)

(

~ _i A

u

t

= ~

(

_i

)

B

u

t

and ~

(

_i

)

A

u

f

=

f

_B~

(

u

_i

)

(i.e., 1 – ~

(

_i

)

A

u

f

= 1 –

f

_B~

(

u

_i

)

),

where 1 ≤ i ≤ n. Therefore, the vague sets à and

B

~

are identical. Q. E. D.

Property 4: H(Ã,

B

~

) = H(

B

~

, Ã). Proof: Because H(Ã,

B

~

)

∑

=

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

₋

−

=

n i i B i A

u

S

V

u

V

S

n

1 ~ ~

2

))

(

(

))

(

(

1

1

and H(

B

~

, Ã)

∑

=

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

−

−

=

n i i A i B

u

S

V

u

V

S

n

1 ~ ~

2

))

(

(

)

(

(

1

1

, and because

∑

= ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ ₋ − n i i B i A u SV u V S n ₁ ~ ~ 2 )) ( ( )) ( ( 1 1 =

∑

= ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ ₋ − n i i A i B u SV u V S n ₁ ~ ~ 2 )) ( ( ) ( ( 1 1 ,

Example 1: Let à and

B

~

be two vague sets of the universe of discourse U, U = {u1, u2, u3, u4, u5},

à = [0.2, 0.4]/u1 + [0.3, 0.5]/u2 + [0.5, 0.7]/u3 + [0.7, 0.9]/u4 + [0.8, 1]/u5

B

~

= [0.3, 0.5]/u1 + [0.4, 0.6]/u2 + [0.6, 0.8]/u3 + [0.7, 0.9]/u4 + [0.8, 1]/u5,

where

)

(

₁ ~

u

V

A = [0.2, 0.4],

V

B~

(

u

1

)

= [0.3, 0.5],

)

(

₂ ~

u

V

A = [0.3, 0.5],

V

B~

(

u

2

)

= [0.4, 0.6],

)

(

₃ ~

u

V

A = [0.5, 0.7],

V

B~

(

u

3

)

= [0.6, 0.8],

)

(

₄ ~

u

V

A = [0.7, 0.9],

V

B~

(

u

4

)

= [0.7, 0.9],

)

(

₅ ~

u

V

A = [0.8, 1],

V

B~

(

u

5

)

= [0.8, 1]. By applying Eq. (5), we can get

))

(

(

V

~

u

₁

S

A = 0.2 – 0.6 = –0.4,

))

(

(

V

~

u

₂

S

A = 0.3 – 0.5 = –0.2,

))

(

(

V

~

u

₃

S

A = 0.5 – 0.3 = 0.2,

))

(

(

V

~

u

₄

S

A = 0.7 – 0.1 = 0.6,

))

(

(

V

~

u

₅

S

A = 0.8 – 0 = 0.8,

))

(

(

V

~

u

₁

S

B = 0.3 – 0.5 = –0.2,

))

(

(

V

~

u

₂

S

B = 0.4 – 0.4 = 0,

))

(

(

V

~

u

₃

S

B = 0.6 – 0.2 = 0.4,

))

(

(

V

~

u

₄

S

B = 0.7 – 0.1 = 0.6,

))

(

(

V

~

u

₅

S

B = 0.8 – 0 = 0.8.

By applying Eq. (7), the degree of similarity H(Ã,

B

~

) between the vague sets à and

B

~

can be evaluated, shown as follows: H(Ã,

B

~

)

∑

=

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

−

−

=

5 1 ~ ~

2

))

(

(

))

(

(

1

5

1

i i B i A

u

S

V

u

V

S

_⎢

⎣

⎡

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

₋

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

₋

₋

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

₋

₋

₋

−

=

2

4

.

0

2

.

0

1

2

0

2

.

0

1

2

)

2

.

0

(

4

.

0

1

(

5

1

_⎥

⎦

⎤

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

₋

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

₋

−

2

8

.

0

8

.

0

1

2

6

.

0

6

.

0

1

=

(

0

.

9

0

.

9

0

.

9

1

1

)

5

1

+

+

+

+

= 0.94.

A Review of Biswas’ Methods for Students’ Answerscripts Evaluation

Biswas (1995) used the matching function S to measure the degree of similarity between two fuzzy sets (Zadeh, 1965). Let

A

and

B

be the vector representation of the fuzzy sets A and B, respectively. Then, the degree of similarity S(

A

,

B

) between the fuzzy sets A and B can be calculated as follows (Chen, 1988):

S(

A

,

B

) =

)

,

(

A

A

B

B

Max

B

A

⋅

⋅

⋅

_{, (8)}

where S(

A

,

B

)

∈

[0, 1]. The larger the value of S(

A

,

B

), the higher the similarity between the fuzzy sets A and B. Biswas (1995) presented a “fuzzy evaluation method” (fem) for evaluating students’ answerscripts, based on the matching function S. He used five fuzzy linguistic hedges, called Standard Fuzzy Sets (SFS), for students’ answerscripts evaluation, i.e., E (excellent), V (very good), G (good), S (satisfactory) and U (unsatisfactory), where

X = {0%, 20%, 40%, 60%, 80%, 100%}, E = {(0%, 0), (20%, 0), (40%, 0.8), (60%, 0.9), (80%, 1), (100%, 1)}, V = {(0%, 0), (20%, 0), (40%, 0.8), (60%, 0.9), (80%, 0.9), (100%, 0.8)}, G = {(0%, 0), (20%, 0.1), (40%, 0.8), (60%, 0.9), (80%, 0.4), (100%, 0.2)}, S = {(0%, 0.4), (20%, 0.4), (40%, 0.9), (60%, 0.6), (80%, 0.2), (100%, 0)}, U = {(0%, 1), (20%, 1), (40%, 0.4), (60%, 0.2), (80%, 0), (100%, 0)}.

He used the vector representation method to represent the fuzzy sets E, V, G, S and U by the vectors

E

,

V

,

G

,

S

and U , respectively, where

E

= <0, 0, 0.8, 0.9, 1, 1>,

V

= <0, 0, 0.8, 0.9, 0.9, 0.8>,

G

= <0, 0.1, 0.8, 0.9, 0.4, 0.2>,

S

= <0.4, 0.4, 0.9, 0.6, 0.2, 0>,

U = <1, 1, 0.4, 0.2, 0, 0>.

Biswas pointed out that “A”, “B”, “C”, “D” and “E” are letter grades, where 0 ≤ E < 30, 30 ≤ D < 50, 50 ≤ C < 70, 70 ≤ B < 90 and 90 ≤ A ≤ 100. Furthermore, he presented the concept of “points”, where the mid-grade-points of the letter grades A, B, C, D and E are P(A), P(B), P(C), P(D) and P(E), respectively, P(A) = 95, P(B) = 80,

P(C) = 60, P(D) = 40 and P(E) = 15. Assume that an evaluator evaluates the first question (i.e., Q.1) of the

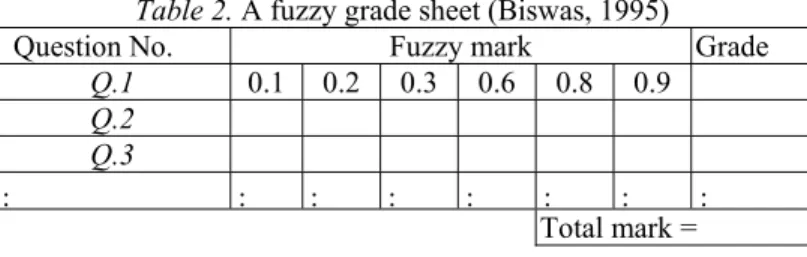
answerscript of a student using a fuzzy grade sheet as shown in Table 2.

Table 2. A fuzzy grade sheet (Biswas, 1995)

Question No. Fuzzy mark Grade

Q.1 0.1 0.2 0.3 0.6 0.8 0.9

Q.2 Q.3

… … … …

Total mark =

In the second row of Table 2, the fuzzy marks 0.1, 0.2, 0.3, 0.6, 0.8 and 0.9, awarded to the answer of question Q.1, indicate that the degrees of the evaluator’s satisfaction for that answer are 0%, 20%, 40%, 60%, 80% and 100%, respectively.

In the following, we briefly review Biswas’ method (1995) for students’ answerscript evaluation as follows: Step 1: For each question in the answerscript repeatedly perform the following tasks:

columns shown in Table 2, where 1 ≤ i ≤ n. Let F_i be the vector representation of Fi, where 1 ≤ i ≤ n.

(2) Based on Eq. (8), calculate the degrees of similarity S(

E

,F_i ), S(

V

,F_i ), S(

G

,F_i ), S(

S

,F_i ) and S(U ,F_i ), respectively, where

E

,

V

,

G

,

S

and U are the vector representations of the standard fuzzy sets E (excellent), V (very good), G (good), S (satisfactory) and U (unsatisfactory), respectively, and 1 ≤ i ≤ n.

(3) Find the maximum value among the values of S(

E

,F_i ), S(

V

,F_i ), S(

G

,F_i ), S(

S

,F_i ) and S(U ,F_i ).

Assume that S(

V

,F_i ) is the maximum value among the values of S(

E

,F_i ), S(

V

,F_i ), S(

G

,F_i ), S(

S

,F_i )

and S(U ,F_i ), then award the letter grade “B” to the question Q.i due to the fact that the letter grade “B”

corresponds to the standard fuzzy set V (very good). If S(

E

,F_i ) = S(

V

,F_i ) is the maximum value among the

values of S(

E

,F_i ), S(

V

,F_i ), S(

G

,F_i ), S(

S

,F_i ) and S(U ,F_i ), then award the letter grade “A” to the

question Q.i due to the fact that the letter grade “A” corresponds to the standard fuzzy set E (excellent). Step 2: Calculate the total mark of the student as follows:

Total Mark =

100

1

×

∑

=

×

n i i

g

P

i

Q

T

1

)],

(

)

.

(

[

(9)

where T(Q.i) denotes the mark allotted to Q.i in the question paper, gi denotes the grade awarded to Q.i by Step 1 of

the algorithm, P(gi) denotes the mid-grade-point of gi, and 1 ≤ i ≤ n. Put this total score in the appropriate box at the

bottom of the fuzzy grade sheet.

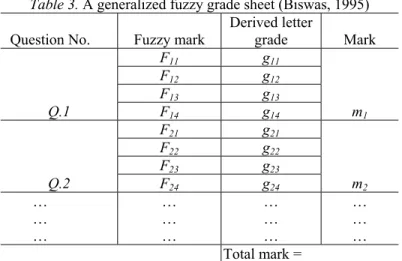
Biswas (1995) also presented a generalized fuzzy evaluation method (gfem) for students’ answerscripts evaluation, where a generalized fuzzy grade sheet shown in Table 3 is used to evaluate the students’ answerscripts.

Table 3. A generalized fuzzy grade sheet (Biswas, 1995)

Question No. Fuzzy mark Derived letter grade Mark

Q.1 F11 g11 m1 F12 g12 F13 g13 F14 g14 Q.2 F21 g21 m2 F22 g22 F23 g23 F24 g24 … … … … … … … … … … … … Total mark =

In the generalized fuzzy grade sheet shown in Table 3, for all j = 1, 2, 3, 4 and for all i, gij denotes the derived letter

grade by the fuzzy evaluation method fem for the awarded fuzzy mark Fij and mi denotes the derived mark awarded

to the question Q.i, where

mi =

400

1

×

T (Q.i)

×

∑

= 4 1

)

(

j ij

g

P

, (10) and the Total Mark =

.

1

∑

= n i i

m

A New Method for Evaluating Students’ Answerscripts Based on the Similarity Measure

between Vague Sets

In this section, we present a new method for evaluating students’ answerscripts based on the similarity measure between vague sets. Let X be the universe of discourse. We use five fuzzy linguistic hedges, called Standard Vague Sets (SVS), for students’ answerscripts evaluation, i.e.,

E

~

(excellent),

V

~

(very good),

G

~

(good),

S

~

(satisfactory) and

U

~

(unsatisfactory), where

X = {0%, 20%, 40%, 60%, 80%, 100%},

E

~

= [0, 0]/0% + [0, 0]/20% + [0, 0]/40% + [0.4, 0.5]/60% + [0.8, 0.9]/80% + [1, 1]/100%,

V

~

= [0, 0]/0% + [0, 0]/20% + [0, 0]/40% + [0.4, 0.5]/60% + [1, 1]/80% + [0.7, 0.8]/100%,

G

~

= [0, 0]/0% + [0, 0]/20% + [0.4, 0.5]/40% + [1, 1]/60% + [0.8, 0.9]/80% + [0.4, 0.5]/100%,

S

~

= [0, 0]/0% + [0.4, 0.5]/20% + [1, 1]/40% + [0.8, 0.9]/60% + [0.4, 0.5]/80% + [0, 0]/100%,

U

~

= [1, 1]/0% + [1, 1]/20% + [0.4, 0.5]/40% + [0.2, 0.3]/60% + [0, 0]/80% + [0, 0]/100%.

Assume that “A”, “B”, “C”, “D” and “E” are letter grades, where 0 ≤ E < 30, 30 ≤ D < 50, 50 ≤ C < 70, 70 ≤ B < 90 and 90 ≤ A ≤ 100. Assume that an evaluator evaluates the first question (i.e., Q.1) of a student’s answerscript, using a vague grade sheet as shown in Table 4.

Table 4. A vague grade sheet

Question No. Vague mark

Derived letter grade Q.1 [0, 0] [0.1, 0.2] [0.3, 0.4] [0.6, 0.7] [0.7, 0.8] [1, 1] Q.2 Q.3 … … … … Q.n Total mark =

In the second row of the vague grade sheet shown in Table 4, the vague marks [0, 0], [0.1, 0.2], [0.3, 0.4], [0.6, 0.7], [0.7, 0.8] and [1, 1], awarded to the answer of question Q.1, indicate that the degrees of the evaluator’s satisfaction for that answer are 0%, 20%, 40%, 60%, 80% and 100%, respectively. Let the vague mark of the answer of question

Q.1 be denoted by 1

~

F

. Then, we can see that

1

~

F

is a vague set of the universe of discourse X, where

X = {0%, 20%, 40%, 60%, 80%, 100%}, 1

~

F

= [0, 0]/0% + [0.1, 0.2]/20% + [0.3, 0.4]/40% + [0.6, 0.7]/60% + [0.7, 0.8]/80% + [1, 1]/100%.

The proposed vague evaluation method (VEM) for students’ answerscripts evaluation is presented as follows: Step 1: For each question in the answerscript repeatedly perform the following tasks:

(1) The evaluator awards a vague mark

F

~

_i represented by a vague set to each question Q.i by his/her judgment and fills up each cell of the ith row for the first seven columns shown in Table 4, where 1 ≤ i ≤ n.

(2) Based on Eq. (7), calculate the degrees of similarity H(

E

~

,

F

~

_i), H(

V

~

,

F

~

_i), H(

G

~

,

F

~

_i), H(

S

~

,

F

~

_i) and H(

U

~

,

F

~

_i), respectively, where

E

~

(excellent),

V

~

(very good),

G

~

(good),

S

~

(satisfactory) and

U

~

(unsatisfactory) are standard vague sets.

(3) Find the maximum value among the values of H(

E

~

,

F

~

_i), H(

V

~

,

F

~

_i), H(

G

~

,

F

~

_i), H(

S

~

,

F

~

_i) and H(

U

~

,

F

~

_i). If H(W~,F~_i) is the largest value among the values of H(

E

~

,

F

~

_i), H(

V

~

,

F

~

_i), H(

G

~

,

F

~

_i), H(

S

~

,

F

~

_i) and H(

U

~

,

F

~

_i),

whereW~

∈

{

E

~

,

V

~

,

G

~

,

S

~

,

U

~

}, then translate the standard vague set W~ into the corresponding letter grade,

where the standard vague set

E

~

is translated into the letter grade “A”, the standard vague set

V

~

is translated into the letter grade “B”, the standard vague set

G

~

is translated into the letter grade “C”, the standard vague set

S

~

is translated into the letter grade “D”, and the standard vague set

U

~

is translated into the letter grade “E”. For example, assume that H(

V

~

,

F

~

_i) is the maximum value among the values of H(

E

~

,

F

~

_i), H(

V

~

,

F

~

_i), H(

G

~

,

F

~

_i), H(

S

~

,

F

~

_i) and H(

U

~

,

F

~

_i), then award grade “B” to the question Q.i due to the fact that the letter

grade “B” corresponds to the standard vague set

V

~

(very good). If H(

E

~

,

F

~

_i) = H(

V

~

,

F

~

_i) is the maximum

value among the values of H(

E

~

,

F

~

_i), H(

V

~

,

F

~

_i), H(

G

~

,

F

~

_i), H(

S

~

,

F

~

_i) and H(

U

~

,

F

~

_i), then award the letter

grade “A” to the question Q.i due to the fact that the letter grade “A” corresponds to the standard vague set

E

~

(excellent).

Step 2: Calculate the total mark of the student as follows:

Total Mark = 100 1

_×

)], ~ , ~ ( ) ( ) . ( [ 1 i ∑ = × × n i F w H i g K i Q T (11)

where T(Q.i) denotes the mark allotted to the question Q.i in the question paper, gi denotes the letter grade awarded

to Q.i by Step 1, K(gi) denotes the derived grade-point of the letter grade gi based on the index of optimismλ

determined by the evaluator, where λ

∈

[0, 1], H(W~,F~i) is the maximum value among the values of H(

E

~

,

F

~

_i),

H(

V

~

,

F

~

_i), H(

G

~

,

F

~

_i), H(

S

~

,

F

~

_i) and H(

U

~

,

F

~

_i), W~

∈

{

E

~

,

V

~

,

G

~

,

S

~

,

U

~

}, such that the derived letter grade awarded to the question Q.i is gi, and 1 ≤ i ≤ n. If 0 ≤ λ < 0.5, then the evaluator is a pessimistic evaluator. If λ = 0.5,

then the evaluator is a normal evaluator. If 0.5 < λ ≤ 1.0, then the evaluator is an optimistic evaluator. Assume that the derived letter grade obtained in Step 1 with respect to the question Q.i is gi, where gi

∈

{A, B, C, D, E} and0 ≤ y1

≤ gi≤ y2 ≤ 100,then the derived grade-point K(gi) shown in Eq. (8) is calculated as follows:

K(gi) = (1 – λ)

×

y1 + λ

×

y2, (12)

where λ is the index of optimismdetermined by the evaluator, λ

∈

[0, 1], and 0 ≤ y1 ≤ K(gi) ≤ y2 ≤ 100. Put the

derived total mark in the appropriate box at the bottom of the vague grade sheet.

Example 2: Consider a student’s answerscript to an examination of 100 marks. Assume that in total there are four

questions to be answered: TOTAL MARKS = 100, Q.1 carries 30 marks, Q.2 carries 30 marks, Q.3 carries 20 marks, Q.4 carries 20 marks.

Assume that an evaluator awards the student’s answerscript using the vague grade sheet shown in Table 5, where the index of optimismλ determined by the evaluator is 0.60, i.e.,λ = 0.60. Assume that “A”, “B”, “C”, “D” and “E” are letter grades, where 0 ≤ E < 30, 30 ≤ D < 50, 50 ≤ C < 70, 70 ≤ B < 90 and 90 ≤ A ≤ 100.

Table 5. Vague grade sheet of Example 2

Question No. Vague mark Derived letter grade

Q.1 [0, 0] [0, 0] [0, 0] [0.4, 0.5] [1, 1] [0.5, 0.6]

Q.2 [0, 0] [0, 0] [0, 0] [0.4, 0.5] [0.8, 0.9] [1, 1]

Q.3 [0, 0] [0.4, 0.5] [1, 1] [0.6, 0.7] [0.4, 0.5] [0, 0]

Q.4 [0.8, 0.9] [0.5, 0.6] [0.2, 0.3] [0, 0] [0, 0] [0, 0] Total mark =

From Table 5, we can see that the vague marks of the questions Q.1, Q.2, Q.3 and Q.4 represented by vague sets are

_F

~

₁,

_F

~

₂,

_F

~

₃ and

F

~

₄, respectively, where

1

~

F

= [0, 0]/0% + [0, 0]/20% + [0, 0]/40% + [0.4, 0.5]/60% + [1, 1]/80% + [0.5, 0.6]/100%, 2

~

F

= [0, 0]/0% + [0, 0]/20% + [0, 0]/40% + [0.4, 0.5]/60% + [0.8, 0.9]/80% + [1, 1]/100%, 3

~

F

= [0, 0]/0% + [0.4, 0.5]/20% + [1, 1]/40% + [0.6, 0.7]/60% + [0.4, 0.5]/80% + [0, 0]/100%, 4

~

F

= [0.8, 0.9]/0% + [0.5, 0.6]/20% + [0.2, 0.3]/40% + [0, 0]/60% + [0, 0]/80% + [0, 0]/100%.

[Step 1] According to the standard vague sets

E

~

,

V

~

,

G

~

,

S

~

,

U

~

and the vague marks

F

~

₁,

F

~

₂,

F

~

₃,

F

~

₄, we can get the vague values, as shown in Table 6.

Table 6. Vague values of Example 2

t

V

E~

(

t

)

V

V~

(

t

)

V

G~

(

t

)

V

S~

(

t

)

V

U~

(

t

)

V

F~1

(

t

)

V

F~2

(

t

)

V

F~3

(

t

)

V

F~4

(

t

)

0 % [0, 0] [0, 0] [0, 0] [0, 0] [1, 1] [0, 0] [0, 0] [0, 0] [0.8, 0.9] 20 % [0, 0] [0, 0] [0, 0] [0.4, 0.5] [1, 1] [0, 0] [0, 0] [0.4, 0.5] [0.5, 0.6] 40 % [0, 0] [0, 0] [0.4, 0.5] [1, 1] [0.4, 0.5] [0, 0] [0, 0] [1, 1] [0.2, 0.3] 60 % [0.4, 0.5] [0.4, 0.5] [1, 1] [0.8, 0.9] [0.2, 0.3] [0.4, 0.5] [0.4, 0.5] [0.6, 0.7] [0, 0] 80 % [0.8, 0.9] [1, 1] [0.8, 0.9] [0.4, 0.5] [0, 0] [1, 1] [0.8, 0.9] [0.4, 0.5] [0, 0] 100 % [1, 1] [0.7, 0.8] [0.4, 0.5] [0, 0] [0, 0] [0.5, 0.6] [1, 1] [0, 0] [0, 0] By applying Eq. (5), we can get scores of the vague values, as shown in Table 7.

Table 7. Scores of the vague values of Example 2

t

S

(

V

E~

(

t

))

S

(

V

V~

(

t

))

S

(

V

G~

(

t

))

S

(

V

S~

(

t

))

S

(

V

U~

(

t

))

S

(

V

F~1

(

t

))

S

(

V

F~2

(

t

))

S

(

V

F~3

(

t

))

S

(

V

F~4

(

t

))

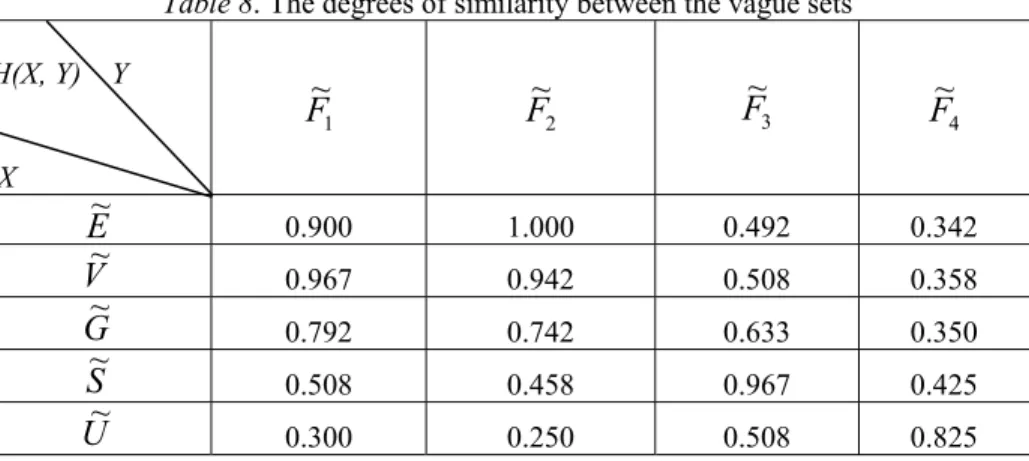
0 % -1 -1 -1 -1 1 -1 -1 -1 0.7 20 % -1 -1 -1 -0.1 1 -1 -1 -0.1 0.1 40 % -1 -1 -0.1 1 -0.1 -1 -1 1 -0.5 60 % -0.1 -0.1 1 0.7 -0.5 -0.1 -0.1 0.3 -1 80 % 0.7 1 0.7 -0.1 -1 1 0.7 -0.1 -1 100 % 1 0.5 -0.1 -1 -1 0.1 1 -1 -1

Table 8. The degrees of similarity between the vague sets

H(X, Y) Y X 1

~

F

F

~

₂ 3

~

F

F

~

₄

E

~

0.900 1.000 0.492 0.342

V

~

0.967 0.942 0.508 0.358

G

~

0.792 0.742 0.633 0.350

S

~

0.508 0.458 0.967 0.425

U

~

0.300 0.250 0.508 0.825

By applying Eq. (7), we can get the degree of similarity H(X, Y) between the vague values X and Y, where

X

∈

{

E

~

,

V

~

,

G

~

,

S

~

,

U

~

} and Y

∈

{

F

~

₁,

F

~

₂,

F

~

₃,

F

~

₃}, as shown in Table 8.

Because H(

V

~

,

F

~

₁) is the maximum value among the values of H(

E

~

,

F

~

₁), H(

V

~

,

F

~

₁), H(

G

~

,

F

~

₁), H(

S

~

,

F

~

₁)

and H(

U

~

,

F

~

₁), we award grade “B” to the question Q.1 due to the fact that the letter grade “B” corresponds to the

standard vague set

V

~

(very good).

Because H(

E

~

,

F

~

₂) is the maximum value among the values of H(

E

~

,

F

~

₂), H(

V

~

,

F

~

₂), H(

G

~

,

F

~

₂), H(

S

~

,

F

~

₂)

and H(

U

~

,

F

~

₂), we award grade “A” to the question Q.2 due to the fact that the letter grade “A” corresponds to the

standard vague set

E

~

(excellent).

Because H(

S

~

,

F

~

₃) is the maximum value among the values of H(

E

~

,

F

~

₃), H(

V

~

,

F

~

₃), H(

G

~

,

F

~

₃), H(

S

~

,

F

~

₃)

and H(

U

~

,

F

~

₃), we award grade “D” to the question Q.3 due to the fact that the letter grade “D” corresponds to the

standard vague set

S

~

(satisfactory).

Because H(

U

~

,

F

~

₄) is the maximum value among the values of H(

E

~

,

F

~

₄), H(

V

~

,

F

~

₄), H(

G

~

,

F

~

₄), H(

S

~

,

F

~

₄)

and H(

U

~

,

F

~

₄), we award grade “E” to the question Q.4 due to the fact that the letter grade “E” corresponds to the

standard vague set

U

~

(unsatisfactory).

[Step 2] Because 90 ≤ A ≤ 100, 70 ≤ B < 90, 30 ≤ D < 50 and 0 ≤ E < 30, where “A”, “B”, “D” and “E” are letter grades, and the index of optimismλ determined by the evaluator is 0.60 (i.e.,λ = 0.60), based on Eq. (12), we can get the following results:

K(A) = (1 – 0.60) × 90 + 0.60 × 100 = 96, K(B) = (1 – 0.60) × 70 + 0.60 × 90 = 82, K(D) = (1 – 0.60) × 30 + 0.60 × 50 = 42, K(E) = (1 – 0.60) × 0 + 0.60 × 30 = 18.

Because the questions Q.1, Q.2, Q.3 and Q.4 carry 30 marks, 30 marks, 20 marks and 20 marks, respectively, and because H(

V

~

,

F

~

₁) = 0.967, H(

E

~

,

F

~

₂) = 1.000, H(

S

~

,

F

~

₃) = 0.967 and H(

U

~

,

F

~

₄) = 0.825, based on Eq. (11), the

total mark of the student is evaluated as follows:

100

1

(30

×

82

×

0.967 + 30

×

96

×

1.000 + 20

×

42

×

0.967 + 20

×

18

×

0.825) =

100

1

(2378.82 + 2880 + 812.28 + 297) = 63.681

= 64 (assuming that no half mark is given in the total mark).

A Generalized Method for Evaluating Students’ Answerscripts Based on the Similarity

Measure between Vague Sets

In this section, we present a generalized vague evaluation method (GVEM) for students’ answerscripts evaluation based on the similarity measure between vague sets, where a generalized vague grade sheet shown in Table 9 is used to evaluate the students’ answerscripts.

Table 9. A generalized vague grade sheet

Question No. Sub-questions Vague mark Derived letter grade Mark

Q.11 11

~

F g11

~

Q.13 13 ~ F g13 Q.14 14 ~ F g₁₄ Q.2 Q.21 21 ~ F g21 m2 Q.22 22 ~ F g22 Q.23 23 ~ F g23 Q.24 24 ~ F g₂₄ … … … … … Q.n Q.n1 1 ~ n F g_n1 mn Q.n2 2 ~ n F gn2 Q.n3 3 ~ n F gn3 Q.n4 4 ~ n F gn4 Total mark =

In the generalized vague grade sheet shown in Table 9, each question Q.i consists of four sub-questions, i.e., Q.i1,

Q.i2, Q.i3 and Q.i4. For all j = 1, 2, 3, 4 and for all i, gij is the derived letter grade by the proposed vague evaluation

method VEM of the awarded vague mark

_F

~

_ij with respect to the sub-question Q.ij, and mi is the derived mark

awarded to the question Q.i,

mi =

400

1

×

T (Q.i)

×

4[ ( ) (~, )], 1 ij j ij F w H g K ×

∑

= (13) and Total Mark =

.

1

∑

= n i i

m

where T(Q.i) denotes the mark allotted to Q.i in the question paper, gij denotes the derived letter grade awarded to

Q.i, and K(gij) denotes the derived grade-point of the letter grade gij based on the index of optimismλ determined by

the evaluator, whereλ

_∈

[0, 1], H(W~,F~_ij) is the maximum value among the values of H(

E

~

,F~_ij), H(

V

~

,F~_ij), H(

G

~

,F~_ij), H(

S

~

,F~_ij) and H(

U

~

,F~_ij), W~

∈

{

E

~

,

V

~

,

G

~

,

S

~

,

U

~

}, such that the derived letter grade awarded to the question Q.ij is gij, 1 ≤ j ≤ 4, and 1 ≤ i ≤ n. If 0 ≤λ < 0.5, then the evaluator is a pessimistic evaluator. Ifλ = 0.5, then

the evaluator is a normal evaluator. If 0.5 <λ ≤ 1.0, then the evaluator is an optimistic evaluator. Assume that the derived letter grade with respect to the sub-question Q.ij is gij, where gij

∈

{A, B, C, D, E} and0 ≤ y1 ≤ gij≤ y2 ≤ 100,

then the derived grade-point K(gij) shown in Eq. (13) is calculated as follows:

K(gij) = (1 –λ )

×

y1 +λ

×

y2, (14)

whereλ is the index of optimismdetermined by the evaluator,λ

∈

[0, 1], and 0 ≤ y1 ≤ K(gij) ≤ y2 ≤ 100. Put the

derived total mark in the appropriate box at the bottom of the generalized vague grade sheet.

Experimental Results

We have made an experiment to compare the evaluating results of the proposed method with the Biswas’ method (1995) for different days. In our experiment, there are four questions to be answered in a student’s answerscript, where

TOTAL MARKS = 100,

Q.2 carries 25 marks, Q.3 carries 25 marks, Q.4 carries 30 marks.

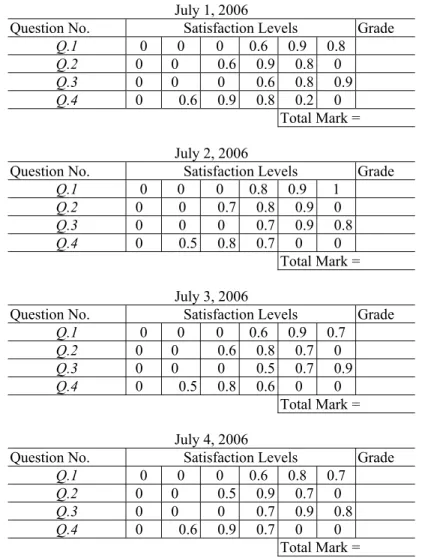
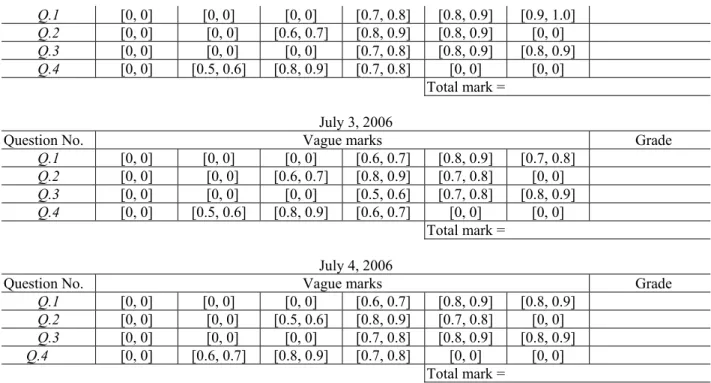
Assume that the index of optimismλ of the evaluator is 0.60 (i.e., λ = 0.60). The evaluator uses Biswas’ method (1995) and the proposed method to evaluate the student’s answerscript on different days, respectively. The results are shown in Fig. 2 and Fig. 3, respectively. A comparison of the evaluating results of the student’s answerscript is shown in Table 10. From Table 10, we can see that the proposed method is more stable to evaluate students’ answerscripts than Biswas’ method (1995). It can evaluate students’ answerscripts in a more flexible and more intelligent manner.

July 1, 2006

Question No. Satisfaction Levels Grade

Q.1 0 0 0 0.6 0.9 0.8 Q.2 0 0 0.6 0.9 0.8 0 Q.3 0 0 0 0.6 0.8 0.9 Q.4 0 0.6 0.9 0.8 0.2 0 Total Mark = July 2, 2006

Question No. Satisfaction Levels Grade

Q.1 0 0 0 0.8 0.9 1 Q.2 0 0 0.7 0.8 0.9 0 Q.3 0 0 0 0.7 0.9 0.8 Q.4 0 0.5 0.8 0.7 0 0 Total Mark = July 3, 2006

Question No. Satisfaction Levels Grade

Q.1 0 0 0 0.6 0.9 0.7 Q.2 0 0 0.6 0.8 0.7 0 Q.3 0 0 0 0.5 0.7 0.9 Q.4 0 0.5 0.8 0.6 0 0 Total Mark = July 4, 2006

Question No. Satisfaction Levels Grade

Q.1 0 0 0 0.6 0.8 0.7

Q.2 0 0 0.5 0.9 0.7 0

Q.3 0 0 0 0.7 0.9 0.8

Q.4 0 0.6 0.9 0.7 0 0

Total Mark =

Figure 2. Evaluating the student’s answerscript at different days using Biswas’ method (1995)

July 1, 2006

Question No. Vague marks Grade

Q.1 [0, 0] [0, 0] [0, 0] [0.6, 0.7] [0.8, 0.9] [0.8, 0.9] Q.2 [0, 0] [0, 0] [0.6, 0.7] [0.8, 0.9] [0.8, 0.9] [0, 0] Q.3 [0, 0] [0, 0] [0, 0] [0.6, 0.7] [0.8, 0.9] [0.8, 0.9] Q.4 [0, 0] [0.5, 0.6] [0.8, 0.9] [0.7, 0.8] [0.1, 0.2] [0, 0] Total mark = July 2, 2006

Q.1 [0, 0] [0, 0] [0, 0] [0.7, 0.8] [0.8, 0.9] [0.9, 1.0] Q.2 [0, 0] [0, 0] [0.6, 0.7] [0.8, 0.9] [0.8, 0.9] [0, 0] Q.3 [0, 0] [0, 0] [0, 0] [0.7, 0.8] [0.8, 0.9] [0.8, 0.9] Q.4 [0, 0] [0.5, 0.6] [0.8, 0.9] [0.7, 0.8] [0, 0] [0, 0] Total mark = July 3, 2006

Question No. Vague marks Grade

Q.1 [0, 0] [0, 0] [0, 0] [0.6, 0.7] [0.8, 0.9] [0.7, 0.8] Q.2 [0, 0] [0, 0] [0.6, 0.7] [0.8, 0.9] [0.7, 0.8] [0, 0] Q.3 [0, 0] [0, 0] [0, 0] [0.5, 0.6] [0.7, 0.8] [0.8, 0.9] Q.4 [0, 0] [0.5, 0.6] [0.8, 0.9] [0.6, 0.7] [0, 0] [0, 0] Total mark = July 4, 2006

Question No. Vague marks Grade

Q.1 [0, 0] [0, 0] [0, 0] [0.6, 0.7] [0.8, 0.9] [0.8, 0.9]

Q.2 [0, 0] [0, 0] [0.5, 0.6] [0.8, 0.9] [0.7, 0.8] [0, 0]

Q.3 [0, 0] [0, 0] [0, 0] [0.7, 0.8] [0.8, 0.9] [0.8, 0.9]

Q.4 [0, 0] [0.6, 0.7] [0.8, 0.9] [0.7, 0.8] [0, 0] [0, 0]

Total mark =

Figure 3. Evaluating the student’s answerscript at different days using the proposed method Table 10. A comparison of the evaluating results for different methods

Methods Total

mark

Days Biswas’ method (1995) The proposed method

July 1, 2006 69 68

July 2, 2006 72 68

July 3, 2006 55 68

July 4, 2006 55 68

The Merits of the Proposed Methods

The proposed methods have the following advantages:

(1) The proposed methods are more flexible and more intelligent than Biswas’ methods (1995) due to the fact that we use vague sets rather than fuzzy sets to represent the vague mark of each question, where the evaluator can use vague values to indicate the degree of the evaluator’s satisfaction for each question. Especially, the proposed methods are particularly useful when the assessment involves subjective evaluation.

(2) The proposed methods are more stable to evaluate students’ answerscripts than Biswas’ methods (1995). They can evaluate students’ answerscripts in a more flexible and more intelligent manner.

Conclusions

In this paper, we have presented two new methods for evaluating students’ answerscripts based on the similarity measure between vague sets. The vague marks awarded to the answers in the students’ answerscripts are represented by vague sets, where each element belonging to a vague set is represented by a vague value. An index of optimismλ determined by the evaluator is used to indicate the degree of optimism of the evaluator, whereλ

_∈

[0, 1]. Because the proposed methods use vague sets to evaluate students’ answerscripts rather than fuzzy sets, they can evaluate students’ answerscripts in a more flexible and more intelligent manner. The experimental results show that

the proposed methods can evaluate students’ answerscripts more stable than Biswas’ methods (1995).

Acknowledgements

The authors would like to thank Professor Jason Chiyu Chan, Department of Education, National Chengchi University, Taipei, Taiwan, Republic of China, for providing very helpful comments and suggestions. This work was supported in part by the National Science Council, Republic of China, under Grant NSC 95-2221-E-011-117-MY2.

References

Biswas, R. (1995). An application of fuzzy sets in students’ evaluation. Fuzzy Sets and Systems, 74 (2), 187-194. Chang, D. F., & Sun, C. M. (1993). Fuzzy assessment of learning performance of junior high school students. Paper

presented at the First National Symposium on Fuzzy Theory and Applications, June 25-26, 1993, Hsinchu, Taiwan.

Chen, S. M. (1988). A new approach to handling fuzzy decisionmaking problems. IEEE Transactions on Systems,

Man, and Cybernetics, 18 (6), 1012-1016.

Chen, S. M. (1995a). Arithmetic operations between vague sets. Paper presented at the International Joint

Conference of CFSA/IFIS/SOFT’95 on Fuzzy Theory and Applications, December 7-9, 1995, Taipei, Taiwan.

Chen, S. M. (1995b). Measures of similarity between vague sets. Fuzzy Sets and Systems, 74 (2), 217-223.

Chen, S. M. (1997). Similarity measures between vague sets and between elements. IEEE Transactions on Systems,

Man, and Cybernetics-Part B: Cybernetics, 27 (1), 153-158.

Chen, S. M. (1999). Evaluating the rate of aggregative risk in software development using fuzzy set theory.

Cybernetics and Systems, 30 (1), 57-75.

Chen, S. M., & Lee, C. H. (1999). New methods for students’ evaluating using fuzzy sets. Fuzzy Sets and Systems,

104 (2), 209-218.

Chen, S. M., & Wang, J. Y. (1995). Document retrieval using knowledge-based fuzzy information retrieval techniques. IEEE Transactions on Systems, Man, and Cybernetics, 25 (5), 793-803.

Cheng, C. H., & Yang, K. L. (1998). Using fuzzy sets in education grading system. Journal of Chinese Fuzzy

Systems Association, 4 (2), 81-89.

Chiang, T .T., & Lin C. M. (1994). Application of fuzzy theory to teaching assessment. Paper presented at the 1994

Second National Conference on Fuzzy Theory and Applications, September 15-17, 1994, Taipei, Taiwan.

Frair, L. (1995). Student peer evaluations using the analytic hierarchy process method. Paper presented at the

Frontiers in Education Conference, November 1-4, 1995, Atlanta, GA, USA.

Gau, W. L., & Buehrer, D. J. (1993). Vague sets. IEEE Transactions on Systems, Man, and Cybernetics, 23 (2), 610-614.

Echauz, J. R., & Vachtsevanos, G. J. (1995). Fuzzy grading system. IEEE Transactions on Education, 38 (2), 158-165.

Hwang, G. J., Lin, B. M. T., & Lin, T. L. (2006). An effective approach for test-sheet composition with large-scale item banks, Computers & Education, 46 (2), 122-139.