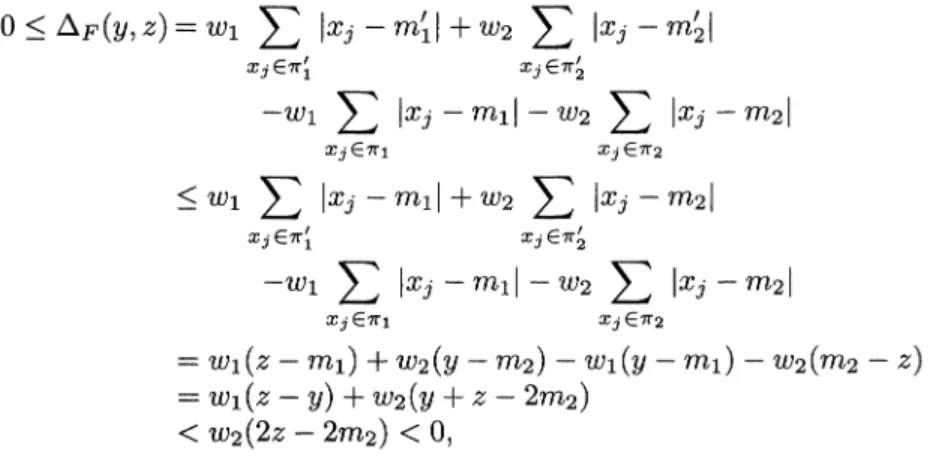Optimality of nested partitions and its application to cluster analysis

OPTIMALITY OF

NESTED PARTITIONS AND ITS APPLICATION

TO CLUSTER

ANALYSIS*

E.

BOROSt

AND F. K. HWANG$

Abstract. Apartition ofasetN ofndistinctnumbersiscalled nestediffour numbersa

_<

b<

c< dinNsuch that a andcare in onepartwhile band d in another do not exist. Apartitionis calledap-partition ifthe number ofpartsisspecifiedat p and ashape-partition if the sizesofthe pparts arealsospecified. There areexponentially manyp-partitions but only polynomiMlymany nested p-partitions. In this paperweconsider these notions in d-dimensional Euclidean spaces and giveageneralconditiononthe cost structure for whichanoptimal shape-partitionisalwaysnested. Weillustrate applicationsofourresults tosomeclustering problems, generalizesomeknownresults in thisway, and proposesomeopenproblems.

Keywords, clustering,nested partitions AMS subject classifications. 62H30, 05A18

1. Introduction. Consider the problem of partitioning a set

N

of n distinct

numbersintononempty disjoint

parts.

The partitioniscalledan open-partition if the

number of parts isnot prespecified and calleda p-partition ifthe numberisspecified

tobep

If,

furthermore aset

{nl

np}

with

_-.=1

P

n

n is prespecifiedtobe the

setofsizesof thepparts, then thepartition iscalledashape-partition,shape referring

tothe set

{ni}.

Often,

oneencountersthe problem of findinganoptimalpartition givenacost

(of

partition)

function.

However,

the brute force approach ofcomparing the costs of all

partitions is too time-consuming duetothelarge number ofpartitions.

For

example,

usingthe principle of

inclusion-exclusion,

thenumber ofp-partitions can beshownto

be

(1)

e(n,p)

E(-1)

k

(p-k)

.

k=0

Thenumber ofopen-partitions

n

(2)

#(n)

p=l

is represented

by

the Bell numbers whosefirst 10 terms are

1, 2,

5, 15, 52, 203, 877,

4140, 21147,

115975.

Even

for the shape-partition, the number is

(3)

:(n,... ,np)=

_P

n

V[n-p+l

Hi--1

hi.1lj--1

PJ"

wherepj isthe number of parts ofsize j. Thisnumberiseasilyseentobe exponential in neven forp 2.

Received by the editorsAugust 4, 1994; acceptedfor publication (in revised form) April 20,

1995. This paper isarevisedversionofRUTCORResearchReport 7,1993.

RUTCOR, Rutgers University, New Brunswick, NJ 08904 (boros@rutcor.rutgers.edu). The researchofthisauthorwassupported inpartbyOfficeof Naval Research grantsN00014-92-J-1375 andN00014-92-J-4083andbyAirForceOfficeofScientificResearch grantF49620-95-1-0233.

Department ofApplied Mathematics, Chiao-Tung University, Hsin-Chu, Taiwan 30050 ROC

fhwang@math.nctu.edu.tw).

1153

One

way to dealwiththecombinatorialproblem of hugepartition spaces is tolook for small subspaces which,

nevertheless,

also contain optimal partitions.

One

well-studiedsubspaceconsistsofconsecutivepartitions

[3,9]

whicharecharacterizedby the

requirement that each part ofaconsecutivepartition consists of numbersconsecutive

in

N.

In

thissubspace each p-partition correspondsto a way ofinserting p- 1 bars

intothe n- 1 spaces between the n numbers. The number ofp-partitions isthus

(

-1

/

(4)

#c(n,p)

1

apolynomial function ofnforfixed p.

For

shape-partitions, thenumberiseasilyseen

to be

p

n--p+l

j=l

PJ

Whenthe "consecutive" subspace is not known to contain anoptimal partition,

onehas tosearch other subspaces.

Boros

and

Hammer

[2]

raisedthenotionof

nested

partitions, which isdefined by the nonexistenceoffour numbers a b c d in

N

such

that a andc belong to one part, while b and d belongto another.

Note

that a

consecutive partition is always

nested,

but not vice versa. They demonstrated some

cost functions which guarantee that an optimal p-partition is nested.

Hwang

and Mallows

[I0]

showed that the number of nestedp-partitions is

(6)

N(,p)--

\p-1]\p],

again, a polynomialfunction ofnfor fixed p.

The notions of "consecutiveness" and nestedness have been extended to

vec-tots

(points

ind-dimensional

spaces).

We

now extend themfurther to d-dimensional multisets.

Let

X

_{{Xl,X2,... ,x}}

C

]d

be a multisetofd-dimensional points, i.e.,

elements of

X

may coincide.

Furthermore,

let

_conv(X)

denote the convex hull of

X,

and letconv*

_(X)

denote therelative interiorof

cony(X).

A

partition

_{(1,..., p)}

ofthe multiset

X

(identical

points are treated as separated entities in a

partition)

is

called consecutive

_(see

[1])

ifcony*

_(i)

gcony*

_(j)

₀

for all 1

_<

i,j

_<

p.

It

iscalled

nested

(see

[2])

iffor all 1

_<

i,j

<_

p, eitheriN

conv*(j)

0

or rjN

conv*()

0.

Again, consecutiveness implies nestedness.

In

this paper we give a sufficient

condi-tion on the cost function such that an optimal shape-partition is always nested.

A

by-product isa sufficient conditionfor theexistence ofaconsecutive optimal

shape-partition.

In

particular,they leadtoan extension ofFisher’sresult

[6]

onaclustering problem fromone dimensionto d dimensions whichhe long desired.

2. The mainresults.

In

this section we deriveageneralcondition which guar-antees that every optimal shape-partition is nested.

We

first consider a shape with

onlytwo parts, and thenwe extend theresult to generalp.

Consider amultiset

X

ofd-dimensional points, d

_

i, and a partition ofit into two parts,

(7, r2). Let,

furthermore,

F(7)

denotethe cost ofpartition

.

Let

r be a partition obtained from r by interchanging two points, x and Y 2.

Clearly,

has the same shape as

.

We

will consider

F()

F()

as a function

_AF(x,

y)

ofx and y, i.e.,

_AF

7 72 ---*

P.

More

precisely, letus consider

acontinuous, real-valuedmapping

A

overthe space

d

d

satisfying the following

conditions:

A(x,

y)-

As(x,

y)

for all x

e

71"1 and y

e

2,

A(z,

z)-

0 for all z E

]d.

Suchamapping

_A

existsandcannaturallybe consideredas acontinuous extension

of

As,

forif x E 1and y s2happento coincide

(X

isa

multiset),

then

As(x,

y)

0 since the

switch

ofidentical elements does not change the partition.

Let

us remark that in most cases, when

F

is given in an algebraic

form,

the formula for

As

will

automa/icallydefinesuch an extension.

For

a fixed vector x sl let us introduce the notation

g(y)

A(x,y)

and,

analogously, let

_gy(x)

AF(x

y),

ifwe want toemphasize that y s2 isfixed now.

Let,

furthermore,

_X+(g)

{x

Idlg(x)

>_

0},

and let

Y+(g)

{y

]dlg(y

>_

0}.

We

arereadynowto stateasufficient conditionforashape-partition tobe nested.

THEOREM

2.1.

For

a shape-partition problem let

(l,r2)

be an optimal partition. Further let us suppose that either

_for

every x 1, the set

Y+(g)

is a

convex set with x being a boundary point, or

_for

every y 2, the set

X+

(g)

is a

conve

_x

setwithy being a boundarypoint. Then7-

(1,

r2)

is nested.

Proof.

Let

us assume that for every y r2, theset

X+

(gy)

is a convex set with ybeingaboundarypoint. Since isoptimal, i.e., itscost

F(r)

isminimal among all partitionsofthesame shape,

_gs(x)

>_

0for all x

s

and all y E2, implying

(8)

71 C

X+

_(gy)

forally 2. Sincefor each y 2theset

X

+

(g)

isconvex withy beingaboundary point, theintersectionofall these sets

x+-yETr2

isalsoconvex and nopoint of2 belongsto its interior. Since

conv*(l)

follows,,

which proves that is nested. The other case is

analogous.

Sometimes,

it is easier to use Theorem 2.1 when the conditions are specified on

and *. thefunctions

₉

_9x

A

reM-valued function

_f(x)

is called quasi concave ifover any interval

[a, b]

{ca

+

(1 -c)bl0

_<

a

_<

_1}

it always attains its minimum over

[a, b]

at one of the

endpoints. The function

_f

is called strictly quasi concave ifno internal point ofan

interval can be a minimum

(over

that

interval).

It

is well known that a

(strictly)

concave function is

(strictly)

quasi concave.

COROLLARY

2.2.

Let

X

be a given multiset with

F

being the cost

_function

_of

its

partitions, as

_before.

_If

either

g

_for

any x

X

or

g

_for

anyy

X

is strictly quasi

concave, then every optimal shape-partition is nested.

Proof.

Let

usassume that

_g

for anyy E

X

is strictly quasi concave. The other

case can be treated analogously.

Let

us consider anoptimal shape-partition

(,

2).

Accordingto the previ-ous

theorem,

if

X

+

(gy)

isconvex having y on its boundary for everyy

is necessarily nested.

Let

us observe first that for every y r2, thepoint y must be aboundarypoint

of

X+

_(g),

since

g

is strictly quasi concave. This implies that if is not

nested,

then,

by Theorem

2.1,

there isavector yE7c2 forwhichthe set

X +

(gy)

isnotconvex. Then there must exist points

u,

v E

X +

_(g)

and w cu

+

_{(1 -c)v}

X+

_(g)

for

some 0

<

c

<

1,

i.e., for

_whichgy(u)

>_

0,

_g(v)

>

_Owhilegv(w)

<

0.

_Sincegv

is

continuous, the interval

In,

v]

has aninternalminimum, contradictingthestrictquasi concavity of

g.

THEOREM

2.3.

Suppose

that thecost

_function

hasthestructure

F(r)

LIP__1

f

(Tri)

i.e.,

F(Tc)

is the sum

_of

independent values associated with each

_of

the parts.

In

this

case,

_if

every optimalshape-partitionisnestedholds

_for

p 2, thenitholds

_for

p

>

2.

Proof.

Let

r be an optimal shape-partition.

By

Theorem 2.1, any two parts of

r must be a nested partition oftheir elements or we would be able to reduce

F(r)

by making them

nested,

which contradicts the assumption that 7r is optimal.

By

the definition of a nested partition, r is nested if any two parts of 7r are pairwise

nested.

Interestingly, thearguments used to establishnested optimal partitions are also applicable forconsecutiveoptimalpartitions,forwhichmoreefficientalgorithmsexist.

THEOREM

2.4. Consider a shape-partitionproblem and let r be an optimal

par-tition.

Suppose

that

_for

every pair

(7c,

7cj)

and

_for

every x rj,

Y+

(g)

is a convex

set with x on its boundary, and

_for

everyy 7rj,

X

+

(g)

is a convex sethaving y as

a boundarypoint. Then every optimal partitionis consecutive.

Proof.

First consider the case oftwo parts.

Let

7r be an optimal partition.

We

havearguedin theproof of Theorem 2.1 that

X

+

_(g)

beinga convexsethaving yon itsboundaryimplies thatnoy r2is in

conv*(Trl).

Similarly,

Y+(g)

being aconvex set with x being the

boundary

implies that no x 7rl is in

conv*(r2).

Hence

7r is

consecutive. The resultisthen extended togeneralppartsby anargument analogous

totheproof ofTheorem 2.3.

COROLLARY

2.5.

Suppose

that both

g

and

_gv

are strictlyquasi concave

_for

every x and y, respectively. Then every optimal shape-partition is consecutive.

Sincean open-partition must beap-partition for somep, and ap-partition must

be a shape-partitionfor some shape, results inthis section also applyto p-partitions and open-partitions.

3. Applications to clustering.

In

aclustering problem, onepartitionsagiven setofpoints intoclusters usuallywith points in thesame cluster close toeach

other,

though closeness can be defined in various ways.

It

is very rare for a clustering problem to have a polynomial-time algorithm for exact optimal clustering, due to theusually large number ofpossible clusterings.

One

ofthe few exceptions isdue to Fisherwhowas one of the first to use consecutive partitions. Fisher

[6]

considered a

one-dimensionalclustering problem where thegoal istominimizethesumofsquares,

i.e., the cost ofa partition r

(7c1,...,

7rp)

is

P

i=1xjTr

where5iistheaverage ofthe numbersin7ri.

He

proved thatthereexists a consecutive

optimal p-partition, even when there is a weight

_w.

associated to each number xj. Since every open-partition must be a p-partition for some p, this also implies the existenceofa consecutive optimal open-partition. Fisher wrote

[6,

pp.

796-797]:

"It

would ofcoursebemost desirable to develop, both theoreticallyandcomputationally,

a distance criterion that is defined in more than one dimension.

An

example of the need for such a formulation is shown, in a multivariate stratification problem

encountered in a sample survey by Hagood and

Bernert

[8].

Of course involved in

any suchapproachisarelevant system of weighing the different dimensionstoreflect

their relative importance in determining distance."

Gower

[7]

studied three criteria

commonly adopted in the literature of cluster analysis for multivariate data.

One

of

which,

attributed to Edwards and Cavalli-Sforza

[5],

is to divide the data into

two disjoint subsets with a minimum sum of squares, a special case of Fisher’s d-dimensionalproblemwith p 2.

Unfortunately,

Fisher’sproof technique ofthe one-dimensionalcasecannothandle

a weight function associated with the dimensions.

Gower

proved the existence of

consecutive

optimal partitions for p 2 and without dimension weight.

We

now

consider the general case.

Suppose

that xj

(Xjl,... ,Xjd)

and uk is the positive

weight ofdimension

k,

k

1,...,

d. Consider thecost function

(10)

where yj

(x/rXjl,

v/Xj2,...,

XflXjd)

and

--xj6,

y/l l

is themean

(cen-troid)

of the vectors yj for xj E

r (and

where the product ofthe vectors denotes their inner

product).

In

the followingtheorem weshallreplaceyj in

(10)

byxj for uniformity andalso

generalizeit by introducing aweight function

_w

associated topart i.

THEOREM 3.1.

Suppose

that

p

(11)

F(r)

E

w

E

(xj

)2,

i--1

_x

r

where

_{w >}

0

and-2

is the centroid

(mean,

inthis

case)

of

the d-dimensional points

in

r.

Then an optimal shape-partitionmust be nested.

Proof.

By

Theorem 2.3 it isenough to prove the above statement forthecase of p=2.

Let

be an optimal shape-partition and let r be thepartitionobtained from r

by interchanging y E rl andz r2.

Let

and denote the centroidsof

r

and

r,

respectively. Then 0

<_ AF(y,

z)

wl

Xl)

E

(Xj

51)2

XjTr XjTrl Wl nl 2

Xj

fr Xj

E

Xj--xjer, nl

View the above expression as a function of real y and z

(vectors)

with the given coefficient

₍₁

and

52

are treated as

fixed)

and define

g(y)

and

_g(z)

accordingly.

Sincethesum of thecoefficients of the z2 term andthe

y2

term isnegative, at least

one of them is negative, say, the coefficient of the z2 term. Since

g(y)

is separable

inthe dimensionof y, it is easilyverifiedthat the negative coefficient of the z2 term

implies thatthe Hessian is negative-definite.

Hence

g

is strictly concave. Since the

coefficients of

y2

and z2 _{are independent of the particular selection of y and}

_z,

_we

can conclude that

g

isstrictly concave for all z E 2.

By

Corollary

2.2 an optimal

shape-partition thus mustbe nested. Cl

COROLLARY

3.2.

_If

(12)

IWl

W21

Wl W2

nl n2

then every optimal shape-partition is consecutive.

Proof.

The proof of

Corollary

3.2 follows immediately from Corollary 2.5.

In

particular, if

_w

1 for all i, then the conditionof Corollary 3.2 issatisfied.

Thuswehave extendedFisher’ssum-of-squares result to d-dimensional points.

By

setting

w

0 for

_n

1 and

w

1/(n-

1)

for

_{n >_}

2,

F()

in Theorem 3.1 represents the sum ofvariances

_(for

multidimensional points, each variance is

weightedsumoverthed

dimensions).

Therefore all shape-partitions tominimize the sumofvariancesare nested.

It

isalso easily verified that

(12)

holdsif

_In1

_n21

_<

1.

Hence

we havethe following result.

COROLLARY

3.3. Consider apartitioning problem where the part-sizes can

dif-fer

by at most 1. Then every optimalpartition minimizing the sum

_of

variances is consecutive.

One

may feelthatperhaps for anarbitrary shapethereexists aconsecutive

opti-malpartition.

We

now give aone-dimensional exampleto showthat Corollary 3.3 is

tight, i.e., ifthepart-size can differ by 2, thenno optimalpartition is consecutive.

Let

N

{0,

13,

14, 14, 15,

28}

and the shape be

{2,

4}.

Then

{14, 14},

2

{0,

13,

15,

28}

is the optimal shape-partition minimizing the sum ofvariances.

But

{1,

2}

is not a consecutive partition.

Another consequence of

Corollary

2.2 is astrengthening ofTheorem 1.2 of

[2].

THEOREM

3.4.

Suppose

that

p

()

F()

(x

x),

i=1 xj,Xk

wherewi

>

O. Then every optimal shape-partition is nested.

Proof.

By

Theorem 2 again, it is enough to consider p 2.

Let

y E 7rl and z Er2. Then

(14)

/F(Y,Z)--

Wl

E

((Z

Xj)2

(y__

Xj)2)

xjErl

+

((

x)

(

x)

)

xj r2

y[w2(n2

1)

Wl

(nl

--

1)]

+

z2[wl

(nl

1)

w2(n2

+

1)]

--

2(W

--w2)yz

_"

2y

[W

lxGvIE

Xj W2 xjr2

_x

r

where nl and

n

denote the cardinalities of1 and r2, respectively. Since the sum ofthe coefficients of

y2

and z2 _is

_-2(Wl

+

w2)

<

0,

at leastone of them is negative,

implying that at least oneof

g

or

_gv

is strictlyconcave.

Thus,

by

Corollary 2.2,

we

can concludethat an optimal shape-partitionmustbe nested. If both

y2

and z2 _have

nonpositive coefficients inthe aboveproof, i.e., if

(15)

[win1-

w2n2[

Wl--w2,

then by

Corollary

2.5 anoptimal shape-partition must beconsecutive. This

observa-tionyields thefollowing interestingconsequence.

COROLLARY

3.5. Consider ashape-partitioningproblem where

p

(16)

F(r)

E E

(xj

xk)

2

i--1xj,Xk7ri

andinwhich the part-sizes can

_differ

by at most2. Then every optimal shape-partition

is consecutive.

Boros

and

Hammer

studieda one-dimensional clustering problemwith

p

(17)

F(Tr)

E E

andproved that every optimalp-partition isnested. This,

however,

may not be true

for shape-partitions.

In

this paper, instead of the absolute difference between two

numbers,

we consider the absolute difference between a number and the centroid of

thepart, with apart-weight. THEOREM3.6.

Suppose

that

p

(18)

F(Tr)

E

wi

E

IxJ

rnl’

FIG. 1. The ordering_ofy’s andz’swhenwl >_w2.

where

_{w >}

0 and

_m

is the median

_of

the set7r. Then every optimal shape-partition

is nested.

Proof.

By

Theorem 2.3 it is sufficient to considerp 2.

Let

y E 7rl and z E 7r2.

Let

r’

(r,

r)

be obtainedfrom 7r by interchanging y and

z,

and let

m

and

m

be the medians of

_7r

and

_7r.

Without loss of generality, assume m

<_

m2.

Case

i. y,z

>_

m2. Then

m

ml and

m

m2.

(19)

0

< (, )= (z

.)

+

:(

n:)

(

n)

:(z

n:)

(1

)(z

).

So

z-y has the same sign as

w

-w2.

Case

ii.

_{m _<}

y,z

<_

m2. Then

m

m and

m

m2.

(20)

0

<

a(,

z)=

(z

.)

+

(n

)

(

n)

(n

z)

(

+

)(z

).

Soz>_y.

Case

iii. y, z

<

_m.

Then

m

_m

and

m

m2.

(21)

0<

(,

)=

(n

)

+

.(.

)

(.

)

(n

z)

(

)(

z).

So

y z has thesame signas _{wl w2.}

First consider

_{w >_}

w2, then the ordering of y 7r and z 7r2 in the three intervals separated byml andm2 is shownin Figure 1.

We

willshow that ay r, y

>_

m2 and a z 7r2, m

_<

z

<

m2 cannot coexist.

Thiswill imply that the partition isnested.

Suppose

tothecontrary that such apair

(y,

z)

exists. Then

0

_(,z)=

_i

₊

x

x

x2 --Wl

]Xj--taXI-

w2

Ixj

xj

l(Z

)

+

:(

:)

(u

)

:(

z)

< w2(2z-

2m2) <

0,

an absurdity.

Next

consider

_{w _<}

w2; then the possible ordering of the

y’s

and

z’s

is asshown

inFigure 2.

FIG. 2. Theordering _ofy’s andz’swhenwl<_w2.

We

can showin a similarfashion that z

<

m and m

<

y

_<

m2 cannot coexist.

Thus thepartition isnested.

One

can also observe that ifWl w2, then the only order of the elements ofrl

andr2 satisfying all conditions inthe above proofis y Y z

z,

implying hence the following

corollary

(for

a differentproof, seealso

[9]).

COROLLARY

3.7.

_If

P

i=1

_x

where mi denotes the median

of

the set ri, then

every

optimal shape-partition is

consecutive.

4.

Some

concluding remarks.

Boros

and

Hammer

proved that if

_F(r)

-i=1

7ri

x,ye=

x

_Yl

for one-dimensional points or if

_E(r)

-x,ye

_(-

y)2

for d-dimensional points, then an optimal partition is nested.

We

generalized their

result bygivingabroadsufficient condition derivedfromanovelgeometric

argument.

We

applied this condition to obtain the d-dimensional version ofFisher’s clustering problem which he proposed but couldn’tprove.

Since the concept of nested partition is fairly

recent,

there are still many

unex-plored issues.

We

raisethe following questions.

(i)

Clearly,

a partition r

(h,..., p)

isnested ifand onlyifforany i andj,

(,

j)

isa nestedpartitionof the elementsin

r

t3

rg. Does

theexistenceof

a nested optimal 2-partition guarantee the existence of a nested optimal p-partitionfor general

p?

An

affirmative answer was recentlygiven by

Hwang,

Rothblum,

and

Yao

[II]

forone-dimensional points but the problem for

gen-eraldimension remainsopen.

(ii)

For

the subspace of consecutive partitions

(in

one

dimension),

there exist an

O(n2)-time

dynamic programming algorithm to find an optimal open-partition

[9]

and an

O(pn2)-time

algorithm to find an optimal p-partition.

From

(6),

there exists an

O(n2p-2)-time

algorithmto find anoptimal nested

p-partition.

Does

there exist a better dynamic programming algorithm for thesubspace of nested p-partitions?

Note

that sinceany subsetcanbe apart

in a nested open partition, for a general cost

function,

one must inspect at least 2n _{cost terms to find anoptimal nested open-partition.}

For

the one-dimensional case, it seems quite plausible to conjecture that there

al-ways existsaconsecutive optimalpartition.

However,

acounterexamplewasrecently

given by

Chang

and

Hwang

[4]

in which the optimal partition is nested but is not

consecutive.

REFERENCES

[1] E. R. BARNES, A. J. HOFFMAN,AND W. G. ROTHBLUM, Onoptimal partitions having disjoint

convexandconic hulls,Math. Programming,54 (1992), pp. 69-86.

[2] E. BOROS AND P. L. HAMMER, On clustering problems with connected optima in Euclidean spaces, DiscreteMath., 75(1989), pp. 81-88.

[3] A. K.CHAKRAVARTY,J.B.ORLIN,ANDU. I. ROTHBLUM, Apartitioningproblemwithadditive

objectivewithanapplication to optimal inventory groupingforjoint replenishment,Oper.

Res., 30(1982), pp. 1018-1022.

[4] G.J. CHANGANDF. K. HWANG,Optimality_ofconsecutiveand nested tree partitions, to appear.

[5]

n.

W. F. EDWARDSANDL. L. CAVALLI-SFORZA, A method_forclusteranalysis, Biometrics,21

(1965),pp. 362-375.

[6] W. D. FISHER, On groupingfor maximumhomogeneity, J. Amer. Statist. Assoc., 53 (1958),

pp. 789-798.

[7] J. C.GOWER, Somedistance properties oflatentrootsand vector methods used in multivariate analysis, Biometrika, 53(1966), pp. 325-338.

[8] M.J.HAGOODANDE.H.BERNERT, Componentindexesasabasis_forstratificationinsampling,

J. Amer.Statist. Assoc.,40 (1945), pp. 330-341.

[9] F. K. HWANG, Optimalpartitions, J. Optim. TheoryAppl., 34 (1981), pp. 1-10.

[10] F. Z. HWANG AND C. L. MALLOWS, The numbers _ofnestedpartitions andinner-consecutive

partitions,J.Combin. Theory Ser.A, 70(1995), pp. 323-333.

[11] F. K. HWANG, U. G. ROTHBLUM, ANDY. C.YAO, Localizing combinatorial properties _of

par-titions, DiscreteMath.,to appear.