Automata
⋆Fang Yu, Tevfik Bultan, and Oscar H. Ibarra
Department of Computer Science, University of California, Santa Barbara, CA, USA
{yuf, bultan, ibarra}@cs.ucsb.edu
Abstract. Verification of string manipulation operations is a crucial problem in computer security. In this paper, we present a new relational string verification technique based on multi-track automata. Our approach is capable of verifying properties that depend on relations among string variables. This enables us to prove that vulnerabilities that result from improper string manipulation do not ex-ist in a given program. Our main contributions in this paper can be summarized as follows: (1) We formally characterize the string verification problem as the reach-ability analysis of string systems and show decidreach-ability/undecidreach-ability results for several string analysis problems. (2) We develop a sound symbolic analysis tech-nique for string verification that over-approximates the reachable states of a given string system using multi-track automata and summarization. (3) We evaluate the presented techniques with respect to several string analysis benchmarks extracted from real web applications.
1
Introduction
The most important Web application vulnerabilities are due to inadequate manipulation of string variables [10]. In this paper we investigate the string verification problem: Given a program that manipulates strings, we want to verify assertions about string variables. For example, we may want to check that at a certain program point a string variable cannot contain a specific set of characters. This type of checks can be used to prevent SQL injection attacks where a malicious user includes special characters in the input string to inject unintended commands to the queries that the Web application constructs (using the input provided by the user) and sends to a backend database. As another example, we may want to check that at a certain program point a string variable should be prefix or suffix of another string variable. This type of checks can be used to prevent Malicious File Execution (MFE) attacks where Web application developers concatenate potentially hostile user input with file functions that lead to inclusion or execution of untrusted files by the Web server.
We formalize the string verification problem as reachability analysis of string
sys-tems (Section 2). After demonstrating that the string analysis problem is undecidable
in general, we present and implement a forward symbolic reachability analysis tech-nique that computes an over-approximation of the reachable states of a string system using widening and summarization (Section 4). We use multi-track deterministic finite
automata (DFAs) as a symbolic representation to encode the set of possible values that string variables can take at a given program point. Unlike prior string analysis tech-niques, our analysis is relational, i.e., it is able to keep track of the relationships among the string variables, improving the precision of the string analysis and enabling ver-ification of invariants such asX1 = X2 whereX1 andX2 are string variables. We develop the precise construction of multi-track DFAs for linear word equations, such asc1X1c2 = c′1X2c′2and show that non-linear word equations (such asX1= X2X3) cannot be characterized precisely as a multi-track DFA (Section 3). We propose a reg-ular approximation for non-linear equations and show how these constructions can be used to compute the post-condition of branch conditions and assignment statements that involve concatenation. We use summarization for inter-procedural analysis by generat-ing a multi-track automaton (transducer) characterizgenerat-ing the relationship between the input parameters and the return values of each procedure (Section 4). To be able to use procedure summaries during our reachability analysis we align multi-track automata so that normalized automata are closed under intersection. We implemented these al-gorithms using the MONA automata package [5] and analyzed several PHP programs demonstrating the effectiveness of our string analysis techniques (Section 5).
Related Work. The use of automata as a symbolic representation for verification has
been investigated in other contexts [4]. In this paper, we focus on verification of string manipulation operations, which is essential to detect and prevent crucial web vulnera-bilities. Due to its importance in security, string analysis has been widely studied. One influential approach has been grammar-based string analysis that statically computes an over-approximation of the values of string expressions in Java programs [6] which has also been used to check for various types of errors in Web applications [8, 9, 12]. In [9, 12], multi-track DFAs, known as transducers, are used to model replacement operations. There are also several recent string analysis tools that use symbolic string analysis based on DFA encodings [7, 11, 14, 15]. Some of them are based on symbolic execution and use a DFA representation to model and verify the string manipulation operations in Java programs [7, 11]. In our earlier work, we have used a DFA based symbolic reachability analysis to verify the correctness of string sanitization operations in PHP programs [13–15]. Unlike the approach we proposed in this paper, all of the re-sults mentioned above use single track DFA and encode the reachable configurations of each string variable separately. Our multi-track automata encoding not only improves the precision of the string analysis but also enables verification of properties that cannot be verified with the previous approaches.
We have also investigated the boundary of decidability for the string verification problem. Bjørner et al. [2] show the undecidability result with replacement operation. In this paper we consider only concatenation and show that string verification problem is undecidable even for deterministic string systems with only three unary string variables and non-deterministic string systems with only two string variables if the comparison of two variables are allowed.
2
String Systems
We define the syntax of string systems in Figure 1. We only consider string variables and hence variable declarations need not specify a type. All statements are labeled. We
prog ::= decl∗func∗ decl ::=declid+;
func ::= id (id∗)begindecl∗lstmt+ end lstmt ::= l:stmt
stmt ::= seqstmt|ifexpthen gotol;|gotoL; where L is a set of labels
|inputid;|outputexp;|assertexp; seqstmt::=id := sexp;| id :=callid (sexp∗); exp ::= bexp| exp ∧ exp | ¬ exp
bexp ::= atom = sexp
sexp ::= sexp.atom| atom | suffix(id) | prefix(id) atom ::= id| c, where c is a string constant
Fig. 1. The syntax of string systems
only consider one string operation (concatenation) in our formal model; however, our symbolic string analysis techniques can be extended to handle complex string opera-tions (such as replacement [14]). Function calls use call-by-value parameter passing. We allow goto statements to be non-deterministic (if a goto statement has multiple tar-get labels, then one of them is chosen non-deterministically). If a string system contains a non-deterministic goto statement it is called a non-deterministic string system, other-wise, it is called a deterministic string system.
There are several attributes we can use to classify string systems such as deter-ministic (D) or non-deterministic (N ) string systems, the number of variables in the string systems, and the alphabet used by the string variables, e.g., unary (U ), binary (B), or arbitrary (K) alphabet. Finally, we can restrict the set of string expressions that can be used in the assignment and conditional branch instructions. As an instance, N B(X1, X2)XXi1:=X=X2icdenotes a non-deterministic string system with a binary alphabet
and two string variables (X1 andX2) where variables can only concatenate constant strings from the right and compared to each other. We usea to denote a single symbol, andc, d to denote constant strings. c = prefix (Xi) evaluates to true if c is a prefix of Xi, andc = suffix (Xi) evaluates to true if c is a suffix of Xi. We define the reachability
problem for string systems is the problem of deciding, given a string system and a
con-figuration (i.e., the instruction label and the values of the variables), whether at some point during a computation, the configuration will be reached. We have the following results:
Theorem 1. The reachability problem for:
1. N B(X1, X2)XXi1:=X=X2icis undecidable,
2. DU (X1, X2, X3)XXi1:=X=X3i,Xc 2=X3is undecidable,
3. DU (X1, X2, X3, X4)XXi1:=X=X3i,Xc 2=X4is undecidable,
4. N U (X1, X2)XXi1:=X=X2i,c=Xc i,c=prefix (Xi),c=suffix(Xi)is decidable,
5. N K(X1, X2, . . . , Xk)c=XXi:=dXi,c=prefix (Xic i),c=suffix (Xi)is decidable, and
6. DK(X1, X2, , . . . , Xk)
Xi:=Xia,Xi:=aXi
X1=X2,c=Xi,c=prefix (Xi),c=suffix(Xi)is decidable.
Theorem 1 demonstrates the complexity boundaries for verification of string sys-tems. Theorem 1.1, 1.2 and 1.3 show that the string verification problem can be
unde-cidable even when we restrict a non-deterministic string system to two binary variables, or a deterministic string system to three unary variables or four unary variables with specific comparisons. Theorem 1.4 shows that the three variables in Theorem 1.2 are necessary in the sense that when there are only two variables, reachability is decid-able, even when the string system is nondeterministic. Theorem 1.5 and 1.6, on the other hand, demonstrate that there are non-trivial string verification problems that are decidable. Since the general string verification problem is undecidable, it is necessary to develop conservative approximation techniques for verification of string systems. In this paper we propose a sound string verification approach based on symbolic reachabil-ity analysis with conservative approximations where multi-track automata are used as a symbolic representation. Some examples of string systems that can be verified using our analysis are given in [16].
3
Regular Approximation of Word Equations
Our string analysis is based on the following observations: (1) The transitions and the configurations of a string system can be symbolically represented using word equations with existential quantification, (2) word equations can be represented/approximated us-ing multi-track DFAs, which are closed under intersection, union, complement, and projection, and (3) the operations required during reachability analysis (such as equiv-alence checking) can be computed on DFAs.
Multi-track DFAs A multi-track DFA is a DFA but over the alphabet that consists of
many tracks. Ann-track alphabet is defined as (Σ ∪ {λ})n, whereλ 6∈ Σ is a special symbol for padding. We usew[i] (1 ≤ i ≤ n) to denote the ithtrack ofw ∈ (Σ ∪{λ})n. An aligned multi-track DFA is a multi-track DFA where all tracks are left justified (i.e., λ’s are right justified). That is, if w is accepted by an aligned n-track DFA M , then for1 ≤ i ≤ n, w[i] ∈ Σ∗λ∗. We also usew[i] ∈ Σˆ ∗ to denote the longestλ-free prefix ofw[i]. It is clear that aligned multi-track DFA languages are closed under inter-section, union, and homomorphism. LetMu be the alignedn-track DFA that accepts the (aligned) universe, i.e.,{w | ∀i.w[i] ∈ Σ∗λ∗}. The complement of the language accepted by an alignedn-track DFA M is defined by complement modulo alignment, i.e., the intersection of the complement ofL(M ) with L(Mu). For the following de-scriptions, a multi-track DFA is an aligned multi-track DFA unless we explicitly state otherwise.
Word Equations A word equation is an equality relation of two words that concatenate
variables from a finite setX and words from a finite set of constants C. The general form of word equations is defined asv1. . . vn = v1′ . . . v′m, where∀i, vi, v′i ∈ X ∪ C. The following theorem identifies the basic forms of word equations. For example, a word equationf : X1 = X2dX3X4 is equivalent to ∃Xk1, Xk2.X1 = X2Xk1 ∧ Xk1 =
dXk2∧ Xk2= X3X4.
Theorem 2. Word equations and Boolean combinations (¬, ∧ and ∨) of these
equa-tions can be expressed using equaequa-tions of the formX1= X2c, X1= cX2,c = X1X2, X1= X2X3, Boolean combinations of such equations and existential quantification.
Letf be a word equation over X= {X1, X2, . . . , Xn} and f [c/X] denote a new equation where X is replaced with c for all X that appears in f . We say that an n-track DFAM under-approximates f if for all w ∈ L(M ), f [ ˆw[1]/X1, . . . , ˆw[n]/Xn] holds. We say that ann-track DFA M over-approximates f if for any s1, . . . , sn∈ Σ∗ wheref [s1/X1, . . . , sn/Xn] holds, there exists w ∈ L(M ) such that for all 1 ≤ i ≤ n, ˆw[i] = si. We callM precise with respect to f if M both under-approximates and over-approximatesf .
Definition 1. A word equationf is regularly expressible if and only if there exists a
multi-track DFAM such that M is precise with respect to f .
Theorem 3. 1. X1 = X2c, X1= cX2, andc = X1X2are regularly expressible, as
well as their Boolean combinations.
2. X1= cX2is regularly expressible but the correspondingM has exponential
num-ber of states in the length ofc.
3. X1= X2X3is not regularly expressible.
We are able to compute multi-track DFAs that are precise with respect to word equa-tions:X1 = X2c, X1= cX2, andc = X1X2. SinceX1= X2X3is not regularly ex-pressible, below, we describe how to compute DFAs that approximate such non-linear word equations. Using the DFA constructions for these four basic forms we can con-struct multi-track DFAs for all word equations and their Boolean combinations (if the word equation contains a non-linear term then the constructed DFA will approximate the equation, otherwise it will be precise). The Boolean operations conjunction, dis-junction and negation can be handled with intersection, union, and complement mod-ulo alignment of the multi-track DFAs, respectively. Existential quantification on the other hand, can be handled using homomorphism, where given a word equationf and a multi-track automatonM such that M is precise with respect to f , then the multi-track automaton M ⇂i is precise with respect to ∃Xi.f where M ⇂i denotes the result of erasing theithtrack (by homomorphism) ofM .
Construction ofX1 = X2X3 Since Theorem 3 shows thatX1 = X2X3 is not reg-ularly expressible, it is necessary to construct a conservative (over or under) approx-imation of X1 = X2X3. We first propose an over approximation construction for X1 = X2X3. LetM1 = hQ1, Σ, δ1, I1, F1i, M2 = hQ2, Σ, δ2, I2, F2i, and M3 = hQ3, Σ, δ3, I3, F3i accept values of X1, X2, and X3, respectively. M = hQ, (Σ ∪ {λ})3, δ, I, F i is constructed as follows.
– Q ⊆ Q1× Q2× Q3× Q3, – I = (I1, I2, I3, I3),
– ∀a, b ∈ Σ, δ((r, p, s, s′), (a, a, b)) = (δ1(r, a), δ2(p, a), δ3(s, b), s′),
– ∀a, b ∈ Σ, p ∈ F2, s 6∈ F3, δ((r, p, s, s′), (a, λ, b)) = (δ1(r, a), p, δ3(s, b), δ3(s′, a)), – ∀a ∈ Σ, p ∈ F2, s ∈ F3, δ((r, p, s, s′), (a, λ, λ)) = (δ1(r, a), p, s, δ3(s′, a)), – ∀a ∈ Σ, p 6∈ F2, s ∈ F3, δ((r, p, s, s′), (a, a, λ)) = (δ1(r, a), δ2(p, a), s, s′), – F = {(r, p, s, s′) | r ∈ F
The intuition is as follows:M traces M1,M2andM3on the first, second and third tracks, respectively, and makes sure that the first and second tracks match each other. After reaching an accepting state in M2, M enforces the second track to be λ and starts to traceM3on the first track to ensure the rest (suffix) is accepted byM3.|Q| is O(|Q1| × |Q2| × |Q3| + |Q1| × |Q3| × |Q3|). For all w ∈ L(M ), the following hold:
– w[1] ∈ L(Mˆ 1), ˆw[2] ∈ L(M2), ˆw[3] ∈ L(M3), – w[1] = ˆˆ w[2]w′andw′∈ L(M3),
Note that w′ may not be equal to w[3], i.e., there exists w ∈ L(M ), ˆˆ w[1] 6= ˆ
w[2] ˆw[3], and hence M is not precise with respect to X1= X2X3. On the other hand, for anyw such that ˆw[1] = ˆw[2] ˆw[3], we have w ∈ L(M ), hence M is a regular
over-approximation ofX1= X2X3.
Below, we describe how to construct a regular under-approximation ofX1= X2X3 (which is necessary for conservative approximation of its complement set). We use the idea that ifL(M2) is a finite set language, one can construct the DFA M that satisfies X1 = X2X3 by explicitly taking the union of the construction of X1 = cX3 for all c ∈ L(M2). If L(M2) is an infinite set language, we construct a regular under-approximation ofX1 = X2X3 by considering a (finite) subset ofL(M2) where the length is bounded. Formally speaking, for eachk ≥ 0 we can construct Mk, so that w ∈ L(Mk), ˆw[1] = ˆw[2] ˆw[3], ˆw[1] ∈ L(M1), ˆw[3] ∈ L(M3), ˆw[2] ∈ L(M2) and | ˆw[2]| ≤ k. It follows that Mk is a regular under-approximation of X1 = X2X3. If L(M2) is a finite set language, there exists k (the length of the longest accepted word) whereL(Mk) is precise with respect to X1= X2X3. IfL(M2) is an infinite set language, there does not exist suchk so that L(Mk) is precise with respect to X1 = X2X3, as we have proven non-regularity ofX1= X2X3.
4
Symbolic Reachability Analysis
Our symbolic reachability analysis involves two main steps: forward fixpoint computa-tion and summarizacomputa-tion.
Forward Fixpoint Computation The first phase of our analysis is a standard forward
fixpoint computation on multi-track DFAs. Each program point is associated with a single multi-track DFA, where each track is associated with a single string variable X ∈ X. We use M [l] to denote the multi-track automaton at the program label l. The forward fixpoint computation algorithm is a standard work-queue algorithm. Initially, for all labelsl, L(M [l]) = ∅. We iteratively compute the post-images of the statements and join the results to the corresponding automata. For astmt in the form: X:= sexp, the post-image is computed as:
POST(M, stmt) ≡ (∃X.M ∩CONSTRUCT(X′ = sexp, +))[X/X′].
CONSTRUCT(exp, b) returns the DFA that accepts a regular approximation of exp, where b ∈ {+, −} indicates the direction (over or under, respectively) of approximation if needed. During the construction, we recursively push the negations (¬) (and flip the di-rection) inside to the basic expressions (bexp), and use the corresponding construction
f(X) begin 1: goto 2, 3; 2: X: = call f(X.a); 3: return X; end
Fig. 2. A function and its summary DFA
of multi-track DFAs discussed in the previous section. We use function summaries to handle function calls. Each functionf is summarized as a finite state transducer, de-noted asMf, which captures the relations among input variables (parameters), denoted asXp, and return values. The return values are tracked in the output track, denoted as Xo. We discuss the generation of the transducerMfbelow. For astmt in the form X:=
callf (e1, . . . , en), the post-image is computed as:
POST(M, stmt) ≡ (∃X, Xp1, . . . Xpn.M ∩ MI ∩ Mf)[X/Xo],
whereMI = CONSTRUCT( V
iXpi = ei,+). The process terminates when we reach
a fixpoint. To accelerate the fixpoint computation, we extend our automata widening operator [14], denoted as∇, to multi-track automata. We identify equivalence classes according to specific equivalence conditions and merge states in the same equivalence class [1, 3]. The following lemma shows that the equality relations among tracks are preserved while widening multi-track automata.
Lemma 1. ifL(M ) ⊆ L(x = y) and L(M′) ⊆ L(x = y), L(M ∇M′) ⊆ L(x = y).
Summarization We compute procedure summaries in order to handle procedure calls.
We assume parameter-passing with call-by-value semantics and we are able to handle recursion. Each functionf is summarized as a multi-track DFA, denoted as Mf, that captures the relation among its input variables and return values.
Consider the recursive functionf shown in Figure 2 with one parameter. f non-deterministically returns its input (goto 3) or makes a self call (goto 2) by concatenating its input and a constanta. The generated summary for this function is also shown in Figure 2.Mf is a2-track DFA, where the first track is associated with its parameter Xp1, and the second track is associated with Xo representing the return values. The
edge(Σ, Σ) represents a set of identity edges. In other words, δ(q, (Σ, Σ)) = q′means ∀a ∈ Σ, δ(q, (a, a)) = q′. The summary DFAMfprecisely captures the relationXo= Xp1.a∗between the input variable and the return values.
During the summarization phase, (possibly recursive) functions are summarized as unaligned multi-track DFAs that specify the relations among their inputs and return values. We first build (possibly cyclic) dependency graphs to specify how the inputs flow to the return values. Each node in the dependency graph is associated with an unaligned multi-track DFA that traces the relation among inputs and the value of that node. An unaligned multi-track DFA is a multi-track DFA whereλs might not be right justified. Return values of a function are represented with an auxiliary output track. Given a functionf with n parameters, Mfis an unaligned(n + 1)-track DFA, where n
tracks represent then input parameters and one track Xois the output track representing the return values. We iteratively compute post images of reachable relations and join the results until we reach a fixpoint. Upon termination, the summary is the union of the unaligned DFAs associated with the return nodes. To compose these summaries at the call site, we also propose an alignment algorithm to align (so thatλ’s are right justified) an unaligned multi-track DFA.
Once the summary DFAMf has been computed, it is not necessary to reanalyze the body of f . To compute the post-image of a call to f we intersect the values of input parameters withMfand use existential quantification to obtain the return values. LetM be a one-track DFA associated with X where L(M ) = {b}.POST(M , X :=
callf (X)) returns M′whereL(M′) = ba∗for the example function shown above. As another example, letM be a 2-track DFA associated with X, Y that is precise with respect to X = Y . ThenPOST(M , X := callf (X)) returns M′ which is precise with respect toX = Y.a∗precisely capturing the relation betweenX and Y after the execution of the function call. As discussed above,M′is computed by(∃X, Xp
1.M ∩
MI∩ Mf)[X/Xo], where L(MI) =CONSTRUCT(Xp1= X, +).
5
Experiments
We evaluate our approach against three kinds of benchmarks: 1) Basic benchmarks, 2) XSS/SQLI benchmarks, and 3) MFE benchmarks. These benchmarks represent typi-cal string manipulating programs along with string properties that address severe web vulnerabilities.
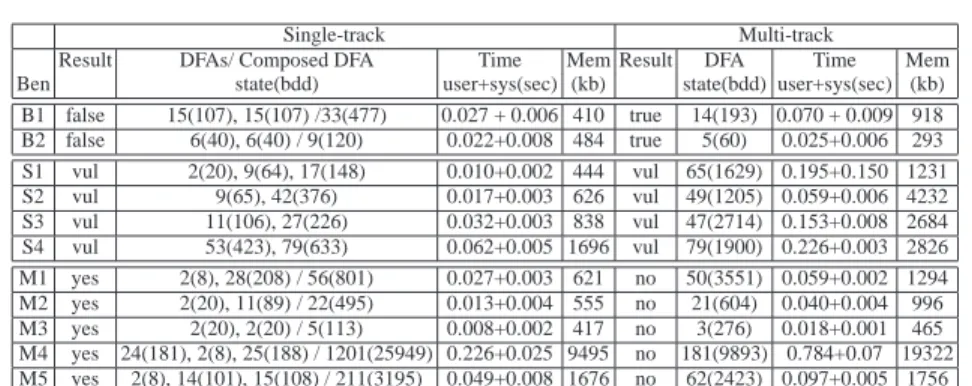
In the first set, we demonstrate that our approach can prove implicit equality prop-erties of string systems. We wrote two small programs. CheckBranch (B1) has if branch (X1= X2) and else branch (X16= X2). In the else branch, we assign a constant string c to X1and then assign the same constant string toX2. We check at the merge point whetherX1= X2. In CheckLoop (B2) we assign variablesX1andX2the same con-stant string at the beginning, and iteratively append another concon-stant string to both in an infinite loop. We check whetherX1= X2at the loop exit. LetM accept the values ofX1andX2upon termination. The equality assertion holds whenL(M ) ⊆ L(Ma), whereMaisCONSTRUCT(X1 = X2,−). We use ”−” to construct (under approxima-tion) automata for assertions to ensure the soundness of our analysis. Using multi-track DFAs, we prove the equality property (result “true”) whereas we are unable to prove it using single-track DFAs (result “false”) as shown in Table 1 (B1 and B2). Though these benchmark examples are simple, to the best of our knowledge, there are no other string analysis tools that can prove equality properties in these benchmarks.
In the second set, we check existence of Cross-Site Scripting (XSS) and SQL Injec-tion (SQLI) vulnerabilities in Web applicaInjec-tions with known vulnerabilities. We check whether at a specific program point, a sensitive function may take an attack string as its input. If so, we say that the program is vulnerable with respect to the given attack pattern. To identify XSS/SQLI attacks, we check intersection emptiness against all pos-sible input values that reach a sensitive function at a given program point and the attack strings specified as a regular language. Though one can check such vulnerabilities using single-track DFAs [14], using multi-track automata, we can precisely interpret branch
conditions, such as$www=$url, that cannot be precisely expressed using single-track automata, and obtain more accurate characterization of inputs of the sensitive functions. For the vulnerabilities identified in these benchmarks (S1 to S4), we did not observe false alarms that result from the approximation of the branch conditions.
The last set of benchmarks show that the precision that is obtained using multi-track DFAs can help us in removing false alarms generated by single-multi-track automata based string analysis. These benchmarks represent malicious file execution (MFE) at-tacks. Such vulnerabilities are caused because developers directly use or concatenate potentially hostile input with file or stream functions, or improperly trust input files. We systematically searched web applications for program points that execute file func-tions, such asincludeandfopen, whose arguments may be influenced by external inputs. At these program points, we check whether the retrieved files and the external inputs are consistent with what the developers intend. We manually generate a multi-track DFAMvulthat accepts a set of possible violations for each benchmark, and apply our analysis on the sliced program segments. Upon termination, we report that the file function is vulnerable ifL(M ) ∩ L(Mvul) 6= ∅. M is the composed DFA of the listed single-track DFAs in the single-track analysis. As shown in Table 1 (M1 to M5), using multi-track DFAs we are able to verify that MFE vulnerabilities do not exist whereas string analysis using single-track DFAs raises false alarms for all these examples.
We have shown that multi-track DFAs can handle problems that cannot be handled by multiple single-track DFAs, but at the same time, they use more time and memory. For these benchmarks, the cost seems affordable. As shown in Table 1, in all tests, the multi-track DFAs that we computed (even for the composed ones) are smaller than the product of the corresponding single-track DFAs. One advantage of our implementation is symbolic DFA representation (provided by the MONA DFA library [5]), in which transition relations of the DFA are represented as Multi-terminal Binary Decision Dia-grams (MBDDs). Using the symbolic DFA representation we avoid the potential expo-nential blow-up that can be caused by the product alphabet. However, in the worst case the size of the MBDD can still be exponential in the number of tracks.
6
Conclusion
In this paper, we presented a formal characterization of the string verification problem, investigated the decidability boundary for string systems, and presented a novel veri-fication technique for string systems. Our veriveri-fication technique is based on forward symbolic reachability analysis with multi-track automata, conservative approximations of word equations and summarization. We demonstrated the effectiveness of our ap-proach on several benchmarks.
References
1. C. Bartzis and T. Bultan. Widening arithmetic automata. In CAV, pages 321–333, 2004. 2. N. Bjørner, N. Tillmann, and A. Voronkov. Path feasibility analysis for string-manipulating
Single-track Multi-track
Result DFAs/ Composed DFA Time Mem Result DFA Time Mem Ben state(bdd) user+sys(sec) (kb) state(bdd) user+sys(sec) (kb)
B1 false 15(107), 15(107) /33(477) 0.027 + 0.006 410 true 14(193) 0.070 + 0.009 918 B2 false 6(40), 6(40) / 9(120) 0.022+0.008 484 true 5(60) 0.025+0.006 293 S1 vul 2(20), 9(64), 17(148) 0.010+0.002 444 vul 65(1629) 0.195+0.150 1231 S2 vul 9(65), 42(376) 0.017+0.003 626 vul 49(1205) 0.059+0.006 4232 S3 vul 11(106), 27(226) 0.032+0.003 838 vul 47(2714) 0.153+0.008 2684 S4 vul 53(423), 79(633) 0.062+0.005 1696 vul 79(1900) 0.226+0.003 2826 M1 yes 2(8), 28(208) / 56(801) 0.027+0.003 621 no 50(3551) 0.059+0.002 1294 M2 yes 2(20), 11(89) / 22(495) 0.013+0.004 555 no 21(604) 0.040+0.004 996 M3 yes 2(20), 2(20) / 5(113) 0.008+0.002 417 no 3(276) 0.018+0.001 465 M4 yes 24(181), 2(8), 25(188) / 1201(25949) 0.226+0.025 9495 no 181(9893) 0.784+0.07 19322 M5 yes 2(8), 14(101), 15(108) / 211(3195) 0.049+0.008 1676 no 62(2423) 0.097+0.005 1756
Table 1. Experimental results. DFA(s): the minimized DFA(s) associated with the
checked program point. state: number of states. bdd: number of bdd nodes. Bench-mark: Application, script (line number). S1: MyEasyMarket-4.1, trans.php (218). S2: PBLguestbook-1.32, pblguestbook.php(1210), S3:Aphpkb-0.71, saa.php(87), and S4: BloggIT 1.0, admin.php (23). M1: PBLguestbook-1.32, pblguestbook.php(536). M2: MyEasyMarket-4.1, prod.php (94). M3: MyEasyMarket-4.1, prod.php (189). M4: php-fusion-6.01, db backup.php (111). M5: php-php-fusion-6.01, forums prune.php (28).
3. A. Bouajjani, P. Habermehl, and T. Vojnar. Abstract regular model checking. In CAV, pages 372–386, 2004.
4. A. Bouajjani, B. Jonsson, M. Nilsson, and T. Touili. Regular model checking. In CAV, pages 403–418, 2000.
5. BRICS. The MONA project.http://www.brics.dk/mona/.
6. A. S. Christensen, A. Møller, and M. I. Schwartzbach. Precise analysis of string expressions. In SAS, pages 1–18, 2003.
7. X. Fu, X. Lu, B. Peltsverger, S. Chen, K. Qian, and L. Tao. A static analysis framework for detecting sql injection vulnerabilities. In COMPSAC, pages 87–96, 2007.
8. C. Gould, Z. Su, and P. Devanbu. Static checking of dynamically generated queries in database applications. In ICSE, pages 645–654, 2004.
9. Y. Minamide. Static approximation of dynamically generated web pages. In WWW, pages 432–441, 2005.
10. Open Web Application Security Project (OWASP). Top ten project. http://www. owasp.org/, May 2007.
11. D. Shannon, S. Hajra, A. Lee, D. Zhan, and S. Khurshid. Abstracting symbolic execution with string analysis. In TAICPART-MUTATION, pages 13–22, DC, USA, 2007.
12. G. Wassermann and Z. Su. Static detection of cross-site scripting vulnerabilities. In ICSE, pages 171–180, 2008.
13. F. Yu, M. Alkhalaf, and T. Bultan. Stranger: An automata-based string analysis tool for php. In TACAS, pages 154–157, 2010.
14. F. Yu, T. Bultan, M. Cova, and O. H. Ibarra. Symbolic string verification: An automata-based approach. In SPIN, pages 306–324, 2008.
15. F. Yu, T. Bultan, and O. H. Ibarra. Symbolic string verification: Combining string analysis and size analysis. In TACAS, pages 322–336, 2009.
16. F. Yu, T. Bultan, and O. H. Ibarra. Verification of string manipulating programs using multi-track automata. Technical Report 2009-14, Computer Science Department, University of California, Santa Barbara, August 2009.