EFFECTS OF AN IMPURITY ON THE CONDUCTANCE AND THERMOPOWER OF A SADDLE-POINT-POTENTIAL QUANTUM POINT-CONTACT

EfFects

of

an impurity

on

the

conductance

and

thermopovver

of

a

saddle-point-potential

quantum

point

contact

C.

S.

Chu

Institute ofPhysics, National Chiao Tung University, Hsinchu 80050, Taiwan, Republic of China and Department ofElectrophysics, National Chiao Tung University, Hsinchu 80050, Taiwan, Republic Of China

Ming-Hui Chou

Department _ofElectrophysics, National Chiao Tung University, Hsinchu $0050, Taiwan, Republic Of China (Received 18May 1994;revised manuscript received 11July 1994)

The conductance Gand the thermopower

S

of asaddle-point-potential quantum point contact inthe presence of ab-potential impurity are calculated. For the case when an attractive impurity is located inside the quantum point contact, there are dips, peaks, and kinks in G. These structures can be found below and near the band bottom ofsome transverse subbands, respectively. The peaks in Ggive rise to double peaks in

S

and the dips in Ggive rise toashift inthe peak positions of

S,

towards a smaller chemical potential value. In addition, a broad dip in G is found to give

rise to negative thermopower in regions between the peaks of

S.

For the case when an attractive impurity is located in the classical forbidden region for the electrons, we 6nd in G the structures that correspond to resonance tunneling and resonance reaection. The corresponding

S

is found to

show large and negative spikes. Our study shows that structures not so transparent in Gmanifest unequivocally in

S,

rendering

S

avery informative physical quantity to be measured.

I.

INTRODUCTION

The quantum transport in quantum point contacts

(QPC)

has received

a

lot

of

attention, both theoreticali

and experimental, in recent years. These systems are

electrostatically defined narrow constrictions connecting two high-mobility two-dimensional electron gas. The

width W of

a QPC

is small

_(W

—

Ap) enough to ex-hibit quantization efFects, and the corresponding length

L is short enough

(L

«

l, the mean free path) to

make possible the study

of

quantum ballistic transport. In the absence

of

defects and impurities, it is found experimentally ' _{that the conductance G is quantized,}

in units of 2e /h. However, this quantization in G is vulnerable

to

the presence

of

even one impurity in

the constriction, according

to

recent theoretical and experimental ' 2 _{studies. More specifically, theoretical}

studies show that the conductance G can exhibit dip

structures

just

below the threshold

of

a transverse sub-band both in the case

of a

weak attractive short-range

scatterer present in the constriction and in the case

of

attractive long-range scatterers separated from the QPC

by

a

spacer layer. These dip structures in Gare observed in recent experiments. ' _{Thus dip structures in G can}

be used

to

distinguish an attractive scatterer from a re-pulsive scatterer but cannot be used

to

tell an in-plane

scatterer from an off-plane scatterer.

Besides the conductance

G,

thermopower

S

is another physical property of QPC systems in which quantization efFectmanifests unequivocally.

It

was first shown

theoret-ically by Streda that in

a

narrow constriction the ther-mopower

S

exhibits peak structures. His calculation in-volved an ideal narrow constriction

of

which the

longitu-dinal transmission coefficient through the constriction is

a

step function

of

energy, and he concluded that the peak values of

8

are quantized, given by (ks/e) ln2/(i

+

1/2).

These peaks occur when the Fermi energy p equals the

threshold of the

_(i

₊

l)th

transverse subband, starting

from

i

=

1.

Later theoretical studies ' _{show similar}

os-cillations in

S

except that these peak values are modified when the longitudinal transmission coefficient through

the constriction is no longer

a

step function

of

energy, which corresponds

to

the case when the width

of

the

con-striction is changing, either adiabatically or ina

saddle-point-potential

QPC.

is The aforementioned quantum os-cillations are demonstrated in recent experiments.

These peak features render

S

potentially very sensitive to the configuration

of

the

QPC

systems, especially when _p is in the vicinity

of

a

transverse subband threshold.

%e

expect that both G and

S

can be used

to

explore the configuration of

QPC

systems and that they play com-plementary roles in such regard. Hence we consider, in this paper, the effect ofimpurity on

8

in QPC systems.

Our purposes in this work are

to

study and

to

compare

the efFect

of

impurity on the thermopower

S

and the

con-ductance G in

QPC

systems. The QPC is modeled by

a

saddle-point potential which is simple and quite realistic,

giving no sharp corners and containing the essential fea-tures ofthe electrostatically induced QPC bottleneck. The impurity is taken

to

be short range which, in the

case of

a

saddle-point potential

QPC,

is appropriately described by

a

b potential. The efFect

of

the impurity

location on G and

S

is studied by considering the im-purity

to

be located in the central cross section of the

QPC.

Similar study has been carried out by Levinson et al. for Gusing

a

confinement-potential Green's

El'l'I:CTS OFAN IMPURITY ON THE CONDUCTANCE

AND.

.

.

14213

tion method. In this work, we propose

to

apply another method,

a

mode-matching method, to the

QPC

systems.

This method can be easily extended

to

other situations such as applying an external magnetic field

to

the QPC

systems. In addition, new insights are obtained when our analysis includes both the cases for an impurity present inside and outside the

QPC.

An impurity is outside the

QPC

when it is located in the classical forbidden region for the electrons.

For an attractive impurity located inside the QPC, our results show dips and peaks in Gwhich occur below and near the threshold

of

some transverse subbands, respec-tively. Sometimes, when _p is

at

the threshold

of

a

trans-verse subband, the peaks are so small that they appear

more like kinks in

G.

In addition, there is

a

resonance tunneling peak in G in the pinchoK region. The kinks in

G

give rise

to

double peaks in

S

and the dips in G give rise

to

a shift in the peak positions

of

S,

towards

a

smaller chemical potential value. A broad dip in G is found

to

give negative thermopower, in regions between

the peaks

of

S.

The resonance tunneling in the pinchofI' region results in

S

a

large peak followed by a large neg-ative dip. Our study shows

that,

near the threshold

of

a

subband,

S

exhibits

a

relatively large double peak struc-ture even inthe case when Ghas only

a

small kink. This corroborates our intuition that

S

issensitive

to

the QPC con6guration near the threshold

of

a

transverse subband.

For

a

not-too-weak attractive impurity located outaide

the

QPC,

our results show both additional peak and dip which corresponds

to

resonance tunneling and resonance refiection occurring outside the

QPC.

In such

a

regime,

the thermopower

S

of

the

QPC

deviates far &om that

of

its impurity-free counterparts, exhibiting

a

large neg-ative dip followed by

a

large positive spike. On the other

hand,

if

the impurity outside the constriction is strongly

attractive, the above resonant features

of

S

disappear. In

Sec.

II

we develop

a

mode-matching method for the electron scattering in the saddle-point potential

QPC.

The thermopower is, within the Landauer multichannel

approach, ' ' _related

_to

_{the current transmission} coef-6cients. In

Sec.

III

we present some numerical examples

to

illustrate that

S

is very sensitive

to

the con6guration of the

QPC

in the threshold region of a transverse

sub-band. Finally,

Sec. IV

presents

a

conclusion.

transmission coefficient. There is transmission coefficient

~t„„~

(Ref. 21)where

t„„

isthe coefficient appearing in

the scattered wave function and is associated with the nth transmitted

state.

There is also

a

current

trans-mission coefficient

T

which is the ratio between the transmitted current in the nth channel and the incident current in the nth channel. These two transmission

co-efBcients are difFerent when n is difI'erent &om

n'.

So far, this difl'erence has not been emphasized enough and many papers use the term trunsmission coeQcient when they actually are referring

to

current transmission

coef-6cient.

In the following, the total transmitted current is ex-pressed in terms

of

the current transmission coefficient

T„„.

is'2o _{We take the left (right) reservoir}

_to

_have chem-ical _{potential p}

_(p

—

b,y,_{) and} temperature

T

+

b,

T (T).

The total transmitted current, from the left

to

the right reservoir, is given by

J

=

—

—

_dE

_[n~

_(E,

_p,

_T

₊

b,

T)

h

n(E,

IJ,

——

b,_p,

T)]

)

T„„.

_,

n,n'

where

n~(E,

p,

T)

is the Fermi-Dirac distribution

func-tion and

—

e isthe charge ofan electron. In choosing the lower limit

of

the energy integration, we have assumed

that

_p

—

E

&&

k~T,

where

E

is the lowest electron

energy in the reservoir.

Within the linear response regime, the conductance G isobtained &om

_{Eq. (1)}

by taking

AT

=

0, and we have20

2 2 oo

dE

~-

I)

h _g

dE)

where Ap

=

—

eLV.

Similarly, within the linear response regime, the ther-mopower

S

is obtained &om

Eq.

(1)

by taking

J

=

0,

such that20 d

E—

dE

—

dE

i

)

T„„

)

kgT

)

T

dE)

II.

IMPURITY

SCATTERING

IN

SADDLE-POINT POTENTIAL

In this section, we consider

a

saddle-point potential

QPC

which connects two particle and energy reservoirs.

The quant»m transport phenomena are related

to

the

quantum mechanical scattering inthe

QPC.

is' 0_Incident

electron in the nth transverse subband

of

the left reser-voir isscattered inthe

QPC

and gives rise to transmitted

currents in allthe propagating channels inthe right

reser-voir. Westress that in the case

of

multichannel quantum

scattering, we should be more speci6c when referring

to

The current transmission coefficients

T „t

depend onthe

configuration of the

QPC.

In the following, we consider

a

saddle-point potential V,z(2:,

y),

given by

V.p(x,y)

=

U

—

U

x

+ U„y,

(4)

V'-&(*

y)

=

V-

~(*)

~(y

—

y-).

where the electrostatic potential

at

the saddle U istaken

to

be zero. An impurity located in the central cross

sec-tion

of

the saddle-point potential, with the impurity po-tential _{V; ~}given by

assin that the numerical results

ob-tained using

a

b potential V; _{p(z y) as iii q} aie

essentially

t

esame as usi

'

l

f

V as long as the potential range is s or e

tentia or zmp,

than all other relevant length scales. n suc

ca

constant V in

Eq. (5)

is given by

function

V

=

V; p

xydxdy.

E'

=

/i2k2/2m and the

Choosing the energy unit

E

'

—

1&~ where kg is

a

typical Fermi wave length unit

a

=

₍

~,

w

~ ~ ~

v ' the two-dimensional Schrodinger

vector

of

the reservoir, e wo- ' equation becomes

[-V

—

(u

z

+(u„y

+u

b(z)8(y

—

_{y )}

4'(z,

_y)

=E~(z

y)

(6)

re (u

=

/2mU

//iks2, ,

~„=

/2mU„/hk~~, and e

Here,

~

=

m

Cischaracterized V//i~. The con6guration of the

/PC

is

2m ('

.

e

su

u

e,

andy.

In

b the dimensionless parameters

u,

~~, particular, the _{ratio (u„/u~)}

=

_IW,

The unperturbed transverse motion is quantize in o ~2n

+

1~&u and normalized wave

subbands, with energy ~ n

where

H

is the Hermite polynomial and n starts kom zero.

'on

_z

_{along the}

_/PC

The unperturbed wave function

x

or ' h th subband satisfies the equation for an electron in

t

e n su

a

+

(d

z

+

6~ %jan~(z)

=

0, Bx

4

= E

—(2n+

l)~

is the energy for the motion

where

e„=

—

n

along

z

u'iree

t

ion.n. The dependence of

„z

there are two

g„(z)'s,

implied. For every value

of

e„,

there are wo given by22

(a}

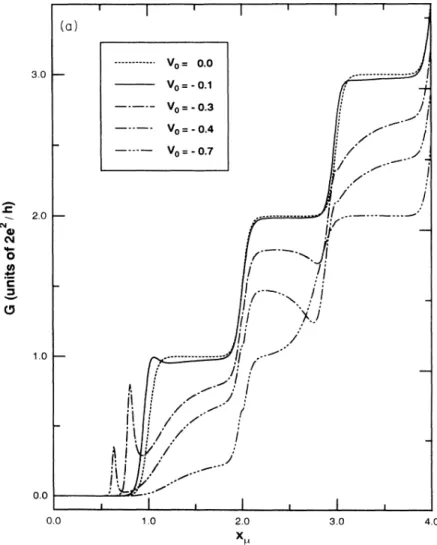
3.0 ~p=

00

~p=

-0.

1 ~p-

-0.

3 ~p=

-0.

4 Vp-

-0.

7 ee eeeeoc ~P'0 % /I l W / 2.

0—

Al

I

CV

0

lA O~ C

FIG.

1.

(a) Conductance G ofof theth PC

v

=

0.0 case cor-as afunction of

x„.

T

evo

=

responds to an ideal Q

PC.

Four other

im-=

—

_0.1

—

_0.3,

—

0.4, and purity strengths: v

=

—

. ,

—

.

,

—

.

, d

—

0.7 are s own.h . The impurity is located at the center ofthe

+PC.

(b) Thermopower

S

ofthe

/PC

as afunction of

_z„

for the same

x

=2.

shows detail

8

structures near

x„=

0.0

0.0 2.0

50 ErveCTS OFAN IMPURITY ON THECONDUCTANCE

AND.

. .

14215

(

—

im

xl

@„(x)=

xg(u

exp ~

xMi

—

+i

",

—,

mu

x

(4

4~

2

₎

(10)

Here,

Q,

_{(@ )} is an even (odd) function

of

z

and

M(a,

b,z)is Kummer's function.

Using

g„,

and

Q„,

we construct

a

state

_Q„;„(z)

[tp„,

„f

(x)

jwhich has only positive (negative) current

den-sity in the asymptotic region

(x

~

—

oo).

Similarly, we construct

a

state

g„„t

which has only positive current density in the asymptotic region

z

~

+oo.

The results are

where

4-,

'-(*)

=

4-(*)

+

~-

@-(*)

@-,

-~(*) =

0-o(*) +&-@

.

(&)

4e.,ref(+)

=

4rao(+)

+

7'

Wne(+)&

i

—

i

(

ere„l

.

.

f xe„'t

cosh

—

ssznh

4~

&4~.

₎

&4~.

& 2

(i

&4+

'4~. )

and 'Yn

=

_Pn

=

—

o'~.

With an impurity located

at

(z,

y)

=

(0,

y

),

the scat-tering wave function

of

an nth subband electron with

total

energy

E

and incident from the left-hand side can bewritten in the form

y)y„;

(&)+)

&

„y

_(y)@

„f(x),

&&0,

~.

'(*

y)

=

&

)

t„,

„y„,

(y)y„,

.

„,

(*),

*&0.

atching the wave function

4+

at

x

=

0 and integrating the Schrodinger equation across

x

=

0 leads

to

two matrix

equations

0

Ol ~

~

C lO

-

& (b) ll s.o ~!',

!i

ii

!i

2.0 I Il

I/I

/I

l 1.0 0.2 0.0 I

I'

j I 2.0 V,= OO Vo=-O.i Vo

=-03

V,

=-0.

4 Vo

=-0.

7

FIG.

1.(Continued). 0.0 1.0 2.0 X 3.0

where

cx+

pK = PT,

1+R=

JT,

(n)

„=

n„h

(P)

=P

~.

,

(&)-

=

_~-~-,

(R)

„=

r

(T)

- =&-,

2v~

(&)-

=

~-

—

4 (u-)

4-(u-)P-.

(14)

(»)

forward to show from

Eq. (17)

that, in the case of no impurity (v

=

0), t

=

b [1

+

exp (

—

me /w )j which is the well-known result for

a

perfect saddle-point

potential.

'

The incident current

J;„,

is given by

8

J

nine

=

hm &o(~n one

+

4no) (~nOne

+

/no)

K~—OO Ox

and the transmitted current

J„

_t,

„

in the nth channel is given by

From

Eq. (14)

and

_{Eq. (15),}

we obtain the transmission coefficients

t

„,

which isthe matrix element

of

T

and is given by

&=(&

—

»)

'(~

—

_~)

The matrix

T

is symmetric because both

_(P

—

_p

_J)

and

(n

—

p)

are symmetric. In deriving the above

ma-trix

equations, we have used the relations

_Q„,

₍₀₎

=

1,

g„',

(0)

=

g„(0)

=

0, and @„' (0)

=

+id,

where the

prime means derivative with respect

to

z.

It

is

straight-g„,

„.

„=

hm

C.

i

t„„~'

(P.

y.

.

+

0.

.

)

X~OO

x

—

(P-

0-

~

+

&-

-)

'

Here,

C

is adimensionless constant.

The current transmission coefficient

_T„„

is given by

(19)

Jn',tran

Jn,inc (20)

Finally, substituting

Eqs. (18)

and

(19)

into

Eq. (20),

and taking the required asymptotic limit, we have

3.

0—

Vo= 0.00 Vo=-0.10 V,=

-0.

30 Vo=-0.50 Vo=

-0.

55 2.0

—

(p)

I

CV

0

th C

1.

0—

~e

$J

/j

ll'

/j

FIG.2. _(a) Conductance i of the

+PC

as a function of

x„.

The impurity is at the edge of the

+PC

when

z„=

2.

1.

The dotted curve corresponds to the ideal

+PC

results and four other impurity strengths are shown. (b)Thermopower

8

ofthe

+PC

asafunction of

z„.

TheconBguration isthe same asin

_(a).

0.0

0.0 1.0 2.0

X

50 EFFECTS OFAN IMPURITY ONTHECONDUCTANCE

AND.

.

.

14217

T„„=

(t „~ exp (n

—

n')

2

r!"

₍₄

_4u X ₂ t,

4+'4~.

)

2 4)~

(2'

)

₍₂₁₎

In the case when there is no impurity,

it

is obvious that

t„„

is diagonal and that

T

„=

~

t

„~

.

III.

NUMERICAL

EXAMPLES

In this section, we present in three different situations

the G and

S

of a

/PC

as

a

function

of

the chemical

potential p

of

the reservoir. The effective width

of

the

/PC

is increased as y,increases. In the first situation, an

attractive impurity is fixed in its location, closer

to

the

symmetry axis, such that the impurity is always inaide

the

/PC.

In the second situation, an attractive impurity

is, again, fixed in its position but is

at

a

greater distance from the symmetry axis such that it is outside the

/PC

in the lower p, regime and is inside the system in the

higher

_p

regime. The effect of the impurity strength is also examined in the above two situations. Finally, in

the third situation, the strength

of

the impurity is fixed while its transverse location is changing.

We take the

/PC

to

be that in

a

high-mobility GaAs-Al Gaq As with typical electron density n

2.

5

x

10~~

cm,

m'

=

_0.

₀₆₇

_m„and

_A»

=

₅₀₀ A. Thus our choice

of

length scale

a'

=

k& ——

79.

6A, and energy scale

E'

=

5~k&s/2m'

=

9meV

=

104

K.

In all the fol-lowing numerical examples, we have chosen

k~T

=

0.

01

(T

1K),

u

=

0.

125,

andw„= 0.5.

Withsuchchoice ofparameters, the

/PC's

effective length

to

width ratio

I/W

=

4.

In the following numerical examples, the im-purity potentials v were, in fact, rescaled and became

vo cue

In Figs.

1(a)

and

_1(b),

we plot the variation of G and

S,

respectively, of

a

/PC

as

a

function of the

chemi-cal potential p,

.

For convenient purposes, the abscissa is

given by

z„

z„=

-!

—

+1

/, 1

(p,

&~s

)

(22)

which truncated integer value is the number of propa-gating channels below p,

.

The effective half-width

of

the

/PC

is given by y

g(2z„—

1)/u& for

z„)

0.5.

An

attractive impurity is located

at

(z,

y )

=

(0,

0).

Our results include cases

of

five impurity strengths: v

0.

3

I

02

(b)

II 0.1 _II! I[

0

Q

c

lO 0.0

—

'~

-0.1 -0.

2—

I I I !I I

z/

"

Vo= O.0O Vo=

-0.

10 Vo=

030

V,

=-o.

so V,

=-o.

ss

FIG.

2. (Continued). -0.

3

1.

0

1.

5 2.0 2.5 3.0 3.5

0.

0,

—

0.

1,

—

0.

3,

—

0.

4, and

—

0.

7.

Except in the pinchoK region

(x„(

1),

the impurity remains inside the

QPC.

There is, in the pinchoK region, no propagating chan-nel in the QPC so that transmission occurs only through tunneling which gives rise

to

a

peak in G, as is shown in

Fig.

1(a).

For a more attractive impurity, this peak in G occurs

at a

lower

x„and

with

a

lower peak height.

These features are consistent with the interpretation

of

such

a

peak in terms

of

resonant tunneling transmission.

In the case

of a

more attractive impurity, the resonant

peak in G occurs

at

a

lower

x„because

p, has

to

line

up with

a

lower quasibound

state.

On the other hand, in the saddle-point potential configuration, the effective tunneling distance is increased, rendering the peak height in G

to

be lowered. For an even more attractive impu-rity, such as v &

—

0.

7in

Fig. 1(a),

there is no resonant

peak because the impurity quasibound state is too deep

to

allow resonant tunneling

to

occur. For the case of

thermopower, in this pinchoK region, the resonant tun-neling gives rise

to

a pair

of

positive peak and negative dip structures, with the peak locating on the lower

_x„

side. We Gnd that this peak-dip structure can be

under-stood qualitatively by noting firstly in

Eq. (3)

that

S

is zero when

P„„,

T„„

is

a

constant near

_p

and, secondly,

that if

P„„,

T„„were

todepend linearly on energy near

p, ,

S

would be proportional

to

the slope of

P„,

T

„.

In

the low temperature regime, as we consider here, we have

,

T„„G,

and the peak-dip structure in

S

isfound

to

reflect qualitatively the slope of the peak in

G.

%ith

this insight, we point out in particular that for the cases

v

= —

0.

3, and

—

0.

4, the former case has a larger peak in G but asmaller peak-dip magnitude. This is related

to

the fact that the former peak has

a

slower rate ofrise and drop. This result demonstrates clearly the G prof-ile

sensitive feature

of

S

in the low temperature regime.

In the region when there are propagating channels, there are dip structures in G

just

below

x„=

3 for the

cases v

= —

0.

3 and

—

0.

4.

Following

a

dip structure.

on the larger

x„side,

G rises more rapidly and has a greater slope than the case for an ideal

QPC.

Thus, ap-plying our Gprofile-sensiti-ve analysis for

S,

the effect of the dip structure in G is

to

give rise

to

alarger peak as well as a shift in the peak location of

S

towards

a

lower

x„value.

This feature is demonstrated in

Fig.

1(b) near

x„=

3.

Furthermore,

a

broad dip, such as the case for

v

=

—

0.

4,gives rise tonegative

S

in the region when

x„

is between 2 and

3.

Besides dip structure in G, there is a

kink in G

at

x„=

2. Similar structures have been found by Levinson et a/. These kinks in Gare not found in nar-row constrictions ofwhich the con6nement potentials are

3.0 i 4 t t 2.

0—

I

hl

0

N

r

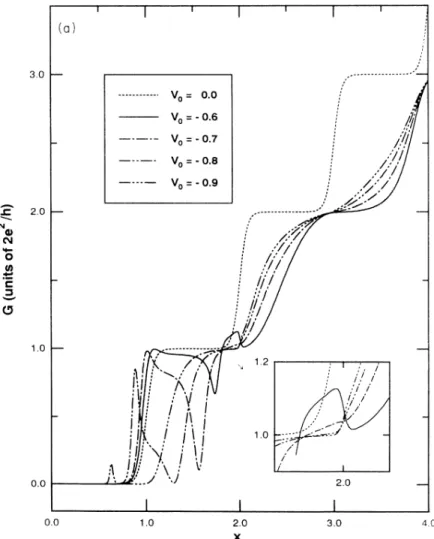
FIG. 3. (a) G vs

z„.

The location ofthe impurity is the same as in 2(a). The figure

shows that a more attractive impurity gives

rise to resonant reBection and transmission

when it is still outside

(z„(

2.1) the QPC.

(b)

S

vs

x„.

Same configuration asin

(a).

0.0

0.0 1.0 2.0

X

50 EFFECTS OFAN IMPURITY ON THECONDUCTANCE

AND.

.

.

14219 independent

of

the longitudinal coordinates. The kink in

G is shown, in

Fig. 1(b), to

give rise to

a

double-peak

structure in

S.

This can be explained with our Gpr-ofile

sensitive analysis. We point out that for v

=

—

0.

7, the

kink in G isbarely recognizable while the corresponding double peak in

S

is quite spectacular, with the higher

peak height almost double that of the ideal

QPC.

Figures

_{2(a), 2(b), 3(a),}

and

3(b)

show the G and

_S,

respectively, for the case when the impurity islocated

at

y

=

2.5.

The impurity strength varies &om v

=

0.

0

to

v

=

—

0.9.

As the chemical potential p, increases,

the effective width ofthe QPC is increasing and the im-purity location changes &om eR'ectively outside

to

inside

the

QPC.

Inparticular, the impurity is at the edge ofthe

QPC

when

x„=

_(u„y

+

1)/2.

We take

u„=

0.

5 so that the critical

_z„

isabout

2.

1.

One main purpose ofplotting

Figs.

2(a)

and

2(b)

is

to

show

that,

for

a

not-so-attractive

impurity (v

(

—

0.

55),

the impurity effect only becomes evident when

it

is electively inside the

QPC.

Figures

3(a)

and

3(b)

show, however, that

a

more attractive im-purity has its effect felt even when it is still electively

outside the

QPC.

From

Fig. 2(a),

we see that for v

=

—

0.

1 and v

—

_0.

_{3, a}

_signi6cant eKect

of

the impurity comes in when x&

)

2.

1.

This is reasonable because the impurity

sects

the transport when it is efFectively inside the

QPC.

The latter impurity gives

a

dip and

a

small peak in Gnear

x„=

3.

The dip-and-peak structure in G

(x„3

and

v

=

—

0.

3)gives rise in

S

to a

positive peak in between two negative dips, as shown in

Fig. 2(b).

As shown in

Figs. 2(a) and

2(b),

the G plateaus as well as the dip

structures in region x~

)

2 are destroyed when the im-purity becomes more attractive. Thus the rising in G

for x&

—

3 becomes less abrupt. The corresponding fea-ture in

S

is

a

gradual shift in the peak of

S,

away &om

the ideal QPC peak

at

x„=

3 and towards

a

smaller

z„value.

Following the shifting

of

peak positions in

S,

these peaks are broadened and their peak height lowered.

In addition, there is

a

peak in G, near

x„=

2, which is

associated with resonance tunneling occurring near the

edge of the

QPC.

This peak becomes more pronounced for

a

more attractive impurity and the corresponding

S

exhibits

a

peak followed by

a

large negative spike. For the casev

=

—

0.

5, the magnitude

of

the negative

S

spike is even greater than the magnitude of the ideal peak in

S.

This isa signature

of

a

pronounced peak in

G.

2.0

a

Ol O~

c

M r 1.0 'I 1.5

—

I' 'I r

:I

I I I a ii II II

os

—

'

I

II

~

'1, I I ! I

II

-o-'sl

ti

l ! -1.0 I t i emaamwm4$w~ 0.0

v,

=

oo

V =-Or6 V =-0.7

vo--o.

8 V =- or9 2.0

FIG.

3. (Continued). -1.5 1.0 1.5 2.0 X 2.5 I 3.0 3.5

3.0

V=00

X

=Q5

= 1.0 I t I I~ = 1.5

X=2Q

2.

0—

O Ol

0

th

c

~tj~Ii

@oooooeresr so+ t~'I

~ ~ 0

FIG.

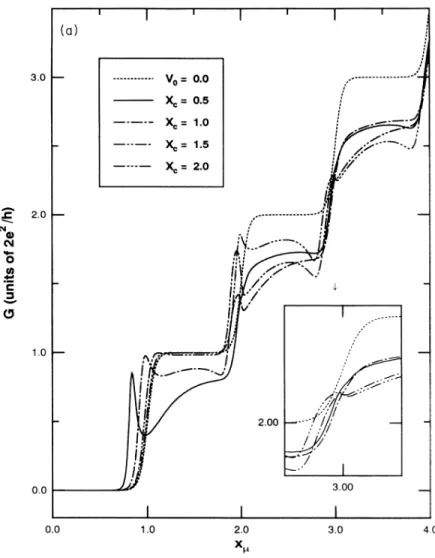
4. (a) Gvs

z„.

The impurity poten-tial vo

=

—

0.3, the ideal QPC curve is given

by the dotted curve. Four impurity positions are shovrn. The impurity is at the edge of the

/PC

when

x,

=

z„.

(b)

S

vs

z„.

Same configuration as in

(a).

1,

0—

0.0 0.0 I 1.0 2.0 X 3.00 3.0 4.0

As the impurity becomes even more attractive, as shown in Figs.

3(a)

and

_3(b),

new G and

S

structures

are developed inthe region

x„&

2,which corresponds

to

resonant reflection and resonant transmission when the

impurity is quite outside the

QPC.

Corresponding tothe resonant reflection dip inG,there is

a

large negative spike following by

a

large positive peak structure in

S.

Note, in particular, that the magnitudes

of

both the spike and

the peak can be up

to

five

to

six times that

of

the ideal

S

peak

at

x„=

1.

This demonstrates that

S

is very sensitive

to

resonant processes in the QPC systems.

Finally, in

_{Figs. 4(a)}

and

4(b),

we plot G and

S

for

a

v

=

—

0.

3 impurity in various positions:

x

0.

5,

1.

0,

1.

5, and

2.

0.

The impurity is at the edge of the

QPC

when

x„=

x,

.

From the results in previous figures, we see that this impurity is a weak attractive scatterer. In the pinchofF region, the

x

=

0.

5 and

1.

0 impurities give rise

to a

resonant tunneling peak in

G.

The

x

=

2.

0 impurity gives rise

to

a

peak inGdue

to

resonant tunnel-ing outside the

QPC.

However, it is interesting to note

that the

x

=

1.

0,

1.

5 impurities contribute

to

peaks in G

near

x„=

2 where the impurities are already inside the

QPC.

Our results show that the impurity with

x,

=

2.0 gives rise

to

alarger G peak

at

x„=

2 while it gives rise

only

to a

kink in G

at

integer

x„=

3.

The corresponding

structure in

S

for this peak consists of

a

negative dip, as shown in

_Fig.

4(b) .

IV.

CONCLUSION

A mode-matching technique has been applied

to

study

the eKectofan impurity onthe conductance and the ther-mopower of

a

saddle-point-potential

QPC.

Our analysis demonstrates the correlation between the conductance

and the thermopower in the low temperature regime.

The correlation is established qualitatively using

a

G-profile serisitive analys-is. We show that

S

is very sensi-tive

to

the impurity near the threshold

of

a

transverse subband. In fact, our results show that

S

is closely

re-lated

to

the slope

of

G.

At integral

x„values,

kinks in G

which are not so transparent can give rise

to

large dou-ble peaks in

S.

Large negative spikes in

S

arise due

to

the presence

of

sharper peaks and dips in

G.

Thus

S

E1'1ACTS OFAN IMPURITY ON THECONDUCTANCE

AND.

. .

14221 1.6 1.2 (b) 0.2 0.0

vo=

OO

Xc=

05

Xc= 1'0 X =

1.

5 X = 2.0 0.8

I

-0.2 2,0

FIG.

4. (Continued). 0.

0—

-0.

4—

1.0 2,0 X 3,0 re6ection dip in

G.

Besides, we have studied the cases when the impurity is outside and inside the

/PC

and have demonstrated the

resonant tunneling and the resonant re8ection occurring outside the

/PC.

Our results show in detail the effect on

S

and G when

a

short-range impurity is around the edge of the

/PC.

Finally, this study shows that both G

and

8

can be used

to

explore the con6guration of

/PC

systems and that they play complementary roles in such

regard.

ACKNOWLEDGMENTS

This work was partially supported by the National

Sci-ence Council

of

the Republic ofChina through Contract No. NSC82-0208-M-009-062.

C.

W.

J.

Beenakker and H. van Houten, in Solid State Physics, edited by H. Ehrenreich and D. Turnbull (Aca-demic, New York, 1991),Vol. 44, p.

1.

B.

J.

van Wees, H.van Houten, C. W.

J.

Beenakker,

J.

G. Williamson,

L.

P.Kouvrenhoven, D.van der Marel, and

C.

T.

Foxon, Phys. Rev. Lett. 80,848(1988).

D.A. Wharam,

T.

J.

Thornton,

R.

Newbury, M. Pepper, H.Ahmed,

J.

E.

F.

Frost, D. G.Hasko, D.

C.

Peacock, D.

A. Ritchie, and G.A.C.Jones,

J.

Phys. C

21,

L209(1988). D.van Marel and

E.

G.Haanapel, Phys. Rev.

B

39,

7811

(1989).

C.

S.

Chu and

R. S.

Sorbello, Phys. Rev.

B 40,

5941

(1989).

P.Bagwell, Phys. Rev.

B 41,

10354

(1990).

E.

Tekman and

S.

Ciraci, Phys. Rev.

B 4$,

7145

(1991).

J.

A.Nixon,

J.

H.Davies, and H.U. Baranger, Phys. Rev.

B

4$, 12638

(1991).

Y.

B.

Levinson, M.

I.

Lubin, and

E.

V.Sukhorukov, Phys. Rev.

B 45, 11936

(1992).

Y.

MLxegaki and D.

K.

Ferry, Phys. Rev.

B

4B, 15218

(1992).

J.

Faist, P. Gueret, and H. Rothuizen, Phys. Rev.

B

42, 3217

(1990).

C. C.

Eugster,

J.

A.del Alamo, M.

R.

Melloch, and M.

J.

Rooks, Phys. Rev.

B

4B, 10 146(1992).

P.Streda,

J.

Phys. Condens. Matter

1,

1025 (1989). C.

R.

Proetto, Phys. Rev.

B

44, 9096

(1991).

Y.Okuyama and N.Tokuda, Phys. Rev.

B

46,2610(1992). L. W. Molenkamp, H. van Houten, C. W.

J.

Beenakker,

R.

Eppenga, and C.

T.

Foxon, Phys. Rev. Lett.

65,

1052

(1990).

L. W.Molenkamp, Th. Gravier, H. van Houten, O.

J.

A. Buijk, M. A. A. Mabesoone, and C.

T.

Foxon, Phys. Rev.

Lett.

88,

3765(1992).

M. Biittiker, Phys. Rev.

B

41,

7906(1990).

M. Buttiker,

Y.

Imry,

R.

Landauer, and S.Pinhas, Phys.

Rev.

B

31,

6207 (1985).

U. Sivan and

Y.

Imry, Phys. Rev.

B 33,

551 (1986).

This de6nition oftransmission coefBcient can be found ina standard quantum mechanics textbook such asL.

l.

SchiK, Quantum Mechanics (McGraw-Hill, New York, 1971),p.

103.

H. A. Fertig and

B.

I.

Halperin, Phys. Rev.

8

36,

7969

(1987).

M. Abramowitz and

I.

A. Stegun, Handbook of