EFFECTIVE BOSON NUMBER CALCULATIONS NEAR THE Z = 64 SUBSHELL

PHYSICAL REVIEW C VOLUME 42, NUMBER 1 _JULY 1990

Effective boson

number

calculations near the

Z

=64

subshell

C.

S.

Han and

D.

S.

Chuu

Department ofElectrophysics, National Chiao Tung University, Hsinchu, Taiwan, Republic

of

China

S.

T.

Hsieh

Department ofPhysics, National Tsing Hua University, Hsinchu, Taiwan, Republic

of

China (Received 21 November 19&9)

The effect ofthe partial subshell closure near Z

=64

is studied byintroducing the effective boson

number in the framework ofthe interacting boson model. The energy spectra and the

8

(E2)values

ofthe Sm, Gd, and Dy isotope series are calculated. It isfound that the agreements between the theoretical results and the observed data arevery satisfactory when the partial closure effect is taken into account byasmooth variation ofthe effective proton-boson numbers.

I.

INTRODUCTION

In recent years there are considerable interests in

studying the subshell closure effects at

Z

=64.

'

It

has been shown ' _{that the}

_Z

₌₆₄

_{subshell had significant} effect for N

~

88 transition nuclei, but disappears asN ap-proaches

90

due to the increasing importance

of

the n-p

interactions. This subshell closure also introduces significant effects on the calculations using the interacting boson model

(IBA).

In

IBA,

the number

of

active bosons

is usually determined by counting particles above, or below the nearest spherical-shell closure. Therefore, the counting

of

the boson numbers becomes ambiguous when

some subshell closure exists. Wolfet

al.

have calculated the magnetic moment

of

the first

2+

states

of

the transi-tional nuclei

Ba,

Nd, Sm, and Gd in the framework

of

IBA-2,

and Gill et

al.

have performed an

IBA

calcula-tion near

Z

=64

subshell. They made the assumption

of

a drastic change in the proton-boson numbers at N

=

88, namely, the assumption

of

a

Z

=64

shell for N 88and a

Z

=50

shell for N

~90.

It

is interesting

to

note that for those nuclei with N 88 the counting schemes from the

Z

=64

subshell yielded better agreement with the experi-mental data. Scholten has proposed a method to calcu-late the number

of

"effective bosons" in a microscopic model.

It

is interesting to see that when the number

of

effective bosons is calculated, it does yield a minimum

value at

Z

=64.

However, the minimum value is about

2.

4 instead

of

0

as required by a full closure structure. This means that there is considerable washing out

of

the shell closure effect at

Z

=64.

A similar result has also been obtained by Maino and Venture using the Nilsson model on the basis

of BCS

approximation. Federman and Pittel, Federman et

al.

, and Chen et

al.

studied

I

the shape transition

of

Zr and Mo isotopes in the frame-work

of

a shell model.

It

was found that the isospin

T

=0

component

of

the n-p interaction is responsible for the onset

of

deformation.

It

was suggested that the pro-motion

of

the neutron into the h9/2 orbit near

N=90

leads to a concurrent polarization

of

protons into the

h»&2 orbit, via the strong npinter-action between parti-cles in spin-orbit partners orbits, and results in an eradi-cation

of

the subshell _gap. However, it is well known that the shell-model single particle level spacings are dependent on the model space. Therefore, the assump-tion

of

sudden disappearance

of

the

Z

=64

subshell at N

=88

made by Wolf et

al.

and Gill et

al.

seems

to

be oversimplified in the sense that itdoes not take the effects

of

partial closure

of

Z

=64

and the smooth neutron num-ber dependence into account. In order to investigate these partial subshell closure effects, some preliminary studies'

'"

on Sm and

Er

isotopes with

N=86

—96

have been done.

It

is found that satisfactory results can be achieved only when smooth variation

of

the proton-boson numbers forN&_{88are considered.}

In this paper, we present a systematic study on the 148—_158Sm 1so—_{1586d, and} 152—_1MDy

isotopes

the effects

of

partial closure and the smooth neutron dependence by considering the effective proton-boson numbers in

IBA.

Aunified Hamiltonian and an

E2

tran-sition operator for each isotope series are used in our cal-culation.

II.

MODEL

In the calculation

of

energy levels, the most general Hamiltonian with nine parameters

of IBA-1

was used

H~=e,

(s

s)+ed(dt

d)+

g

—,

'&(2L+1)CLX[[d

Xd ]

'X[d Xd]' 'j'

'

L=0,2, 4

+(

—

')'

v

[[d

Xd

]'

'X[d

Xs]'

'+[d

Xs

]'

'X[d Xd]' 'j'

'

+(2)

0'0[[d

Xd

]'

'X[s

Xs]'

'+[s

Xs ]'

'X[d Xd]' 'j'

'

+u

_[[d

Xs ]'

'X[d Xs]' 'j'

'+

—,

'u

I[s

Xst]'

'X[s

Xs]'

'j'

' .

For

comparison, two calculations were performed. We first consider the conventional

IBA

(hereafter denoted as

MI).

Then the effective proton-boson numbers are

in-cluded (hereafter denoted as MII) to investigate the par-tial subshell closure effects

of

the

Z

=64

and N

=82.

In both models, the number

of

neutron bosons N is count-ed as usual,

N„=

—,

'(N

—

82) where N is the number

of

neutrons.

For

the proton bosons, N is counted from

Z

=50

closed shell in

MI.

However, in

MII,

we relax all

the shell closure restriction for the proton boson but maintain the only requirement that they must be integers. Therefore, we try different sets

of

proton-boson numbers for the nuclei in each isotope series in our calculations. Once we chose a set

of

N for the isotope series, a least-squares search for the interaction parameters is then car-ried out in the framework

of

IBA

to fit the experimental data

of

these nuclei.

It

was found that the best set forthe effective proton-boson numbers for Sm isotopes is N

=2

for ' Sm, N

=4

for ' Sm, and N

=6

for all other Sm isotopes. The best set

of

the effective proton-boson num-bers

of

the Gd isotopes is N

=2

for ' Gd, N

=5

for

Gd, and N

=7

for all other Gd isotopes.

For

Dy iso-topes, the best set is

N„=5

for ' Dy, N

=7

for ' Dy, and N

=8

for all other Dy isotopes.

It

is worth noting that for each isotope series, both

MI

and

MII

count the same N for N

90.

This is consistent with the disap-pearance

of

the

Z

=64

subshell for N

&90

in this mass region as pointed out in previous works. ' _{However, the}

linear variation

of

N for N 88in

MII

for each isotope series manifests the effects

of

the partial closure and smooth neutron number dependence.

In the calculations, 71 reliable energy levels in Sm, 94

levels in Gd, and 100levels in Dy isotopes were included in the least-squares fittings.

It

is well known that not all the parameters in the Hamiltonian are linearly indepen-dent. Since we are concerned with excitation energies only, the effect

_{of e,}

can be absorbed into ed. Also the parameter uo is kept at zero because it can be absorbed into other parameters. ' The resulting interaction pa-rameters and the overall root-mean-square deviations for Sm, Gd, and Dy isotopes are listed in Table

I.

It

isworth noting that unified interaction parameters can be found for each isotope series.

It

isalso seen from the table that the parameters change smoothly from Sm isotopes to Dy isotopes. ~'I+&I 0 ~~ cd ~I&+I V 'a V U' cd V 6 0 0 U V bQ CJ V V 0 V 'a cd Q 0 ~1++I

4

0 cd CA C@ V C 0 ~& 0 cd

40%

_OO

0

O O

%04

OO Ch DO

000

0

O

0

l OO OO

~

M CO

ooo ooo

I I I I I I O O

000

000

0 0

ev

ooo

mWt

_Q Q

000

I I I I I I

o0OO0OO

_{ooo ooo}

4N~

0oo

I I I

0 0

000

OO cv

ooo

m t

_{0 0}

000

I I I I I I 40 OO M OO o

ooo ooo

I I I I I I

III.

RESULTS OO DO

0

H

0

O Q If) OO OO

0 0 0

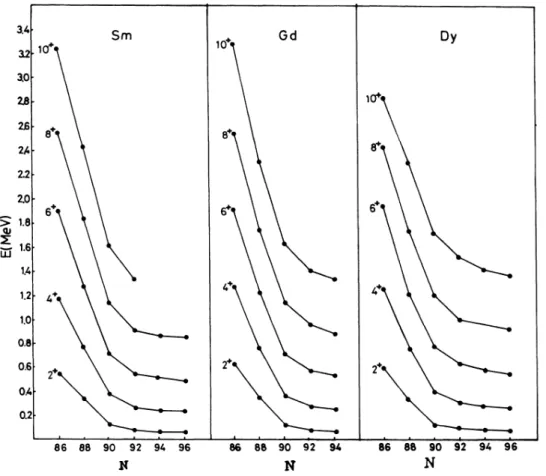
The ground-band levels

of

the Sm, Gd, and Dy

iso-topes are shown in

Fig. 1.

We can see that the energy values for each

J

states change almost linearly for N 88 and become quite flat for

X

90.

This is consistent with the onset

of

the

Z

=64

subshell effect. Furthermore, the linear falling

of

the energy values for each

J

state as N goes from 86to 88 seems tojustify the linear variation

of

the effective proton-boson number

N„

found in

MII

in

each isotope series.

The partial closure effect for

Z

=64

subshell can be in-vestigated by plotting the effective proton-boson numbers versus the number

of

protons for each mass number A as

000

282 C.S.HAN, D. S.CHUU, AND S.

T.

HSIEH 42 3.4 10 Gd Dy

0.

2'

~ 22 20-W 1S

~

1.6

X

UJ 1.4~ 1.2~ 1.0 O. S-0.6 OA~ 0.2 I 86 S8 90 92 94 96 N i 86 88 90 92 94 86 88 QO 92 94 96

FIG.

1.The general trend ofthe experimental ground-band level energies ofthe Sm,Gd,and Dy isotopes.

shown in

Fig. 2. For

A

=150,

there is a clear minimum

N

=2

occurring at

Z

=64.

The nonzero value

of

the minimum indicates that the closure

of

the

Z

=64

sub-shell is not complete but only partial. This result is con-sistent with that obtained _by Scholten as shown in the dashed line

of

the figure. However, in Scholten's result, there is no calculation to study the way the subshell clo-sure will be decreasing as the neutron number

N,

ap-proaches

90.

We have also studied this tendency

of

wash-ing out the subshell closure at

Z

=64

as N

=90.

This can be clearly seen from the figure that the partial closure effect

of Z

=64

starts to decrease as A goes from 152to 154and is completely eliminated at A

=156,

where the curve becomes a straight line indicating the spherical clo-sure

of

Z

=50

for N

~90.

The gradual decreasing

of

the partial closure effect in the mass region A

=150

—

156 manifests the smooth neutron number dependence due to the increasing importance

of

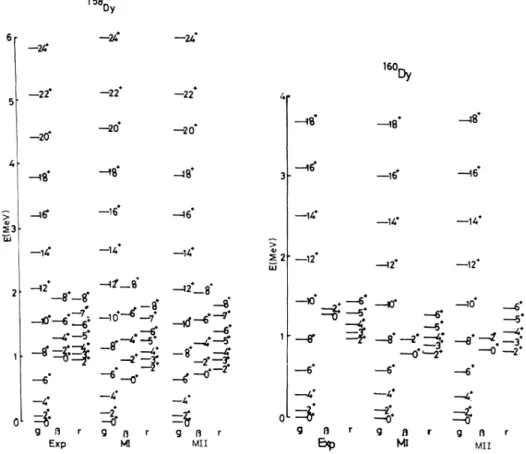
the n-p interaction.

The calculated energy spectra

of

Sm, Gd, and Dy iso-topes compared with the experimental values are shown in Figs. 3—8. In these figures different quasibands are separated in order to have a clear comparison. One can see that the traditional

IBA

(in the column

MB

cannot reproduce well the energy spectra

of

these isotopes. The calculated ground state energies in

MI

in general have much lower values compared

to

the observed data espe-cially for some higher spin states, except for ' Dy and Dy where the calculated values are higher than the

ex-8~ A=156 A=154 6 ~ - A=152 4 ~ A=150 2 62 64 66

FIG.

2. The effective proton-boson numbers versus the

num-ber ofprotons for each mass number A. Thy dashed line is

148 Sm 8 4

—

3 2 0 0 Ol 4J

~

2 8

—

6

—

3 g 4 LaJ

—

2

—

10

—

4

—

2 8

—

2 4

—

4 4 «3 m2 8 «4 0 3

—

12

—

14' 10 ~

—

12

—

8~

—

5 0

—

p' g 0 r Exp

—

0 9 g r Ml MII 0

—

2

—

0 g Q r _{g Q} Exp N

—

2 MII 0" g 0 Exp g 0 r _{g 0} MI MII

FIG.

3. Experimental and calculated energy spectra for ' 'Sm,

"

Sm, and

'"Sm.

31' 5'S 3 )56' 158 2~ 2

—

12

—

3 mo

~

—

2'

—

12 1p ~ 2' 4

—

12 mo

—

8

—

fp 2'

—

0'

—

2 1~ 8 B 8

—

2. p 0 g 0 r g g r g 0 Exp Ml MII 9 0 r _{9 0} g 8 Exp 0~

—

4 0 9 Exp Ml MII

FIG.

4. Experimental and calculated energy spectra for

"

Sm, ' Sm, and

"

Sm.

152 3' M2

—

8 W6 4~

—

12 H2 4-3

—

16 MS M6

—

2

—

₂ -0 ol.

~

Exp 4

—

2 4 —2

—

p' 9 0 MI pL g A MII -6 —4

—

3z2. Lal

—

2 4

—

2 2 2

—

2 g 8 r Exp —B 4 —10 —_6. -6 -2 g f3 r Ml 4 4 4 —2 0 —4 0 —2 0' g A MII 9 0 Exp wp l2 —6 3

—

2' 0 g A Ml

284 C. S.HAN,

D.

S.CHUU, AND S.

T.

HSIEH 42 15 3r P

~4

WO mp

~2

7 2

_—

12

—

12

—

e

0

~o

—

5' i

—

6

—

10

«3

—

8

—

2. 1-

—

8 m2'

—

2

~

~

—

8

—

4

—

_—

2 0

—

5 t

—

5 ~ 4 4 4

~

—

2

—

8' 9 g r Exp

—

4 4 2~ 9 8 MI

~

4 E'xp MII

FIG.

6. Experimental and calculated energy spectra for

"

Gd and

'"Gd.

perimental data. The energy spacings calculated in

MI

are also in considerable _disagreement with the observed data in the

_P

band and the _y band. Some states are even in reversed order in _{the y band}

of

' Dy. Thus the results manifest that the pure

IBA

model is unable to simulate the energy level structure forthe nuclei near

Z

=64.

The reason forthese discrepancies isthat in the calculation

of

the nuclei near

Z

=64

with 86 N 96,the introduction

of

the neutron-proton interaction will become

increasing-ly important when there are more neutrons outside the N

=82

shell, and thus tend to eliminate the

Z

=64

sub-shell closure as mentioned above. Hence, it is reasonable to expect that the calculation which includes the proper number

of

proton bosons will yield better results for the energy level fittings. This is indeed true as shown in the

figures (under the column

MII)

where the effective

156_D &52 +r

—

12'

~p

3I M2 3

—

16 W4 M2' M2 5 4 0 LLI MQ

—

8 2 0' g 9 9 Ex& gI MII 4 4

—

7

—

2

—

4

~+

pi (f 9 Q r G(p

—

s

—

7

4

—

2

—

₀ 9 Q r MII Qi Mo'

—

6 2

-6

~4

WO

~0

~&

—

8 ~Q

—

0' 4

—

₀ 9 8 MII

FIG.

7. Experimental and calculated energy spectra for

"

Dy,

"

Dy, and ' Dy.

1'58 Oy 6-160 5

—

22

—

20

—

22 4

—

20

—

20 4r m8 4-

_~6

3

—

16

—

16 w6'

x3'

YLJ

—

14 2'

_—

8

—

8' r 4 7.

10~ ~o

~4

~

—

4 Qe 9 Q r Exp

—

&6

—

14

—

8

—

10

—

8

~r

r

—

4 o Ml

—

16

—

14 r

—

4 8 r ~

~

0 9 Q r MII

—

14

)

&2

—

12 hl r

—

10

~t

4

—

6 9 Q r

—

14

—

12

—

5' 0

~4

9 g r h4

—

14

—

12

—

10

—

2'. 9 A r MII

FIG.

8. Experimental and calculated energy spectra for

'"Dy

and ' Dy.

TABLE

II.

8(E2)

values (in e b )and branching ratios for Sm isotopes. Theory

This work Previous works Nucleus Sm

'"Sm

152S J,

~Jf

4)~2)

2(~0)

4i

—

+2) 10)

~8)

4)

~22

2,

~0,

23~0

22 +2]

23~2]

23

—

+41 3)

~2)

/4) 3)

~2~/2,

2)~0)

4i

—

+2i

6)~4)

8)~6)

10)~8)

12'

—

+₁₀₎

23~0)

23~2]

23~4)

23~2)

/0, Expt. 0.151 0.25' 0.274

053

0435 0447 0.0106b 0.0036 0.0088b 0.27 0.0387 0.0174 0.296b 24+5 0.67 1.017b 1.2' 139' 1 103 1.123" 0.0163d 0.041 7 0.00416 2.44' MI 0.225 0.399 0.355 0.708 0.934 0.70 0.08 0.09 0.0001 0.14 0.005 0.036 0.165 8.54 0.41 0.68 0.88 0.971 0.907 0.826 0.007 0.011 0.002 1.57 MII 0.131 0.20 0.318 0.566 0.609 0.512 0.05 0.021 0.0035 0.11 0.079 0.025 0.342 20.62 0.861 1.197 1.256 1.220 1.131 1.001 0.0102 0.0267 0.0019 2.618 0.275 0.51b 0 139 0.02b 0.02 0.181b 0.024

109

434

0.673

098

0.41' 0.73' 0.18' 0.008' 0.015' 0.12' 0.029' 0.54' 16.8" 0.75~ 1.0g 0.97g 0.83g

286 C. S.HAN,

D.

S.CHUU, AND S.

T.

HSIEH 42

TABLE

II.

(Continued).

Nucleus

_J;

—

_+Jf

Expt. This work MI

MII

Theory Previous works 154sm 156Sm 158S

23~21/4

31 21/41 43~21/41 22~02/21 62~41/61 6~~4~/61 82~61/81 8P~62/81 51 41/61

21~01

41

—

+21 101~81 121~101 23

—

+01 23 +21

23~4

23~21/0

31~21/41 43—+21/41

21~0

11.9' 0 95' 0.088' &860' 0.2' 0.08' 54' &0.06' &58' 0.43' O.922' 1.186d 1497 1.538 1.565 0.013 O.O2' 0.0008 1.56" 2.S' o.

oss'

1.22" 1.28" 5.50 0.428 0.0001 50.8 0.081 0.308 128.5 3.59 173.2 0.102 0.657 0.96 1.01 1.05 0.964 0.002 0.012 0.0018 6.0 0.29 0.0013 0.784 0.647 14.28 1.0 0.054 273.7 0.256 0.658 330.8 4.55 175 0.391 0.978 1.364 1.416 1.333 1.212 0.0068 0.018 0.0012 2.65 1.0 0.111 1.089 1.205 'Reference 17. Reference 18. 'Reference 19. Reference 20. 'Reference 21. 'Reference 22. ~Reference 15. "Reference 23.

TABLE

III. B(E2)

values (ine b )forGd isotopes. Theory Nucleus

J;~Jf

Expt. This work MI

MII

Previous work 1526d 1546d

21~01

41—+21

61~41

41

—

+2q 22~21 22~01 2p~02 21

—

+01 41 41 81

—

+61 101

~81

02~21 22~01 2P~21 2P~41 42~21 42 62~41 6q

—

+61 0.33' 0.64' 0.95' 0.096' 0.077' 0.0014' 0.21' 0.773' 1.178' 139' 1.526' 173' 0.258' 0.004 0.033' 0.09' 0003' 0.071' 0.0027'

0.

033' 0.506 0.803 0.68 0.017

0.

201

0.

049 0.085 0.545 1.07 1.16 1.17 1.11 0.03 0.027 0.018

0.

005 0.009 0.001 7 0.0013 0.009 0.463 0.77 0.84 0.036 0.116 0.027 0.263 0.954 1.132 1.385 1.345 1.235

0.

02

0.

017

0.

017 0.021 0.027 0.018

0.

047

0.

019

033

O.62Ob 0.76 O.O6b o.164b O.O26b 0773' 1.098' 119' 1.20' 1.18' 0.136'

0.

0168 0.025' 0.087' 0.016' 0.089' 0 013' 0.008 5' 0.33' 0.69' 0.79 O.O11d 0.006' 0.009' 0.87' 1.18' 1.17'

Table

III.

(Continued). Nucleus

_J;~Jg

Expt. This work MI MII Theory Previous work 156g,_d

23~0]

23 +2]

23~4]

31~21

3]

~4]

43~2]

43 4] 43 5]

~4]

2]

~0]

4] 4] 10]

~8]

12,—+10,

02~2]

22—+0]

22~2]

22~4]

42—+2]

42~4]

42~6]

23~2]

23~4]

3]

~2]

3]~4]

43~2

43

~4]

5]

~4]

5]

~6]

0.00459 0.0 0.001 39 0.0103 0.01 0.001 4 0.01 0.0043 0.0074 0.914' 1.299' 1.470' 1.57' 159' 1.45' 0.029' 0.00316 0.016' 0.018' 0.

0061'

0.014' 0.009 1' 0.035 5' 0.003 2' 0.0364' 0.028' 0.007 8' 0.046' 0.029 5' 0.041' 0.005 0.071 0.0043 0.011 0.055 0.0013 0.061 0.0039 0.0011 0.86 1.12 1.29 1.28 1.23 1.22 0.197 0.001 0.0028 0.007 9 0.011 0.003 0.012 0.026 0.0014 0.0028 0.005 0.0025 0.0021 0.0001 0.003 0.0067 0.027 0.0012 0.0082 0.017 0.0048 0.028 0.0036 0.0034 1.04 1.45 1.53 1.50 1.42 1.26 0.124 0.002 3 0.015 0.043 0.045 0.035 0.048 0.023 0.0038 0.008 0.015 0.002 6 0,005 0.0006 0.014 0.0052 0.01' 0.00038 0.0176 0.01 0.0019 0.01 0.00081 0.01 0914' 1.286' 1.38' 1.38' 134' 1.26' 0.025' 0.004 0.006' 0.015' 0.0047' 0.004 8' 0.014 8' 0 0333' 0.0023' 0 037' 0019' 0.

011'

0 039' 0.0289' 0.025' 'Reference 24. bReference 25. 'Reference 26 Reference 15 'Reference 27

2]~0]

23~0]

23~2]

23~4]

43~2]

43

—

+4] 43 61

22~0

2p 2]

22~4]

31 21 3] 4] 4, 2, 42 4]

42~6]

5]

~4]

5]

~6]

43~23 42~22 5]

—

+3] 43~22

43~3]

1.008' 0.0016' 0.001 2' 0.0071' 0.004' 0.0022' 0 0094' 0.016 9' 0.029' 0.0013' 0.0297' 0.0177' 0.006' 0.04' &0.01' 0.023 5' 0.0194' 137e 0.6' 1.01' 0 037' 0.14' 0.75 0.0005 0.0017 0.06 0.008 0.0082 0.0004 0.031 0.03 0.067 0.0017 0.0058 0.014 0.013 0.034 0.002 0.016 0.25 0.57 0.49 0.504 0.637 1.13 0.013 0.0002 0.018 0.007 0.029 0.0024 0.030 0.057 0.077 0.0012 0.006 0.037 0.018 0.07 Q.OQO8 0.014 1.3 0.48 0.66 0.35 0.67 1.008' 00019e 0.000 4' 0.0034' 0004 7' 0.001 5' 0.0056' 0.0236' 0 039' 00019' 0043e 0.021' 0.009 2' 0.04' 0.0028' Q035e 0.028' 1 13' 0.42' 0 70' 0.0207' 0.16'

288 C. S.HAN,

D.

S.CHUU, AND S.

T.

HSIEH 42

TABLEIV.

B(E)

values (in

e'b')

and branching ratios for Dy isotopes. Theory

This work Previous work Nucleus 154D 156D 158Dy 'Reference 28. Reference 15. 'Reference 25. Reference 29. 'Reference 30.

J,

~Jf

22~0l/2l 42~2~/4l 62 4z/6l

2l~ol

42~22 6q

~42

10q~82 12'

~

102

142~

122 42 4l

42~2l

62~6l

62~4,

82~8(

102~10)

102~8(

122~

12l

122~

10l

142~

12( 2l

—

+Ol Expt. 0.015' 5.

1+0.

5' 14+2' 3.79' 1.29 1.42

149

1.53 1.S6' 1.58d 0.054 0.0024 0.078 O.OO14' o.os4d o.ooo6' 0.077" 0.001" &0.32' o.oo6d &0.0015d 093' 0.095 2.13 1.15 1.04 0.75 1.15 1.19 1.13 0.86 0.68 0.098 0.018 0.53 0.011 0.031 0.0029 0.014 0.0046 0.012 0.0017 0.0033 1.34 0.051 2.92 6.82 1.17 0.792 1.25 1.36 1.32 0.97 0.80 0.09 0.079 0.76 0.0045 0.057 0.0017 0.038 0.002 0.036 0.0053 0.0023 1.40 O.O1lb 1.11b 2.16b 1.O1' O.7S' 1.07 1.O1b 0.81 o.s6' O.27'

proton-boson number is taken into account. The results

in

MII

show that the calculated ground-band energy lev-els are in good agreement with the observed data. The energy spacings

of

the levels in

_p

_{and y bands improved}

much better. The level ordering in the _y band

of

' Dy is also well reproduced.

To

test the wave function, we also calculate the elec-tromagnetic transitions. The general form

of

the

E2

operator was used,

T'

'=a[(d

Xs+s

Xd)'

'+P(dtXd)' ']

(2)

The parameters

a

and

_p

were determined directly from least-squares fitting

to

the observed

8

(E2)

values. There are abundant observed

8

(E2)

data for the Sm, Gd, and Dy isotopes. We have calculated the

8(E2)

both in

MI

and in

MII.

In the calculation

of

MII,

itis interesting to note that a unified parameter

a=0.

165 and

p=

—

0.

105 can be found to reproduce the

8(E2)

values quite well

for all the three isotope series. The resulting values

of

a

and

_p

obtained in our calculation agree approximately with those obtained in previous works. ' ' A similar calculation is also performed in

MI

with unified pararne-ters

a=0.

135and

p=0.

115.

In general, the results in

MII

are much better than those in

MI.

Tables

II, III,

and IV show the

8

(E2)

values and some branching

ra-tios. Some results

of

the previous works are also included for comparison.

It

can be seen from the tables that our calculated results in

MII

are in better agreement with the observed values than those in

MI,

especially for the tran-sitions within the ground band.

For

the cross band tran-sitions the agreement is also more satisfactory for the

MII

calculation.

IV. CONCLUSIONS

This paper presents a scheme tostudy the effect

of

sub-shell closure at

Z

=64

for the Sm, Gd, and Dy isotopes in the framework

of IBA.

Wefound that large discrepan-cies occur when

Z

=

50and N

=

82 is treated as a closed shell in this mass region. But this discrepancy can be im-proved very much when the partial subshell closure effect at

Z

=64

is taken into account. Therefore, in presenting a scheme for calculating nuclei near

Z

=64,

it is neces-sary torecognize not only that there is a subshell closure at

Z

=64,

but also that the neutron-proton interaction among nucleons will gradually wash out the subshell gap

when there are more neutrons outside the N

=82

shell. The existence

of

partial subshell closure causes ambigui-ties in counting boson numbers in the IBA-type calcula-tions. Lacking a precise microscopic counting scheme,

effective boson numbers in the phenomenological calcula-tions.

It

is found that the energy spectra and the

B(E2)

values

of

the Sm, Gd, and Dy isotopes can be well ex-plained when the partial subshell closure effect is taken into account by gradually increasing the effective proton bosons asN approaches

90.

The results

of

our phenome-nological calculations indicate that the effective boson

ap-proach in

IBA

is a rather encouraging approach.

It

may be helpful

to

study the foundation

of

this approach in a more microscopic model, such as the shell model which can manifest the effects

of

the n-p interaction explicitly.

This work was supported by the National Science Council

of

Taiwan, Republic

of

China.

'R. F.

Casten, D. D.Warner, D. S.Brenner, and

R.

L.Gill, Phys. Rev.Lett. 47,143(1981).

A. Wolf, D. D.Warner, and N. Benczer-Koller, Phys. Lett. 158B,7(1985).

R.

L.Gill, R.

F.

Casten, D. D.Warner, D. S.Brenner, and W.

B.

Walters, Phys. Lett.118B,251(1982).

4A. Wolf, Z.Berant, D. D.Warner,

R.

L.Gill, M. Schmid,

R.

E.

Chrien, G.Peaslee, H.Yamamoto,

J.

C.Hill,

F. K.

Wohn,

C.Chung, and W.

B.

Walters, Phys. Lett. 123B,165(1983).

50.

Scholten, Phys. Lett. 127B,144(1983).

G.Maino and A.Venture, Lett.Nuovo Cimento 39,89(1984).

7P. Federman and S.Pittel, Phys. Rev.C 20,820(1979). P. Federman, S. Pittel, and

R.

Campos, Phys. Lett. 82B, 9

(1979).

L.M. Chen, S.

T.

Hsieh, H. C. Chiang, and D. S.Chuu, Il Nuova Cimento 101A,185(1989).

' _S.

_T.

_{Hsieh, H.C.Chiang, M. M.King Yen, and D. S.Chuu,}

J.

Phys. G 12, L167 (1986).

D. S.Chuu, C.S.Han, and S.

T.

Hsieh, Nucl. Phys. A482, 679 (1988).

A. Arima and

F.

Iachello, Phys. Rev. Lett. 35, 1069(1975);

Ann. Phys. (N.Y.)99,253 (1976);111,201(1978);Phys. Rev. Lett. 40,385(1978);Ann. Phys. (N.

Y.

)123,468(1979);Annu. Rev.Nucl. Part. Sci.31,75(1981).

O.Scholten, Ph.D.thesis, University ofGroningen, 1980. '

_R.

_{Bijker, A.}

_E.

_{Dieperink, O. Scholten, and}

_R.

_Spanhoff,

Nucl. Phys. A344, 207(1980).

D. S. Chuu, C. S.Han, S.

T.

Hsieh, and M. M. King Yen, Phys. Rev. C 30, 1300 (1984).

M. M.King Yen, S.

T.

Hsieh, H.C.Chiang, and

D.

S.Chuu, Phys. Rev. C 29,688(1984).

R.

M.Diamond,

F.

S.Stephens,

K.

Nakai, and

R.

Nordhagen, Phys. Rev. C 3,344(1971).

'

_T.

_Tamura,

_K.

_{Weeks, and}

_T.

_{Kishimoto, Phys. Rev. C 20,} 307(1979).

' _S.

_K.

_Bhardwaj,

_K.

_K.

_Gupta,

_J.

_B.

_{Gupta, and D.}

_K.

_Gupta, Phys. Rev.C 27,872(1983).

K. K.

Gupta, V.P.Varshney, and D.

K.

Gupta, Phys. Rev. C 26,685(1982).

'J.

Konijn,

J.

B.

R.

Berkhout, W. H. A. Hesselink,

J.

J.

Van Ruijven, P.Van Nes, H. Verheul,

F.

W. N. De Boer, C.A.

Fields,

E.

Sugarbaker, P. M. Walker, and

R.

Bijker, Nucl. Phys. A373,397 (1982).

S.Davydov and V. L.Ovcharenko, Yad. Fiz. 3, 1011 (1966)

[Sov.

J.

Nucl. Phys. 3, 740 (1966)].

J.

B.

Wilhelmy, S.G.Thompson,

R.

C.Jared, and

E.

Cheifetz, Phys. Rev.Lett. 25, 1122 (1970).

N.

R.

Johnson,

I.

R.

Lee,

F.

K.

McGowan,

T.

T.

Sugihara, S. W. Yates, and M. W.Guidry, Phys. Rev.C26, 1004(1982).

T.

Grotdal,

K.

Nybo,

T.

Thorsteinsen, and

B.

Elbek, Nucl.

Phys. A110,385(1968).

K.

Kumar and

J.

B.

Gupta, Nucl. Phys. A304, 295(1978). P. Van Isacker,

K.

Heyde, M. Waroquire, and

G.

Wenes,

Nucl. Phys. A380,383 (1982)~

W. W. Bowman,

T.

T.

Sugihara, and

F.

R.

Hamiter, Phys.

Rev. C3,1275(1971).

H.

R.

Andrews, D.Ward,

R.

L.Graham, and

J.

S.Geiger, Nucl. Phys. A219, 141(1974).

J.

Ben-Zvi, A.

E.

Blaugrund,

Y.

Dar, G.Goldring,

J.

Hess, M. W.Sachs,

E.

Z.Skurnik, and

Y.

Wolfson, Nucl. Phys. A117,