BIT 32 (1992), 403-412.
T H E M O S T V I T A L E D G E S W I T H R E S P E C T T O T H E N U M B E R O F S P A N N I N G T R E E S I N T W O - T E R M I N A L S E R I E S - P A R A L L E L G R A P H S
R O N G - H O N G JAN, LIH-HSING HSU and YUEH-YING LEE Department of lnformation and Computer Science, National Chiao Tung University
Hsinchu 30050, Taiwan, R.O.C.
Abstract.
A set E' of k edges in a multigraph G = (1I, E) is said to be a k most vital edge set (k-MVE set) if these edges being removed from G, the resultant graph G' = (V,E - E') has minimum number of spanning trees. The problem of finding a k-MVE set for two-terminal series-parallel graphs is considered in this paper. We present an O(IEI) time algorithm for the case k = 1, and an O(I VI k + IEI) time algorithm for arbitrary k.
C.R. Category: G.2.2.
Keywords: most vital edges, spanning trees, two-terminal series-parallel graphs.
1. Introduction and definitions.
In many applications the network designer may want to know which edges in the network are most important to him; if these edges are removed from the network there will be a significant decrease in its performance. Such edges are called the most vital edges in a network. Several papers [2, 4, 7] have been presented to find the most vital edges. However, they only address the effect on the shortest path or the maximum flow in the network. For example, the problem considered in [4] is to find a set of edges in a network whose removal from the network results in the greatest increase in the length of the shortest path between two specified nodes. In this paper, we will consider the effect on the number of spanning trees in the network.
The number of spanning trees is an important parameter in design and analysis of network reliability [3]. A computer communication network can be modelled as a graph with p vertices and q edges; vertices represent computers in the network, and edges represent communication links. Assume that the vertices are perfectly reliable and each edge may work (or fail) independently with the probability p (or 1 - p).
4 0 4 RONG-HONG JAN, LIH-HSING HSU AND YUEH-YING LEE
Therefore, ifp is close to zero, the all-terminal reliability R(G) of the network G can be estimated by
R(G) ~ z(G) pP- 1(1 -- p)q-P+ i
where z(G) is the number of spanning trees of G.
Most graph-theoretic terms used in this paper are standard (e.g., [6]). Here, we limit ourselves to defining the most commonly used terms and those that may produce confusion. Let G = (V, E) be a multigraph, where V is the vertex set of G and E is the edge set of G. Let p = IV[ and q = IE[. A spannino subgraph of G = ( E E ) is a subgraph H = (V,E'), where E ' c E. A simple 9raph is a graph G with the multiplicity of every edge in G equal to one.
A spanning subgraph H of a connected graph G is called a spanning tree of G if H forms a tree. There are usually many spanning trees in a connected graph. We use z(G) to denote the number of spanning trees in G. Let E' be a subset of E in graph G = (V, E). We use G -- E' to denote the graph G' = (V, E -- E'). In particular, we use G - e to denote the graph G - {e}. An edge e* is called a most vital ed9 e in graph G, if z(G - e*) < v(G - e) for all edges e ~ E. The problem of finding such an edge is called the 1-MVE problem. A subset E* of E with
IE*I
= k is called a k most vital edge set (k-MVE set) of G if ~(G - E*) < z(G - E') for all E' c E with IE'I = k. The problem of finding such a subset is called the k-MVE problem.In this paper, both the 1-MVE problem and k-MVE problem are considered for a special class of graphs called two-terminal series-parallel graphs [5], The formal description of two-terminal series-parallel graphs will be given in the next section. Many NP-complete problems in general graphs can be solved by polynomial-time algorithms in this class of graphs [8, 11]. We are going to present an O(q) time algorithm to solve the 1-MVE problem and an O(/~' + q) time algorithm to solve the k-MVE problem.
2. Two-terminal series-parallel graphs
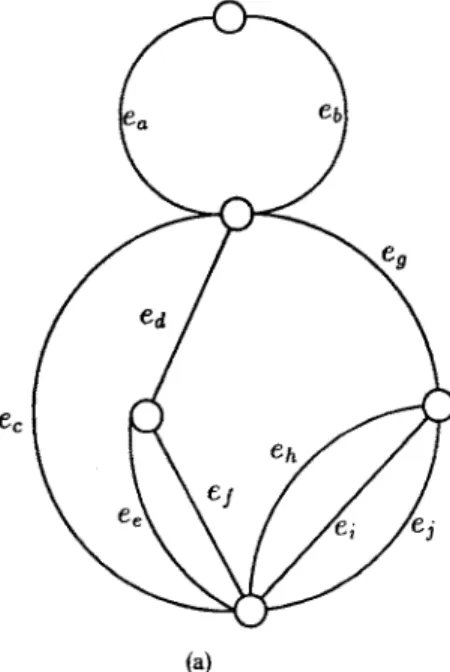
Two-terminal series-parallel graphs are derived from the concept of series-paral- lel networks (SPN). Series-parallel networks often occur in practice since they correspond to boolean formulas (with serial connection implementing logical-AND and parallel connection implementing logical-OR). For example, an SPN shown in Fig. 1, corresponds to the boolean formula [a v b] A [C v (d A (e v f)) v (g A (h v i v j))]. An SPN can be represented by a two-terminal series-parallel graph, an edge-labelled graph with two distinguished vertices called terminals. Formally, a two-terminal series-parallel (TTSP) 9raph of type k, where k ~ {L, P, S} (which mean leaf, parallel and series), is recursively defined as follows.
1. A graph G, which contains only one edge labelled by ex with its two endpoints as terminals, is a TTSP graph of type L.
THE MOST VITAL EDGES WITH RESPECT TO THE NUMBER O F . . . 405 by identifying all a~ together, we get a new vertex a and identifying all bi together, we get a new vertex b. The resultant graph G is a TTSP graph of type P with two terminals (a, b).
3. If the TTSP graphs G~, i = 1, 2, . . . . h, with terminals (a~, hi) are not of type S, then by identifying terminals bi and ai+l together, for i = 1,2 .... , h - 1, we get a graph G with terminals (al, bh). The resultant graph G is a TTSP graph of type S with two terminals (a~, bh).
For example, Fig. 2(a) shows a TTSP graph representing the SPN shown in Fig. 1.
cl
a I
dl
t
I
I
e~Figure 1 An S-type series-parallel network Figure 2(a) The TTSP graph of Figure 1
For convenience we describe a TTSP graph G with a tree structure, 7(G), called the parsing tree of G. For example, Fig. 2(b) is the parsing tree of the TTSP graph G shown in Fig. 2(a). Every node x in T(G), along with all of its descendant nodes induces a subtree T~ which describes a TTSP subgraph Gx of G. Each leaf node labelled by x in T(G) corresponds to an L-type TI'SP subgraph which contains only one edge e,~ in the TTSP graph G. Every internal node x is labelled by S or P according to the type of the TTSP subgraph Gx. If the node x in T(G) is a child node of the root r, then G~ is called a child T T S P subgraph of G.
Now, the procedure for evaluating z(G) for the TTSP graph G is described. In order to compute the value of z(G), we introduce a spanning subgraph, called bush [10], of the TTSP graph G. Let G = (V, E) be a TTSP graph with two terminals a and b. A spanning subgraph of G is called a bush of G if it is composed of two disjoint,
406 RONG-HONG JAN, LII-I-HSING HSU AND YUEH-YING LEE
P l )
(b)
Fig. 2(b) The parsing tree of Figure 2(a)
rooted trees: one rooted at terminal a and the other rooted at terminal b. F o r example, Fig. 3 shows two bushes of the T T S P graph G in Fig. 2(a). Let
z'(G)
denote the number of bushes in G.©
L/
Figure 3 Two of bushes of TTSP graph G, shown in Figure 2(a)
Let G be a T T S P graph. Obviously, z(G) > 1 and
z'(G)
> 1. Moreover, if G is of type L, z(G) = z'(G) = 1. If G is of type S with child T T S P subgraphsG1, G2 . . . Gh,
then the union of any spanning tree of Gi, for i = 1, 2 . . . h, forms a spanning tree of G. O n the other hand, a bush of G can be divided into a bush of Gi for some fixed i,
h
and spanning trees for all Gj with j ~ i. Thus, z(G) = 1~,=1
z(G,)
and z'(G) = ~ = 1 [z'(G,)I-I~=~,j,, z(Gj)] = z(G) ~ = 1 (z'(G,)/z(G,)).
If G is of type P with child T T S PT H E M O S T V I T A L E D G E S W I T H R E S P E C T T O T H E N U M B E R O F . . . 407
subgraphs G 1, G 2 , . . . , Gh, then the union of any bush of Gi, for i : I, 2 . . . h, forms a bush of G. Moreover, any spanning tree of G can be decomposed into a spanning tree of Gi for some fixed i, and bushes for all Gj withj # i. Thus, z'(G) = ~ih= 1 z'(Gi) and z(G) = ~ = 1 [ ( i)I-[j:l,#,i
Therefore, the values of z(G) and z'(G) can be determined by computing z(G~) and z'(Gx) level by level for every node x in the parsing tree T(G). If the input form for the TTSP graph is a link-list structure, the graph can be translated into its parsing tree in O(q) time by the algorithm proposed by Valdes, Tarjan and Lawler [9]. The following theorem is obtained.
THEOREM 1. 1. z(G) = z'(G) = 1 if G is of type L.
2. I f G is of type S with child TTSP subgraphs G1, G2, . . . . Gh, then
h h z'(Gi)
• (G) = i=lI~ z(Gt) and z'(G) = z(G),~l.= z(Gi) " 3. I f G is of type P with child T T S P subgraphs G1, G z , . . . , Gh, then
h h z(Gi)
z'(G) = I-[ z'(G,) and z(G) = "c'(G) ~ z'(Gi)"
i = 1 i = 1
4. Given the T T S P graph G, there is an O(q) time algorithm that evaluates [z(G~), z'(G~)]~ for every node x in parsing tree T(G).
3. The most vital edge.
To be direct, we may compute z(G - e) for every edge e in the TTSP graph G. If the graph G - e is not a TTSP graph, then z(G - e) = 0. Otherwise, z(G - e) can be found by theorem 1. The most vital edge in G is thus easily obtained. However, this method takes O(q 2) time. In this section, a linear time algorithm for finding the most vital edge in a TTSP graph will be presented.
First, given an L-type TTSP graph G which contains only the edge e, the value of z(G - e) is 0 and the value ofz'(G - e) is 1. Then, for any TTSP graph G with an edge el, z(G - ei) and z'(G - e,) can be determined recursively by the following equations. LEMMA 1. Given the T T S P graph G with the child T T S P subgraphs G1, G2 . . . . , Gh, for each edge ei e Gi, i = 1, 2 , . . . , h, we have:
1. I f G is of type S, then
l_
z (G - ei)[ z(Gi)
1 O 1 v z ( G i _ e , ) ~
z'(G) z'(Gi) l/[_z'(Gi -- ei)J (1)
408 R O N G - H O N G JAN, LIH-HSING HSU AND YUEH-YING LEE
2. I f G is o f type P, then
[,(G -e,) l _ ,'(G) [, z(O) ,(G,)lF:!~,_eal
T'(G -
e3_l z'(Gi) 0 z'(G)
1~'(G')_]L~
(G( - ei)_l"
(2)PROOF. 1. Let G be of type S with the TTSP subgraphs G1, G2 . . . . , G~ and let edge e~ be an edge in child subgraph Gi. The removal of edge e~ from G influences neither the number of spanning trees nor the number of bushes in any other child subgraph G~,j = 1, 2 . . . h, and j ~ i.
(a) If the subgraph Gi contains only the edge ei, then z ( G t ) = z ( G i - e~)= O, z'(Gi - ei) = i, a n d ~(G - ei) = 0. The right hand side of equation (1) is equal to [0, z(G)]'. Note that
z'(G - ei) ; ~'(6~ - e3 1--[ ~(Gj) +
~'(G~)~(G~- e3
1-I
~(Gj)
j = 1 , j # i s= 1 , s ~ i L j = I , j c s , i h = I-[z(Gj)
=z(G).
j = 1 ,j-f: iThus, the left hand side of (1) is also equal to [0, z(G)] ~.
(b) Ifsubgraph Gi contains more than one edge, then z(Gi - e~) ~ O. By Theorem 1,
~(G)
z(G - el) = z(Gi - e,) ]--I "c(Gj) = z(Gi - e , ) - -
i = L i ' i z(Gi) and z'(G - e,) = z(G - ei) + , z(G) f V ~ { ( G j)
= ~(G,- e , r ~ L j ~ ,
z(Gj)
~(a) f~(G~
"[- z'(G)
Using matrix form, equation (1) holds. 2. Similary, we can obtain equation (2).z'(Gi - e~) ]
z(G,-
,,(G,) 1
z(G,) J + z(G, ei)] z'(Gi) 1
z'(O, - e~)[.
z(Gi) .] + )
With this observation, we define the T-evaluation matrix Mx for each node x, whose parent is node y, in the parsing tree T(G) as:
Mx = z(G2i" z'(G,) ~'(G~) if the parent node y is of type S, L z(Gy) T(G~)
T H E MOST V I T A L E D G E S W I T H R E S P E C T T O T H E N U M B E R O F . , . 409
Mx - z ' ( G ~ z'(G~) z'(G~) i f the parent node y is of type P and
L
0 1Mx = [10 O1] if node x is the root of T(G).
Given a leaf node x in T(G), it is clear that [z(Gx - e~), z'(G~, - e~)] t = [0, l y . Let x = Xo, Xl,X2 . . . . ,x, = r be the unique path from x to the root r. Then,
[
z(G - e~)I = M~ M,. ...Mxo[Ol].
z'(G - e,)] -'
With this equation, the 1-MVE problem of the TTSP graph can be solved by z(G - e*) = min {z(G - e~,)le~ is a leaf node in T(G)}. Obviously, this method takes O(q 2) time, so we will introduce another data structure called a preserving matrix to improve the time complexity of the algorithm. The preserving matrix Px of node x in the parsing tree T(G) can be determined recursively as follows.
P~ = M,, if node x is the root node in T(G),
P~ = Py. M~ if node x is a non-root node with its parent node y,
where Mx is the z-evaluation matrix of node x and Py is the preserving matrix of node y. It is clear that ifx is a leaf node in T(G) and x = Xo, xl, x2,. •. x, = r be the unique path from x to the root r, then
<
z'(G - e~)J
With this preserving matrix, the following algorithm can be used to solve the 1-MVE problem of the TTSP graph in linear time.
Algorithm 1
S t e p l Evaluate[x(Gx),{(Gx)]tforeachnodexintheparsingtree T(G)bypostorder traversal [1].
Step 2 For every non-root node x with its parent y, compute the r-evaluation matrix Mx and thus, get the preserving matrix Px = Py. M~ by preorder traversal [1] in the parsing tree T(G).
Step 3 Compute T(G -- ex) for every leaf node x using
[z(G-ex)7= e 0
z ' ( G - e x ) J # [ 1 ] "
Step 4 Choose the most vital edge from the results obtained in step 3. That is, choose e* such that z(G -- e*) = m i n { z ( G -- e)le is an edge in TTSP graph G}. Obviously, algorithm 1 takes O(q) time.
410 RONG-HONG JAN, LIH-HSING HSU AND YUEH-YING LEE 4. The k most vital edge set.
In this section, the k-MVE problem is discussed. First, we will use k = 2 and 4 as examples, and then we will extend them to the general case. Note that the 2-MVE set does not necessarily contain the I-MVE set. For example, the 1-MVE set for the TTSP graph shown in Fig. 2(a) is {ca} while the 2-MVE set is {ca, e~}.
If E* = (ei, e2} is a 2-MVE set for TTSP graph G, edge el is obviously the most vital edge in the subgraph G - e2. Hence, a direct way of finding a 2-MVE set of G is to find a 1-MVE set in the subgraph G - e for each e in the TTSP graph G, respectively. Since there are O(q) edges and each takes O(q) time by using Algorithm 1, it will take O(q z) time to find a 2-MVE set in a TTSP graph. However, the time complexity can be reduced to O(p 2 + q). It is known that every TTSP graph is connected. Thus, p ~ q + 1. Since there may exist a lot of parallel edges connecting any two vertices, p may be much smaller than q.
Let G = (V, E) be a TTSP graph. The reduced weighted T T S P graph RG = (VR, E R ) of G is a simple graph, where V = VR and vertices x,y in R~ are joined by an edge if and only if they are joined by some edges in the TTSP graph G. Moreover, the edge multiplicity for edge e = (u, v) in G, denoted as re(e), is assigned to the corresponding edge e = (u, v) in R~. Similarly, we can associate the multiplicity of edges in G with the corresponding leaf node of the parsing tree T(R~) of RG. For example, Fig. 4(a) is the reduced weighted TTSP graph R~ of TTSP graph G shown in Figi 2(a). Fig. 4(b) is the parsing tree T(R~) of R~. Let G - ke, where k <_ re(e), denote the graph
= (V, E - / ~ ) in which the set/~ contains k copies of the edge e,
Observe that every subset E' of E with IE'I = 2 is composed of two edges, which are either parallel edges in G (i.e., two such edges represented by one edge in graph RG), or non-parallel edges in G (i.e., two such edges represented by two edges in graph RG). We can solve a 2-MVE problem in a reduced weighted TTSP by the following algorithm.
Algorithm 2
Step 1 Transfer the parsing tree T(G) of the TTSP graph G to the parsing tree T(RG) of the reduced weighted TTSP graph Ro.
Step 2 Evaluate [z(R~), z'(RGx)] t for each node x in the parsing tree T(Ro) by postorder traversal.
Step 3 Compute z(G - 2e) for every edge e in RG with an edge multiplicity of at least two.
Step 4 For each graph R~-e,, el ~ ER, compute z((G - - e l ) - - e j) where ej ~ E R and ej v ~ ei.
Step 5 Choose the 2-MVE set from the results obtained in step 3 and step 4. That is, choose edge set E* = {e~, e~} such that z(G - E*) = rain {z(G -
e')tE'
= E and 1E'I = 2}.THE MOST VITAL EDGES WITH RESPECT TO THE NUMBER O F . . . 411
el, (2 t
e2,(I
1
(
e~, (y): y indicates the corresponding edge multiplicity of edge e~ (a)
S
I'
xt.: y indicates the corresponding edge multiplicity of leaf node x (b)
Figure 4(a) The reduced weighted TTSP graph of Figure 2(a) (b) The parsing tree of Figure 4(a)
The evaluation of [z(R~.), z(R~x)] t in the parsing tree T ( R ~ ) is the same as the evaluation of [z(Gx), z'(Gx)] t in Theorem 1. The only difference is [z(R~x), z'(R~x)]'
= I-m(ex), 1] t if the graph R~x is of type L and rn(e~) is its multiplicity. Similarly, the evaluation of [ z ( G - e ~ ) , z ' ( G - ex)] t in the parsing tree T ( R ~ ) is [ z ( G - ex),
z'(G - e~)]' = M~ M ~ . _ I . . . M~o[m(e~) -- 1, 1] 7, ifxo, x l , x z , . . . , xn = r is the unique path from leaf node x to the root r in the parsing tree T(R~). Moreover, [z(G - ke~), z'(G - kex)] t = MxnM~, - 1"'" Mxo[m(e~) - k, 1]', where m(ex) > k. In Algorithm 2, step 1 takes O(q) time. Since R6 = (V, ER) is a planar graph, IERI -- O(p). Thus, steps 2 and 3 take O(p) time and step 4 takes O(p 2) time. The algorithm takes O(p 2 + q) time total.
Now, we will discuss the case k = 4. It is observed that every edge subset E' with IE'I = 4 is composed of four edges in the TTSP graph G, which may be four parallel edges, three parallel edges together with another edge, two parallel edges together with another two parallel edges, two parallel edges together with two non-parallel
412 RONG-HONG JAN, LIH-HSING HSU AND YU'EH-YING LEE
edges or four non-parallel edges. In short, we can write 4 = 4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1. Using the same idea as in the case k = 2, the time complexity for solving a 4-MVE problem is O(p 4 + p3 + 2p2 + p + q) = O(p4 + q). As in the discussion above, a k-MVE problem can also be solved in a similar way. The time complexity is O(dkp k + dk- tp k- 1 + . . . + d2p2 + d i p + q), where d~ is the number of integer partitions of integer k being divided into exactly i parts. Let n~ denote the number of ordered integer partitions of integer k being divided into exactly i parts. F o r example, da = 1 and rr3 = 3, when k = 4 and i = 3. Note that 4 = 2 + 1 + 1 when the order of 1 and 2 is ignored and 4 = 2 + 1 + 1 = 1 + 2 + 1 = 1 + 1 + 2 when the order is taken into account. Obviously, d~ < rc~. Since rc~ = C ( k - 1 , i - 1 ) < C(k,i), where C(m,n) is the binomial coefficient,
dkp k + d k - l p k-1 + . . . + d2p z + dip + q < (p + 1) k + q. Therefore, the k-MVE problem can be solved in O(p ~ + q) time.
5. Conclusions.
In this paper, an O(q) time algorithm for solving a 1-MVE problem in a T T S P graph is presented, where q is the number of edges in the graph. A reduction method is also proposed to solve a k-MVE problem in O(p k + q) time, where p is the number of vertices in the graph.
REFERENCES
1. A.V. Aho, J. E. Hopcroft and J. D. Ullman, The Design and Analysis of Computer Algorithms, 54-55, Addison-Wesley, Reading, MA, 1974.
2. M. O. Ball, B. L. Golden and R. V. Vohra, Finding the most vital arcs in a network, Operations Research Letters, 8, 73-76 (1989).
3. C.J. Colbourn, The Combinatorics of Network Reliability, 49-53, Oxford University Press, Oxford, England, 1987.
4. H. W. Corley and D. Y. Sha, Most vital links and nodes in weighted networks, Operations Research Letters, t, 157-160 (1982).
5. R. J. Duffin, Topology of series-parallel networks, Journal of Mathematical Analysis and Applica- tions, 10, 303-318 (1965).
6. R. Gould, Graph Theory, Benjamin/Cummings, Menlo Park, CA, 1988.
7. S.H. Lubore, H. D. Ratliffand G. T. Sicilia, Determining the most vital links in aflow network, Naval Research Logistics Quarterly, 17, 497-502 (1970).
8. H. D. Ratliff and A. S. Rosenthal, Order-picking in a rectangular warehouse: A solvable case of the traveling salesman problem, Operations Research, 507-521 (1983).
9. J, Valdes, R. Tarjan, and E. L. Lawler, The recognition of series parallel digraphs, SIAM Journal on Computing, 11,298-313 (1982).
10. J.A. Wald and C. J. Colbourn, Steinertrees, partial2-trees, andminimumlFInetworks, Networks, t3, 159-167 (1983).
11. Y.L. Wang, R. S. Chang and P. R. Chang, The tour problems in two-terminal series-parallel graphs, to appear in BIT.