1 / 27
Mining Rules from an Incomplete Data Set with a
High Missing Rate
Tzung-Pei Hong
1, 2and Chih-Wei Wu
31Department of Computer Science and Information Engineering National University of Kaohsiung, Kaohsiung, 811, Taiwan
2Department of Computer Science and Engineering National Sun Yat-sen University, Kaohsiung, 804, Taiwan
3Department of Electrical Engineering
National University of Kaohsiung, Kaohsiung, 811, Taiwan tphong@nuk.edu.tw, wuchinwei@yahoo.com.tw
Abstract
The problem of recovering missing values from a dataset has become an important research issue in the field of data mining and machine learning. In this thesis, we introduce an iterative missing-value completion method based on the RAR (Robust Association Rules) support values to extract useful association rules for inferring missing values in an iterative way. It consists of three phases. The first phase uses the association rules to roughly complete the missing values. The second phase iteratively reduces the minimum support to gather more association rules to complete the rest of missing values. The third phase uses the association rules from the completed dataset to correct the missing values that have been filled in. Experimental results show the proposed approaches have good accuracy and data recovery even when the missing-value rate is high.
2 / 27
Keywords: association rule, data mining, missing value, incomplete data, support.
1. Introduction
Modern enterprise use knowledge management techniques to obtaining competitive advantages. An effective knowledge management uses proper tools to extract business knowledge from large datasets [4][8]. Machine learning and data mining are thus two kinds of important techniques for achieving the purpose. They attempt to mine hidden and useful business knowledge from large datasets [1][2][3][14]. Most learning or mining approaches derive rules from complete data sets. If some attribute values are unknown in a dataset, it is called incomplete.
In the past, several methods were proposed to handle the problem of incomplete datasets [6][7][10][12][13][15]. A commonly-used solution to processing missing attribute values is to ignore the tuples which contain missing attribute values. This method may disregard important information within the data and a significant amount of data could be discarded. Some other methods, such as using association rules as an aid to complete the missing values are shown to have acceptable prediction accuracy. For example, Ragel and Cremilleux proposed the Robust Association Rules (RAR) to reduce the impact of missing values in a database [11]. However the performance of the above approaches may degrade when the missing ratio of an incomplete dataset is
3 / 27 high.
To deal with this disadvantage, we introduce an iterative missing-value completion method to fully infer the missing attribute values by combining an iterative mechanism and data mining techniques. The method uses the RAR support criterion [11] to extract useful association rules for inferring the missing values in an iterative way. It consists of three phases. The first phase uses the association rules which are mined from an original incomplete dataset to roughly complete the missing values. The second phase uses the reduced minimum support to gather more association rules from the original incomplete dataset to complete the rest of missing values from phase 1 in an iterative way until no missing values exist. The third phase uses the association rules from the completed dataset to correct the missing values that have been filled in according to the association rules until the missing values converge. Experiments on two datasets are also made to show the performance of the proposed approach.
The remainder of the paper is organized as follows. Some related works are briefly reviewed in Section 2. The proposed algorithm for mining association rules and guessing missing values at the same time is described in Section 3. An example to illustrate the proposed algorithm is given in Section 4. Experimental results of the
4 / 27
proposed algorithm are shown in Section 5. Conclusions and future works are finally given in Section 6.
2. Review of Some Related Works
The goal of data mining is to discover important associations among attributes such that the presence of some items in a tuple will imply the presence of some other items. An association rule is an expression X→Y, where X is a set of attributes and Y is usually a single attribute. It means in the set of tuples, if all the attributes in X exist in a transaction, then Y is also in the tuple with a high probability. To achieve this purpose, Agrawal and his co-workers proposed several mining algorithms based on the concept of large itemsets to find association rules [1]. They divided the mining process into the following steps.
Step 1: Generate candidate itemsets and count their frequencies by scanning the dataset.
Step 2: Consider an itemset as a large (frequent) itemset if the number of the tuples in which the itemset appears is equal to or larger than a pre-defined threshold value (called minimum support).
5 / 27
items are processed first. Large itemsets containing only single items are then combined to form candidate itemsets with two items. This process is repeated until all large itemsets have been found.
Step 5: Form all possible association combinations for each large itemset, and calculate their confidences.
Step 6: Output the rules with their confidence values larger than a predefined threshold (called minimum confidence) as association rules.
Ragel and Cremilleux then proposed the Robust‐Association‐Rules (RAR) approach to mine association rules in an incomplete dataset [11][12]. Instead of deleting the tuples with missing attribute values, RAR partially disabled the tuples with missing attribute values to ease the issue of lost rules. They also re‐defined the support and the confidence calculation for association rules. The rules which are mined with the RAR approach can then be used to recover the missing values in a dataset [12]. Formally, let the tuple set (X) for an itemset X be defined as follows:
}, ,
| { )
(X Tup X Tup TupD
where D is a given data set and Tup represents a tuple in the data set D. X Tup represents Tup has the itemset X. Besides, let Dis(X) be the set of disabled (missing) data with the itemset X. It is defined as follows:
6 / 27 }, , ?, , | { )
(X Tup A X A X Tup Tup D
Dis
where the symbol ‘?’ denotes a missing attribute value. A is thus a missing attribute belonging to X. The RAR support for an itemset X based on the approach is thus defined as: . | ) ( | | | | ) ( | ) ( Y X Dis D X X Sup
The confidence for an association rule X → Y based on the RAR approach is defined as follows: . | ) ( ) ( | ) ( | ) ( | ) ( X Y Dis X Y X Y X Conf
Ragel and Cremilleux then proposed the Missing-Values Completion (MVC) approach [5] based on the RAR method to recover multiple missing values in a dataset. The approach first applies RAR to discover all association rules. It then applies the most appropriate rule to fill in a single missing value in a tuple.
3. The Proposed Approach
In this section, we propose the iterative missing-value completion method with the RAR support to extract the association rules from an incomplete dataset with a
7 / 27
high missing rate. It consists of three phases. The first phase uses the association rules which are mined from the original incomplete dataset to roughly complete missing values. The second phase uses the reduced minimum supports to gather more association rules from the originally incomplete dataset to complete the rest of missing values in an iterative way until no missing values exist. The third phase uses the association rules from the completed dataset to correct the missing values that have been filled into predicted values until convergence. The details of the proposed algorithm are stated below.
The proposed algorithm for mining rules and completing missing values:
INPUT: An incomplete dataset D with n tuples, a set of m attributes A, each with a set of values, the minimum support threshold minSup, the minimum confidence threshold minConf.
OUTPUT: A set of association rules and a complete dataset with completed missing values.
PHASE 1:
STEP 1: Find the RAR-support values of all the 1-itemsets. If the support of a 1-itemset X is not less than the threshold minSup, put it in the set of frequent
8 / 27 (large) 1-itemsets, L1.
STEP 2: Iteratively find the other frequent itemsets with more than one item in an Apriori-like way using the RAR-Support evaluation. The set of frequent (large) k-itemsets is called Lk.
STEP 3: Find the confidence value of each possible candidate association rule generated from the frequent itemsets. Here, only the rules with only one item in the consequence are handled. If the confidence of a candidate association rule is not less than the threshold minConf, put it in the set of association rules, AR.
STEP 4: Use the set of association rules to infer the missing values of the incomplete dataset by the following sub-steps.
SUBSTEP 4.1: If there is only one association rule which can be used to derive the missing value of an attribute in a tuple, then use the rule. SUBSTEP 4.2: If there is more than one association rule which can be used to
derive the missing value of an attribute in an tuple, then use the one with the maximum RAR-confidence value; if more than one rule have the same maximum RAR-conference values, then use the one with the maximum RAR-support value; if the maximum
9 / 27
RAR-support values are still the same, then keep the value still missing if the rules derive different values. Let the updated dataset as D’.
STEP 5: Check the dataset; if there are still missing values in the dataset, execute Phase 2; otherwise, execute Phase3.
PHASE 2:
STEP 6: Let y = 1, where y is used to control the reduced minimum support value and the reduced minimum confidence threshold.
STEP 7: Set the reduced minimum support threshold RedMinSup = minSup/ry and the reduced minimum confidence threshold RedMinConf = minConf/ry, where r is the reduced coefficient.
STEP 8: For each tuple still with missing values, find the set of originally non-missing attribute-value pairs in the tuple from the original dataset D and form the candidate 2-itemsets, with one item from the set of non-missing attribute-value pairs and the other from the possible values in a missing value.
10 / 27
original dataset D; If the RAR-support of a candidate 2-itemset X is not less than the reduced support threshold RedMinSup, put it in the set of reduced frequent (large) 2-itemsets, L2’.
STEP 10: Find the confidence value of each possible candidate association rule generated from the frequent 2-itemsets, L2’, generated in STEP 9. If the
confidence of a candidate association rule is not less than the reduced confident threshold, put it in the set of reduced association rules, AR’. STEP 11: Use the set of association rules AR’ to infer the missing values of the
updated dataset D’ by the following sub-steps.
SUBSTEP 11.1: If there is only one association rule which can be used to derive the missing value of an attribute in a tuple, then use the rule. SUBSTEP 11.2: If there is more than one association rule which can be used to
derive the missing value of an attribute in a tuple, then use the one with the maximum RAR-confidence value. If more than one rule have the same maximum RAR-conference values, then use the one with the maximum RAR-support value. If the maximum RAR-support values are still the same and the rules derive different values, then keep the missing value still unknown.
11 / 27
STEP 12: y = y + 1 and repeat STEPs 7 to 11 until there are no missing values in the updated dataset excluding the tuples with all their attribute values missing or y gets to a predefined value.
STEP 13: If there is still a missing value for an attribute, fill in the most frequent value (based on the RAR support) of the attribute in the original dataset D.
PHASE 3:
STEP 14: Find the new set of association rules, AR’ from the updated dataset D’ (which is complete now) in a way similar to STEPS 1 to 3 in Phase 1 using the traditional support and confidence (due to no missing values), but only focusing on the items in the tuples with originally missing values in D. STEP 15: Use the set of association rules to infer the missing values of the originally
incomplete dataset by the following sub-steps.
SUBSTEP 15.1: If there is only one association rule which can be used to derive the missing value of an attribute in a tuple, then use the rule.
SUBSTEP 15.2: If there is more than one association rule which can be used to derive the missing value of an attribute in an tuple,
12 / 27
then use the one with the maximum RAR-confidence value; if more than one rule have the same maximum RAR-conference values, then use the one with the maximum RAR-support value; if the maximum RAR-support values are still the same and the rules derive different values, then keep the value the same as that in the updated dataset D’.
STEP 16: Compare the missing values before and after dataset update. If they are not the same, repeat STEPS 14 to 16 using the new updated D’. If they are the same (meaning convergence), then do the next step.
STEP 17: Output the final association rules and the updated dataset.
After STEP 17, the filled-in missing values have converged, and the association rules will not be changed as well. Through the iterative processing until convergence, the bad influence of the missing values wrongly guessed at the beginning can be reduced.
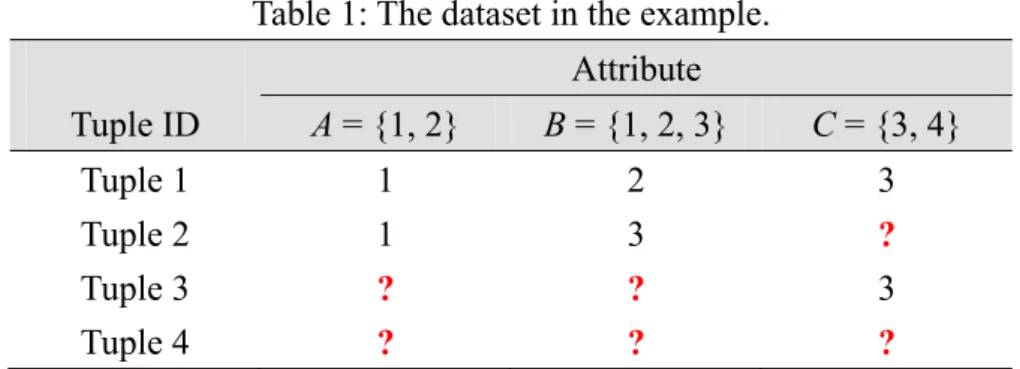
Note that tuples with all values missing may possibly appear in a dataset. Take the data in Table 3 as an example, in which all the values in tuple 4 are missing. From
13 / 27
STEP 8, since A = 1 and B = 3 are known in tuple 2 and the value of C is unknown, the set of candidate 2-itemsets generated thus includes (A1, C3), (A1, C4), (B3, C3), and (B3, C4). Similarly, the set of candidate 2-itemsets generated from tuple 3 includes (A1, C3), (A2, C3), (B1, C3), (B2, C3), and (B3, C3). Thus, only a partial set of possible candidate 2-itemsets needs to be checked, such that the computation time can be reduced. The algorithm will check only these candidates to extract useful association rules and infer missing values. STEP 14 also uses the same way to generate the candidates.
Table 1: The dataset in the example. Attribute Tuple ID A = {1, 2} B = {1, 2, 3} C = {3, 4} Tuple 1 1 2 3 Tuple 2 1 3 ? Tuple 3 ? ? 3 Tuple 4 ? ? ?
In Table 3, all the values in tuple 4 are missing. Thus, no candidate will be generated in STEP 8. For this case, STEP 13 is used to fill the initial missing values. That is, the most frequent value of the attribute based on the RAR support in the original dataset is used.
14 / 27
4. An Example
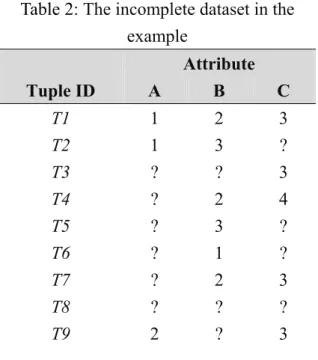
In this section, an example is given to show how the proposed algorithm can be used to find useful association rules and fill in missing values in an incomplete dataset with a high percentage of missing data. As an example, the incomplete dataset in Table 4 is used to demonstrate the idea. In Table 4, there are twelve tuples and three attributes, A, B, C. The values of the attributes are shown as follows: A = {1, 2}, B =
{1, 2, 3} and C = {3, 4}. Each attribute has 50% missing values in this example.
Assume the minSup threshold is set at 50% and the minConf threshold is set at 50%. The proposed algorithm processes this incomplete data set as follows.
Table 2: The incomplete dataset in the example Attribute Tuple ID A B C T1 1 2 3 T2 1 3 ? T3 ? ? 3 T4 ? 2 4 T5 ? 3 ? T6 ? 1 ? T7 ? 2 3 T8 ? ? ? T9 2 ? 3
15 / 27
T10 2 ? ?
T11 2 ? 3
T12 2 ? ?
Phase 1 first uses the association rules which are mined from original incomplete dataset to roughly complete the missing values. All the association rules with their RAR support values and RAR confidence values are shown in Table 6.
Table 3: The association rules with support and confidence values after STEP 3
Rule ID X → Y Sup Conf
R1 C3 → A2 0.67 0.67
R2 C3 → B2 0.67 1.00
R3 A2 → C3 0.67 1.00
R4 B2 → C3 0.67 0.67
The association rules in Table 6 are used to roughly infer the missing values in the incomplete dataset. The results after this step are shown in Table 7.
Table 4: The dataset after STEP 4
Attribute Tuple ID A B C T1 1 2 3 T2 1 3 ? T3 ?=2 ?=2 3 T4 ? 2 4 T5 ? 3 ?
16 / 27 T6 ? 1 ? T7 ?=2 2 3 T8 ? ? ? T9 2 ?=2 3 T10 2 ? ?=3 T11 2 ?=2 3 T12 2 ? ?=3
Phase 2 then uses the reduced minimum support to gather more association rules from the original incomplete dataset to complete the rest of missing values from phase 1. The support and the confidence thresholds are decreased as follows:
redMinSup = minSup / 2y = 0.5 / 21 = 0.25, and
redMinConf = minConf / 2y = 0.5 / 21 = 0.25.
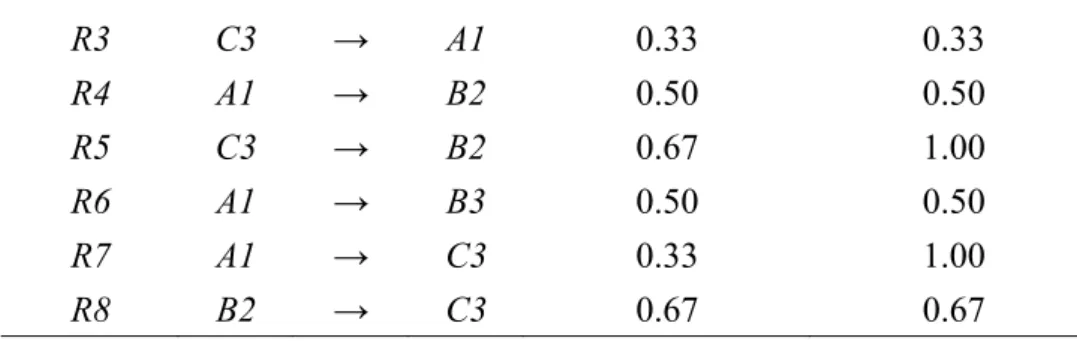
For the tuples still with missing values, the originally non-missing attribute-value pairs in those tuples are first identified. The candidate 2-itemsets are then formed, with one item from the set of originally non-missing attribute-value pairs and the other from the possible values of the attributes with missing values. The reduced association rules with their support and confidence values are shown in Table 10.
Table 5: The reduced association rules with their support and confidence values
Rule ID X → Y Sup Conf
R1 B2 → A1 0.50 1.00
17 / 27 R3 C3 → A1 0.33 0.33 R4 A1 → B2 0.50 0.50 R5 C3 → B2 0.67 1.00 R6 A1 → B3 0.50 0.50 R7 A1 → C3 0.33 1.00 R8 B2 → C3 0.67 0.67
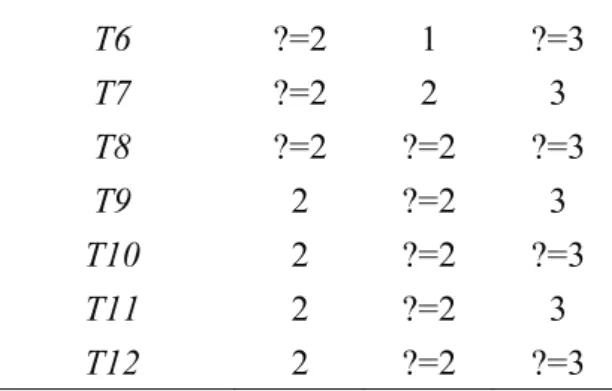
The set of reduced association rules AR’ is then used to assign the missing values which have not yet been filled in. If there is more than one association rule which can be used to derive the missing value of an attribute, then use the one with the maximum RAR-confidence value. The above steps are repeated until there are no missing values in the updated dataset excluding the tuples with all their attribute values missing or y gets to a predefined value. If there is still a missing value for an attribute, the most frequent value (based on the RAR support) of the attribute in the original dataset D is used to assign it. The results after this phase are shown in Table 13. After the step, all missing values are filled in and Phase 3 begins to adjust the values.
Table 6: The dataset after Phase 2
Attribute Tuple ID A B C T1 1 2 3 T2 1 3 ?=3 T3 ?=2 ?=2 3 T4 ?=1 2 4 T5 ?=1 3 ?=3
18 / 27 T6 ?=2 1 ?=3 T7 ?=2 2 3 T8 ?=2 ?=2 ?=3 T9 2 ?=2 3 T10 2 ?=2 ?=3 T11 2 ?=2 3 T12 2 ?=2 ?=3
Phase 3 then uses the association rules from the completed dataset to correct the missing values that have been filled into predicted values until convergence. The new set of association rules, AR’, are found from the updated dataset D’ and is used to adjust the previously filled-in missing values in the dataset. The results after this step are shown in Table 15, where the first number in a missing slot represents the previous guess and the second one represents the current guess after the adjustment.
Table 7: The dataset after adjustment Attribute Tuple ID A B C T1 1 2 3 T2 1 3 ? = 3, 3 T3 ? = 2, 2 ? = 2, 2 3 T4 ? = 1, 2 2 4 T5 ? = 1, 2 3 ? = 3, 3 T6 ? = 2, 2 1 ? = 3, 3 T7 ? = 2, 2 2 3 T8 ? = 2, 2 ? = 2, 2 ? = 3, 3 T9 2 ? = 2, 2 3 T10 2 ? = 2, 2 ? = 3, 3
19 / 27
T11 2 ? = 2, 2 3
T12 2 ? = 2, 2 ? = 3, 3
The guessed missing values before and after adjustment are compared. In this example, the results of the missing values guessed in tuples 4 and 5 are different, and thus STEPs 14 to 16 are repeated again. The results of guessed missing values are the same as those in the first iteration. The final association rules and the completed dataset are then output to users.
5. Experimental Results
In this thesis, experiments were made to show the performance of the proposed approach. All the experiments were performed on an Intel Core 2 Duo E8400 (3GHz) PC with 2 GB main memory, running the Windows XP Professional operating systems. The proposed algorithm was implemented on two real datasets, Teaching Assistant Evaluation and Tic-Tac-Toe, which were taken from the UCI Machine Learning Repository. Table 18 lists a summary of the two datasets and the used thresholds in the experiments. Each attribute in Teaching Assistant Evaluation and in Tic-Tac-Toe was randomly assigned different missing rates from 5% to 50%.
20 / 27
Table 8: Characteristics of the two experimental datasets and the used threshold values.
Dataset Tuple number Attribute number Missing rate minSup minConf
TAE 151 5 5% - 50% 50% 50%
Tic-Tac-Toe 958 9 5% - 50% 50% 50%
The robust association-rule (RAR) algorithm was also executed as a comparison to the proposed iterative mining algorithm. In order to evaluate the proformance of the proposed iterative mining algorithm, two measures including accuracy and recovery are defined. Let |mv| denote the number of missing values in a dataset, |crmv| denotes the number of correctly recovered missing values, and |rmv| denotes the number of recovered missing values, which may be or may not be correct. Accuracy is then defined as follows:
accuracy = |crmv| / |mv|,
which means the number of correct guesses over the total number of missing values. Recovery is defined as follows:
recovery = |rmv| / |mv|,
which means the number of guesses over the total number of missing values. Note that if a missing value can’t be recovered by any association rule, it is thought of a wrongly recovered missing value.
21 / 27
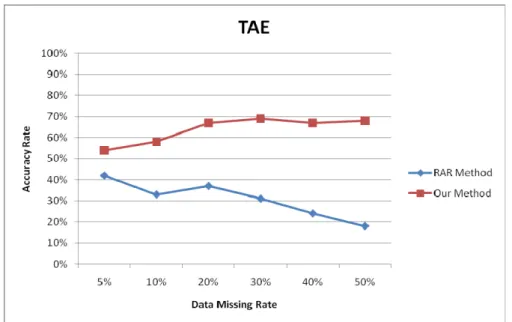
proposed method over various data missing rates on the TAE dataset. It could be seen from the figure that our proposed method had a better precision than RAR-MVC.
Figure 1: The comparison of accuracy for our method and RAR-MVC on TAE.
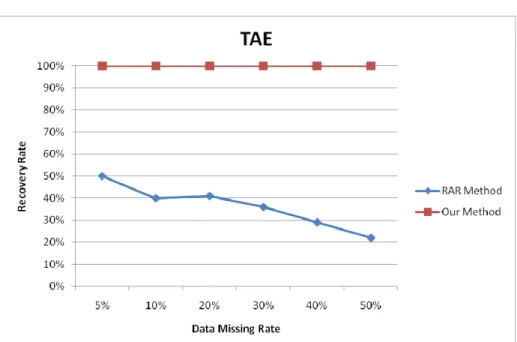
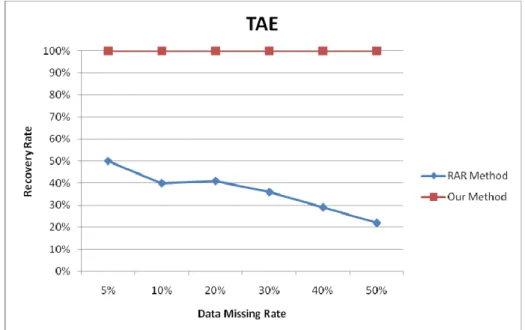
Note that when the data rate was high, the number of missing values would become large and thus the RAR-MVC approach would get a decreasing accuracy along with the growth of missing rates. Our proposed approach, however, kept nearly stable along with the growth of missing rates. Figure 2 then shows the recovery rates generated by our proposed method and RAR-MVC over various data missing rates on the TAE dataset. From this figure, it could be observed that our proposed method always had the recovery rate of 100% since all the values were guessed. RAR-MVC, however, had the recovery rate decreasing along with the growth of the missing rates.
22 / 27 .
Figure 2: The comparison of recovery rates for our method and RAR-MVC on TAE.
Figure 3 then shows the accuracy obtained by our approach and by RAR-MVC for different data missing rates on the Tic-Tac-Toe dataset. The results are similar to those for the TAE data set.
23 / 27
Figure 3: The comparison of accuracy for our method and RAR-MVC on Tic-Tac-Toe.
At last, Figure 4 shows the recovery rates obtained by our method and by RAR-MVC on the Tic-Tac-Toe dataset. The results were also similar to those for the TAE data set.
Figure 4: The comparison of recovery rates for our method and RAR-MVC on Tic-Tac-Toe.
24 / 27
6. Conclusion and Future Work
The recovery of missing values is an important issue in data preprocessing. In this paper, we have proposed an iterative approach to fully recover all the missing attribute values based on the association between different attribute values in a dataset.
The proposed approach consists of three phases, respectively for roughly assigning proper values, filling in the remaining missing values, and adjusting the assigned missing values. The experimental results also indicate when the missing rate of a dataset is small, the accuracy of our proposed method is a little higher than the RAR-MVC approach. Along with the increase of the missing rates, the proposed method has a more significant effect. As to the recovery rate, it could be observed that our method allways performed better than the RAR approach. The reason is that our method uses the iterative mechanism to recover all the missing values. Our approach can thus raise accuracy and recovery rates of predicted missing values. In the future, we will further extend this approach to incomplete temporal databases.
25 / 27
References
[1] R. Agrawal, T. Imielinksi and A. Swami, “Mining association rules between
sets of items in large database,“ The 1993 ACM SIGMOD Conference on
Management of Data, 1993, pp. 207 – 216.
[2] R. Agrawal, T. Imielinksi and A. Swami, “Database mining: a performance perspective,” IEEE Transactions on Knowledge and Data Engineering, Vol. 5, No. 6, 1993, pp. 914-925.
[3] R. Agrawal and R. Srikant, “Fast algorithm for mining association rules,” The International Conference on Very Large Data Bases, 1994, pp. 487-499. [4] M. Y. Chen and A. P. Chen, “Knowledge management performance evaluation:
a decade review from 1995 to 2004,” Journal of Information Science, Vol. 32, No. 1, 2006, pp. 17–38.
[5] T. P. Hong, L. H. Tseng and S. L. Wang, “Learning rules from incomplete training examples by rough sets,” Expert Systems with Applications, Vol. 22, No. 4, 2002, pp. 285-293.
[6] M. Kryszkiewicz, “Probabilistic Approach to Association Rules in Incomplete Databases,” Lecture Notes in Computer Science, Vol. 1846, 2000, pp. 133-138. [7] J. R. Nayak and D. J. Cook, “Approximate association rule mining,” The
26 / 27
Fourteenth International Florida Artificial Intelligence Research Society Conference, 2001, pp. 259-263.
[8] M. B. Nunes, F. Annansingh and B. Eaglestone, “Knowledge management issues in knowledge-intensive SMEs,” Journal of Documentation, Vol. 62, No. 1, 2006, pp. 101–19.
[9] T. Orchard and M. A. Woodbury, “A missing information principle: theory and
applications,” The 6th Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1, 1972, pp. 697-715.
[10] G. Protaziuk and H. Rybinski, “Discovering association rules in incomplete transactional databases,” Lecture Notes in Computer Science, Vol. 4374, 2007, pp. 308-328.
[11] A. Ragel and B. Cremilleux, “Treatment of missing values for association rules,” Lecture Notes in Computer Science, Vol. 1394, 1998, pp. 258-270. [12] A. Ragel and B. Cremilleux, “MVC – a preprocessing method to deal with
missing values,” Knowledge-Based Systems, Vol. 12, No. 5, 1999, pp. 285–291.
[13] J. J. Shen, C. C. Chang and Y. C. Li, “Combined association rules for dealing with missing values,” Journal of Information Science, Vol. 33, No, 4, 2007, pp.
27 / 27 468–480.
[14] R. Srikant, Q. Vu and R. Agrawal,, “Mining association rules with item constraints,” The Third International Conference on Knowledge Discovery and
Data Mining, 1997, pp. 67 – 73.
[15] C. H. Wu, C. H. Wun and H. J. Chou, “Using association rules for completing missing data,” The Fourth International Conference on Hybrid Intelligent Systems, 2004, pp. 236-241.