探討平面圖的d維矩形表示法 - 政大學術集成

全文

(1)國立政治大學應用數學系數學教學碩士在職專班碩士學位論文. 治政大 A Study on Strict d-box Representations of 立 ‧ 國. 學. Planar Graphs. 探討平面圖的 d 維矩形表示法. ‧. n. er. io. sit. y. Nat. al. Ch. engchi. i n U. v. 碩專班學生：劉淑慧撰指導教授：張宜武博士. 中華民國 102 年 1 月 10 日.

(2) Abstract We study strict d-box representations of planar graphs. We prove that a 4-connected planar triangulation graph G has a strict 2-box representation. We extend this result to that every planar graph has a strict 3-box representation. Our goal is to provide some fresh insights into the current status of research in the area while suggesting directions for the future.. keywords: interval graphs; 4-connected planar triangulation graph; strict d-box representation.. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. i. i n U. v.

(3) 中文摘要. 本文我們探討平面圖形的嚴格 d 維矩形表示法。我們證明了四連通三角平面圖有嚴格的二維矩形表示法，而且我們推廣到每一個平面圖都有嚴格的三維矩形表示法。我們的目標是希望能在平面圖矩形表示法的現今地位上，提供新的洞悉,並給未來學習者一個方向。關鍵詞：區間圖，四連通三角平面圖，嚴格 d 維矩形表示法。. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. ii. i n U. v.

(4) Contents Abstrat. i. 中文摘要. ii. 1. Introduction. 1. 2. Strict 2-box representation. 4. 2.1. Defitions and theprem of cyclically 4-edge-connected planar graphs and 4-connected planar triangulation graphs………………………………... 4. 2.2. Planar graphs have strict a 2-box representations by at least two boxes……..8. 立. 10. 學. A strict 2-box representation for 4-connected planar triangulation graphs……………………………………………………………….…….. 10. 3.2. A strict 3-box representation for planar graphs………………………….….18. ‧. 3.1. al. n. References. Ch. engchi. er. io. Open problems and further directions of study. sit. y. Nat. 4. Some results on d-box representation. ‧ 國. 3. 政治大. i n U. v. 23 24.

(5) 1. Introduction In graph theory, an intersection graph of a set system is the graph whose. vertices are the sets such that two vertices are adjacent if and only if the sets intersect. The interval graphs were introduced to study intersecting intervals on the real line. Each vertex v in an interval graph G = (V, E) is associated with an interval Iv , and if two vertices are connected by an edge in G , then the intersection of their associated intervals is nonempty. Some of the intervals may have nonempty intersection, and the others have empty intersection.. 政治大 pletely. Instead of representing 立 a vertex by one interval it may be represented by a W. T. Trotter [6] tells us that interval graphs have been characterized com-. specified number of intervals or an interval of higher dimensions. In the case of a. ‧ 國. 學. specified number of intervals, Scheinerman and West [4] proved that every planar graph is an intersection graph such that each vertex is represented by at most three. ‧. intervals on the real line. In the case of higher dimensions, Scheinerman [3] proved. sit. y. Nat. that in two dimensions two rectangles for each vertex are sufficient to represent any. io. er. planar graph. And Melinkov [2] charactherizes the planar graphs whose vertices can be represented by horizontal intervals in the plane such that two interval are. n. al. i n U. v. adjacent if they can be joined by a vertical line not intersecting any other inter-. Ch. engchi. val. Duchet, Hamidoune, Las Vergnas, and Meyniel [1] proved that every maximal planar graph has such a representation. We adopt that a vertex is represented in higher dimensions. So we say that a graph G has a d-box representation (i.e. d-dimensional closed intervals) if G is an intersection graph such that the sets are closed d-boxes in Rd . In this paper, we want to discuss the strict d-box representation, it means that a graph is a d-box representation and no two of which have an interior point in common and such that two boxes which intersect have precisely a (d−1)-box in common. If a graph G is a strict 2-box representation(d = 2) , then all vertices of G are drawn as rectangles. 1.

(6) and all edges are drawn as a horizontal or a vertical line segment. If there four edges form the four “outer corners”, then the representation is called rectangular representation. In 1953, Ungar [7] proved that every cubic cyclically 4-edge-connected graph has a plane representation such that each face is bounded by a rectangle. And Ungar showed that any plane embedding T of a cyclically 4-edge-connected planar cubic graph G has a rectangular drawing if four vertices of degree 2 are inserted on some edges on the outer face. Carsten Thomassen [5] generalizing the results of Ungar, C. Thomassen obtains. 政治大. a necessary and sufficient condition for a plane graph T with the maximum degree. 立. 4 ≤ 3 to have a rectangular representation when a quadruplet of vertices of degree 2. ‧ 國. 學. on F0 (T) are designated as corners for a rectangular representation. He prove that every planar graph is the intersection graph of a collection of three-dimensional. ‧. boxes, with intersections occurring only in the boundaries of the boxes. In 1984, C. Thomassen [8] characterizes the graphs that have such representations in the. Nat. sit. y. plane, called strict d-boxes graph if G is an intersection graph such that the sets. io. er. are closed d-boxes in Rd . These are precisely the proper subgraphs of 4-connected planar triangulations, which we characterize by forbidden subgraphs. He prove that. n. al. Ch. i n U. v. every planar graph is a strict 3-box graph. And E. R. Scheinerman [3] showed that. engchi. every planar graph has a strict representation using at most two rectangles per vertex. In our article, we discuss a strict 2-box representation and a strict 3-box representation . In Chapter 1, we introduce intersection graphs, interval graphs, and the definition of a strict d-boxes representation. In Chapter 2, we introduce the definitions, propositions and the theorem of strict 2-boxes graphs. In Chapter 3, we show a strict 2-box representation for a 4-connected planar triangulation and then we extend to a strict 3-box representation for planar graphs. In Chapter 4, we mention. 2.

(7) some open problems and further directions of research.. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 3. i n U. v.

(8) 2 2.1. Strict 2-box representation Definitions and theorems of cyclically 4-edge-connected planar graphs and 4-connected planar triangulation graphs In this section we give some definitions and present preliminary results. Be-. cause Theorem 2.13(Ungar, 1953 [7]) showed that a cyclically 4-edge-connected planar graph G has a strict 2-box representation. Definition 2.1. The graphs can be drawn in the plane without crossing edges, such. 政治大. graphs are planar.. 立. Definition 2.2. A graph G is called cubic if the degree of v is 3 for every vetex v.. ‧ 國. 學. Definition 2.3. A graph G is called 4-edge-connected if the removal of at least 4 edges leaves a graph such that the graph has more than one component.. ‧. Definition 2.4. A planar graph G is called cyclically 4-edge-connected planar. y. Nat. io. sit. graph if G is cubic and G is 4-edge-connected graph.. n. al. er. Example 2.5. Consider the graph in Figure 1 is cyclically 4-edge-connected graph,. i n U. v. But the graph in Figure 2 is not cyclically 4-edge-connected graph, since the removal. Ch. engchi. of the three edges drawn by thick dotted lines leave a graph such that the graph has more than one component.. Figure 1: A cyclically 4-edge con-. Figure 2: not a cyclically 4-edge con-. nected graph. nected graph. 4.

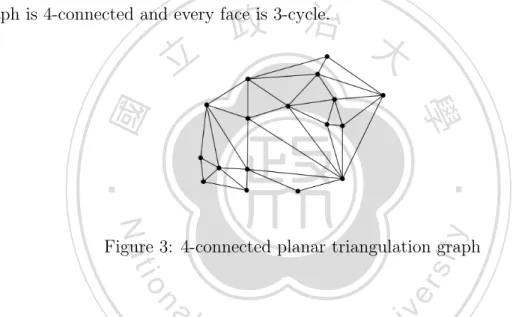
(9) We will discuss the strict 2-box representation for 4-connected planar triangulation in section 3.1. So we gives some of the definitions for 4-connected planar triangulation. Definition 2.6. A graph G is called 4-connected if the removal of at least 4 vertices leaves a graph such that the graph has more than one component. Definition 2.7. A triangulation is a simple plane graph where every face boundary is 3-cycle. Definition 2.8. A graph is called 4-connected planar triangulation if the planar. 政治大. graph is 4-connected and every face is 3-cycle.. 立. ‧. ‧ 國. 學 y. Nat. er. io. sit. Figure 3: 4-connected planar triangulation graph. al. n. v i n C 4-edge-connected Example 2.9. G is a cyclically U and hence the dual graph h e n g c h i graph H of G is a 4-connected planar triangulation.. Figure 4: The left is a 4-edge-connected graph and the right is a 4-connected planar triangulation. 5.

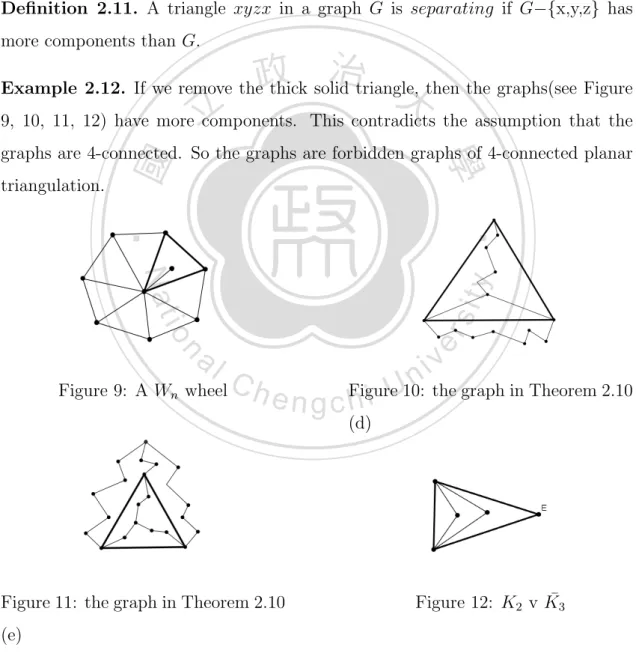
(10) The following theorem could help us to check if a given graph is 4-connected planar triangulation. It also gives us a way to construct graphs that are not 4connected planar triangulation from the forbidden graphs. Theorem 2.10 (Carsten Thomassen, Interval of Planar Graphs). The graphs which are not proper subgraphs of 4-connected planar triangulations and which are edgeminimal with that property are precisely the following:. (a) The triangle-free subdivisions of the Kuratowski graphs K5 and K3,3 . (b) The planar triangulations with no separating K3 . (i.e. K4 and the 4-connected planar triangulations). 立. 政治大. (c) The graphs obtained from a wheel Wn of order n ≥ 5 by adding a vertex and. ‧ 國. 學. joining it to the center of the wheel(see Figure 5).. (d) Any graph obtained from K4 by subdividing one edge xy and adding an addi-. ‧. tional path of length at least 2 between the two other vertices of the K4 (see. sit. y. Nat. Figure 6).. er. io. (e) Any graph which is obtained from K5 with one missing edge by subdividing edges incident with the missing edge(in such a way that the graph does not contain a. n. al. Ch. graph described under(d), see Figure 7).. engchi. i n U. v. (f ) The graph K2 v K¯3 (see Figure 8).. Figure 5: A Wn wheel. Figure 6: the graph in Theorem 2.10 (d). 6.

(11) Figure 8: K2 v K¯3. Figure 7: the graph in Theorem 2.10 (e). Definition 2.11. A triangle xyzx in a graph G is separating if G−{x,y,z} has more components than G.. 政治大. Example 2.12. If we remove the thick solid triangle, then the graphs(see Figure. 立. 9, 10, 11, 12) have more components. This contradicts the assumption that the. ‧. ‧ 國. triangulation.. 學. graphs are 4-connected. So the graphs are forbidden graphs of 4-connected planar. er. io. sit. y. Nat. al. n. v i n wheel C h e n g c Figure h i U10: the graph in Theorem 2.10. Figure 9: A Wn. (d). Figure 12: K2 v K¯3. Figure 11: the graph in Theorem 2.10 (e). 7.

(12) 2.2. Planar graphs have strict 2-box representations by at least two boxes. Theorem 2.13. (Ungar, 1953 [7]) A cyclically 4-edge-connected planar graph G has a plane representation(strict 2-box representation).. Because a cyclically 4-edge-connected planar graph has no separating triangle, So we have the corollary as following: Corollary 2.14. (C. Thomssen, 1986 [8]) Any planar graph with no separating. 政治大 Theorem 2.15. (C. Thomssen, 立 1986 [8]) A graph G is a strict rectangle graph if triangle has a strict rectangle representation.. ‧ 國. 學. and only if G is a proper subgraph of some 4-connected planar triangulation H.. We also obtain an extension of the result of Scheinerman that any planar. ‧. graph has a rectangle representation(2-box representation) such that each vertex is. sit. y. Nat. represented by at most two rectangles.. al. er. io. Corollary 2.16. (E. R. Scheinerman, 1984 [3]) Every planar graph has a strict. n. rectangle representation in R2 such that each vertex is represented by at most two rectangles.. Ch. engchi. i n U. v. Proposition 2.17. (C. Thomssen, 1986 [8]) Every planar graph G is the union of two triangle free graphs. Lemma 2.18. If G is a planar graph not containing any subgraph described in Theorem2.12(c), then G contains a 4-connected planar triangulation if and only if some component of G is a 4-connected planar triangulation.. 8.

(13) 3 3.1. Some results on d-box representation A strict 2-box representation for 4-connected planar triangulation graphs In this section we use two ways to draw the strict 2-box representation for. 4-connected planar triangulation graph, and give some examples to show how to draw them. We try to extended the way to draw a strict 3-box representation in next section.. 政治大 graph such that the sets are closed d-boxes in R , no two of which have an interior 立 Definition 3.1. A graph G is a strict d-box representation if G is an intersection d. point in common and such that two boxes which intersect have precisely a (d − 1)-. ‧ 國. 學. box in common.. ‧. Example 3.2. If a graph G is a strict 1-box representation, then the vertex can be drawn by a 1-dimensional closed interval and the two intervals which intersect. Nat. n. al. er. io. sit. y. have precisely a 0-box in common(see Figure 13).. Ch. engchi. i n U. v. Figure 13: 1-box representation. Example 3.3. A graph G is a strict 2-box representation if all vertices of G are drawn as rectangles, and all edges are drawn as a horizontal or a vertical line segment(see Figure 14). If there four edges form the four “outer corners”, then the representation is called rectangular representation(see Figure 15).. 9.

(14) Figure 14: A strict 2-box representa-. Figure 15: a correspond rectangular. tion. representation. 政治大. We adopt that strict 2-box representation in this article is the graph in Figure 14.. 立. ‧ 國. 學. Remark 3.4. By Theorem2.13, we know that a cubic 4-edge-connected planar graph G has a strict 2-box representation. And we can think of G as a “geometric dual graph” of interval system. That means that the strict 2-box representation is pre-. ‧. cisely the proper subgraphs of the 4-connect planar triangulations.. y. Nat. sit. Example 3.5. Consider the graph G in Figure 16 is a cubic 4-edge-connected. al. er. io. planar graph, and G has a strict 2-box representation. Then the graph H in Figure. n. 17 is a dual graph of G, and we can see H is a 4-connected planar triangulation graph.. Ch. engchi. i n U. v. Figure 16: G is a cubic 4-edge con-. Figure 17: H is a 4-connected planar. nected planar. triangulation. 10.

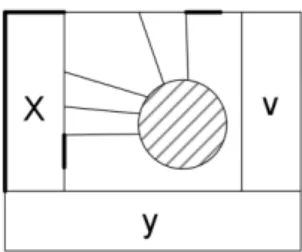
(15) The following theorem could help us to check that if a given graph has a strict 2-box representation. It also gives us the forbidden configurations for strict 2-box representations. Theorem 3.6. (Carsten Thomassen, 1986, [6]) If we draw a facial cycle C of a cubic planar G as a rectangle R such that none of its corners are vertices of C, then by Carsten Thomassen [5] this can be extended to a rectangular representation(a strict 2-box representation) of G inside R if and only if. (a) For each vertex x not in C, there is only one set of three edges that separates x. 政治大 (b) Each connected component 立 of G − V (C) is joined to two opposite sides of R from C, namely the set of edges incident x(see Figure 18);. ‧ 國. 學. and each chord of C( if any ) joins two opposite sides of R (see Figure 19); (c) For each connected component H of G − V (C) and each edge e of G, H is in. n. al. er. io. sit. y. Nat Figure 18: (a). ‧. G − e joined to at least two sides of R (see Figure 20).. Ch. engchi. Figure 19: (b). i n U. v. Figure 20: (c). Theorem 3.7. (Carsten Thomassen extension of Ungar’s result) Let G be a 4connected planar triangulation graph and let zyxz and zyvz be two triangles of G(see Figure 21). Then the dual graph H of G has a strict 2-box representation such that z corresponds to the unbounded face and such that x, y, and v correspond to rectangles as shown in Figure 22.. 11.

(16) Figure 21: two triangles zyxz and. Figure 22:. zyvz. rectangle. x, y, z, v correspond to. Proof. In order to show that the configuration in Figure 22 can be extend to a. 政治大 It suffices to show 立 that none of the forbidden configurations indicated in. rectangular representation of H we apply Theorem 3.6(Carsten Thomassen, 1986, [6]).. ‧ 國. 學. Theorem 3.6 occurs.. case1: One such configuration is indicated in Figure 23.Clearly, if the removal of the. ‧. three thick solid lines leaves the graph, the shaded area will be a component.. n. al. er. io. sit. y. Nat. Obviously, this contradicts the assumption that G is 4-connected.. Ch. engchi. i n U. v. Figure 23: the removal of three thick solid lines. case2: One such configuration is indicated in Figure 24 and 25. If the removal of the three or four thick solid lines leaves the graph, then the shaded area will be a component.Obviously, this contradicts the assumption that G is 4-connected.. 12.

(17) Figure 24: the removal of four thick. Figure 25: the removal of three thick. solid lines. solid lines. case3: Another configuration is indicated in Figure 26 and 27. If the removal of the three or four thick solid lines leaves the graph, then the shaded area will be a. 政治大. component. Clearly, this contradicts the assumption that G is 4-connected.. 立. ‧. ‧ 國. 學 y. Nat. solid lines. solid lines. Ch. engchi. er. n. al. sit. Figure 27: the removal of three thick. io. Figure 26: the removal of four thick. i n U. v. Finally the forbidden configuration in Theorem 3.6 do not occur and the proof is complete.. Moreover, we try to look at two examples(Example 3.8 and 3.9 ). It gives us clear picture how to draw a strict 2-box representation, and show that the two triangles we choose are drawn by Theorem3.7. Example 3.8. There is a 4-connected triangulation graph in Figure 28. We choose two triangles cdf c, and cf hc. Let the rectangle which c corresponds to be the unbounded face, and draw d, f and h correspond to rectangles as shown in Figure 29. By Theorem 3.7, we get a strict 2-box representation.. 13.

(18) Figure 28: A 4-connected triangula-. Figure 29: A graph in Figure 28 corre-. tion graph and we choose two trian-. sponding strict 2-box representation. gles cdf c, and cf hc. 治政大strict 2-box representation in We choose another two triangles and get another 立 the following example. ‧ 國. 學. Example 3.9. There is a 4-connected triangulation graph in Figure 30. We choose two triangles cdac, and cdf c. Let the rectangle which c corresponds to be the. ‧. unbounded face, and draw a, d and f correspond to rectangles as shown in Figure. n. al. y. er. io. sit. Nat. 31. By Theorem 3.7, we get a strict 2-box representation.. Ch. engchi. i n U. v. Figure 30: A 4-connected triangula-. Figure 31: A graph in Figure 30 corre-. tion graph and we choose two trian-. sponding strict 2-box representation. gles cdac, and cdf c. 14.

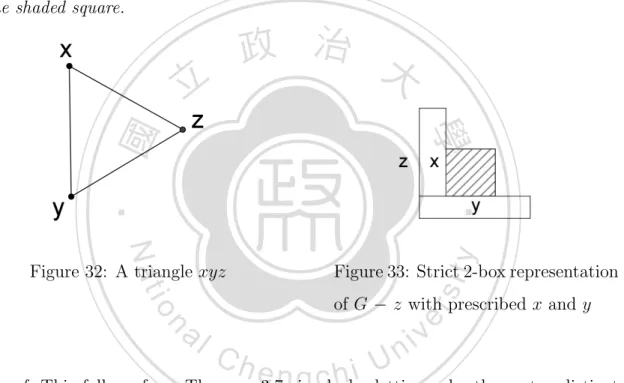
(19) Consider G is 4-connected triangulation grpah. If we can’t find two triangles zyxz and zuvz which is described by Theorem 3.7 in G. We can choose a triangle zxyz in G to be a unbounded face, and draw a strict 2-box representation. That means we can choose any triangle in G, and we have the corresponding strict 2-box representation. Corollary 3.10. Let G be a 4-connected planar triangulation graph and zxyz a triangle in G(see Figure 32). Then G − z has a strict 2-box representation such that x and y are represented as shown in Figure 33 and all other rectangles are in the shaded square.. 政治大. 立. ‧. ‧ 國. 學 y. Nat. of G − z with prescribed x and y. n. er. io. al. Figure 33: Strict 2-box representation. sit. Figure 32: A triangle xyz. Ch. engchi. i n U. v. Proof. This follows from Theorem 3.7 simply by letting v be the vertex distinct from x, y, z such that vyzv is a triangle.. Moreover, we try to look at two examples(Example 3.11 and 3.12). It gives us clear picture how to draw a strict 2-box representation.. 15.

(20) Example 3.11. There is a 4-connected triangulation graph in Figure 34. We choose agha, and let the rectangle which h corresponds to be the outer face, and draw the strict rectangle representation of G − h with prescribed a and g by Corollary 3.10, and that is a strict 2-box representation in Figure 35. We get a strict 2-box representation.. 學. ‧ 國. 立. 政治大. Figure 34: we choose a triangle agha. Figure 35: strict 2-box representation. ‧. Example 3.12. There is a 4-connected triangulation graph in Figure 36. We choose. y. Nat. sit. cdf c, and let the rectangle which f corresponds to be the outer face, and draw the. al. er. io. strict rectangle representation of G − f with prescribed c and d by Theorem 3.9,. v. n. and that is a strict 2-box representation in Figure 37. We get another strict 2-box representation.. Ch. engchi. Figure 36: we choose a triangle cdf c. i n U. Figure 37: strict 2-box representation. 16.

(21) 3.2. A strict 3-box representation for planar graphs In this section we mention a strict 3-box representation by extending Corollary. 3.10. Now we provide some definitions and short proofs of 3-box representation for planar graph. Definition 3.13. If a graph G is a strict 3-box representation, then the vertex can be drawn by a 3-dimensional closed interval and the two box which intersect have precisely a 2-box in common(see Figure 38).. 立. 政治大. ‧. ‧ 國. 學 y. Nat. n. al. er. io. sit. Figure 38: strict 3-box representation. i n U. v. By Theorem 2.10(c), we know that the graph wheel W5 is the forbidden graph of. Ch. engchi. strict 2-box representation. By Corollary 2.16, E. R. Scheinerman tells us that every planar graph has a strict rectangle representation in R2 (strict 2-box representation) such that each vertex is represented by at most two rectangles. We show that the graph wheel W5 has a strict 2-box representation such that each vertex is presented by at most two rectangles, and it can be drawn by a strict 3-box representation. Example 3.14. A planar graph wheel W5 (see Figure 39) which is the forbidden graph of a strict 2-box representation. It can be drawn by a strict 2-box representation, and each vertex is represented by at most two rectangles(see Figure 40). We also draw it by a strict 3-box representation, and each vertex is represented by one box(see Figure 41).. 17.

(22) Figure 39: planar. A. Figure 40: strict. Figure 41: strict. graph. 2-box represen-. 3-box represen-. tation. tation. wheel W5. 政治大. We give some definition for the strict 3-box representation.. 立. Definition 3.15. Suppose the boxes Bx ,By , and Bz in R3 such that Bx ⊃ {0}. ‧ 國. 學. × [0,k] × [0,k], By By ⊃ [0,k] × {0} × [0,k], Bz ⊃ [0,k]×[0,k] × {0}, and for i ∈ {x, y, z} and k is positive integer, Bi contains no point with positive i-coordinate.. 42).. ‧. Then we say the origin is an inner corner of the boxes Bx , By , and Bz (see Figure. n. er. io. sit. y. Nat. al. Ch. engchi. i n U. v. Figure 42: inner corner. Definition 3.16. If there exists a positive real number ε such that the box (0,ε]×(0,ε]×(0,ε] intersects no box in the box system, then we say it is an empty inner corner. We recall the Corollary 3.10, and we can extend to the strict 3-box representation. The following Corollary help us to check that if a given graph has a strict. 18.

(23) 3-box representation. Corollary 3.17. Let G be a 4-connected triangulation and xyzx a triangle in G. Suppose the boxes Bx , By , and Bz is an original inner corner.Then Bx , By , Bz can be extended to a strict box representation of G in R3 such that all other boxes are in the box [0, 1] × [0, 1] × [0, 1], and all vertices not adjacent to z are in the box [0, 1] × [0, 1] × [2/3, 1](see Figure 43).. 立. 政治大. ‧ 國. 學. Figure 43: all vertices not adjacent to z are in the box [0, 1] × [0, 1] × [2/3, 1]. ‧. Nat. sit. y. We want to discuss every planar graph has a strict 3-box representation, so we. io. er. need to prove that every planar triangulation has a strict 3-box representation.. al. n. v i n Cxyzx tion graph G, then the triangle a f acial triangle. h e isncalled gchi U. Definition 3.18. If there is no vertex in the triangle xyzx of the planar triangula-. Theorem 3.19. Every planar triangulation G has a strict box representation in R3 0. 0. 0. such that every facial triangle except possibly one prescribed facial triangle x y z x. 0. has an empty inner corner. 0. 0. 0. 0. Proof. Let x y z x be any triangle that we choose.If G has a separating triangle xyzx we choose it such that the number of vertices in the component of G−{x,y,z} 0. 0. 0. 0. not intersecting x y z x is smallest possible. Suppose G = G1 ∪ G2 where G1 and G2 are planar triangulations with precisely 0. 0. 0. 0. xyzx in common, and G2 contains x y z x , G1 is 4-connected or isomorphic to K4 .. 19.

(24) case1: G1 is isomorphic to K4 0. 0. 0. 0. Let G2 = xyzx = x y z x (see Figure 44). We can choose the separating triangle xyvx. Clearly, the vertex v can be drawn the box Bv and the triangle xyvx and yzvy have empty inner corners(see Figure 45).. Figure 45: The strict 3-box representation of the graph 治政in Figure 44. 大. Figure 44: G1 is a K4. 立. ‧ 國. 學. case2: G1 is 4-connected, not k4. 0. 0. 0. 0. If G is 4-connected, we put G = G1 and let G2 = xyzx = x y z x . Then we. ‧. represent G2 such that x, y, and z are encoded as in Corollary 3.17 (If G2 has more than three vertices, this can be done by the induction hypothesis). And. y. Nat. sit. we modify the representation in Corollary 3.17.. al. er. io. For each vertex u in G1 −{x,y,z} which is adjacent to z we cut off from its. n. box a box of the form (1 − ε,1] × I1 × I2 or I1 × (1 − ε,1] × I2 , where I1 ,. Ch. i n U. v. I2 are intervals and ε is a small positive number such that different values for. engchi. ε are used for different vertices u.. In other words, every vertex u can be drawn in the B1 or B2 (see Figure 46). In this way we create an inner empty conner(close to the plane with equation x=1 or y=1)for each facial triangle that contaions z. In order to achieve the same for all other facial triangles as well we translate all other boxes corresponding to vertices of G1 −{x,y,z} a little upwards, i.e.,the vector of translation is of the form (0,0,ε)where ε is a small positive number and different values for ε are used for different vertices. In this way each facial triangle in G1 not containing z gets an inner empty corner close to one of the planes with equation z=1, z=1/2.. 20.

(25) Figure 46: B1 is the box (1 − ε,1] × I1 × I2 and B2 is the box I1 × (1 − ε,1] × I2. 政治大. 立. Since every planar graph is an induced subgraph of a planar triangulation, then. ‧ 國. 學. we have the following theorem.. Theorem 3.20. Every planar graph has a strict box representation in R3 .. ‧. y. Nat. Proof. Suppose G is a planar graph, and given a vertex v in any face which is not. sit. triangle. Drawing some edge from v to the vertices of the face, then we get a new 0. 0. er. io. planar triangulation graph G (see Figure 47). By Theorem 3.19, G has a strict. al. n. v i n the graph G, then we get theCstrict representation of G. h e n3-box gchi U. 3-box representation. If the removal of the box corresponding to the vertex v leaves So the proof is. complete.. Figure 47: draw a vertex v in the face which is not triangle. 21.

(26) 4. Open problems and further directions of study In our article, we have presented the forbidden subgraph of 4-connected planar. triangulation and the strict 2-box representation. We also show that every planar has a strict 3-box representation. There are still some open problems from our article and we mention them in the following.. 1 Does every 3-connected planar graph have a strict 2-box representation? 2 Does every 2-connected planar graph have a strict 2-box representation?. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 22. i n U. v.

(27) References [1] P. Duchet, Y. Hamidoune, M. Las Vergas, and H. Meyniel, Representing a planar graph by vertical lines joing different levels, Discrete Math. 46(1983), 221-332. [2] L. A. Melnikov, Problem at the ”Sixth Hungar. Colloq. on Combinatorics”, Eger, 1981. [3] E. R. Scheinerman, ”Intersection Classes and Multiple Intersection Parame-. 政治大 E. R. Scheinerman and D. B. West, ”The interval number of a planar graph: 立 ters”, Ph. D. thesis, Princetion Uni., 1984.. [4]. Three intervals suffice, J. Combin. Theory Ser. B 35 (1983), 224-239.. ‧ 國. 學. [5] C. Thomassen, Plane representations of graphs, in ”Progress in Graph The-. 1984.. ‧. ory”, (J. A. Bondy and U. S. Murty, Eds.), pp.43-69, Academic Press, Toronto,. y. Nat. io. sit. [6] W. T. Trotter, Graphs and partially ordered sets, in ”Selected Topics in Graph. n. al. er. Theory 2”, (L. W. Beineke and R. J. Wilson, Eds.), pp.237-268, Academic Press, London, 1983.. Ch. engchi. i n U. v. [7] P. Unger, On diagrams representing maps, J. London Math. Soc. 28 (1953), pp.336-342 [8] C. Thomassen, ”Interval representations of planar graphs, Journal of Combinatorial Theory, Series B, pp.9-20, 1986.. 23.

(28)