SHELL-MODEL CALCULATIONS OF ONE-HOLE STATES IN THE NUCLEI OF A = 41-43

Shell-model

calculations

of

one-hole states

in

the

nuclei

of

A

=41

—

43

D.

S.

Chuu and

C. S.

Han

Department

of

Electrophysics, National Chiao Tu-ng University, Hsinchu, Taiwan, Republic

of

China

S.

T.

Hsieh

Department

of

Physics, National Tsing Hua University, Hsinchu, Taiwan, Republic

of

China

M. M.

King Yen

Department

of

Nuclear Engineering, National Tsing Hua University, Hsinchu, Taiwan, Republic

of

China (Received 17 February 1982)

The one-hole states ofA

=41

—

43nuclei are calculated with amodel space spanning the (f7/2p3/2)" (d3/2si/2) ' configurations. The two-body effective interaction is assumed to

be the modified surface-delta type. Energy spectra and spectroscopic factors are calculated and compared with the observed values. Satisfactory results are obtained.

NUCLEAR STRUCTURE A

=41

—

43,calculated effective interaction, energy spectra, spectroscopic factors.

I.

INTRODUCTION

The nuclei in the

lf-2p

shell have long been

of

in-terest to both experimental and theoretical nuclear physicists. Extensive studies have been done' 2 _for

the normal parity states

of

the nuclei in this region.

For

the non-normal parity levels, however, the situ-ation isless well understood. This paper will give a systematic study

of

the one-hole states in the mass region

of

A=41

—

43 within the framework

of

the

shell model. The particles are assumed

to

be distri-buted in the 1_{f7/2 and 2p3/2} orbitals and one hole is

assumed tobe in the 1d3&z or2s&&q orbital.

A least-squares fit calculation on the non-normal parity states in

lf-2p

shell nuclei has been per-formed by Dieperink and Brussard within the description

of

the (lf7/2)"(ld3/2) ' configuration. In their results, only the low-lying energy levels can be reproduced and the calculated transition rates are not in agreement with the observed values. This discrepancy isdue to the fact that the configuration space they used is too small. Later, Hsieh et

al.

'

calculated the non-normal parity states for the

nu-clei in the

A=39

—

41 region by expanding the

model space to include the complete

(lf-2p)

shell

and single-hole states in the (2s,ld) shell. Some dis-tinct improvements were obtained. The spectro-scopic factors and electromagnetic (EM) transition rates obtained were in reasonably good agreement

with experimental data.

For

the heavier mass

re-gion

A=42,

the extended model space has not yet

been employed. Lawson and Muller-Arnke have studied the magnetic moment

of

the

(3/2)

i+ _{state in} Scand found that this state does not have apure

(f

7/2) (d3/2 ) ' configuration. The lifetime and

magnetic moment can only be accounted for

simul-taneously by extending the model space to include about

10% of

_{the (f7/2) (si/2)} ' admixture. The importance

of

the s~&z hole state can also be seen in

the spectrum

of

potassium isotopes; the

l=0

hole strength steadily decreases in energy with increasing mass. From the

/=1

single-particle strength

ob-served for levels around 1 MeV in Ca, it is clear that the contribution

of

the_p3/2 orbital for nuclei

of

A &42 is also important. Johnstone recently re-ported calculations for the one-hole states in

potas-sium isotopes

(A=40

—

46) using a model space based on the

(f

7/2~P3/2 )"(d3/2,$1/2)

configuration. The matrix elements

of

the residual interaction are treated as free parameters which are determined by aleast-squares fit tothe observed

en-ergy levels; good agreement is achieved in his re-sults. The works mentioned above encourage us to reinvestigate the one-hole states in the mass region

of

A

=41

—

43.

A better systematic prediction is ex-pected

if

we expand the original model space (lf7/2,ldll/2 ') to include the active particle orbit 2p3&z and the active hole orbit 2s&&z.

It

is hoped

that so doing, and considering only one-particle, in-stead

of

multiparticle, excitation from the 1d3/p or

on the energy level calculation is expected to be small. The reason is as follows. The spurious states are distributed in the space within laic@

of

excita-tion, and our model space contains only part

of

them. Furthermore, the intensities

of

the low-lying

states are rather concentrated in certain components

of

the basis states. Thus, the effect

of

spurious states is negligible except in the calculation

of

El

transition rates, which weare not interested in.

II.

THEMODEL

In this calculation, we consider the one-hole states

of

A=41

—

43 nuclei; the nucleus Ca is as-sumed to be the core. The active nucleons are dis-tributed in the lf7/p and 2p3/2 orbitals and one

ac-tive hole is allowed in the 1d3/2 or2s&/2 orbital. In

order to obtain a model space

of

manageable size,

we neglect the 2p~/2 orbital. This should not

intro-duce significant errors since the _2p&/2 lies about 4 MeV above the lf7/2 orbital. Also, according to the Kuo-Brown matrix elements, the _f7/2 p'[/2

in-teraction is very weakly attractive. The omission

of

the lds/2 and 1_{f5/2 orbitals from the model space} is

quite reasonable because the splitting

of

the

ob-served single-particle levels

of

2s~/2-1d_5/2 and

1

f

5/2-2p3/p are much larger than those

of

ldll/g-2s)/2 and 2p3/2 lf7/2 Within this model space we diagonalize an effective one-body plus

two-body Hamiltonian. We identify the resulting

eigenvalues with observed energy levels and use the eigenvectors as wave functions to calculate various observables.

The effective Hamiltonian in this space has the orm

H =Ho+Hpp+Hgp

.

Here Ho is the Hamiltonian

of

the single particle in the effective field

of

the core. The single-particle

energies for active orbitals were chosen initially from the observed single-particle spectra

of

the masses

39,

40, and

41.

H&& represents the effective two-body interactions between the particles in the

1_{f7/2 and 2p3/2} orbitals, while II~~ represents the effective interaction between the hole in the 1d3/2

or 2s&/2 orbital and the particle in the lf7/2 arid 2pq/2 orbitals. The two-body effective interactions

are assumed tobe the modified surface delta form

VJ.

=4rrAr(Q,

_J

)+Br,

T=0,

1,

With this prescription we carry out a least-squares fit calculation on the energy spectra

of

'"

_Ca,

'

'

_K,

_and

_{Sc. For}

_{the input}

experi-mental data, we include in principle all the available

low-lying levels with reliable

J

assignments up to

the point that the first level with an uncertain

J"

assignment appears. Forty-three energy levels are included in the calculation. The eight interaction strengths (AO,A~,BO, B~)zz and (AO,

A„BO,

B~)~~

and the ld&/2-2s&/2, lf7/2-ld&/2, and 2ps/2-id&/r

single-particle energy spacings are varied until the discrepancy between the calculated and observed

en-ergy levels is minimized. The overall rms deviation is

0.

26 MeV. The best-fit interaction strengths and single-particle energy spacings are listed in Table

I.

The center-of-mass spurious states have not been re-moved in the calculation.

A. Energy spectra

TABLE

I.

The particle-particle and hole-particle in-teraction strengths and the single-particle energy spacings (inMeV). hp

—

1.73

—

0.57

—

0.03 0.02 Bp 2.20

—

2.02

—

0.66

—

0.32 1tg3/2 2s~/z 1f7/2 1d3/2 2p3/2 183/2 1.68 5.71 6.66

The calculated energy spectra produced by the

hest fit parameters together with the observed

values are shown in Figs. 1

—

3.

The experimental data are taken from Endt and Leun. Those levels

that are included in the least-squares fits are marked with an asterisk. The excitation energies

of

the one hole states were made to fitthe observed en-ergies relative to the ground state energies

of

the nuclei with

A=41

—

43.

Since we are only con-cerned with the energy spacings relative to the ground states in our calculation, itis hoped that the adjustable single-particle energies may absorb the discrepancy due to the effect

of

neglecting the three-hole configuration.

6

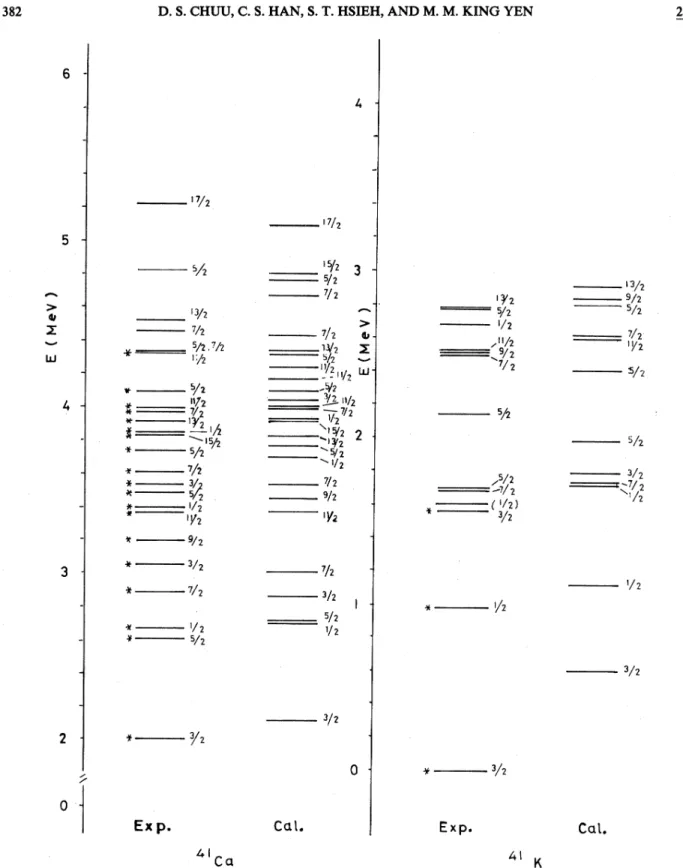
4 I72 I_7/2 3 I 3/2 7/2 5/2,'/2 I:/2 5/g Ii/2 lg~ i/2

~

I_5/2 5/2 I/2 I 2 9/2 3/2 7/2 I/2 5/2 i_5/& 5/2 7/2

a.

13/2 5/2 I_l/2 gp ~/2 _il/2

~

7/2 l I/ i/2 N_I/ 7/2 9/2 3/2 I 5/2 &/2 I$2 5/g I/2 I_I/2 9/2 7/2 5/2 —-&/2 (I/2) 3 I3/2 9/2 -5/2 7/2 I_/12 3/2 -7/2 41/ I/2 3/2 2 3/2

0

0

Ex

p.

Ca

l.

Exp.

4l

FIG.

1. Experimental and theoretical even parity energy spectra fortheA

=41

nuclei.

The energy spectra

of

even parity levels for

2=41

nuclei are shown in

Fig. 1.

The agreement

between calculated and observed energies is

reason-ably good for most

of

the levels.

For 'Ca

our

cal-culafed

E

=(3/2)+

rotational band based on the

2.

01 MeV

(3/2)+

level is similar to the results

ob-tained by Hsieh et

al.

using the complete (1

f

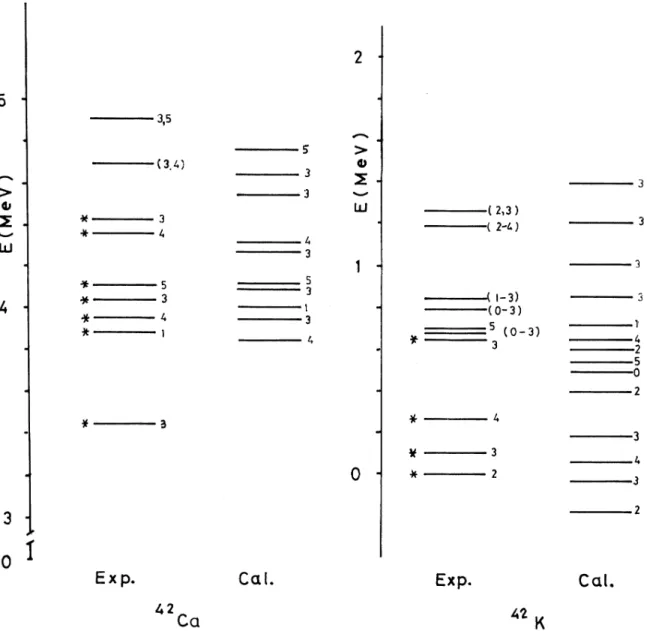
2p)"(2sld) ' configuration space. This seems to

— 3,5 (2i3) (2-4) f, ~-3)

(o-3)

5

_(o-33

3 1' 4 2 5 --0

Exp.

Ca l.

_Exp.

_Cal.

42

FIG.

2. Experimental and theoretical odd parity energy spectra for theA

=42

nuclei.

indicate that the inclusion

of

the _d5/q

',

_f5/2, and

p~~2 orbitals is not necessary.

For

some lower-lying levels, the intensities

of

(s~/2

f

7/p) and

(s]/2 p3/2) are rather strong.

For

example, the cal-culated (1/2)~+

(T=3/2)

state is dominated by the

(s)/2 'f7/2 ) configuration. This seems to justify

the necessity

of

the inclusion

of

s&~2 and p3/2

con-figuration space at least. The four high spin states populated in the

K(a,

d)

'Ca

experiment' can be

well reproduced in our model. The lowest

(11/2)+,

(13/2)+, (15/2)+,

and

(17/2)+

levels are given at

3.

39,

3.

83,

3.91,

and

5.

11MeV, and are observed at

3.

37,

3.

92,

3.

83, and

5.

22 MeV, respectively.

For

'K,

the calculated

(3/2)

t state gives a large

discrepancy

of

about

0.

6MeV compared to the ob-served one. In fact, this is one

of

the worst fittings in this mass region. The level observed at

1.

56MeV has been suggested" to be

J

=(1/2)+.

Our calcu-lated (I/2)z+ state at 1.67MeV supports this

predic-tion.

Figure 2 shows the results for the odd parity states

of

nuclei with

A=42.

For

Ca, most

of

the

levels are reproduced reasonably well, except the 3~

state. The calculated energy value for this state is displaced about

0.

49MeV from the observed value. The level at

4.

67 MeV is tentatively assigned as

J

=(3

—

4)

.

The fitted 34 state at

4.

56 MeV seems to favor a 3 state at

4.

67 MeV.

For

K,

-'/z-'Xz) i_3/z i)/z (3/z,s/z) i_s/z s/z ('/z 7/z) 9/z l_i/z S/2 (3/z~s/z) ih 7/z 2 5/2 3/2 (3/z,s/z) 7h 3/z s/z _3/z (3/z,s/z) 3/z

Ex

p.

C

a

l.

Ex

_p.

C

al.

Cal.

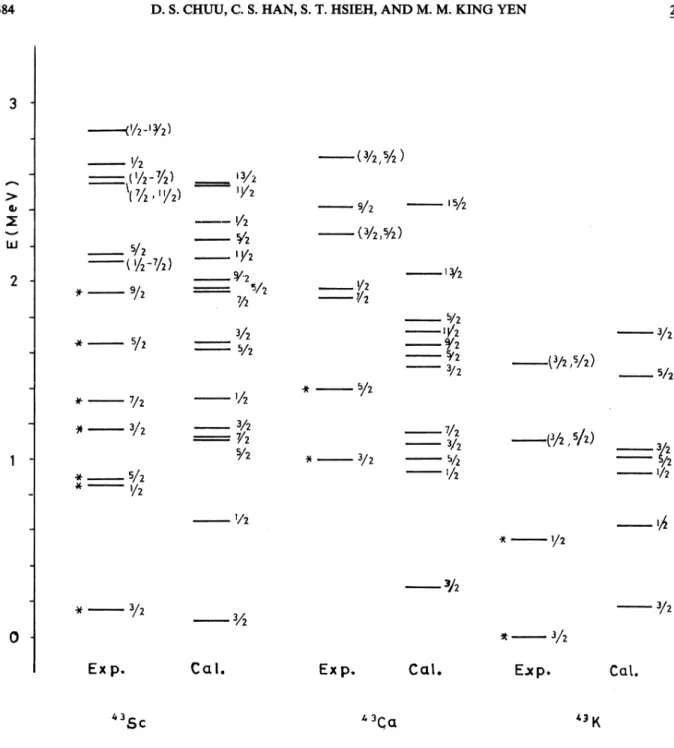
43 4

_3qa

FIG. 3. Experimental and theoretical even parity energy spectra forthe

2

=43

nuclei.

most

of

the calculated states have counterparts in

the observed level scheme. The states at

0.

68,

0.

79,

0.

84,

1.

19,and

1.

26 MeV are uncertainly assigned as

J

=(0

—

3),

(0

—

3),

(l

—

3),

(2

—

4),

and (2

—

3)

.

Our calculated states at

0.

54,

0.

72,

0.

84,

1.01,

and

1.

20 MeV seem to suggest that these five

levels are

0~,

1&,

33,

34,

and 35 states, respective-ly.

The energy spectra for the even parity states

of

nuclei with A

=43

are presented in

Fig.

3.

The

cal-culated energy levels in

Sc

are in reasonably good agreement with experimental values, especially the (3/2)~+, (3/2)z+, and (5/2)~+ states. A pickup reaction' leading tothe (3/2)+& state indicates that this state may be a pure d3&2 hole state. But as

mentioned above, Lawson and Miiller-Arnke have

shown that the observed smaller

B

(M2)

values can

only be explained

if

some (s~/z) '(f7/z) admixture is included. Our calculation shows that the (3/2)~+ state contains about

5% of

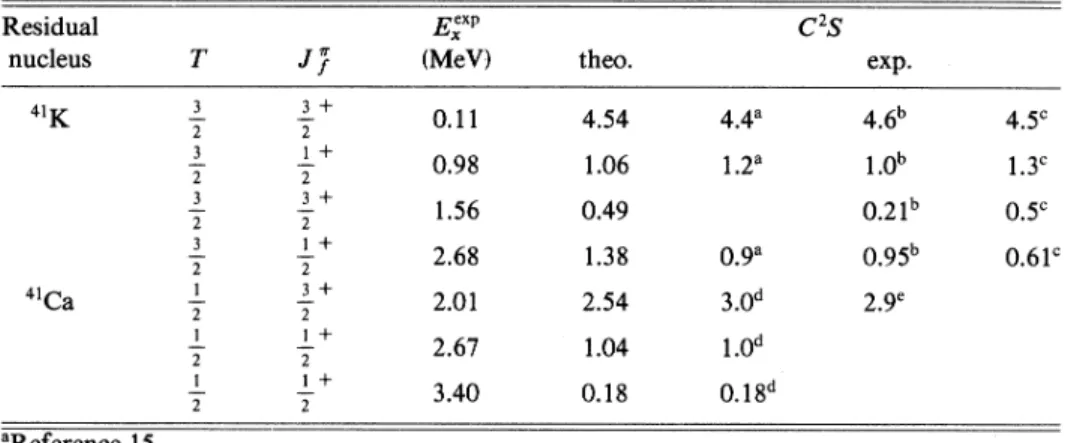
the s~~2 ' hole

com-41K 4'Ca 3 2 3 2 3 2 3 2 1 2 1 2 1 2

3+

2

1+

2

3+

2 1+ 2

3+

2

1+

2 1+ 2 0.11 0.98 1.56 2.68 2.01 2.67 3.40 4.54 1.06 0.49 1.38 2.54 1.04 0.18

44'

1.2'

09'

30d 1.0 0.18 4.6b 1.Ob O.21b

095

2.

9'

4.5' 1.3' 0.5' 0.61' 'Reference 15. bReference 13. 'Reference 14. References 16and 17. 'Reference 18.

ponent.

For

Ca,the agreement between calculated and experimental energy levels is not as good as in the case

of

Sc.

The calculated excitation energy

for the (3/2)i+ state lies

0.

71 MeV below the ob-served one. In fact, the fit to this state is the worst

of

all the fittings. The reason for this discrepancy may be that the interaction we used is oversimpli-fied.

For

K,

most

of

the levels came from the

Ca(d, He) and Ca(t,

a)

reactions. '

'

Our calcu-lated results are satisfactory.

B.

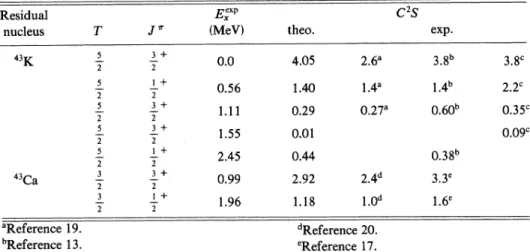
Spectroscopic factors

Table

II

shows the spectroscopic factors

of

'K

and

'Ca

for

l=0

and

1=2

proton and neutron pickup reactions on Ca. Our calculated values for this mass number agree very well with the observed data. The calculated value for the

(5/2)+

states are zero due to the neglect

of

the d5&2 ' hole in the

model space.

For 'Ca

no experimental

l=2

reac-tion has been found for the

(5/2)+

level at 2.61 MeV. Thus, the omission

of

the _dz/2 orbital is reasonable for low-lying levels. However, the ob-served strength is

0.

17 for the

(3/2)+

level at

3.

53 MeV and reaches

0.

39 for the

(5/2)+

level at

3.

74 MeV. Our calculated value

of

0.

01 for the

(3/2)+

level at

3.

53 MeV istoo much underestimated. Table

III

shows the spectroscopic information

of

K

for the

l=2

pickup reaction on Ca. The main components

of

the wave functions for these four

levels are

3/2,

f7/2 Ti——_—,

,

Ji)T

p

J

—

1 3

TABLE

III.

Theexperimental and theoretical spectro-scopic factors of Kfor

l=2

pickup reactions on Ca.

Residual nucleus K 'Reference 15. Eexp_r (MeV) 0.00 0.11 0.26 0.70 theo. 0.43 0.47 1~18 1.31

CS

exp.

'

0.45 0.88 1.1 1.4

where

J,

is mainly —,for the

J"=4

and 5 states,

but is split into —, and —, for the

J

=2

and 3

states. Our calculated value

of

0.

47 for the 3 state at

0.

11 MeV is underestimated compared tothe

ob-served value

of

0.

88. This is because the wave func-tion is spread too much in this state.

The calculated and experimental spectroscopic factors

of"

K

and Ca for the

1=0

and

1=2

_{p or} n

pickup reactions on Ca are listed in Table

IV.

The results for most

of

the states are in good agree-ment with the experimental results.

For

Ca, the calculated value forthe

(5/2)+

state at 1.39MeV is zero. The experimental value for this state is also

very small; however, the null result is due to the neglect

of

the d5/2 orbital in our model. The level

at 2.27 MeV is uncertainly assigned as

J

=(3/2,

5/2)2+. Our calculated strength

of

the (3/2)2+ state is only

0.

06, while the experiment

yields about

0.

2.

For

K

the levels at

1.11, 1.

55,

and

2.

67 MeV (not shown in

Fig.

3) are all

tenta-tively assigned to be

J

=(3/2,

5/2)+.

The good agreement

of

the calculated and experimental

TABLE IV. The experimental and theoretica1 spectroscopic factors of

'K

and Ca for

l=0

and

l=2

pickup reactions on Ca.

Residual nucleus 43K 43Ca 5 2 5 2 5 2 5 2 5 2 3 2 3 2 1+ 2

3+

2

3+

2 ]+ 2

3+

2

1+

2 EexP {MeV) 0.0 0.56 1.55 2.45 0.99 1.96 theo. 4.05 1.40 0.29 0.01 2.92 1.18 268 1.4' 0.27' 2.4d 1.0d

CS

exp.

38

1.4b 0.60' 0.38b 33' 16e 3.8' 2.2' 0.35' 0.09' 'Reference 19. Reference 13. 'Reference 14. Reference 20. 'Reference 17.

strengths strongly supports the

(3/2)+

assignment for levels at both

1.

11 and

1.

55 MeV. This is con-sistent with the result obtained in the calculation

of

the energy levels. The calculated value for the

(3/2)+

level at the 2.67MeV state is

0.

02,which is

much smaller than the observed value

of

0.

47.

To

further test the wave functions obtained in our model, we calculated the

EM

transition rates

using the experimental gamma energies. In general, the agreement between the calculated and observed

values issatisfactory.

C. Comparison ofour model space with the simple

(f

7/2, d3/2 ors~/2 ')configuration

In order to test the significance

of

our model space, we calculated the intensities

of

the com-ponents

of

our wave functions which are seen in the coupling

of

the

s,

/2 or d3/2 hole to the simple f7/3 structure.

The calculated intensity

of

the (f7/3 d3/2

',

or s~/3 ')component increases, in general, as the mass

number decreases.

For

an individual mass number, higher isospin states, in general, give a larger inten-sity

of

the component (f7/2 d3/3 ol sf/2

').

Our

results also show that the intensity

of

the com-ponent (f7/3 Sf/3 ) is small compared to that

of

the component (f7/2 d3/3 ) One important point

that has to be mentioned here is that even for cer-tain low lying states, such as (1/2)& and (1/2)2 states in

'K,

the

(1/2)l,

(5/2)2, and (3/2)3 states in 'Ca, the

(1/2)l

state in Ca, and the (1/2)~ and (3/2)3 states in

K,

the intensity

of

(f7/q,s~/2 ')is

larger than

32%

and cannot beneglected.

The intensities

of

the component (f7/2, d3/3

',

or

s~/3 ') contained in the wave functions for the

yrast states are larger than

77%,

in general. Excep-tions are the

(9/2)l, (11

/2)~, and

(13/2)l

states in

'Ca; the

3,

and 1~ states in Ca; and the (3/2)~,

(1/2)l,

(5/2)&, (7/2)&, (9/2)&, and

(11/2)l

states in

Sc.

All

of

them are smaller than

47%.

This man-ifests the fact that the simple model cannot account for the lower isospin states, and the inclusion

of

the p3/2 configuration space seems to be necessary in

this mass region.

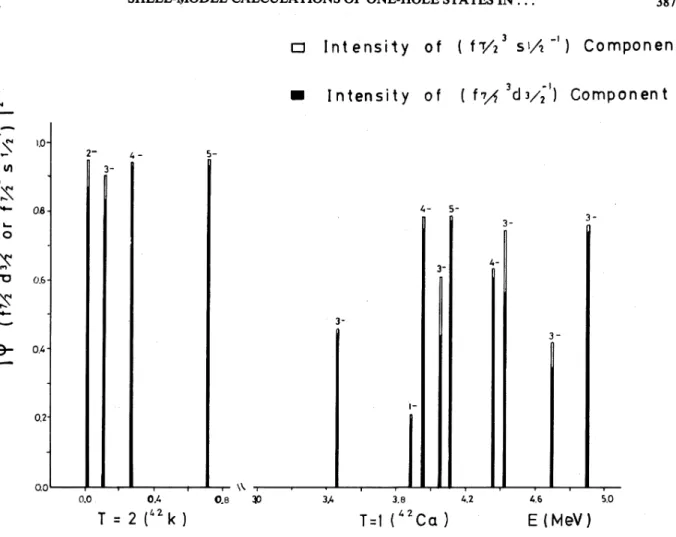
Figure 4shows atypical result for the calculation

of

3=42

nuclei.

For

K,

the intensities

of

the compo~e~t (f7/33d3/3 —1 ol s]/2

—

1)for the low ly-ing states are larger than 90%%uo. Therefore, the

sim-ple model is suitable to account for the level struc-tures

of

this nuclei. However, for 4Ca, the

interisi-ties are smaller than 80%%uo. Especially, the 1&, 3&,

and 34states give only

22%,

46%,

and

43%

intensi-ties

of

the component _(f7/3 d3/3

',

or sl/2

').

Furthermore, larger intensities

of

the component

(f

7/3 $ ]/2 ') are also exhibited in the 2~ and 3&

states

of K,

and the 32,33,and 34states in Ca.

In conclusion, the simple model is only able to account for most

of

the low lying states

of

nuclei with a small mass number, and is only suitable for the calculation

of

higher isospin states for individu-al mass numbers.

For

nuclei with a large mass

number, or for states with lower isospin, enlarging

the model space becomes more important.

III.

CONCLUSION

In this paper we have presented a systematic

study on the one hole states for the nuclei

of

ef-intensity

of

(

f7+

l.

0-0

Oa- 4- 5-3- 3 3 0.4-3w 3- 0,2-0.0 0.0 _0.8 I 4.2 I 4.6

E

(MeV)

5.0

FIG.

4. The intensities ofthe component (f7/2 d3/2 ',ors~/2 ')forthe states in Kand Ca.

fective interaction, the calculated energy spectra are in reasonably good agreement with the experimental data, and some definite predictions are made on the spin-parity assignment for afew low-lying levels

of

ambiguous experimental spin-parity determination in

K,

Ca, and

K.

We have assumed an inert

Ca core and allowed active s&/l d3/2 f7/2 and

p3/2 orbitals. The omission

of

f

s/z, pl/2, and ds/2

orbitals from the model space will not yield signifi-cant errors because they lie at about

4

to 6 MeV

away from the f7/2 level. The contributions

of

the p3/g and s&/2 orbitals are, however, rather

impor-tant even for some low-lying states. This clearly in-dicates that any shell-model calculation which at-tempts to successfully account for the non-normal parity levels

of

the range

of

nuclei with mass A&40 will have touse amodel space spanning at least the s]/l d3/2

f

7/2 and p3/2 single-particle orbitals.

We have also calculated the spectroscopic factors

to test the wave functions obtained. The calculated spectroscopic factors are in good agreement with

the experiment. The I

=2

pickup reactions on Ca

for the 3& state

of

K

do not agree as well as the

others, because the wave function

of

this state is spread too much. This discrepancy may be im-proved by enlarging the model space. The model space is tested by comparing the intensities

of

the picture

of

coupling sl/2 and d3/l holes tothe simple

f

7/2 structure. Our results show that in this mass

region, the p3/2 and s&/2 orbitals seem tobe

neces-sary.

In conclusion, the one-hole states for /I

=41

—

43 nuclei can be well explained within the conventional

shell model by using a model space

of

(f7/2 lp)/(2d3/2 s]/2) ' configurations ~

This work was supported by the National Science Council

of

the Republic

of

China.

J.

B.

McGrory, Phys. Rev.C8,693 (1973)~

D.H. Gloeckner,

R.

D. Lawson, and

F. J.

D.Serduke, Phys. Rev.C 7, 1913 (1973).

D.Banerjee and G. Oberlechner, Phys. Rev. C 7,2437

(1973).

4A.

_{E. L.}

Dieperink and P.

J.

Brussard, Nucl. Phys.

A106,177(1968).

5S.

T.

Hsieh,

K. T.

Knopfle, and G.

J.

Wagner, Nucl. Phys. A254, 141(1975).

R. D.

Lawson and A. Miiller-Arnke, Phys. Rev. C 16, 1609 (1977)~

~P.M. Endt and C.Van der Leun, Nucl. Phys. A310, 1 (1978).

~I.P.Johnstone, Phys. Rev. C22, 2561(1980).

R.

R.

Scheerbaum, Phys. Lett.

618,

151(1976).

H. Nann, W.S.Chien, A. Saha, and

B.

H.Wildenthal, Phys. Rev. C12, 1524(1975).

'D.

F.

Beckstrand and

E. B.

Shera, Phys. Rev. C3, 208

(1971).

G.Mairle and G.

J.

Wagner, Z.Phys. 251,404(1972). ' _{P.Doll, G.}

_J.

_Wagner,

_{K. T.}

_{Knopfle, and G. Marie,}

Nucl. Phys. A263, 210(1976).

~4R.Santo,

R.

Stock,

J.

H. Bjerregaard, O. Hansen, O.

Nathan,

R.

Chapman, and S. Hinds, Nucl. Phys.

A118, 409 (1968).

J.

L.Yntema, Phys. Rev. 186, 1144(1969).

U.Lynen,

R.

Bock,

R.

Santo, and

R.

Stock, Phys. Lett. 25B, 9 (1969).

U.Lynen, thesis, University ofHeidelberg, 1967.

'

_J.

_{Rapaport, W.}

_E.

_{Dorenbusch, and}

_T.

_{A. Betote,} Nucl. Phys. A177,307(1971).

D.Dehnhard and M.

E.

Cage, Nucl. Phys. A230, 393 (1974).

P. Martin, M. Buenerd, Y. Dupont, and M. Chabre, Nucl. Phys. A185,465(1972).