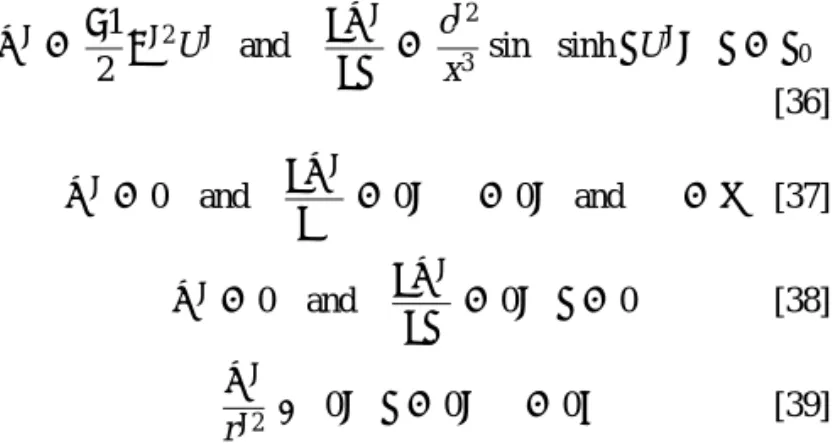Electrophoretic Motion of a Charge-Regulated Sphere
Normal to a Plane
Yu-Po Tang, Ming-Hui Chih, Eric Lee, and Jyh-Ping Hsu1
Department of Chemical Engineering, National Taiwan University, Taipei, Taiwan 10617, Republic of China
Received March 1, 2001; accepted June 8, 2001; published online August 16, 2001
The electrophoresis of a charge-regulated spherical particle nor-mal to a planar surface is analyzed theoretically. The present study extends previous analyses in that the surface of the particle assumes a general charged condition, which simulates biocolloids and par-ticles covered by an artificial membrane, and an arbitrary, double layer thicknessκa, κ, and a being respectively the reciprocal Debye length and particle radius. We conclude that the thinner the dou-ble layer and/or the larger the particle-surface distance, the greater the mobility of the particle. If the concentration of the dissociable functional groups on particle surface Nsis low, the absolute mobil-ity of a particle decreases with the increase inκa, and the reverse is true if Nsis high. For a medium Ns, the absolute mobility has a local maximum asκa varies. We show that the higher the pH of the liquid phase, the smaller the absolute mobility. °C2001 Academic Press
Key Words: electrophoresis; charge-regulated particle; boundary
effect; particle-planar surface interaction.
INTRODUCTION
The electrophoresis of spherical particles has been studied extensively for both dilute dispersions (1–9) and concentrated dispersions (10–14). Reported results range from analytical solution for low potential and thin double layer to numerical solution for arbitrary potential and double layer thickness. The effect of the presence of a boundary on the electrophoretic behavior of a particle has also been examined. Zydeny (15) and Lee et al. (16, 17), for example, discussed the electrophoretic behavior of a sphere in a spherical cavity. Morrison and Stukel (18) considered the electrophoresis of a sphere normal to a plane for the case of thin double layer and low surface potential. The problem was solved by adopting bispherical coordinates, and it was concluded that the presence of the plane has the effect of reducing the mobility of the particle, and the closer the distance between the particle and the plane the more significant the effect. Keh and Lien (19), however, pointed out that the analysis of Morrison and Stukel is flawed. Keh and Anderson (20) examined the boundary effect of electrophoresis by considering
1To whom correspondence should be addressed. Fax: 886-2-23623040.
E-mail: jphsu@ccms.ntu.edu.tw.
three types of problems: a particle moves normal to a plane, a particle moves parallel to a plane, and a particle moves along the axis of a cylindrical cavity. A reflection method was applied, and an analytical solution was derived under the conditions of low electrical potential and infinitely thin double layer. They con-clude the following: (a) The flow field has the effect of reducing the electrophoretic velocity of a particle. (b) The presence of a boundary has the effect of changing the electrical interaction be-tween a particle and the applied electric field. (c) If the boundary is charged, an electroosmotic effect will be induced. The analy-sis was extended by Ennis and Anderson (21) to a finite, double layer thickness, but the double layer is not allowed to reach the boundary. It was found that the double layer surrounding a particle has the effect of reducing its electrophoretic velocity. Feng and Wu (22) considered the electrophoretic motion of an arbitrary prolate body of revolution normal to a conducting plane under the condition of a thin double layer. In a recent study, Shugai and Carnie (23) adopted the method of Teubner (24) to solve the electrophoresis of a colloidal particle normal to a plane for the case of low electrical potential and arbitrary, double layer thickness. Two types of boundary conditions are considered: constant surface potential and constant surface charge density. It was shown that when the double layer is close to the boundary the method adopted is more accurate than the reflection method. As pointed out by Krozel and Saville (25), constant surface potential and constant surface charge density are idealized conditions which represent two limiting cases, and in practice, the charged condition is between these two limits.
In the present study, we consider the electrophoresis of a charge-regulated sphere normal to a planar surface. If the elec-trical potential is low, the surface condition of the latter can be approximated by a linear combination of constant potential and constant charge. In other words, the results in the literature are extended to a more general case. A typical example of the type of particle examined includes biocolloids, such as biological cells and microorganisms, and particles covered by an artificial mem-brane layer. In addition to a more detailed understanding about the boundary effect on electrophoresis, the present analysis has potential applications in processes which involve the interaction between a charged entity and a surface—For instance, electrode-position and cellular adhesion to surfaces, to name a few.
121 0021-9797/01 $35.00
Copyright°C2001 by Academic Press All rights of reproduction in any form reserved.
THEORY
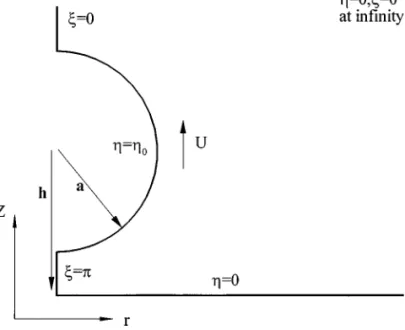
We consider the electrophoresis of a sphere of radius a to-ward a planar surface. The distance between the center of the particle and the surface is h. The liquid phase contains z1: z2 electrolyte, z1and z2being respectively the valence of cations and that of anions. The electroneutrality in the bulk liquid phase requires that n20= n10/α, n10and n20are respectively the bulk concentration of cations and that of anions, andα is constant. Referring to Fig. 1, a uniform electric field Ezwith strength Ezis
applied in the Z direction and the particle moves with velocity
U. The bispherical coordinates (ξ, η, φ) are adopted in which η = 0 represents the planar surface and η = η0 represents the surface of the particle. The present coordinates are related to the cylindrical coordinates (ω, θ, Z) by (24)
z= c sinhη
coshη − cos ξ [1]
ω = c sinξ
coshη − cos ξ, [2]
where c is the focal length and 0≤ η ≤ η0, 0≤ ξ ≤ π. Suppose that the liquid phase is incompressible with constant physical properties.
We assume that the electrical potential of the system under consideration can be described by the Poission equation
∇2φ = −ρ ε = − 2 X j=1 zjenj ε , [3]
whereρ and ε are respectively the space charge density and
FIG. 1. The bispherical coordinates (ξ, η, φ) adopted, where η = 0 and η =
η0represent respectively the plane and particle surface. a is particle readius and h
is the distance between the center of the particle and the plane. A uniform electric field Ezis applied in the Z direction, and the particle moves with velocity U.
the permittivity of the liquid phase, e is the elementary charge, and njand zjare respectively the number concentration and the
valence of ionic species j .
Suppose that the flow field can be described by the Navier– Stokes equation in the creeping flow regime
*
∇ · v = 0 [4]
µ∇2v−∇ p − ρ* ∇φ = 0,* [5] where p andµ are respectively the pressure and the viscosity.
For convenience,φ is expressed as a sum of φ1 andφ2 (6). The former represents the potential in the absence of applied electric field, that is, the equilibrium potential, and the latter is a perturbed potential, which arises from the applied electric field. Suppose that the spatial variation of the ionic concentration at equilibrium follows the Boltzmann distribution
nj = nj 0exp µ −zjeφ1 kBT ¶ . [6]
If the potential is low, this expression andρ can be approximated respectively by nj ∼= nj 0 µ 1−zjeφ1 kBT ¶ [7] and ρ ∼= 2 X j=1 zjenj 0 µ 1−zjeφ1 kBT ¶ . [7a]
Substituting Eq. [7] into Eq. [3] and defining φ∗j = φj/(kBT/
z1e) and n∗j = nj/n10, we obtain
∇2φ∗ 1 = (κa)
2φ∗
1, [8]
where the reciprocal Debye length κ and the scaled Laplace operator∇2are defined respectively by
κ = " 2 X j=1 nj 0(ezj)2/εkBT #1/2 [9] and ∇2= x2 c∗2 · ∂2 ∂η2 + ∂2 ∂ξ2− sinhη x ∂ ∂η+ cosξ cosh η − 1 x sinξ ∂ ∂ξ ¸ , [10] with c∗= c/a and x = cosh η − cos ξ. Since φ = φ1+ φ2, Eqs. [3] and [8] lead to
∇2φ∗ 2 = ∇
2φ∗− ∇2φ∗
Taking the curl of Eq. [5] and adopting the stream function representation, we obtain
µiϕ
ωE
4ψ − ∇ × (ρ∇φ) = 0, [12]
whereω = c sin ξ/x is the distance from the symmetric axis. Theη- and the ξ-components of the velocity, vηandvξ, can be expressed as vη = x2 c2sinξ ∂ψ ∂ξ [13] vξ = −x 2 c2sinξ ∂ψ ∂η. [14]
Substituting Eq. [7a] into Eq. [12] and defining the scaled stream functionψ∗asψ∗= ψ/(kBT/z1e)2εa/µ, we have
E4ψ∗= −(κa)2x sinξ c∗ µ∂φ∗ 1 ∂ξ ∂φ∗ 2 ∂η − ∂φ∗ 1 ∂η ∂φ∗ 2 ∂ξ ¶ , [15]
where E4= E2E2, and E2is defined by
E2= x 2 c∗2 · ∂2 ∂η2 + ∂2 ∂ξ2 + sinhη x ∂ ∂η+ 1− cos ξ cosh η x sinξ ∂ ∂ξ ¸ . [16] The boundary conditions associated with Eqs. [8], [11], and [15] are assumed as follows. For the equilibrium potentialφ1we assume that it vanishes at a point far away from the sphere; that is,
φ∗
1 = 0, η = 0, ξ = 0, ξ = π, and η = 0. [17] The symmetric nature of the present system requires that
∂φ∗
1
∂ξ = 0, ξ = 0, and ξ = π. [18]
Suppose that the dissociation of the functional groups on the particle surface can be expressed by (27)
A H ⇔ A−+ H+. [19]
Let Ka be the dissociation constant of this expression. Then
Ka=
[ A−] [H+]S
[ A H ] . [20]
The subscript S denotes surface property. Suppose that the
spatial variation of [H+] follows Boltzmann distribution
[H+]S = [H+]bexp µ −eφ1 kBT ¶ . [21]
The subscript b denotes bulk liquid property. If we let NSbe the
concentration of dissociable functional groups on the particle surface, then NS = [A−]+ [AH]. [22] Equations [20]–[22] yield [ A−]= NS 1+[H+]b Ka exp ¡ −eφ1 kBT ¢. [23]
The surface charge concentrationσ can be expressed as
σ = −e[A−]. [24]
Equations [23] and [24] lead to
σ = − eNS 1+[H+]b Ka exp ¡ −eφ1 kBT ¢. [25]
Ifφ1is low, this expression can be approximated by
σ = σ|φ1=,0+ dσ dφ1 ¯¯ ¯¯ φ1=0 (φ1− 0) = −eNS {1 + [H+]b/Ka}− (e2NS/kBT ){[H+]b/Ka} {1 + [H+]b/Ka}2 φ1. [26] We assume that the dielectric constant of the solid phase is much smaller than that of the liquid phase. Then
σ = −ε∇φ · n. [27]
In bispherical coordinates, this expression becomes
σ = εx
c
∂φ1
∂η . [28]
Equations [26] and [28] yield x c∗ 1+ [H+]b/Ka (e2N Sa/εkBT ) dφ1∗ dη∗ + [H+]b/Ka 1+ [H+]b/Kaφ ∗ 1 = −1. [29] If we let A= (e2NSa/εkBT ) and B= [H+]b/Ka, then this
expression can be rewritten as x c∗ 1+ B A dφ∗1 dη∗ + B 1+ Bφ ∗ 1 = −1 . [30]
This condition needs to be satisfied on the particle surface. Note that if the surface potential of the particle remains constant, then Eq. [30] becomes
φ∗
1 = 1, η = η0. [31]
For the perturbed potentialφ2, since the electric field Ez is in
the Z direction, we have
∂φ∗ 2 ∂η = 0, η = η0 [32] ∂φ∗ 2 ∂ξ = 0, ξ = 0, and ξ = π [33] φ∗ 2 = −E∗z· r∗, η = 0, η = η0, ξ = 0, and η = 0, [34]
where E∗z(=Ez/(kBT/(z1e/a))) is the scaled electric field, r∗is the position vector from the center of the particle, r∗= r∗· ir, r∗= r/a, r being the distance from the center of the particle. In bispherical coordinates, r∗can be expressed as
r∗ = c∗ µ coshη + cos ξ x ¶1/2 . [35]
At steady state the particle moves with velocity U and the fluid at infinity is stationary; therefore the boundary conditions for the flow field can be assumed as
ψ∗ =−1
2 ω
∗2U∗ and ∂ψ∗
∂η =
c∗2
x3 sinξ sinh ηU
∗, η = η 0 [36] ψ∗= 0 and ∂ψ∗ ∂ξ = 0, ξ = 0, and ξ = π [37] ψ∗= 0 and ∂ψ∗ ∂η = 0, η = 0 [38] ψ∗ r∗2 → 0, η = 0, ξ = 0. [39]
In these expressions,ω∗= c∗sinξ/x and U∗= U/(kT/ez1)2ε/
µa.
The forces acting on the particle include the electric force FE z
and the hybrodynamic force FDz, which can be evaluated by
FE z= 2π π Z 0 σ(−∇φ) δS [40] FDz= µπ π Z 0 ω3 ∂ ∂n E2ψ ω2 δS− π π Z 0 ω2ρ∂φ ∂S δS, [41] where s denotes a tangential surface. Substituting Eq. [28] into
Eq. [40] yields FE z∗ = 2π π Z 0 −sinξ x ∂φ ∂η × µ (1− cosh η cos ξ)∂φ ∗ ∂η − sinh η sin ξ ∂φ∗ ∂ξ ¶ dξ. [42]
Substituting Eq. [7a] into Eq. [41] gives
FDz∗ = π π Z 0 −ω∗3 ∂ ∂η E2ψ∗ ω∗2 dξ + (κa)2π × π Z 0 c∗2 x2 sin 2ξφ∗ 1 ∂φ∗ ∂ξ dξ. [43]
Following the same treatment as that of O’Brien and White (6), the problem under consideration is dencomposed into two sub-problems. In the first the particle moves with constant velocity in the absence of the applied electric field, and in the second the particle is held constant when the external electric field is ap-plied. If we let f1and f2be the net forces acting on the particle in these two problems, then f1= χU∗and f2= β E∗, whereχ and
β are constant. Since the net force acting on the particle vanishes
at the steady state, we have f1+ f2= 0, which implies that the mobility of the particle can be expressed as U∗/E∗= −β/χ.
RESULTS AND DISCUSSION
Figure 2 illustrates the variation of the scaled electrophoretic mobility (U∗/E∗) as a function of η0 at various κa, and the variation of (U∗/E∗) as a function of κa at various η0 is
FIG. 2. Variation of scaled electrophoretic mobility (U∗/E∗) as a function ofη0 at various, double layer thicknessesκa for the case when the surface
FIG. 3. Variation of scaled electrophoretic mobility (U∗/E∗) as a function ofκa at various distances between the particle and plane η0for the case when
the surface potential of the particle remains constant.
presented in Fig. 3. Sinceη0 = cosh−1(h/a) a and h being re-spectively the radius of a particle and the distance between the center of the particle and the surface,η0is as a measure for the relative distance between the particle and the surface. Figure 2 shows that for a fixedκa the scaled mobility increases with the increase inη0; that is, the presence of the surface has the effect of retarding the movement of the particle. Therefore, the larger theη0, the greater the distance between the particle and the sur-face, and the less the influence of the latter on the movement of the former. This is consistent with previous results (21, 22). Apparently, ifη0→ ∞ the mobility of the particle approaches that of an isolated particle. Figure 3 reveals that for a fixedη0, (U∗/E∗) increases withκa. This is because the smaller the κa the thicker the double layer surrounding the particle, and the more easily it feels the presence of the surface. Note that if
κa is smaller than a certain critical value, (U∗/E∗) becomes
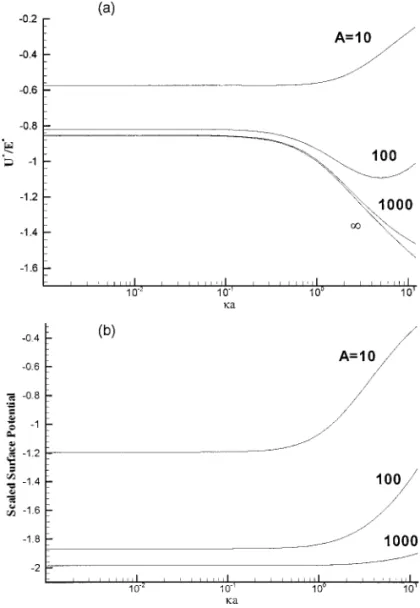
independent of κa. This critical value is on the order of the surface-to-surface distance between the particle and the surface. The variation of the scaled electrophoretic mobility (U∗/E∗) as a function of κa at various A is illustrated in Fig. 4a, and the corresponding variation in the surface potential is presented in Fig. 4b. According to its definition (=e2N
Sa/εkBT ), A is
a measure of the concentration of the dissociable functional groups on the particle surface; the larger the value of A the greater the number of dissociable functional groups. Figure 4a reveals that if A is small, the absolute mobility |U∗/E∗| de-creases with the increase inκa. However, if A is large, |U∗/E∗| increases with the increase inκa. For a Medium A, |U∗/E∗| exhibits a local maximum asκa varies. These trends reveal that the mobility is controlled by two competing factors. The first factor is of hydrodynamic nature. It is known that for both an isolated particle and a concentrated dispersion, the thinner the double layer the larger the mobility (6, 17). That is,|U∗/E∗| increases withκa. This is pronounced if the double layer does
not touch the planar surface. As A→ ∞, the particle has a constant potential surface, and therefore the qualitative behavior of|U∗/E∗| as κa varies for the case A is large (=1000) similar to that of Fig. 3. Note that a particle is positively charged in the latter and is negatively charged in the former. The second controlling factor is the variation of the surface potential of a particle. As can be seen from Fig. 4b, the absolute surface potential decreases with the increase inκa. This is because the thinner the double layer the smaller the space available for the distribution of dissociated ionic species, which leads to a smaller degree of dissociation of the functional groups on the particle surface. This yields a lower surface charge density and a smaller mobility. This effect is pronounced if A is small. For a medium value of A (=100), the competition of the two controlling factors yields a local maximum in|U∗/E∗| as κa varies.
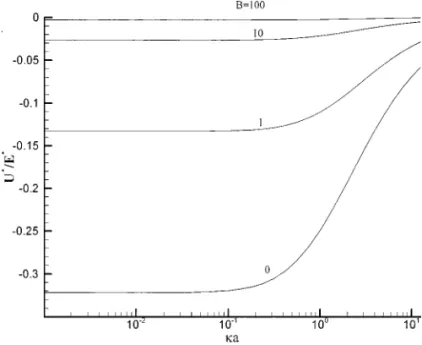
The variation of the scaled electrophoretic mobility (U∗/E∗) as a function ofκa at various B is illustrated in Fig. 5. This figure suggests that ifκa is constant, |U∗/E∗| decreases with the increase in B. The definition of B (=[H+]b/Ka) indicates that for a fixed Ka it is a measure of [H+] in the bulk liquid
phase. The larger the value of B the higher the [H+], which
FIG. 4. Variation of scaled electrophoretic mobility (U∗/E∗), (a), and scaled surface potential, (b), as a function ofκa at various A for the case
FIG. 5. Variation of scaled electrophoretic mobility (U∗/E∗) as a function ofκa at various B for the case η0= 1.317 and A = 1.
leads to a lower degree of dissociation of the functional groups on particle surface. Therefore the surface charge density becomes lower, and the mobility becomes smaller. On the other hand, if [H+] is low, the surface charge density is high, and the absolute mobility becomes large, as illustrated in Fig. 5. This figure also shows that if B is very large (B= 100), the dissociation of the functional groups on the particle surface is negligible, and the mobility vanishes essentially. On the other hand, if B is small,
|U∗/E∗| is large. If B = 0, the dissociation of surface functional
groups is complete, and the present model reduces to a constant surface charge model. However, as mentioned previously, since the mobility is still influenced by the thickness of a double layer,
FIG. 6. Variation of scaled electrophoretic mobility (U∗/E∗) as a function ofη0at various A for the caseκa = 10 and B = 1.
|U∗/E∗| starts to decrease with the increase in κa if the latter is
sufficiently large.
Figure 6 summarizes the variation of the scaled electro-phoretic mobility (U∗/E∗) as a function ofη0at various A. For a fixed A, the qualitative behavior of the variation of (U∗/E∗) as a function ofη0is similar to that shown in Fig. 2. For a fixedη0, the qualitative behavior of the variation of (U∗/E∗) as a function of A is similar to that illustrated in Fig. 4.
CONCLUSION
Bispherical coordinates coupled with an orthogonal col-location procedure are adopted to solve the problem of the electrophoresis of a charge-regulated sphere normal to a plane. The method used is applicable to an arbitrary, double layer thickness. The charged conditions on particle surface are found to have a profound in fluence on its qualitative behavior. For instance, for a medium level of concentration of the dissociable functional groups on the surface of a particle, its electrophoretic mobility may have a local maximum as the thickness of the double layer varies.
ACKNOWLEDGMENT
This work is supported by the National Science Council of the Republic of China.
REFERENCES
1. Von Smoluchowski, M., Z. Phys. Chem. 92, 129 (1918). 2. Huckel, E., Phys. Z. 25, 204 (1924).
3. Henry, D. C., Proc. R. Soc. London Ser. A 133, 106 (1931). 4. Booth, F., Proc. R. Soc. London Ser. A 203, 514 (1950).
5. Wiersema, P. H., Loeb, A. L., and Overbeek, J. Th. G., J. Colloid Interface
Sci. 22, 78 (1996).
6. O’Brien, R. W., and White, L. R., J. Chem. Soc. Faraday Trans. 2 74, 1607 (1978).
7. O’Brien, R. W., and Hunter, R. J., Can. J. Chem. 59, 1878 (1981). 8. Ohshima, H., Healy, T. W., and White, L. R., J. Chem. Soc. Faraday Trans.
2 79, 1613 (1983).
9. Ohshima, H., Adv. Colloid Interface Sci. 62, 189 (1995).
10. Levine, S., and Neale, G. H., J. Colloid Interface Sci. 47, 520 (1974). 11. Kozak, M. W., and Davis, E. J., J. Colloid Interface Sci. 127, 497 (1989). 12. Kozak, M. W., and Davis, E. J., J. Colloid Interface Sci. 129, 166 (1989). 13. Ohshima, H., J. Colloid Interface Sci. 188, 481 (1997).
14. Lee, E., Chu, J. W., and Hsu, J. P., J. Colloid Interface Sci. 209, 240 (1999). 15. Zydney, A. L., J. Colloid Interface Sci. 169, 476 (1995).
16. Lee, E., Chu, J. W., and Hsu, J. P., J. Colloid Interface Sci. 196, 316 (1997). 17. Lee, E., Chu, J. W., and Hsu, J. P., J. Colloid Interface Sci. 205, 65 (1998). 18. Morrison, F. A., and Stukel, J. J., J. Colloid Interface Sci. 33, 88 (1969). 19. Keh, H. J., and Lien, L. C., J. Chin. Inst. Chem. Eng. 20, 283 (1989). 20. Keh, H. J., and Anderson, J. L., J. Fluid Mech. 153, 417 (1985). 21. Ennis, J., and Anderson, J. L., J. Colloid Interface Sci. 185, 497 (1997). 22. Feng, J. J., and Wu, W. Y., J. Fluid Mech. 264, 41 (1994).
23. Shugai, A. A., and Carnie, S. L., J. Colloid Interface Sci. 213, 298 (1997). 24. Teubner, M., J. Chem. Phys. 76, 11 (1982).
25. Krozel, J. W., and Saville, D. A., J. Colloid Interface Sci. 150, 365 (1992). 26. Happel, J., “Low Reynolds Number Hydrodynamics.” Noordhoff, Leyden,
1973.