Planning the e-Scrap Reverse Production System
Under Uncertainty in the State of Georgia:
A Case Study
I-Hsuan Hong, Tiravat Assavapokee, Jane Ammons, Chuck Boelkins, Kennon Gilliam, Devon Oudit,
Matthew J. Realff, Juan Martín Vannícola, and Wuthichai Wongthatsanekorn
Abstract—Due to legislative requirements, environmental
con-cerns, and market image, the disposition of end-of-life e-scrap is attracting tremendous attention in many parts of the world today. Effective management of returned used product flows can have a great impact on the profitability and resulting financial viability of associated e-scrap reverse production systems. However, designing efficient e-scrap reverse production systems is complicated by the high degree of uncertainty surrounding several key factors. Very few examples of this complex design problem are documented in the academic literature. This paper contributes as analysis of a new, large-scale application that designs an infrastructure to process used televisions, monitors, and computer central pro-cessing units (CPUs) in the state of Georgia in the U.S. The case study employs a scenario-based robust optimization model for supporting strategic e-scrap reverse production infrastructure design decisions under uncertainty. A mixed integer linear pro-gramming (MILP) model is used to maximize the system net profit for specified deterministic parameter values in each scenario, and then a min–max robust optimization methodology finds a robust solution for all of the scenarios.
Index Terms—Electronics recycling, reverse production systems,
robust optimization.
I. INTRODUCTION
E
LECTRONICS are ubiquitous in current society. Their va-riety and volumes today make it inevitable that we inherit significant reuse/recycling/disposal challenges, including col-lection, transportation and processing costs along with seriousManuscript received August 30, 2005; revised February 27, 2006. This work was supported in part by the National Science Foundation under Grants DMI 9800198 and DMI 0200162, the Consortium for Competitiveness in Apparel, Carpet, and Textile Industries (CCACTI) of the State of Georgia, and the P2AD of the Georgia Department of Natural Resources.
I-H. Hong was with the Industrial and Systems Engineering Department, Georgia Institute of Technology, Atlanta, GA 30332-0205 USA. He is now with National Chiao Tung University, Hsinchu 300,Taiwan, R.O.C..
T. Assavapokee is with the Industrial Engineering Department, University of Houston, Houston, TX 77204-4008 USA.
J. Ammons, K. Gilliam, D. Oudit, J. M. Vannícola, and W. Wongthatsanekorn are with the Industrial and Systems Engineering Department, Georgia Institute of Technology, Atlanta, GA 30332-0205 USA.
C. Boelkins is with the Pollution Prevention Assistance Division, Georgia Department of Natural Resources, Atlanta, GA 30334 USA.
M. J. Realff is with the Chemical and Biomolecular Engineering Department, Georgia Institute of Technology, Atlanta, GA 30332-0100 USA.
Color versions of Figs. 1, 5, 7, 10, and 11 are available online at http://ieeex-plore.ieee.org.
Digital Object Identifier 10.1109/TEPM.2006.881769
hazardous waste concerns (lead, cadmium, mercury, etc.). How-ever, with challenge comes opportunity. In this case, the oppor-tunity is to view the scrap electronics (e-scrap) as resource, and to capture value from the returned stream of used electronics.
This paper presents a case study for the design of a large-scale system for collecting, transporting, and processing used elec-tronics in the state of Georgia in the U.S. Data used in our case study are collected from a variety of sources and through in-teraction with industry. Our objective is to maximize the finan-cial viability of the infrastructure and minimize the deviation of performance from the optimal investment when faced with key uncertainties. Due to their predominance in the waste stream, our primary focus at this time is a subset of the used electronics stream: televisions (TVs), CPUs, and monitors.
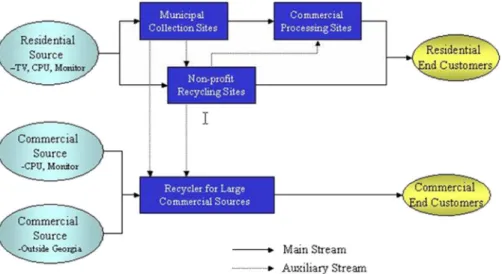
The problem is definitely large scale. For example, we pre-dict that more than 5 570 000 lb of used televisions, 3 300 000 lb of used computer monitors, and 1 800 000 lb of used CPUs could be collected and processed in the state of Georgia each year if 30% of Georgia residents with something to recycle par-ticipate in the system. With interviews with the state government agency, consortia, and industry firms, we consider the configura-tion of a regional electronics recycling system with local munic-ipal collection sites and a host of processors ranging from large and small commercial firms to nonprofit organizations [1]–[3]. An illustration of the physical flows of the reverse production system (RPS) for Georgia’s used electronics is shown in Fig. 1. Municipal collection sites and nonprofit recycling sites are as-sumed to collect e-scrap, including TVs, CPUs, and monitors, supplied by residential and small business sectors. Commercial processing sites collect after-sorted e-scrap from several local municipal or nonprofit recycling sites for further processing. In addition, recyclers for large commercial sources focus on col-lection and processing of e-scrap of CPUs and monitors from business sources. Different sites may involve different functions and different contact parties. For example, recyclers for large commercial sources may only contract with business sources for e-scrap collection and processing, while other commercial processing sites may handle after-sorted e-scrap from both mu-nicipal and nonprofit collection sites.
The remainder of the paper is organized as follows. In Section II, we overview the underlying technical background and previous literature. The mathematical programming ap-proach we utilize is presented in Section III. Section IV details the regional case study for the state of Georgia. Discussion of the case study and conclusions are presented in Section V. 1521-334X/$20.00 © 2006 IEEE
Fig. 1. Physical flow of used electronics.
II. BACKGROUND ANDLITERATUREREVEIW
The design and analysis of reverse production systems have developed as topics of recent interest. Alternative views and models for the general problem can be found in sources such as Ammons et al. [4] and Guide et al. [5]. Flapper [6], [7], Dowlatshahi [8], and Fleishmann et al. [9] give systematic overviews of the logistic aspects of reuse and recycling system. Fleischmann et al. [10] also present a characterization of logistic networks for product recovery. Carter and Ellram [11] and Kang and Schoenung [12] give reviews of the literature on reverse logistics and U.S. infrastructure and technology options in electronic waste recycling. Spengler et al. [13] and Gungor and Gupta [14] present product recovery integrated with environmental issues and a comprehensive bibliography in this area. Spengler et al. [15] later present a MILP model for integrated planning of acquisition, disassembly, and bulk recycling in e-scrap recovery. The safety stock planning in a general supply chain with the integration of external and internal product return and reuse is discussed in [16]. Hirsch et al. [17] propose a simulation tool to analyze the behavior of a given logistic infrastructure on the basis of predefined parameters. Guide et al. [18] also use simulation to evaluate the performance of alternative workflow control rules in a re-manufacturing environment. Research on reverse supply chain design for specific materials such as refrigerators, copiers, and electronics includes Krikke et al. [19], Krikke et al. [20], and Sodhi and Reimer [21]. Nagurney and Toyasaki [22] take another perspective viewing several independent agents in elec-tronics recycling systems, and analyze the individual behavior of acquisition and flow decisions.
The approach used in this paper is termed robust, or “worst case,” optimization. Kouvelis an Yu [23] propose the definition of robust optimization including absolute, relative, and minimax robustness criteria. This case study employs the measure of min-imax robust deviation, in which the robust solution is one that minimizes the maximum deviation from the optimal value for all possible realizations of the parameters in the model.
The uncertainties may have critical impact on the design of reverse production systems. A simple, but limited, approach
for understanding the impact of uncertainty is traditional sce-nario/parametric analysis [24]. Alternatively, Listes and Dekker [25] demonstrate the application of conventional stochastic pro-gramming to the sand recycling case study reported earlier by Barros et al. [26]. However, assumptions on the distributions of parameters are required for such an approach and the objective is the maximization of the expected value. It is not clear that an expected value function is the appropriate objective for ac-tual strategic decisions in cases like these. Other examples of applying stochastic programming for planning and product dis-tribution/recovery problems include Clay and Grossmann [27] and Inderfurth et al. [28]. Yu and Li [29] present the use of ro-bust optimization model for a stochastic logistics problem.
Mulvey et al. [30] make a strong case for the application of robust optimization using a minimax objective function as su-perior to stochastic optimization when dealing with single or in-frequent decisions involving great uncertainty. This observation is the basis for our previous results for uncertain reverse pro-duction system infrastructure determination where robust opti-mization is applied using scenarios to represent uncertainty [24]. Other work applying robust optimization to the forward/reverse logistic problem includes Genaro et al. [31]. Mausser and La-guna [32] describe a formulation for a robust mixed integer pro-gramming (MIP) problem for certain types of parameter ranges. This formulation uses the fact that the parameters found only in the objective function can be set to their extreme values; how-ever, this approach only allows for uncertainty in objective func-tion and can not deal with uncertainty in other parameters in the mathematical model.
In contrast, the case study presented here applies robust op-timization to reverse production system design while explicitly considering the impact of uncertainty on parameters in the con-straint matrix and the right-hand side. Probability distributions are not required or used in this approach, so there is no need to estimate (or speculate upon) them. Compared to previous work, the case study is also distinguished by its solution of a very large scale robust optimization problem. As Section IV docu-ments, the approach addresses more than a million continuous variables, thousands of discrete variables, and more than a mil-lion constraints.
Fig. 2. General form of mixed integer linear programming model.
III. METHODOLOGY
A deterministic mixed integer programming (MILP) model is used to design the reverse production system and determine the flows in the resulting network, where the objective is to max-imize the profit of the system, subject to a set of constraints that enforce material balances and other prescriptions that en-sure network feasibility. The continuous decisions, denoted by the set , are the material flows in the resulting network and processed amounts for the particular tasks.
The discrete decisions, denoted by the set , include site opening decisions, task location decisions, and transportation selection among locations. It is assumed that a superset of po-tential locations for various tasks is already known to the deci-sion maker, and that the network of possible production routes from product to recycled materials is defined. Site opening de-cision variables refer to location selections in the infrastructure design. The second class of discrete variables, task location de-cisions, indicates that the tasks can be restricted to be located at certain subsets of locations (and then only if the location itself is open). If no integer variable for a task takes a nonzero value then the task is not selected. The third class of discrete variables refers to the transportation selection among locations. The ma-terial flows are forced through the subset of locations that are open.
In this way, we can represent a superstructure of recycling tasks (such as various levels of processing and disassembly). Through material balances we force a feasible combination of tasks to be selected so that no material is left in a state in which it cannot be sold or disposed of and where several tasks may be left out completely. The superstructure of tasks are tailored by specific processing alternatives for different product types. As we have previously reported in [33], the MILP model takes the general form shown in Fig. 2. This generic representation sep-arating the task structure and site connectivity has been of sig-nificant value in chemical engineering scheduling and planning formulations and empirically has provided reasonable compu-tational behavior (see [34] and [35]).
Mixed Integer Linear Programming Approach for the Sce-nario-Based Robust RPS Design: The fundamental goal of strategic design models for RPS is to allow “good” long-term infrastructure decisions, strategically committing significant resources, development effort, and future operational viability to a particular configuration design. As we have pointed out, uncertainty plays a significant role in strategic decisions in RPS design, and the above model does not incorporate this uncertainty. The model has been extended to consider limited forms of uncertainty in the parameters such as collected volume
Fig. 3. General statement of robust scenario model.
and prices, and we have focused on using a scenario-based approach coupled with a robust objective function [24]. The scenarios are defined by deterministic values of parameters that are thought to represent likely situations predicted by an expert. The expert is not required to assign any probability to the scenarios. The expert should require that the solution be “robust” if the parameter combination in the scenario should be the one that actually occurs in the future. We have used the measure of robust deviation defined by Kouvelis and Yu [23], such that for each scenario we will subtract the objective function value of a specified robust solution from the objective function value (net profit) of the RPS model optimal solution. For the given robust solution, the largest, or maximum devia-tion is determined across all scenarios. The “optimal” robust solution will be the one with the minimum maximum deviation. This captures a notion of “risk”—the decision maker wants to protect her/himself from doing very poorly in a given scenario when she/he could have done much better by making a different set of choices.
To execute the robust approach, we first solve the MILP model to optimality for each specified scenario. This fixes the set of variables that are optimal for the scenario. In other words, define as the set of all specified scenarios, and solve the MILP model for each scenario . The optimal objec-tive function value (net profit) of the RPS model for scenario is denoted by . We define a configuration to be the set of variables that have the value of 1 in the solution. We use to denote a configuration that is to be evaluated against sce-narios in the set . The evaluation takes the form of finding the optimal value of the configuration when the parameters are set to the values in scenario , and we denote this as . A robust configuration is a configuration that minimizes the maximum deviation of and across all the scenarios in the set . The degrees of freedom that the robust configuration is allowed to manipulate are the continuous operational variables . The robust model is stated in Fig. 3. With the following notation:
optimal solution net profit for scenario ; net profit of robust solution for scenario .
Application of the deterministic model and the robust scenario model are both demonstrated in a case study of developing re-cycling infrastructure for electronics for the state of Georgia in the U.S.
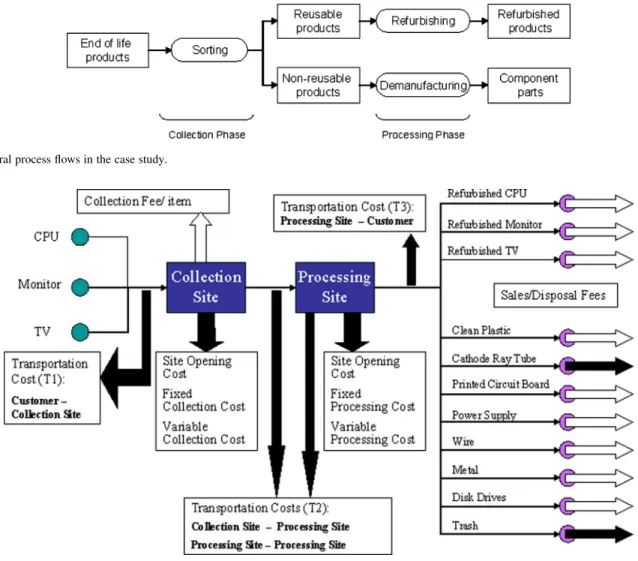
Fig. 4. General process flows in the case study.
Fig. 5. Cash flow diagram with costs in black arrows and profits in white arrows.
IV. CASESTUDY
We want to plan a regional e-scrap processing infrastructure to handle the used electronics that are accumulating within the state of Georgia, an area covering approximately 57 906 square miles (149 911 square km) with an estimated population of 8.4 million people. In the following sections, we develop our data required for problem definition, including e-scrap supply infor-mation, collection site characteristics, processing site descrip-tions, transportation alternatives, and transportation and pro-cessing costs. Then we define the scenarios to be studied based on key uncertainties in participation rate, capacity utilization in collection facilities, and reusability percentages of collected equipment. Optimal solutions are obtained for each of the sce-narios, and then a corresponding robust infrastructure solution is found.
A. Case Study Overview and Input Data
This case study is concerned with designing the infrastruc-ture for the product recovery processes for electronic equipment collected from the residential and business sectors in Georgia. At this initial stage, we consider the predominant physical in-puts to the system to be used televisions, computer monitors, and CPUs. We assume that no material may go deliberately un-collected; in other words the variables that represent the inflow
of the material to the system must equal to the amount avail-able for collection. We consider three general major processes: sorting, refurbishing, and demanufacturing processes conducted in each associated site. The general process flows are detailed in Fig. 4. In general, any sites involving the collection phase per-form the sorting process to initially separate end-of-life products into reusable or nonreusable items, and sites in the processing phase may take refurbishing or/and demanufacturing processes for product recovery. We note that one physical site may involve one or more processes of sorting, refurbishing, and turing processes. The outputs after refurbishing or demanufac-turing process are several categories of refurbished units, com-ponent parts, and materials listed in Fig. 5. The financial flows, depicting profits and costs in white and black shades, are also indicated in Fig. 5.
To accomplish this RPS design with maximum profit or with minimum budget, an effective infrastructure of collection sites, processing sites and transportation network is required. For this case study, we divide the State of Georgia into 12 different re-gions based on service delivery rere-gions defined by Georgia’s Department of Community Affairs (DCA) as shown in Fig. 6 [1]. Each region represents a source of electronic waste streams, a geographically centered collection site and also a demand point for the units after a refurbishing process. The approximate
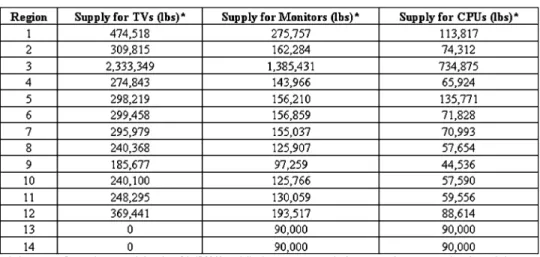
TABLE I
GEORGIA E-SCRAPSUPPLYESTIMATES
Fig. 6. State of Georgia divided into 12 DCA regions.
amount of used electronic equipment available for each region is estimated from its population. The parameters and informa-tion used in the model are detailed in the following subsecinforma-tions that describe e-scrap supply, collection sites, processing sites, demand, and transportation information.
Supply Information: Based upon recycling percentages de-termined from recent studies in Florida [36], we estimate the supply of e-scrap by assuming that on average each resident pro-duces 4 lb of electronic items per year ready for recycling, and studies have shown that between 10%–30% of those residents with something to recycle participate in the collection program. We study how this range affects the design of the network as part of the robust solution approach. We assume that the rela-tive proportions of the collection amounts (in units) for
televi-sions, computer monitors, and CPUs for material collected in Georgia is 35.8:38.5:25.7 and the average weights for televi-sions, computer monitors, and CPUs are 61.6, 30.0, and 20.6 lb, respectively. The proportion amounts and the average weights are from the statistical data of the nearby state, Florida, which is available at http://www.dep.state.fl.us/waste/default.htm.
In addition to the residential and business sources within the state, some Georgia e-scrap processors import business e-scrap from other neighboring states. We represent imported e-scrap as two sources providing obsolescence of computer monitors and CPUs denoted as regions 13 and 14 [2]. Table I shows the esti-mated supply information for each type of electronic equipment from each region under the assumption that 30% of the people who have e-scrap (4 lb of e-scrap per resident) participate in the collection program.
Collection Sites: For the e-scrap originating within the state, we have considered 12 potential state of Georgia government-collection centers located in the center county of each DCA gion. For the imported e-scrap, we have designated external re-gions 13 and 14. Each collection center is assumed to collect televisions, monitors, and CPUs supplied by the small business and resident sources located within a 100 mile transport circle centered at the collection center. We assume that it may be pos-sible for the designated collection sites also to be able to per-form sorting and processing functions. Additionally, this case study includes six nonprofit collection centers throughout the state and one large commercial collection center located in Ma-rietta, Georgia. The large scale collection center is assumed to collect monitors and CPUs supplied by large business sources both inside and outside of Georgia.
The incurred collection cost is separated as fixed, variable, and opening cost. The fixed cost includes the staffing, overhead costs, and the opening cost corresponding to the space rental and utility fees. The variable cost accounts for the rest of the hidden cost and is proportional to the collection amount. The specific numbers used in the study for the collection site information are given in Table II.
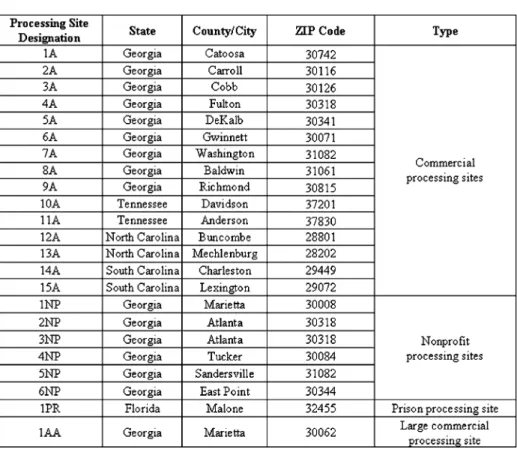
Processing Sites: We consider 15 potential commercial processing sites (nine sites in Georgia, two sites in Tennessee, two sites in North Carolina, and two sites in South Carolina),
TABLE II
COLLECTIONSITEDATAUSED IN THECASESTUDY
TABLE III
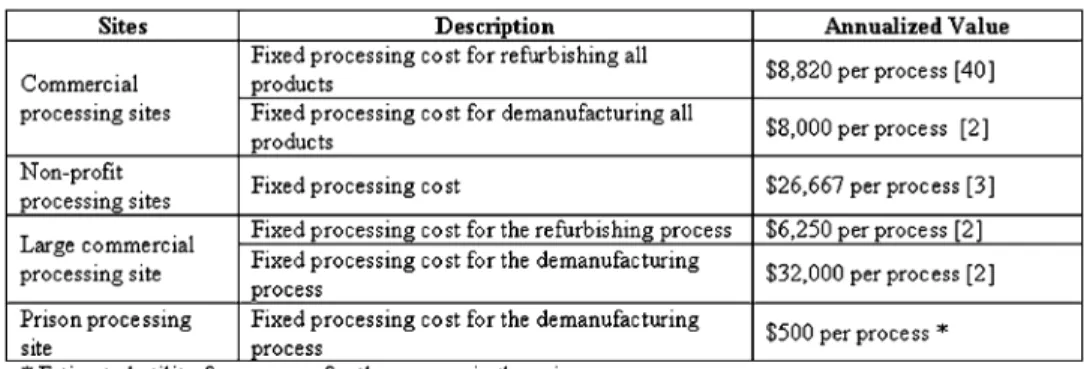
GENERALINFORMATION FORALL23 POTENTIALPROCESSINGSITES[2], [3]
six nonprofit processing sites, one large commercial processing site, and one prison processing site in this case study. Each facility represents an actual refurbishing and/or demanufac-turing facility located in Georgia or nearby states. Refurbishing process includes fixing and replacing operations for the broken parts. Demanufacturing process refers to the combination of disassembly, mechanical fragmentation and separation of mate-rials. Table III contains general information for all 23 potential processing sites considered in this case study.
For each processing site, we consider six main potential pro-cesses: television refurbishment, monitor refurbishment, CPU refurbishment, television demanufacturing, monitor demanu-facturing, and CPU demanudemanu-facturing, but not all processing
sites necessarily perform all six processes. The cost information for each of the six processes is presented in Tables IV and V.
Demand and Prices for Demanufactured/Refurbished Equip-ment, Parts, and Recycled Materials: The processing sites provide an output of demanufactured equipment, parts, and recycled material to a set of demand locations. We consider four types of demand sources and estimate the quantities using the assumption that the demand for refurbished products is greater than or equal to the supply of old used products provided by that region. The first type of demand comes from people within Georgia who are interested in buying refurbished electronic equipment. For this type of demand, we use the same 12 DCA regions to designate the demand location. The second type of
TABLE IV
VARIABLECOSTS FORREFURBISHING ANDDEMANUFACTURINGPROCESSES
TABLE V
FIXEDPROCESSINGCOSTS FORPROCESSINGSITES
demand source is the group of recycling facilities interested in buying metal, plastic, cathode ray tubes (CRTs), and other demanufactured materials. We consider a total of five recyclers located in several states: Georgia (metal recycler), Florida (CRT products and electronics recycler), Texas (plastics recy-cler), and Pennsylvania (CRT glass recycler). The third type of demand comes from both resident and commercial sources who are interested in buying refurbished commercial electronic equipment in large batches provided by the large commercial processing site. The demand locations for the third type of demand are assumed to be the same places as those used for the 12 DCA regions. The last type of demand describes landfills to which we can dispose the nonhazardous trash that results from demanufacturing. We consider eight landfills located in Georgia and group them into five demand points located based on the DCA regions. (Landfill location information can be found at http://www.wastebyrail.com/network.html.)
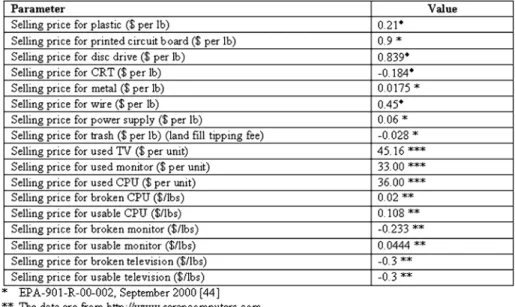
The selling price for each of the refurbished product types and the demanufactured material types is shown in Table VI. Some selling price data are taken from the year 2000, and may not reflect current prices (2005), but all of the other costs and prices are more current.
Transportation Information: We include three types of trans-portation costs. The first type represents the transtrans-portation cost of the people who drive to the collection center and drop off their used electronic equipment. This type of transportation cost is approximated by the gasoline cost ($0.15 per mile) and we as-sume that on average one car carries 50 lb of electronic equip-ment per trip. With this approximation, the transportation cost
per pound per mile is $0.003. This type of transportation cost may be considered as free since it is paid by people who bring e-scrap to the collection center. However, the transportation cost from the e-scrap source to the collection center is still included for a “macro system” perspective.
The second type represents the transportation costs for moving material between collection centers and processing centers, the transportation costs for moving material between processing sites and recycler demand points, and the transporta-tion costs for moving material between processing sites and landfill demand points. We perform this type of transportation with a large truck costing $2 per ton per mile or $0.0009 per pound per mile.
The last type represents the transportation cost for shipping refurbished products from processing sites to customers, which is assumed to be shipped by the private transportation service provider. As a reasonable estimate of the cost of this shipping, we use $0.26 per mile per item—the amount charged by the United Parcel Service (UPS) (cost information is given at http:// www.ups.com).
B. Experimental Design for the Case Study
The data for the state of Georgia case study specifies a large-scale electronics recycling infrastructure design problem. The objective of the problem is to maximize net profit for the system while determining which collection and processing sites to utilize and then what quantities of each item type to process into what materials at each site. We apply our mathematical
TABLE VI
PRICEINFORMATION FORREFURBISHEDPRODUCTS ANDDEMANUFACTUREDMATERIALS
TABLE VII
KEYUNCERTAINTYVALUESETTINGS FOR16 SCENARIOS
programming approach described in Section III to solve the problem.
The results provide a robust configuration for a large scale e-scrap RPS, and the associated net profit (or loss) is predicted. The key uncertain parameters (see [44] and [45]) that we exam-ined are described as follows.
1) Participation rate. For one half of the scenarios, we exam-ined the situation where 10% of the population who have e-scrap (4 lb per resident) contributed at least one used electronic item for collection. For the other half of the sce-narios, we used a participation rate of 30%. In other words, 0.4 lb per resident of e-scrap is collected in the case of 10% participation rate and 1.2 lb per resident is collected in the case of 30% participation rate.
2) Utilization of collection infrastructure. Collection points are more spread out compared to processing points. Thus, the collection capacity is dependent on the geographical segment. In order not to overestimate or underestimate the capacity in the collection facility, we set the low and high level of capacity utilization in the collection infrastructure. For one half of scenarios, we solved problems where col-lection infrastructure only utilizes 45% of colcol-lection ca-pacity. The other half of the scenarios, we solved adopt the level of 75% of collection capacity.
3) CPU and monitor reusability percentages. A key uncer-tainty is the condition of the CPUs and monitors that are collected. We ran one half of our problems assuming reusability rates of (CPU 30%, monitor 25%) and the
TABLE VIII
OPTIMAL ANDROBUSTSOLUTIONS FORGEORGIA E-SCRAPRPS INFRASTRUCTURE
other half with (CPU 10%, monitor 10%). The parameter settings here are based upon several estimates in [44], [46], and [47].
4) Television reusability percentage. Used televisions that cannot be refurbished and resold are an expensive cost. However, many households hold on to their televisions until they no longer work. We assume that the television reusability percentage is lower than the reusability of CPUs and monitors. In this study, we solve one half of the scenarios that only 5% of the collected televisions are in a reusable condition. The other half of the scenarios specify that 10% of the televisions are reusable.
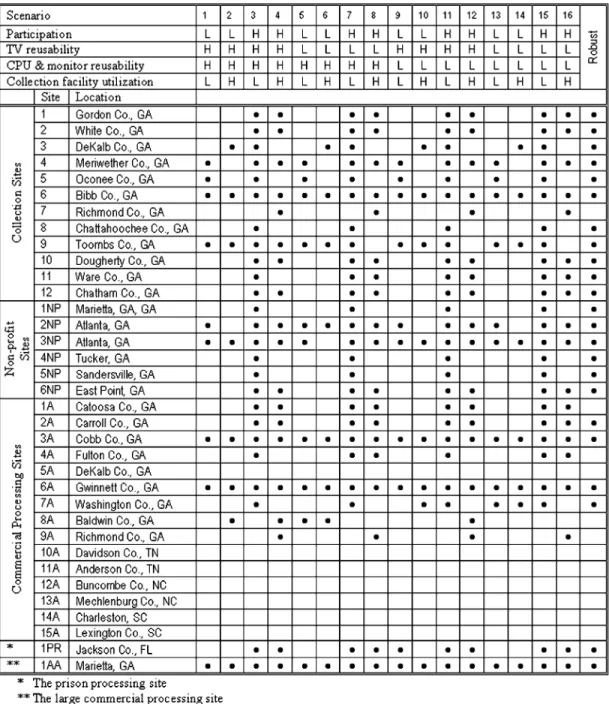
The four types of uncertainty factors, with two levels speci-fied for each factor, result in 2 or 16 scenarios to be studied. In
other words, each scenario describes a unique electronics recy-cling infrastructure design problem to be solved. The 16 prob-lems or scenarios are defined in Table VII.
C. Overall Results
Our case study problems is solved on a Windows 2000-based personal computer with Pentium 1.80 GHz with 1-GBRAMusing C++ program and CPLEX 9.0 [48] for the optimization software. MS-Access and the Visual Basic programming language are used as the case study database and user interface programs. This case study involves in a MILP model with 3500 binary variables, 1.2 million continuous variables, and 1.4 million constraints. When applying a direct solution approach for the robust problem, the optimal solution can not be found. The
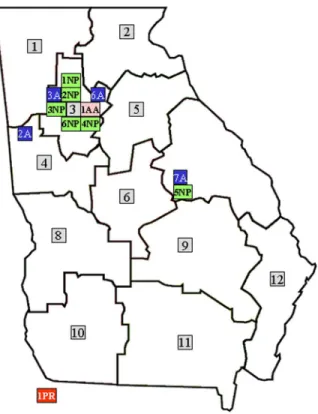
Fig. 7. e-Scrap RPS robust infrastructure solution for the state of Georgia.
computer requires more than 192 h of computational time without returning any feasible solution. A heuristic method [49] is used to solve the case study to optimality for the robust model, and it requires not more than 50 h of computational time.
Using the optimal solutions for the individual scenarios, we solve the robust optimization problem to obtain the robust infra-structure solution. The optimal infrainfra-structure solutions and the robust infrastructure are given in Table VIII. The geographically robust infrastructure solution is also illustrated in Fig. 7. Based upon the robust infrastructure, the corresponding values of con-tinuous variables are obtained for each of the 16 scenarios.
The robust solutions for the individual scenarios can be ex-amined to understand the relative performance of the robust in-frastructure solution in each scenario. Fig. 8 provides a com-parison of the net profit associated with the optimal solution for each scenario to the net profit associated with the robust solution for each scenario. As expected, the value of the optimal solution serves as an upper bound on the value of the robust solution for each scenario.
There are several conclusions that can be drawn from Fig. 8. First, for the input data values detailed in Section IV, it appears that economically viable solutions (i.e., solutions that yield a positive net profit) can be found for several problem scenarios. However, several scenarios are with the estimated negative profits due to the poor setting of data input (i.e., low utilization in collection facilities, and low reusability for items collected). Second, it is clear that two factors of the high utilization in collection facilities and the high reusability rate in e-scrap are preferable directions toward a higher profit. However, the solution indicates that a high participation rate leads to a better profit in high reusability scenarios, but a high participation rate
Fig. 8. Comparison of net profit of the optimal solution to the net profit of the robust solution for each scenario.
Fig. 9. Comparison of net profit of the optimal solution to the net profit with fully utilized collection facilities for each scenario.
results in the poor profit in low reusability scenarios. It implies the impact of participation rates on the profit performance is not always in the same direction, but depends on the case of the reusability level in this case study. Fig. 9 provides a com-parison of the net profit for each scenario to the net profit when collection facilities are fully 100% utilized in the collection capacity. The dark bars in Fig. 9 are the optimal net profits for all scenarios, the same as optimal values shown in Fig. 8, and the gray bars are the profits when collection facilities are fully 100% utilized in associated scenarios. As expected, the net profit value with 100% utilization is also an upper bound for each scenario.
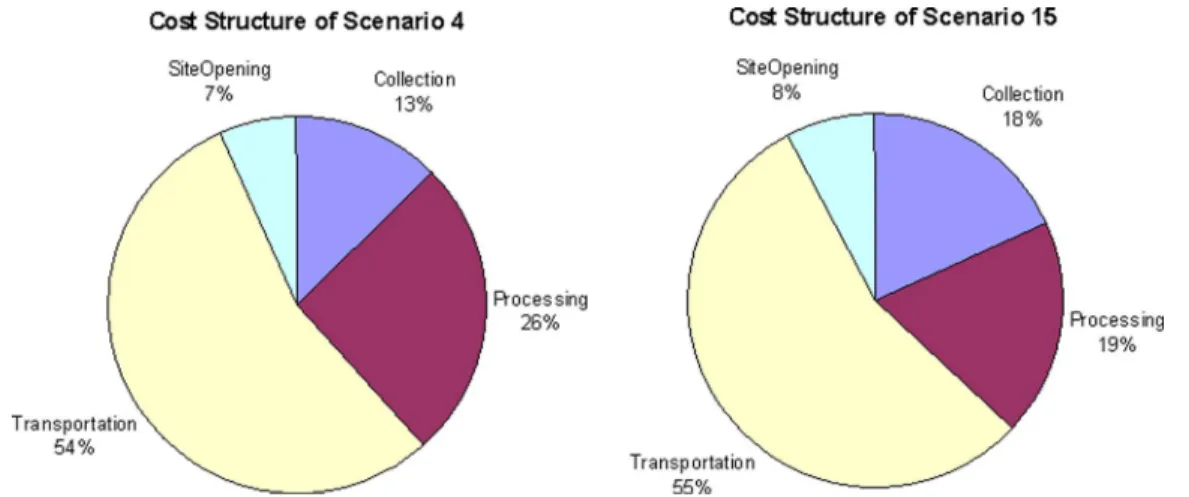
It is also interesting to analyze how the cost burdens compare between highly favorable economic conditions (like Scenario 4, with a high number of reusable televisions, CPUs, and mon-itors collected, and a high collection capacity utilization) and unfavorable ones (like Scenario 15, with many more unusable televisions, CPUs, and monitors, and a low collection capacity utilization). Fig. 10 illustrates this comparison. The transporta-tion costs both in Scenarios 4 and 15 are more than half of the total system costs for electronics recycling (logistics).
Similarly, the relative sources of revenues can be compared when economic conditions are highly favorable (Scenario 4) or when they are not as good (Scenario 15). Fig. 11 illustrates this
Fig. 10. Comparisons of relative costs for highly favorable conditions (Scenario 4) and unfavorable ones (Scenario 15).
Fig. 11. Comparisons of revenue sources for highly favorable conditions (Scenario 4) and unfavorable ones (Scenario 15).
comparison. As expected, under less favorable economic condi-tions the revenue stream is more highly dependent on collection fees as a source of revenue.
V. CONCLUSION ANDEXTENSIONS
In this paper, our method successfully creates a design for used electronics RPS infrastructure in the state of Georgia. It is distinguished from previous approaches to this problem by the way that it captures uncertainty and produces robust solu-tions. The case study is a large scale, with millions of variables and constraints. The problem provides a challenging large scale benchmark data set for other robust optimization solution ap-proaches.
Data based on a variety of sources has been used to approx-imate the regional electronics recycling infrastructure design problem for Georgia. Because very little publically available data exist for this relatively new problem in the U.S., these data may be helpful to other designers of e-scrap collection and pro-cessing systems.
Sixteen alternative problem scenarios have been analyzed to understand how the infrastructure design solutions are affected by key uncertainties in the resident participation rates, the per-centage of used-collected electronics that are reusable, and the capacity utilization in collection facilities. From these solutions, we have learned that the resulting net profits and corresponding
material flows vary greatly depending on the predicted condi-tions. The resulting solutions suggest that an economically vi-able electronics recycling infrastructure is possible for the state of Georgia in several problem scenarios. In fact, this result dis-proves our informal initial hypotheses that the e-scrap collec-tion and processing system is doomed to lose money in many of the scenarios. In other words, the e-scrap collected in the state of Georgia may be seen as a positive financial resource in the case of the high reusability of e-scrap collected, and the corre-sponding collection and processing infrastructure as a source of economic development and job creation.
A key extension of this work is to incorporate additional types of e-scrap including printers, cell phones, telephones, laptop computers, personal digital assistant products (PDAs), etc. in case study analysis, especially with the increasing popularity of mobile products. Also, inclusion of additional collection sites and processing alternatives would extend the study to more comprehensive systems. Several other sources of uncertainty should be investigated, including the uncertain-ties associated with demand quantiuncertain-ties, demand prices, and transportation costs, and their two- and three-way interactions, since these can be critical drivers of revenues and costs. Data security and privacy are other issues that should be examined in more detail in future work since cleaning or erasing the data may cause extra costs in processing e-scrap products. Finally,
investigations on effects of preloading the free software systems or removing the operating systems in refurbished computers are also interesting future directions.
ACKNOWLEDGMENT
The authors would like to thank the reviewers and the asso-ciate editor for their helpful and valuable comments to improve this paper. The authors are grateful for the generous interaction and guidance provided from many industry experts, including J. Powell of Zentech, C. Phillips and the staff of Reboot, N. Nejad of Molam, K. Clark of MARC5R, and B. Donaghue of P2AD. The authors value the input and expertise from Georgia Institute of Technology students R. Bhakta, P. Jagad, A. Jain, C. Spencer, and J. Pas.
REFERENCES
[1] Georgia Department of Community Affairs (DCA), March 2003 [On-line]. Available: http://www.dca.state.ga.us/
[2] N. Nejad, private communication, 2003. [3] C. Phillips, private communication, 2002.
[4] J. C. Ammons, M. J. Realff, and D. E. Newton, “Decision models for reverse production system design,” in Handbook of Environmentally
Conscious Manufacturing, C. N. Madu, Ed. Boston, MA: Kluwer, 2001, pp. 341–362.
[5] V. D. R. Guide, V. R. Daniel, V. Jayaraman, R. Srivastava, and W. C. Benton, “Supply-chain management for recoverable manufacturing systems,” Interfaces, vol. 30, no. 3, pp. 125–145, 2000.
[6] S. D. P. Flapper, “On the operational aspects of reuse,” in Proc. 2nd
Int. Symp. Logistics, Nottingham, U.K., Jul. 1995, pp. 109–118.
[7] ——, “Logistic aspects of reuse: an overview,” in Proc. 1st Int.
Working Seminar on Reuse, Eindhoven, The Netherlands, Nov. 1996,
pp. 109–118.
[8] S. Dowlatshahi, “Developing a theory of reverse logistics,” Interfaces, vol. 30, no. 3, pp. 143–155, 2000.
[9] M. Fleischmann, J. M. Bloemhof-Ruwaard, R. Dekker, E. van der Laan, J. van Nunen, and N. van Wassenhove Luk, “Quantitative models for reverse logistics: a review,” Eur. J. Oper. Res., vol. 103, pp. 1–17, 1997. [10] M. Fleischmann, H. R. Krikke, R. Dekker, and S. D. P. Flapper, “A characterization of logistics networks for product recovery,” Omega, vol. 28, pp. 653–666, 2000.
[11] C. R. Carter and L. M. Ellram, “Reverse logistics: a review of the lit-erature and framework for future investigation,” J. Business Logistics, vol. 19, no. 1, pp. 85–102, 1998.
[12] H.-Y. Kang and J. M. Schoenung, “Electronic waste recycling: a review of U.S. infrastructure and technology options,” Resources,
Conserva-tion, Recycling, vol. 45, pp. 368–400, 2005.
[13] T. Spengler, H. Püchert, T. Penkuhn, and O. Rentz, “Environmental integrated production and recycling management,” Eur. J. Oper.
Re-search, vol. 97, no. 2, pp. 308–326, 1997.
[14] A. Gungor and S. Gupta, “Issues in environmentally conscious manu-facturing and product recovery: A survey,” Comput. Ind. Eng., vol. 36, pp. 811–853, 1999.
[15] T. Spengler, M. Ploog, and M. Schroter, “Integrated planning of ac-quisition, disassembly and bulk recycling: A case study on electronic scrap recovery,” OR Spectrum, vol. 25, pp. 413–442, 2003.
[16] S. Minner, “Strategic safety stocks in reverse logistics supply chain,”
Int. J. Prod. Econ., vol. 71, pp. 417–428, 2001.
[17] B. E. Hirsch, T. Kuhlmann, and J. Schumacher, “Logistics simulation of recycling network,” Comput. Ind., vol. 36, pp. 31–38, 1998. [18] V. D. R. Guide, R. Srivastava, and M. E. Kraus, “Proactive expediting
policies for recoverable manufacturing,” J. Oper. Res. Soc., vol. 49, pp. 479–491, 1998.
[19] H. Krikke, J. Bloemhof-Ruwaard, and L. N. van Wassenhove, “Concur-rent product and closed-loop supply chain design with an application to refrigerators,” Int. J. Prod. Res., vol. 41, no. 16, pp. 3689–3719, 2003. [20] H. R. Krikke, A. van Harten, and P. C. Schuur, “Business case Océ: Reverse logistic network re-design for copiers,” OR Spektrum, vol. 21, pp. 381–409, 1999.
[21] M. S. Sodhi and B. Reimer, “Models for recycling electronics end-of-life products,” OR Spektrum, vol. 23, pp. 91–115, 2001.
[22] A. Nagurney and F. Toyasaki, “Reverse supply chain management and electronic waste recycling: a multitiered network equilibrium frame-work for e-cycling,” Transportation Res. E, vol. 41, pp. 1–28, 2005. [23] P. Kouvelis and G. Yu, Robust Discrete Optimization and its
Applica-tions. Boston, MA: Kluwer, 1997.
[24] M. J. Realff, J. C. Ammons, and D. J. Newton, “Robust reverse pro-duction system design for carpet recycling,” IIE Trans., vol. 36, pp. 767–776, 2004.
[25] O. Listes and R. Dekker, “A stochastic approach to a case study for product recovery network design,” Eur. J. Oper. Res., vol. 160, pp. 268–2872, 2005.
[26] A. I. Barros, R. Dekker, and V. Scholten, “A two-level network for recycling sand: a case study,” Eur. J. Oper. Res., vol. 110, pp. 199–214, 1998.
[27] R. L. Clay and I. E. Grossmann, “A disaggregation algorithm for the optimization of stochastic planning models,” Comput. Chem. Eng., vol. 21, no. 7, pp. 751–774, 1997.
[28] K. Inderfurth, A. G. de Kok, and S. D. P. Flapper, “Product recovery in stochastic remanufacturing systems with multiple reuse options,” Eur.
J. Oper. Res., vol. 133, pp. 130–152, 2001.
[29] C.-S. Yu and H.-L. Li, “A robust optimization model for stochastic logistic problems,” Int. J. Prod. Econ., vol. 64, no. 1, pp. 385–397, 2000.
[30] J. M. Mulvey, R. J. Vanderbei, and S. A. Zenios, “Robust optimization of large-scale systems,” Operations Res., vol. 43, no. 2, pp. 264–281, 1995.
[31] J. G. Genaro, P. Kouvelis, and A. Kurwala, “A robustness approach to uncapacitated network design problems,” Eur. J. Oper. Res., vol. 94, pp. 362–376, 1996.
[32] H. E. Mausser and M. Laguna, “A heuristic to minimax absolute regret for linear programs with interval objective function coefficients,” Eur.
J. Oper. Res., vol. 117, pp. 157–174, 1999.
[33] M. J. Realff, J. C. Ammons, and D. J. Newton, “Carpet recycling: in-frastructure strategic design,” J. Textile Inst., vol. 91, no. 3, pt. 3, pp. 168–186, 2000.
[34] M. J. Realff, N. Shah, and C. C. Pantelides, “Simultaneous design, layout and scheduling of pipeless batch plants,” Comput. Chem. Eng., vol. 20, pp. 869–893, 1996.
[35] N. Shah, C. C. Pantelides, and R. W. H. Sargent, “A general algorithm for short-term scheduling of batch operations—II. Computational is-sues,” Comput. Chem. Eng., vol. 17, pp. 229–244, 1993.
[36] Department of Environmental Protection. Tallahassee, FL [Online]. Available: http://www.dep.state.fl.us/waste/default.htm
[37] D. J. Newton, “A robust approach for planning the strategic infrastruc-ture of reverse production systems,” Ph.D. dissertation, Georgia Inst. Technol., Atlanta, 2000.
[38] M. J. Realff, private communication, 2002, 2002.
[39] Northeast Recycling Council, Inc. (NERC), “Setting up and operating electronics recycling/reuse programs: A manual for municipalities and counties,” Oct. 2001.
[40] “Demanufacturing of electronic equipment for reuse and recycling (DEER2), technology and demonstration center mission need state-ment (MNS),” August 31, 2000, DAAE30-98-C-1050, Revision A. [41] W. Waters, “Electronics recycling vendor survey,” Chelsea Center for
Recycling and Economic Development, Univ. Mass., Tech. Rep. #5, Aug. 1998, p. 25.
[42] J. Pepi, “University of Massachusetts Amherst Scrap Electronics Pro-cessing,” Chelsea Center for Recycling and Economic Development, Univ. Mass., Tech. Rep. #7, Aug. 1998, p. 2.
[43] “Recycling used electronics, report on minnesota’s demonstration project,” Minnesota Office of Environmental Assistance, Jul. 2001, p. 55.
[44] “Electronics re-use and recycling infrastructure development in Mass-achusetts,” Sep. 2000, EPA-901-R-00-002.
[45] “Florida’s strategy for the management of end of life cathode ray tubes (CRTs), computers and other electronic equipment,” Sep. 2, 1999, Dis-cussion paper.
[46] National Recycling Coalition, [Online]. Available: http://www.nrc-re-cycle.org/resources/electronics/trends.htm
[47] “CompuMentor, Islands in the wastestream—Baseline sudy of non-commercial computer reuse in the United States,” Fall, 2004 [Online]. Available: http://www.compumento.com
[48] “CPLEX 9.0 User Manual,” ILOG, Oct. 2003.
[49] T. Assavapokee, M. J. Realff, J. C. Ammons, and I-H. Hong, “Sce-nario relaxation algorithm for finite sce“Sce-nario based min-max regret and min-max relative regret robust optimization,” Comput. Oper. Res., to be published.
I-Hsuan Hong received the M.S. degree in industrial engineering from National Taiwan University, Taipei, Taiwan, R.O.C., and the Ph.D. degree in industrial and systems engineering from the Georgia Institute of Technology, Atlanta, in 2006
In 2006, he joined the faculty of National Chiao-Tung University, Hsinchu, Taiwan, as an Assistant Professor. His research areas include reverse logistics systems, competition models in multiechelon supply chains, and application and methodologies for game theory.
Tiravat Assavapokee received the Ph.D. degree in industrial and systems engineering from the Georgia Institute of Technology, Atlanta, in 2004
He has been an Assistant Professor of Industrial Engineering at the University of Houston, Houston, TX, since August 2004. As a Researcher, he is currently focused on the modeling and analysis of problems and algorithms in logistics planning, city evacuation planning, and forward and reverse supply chain system design. He has particular interests in algorithm development and applications of robust optimization, stochastic programming, stochastic dynamic programming, and simulation-based optimization. His current projects include city evacuation planning from natural disaster, robust strategic design of reverse production system of electronic products and carpets, min–max regret robust algorithms for interval data uncertainty, min–max regret robust algorithms for full factorial design scenarios, relaxation algorithms for min–max regret robust optimization, and applications of accelerated Benders’ decomposition algorithms on robust optimization and stochastic programming.
Jane Ammons received the B.S. and M.S. degrees in industrial engineering from the University of Al-abama, Tuscaloosa, and the Ph.D. degree in industrial and systems engineering from the Georgia Institute of Technology (Georgia Tech), Atlanta.
She serves as the Georgia Tech Associate Dean of Engineering for Faculty Affairs, the NSF ADVANCE Professor of Engineering, and Professor of Industrial and Systems Engineering. Her areas of expertise in-clude production systems design and analysis, man-ufacturing systems, reverse logistics, and continuous quality improvement. In addition to her academic experience, she has worked as a Plant Engineer for an industrial manufacturer.
Dr. Ammons is a member of SME, INFORMS, and ASEE, and has been elected a Fellow of IIE and is a registered Professional Engineer.
Chuck Boelkins is a graduate of Oberlin College, Oberlin, OH, and received the Ph.D. degree in research design and analysis from Stanford University, Stanford, CA.
He is a Resource Recovery Specialist with the Pollution Prevention Assis-tance Division, Georgia Department of Natural Resources, Atlanta. He has been actively managing residential and industrial materials recovery, reuse, and recy-cling for 14 years. He served as a Technical Advisor to the Georgia Computer Equipment Disposal and Recycling Council from 2002 to 2005. He previously served on the research faculty at the Stanford School of Medicine and the Har-vard University School of Public Health.
Dr. Boelkins is a member of Sigma Xi and the Georgia and National Recy-cling Coalitions.
Kennon Gilliam received the B.S. degree in environmental engineering and the M.S. degree in operations research from the Georgia Institute of Technology (Georgia Tech), Atlanta, in December 2003 while on assignment with the U.S. Army. The work in this paper in part was done during his study at Georgia Tech.
Devon Oudit received the M.S. degree in industrial engineering from the Georgia Institute of Technology, Atlanta, in December 2002. The work in this paper in part was done during his study at Georgia Tech.
Matthew J. Realff received the B.S. degree from Imperial College London, U.K., in 1986 and the Ph.D. degree from the Massachusetts Institute of Technology, Cambridge, in 1992.
He is the David I. J. Wang Associate Professor of Chemical and Biomolecular Engineering at the Georgia Institute of Technology, Atlanta. He works in the area of Reverse Production System Design and in Process Planning and Operation.
Juan Martín Vannícola contributed to the research team during a visit to the Georgia Institute of Technology, Atlanta, while studying at the Instituto Tecnols-gico de Buenos Aires (ITBA), Argentina. After finishing his degree at ITBA, he continued his graduate studies at Eindhoven University, Eindhoven, The Nether-lands.
Wuthichai Wongthatsanekorn received the B.S. de-gree in industrial engineering from Columbia Uni-versity, New York, in 2000, the M.S. degree in op-erations research from the University of Michigan, Ann Arbor, in 2001, and the Ph.D. degree in indus-trial and systems engineering from the Georgia Insti-tute of Technology, Atlanta.
His primary area of interest is the modeling and analysis of practical supply chain and logistics prob-lems.