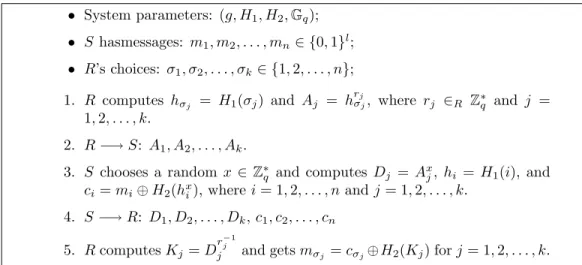具隱私性之資料擷取：忘卻式傳輸與播送

國

立

交

通

大

學

資訊工程學系

博

士

論

文

具隱私性之資料擷取：忘卻式傳輸與播送

Privacy-Preserving Data Retrieval: Oblivious Transfer and Cast

研 究 生：朱成康

指導教授：曾文貴 教授

具隱私性之資料擷取：忘卻式傳輸與播送

Privacy-Preserving Data Retrieval: Oblivious Transfer and Cast

研 究 生：朱成康 Student：Cheng-Kang Chu

指導教授：曾文貴 博士 Advisor：Dr. Wen-Guey Tzeng

國 立 交 通 大 學

資 訊 工 程 學 系

博 士 論 文

A Dissertation

Submitted to Department of Computer Science

College of Computer Science

National Chiao Tung University

in partial Fulfillment of the Requirements

for the Degree of

Doctor of Philosophy

in

Computer Science

June 2008

Hsinchu, Taiwan, Republic of China

i

具隱私性之資料擷取：忘卻式傳輸與播送

學生：朱成康

指導教授：曾文貴 博士

國立交通大學資訊工程學系

摘要

具隱私性之資料擷取一直是密碼學上一個重要的課題，它可以讓

使用者在取得資料的同時，也保有隱私性。在本論文裡面，我們對於

這個課題有兩個貢獻。首先，我們提出了一些有效率的忘卻式傳輸機

制。忘卻式傳輸包含了一個傳送者與一個接收者，傳送者有一些訊息

在手上，而接收者想取得其中的某幾個訊息。對此，安全性的要求在

於接收者只能取得他想要的那部分訊息，而且不能讓傳送者知道他的

選擇。忘卻式傳輸的發展分為一些類別，例如 2 選 1、n 選 1、n 選 k、

動態、條件忘卻式傳輸等等。本論文裡我們提出數個 n 選 k 及一個動

態忘卻式傳輸機制。

接著，我們提出一個新的概念，稱為『條件忘卻式播送』。與忘

卻式傳輸不同，這種系統有三個參與者：一個傳送者及兩個接收者。

傳送者有一個訊息，而接收者擁有他們各自的秘密值。當接收者的兩

個秘密值符合某個我們定義的條件，那麼兩個接收者即可從傳送者那

邊取得訊息。此概念安全性的要求在於，每位參與者都不能知道另外

兩位手中的秘密。同時，我們也提出一些條件忘卻式播送的變形。對

於這些概念及變形，我們提出了一些實際的機制，針對的是「相等」

、

「不相等」

、

「大於」等基本的條件，有了這些基本的機制，便可延伸

設計出更複雜的密碼協定。

關鍵字：忘卻式傳輸，動態忘卻式傳輸，忘卻式播送，條件忘卻式播

送

Privacy-Preserving Data Retrieval:

Oblivious Transfer and Cast

Student: Cheng-Kang Chu Advisor: Dr. Wen-Guey Tzeng Department of Computer Science

National Chiao Tung University

Abstract

Privacy-preserving data retrieval is an important cryptographic issue. It allows users to privately obtain some data they need. In this thesis, we have a two-fold contribution to privacy-preserving data retrieval. Firstly, we give some efficient oblivious transfer (OT) constructions. OT involves two parties: a sender S and a receiver R. The sender S has several messages of which the receiver R wants to get some. The security requirement is that S wants

R to get the messages of his choices only, and R does not want S to know

what he chooses. OT was developed in several types, such as 1-out-of-2 OT, 1-out-of-n OT, k-out-of-n OT, adaptive OT, conditional OT. We propose several efficient k-out-of-n OT schemes and an adaptive OT scheme.

Then, we introduce a new notion of conditional oblivious cast (COC), which involves three parties: a sender S and two receivers A and B. Re-ceivers A and B own secrets x and y, respectively, and the sender S holds a message m. In a COC scheme for a predicate Q (Q-COC), A and B get

party does not leak his secret to the other two parties except the informa-tion that can be inferred from the result. We also extend COC to different settings: only one receiver gets the message or S sends two messages at a time. We give definitions for COC and propose COC schemes for “equality”, “inequality”, and “greater than” predicates. These are fundamental schemes for constructing more complex secure multi-party protocols. Finally, we pro-vide new constructions of three-party oblivious cast, which are more efficient in communication complexity than previous schemes.

Keywords: oblivious transfer, adaptive oblivious transfer, oblivious cast, conditional oblivious cast

v

誌

謝

首先感謝我的指導老師曾文貴教授，在我碩士班及博士班總共九

年的學習過程中，帶領我深入密碼學的領域，老師認真積極的教學態

度，使我受益良多。另外，我要感謝口試委員，成大賴溪松教授、台

科大吳宗成教授、清大孫宏民教授、警大王旭正教授、交大陳榮傑教

授、交大謝續平教授、交大蔡錫鈞教授與交大黃世昆教授，在論文上

給我許多建議與指導，讓我的論文更加完善。除此之外，我也要感謝

學長胡智明教授特別北上來給我鼓勵，以及實驗室學弟妹，孝盈、煥

宗和其他的碩士班同學的幫忙。

最後，我要感謝我的家人及季穎，不論在精神或物質上都給我極大的

支持，讓我在無後顧之憂的情況下可以順利完成學業。在此，謹以此

文獻給所有我想要感謝的人。

Contents

2 Previous Works 10

2.1 Oblivious Transfer . . . 10 2.2 Oblivious Cast . . . 17 3 k-out-of-n Oblivious Transfer 19 3.1 Preliminaries . . . 19 3.2 OTk

3.2.1 The Scheme for Semi-Honest Receiver . . . 23

3.2.2 The Scheme for Malicious Receiver . . . 27

3.3 OTk n with Unconditional Security of Sender . . . 30

3.3.1 The Generic Construction . . . 31

3.3.2 Concrete Construction . . . 38

3.4 OT with Adaptive Queries . . . 42

4 Conditional Oblivious Cast 46 4.1 Preliminaries . . . 46

4.1.1 Definitions . . . 46

4.1.2 Backgrounds . . . 51

4.2 Conditional Oblivious Cast: Type I . . . 55

4.2.1 COC-I for “Equality” Predicate . . . 55

4.2.2 COC-I for “Inequality” Predicate . . . 59

4.2.3 COC-I for “Greater Than” Predicate . . . 64

4.3 Conditional Oblivious Cast: Type II . . . 65

4.3.1 COC-II for “Equality” Predicate . . . 65

4.3.2 COC-II for “Greater Than” Predicate . . . 66

4.3.3 A General Transformation from COC-II to COC-III . . 69

4.4 COC Against Malicious Parties and Collusion . . . 69

4.5 Extensions . . . 77

4.5.1 Constructions of Oblivious Cast . . . 77

5 Conclusion 83

Chapter 1

Introduction

Electronic commerce (eCommerce) is a very popular and important service on Internet nowadays. People can buy anything they need by just clicking buttons at home. In most situations, users’ personal data (e.g. credit card numbers) are well encrypted. However, there is no guarantee of users’ privacy. Why should we tell these merchants which music we like or which book we want to buy? Could we conceal our choices from the merchant?

Privacy-preserving data retrieval allows users privately obtaining some data they need from a sender. In many applications, users’ privacy should be well protected. For example, researchers should be able to query a database without revealing which topics they are interested in, and bidders should be able to bid for a secret without exposing their prices.

In fact, we can use a general secure multi-party computation protocol to fulfill the above requirements. However, we are seeking for more efficient solutions of some specific cases. In this thesis, we discuss privacy-preserving data retrieval for two-party and three-party cases. We focus on oblivious

transfer (OT) and conditional oblivious cast (COC) protocols for these two cases, respectively. In this chapter, we first introduce the concepts of OT and COC, and then state our results to the both notions.

1.1

Oblivious Transfer

Oblivious transfer (OT) is an important cryptographic protocol. It protects users’ privacy from exposing their choices and preserves merchants’ security. In other words, by invoking OT, a buyer only gets the paid goods, and a merchant doesn’t know which ones are chosen. Moreover, OT is an important building block of cryptographic protocols [GV87, Kil88, Yao86].

An oblivious transfer scheme involves two parties: a sender S and a re-ceiver R. S has several messages and R wants to obtain some of them via interaction with S. There are two security requirements for oblivious transfer: (1) R obtains the chosen messages only; (2) S doesn’t know which messages are chosen. The original OT was proposed by Rabin [Rab81]. Then it was developed in the following main types:

• Rabin’s OT: S sends a message to R, and R gets the message with

probability 1/2. On the other hand, S doesn’t know whether R gets the message or not.

• 1-out-of-2 OT (OT1

2): S has two messages m1 and m2, and allows R

to obtain exactly one of them. In addition, S remains oblivious to R’s choice.

• 1-out-of-n OT (OT1

n): An extension of OT12 for the case that S has n

messages.

• k-out-of-n OT (OTk

n): Similar to OT1n except that R obtains k out of

n messages from S.

We are concerned about the most general case - OTk

n in this work. A

straightforward solution for OTk

n is to run OT1nk times independently.

How-ever, this needs k times the cost of OT1

n. So we hope to develop a direct

construction for OTk

n. Security of OT is also an interesting issue. Since it is

impossible to provide unconditional security for both sender and receiver, we consider the unconditional security for each party separately, and the security of the other side is computational. Users can choose appropriate schemes in various applications with different security settings.

Oblivious transfer with adaptive queries (Adpt-OT) allows R to query messages one by one adaptively [NP99b, OK04]. For this setting, S first commits messages to R in the commitment phase. Then in the transfer phase, R makes queries of messages one by one. Adaptive OT is natural and has many applications, such as oblivious search, oblivious database queries, private information retrieval.

1.2

Conditional Oblivious Cast

Instead of depending on R’s choices solely, conditional oblivious transfer (COT) [COR99, BK04] lets R get the message m under some condition.

For example, in a Q-COT scheme, S and R have their own secrets x and y respectively, and R gets m from S if and only if Q(x, y) = 1. Furthermore,

S can not get the result of the condition on x and y.

Three-party oblivious cast (OC) [Bla96, FGMO01] is a generalization of OT to the three-party case: one sender S with a secret bit and two receivers

A and B. The bit is received by exactly one receiver, each with probability

1/2. We further generalize oblivious cast to conditional oblivious cast (COC), where the receivers A and B have their own secrets and can get messages from S if and only if some condition of their secrets holds. The main idea of COC is to separate the role of the secret holder from the message holder S in COT. A COC scheme that meets the requirements of our definitions can be easily transferred to a COT scheme.

For some predicate Q, let the receivers A and B hold secrets x and y, respectively. We discuss three types of COC:

• Q-COC-I: S has a message m. A and B get m if and only if Q(x, y) = 1; • Q-COC-II: S has two messages m0 and m1. A and B get m1 if and

only if Q(x, y) = 1 and m0 if and only if Q(x, y) = 0;

• Q-COC-III: S has a message m. A gets m if and only if Q(x, y) = 1

and B gets m if and only if Q(x, y) = 0.

In all types of COC, the secret x (resp. y) can not be revealed to either the receiver B (resp. A) or the sender S.

COC not only covers all functionalities of COT, but also broadens the range of its applications. We provide three examples here:

• Three-party priced oblivious transfer: Aiello et al. [AIR01] introduced

the notion of “priced oblivious transfer”, which protects the privacy of a customer’s purchase from a vendor. In their setting, the buyer needs to deposit some amount of money in each vendor. This is not practical if a buyer wants to purchase various goods from various vendors. By our COC schemes, we have a generalized priced OT such that the buyer can deposit the money in one bank only. When the buyer wants to buy an item from a vendor, he sends the corresponding price and the bank sends the buyer’s current balance in encrypted form to the vendor. The vendor then sends the item so that the buyer can get it if the balance is above the price.

• Oblivious two-bidder system: A party S has a secret for selling, and A and B are two bidders. The winner can obtain the secret from S

directly. At the end, S has no idea who the winner is. This system can be constructed from COC-III for the “greater than” predicate immedi-ately.

• Oblivious authenticated information retrieval: A user can anonymously

get messages from a server if he passes the authentication procedure provided by another party. For instance, consider a mobile download-ing service which lets users download music, games, movies, etc. from

various merchants without revealing their identities. Assume that a mo-bile phone has no extra memory to store the subscription information. Users first apply the service to the mobile communication company, and the company provides an encrypted subscription list of IMSIs (In-ternational Mobile Subscriber Identity) to the content provider. When a user wants to download a game, his mobile phone sends its encrypted IMSI to the content provider. The content provider then sends the game and the user can get it if the IMSI is in the subscription list. In this case, the user’s identity (IMSI) is anonymous to the content provider.

1.3

Our Results

In this thesis, we propose several efficient k-out-of-n OT and COC construc-tions. For OTk

n, we provide solutions for three different classes: OT with

unconditional security of receiver (OTk

n-I), OT with unconditional security

of sender (OTk

n-II), and OT with adaptive queries (Adpt-OT).

• In the case of unconditional receiver’s security, we propose two schemes

Semi-OTk

n-I and Mal-OTkn-I with two rounds only, in which R sends

O(k) messages to S, and S sends O(n) messages back to R. Semi-OTk n

-I is secure against semi-honest receivers if the Decisional Diffie-Hellman (DDH) problem holds. Mal-OTk

n-I can be proved secure against

Semi-OTk

n-I Mal-OTkn-I [MZV02] [WZW03]

rounds 2 2 2 3

messages† _{(R → S) k k 2n k}

messages† _{(S → R) 2n n + k 2n n + k}

made to adaptiveness No Yes No Yes security proof Yes Yes (RO) No No

† _{The number of group elements.}

Table 1.1: Comparison between OTk

n schemes with unconditional receiver’s

security in communication cost.

problem in the random oracle model. When k = 1, the schemes are as efficient as the OT1

n schemes in [Tze04]. The schemes also have

the nice property of universal parameters, that is, each pair of R and

S need not hold any secret before performing the protocol. The

sys-tem parameters can be used by all senders and receivers without any trapdoor specification. Our OTk

n schemes in this class are the most

efficient ones in terms of the communication cost, either in rounds or the number of messages. We summarize the comparison between ours and other efficient works in this class in Table 1.1. Preliminary versions of these results have been previously published [CT05, CT08].

• In the case of unconditional sender’s security, we first propose a generic

construction Gen-OTk

n-II where any multiplicatively homomorphic

en-cryption scheme whose plaintext space has a prime order can be ap-plied. The query phase of the construction is still two-round. The receiver’s security is based on the semantic security of the underlying

encryption scheme only. Then we provide a concrete construction Con-OTk

n-II with only two rounds. The receiver’s security is based on the

DDH problem and can be proved in the standard model. For some cases of k and n, our Con-OTk

n-II scheme is the most efficient scheme

in terms of the communication cost1_{. Preliminary versions of these}

results have been previously published [CT08].

• For OT with adaptive queries, we extend our Mal-OTk

n-I scheme to an

adaptive OT scheme, named Adpt-OTk

n. In this scheme, S first sends

O(n) messages to R in one round in the commitment phase. For each

query of R, only O(1) messages are exchanged and O(1) operations are performed. Our construction is as efficient as the work of Ogata and Kurosawa [OK04], which is the most efficient adaptive OT scheme up to now. Preliminary versions of these results have been previously published [CT05, CT08].

For COC, we propose COC-I and COC-II schemes for “equality”, “in-equality”, and “greater than” predicates. These are fundamental schemes for constructing more complex secure interactive protocols. Then we also pro-vide a general transformation from COC-II schemes to COC-III schemes. Our schemes are efficiently constructed via homomorphic encryption schemes. We first prove our schemes secure against semi-honest and non-collusive parties, and then modify them to be secure against malicious parties. We also

pro-1_{For the scheme with unconditional sender’s security, one may perform the schemes of}

pose some OC schemes based on our COC-III scheme and homomorphic cryptosystems. Our schemes are more efficient in communication complexity than the previous one. Finally, we give some extensions of COC. Preliminary versions of these results have been previously published [CT06].

Chapter 2

Previous Works

In this chapter we provide a detailed survey of various OT and OC, respec-tively.

2.1

Oblivious Transfer

In 1981, Rabin [Rab81] first introduced the notion of OT. Then, OT was developed in several basic types:

• Rabin’s OT: S sends a message to R, and R gets the message with

probability 1/2. On the other hand, S does not know whether R gets the message. Rabin [Rab81] presented an implementation to obliv-iously transfer one-bit message, based on quadratic roots modulo a composite. Even, Goldreich and Lempel [EGL82] provided another implementation based on general public-key encryptions. Berger, Per-alta and Tedrick [BPT84] also proposed a provably secure scheme. Beaver [Bea92] provided another scheme by fixing Boer’s [Boe90] inse-cure implementation. Fischer, Micali and Rackoff [FMR96] also fixed

Rabin’s implementation so that it can be proved secure assuming only the factoring problem holds.

• 1-out-of-2 OT (OT1

2): S has two messages m1 and m2, and wishes R

to obtain exactly one of them. In addition, S remains oblivious to R’s choice. The notion of OT1

2originated with the work of Wiesner [Wie83],

which is also the beginning of quantum cryptography. Even, Goldre-ich and Lempel [EGL85] proposed such extension of OT1

2, in which

R gets either message with probability 1/2. Brassard, Cr´epeau and

Robert [BCR86b] give us the new notion of OT1

2 such that R can get the

message at his choosing. Cr´epeau and Kilian [CK88] provided another bit-OT1

2 (the messages are only one-bit) scheme from the weakened

security assumptions. Then many other OT1

2 schemes are continually

proposed [BM89, CS91, Boe90, SP90, SCP95, BC97, Cr´e97, Cac98, CMO00, AIR01, Hai04, Kal05, WW06, CS06, Wul07].

• 1-out-of-n OT (OT1

n): OT1n is an extension of OT12 for the case that

S has n messages. Brassard, Cr´epeau and Robert [BCR86a] first

pro-posed OT1

nin the name ”all-or-nothing disclosure of secrets” (ANDOS).

After that, OT1

n has become an important research topic in

crypto-graphic protocol design. Some OT1

n schemes are built by invoking

ba-sis OT1

2 several times [BCR86b, BCS96, NP99a], and the others are

constructed directly from basic cryptographic techniques [SS90, NR94, Ste98, NP01, Tze04, Lip07, LL07]. Some OT1

computational private information retrieval (CPIR) have polylogarith-mic communication cost [Cha04, Lip05].

• k-out-of-n OT (OTk

n): R obtains k out of n messages from S. Bellare

and Micali [BM89] first proposed an OTn−1

n scheme. Santis, Crescenzo,

and Persiano [SCP95] extended their OT1

2 scheme to an OTkn scheme.

Ishai and Kushilevitz [IK97] also provided a bit-OTk

n scheme by

invok-ing OT1

2several times. Naor and Pinkas [NP99a] proposed a non-trivial

OTk

n scheme. The scheme invokes a basis OT12 scheme O(wk log n)

times, where w > log δ/ log(k4_/√_{n) and δ is the probability that}

R can obtain more than k messages. It works only for k ≤ n1/4_.

Mu, Zhang, and Varadharajan [MZV02] presented some efficient OTk n

schemes. These schemes are designed from cryptographic functions di-rectly. The most efficient one is a non-interactive one. To be compared fairly, the setup phase of establishing shared key pairs of a public-key cryptosystem should be included. Thus, the scheme is two-round and

R and S send each other O(n) messages. However, the choices of R

cannot be made adaptive since R’s choices are sent to S first and the message commitments are dependent on the choices. Wu, Zhang, and Wang [WZW03] also provided a three-round OTk

nbased on the two-lock

cryptosystem. Recently, Green and Hohenberger [GH07] presented an OTk

n and an adaptive OT schemes in the full-simulation model which

Relations between basic types of OT Cr´epeau [Cr´e87] proved that Rabin’s OT and OT1

2 are computationally equivalent. However, it needs to

reduce bit-OT1

2 to string-OT12 first, and then reduce string-OT12 to Rabin’s

OT. Kurosawa and Koshiba [KK07] provided a direct reduction of string-OT1 2

to Rabin’s OT. Certainly, OTk

n implies OT1nand OT1nimplies OT12 by setting

k = 1 and n = 2, respectively. There are also some reductions from OT1

n to

OT1

2 [BCR86b, BCS96, NP99a]. Moreover, OTkncan be easily constructed by

invoking OT1

nk times independently. Therefore, these four basic types of OT

are computationally equivalent. Other reductions between OTs are discussed in [CK88, BC97, Cac98, DM99, DKS99, DS01, IKNP03, DFMS04, Nie07].

Besides, there are various types of OT developed in different models and applications:

• Adaptive OT (Adpt-OT): The OT scheme allows R to query messages

one by one adaptively, i.e. the ith chosen message depends on the previous i − 1 messages. The notion was first introduced by Naor and Pinkas [NP99b]. In one of their schemes (the two-dimensional one), each query needs invoke the basis OT1_√

n scheme twice, in which

each invocation of OT1_√

n needs O(

√

n) initialization work. In another

scheme, each adaptive query of messages need invoke the basis OT2 1

protocol log n times. Ogata and Kurosawa [OK04] proposed an efficient adaptive OT scheme based on the RSA cryptosystem. Each S needs a trapdoor (the RSA modulus) specific to him. The scheme is as efficient

as our Adpt-OTk

n scheme. But, if the adaptive OT scheme is converted

to a non-adaptive one, it needs 3 rounds (In the first round, S sends the modulus N to R). There are some recent works [GH07, CNs07] introducing adaptive OT in the full-simulation model. These schemes achieve the stronger security requirement but loss a degree of efficiency.

• Conditional OT (COT): S holds a secret x and a message m, and R

holds a secret y such that R gets m from S if and only if Q(x, y) is evaluated as true for some condition Q. COT was first proposed by Crescenzo, Ostrovsky and Rajagopalan [COR99]. They focus on pro-viding “all-or-nothing” transfer of the message from S to R by the con-dition. Blake et al. [BK04] strengthened COT to strong COT (SCOT), which provides ”1-out-of-2” message transfer from S to R by the con-dition. Our notion of COC is to split the role of S who owns a message and a secret into two roles of a message sender and a secret holder. The main difference in design techniques is that, in COT, the secure compu-tation is done by S with a masked input and a plain input, whereas the secure computation in our COC schemes is done by S with two masked inputs. A COC scheme that meets the requirements of our definitions can be easily transferred to a COT or SCOT scheme.

• Verifiable OT (VOT): R can verify that the messages he gets from S are

indeed the messages S had committed. Cr´epeau [Cr´e89] first proposed a basic bit-VOT1

immedi-ately obtained by the general transformation [BCR86b]. Cr´epeau, van de Graaf, and Tapp [CvdGT95] provided a more efficient scheme in the name “committed oblivious transfer” by using OT1

2 and BC (bit

commitment) as black boxes. Cramer and Damg˚ard [CD97] presented another solution based on their zero-knowledge proof system. Cachin and Camenisch [CC00] proposed a simple and efficient VOT1

2 based on

the DDH assumption. Ambainis, Jakobsson and Lipmaa [AJL04] pro-vided a VOT1

n based on the OT1n scheme proposed in [NP01]. There

are also other variants of OT with verifiable property [JS02, Lip03, GMY04, KSV07].

• Distributed OT (DOT): S is divided between several servers, and R

must contact a threshold of these servers to perform the OT protocol. Compared to the single-server based OT, DOT has the advantage of better efficiency and security. Gertner and Malkin [GM97] first intro-duced the notion of DOT and presented an implementation of DOT1

n.

Naor and Pinkas [NP00] provided a solution of DOT1

2 (it can also be

ex-tended to DOT1

n by their reduction [NP99a]). Blundo, D’Arco, Santis

and Stinson [BDSS02] also constructed some DOT1

n schemes. Nikov,

Nikova, Preneel and Vandewalle [NNPV02] further generalized the re-sult of Blundo et. al. Tzeng [Tze04] proposed a DOT1

n scheme based

on his OT1

n scheme in the name ”threshold oblivious transfer”.

third party, the proxy, which serves as the receiver’s proxy for learning the output. Naor, Pinkas, and Sumner [NPS99] first introduced this no-tion and provided an implementano-tion of POT1

2. Juels and Szydlo [JS02]

also proposed another verifiable POT scheme. These two POT schemes are both used in the auction systems.

• OT in the bounded storage model: The bounded storage model, first

introduced by Maurer [Mau90], assumes that there is only a bound on the adversary’s storage capacity, i.e. no limitation on the computa-tional power of the adversary. In the bounded storage model, provably everlasting security can be achieved efficiently without any complex-ity assumption [CM97, AR99, ADR02, DR02, DM02, Lu02, Vad03]. The first OT1

2 scheme in this model was proposed by Cachin, Cr´epeau

and Marcil [CCM98]. They put the storage bound on R (the case where the bound is placed on S is equivalent by the reversibility of OT [CS91]). The storage requirement for the two parties is O(N2/3_),

where N is the (very large) number of public random bits, and the successful probability of dishonest R is at most O(N−1/3_{), which is not}

small enough. Ding [Din01] provided a more efficient OT1

2 scheme with

O(√kN ) storage requirement and 2−O(k) _{successful probability of}

dis-honest R who stores O(N) bits, where k is a security parameter. Hong, Chang and Ryu [HCR02] extended Ding’s work to get an OT1

n scheme

of interaction. Ding, Harnik, Rosen and Shaltiel [DHRS04] provided a constant round OT1

2 scheme. The two parties in their work need

only exchange 5 messages. They also improved other parameters, such as the number of bits transferred and the probability of immaturely aborting the protocol due to the failure.

There are also some related works designed for particular considera-tions [Bea95, Bea96, GM00, HKN+_{05, LL06]. For the relation between}

OT and other cryptographic primitives, Kilian [Kil88] showed that OT is complete in the sense that every secure multiparty computation can be implemented using OT. Impagliazzo and Luby [IL89] proved that OT im-plies the existence of one-way functions (OWF). Moreover, Impagliazzo and Rudich [IR89] showed that OT is probably stronger than OWF, that is, the construction of OT using OWF as a black box is as hard as separating P from NP . Gertner, Kannan, Malkin, Reingold and Viswanathan [GKM+_00]

studied the relationships among public-key encryption (PKE) and OT. They showed that PKE and OT are incomparable under black-box reductions.

2.2

Oblivious Cast

Blaze [Bla96] introduced the notion of k-out-of-n OC, e.g. there are n re-ceivers and k of them get the message from the sender. He provided a concrete construction by using the blind signature scheme and anonymous communication mechanism. Fitzi et al. [FGMO01] treated OC as a primitive

for the secure multi-party computation. They proved that three-party OC is complete when the corrupted parties is less than one half.

Chapter 3

k-out-of-n Oblivious Transfer

We propose several OTk

n schemes in different security classes in this chapter.

3.1

Preliminaries

Involved parties. An OT scheme has two involved parties: a sender and a

receiver. Both are polynomial-time-bounded probabilistic Turing machines (PPTM). A party is semi-honest (or passive, honest-but-curious) if it does not deviate from the steps defined in the protocol, but tries to compute extra information from received messages. A party is malicious (or active) if it can deviate from the specified steps in any way in order to get extra information. A malicious sender may cheat in order or content of his possessed sages. To prevent the cheat, we can require the sender to commit the mes-sages first [CNs07, GH07]. But we don’t stress on this issue here because we should handle it at the application level above the OT. Actually, most merchants which play the roles of senders act honestly in order to keep their reputation. Therefore, we consider the OT scheme with semi-honest senders

and semi-honest/malicious receivers only.

Indistinguishability. Two distribution ensembles {Xn}n∈N and {Yn}n∈N

are computationally indistinguishable if for any PPTM D and any polynomial

p(n), there is n0 such that for every n ≥ n0

| Pr

x←Xn

[D(x) = 1] − Pr

x←Yn

[D(x) = 1]| ≤ 1/p(n).

Ideal Model. In the ideal model, the sender sends all messages and the

receiver sends all choices to a trusted third party (TTP). The TTP then sends the chosen messages to the receiver. This is the securest way to implement OT.

Security model. Assume that S holds n messages m1, m2, . . . , mn and R

has k choices σ1, σ2, . . . , σk. For OT with honest sender and honest receiver,

we have the following security requirements:

1. Receiver’s security - indistinguishability: for any two different sets of choices C = {σ1, σ2, . . . , σk} and C0 = {σ01, σ02, . . . , σk0}, the transcripts,

corresponding to C and C0_{, received by the sender are indistinguishable.}

If the received messages of S for C and C0 _{are identically distributed,}

the choices of R are unconditionally secure.

2. Sender’s security - indistinguishability: for any set of choices C =

{σ1, σ2, . . . , σk}, the unchosen messages should be indistinguishable

from the random ones. If the ciphertexts of unchosen messages are uniformly distributed for R, the security of S is unconditional.

On the other hand, the OT with honest sender and malicious receiver should meet the following security requirements:

1. Receiver’s security - indistinguishability: the same as the case of the semi-honest receiver.

2. Sender’s security - compared with the ideal model: for any receiver R in the real OT scheme, there is a simulator R0 _{in the ideal model such}

that the outputs of R and R0 _{are indistinguishable.}

Computational model. Let Gq be a subgroup of Z∗p with prime order q,

where p = 2q + 1 is also prime. Let g be a generator of Gq. We use gx to

denote the abbreviation of gx _{mod p, where x ∈ Z}

q. Let x ∈R X denote that

x is chosen uniformly and independently from the set X.

Computational assumptions. We assume that the hardness of the

Deci-sional Diffie-Hellman (DDH) problem and the Chosen-Target Computational Diffie-Hellman (CT-CDH) problem.

Assumption 1 (Decisional Diffie-Hellman (DDH)) The following two

distribution ensembles are computationally indistinguishable:

• Y1 = {(g, ga, gb, gab)}Gq, where g is a generator of Gq, and a, b ∈RZq.

• Y2 = {(g, ga, gb, gc)}Gq, where g is a generator of Gq, and a, b, c ∈RZq.

The CT-CDH assumption, introduced by Boldyreva [Bol03], is analogous to the chosen-target RSA inversion assumption defined by Bellare, et al. [BNPS01]

S, R a sender and a receiver

Gq a cyclic group with prime order q

g, h generators of group Gq mi’s sender’s messages σi’s receiver’s choices f1, f2 polynomials ai’s coefficients of f1 bi’s coefficients of f2 H1, H2 hash functions E an encryption scheme

G, E, D key generation, encryption and decryption functions pk, sk a pair of public key and secret key

M message space of an encryption scheme

λ a security parameter

Table 3.1: Common notations for our OT constructions

Assumption 2 (Chosen-Target Computational Diffie-Hellman (CT-CDH)) Let H1 : {0, 1}∗ → Gq be a cryptographic hash function. The

adver-sary A is given input (q, g, gx_{, H}

1) and two oracles: target oracle TG(·) that

returns a random element wi ∈ Gq at the ith query and helper oracle HG(·)

that returns (·)x_{. Let q}

T and qH be the number of queries A made to the

target oracle and helper oracle, respectively. The probability that A outputs k pairs ((v1, j1), (v2, j2), . . . , (vk, jk)), where vi = (wji)

x _{for i ∈ {1, 2, . . . , k},}

qH < k ≤ qT, is negligible.

Finally, we list some common notations used in this chapter in Table 3.1 for quick reference.

• System parameters: (g, h, Gq);

• S has messages: m1, m2, . . . , mn ∈ Gq;

• R’s choices: σ1, σ2, . . . , σk∈ {1, 2, . . . , n};

1. R chooses two polynomials f1(x) = a0+ a1x + · · · + ak−1xk−1+ xk and

f2(x) = b0+ b1x + · · · + bk−1xk−1+ xk where a0, a1, . . . , ak−1∈RZq and

b0+ b1x + · · · + bk−1xk−1+ xk ≡ (x − σ1)(x − σ2) · · · (x − σk) mod q.

2. R −→ S : A0= ga0hb0, A1= ga1hb1, . . . , Ak−1= gak−1hbk−1.

3. S computes ci = (gri, miBiri) where ri ∈R Zq and Bi = gf1(i)hf2(i) =

A0Ai1· · · Ai k−1 k−1(gh)i k mod p, for i = 1, 2, . . . , n. 4. S −→ R: c1, c2, . . . , cn. 5. Let ci= (Ui, Vi). R computes mσi = Vσi/U f1(σi)

σi mod p for each σi.

Figure 3.1: Semi-OTk

n-I: k-out-of-n OT against semi-honest receiver

3.2

OT

n

with Unconditional Security of

Re-ceiver

In this section we introduce OTk

n with unconditional receiver’s security. We

provide two schemes which are secure against semi-honest receiver in the standard model and secure against malicious receiver in the random oracle model respectively.

3.2.1

The Scheme for Semi-Honest Receiver

The sender S has n secret messages m1, m2, . . . , mn. Assume that the

mes-sage space is Gq. The receiver R wants to get mσ1, mσ2, . . . , mσk without

revealing any information about σ1, σ2, . . . , σk. The protocol Semi-OTkn-I is

depicted in Figure 3.1.

For system parameters, let g, h be two generators of Gqwhere loggh is

can be used repeatedly by all possible senders and receivers as long as the value log_gh is not revealed. Therefore, (g, h, Gq) are universal parameters.

The receiver R first constructs a k-degree polynomial f2(x) such that

f2(i) = 0 if and only if i ∈ {σ1, . . . , σk}. Then R chooses another random

k-degree polynomial f1(x) to mask the chosen polynomial f2(x). The masked

choices A0, A1, . . . , Ak−1 are sent to the sender S.

When S receives these queries, he first computes Bi = gf1(i)hf2(i) by

computing A0Ai1· · · Ai

k−1 k−1(gh)i

k

mod p. Because of the random polynomial

f1(x), S does not know which f2(i) is equal to zero, for i = 1, 2, . . . , n. Then

S treats Bi as the public key and encrypts each message mi by the ElGamal

cryptosystem. The encrypted messages c1, c2, . . . , cn are sent to R.

For each ci, i ∈ {σ1, σ2, . . . , σk}, since Bi = gf1(i)hf2(i) = gf1(i)h0 = gf2(i),

R can get these messages by the decryption of ElGamal cryptosystem with

secret key f1(i). If i /∈ {σ1, σ2, . . . , σk}, since R can not compute (gf1(i)hf2(i))ri

with the knowledge of gri, f

1(i) and f2(i) only, the message mi is unknown

to R.

Correctness. Let ci = (Ui, Vi), we can check that the chosen messages

mσi, i = 1, 2, . . . , k, are computed as Vσi/U f1(σi) σi = mσi · (g f1(σi)_hf2(σi)₎rσi_/grσif1(σi) = mσi · (g f1(σi)_{· 1)}rσi_/grσif1(σi) = mσi.

Theorem 1 For scheme Semi-OTk

n-I, R’s choices are unconditionally

se-cure.

Proof 1 For any tuple (A0, A1, . . . , Ak−1) sent by R, we have a pair of

tu-ples (a0

0, a01, . . . , a0k−1) and (b00, b01, . . . , b0k−1) to represent all possible choices

σ0

1, σ20, . . . , σ0k so that Ai = ga 0

ihb0i for i = 0, 1, . . . , k − 1. Thus, the receiver

R’s choices are unconditionally secure.

2

Theorem 2 Scheme Semi-OTk

n-I meets the sender’s security requirement.

If the DDH assumption holds and R is semi-honest, R gets no information about messages mi for i /∈ {σ1, σ2, . . . , σk}.

Proof 2 We show that for all i /∈ {σ1, σ2, . . . , σk}, ci’s look random if the

DDH assumption holds. Let I = {1, 2, . . . , n}\{σ1, σ2, . . . , σk} be an ordered

set. Assume that there is a polynomial-time distinguisher D distinguishes the following two distributions:

• C = (g, h, {(grij_{, (g}f1(ij)hf2(ij))rij_)}

ij∈I,j=1,...,n−k),

where rij ∈RZq, and f1 and f2 are chosen as in the protocol;

• X = (g, h, {(grij_{, Xj)}i}

j∈I,j=1,...,n−k),

where rij ∈RZq and Xj ∈R Gq.

Then we can construct another PPTM D0_{, which takes D as a sub-routine,}

• ˜Y1 = {(g, h, ga, ha)}Gq, where g, h are generators of Gq, and a ∈RZq.

• ˜Y2 = {(g, h, ga, gb)}Gq, where g, h are generators of Gq, and a, b ∈RZq.

The difference between ( ˜Y1, ˜Y2) and (Y1, Y2) is that h can’t be 1 in ˜Y1 and ˜Y2.

Machine D0

Input: (g, h, v, w) (either from ˜Y1 or ˜Y2)

1. Randomly select σ1, . . . , σk ∈ {1, . . . , n}.

2. Choose polynomials f1 and f2 according to σi’s as in the protocol.

3. Randomly select l ∈ {1, 2, . . . , n − k}.

4. Output D((Ui1, Vi1), (Ui2, Vi2), . . . , (Uin−k, Vin−k)), where ij ∈ I,

(Uij, Vij) =    (grij_{, (g}f1(ij)hf2(ij))rij_{) if j ∈ {1, . . . , l − 1}} (v, vf1(ij)wf2(ij)) if j = l (grij_{, X} j) if j ∈ {l + 1, . . . , n − k} , and rij ∈RZq, Xj ∈R Gq.

Assume that D distinguishes C and X with non-negligible advantage ε. Let α = (g, h, v, w) and ~Cl = (g, h, {(Uij, Vij)}ij∈I,j=1,...,n−k) where

(Uij, Vij) =

½

(grij_{, (g}f1(ij)hf2(ij))rij_{) if j ∈ {1, . . . , l}}

(grij_{, Xj) if j ∈ {l + 1, . . . , n − k}} ,

and rij ∈R Zq and Xj ∈R Gq. Note that ~Cn−k = C and ~C0 = X. If α is

chosen from ˜Y1, then

Pr α∈ ˜Y1 [D0(α) = 1] = Pr[D0( ˜Y1) = 1] = 1 n − k n−k X l=1 Pr[D( ~Cl) = 1].

If α is chosen from ˜Y2, then Pr α∈ ˜Y2 [D0_{(α) = 1] = Pr[D}0_{( ˜Y} 2) = 1] = 1 n − k n−k−1_X l=0 Pr[D( ~Cl) = 1]. Therefore, we have Pr[D0_{( ˜Y} 1) = 1] − Pr[D0( ˜Y2) = 1] = 1 n−k( P_n−k l=1 Pr[D( ~Cl) = 1] − P_n−k−1 l∗₌₀ Pr[D( ~C_l) = 1]) = 1 n−k(Pr[D( ~Cn−k) = 1] − Pr[D( ~C0) = 1]) = 1 n−k(Pr[D(C) = 1] − Pr[D(X) = 1]) ≥ ε n−k.

Moreover, since dist( ˜Y1, Y1) = 1/q and dist( ˜Y2, Y2) = 1/q, we can solve

the DDH problem with at least non-negligible advantage ε

n−k − 2q, which is a

contradiction.

2 Complexity. The scheme uses two rounds (steps 2 and 4), the first round

sends k messages and the second round sends 2n messages. For computation,

R computes 3k and S computes (k + 3)n modular exponentiations.

3.2.2

The Scheme for Malicious Receiver

A malicious player may not follow the protocol dutifully. For example, a malicious R might send arbitrary Ai’s in step 2. So we present the scheme

Mal-OTk

n-I which is provable secure against malicious receivers in the random

oracle model. The scheme is depicted in Figure 3.2.

The generator g and group Gq of system parameters are defined as that

in Semi-OTk

collision-• System parameters: (g, H1, H2, Gq); • S hasmessages: m1, m2, . . . , mn ∈ {0, 1}l; • R’s choices: σ1, σ2, . . . , σk∈ {1, 2, . . . , n}; 1. R computes hσj = H1(σj) and Aj = h rj σj, where rj ∈R Z∗q and j = 1, 2, . . . , k. 2. R −→ S: A1, A2, . . . , Ak. 3. S chooses a random x ∈ Z∗

q and computes Dj = Axj, hi = H1(i), and

ci = mi⊕ H2(hxi), where i = 1, 2, . . . , n and j = 1, 2, . . . , k.

4. S −→ R: D1, D2, . . . , Dk, c1, c2, . . . , cn

5. R computes Kj= D

r−1 j

j and gets mσj = cσj⊕H2(Kj) for j = 1, 2, . . . , k.

Figure 3.2: Mal-OTk

n-I: k-out-of-n OT against malicious receiver

resistant hash functions. Let messages be of l-bit length. Assume that CT-CDH is hard under Gq.

Correctness. We can check that the chosen messages mσj, j = 1, 2, . . . , k,

are computed as cσj⊕ H2(Kj) = mσj ⊕ H2(h x σj) ⊕ H2(h x σj) = mσj.

Security analysis. We assume that the random oracle model in this

secu-rity analysis.

Theorem 3 In Mal-OTk

n-I, R’s choices are unconditionally secure.

Proof 3 Since Gq is the group of prime order q, all elements except 1 in Gq

are generators. Given a value A ∈ Gq, for any hi = H1(i), there is an ri

such that A = hri

i . That is, A can be a masked value of any index. Thus the

2

Theorem 4 Even if R is malicious, the scheme Mal-OTk

n-I meets the

re-quirement for the sender’s security in the random oracle model.

Proof 4 Since we treat H2 as a random oracle, the malicious R has to know

Ki = hxi in order to query the hash oracle to get H2(hxi). For each possible

malicious R, we construct a simulator R∗ _{in the ideal model such that the}

outputs of R and R∗ _{are indistinguishable.}

R∗ _{works as follows:}

1. R∗ _{simulates R to obtain A}∗

1, A∗2, . . . , A∗k. When R queries H1 on index

i, we return a random h∗

i (consistent with the previous queries.)

2. R∗ _{simulates S (externally without knowing m}

i’s) on inputs A∗1, A∗2, . . . , A∗ k to obtain x∗, D1∗, D2∗, . . . , D∗k. 3. R∗ _{randomly chooses c}∗ 1, c∗2, . . . , c∗n. 4. R∗ _{simulates R on input (D}∗ 1, D2∗, . . . , D∗k, c∗1, c∗2, . . . , c∗n) and monitors

the queries closely. If R queries H2 on some vj = (h∗j)x ∗

, R∗ _sends

j to the TTP T to obtain mj and returns c∗j ⊕ mj as the hash value

H2((h∗j)x ∗

), otherwise, returns a random value (consistent with previous

queries). 5. Output (A∗

If R obtains k + 1 decryption keys, R∗ _{does not know which k indices are}

really chosen by R. The simulation would fail. Therefore we show that R can obtain at most k decryption keys by assuming the hardness of chosen-target CDH problem. In the above simulation, if R queries H1, we return

a random value output by the target oracle. When R∗ _{simulates S on input}

A∗

1, A∗2, . . . , A∗k, we forward these queries to the helper oracle, and return the

corresponding outputs. Finally, if R queries H2 on legal vji for all 1 ≤ i ≤

k + 1, we can output k + 1 pairs (vji, ji), which contradicts to the CT-CDH

assumption. Thus, R obtains at most k decryption keys.

Let σ1, σ2, . . . , σk be the k choices of R. For the queried legal vσj’s, cσj

is consistent with the returned hash values, for j = 1, 2, . . . , k. Since no other (h∗

l)x ∗

, l 6= σ1, σ2, . . . , σk, can be queried to the H2 hash oracle, cl has

the right distribution (due to the random oracle model). Thus, the output distribution is indistinguishable from that of R.

2 Complexity. Mal-OTk

n-I has two rounds. The first round sends k messages

and the second round sends n + k messages. For computation, R computes 2k, and S computes n + k modular exponentiations.

3.3

OT

with Unconditional Security of Sender

In this section we introduce OTk

n with unconditional sender’s security. We

multiplica-tively homomorphic encryption schemes to it. Then we propose a concrete scheme with more efficient round complexity. Both constructions are proved secure in the standard model.

3.3.1

The Generic Construction

We propose a simple k-out-of-n oblivious transfer framework such that it can be widely used in small-scale applications or cryptographic protocols. Any multiplicatively homomorphic encryption scheme whose plaintext space has a prime order can be applied to this framework. Therefore protocol designers can choose the existing encryption scheme to implement OT in their protocols.

Current OT solutions using additively homomorphic encryption [AIR01, BGN05, LL07] have some security issues. The main problem is that most ad-ditively homomorphic encryption schemes have a composite plaintext space order. Thus the scheme needs either a trusted party to generate public/secret keys or a zero-knowledge proof system to ensure that the public key is well formed. Moreover, direct use of these homomorphic encryption schemes is not secure [Cha04, LL07].

In addition to the generality, our scheme has the following properties.

• The query phase of our construction has only two rounds: the receiver

sends O(k) messages to the sender, and gets O(n) messages back. So it is very efficient and practical to be used as a building block.

• The construction doesn’t need any zero-knowledge proof system but

still remains secure against malicious receivers. This avoids additional rounds or the use of random oracles in the security proofs.

• The receiver’s privacy is preserved if the underlying encryption scheme

is IND-CPA secure. No additional assumption is needed.

Multiplicatively Homomorphic Public Key Encryption. A public key multiplicatively homomorphic encryption scheme E = (G, E, D) is de-fined as follows. Let M be the plaintext space.

• Key generation: on input a security parameter λ, G(λ) outputs a pair

of public and secret keys (pk, sk).

• Encryption: on input a message m ∈ M, Epk(m) outputs a ciphertext

C.

• Decryption: on input a ciphertext C, Dsk(C) outputs the message m.

• Multiplicative homomorphism: for ciphertexts C1 = Epk(m1), C2 =

Epk(m2) and C = Epk(m), we have

1. C1 · C2 = Epk(m1· m2);

2. Cr _{= E}

pk(mr) where r is a known constant.

Note that if M has a prime order, there exists a generator generating all group elements in M.

IND-CPA Security. We define the security game for a public key

encryp-tion scheme E = (G, E, D) as follows.

Setup. The challenger computes (pk, sk) ← G(λ) and outputs the public key pk.

Challenge. The adversary outputs two messages m0and m1. The challenger

chooses a random b ∈ {0, 1} and returns Cb representing the encryption

of mb.

Guess. Finally, the adversary outputs its guess b0 _{and wins the game if}

b = b0_.

We define the advantage of an adversary A in attacking E as the function of the security parameter λ: AdvE,A(λ) = |P r[b = b0] − 1₂|.

Definition 1 (IND-CPA Security) We say that a public key encryption

scheme is IND-CPA secure if no polynomially bounded adversary A has a non-negligible advantage against the challenger in the above game.

Our construction Gen-OTk

n-II is depicted in Figure 3.3. Let E be a

mul-tiplicatively homomorphic encryption scheme and M be the corresponding message space. Note that the order of M needs to be prime. The sender S has

m1, . . . , mn ∈ M and the receiver R has choices σ1, . . . , σk ∈ {1, 2, . . . , n}.

The scheme is divided into two phases: Setup Phase and Query Phase. In the setup phase, R computes his public/secret key pair, and sends

• Let E = (G, E, D) be a multiplicatively homomorphic encryption

scheme;

• S has messages: m1, m2, . . . , mn ∈ M;

• R’s choice: σ1, σ2. . . σk∈ {1, 2, . . . , n};

Setup Phase

1. R computes G(λ) to generate keys (pk, sk) and sends pk to S.

2. S chooses a random m ∈ M, and sends Epk(m) to R.

3. R replies the decryption result m. S aborts if it is incorrect. Query Phase

1. R computes f (x) = a0+ a1x + · · · + ak−1xk−1+ xk = (x − σ1)(x −

σ2) · · · (x − σk) under the appropriate group.

2. R −→ S: (g, A0, A1, . . . , Ak−1), where Ai = Epk(gai) for all i =

0, 1, . . . , k − 1 and g is a generator of M. 3. S −→ R: C1, C2, . . . , Cn, where Ci= Epk(mi) · (A0· Ai1· · · Ai k−1 k−1 · Epk(gi k ))ri

and ri is randomly chosen.

4. R decrypts Cσi and gets mσi for all i = 1, 2, . . . , k.

Figure 3.3: Gen-OTk

n-II: Generic k-out-of-n OT

to prevent R from learning the encrypted messages that R cannot decrypt himself. Note that the setup phase may not be necessary if the protocol that takes this OT construction as a building block already has a key setup for the receiver.

In the query phase, R first sets up a k-degree polynomial f such that

f (σi) = 0 for all 1 ≤ i ≤ k. In order to let S compute f , he puts the

coeffi-cients on the exponent of a generator g, and sends them to S in the encrypted form. Then S computes the following equations for all i ∈ {1, 2, . . . , n} using

the homomorphic property:

Ci = Epk(mi· (gf (i))ri),

where ri is randomly chosen. Note that S has to encrypt the k-th term of

gf (x) _{with coefficient 1 by himself. This is the technique of ensuring that}

f (x) is a non-zero polynomial. Thus only k points makes f zero. R gets k

messages and n − k random values.

Theorem 5 For any malicious receiver, the scheme Gen-OTk

n-II has

information-theoretic sender’s security.

Proof 5 For each malicious receiver R∗_{, we construct a simulator S}

R∗ in the

ideal model such that the output distributions of R∗ _{and S}

R∗ are identical.

SR∗ works as follows.

1. Simulate R∗ _{to obtain (pk, g, A}

0, A1, . . . , Ak−1).

2. Repeatedly rewind R∗ _{to Step 2 of the setup phase and send A}

i·Epk(hi), hi ∈R

M, as challenge ciphertexts to get gaih

i back. Compute gai = gaihi/hi

for all i ∈ {0, 1, . . . , k − 1}.

3. For all i ∈ {1, 2, . . . , n}, compute gf (i) _{using the values g}ai’s and define

the set J = {j|gf (j) _{= 1}, |J| ≤ k.}

4. Send all j ∈ J to the TTP and get mj’s back.

5. Send Ci to R∗ for all i ∈ {1, 2, . . . , n}:

Ci =

½

Epk(mi) if i ∈ J;

6. Output (pk, Epk(m), m, g, A0, A1, . . . , Ak−1, C1, C2, . . . , Cn)

In Step 2 of the simulation, we use the self reducibility properties of the encryption scheme to map an encrypted message to an encryption of a ran-dom message. Then the challenge ciphertext will be indeed the encryption of a random message. After getting the returned answer, we can compute the original message by canceling the random factor. Therefore we can get all messages sent by R∗ _{and thus know R}∗_{’s choices by checking whether}

gf (i) _{= 1. Moreover, since the coefficient of x}k _{in f (x) is 1, we can make}

sure that f (x) will not be a zero polynomial. For a nonzero k-degree polyno-mial, there are at most k indices such that f (i) = 0. So the number of R∗_’s

choices is at most k, and thus we can send these indices to the TTP.

Let’s consider the output distribution of SR∗. First, (pk, g, A₀, . . . , A_k−1)

are outputted by R∗_{. As stated above, the challenge chiphertext is the}

encryp-tion of a random message, so the challenge and response are distributed as in the real scheme. For all i /∈ J (i.e. f (i) 6= 0), the ciphertexts Ci’s would

be encryptions of random messages, which are identically distributed as Ci’s

in the real scheme. On the other hand, as long as i ∈ J, we can get the index i and query the TTP to obtain mi. Therefore all Ci’s are distributed as them

in the real scheme. The scheme can be perfectly simulated and the sender’s security is information-theoretic.

Theorem 6 For any malicious sender, the scheme Gen-OTk

n-II has receiver’s

se-cure.

Proof 6 Let S∗ _{be any possible malicious sender. We can see that the}

chal-lenges of S∗ _{in the setup phase are independent of R’s choices in the query}

phase. Moreover, S∗ _{cannot influence R’s choices before or after R sends}

(g, A0, A1, . . . , Ak−1). So we can prove the receiver’s security by just

consid-ering the values (g, A0, A1, . . . , Ak−1).

Suppose a polynomial time adversary A breaks receiver’s security of Gen-OTk

n-II with non-negligible advantage ε(λ). We can construct another

poly-nomial time adversary B breaking the IND-CPA security of E with advantage ε(λ)/k. Given pk as input, algorithm B works as follows.

1. B gives algorithm A the public key pk and a generator g. 2. A outputs {σ0,1, . . . , σ0,k}, {σ1,1, . . . , σ1,k} ∈ {1, 2, . . . , n}k.

3. B computes the polynomials

• f0(x) = a0,0 + a0,1x + · · · + a0,k−1xk−1 + xk = (x − σ0,1)(x −

σ0,2) · · · (x − σ0,k) and

• f1(x) = a1,0 + a1,1x + · · · + a1,k−1xk−1 + xk = (x − σ1,1)(x −

σ1,2) · · · (x − σ1,k).

4. B randomly chooses a number l ∈ {1, 2, . . . , k} and sends (ga0,l, ga1,l) to

the challenger of E.

6. B sends ~

Cl = (Epk(ga0,0), . . . , Epk(ga0,l−1), C, Epk(ga1,l+1), . . . , Epk(ga1,k−1))

to A.

7. B outputs A’s guess b.

By the hybrid argument (similar to the proof of Theorem 2), we can see that ADVB(λ) ≥

1

kADVA(λ) = ε(λ)

k

So B breaks E with non-negligible advantage ε(λ)/k, which is a contradiction. Gen-OTk

n-II has receiver’s security.

3.3.2

Concrete Construction

Here we propose a concrete OTk

n construction with unconditional sender’s

security. The scheme is more efficient than the generic one. It is extended from the 1-out-of-n OT under the same security condition provided by Naor and Pinkas [NP01].

We present the scheme in Figure 3.4. The main idea of this scheme is the same as Semi-OTk

n-I. R first chooses two polynomials f1(x), f2(x) and a

random value b where f2(x) represents the choices, and f1(x) and b are used

to mask f2(x). By the DDH assumption, Ci = gaibha 0

i can’t be distinguished

from the random value when given gai_{and g}b_{, for i = 0, 1, . . . , k−1. Therefore}

• System parameters: (g, Gq);

• S has messages: m1, m2, . . . , mn ∈ Gq;

• R’s choices: σ1, σ2, . . . , σk∈ {1, 2, . . . , n};

1. R chooses a generator h of Gq, a random b ∈ Zq, and two

polyno-mials f1(x) = a0 + a1x + · · · + ak−1xk−1 + xk and f2(x) = a00 + a0 1x + · · · + a0k−1xk−1 + xk where a0, a1, . . . , ak−1 ∈R Zq and a00 + a0 1x + · · · + a0k−1xk−1+ xk ≡ (x − σ1)(x − σ2) · · · (x − σk) mod q. Let (A0, A1, . . . , Ak−1) = (ga0, ga1, . . . , gak−1), B = gb, (C0, C1, . . . , Ck−1) = (ga0b_ha00, ga1b_ha01, . . . , gak−1b_ha0k−1). 2. R −→ S : (h, A0, A1, . . . , Ak−1, B, C0, C1, . . . , Ck−1).

3. S chooses n random pairs (r1, s1), (r2, s2), · · · , (rn, sn) in Zq, and

com-putes ci = (gf1(i)rigsi, (gf1(i)bhf2(i))ri(gb)si⊕ mi) = (Xirigsi, ZiriBsi ⊕

mi) for i = 1, 2, . . . , n, where Xi = A0Ai1· · · Ai k−1 k−1gi k , Zi = C0C1i· · · Ci k−1 k−1(gh)i k . 4. S −→ R: c1, c2, . . . , cn. 5. Let ci= (Ui, Vi). R computes mσi = U b σi⊕ Vσi for each σi. Figure 3.4: Con-OTk

n-II: concrete k-out-of-n OT with unconditional sender’s

security

Then S encrypts the messages by the similar technique of randomized reduction of DDH from [NR97, Sta96]. The receiver R uses the value b to decrypt the chosen messages, and gets no information about other messages.

Correctness. Let ci = (Ui, Vi), we can check that the chosen messages

mσi, i = 1, 2, . . . , k, are computed as

U_σb_i⊕ Vσi = (g

f1(σi)r_σigs_σi)b_{⊕ (g}f1(σi)b_hf2(σi)₎r_σi(gb₎s_{σi ⊕ m} σi

= gf1(σi)br_σi+bs_{σi ⊕ (g}f1(σi)b_{· 1)}r_σigbs_{σi ⊕ m} σi

= gf1(σi)br_σi+bs_{σi ⊕ g}f1(σi)br_σi+bs_{σi ⊕ m} σi

= mσi.

Security analysis. We now prove the security of Con-OTk n-II.

Theorem 7 For any malicious sender, the scheme Con-OTk

n-II has receiver’s

security if the DDH assumption holds.

Proof 7 Suppose a polynomial time adversary A breaks receiver’s security

of Con-OTk

n-II with non-negligible advantage ε. We can construct another

polynomial time adversary B solving the DDH problem with advantage ε/k. Given a DDH tuple (g, u, v, w) as input, algorithm B works as follows.

1. B gives algorithm A the generator g.

2. A outputs {σ0,1, . . . , σ0,k}, {σ1,1, . . . , σ1,k} ∈ {1, 2, . . . , n}k.

3. B performs the following steps:

(a) randomly choose a number l ∈ {0, 1, . . . , k − 1} and h ∈ Gq;

(b) compute the polynomials • f0 0(x) = a00,0 + a00,1x + · · · + a00,k−1xk−1+ xk = (x − σ0,1)(x − σ0,2) · · · (x − σ0,k) and • f0 1(x) = a01,0 + a01,1x + · · · + a01,k−1xk−1+ xk = (x − σ1,1)(x − σ1,2) · · · (x − σ1,k); (c) randomly choose b ∈ {0, 1};

(d) perform A(h, A0, A1, . . . , Ak−1, v, C0, C1, . . . , Ck−1) where

(Ai, Ci) =    (gai, vaiha0b,i) if i ∈ {0, . . . , l − 1} (u, wha0b,l) if i = l (gai, R iha 0 b,l+1) if i ∈ {l + 1, . . . , k − 1} , and a ∈ Z , R ∈ G .

4. A outputs a guess b0_{. B outputs 1 if b}0 _{= b and 0 otherwise.} Let α = (g, u, v, w). Define ~El = (g, A1, A2, . . . , Ak, gb, C1, C2, . . . , Ck), where (Ai, Ci) = ½ (gai, gaibha0b,i) if i ∈ {0, . . . , l} (gai, R iha 0 b,l+1) if i ∈ {l + 1, . . . , k − 1}

for some ai ∈ Zq and b ∈ Zq. If α is chosen from Y1, then

Pr α∈Y1 [B(α) = 1] = Pr[B(Y1) = 1] = 1 k k X l=1 Pr[A( ~El) = b].

If α is chosen from Y2, then

Pr α∈Y2 [B(α) = 1] = Pr[B(Y2) = 1] = 1 k k−1 X l=0 Pr[A( ~El) = b]. Therefore, we have Pr[B(Y1) = 1] − Pr[B(Y2) = b] = 1 k( k X l=1 Pr[A( ~El) = b] − k−1 X l=0 Pr[A( ~El) = 1]) = 1 k(Pr[A( ~Ek) = b] − Pr[A( ~E0) = b]) ≥ ε k.

So we can solve the DDH problem with at least non-negligible advantage ε k,

which is a contradiction. Con-OTk

n-II has receiver’s security.

2

Theorem 8 The sender’s security of Scheme Con-OTk

n-II is

unconditionally-secure. That is, any receiver R gets no information about messages mi,