Optimal information-dispersal for increasing the reliability of a distributed service

(1)

462 IEEE TRANSACTIONS ON RELIABILITY, VOL. 46, NO. 4, 1997 DECEMBER

Optimal Information- ispersal for

Increasing the eliability of

a

Distributed Service

Hung-Min Sun

Chaoyang Univ.

of

Technology, Taichung

Shiuh-Pyng Shieh,

Member IEEE

National Chiao Tung University, Hsinchu

Key Words - Fault tolerance, Security, Threshold scheme, Distributed server, Data storage.

Summary & Conclusions - This paper investigates the (m, n) information dispersal scheme (IDS) used to support fault-tolerant distributed servers in a distributed system. In an (m, n)-IDS, a file M is broken into n pieces such that any m pieces collected suffice for reconstructing M . The reliability of

an (m, n)-IDS is primarily determined by 3 important factors:

.

n = information dispersal degree (IDD),

. n/m = information expansion ratio (IER),

. P, = success-probability of acquiring a correct piece.

It is difficult to determine the optimal IDS with the highest reliability from very many choices. Our analysis shows:

.

several novel features of (m, n)-IDS which can help reduce the complexity of finding the optimal IDS with the highest reliability;

. that an IDS with a higher IER might not have a higher reliability, even when P, -+ 1.

Based on the theorems given herein, we have developed a

method that reduces the complexity for computing the highest reliability from,

. O(v) [v = number of servers] to O(1) when the ‘upper bound of the IER = 1, or

.

O ( v 2 ) to 0(1) when the ‘upper bound of the IER’ > 1.

1. 1NTR.ODUCTION

Acronyms‘

ID information dispersal IDD ID degree

IDS ID scheme

IER information expansion ratio

Notation n the IDD m [see (m,n)-IDS] n / m (m, n)-IDS the IER.; n / m 2 1

an IDS which breaks a file into n pieces such that any m pieces collected suffice for reconstructing the file; 1 5 m

5

n

lThe singular & plural of an acronym are always spelled the same.

‘U number of available servers

U upper bound of IER P,

Pd(m, n )

Pr{a server can provide the correct information piece}; 0 < P,

<

1 binfc(m; P,, n): Pr{the file can be correctly constructed using the ( m , n)-IDS}

critical probability:

the P, such that Pd(i, 3 ) = P d ( k , 1 )

piece # i of (m,n)-IDS, 1

5

i

5

n

{ (m, n)-IDS; for all m, n, u E N ,

1

5

( n / m ) 5 U , n

5

U}:

feasible IDS set.

P,* ((2, j),

(k,

1 ) )

p,* p,* ((2, ( k , 1 ) ) S,

Fu,v

Other, standard notation is given in “Information for Readers & Authors” at the rear of each issue.

Many desirable services ( eg, file service, authentication service) in a distributed system should be both highly fault-tolerant and secure [13, 161. Therefore, it is desirable to increase the reliability & security of a service by dis- tributing the responsibility of providing the service among many servers. There are many ways to increase the fault tolerance of a service in a distributed system. A com-

mon approach is to replicate the service so that any one of them can perform the service. However, this approach considerably increases the storage cost for maintaining the replication of files, as well as reduces the level of security (if one server is compromised, security is compromised). Another approach is t o use (m,n)-IDS [l, 161 wherein a file

M

is broken into n pieces, S,, 1 5 2 5 n, such that any

m pieces collected do suffice for reconstructing M . These

n pieces can be stored on n different servers (or systems) to improve total reliability. The (m, n)-IDS is able to tolerate up to n - m server failures. With the (m, n)-IDS, not only the reliability & security can be increased, but also the work load can be shared & balanced among servers. Many applications using the (m, n)-ID algorithm were proposed

[3, 5 - 7, 12 - 151. With a limited number of servers and storage resources, it is important to determine the m , n

that give the optimal fault-tolerant capability. This paper:

.

analyzes the influence of IDD, IER., and P,, 001 8-9529/97/$10.00 01997 IEEE

(2)

SUN/SHIEH: OPTIMAL INFORMATION-DISPERSAL FOR INCREASING T H E RELIABILITY OF A SERVICE 463

.

proposes a method to determine the optimal (m,n)-

IDS with the highest reliability, when given the number of servers and an upper bound on IER.

The method reduces the complexity of determining the highest reliability from

O ( v ) to O(1): if the 'upper bound of IER' = 1; O(w2) to 0(1), otherwise.

Assumptions

1. The (m,n)-IDS is used to tolerate the server failures in a distributed system. These n pieces of information are stored on n different servers to improve total reliability.

4

2. All servers have r,he same success probability. 2. INFORMATION DISPERSAL SCHEME The concept of an ( m , n)-IDS is similar to the concept of an (m,n) threshold scheme

[a,

4, 171 in cryptography, in which a master key K is transformed into n shares,

such that unless m shares are collected, the K cannot be reclaimed. The main difference between an IDS and a threshold scheme is that the latter provides security while the former provides reliability.

An example i s an ( m , n)-IDS based on Shamir's threshold scheme [17], as fcdlows. A file is regarded as a bi- nary string which can be divided into m blocks of equal size, where each block is represented as a number: M = (ao,

.

. .

,

~ ~ - 1 ) . Select a prime p such that,

O < a , I p - l , f o r i = O

, . . .

, m - 1 . Let,

be a polynomial of degree m

-

1 over the finite field GF(p). The n pieces are computed from f(x) by:

[Sa = f ( i ) ] mod p , i =

1,.

.

,n.

Given any m pieces

Si,,

for j = 1,.

.

,

m, and

then f(x) can be reconstructed from the Lagrange inter- polating polynomial [9] :

{ i l ,

. . .

,

im}

c

{ 1,.

. .

,

n } ,

Thus, the file

M

can be obtained. 4

3. FUNDAMENTAL THEOREMS

This section discusses the influence of n, m, P, on the total reliability. Section 3.1 studies the reliability of two

classes of IDS to demonstrate the difficulty of selecting an optimal (m,n)-IDS. Each class consists of IDS with the same IER but different IDD. For example, the (1,2)-IDS and the (2,4)-IDS are i n the same class with the IER.=2. Section 3.2 discusses the reliability of IDS with various IER.

3.1 IDS Reliability

Conventional network services use a (1,l)-IDS:

Pd(1,l) = P,.

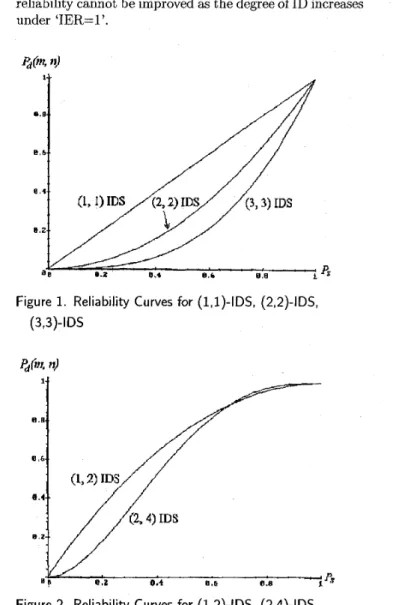
Similarly, the reliabilities of the class (m, m)-IDS which have the same IER.=l can be obtained as follows:

Pd(i,

i) =

P,",

i = 2,.

. .

,m. Thus:

Pd(m, m ) - Pd(n, n ) = P," - P," = P,". (1

-

P,"-")

>

O if m

<

n.

The reliability of an (m, m)-IDS for a fixed P, decreases

as m increases. Figure 1 has reliability curves for a (1,l)- IDS, (2,2)-IDS, and (3,3)-IDS, and shows that the total reliability cannot be improved as the degree of ID increases under 'IER.=l'.

Figure 1. Reliability Curves for (1,l)-IDS, (2,2)-IDS, (3,3)-IDS

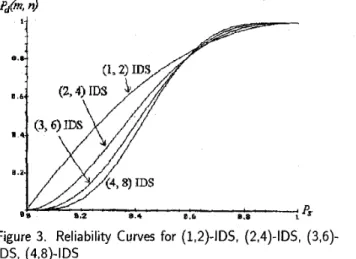
Figure 2. Reliability Curves for (1,2)-IDS, (2,4)-IDS

The class of (m, 2m)-IDS has IER.=2. The reliabilities of a (l,2)-IDS and (2,4)-IDS can be formulated as follows; figure 2 shows their relationship:

(3)

464 IEEE TRANSACTIONS ON RELIABILITY, VOL. 46, NO. 4, 1997 DECEMBER

Pd(l,2)

= binfc(1; Ps,2); Pd(2,4) = binfc(2;

Ps,4).

0 Theorem 3.3

Pd(l,2)

<

Pd(2,4), if

P,

>

2/3 Pd(1,2) = Pd(2,4), if P, = 2/3

P d ( l , 2 )

>

Pd(2,4), if

P,

<

2/3

That is, a (2,4)-IDS is more reliable than a (1,2)-IDS if

P,

>

2/3, and a (1,2)-IDS is more reliable than a (2,4)-IDS if P,

<

2/3. Thus in different P, ranges, the IDS that gives the optimal reliability can be different. Corollary 1 proves that for any two reliability curves of (IC1 ' m , k1 .n)-IDS and

(ka

.

m, kz n)-IDS, there exists exactly one intersection; and, a t the intersection, 0

<

P,

<

1. These intersections can partition probabilities into ranges in which the optimal IDS can be determined.

3.2 Important Properties of IDS

Theorems 3.1 - 3.9 can help find the optimal IDS.

0 Theorem 3.1

Pd(m, n )

<

Pd(m, n

+

k ) , for k

2

1.

Proof; [Omitted].

Theorem 3.1 suggests that a designer use as many servers as possible to distribute the data-pieces of a file, where each server keeps a data-piece. The data-pieces of ( m , n

+

k)-IDS class are all of the same size, and a

collection of m pieces suffices for reconstructing the file.

The ( m , n

+

k)-IDS class can tolerate n

+

k - m server failures. Since the members of (m,n

+

k)-IDS class all need the same number of data-pieces to recover the file, an ( m , n

+

k)-IDS with larger k can tolerate more server

failures and give better total reliability of the file service. For the (m, n

+

k)-IDS class, the data-piece stored in each server need not be changed when new servers join the distributed service - simply distribute a data-piece to each new server. However, the advantage of using larger k is ac-

quired at the expense of higher IER which increases from

n / m to ( n + k ) / m . A higher IER also indicates an increase

of storage cost.

0 Theorem 3.2

Pd(m,n)

>

Pd(m

+

k , n ) , for k

2

1.

Proof. See appendix A.].

Theorem 3.2 does not imply that any IDS with a higher IER always has higher reliability than an IDS with a lower TER. It does suggest that a designer store a larger data- piece on each server if the total number of participated servers is fixed. In the ( m

+

k,n)-IDS class, an IDS with smaller k can give better total reliability a t the expense of higher IER. That is, a larger data-piece must be stored on each one of the n servers. Hence, the IER (which is a measure of storage cost) increases. In the ( m

+

k , n ) -

IDS class, the data-piece stored on each server must be updated when the system configuration (the IDS being used) is changed.

Pd(m,n)

>

Pd(m

+

k , n

+

k ) for k

2

1.

Proof: See appendix A.2.

Theorem 3.3 suggests that a designer use fewer servers in the ( m

+

k , n

+

k)-IDS class of which each IDS member can tolerate the same number of server failures. Although, in the class, each (m

+

k , n

+

k)-IDS has the same fault- tolerance capability, the one with smaller k gives better

reliability, but needs larger IER; ie, the IER decreases as the number of participating servers increases. Among all

(m+k, n+k)-IDS, the ( m , n)-IDS gives the best reliability, but needs the highest IER.

0 Theorem 3.4

Pd(i,

j ) 5 P d ( k , 1 ) if 1 2 j and k 5 a ,

with equality only when I = j and IC = i. Proof: See appendix A.3.

Theorem 3.4 suggests giving larger data-pieces to as

many servers as possible, where each server holds a single data-piece. In this way, fewer data-pieces need be collected to recover the file, and a t the same time the total reliability increases. The advantage is achieved at the expense of higher IER.

0 Theorem 3.5

Pd(i,j)

>

P d ( k , I ) if 1

2

j , k

>

i, and I - k 5 j - z. Proof: See appendix A.4.

Theorem 3.5 shows that the total reliability increases if

.

fewer servers participate (1 2 j ) ;

. each server keeps a larger data-piece ( k

>

2); . more server failures can be tolerated (1 - k

5

j - i).

In the IDS class, the advantage is acquired at the expense of higher IER, where fewer servers are involved but each server keeps a larger data-piece.

0 Theorem 3.6

Given two different IDS, (i,j)-IDS and (k,l)-IDS for

1

2

j , k

>

a , and 1

-

k

>

j - z, there exists exactly one

P,* ( ( i , j ) , ( k , l ) ) such that: Pd(i,.7) Pd(Z, 2) Pd(i,j)

>

Pd(k,

I)

if 0 < ps

<

P,*

((4.71,

( k ,

0)

7 Pd(k, I ) if ps = p,* ((2, j ) , ( k , 1 ) ) 1

Pd(k,L)

if P," ( ( i , j ) , ( k , 1 ) )

<

ps

<

1, =

<

for Zrj, k > i , l - k > j - z .

Proof: See appendix A.5.

Theorem 3.6 indicates that for any two IDS in the IDS class, an IDS can have better reliability in a range of P,,

but worse reliability in the other range. Thus, a particular IDS does not always give better reliability than another. This suggests that a designer must determine the range of

(4)

SUN/SHIEH: OPTIMAL INFORMATION-DISPERSAL FOR INCREASING THE RELIABILITY OF A SERVICE 465

0 Discussion 0 Lemma 4

Theorems 3.4 - 3.6 show that for any two different IDS, (i, j)-IDs and ( k , I)-IDS (let 1 2 j , without loss of gener-

I f infinite subsequence Of

<

xn

>

has an infinite subsequence that ‘Onverges to x, then the sequence

<

x,

>

converges to x. ality):

if

k

5

i then Pd(i,j)

5

Pd(k,I) for all P,,

if

k

>

i and 1

- k

5

j - i then Pd(i,j)

>

Pd(k,I) for all P,

if

k

>

i and I-k

>

j - i then there exists a p i ((i, j ) ,

(k,

I ) ) ,

where:

Proof: Omitted.

Theorem 3.8

ity of (m, n)-IDS and ( k e m, k

-

n)-IDS.

Let Ak = p,* [(m, n ) ,

(k

m, k

.

n ) ] , the critical probabil- Then the sequence

<

Ak

>

converges to m / n .

Proof: See appendix A.9.

Theorem 3.8 shows that the critical probability of

( m , n)-IDS and ( k m, k n)-IDS, P,* [(m, n ) , ( k . m, k

.

n ) ] ,

converges to m / n as k increases. Because the reliabil-

ity curves of

(k

.

m, k n)-IDS vary consistently, the criti-

cal probability of ( m , n)-IDS and ( k

.

m,

k

. n)-IDS, either strictly decreases to m / n or strictly increases to m / n as

k

Discussion Pd(i,j)

>

Pd(k,l) if Ps

<

p,* ((Z,j), ( k , I ) ) ,

Pd(i,j) = Pd(k,I) if Ps = P , * ( ( i , d , ( k , q ) , Pd(i,j)

<

Pd(k,I) if P,

>

P,* ( ( i , j ) , ( k , O ) .

Theorem 3.6 implies corollary 1.

0 Corollary 1

(k2 m, kz n)-IDS, for m

<

n and kl

<

k2. increases.

There exists exactly one P,* for (ki

.

m, ki

.

n)-IDS and Proof: See appendix A.6.

0 Lemma 1

then: Pd(k

-

m, k . n ) M gaufc(-0.5(), for P, = m / n ;

Use a Gaussian approximation of Pd(k. m, k . n ) , evalu-

ated at P, = m / n [ l l ] :

Let p , q be real non-negative numbers such that p f q = 1,

exp

I

(nl - ml)

.

log

(;a)

+

m’. log

(+)I

{

binfc(m’; n’, p ) , for m’ L p

.

n’

for m’

5

p

.

n’.

binf(m’; n’, p ) , Proof: See [8] or [lo].

0 Lemma 2

Pd(k

.

m, k + n ) -+ 0 as k -+ m, for P,

<

m / n and k

2

1

Proof: See appendix A.”.

0 Lemma 3

Pd(k. m, k . n ) t 1 as k --f CO, for m / n

<

P,. Proof: See appendix A.8.

Because gauf(-0.5<) strictly increases to 0.5 as

k

increases, the value of Pd(k.m,

k

en) evaluated at P, = m / n

strictly decreases to 0.5 as k increases. From theorem 3.6,

the critical probability of ( m , n)-IDS and ( k

.

m, k . n)-IDS

(for all k

>

1 ) is larger than m/n. Therefore, the critical

probability of (m, n)-IDS and ( k

.

m , k n)-IDS strictly de-

creases to m / n as k increases. That is, the sequence:

<

Ak > = P,* [(m, n ) , (k

.

m, k

.

n ) ]

strictly decreases to mln. The result has been confirmed

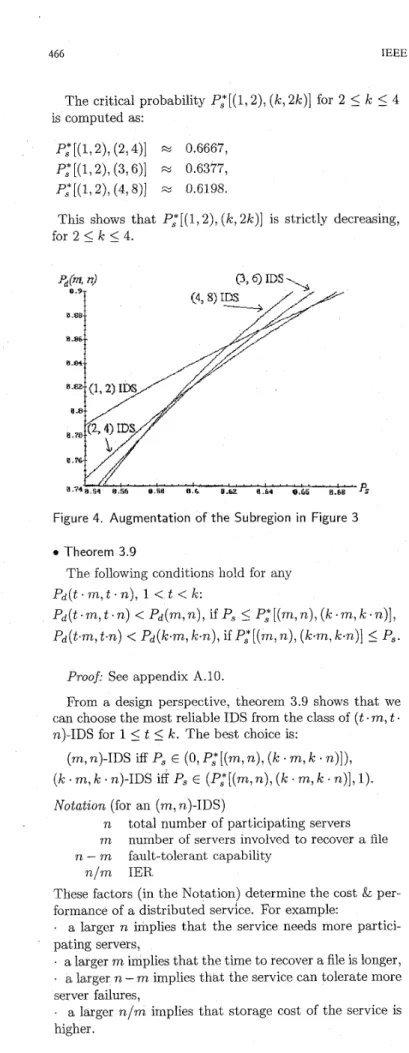
by examining the sequence for n 5 100. As an example,

figure 3 shows the reliabilities of ( k , 2k)-IDS (1

5

k

5

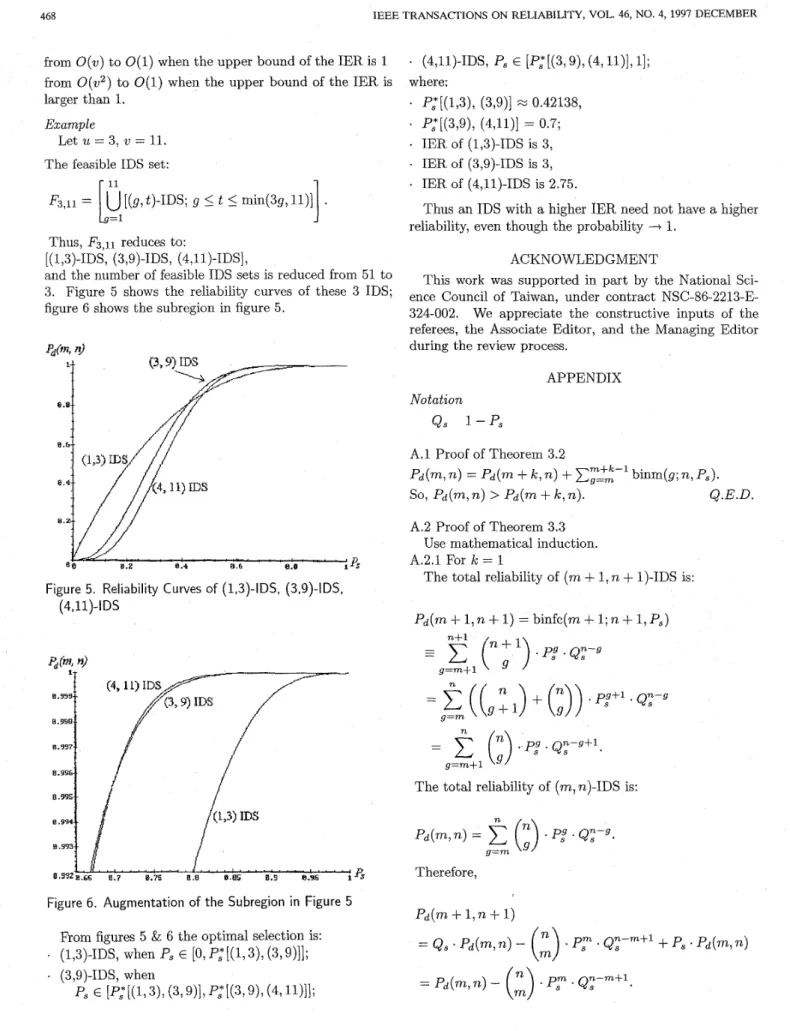
4). Figure 4 augments a subregion in figure 3.

0 Theorem 3.7

As k + 00:

Pd(k.m,k.n) + 0 , for P,

<

m / n ; P d ( k . m , k . n ) -+ I , for

P,

>

m/n.

Proof: This follows from lemmas 2 & 3.

Theorem 3.7 demonstrates a principle to determine the lower bound of IER such that the IDS with the lower bound of IER has better reliability. Given the success

probability of each P,, we should select those IDS whose IER

>

l / P s ; ie, for the class of ( k

.

m, k

.

n)-IDS, the

reliability -+ 1 if IER (= n / m )

>

l/P,. From a design

perspective, theorem 3.7 indicates that if more servers are provided, but the same IER (> l / P s ) is provided, then

the total reliability of the distributed servers increases.

n.2

Figure 3. Reliability Curves for (1,2)-IDS, (2,4)-IDS, (3,6)- IDS, (4,8)-IDS

(5)

466 IEEE TRANSACTIONS ON RELIABILITY, VOL. 46, NO. 4, 1997 DECEMBER

The critical probability P,*[(l,

a),

( k , 2 k ) ] for 2

5

k

5

4 is computed as:

P,*[(1,2), (2,4)] x 0.6667,

P,* [(1,

a),

( 3 , 6 ) ] M _0.6377,

P,*[(l,2), (4, S)] M 0.6198.

This shows that

P,[(l,*

a ) ,

( k , 2k)] is strictly decreasing,

for 2

5

k

5

4.

Figure 4. Augmentation of the Subregion in Figure 3

0 Theorem 3.9

The following conditions hold for any

P d ( t . m , t . n ) , I < t < k :

Pd(t.m,t.n)

<

Pd(m,n), if P,

I:

P , * [ ( m , n ) , ( k . m , k . n ) ] , Pd(t.m, t.n)

<

P d ( k m ,

bn),

if P;[(m,n), ( k m , b n ) ]

5

P,

Proof: See appendix A.10.

From a design perspective, theorem 3.9 shows that we can choose the most reliable IDS from the class of (t ' m, t

.

n)-IDS for 1

5 t 5

k . The best choice is:

( m , n)-IDS iff P, E (0, P:[(m, n), ( k

.

m, k * n ) ] ) ,

( k . m , k . n ) - I D S iff P, E (P;[(m,n),(Ic.m,k.n)],l). Notation (for an ( m , n)-IDS)

n m

total number of participating servers number of servers involved to recover a file

n - m fault-tolerant capability n / m IER

These factors (in the Notation) determine the cost & performance of a distributed service. For example:

. a larger n implies that the service needs more partici- pating servers,

. a larger m implies that the time to recover a file is longer,

.

a larger n

-

m implies that the service can tolerate more

According to the resource & performance constraints, the designer has many possible choices for (m,n)-IDS. Given these IDS, then determine the optimal IDS with the highest reliability. From theorem 3.6, every pair of IDS has at most one critical probability. The optimal IDS for the two ranges (P,

>

P,*, and P,

<

P,)*

are usually different. Given a set of IDS, one of them might be not optimal in all ranges of P,. Therefore, finding optimal IDS

is quite complicated. Based on the theorems 3-1 - 3-9, we give a pseudo-algorithm for finding the possible optimal systems. The input of the algorithm is a set of IDS which the designer can choose according to the resource & performance constraints. The output is the reduced IDS set indicating a possible optimal IDS.

0 Algorithm: Search-t he-Possi ble-0 pti m a [Systems

Input: S [set of IDS with different parameters]

Output: S' [reduced set of IDS indicating possible optimal IDS]

1. Let S ' = S .

2a. Search S' to find the IDS which belong to the same class of ( m , n

+

k)-IDS. Let this IDS be

{ (m, n

+

k,)-IDS}i=l, where

k,

<

k,+l.

2b. Reduce S' by deleting { ( m , n

+

k,)-IDS}i;;.

2c. Repeat this step 2 until no IDS belongs to the same

'

(by theorem 3.1)

class of ( m , n

+

k)-IDS.

3a. Search S' t o find the IDS which belong to the same

class of ( m

+

k,n)-IDS. Let this IDS be { ( m

+

k,, n)-IDS}L=l, where

kg

<

k , + l .

3b. Reduce S' by deleting { ( m

+

k,,n)-IDS}i=2. (by theorem 3.2)

3c. Repeat this step 3 until no IDS belongs to the same class of ( m

+

k , n)-IDS.

4a. Search S' to find the IDS which belong to the same class of ( m

+

k , n

+

{ ( m

+

kg,

n

+

k,)-IDS}&l, where k s

<

k,+l. 4b. Reduce S' by deleting { ( m

+

k,,

n

+

k,)-IDS}&,. 4c. Repeat this step 4 until no IDS belongs to the same

(by theorem 3.3)

class of ( m

+

k , n

+

k)-IDS.

5a. Search S' t o find the IDS which belong to the same

class of ( m . k , n

.

{ ( m

.

k g , n . k,)-IDS}i=I, where k,

<

k , + l .

5b. Reduce S' by deleting { ( m

.

k,, n

.

k , ) - I D S } ~ ~ ~ . (by theorem 3.9)

5c. Repeat this step 5 until no IDS belongs to the same server €ailures,

. a larger n/m implies that storage cost of the service is

(6)

SUN/SHIEH: OPTIMAL INFORMATION-DISPERSAL FOR INCREASING THE RELIABILITY OF A SERVICE

For every pair of IDS in SI, say (i, j)-IDS & ( k , Z)-IDS,

execute the process:

a. if 1

>

j , and k

<

i, then delete (i,j)-IDS from S’; (by theorem 3.4)

b. if 1

>

j , k >

i,

and

1 -

k

<

j

-

i, then delete

( k , Z)-IDS from 5’’; (by theorem 3.5)

c. if 1

<

j , and IC

>

i, then delete (k,l)-IDS from SI; (by theorem 3.4)

d. if 1

<

j , k :4 i, and 1 - k

>

j

-

i, then delete

(i, j)-IDS from SI; (by theorem 3.5)

o u t p u t S’.

EndAlgorithm

Once the reduced IDS set S’ is determined and the success probability of each P, is known, the designer can com- pute & compare the reliabilities of these possible optimal IDS to find the optimal IDS.

Section 4 considers a special case when an upper-bound of the IER and the number of available servers are given. The method uses the properties in theorems 3.1 - 3.9 to

reduce the complexity of finding the optimal IDS. 4. OPTIMAL INFOR.MATION DISPERSAL Theorem 3.2 shows that an ( m l , n)-IDS has higher reliability than an (m2, n)-[DS if ml

<

m2. So, it is reasonable to store higher priority files in the distributed servers a t a higher IER. and lower level files a t a lower IER.; this does not imply that any 11)s with a higher IER always has a higher reliability than an IDS with a lower IER. On the other hand, the number of available servers in a distributed system can change. Based on the analysis in section 3, we propose a method for determining the optimal IDS when an upper-bound of the IER. (depending on the priority of the file) and the number of available servers are given.

Notation

U upper bound 01. the IER v number of available servers

k lv/ul

Given U & v, the feasible IDS set is the set of all possible

IDS that satisfy these conditions. The optimal IDS in each range of P, are elements of the feasible IDS set. Theorems

3.4 & 3.5 show that many IDS of a feasible IDS set are not

optimal in any range of

P,.

Theorem 3.6 shows that an

IDS can be optimal in some range, but not in all ranges. Therefore, a feasible IDS set can be reduced so that all optimal IDS are still included in the reduced feasible

IDS

set. The reduced feasible IDS set is a subset of the feasible IDS set. For any P,, the optimal IDS of

Fu,v

is an element

of the reduced Fu,v.

The feasible IDS set is the union of several partitions. Each partition consists of all (m,n)-IDS for which m is a constant:

467

By theorem 3.1, in each partition:

the (i, i

.

U)-IDS has the highest reliability. Similarly, in each partition:

the

(k

+

j,v)-IDS has the highest reliability. Thus, (1) reduces to:

[(i, t)-IDS; i 5 t

5

i * U],

[ ( k + j , t ) - I D S ; k + j

i

t

<VI,

FU,v = [(i, i

.

u)-IDS; 1

5

i

5 k]

U [ ( k

+

j, v)-IDS;

l < j < v - k ] . (2)

By theorem 3.9, the IDS set:

can be reduced to:

[(i,i. u)-IDS; 1

5

i

5

k ]

[(l, u)-IDS, ( k , ~ * k)-IDS].

By theorem 3.2, in the IDS set:

[(k

+

j , v)-IDS; 1

5

j

5

ZJ

- k],

the

(k

+

I, v)-IDS has the highest reliability. Therefore,

(2) can be reduced to:

[(l, u)-IDS, ( k , U . k)-IDS, ( k

+

1, v)-IDS]. ₍₃₎

If k = v/u, then (3) reduces to: [(l,u)-IDS, (k,v)-IDS,

(k

+

1, w)-IDS].

By theorem 3.2, Pd(k,v)

>

Pd(k

+

1,v). Thus, (3) re-

duces to:

[ ( l , ~ ) - I D S , ( ~ , v ) - I D S ] . (4)

Compare the number of feasible IDS sets with the number of reduced feasible IDS set as follows. The reduced feasible IDS set contains 3 elements (2 elements if k = v/u), ze, the number of elements in the reduced feasible IDS set is Without much loss of generality, let k = v/u. Then, the

OU).

number of the feasible IDS sets is:

[ i J g . u - g + l ) g=l

I

+

[g=k+l

2

( v - g + l )

1

Thus, the number of elements in the feasible IDS set is:

O ( v 2 ) , if U

>

1, O(v), if U = 1.

highest reliability:

(7)

468 IEEE TRANSAClTONS ON RELIABILITY, VOL. 46, NO. 4, 1997 DECEMBER

from O(w) to 0( 1) when the upper bound of the IER is 1 from O(v2) to O(1) when the upper bound of the IER. is larger than 1.

Examp le

Let U = 3, z1 = 11.

The feasible IDS set:

11

F3,11 =

[U

[(g,t)-lDS;

g=1

I

g

5

t

5

min(3g, 1 I)]

Thus, F3,11 reduces to:

and the number of feasible IDS sets is reduced from 51 to 3. Figure 5 shows the reliability curves of these 3 IDS;

figure 6 shows the subregion in figure 5.

[(1,3)-IDS, (3,9)-IDS, (4,l l)-IDS],

8 . 8 . %. 8 .

i3'9r

0.2 8.4 8.6 8.8

Figure 5. Reliability Curves of (1,3)-IDS, (3,9)-IDS, (4,ll)-IDS

Figure 6. Augmentation of the Subregion in Figure 5

* _(4,11)-1W_ps_E_{[P,*[(3,9), (4,11>1,11;} where: * P,*[(1,3), (3,9)] M 0.42138,

.

P,*[(3,9), (4,11)] = 0.7;

.

IER of (1,3)-IDS is 3, . IER of (3,9)-IDS is 3,

.

IER of (4,ll)-IDS is 2.75.

Thus an IDS with a higher IER need not have a higher reliability, even though the probability -+ 1.

ACKNOWLEDGMENT

This work was supported in part by the National Sci- ence Council of Taiwan, under contract NSC-86-2213-E- 324-002. We appreciate the constructive inputs of the referees, the Associate Editor, and the Managing Editor during the review process.

APPENDIX Notation

Q s I - P s

A.1 Proof of Theorem 3.2

binm(g; n, Ps). m + k - l

Pd(m, n ) = pd(m

+

k , n )

+ CgEm

So, Pd(m, n )

>

Pd(m

+

k, n). Q.E.D.

A.2 Proof of Theorem 3.3

A.2.1 For k = 1

Use mathematical induction.

The total reliability of ( m

+

1, n

+

1)-IDS is: Pd(m

+

1 , n

+

1) = binfc(m

+

1 ; n

+

l,Ps)

(8)

Thus, Pd(m, n)

>

Pd(m

+

1, n

+

1), and the theorem holds for k = 1.

=

(!)

> o ,

A.2.2 For k

>

1

Pd(m, n )

>

Pd(m

+

t ,

n

+

t).

Let m’ = m

+

t and n’ = n

+

t ; then from A.2.1,

Pd(m,n)

>

Pd(m

+

t , n

+

t ) = Pd(m‘, n’)

>

Pd(m’

+

1, n’

+

1).

Pd(m, n )

>

Pd(m

+

t -t. 1, n

+

t

+

I), and the theorem holds also when k = t -t 1.

Assume the theorem holds when k = t:

Qs:l

=

[$

(i)

P,”-i. Qj-g

Q,:z

=

[

$ (3

-

Pi!-z

’

, I

1

Therefore,

Q.E.D. _thusPd(2,j)

>

P ~ ( ~ c , I ) when P, -+

o+.

A.3 Proof of Theorem 3.4

By theorem 3.1,

Pd(k,j) 5

Pd(k,

1 ) for 1 2 j ,

j

pd(i,j) = 1

-

(3

.

P,j-”.

Q:,

g=j-i+l

with equality when 1 == j. By theorem 3.2,

with equality when k := i.

Pd(i,j)

5

Pd(k,j) 5

Pd(k,l)

for 1 2 3 and k

L

i,

with equality when 1 == j and k = i. A.4. Proof of Theorem 3.5

Pd(k,l) = 1

-

‘

(i)

.

Pi-”

.

Q:.

Pd(i,j)

5

Pd(k,j) for

k

5

i, g=l-k+l

Therefore,

lim

[3!2]

-

lim [@,:I

-

@ , : 2 ]

P,--r1-

Q;-’+’

Pa-+l- j Q.E.D. = - ( j - i + l ) < O ,

1

Let t = 1

-

j. By theorem 3.3,

[

2 (i)

_.

_{p , “ - g .}

_QZ-J+2-1

(d)

.

p , ” - g . Q:-J+2-1

P d ( 2 , j ) 2 Pd(i

+

t , j

+

t ) =

Pd(i

+

1 - j , l ) , g=l-k+l

with equality when 1 = j. Because 1

-

k

5

j

-

i, then

k 2 i

+

1

-

j. By theorem 3.2, _{@s:2 3}

[

Pd(i

+

1

-

j , 1) 2 Pd(k, I ) , g=J--z+l with pd(i, with l = j Pd(i,

equality when i

+

1 - j =

k.

So,

equality when 1 = j and i

+

1 - j =

k,

or equivalently and i = k. However, IC

>

i. Thus,

j )

> Pd(k,l)

if 1 2 : j, k

>

i, and 1

-

k

5

j

-

i.

j ) 2 Pd(k,l), thus Pd(i, j )

<

Pd(k,

1 ) when P, -

These equations show:

b(P,)

>

0 when

P,

-+ O+, b(P,)

<

0 when

P,

4 1-.

A.5 Proof of Theorem i3.6

A.5.1 Prove:

6(P,)

>

0, when P, ---t (I+,

b(P,)

<

0, when P, +. I-.

Q. E.

D.

A.5.2 Prove (Based on A.5.1.)

+1-

There exists exactly 1 critical P,* such that:

P d ( 4 j ) = Pd(k I ) ,

Pd(i,j)

>

Pd(k,Z) if P,

<

P,*, Pd(i,j)

<

Pd(k,l) if P,*

<

P,.

Because:

then the first derivative of Pd(m,n) is:

(9)

470

Therefore,

Similarly,

IEEE TRANSACTIONS ON RELIABILITY, VOL. 46, NO. 4, 1997 DECEMBER

A.7 Proof of Lemma 2 Let P,

<

m/n.

Lemma 1 shows that:

=

k

.

m

.

log (kin:).

___

Hence, P d ( k . m, k

.

n )

5

exp [@,:I

+

@ ,: 2] Let: fJ'(P,)

>

0 when P, --+

I-.

Let #(P,) = 0. Then, P, = 0, or P, = 1, or Let a = k

-

i, b = ( I

-

k )

-

( j

-

2).

The graph of P," Q: is:

n 1

So, there are at most two solutions in (0,1) for (6). If there is no solution or one solution in (0,1) for (6) then

6'(P,) >_ 0 for all P,. [There is at most one P, such that S'(P,) = 0.1 This implies that 6(P,) is a monotonic increasing function.

6(P,)

>

0 as P, --f 1-, because 6(P,)

>

0 when P, -+ O+.

This contradicts the claim that 6(P,)

<

0 when P, --+ 1-

in A.5.1. Therefore, there are exactly 2 solutions in (0,1) for (6); and there are 3 stationary points for 6(P,) when P, E ( 0 , l ) . However,

S(P,) is a polynomial of P,, and Pd(i, j )

>

Pd(k, I ) when P, 3 Of,

Pd(i,j)

<

Pd(k,I) when P, --+ 1-.

So, there exists exactly 1 P,* such that:

Pd(i,j)

>

Pd(k,I) if P,

<

P,*, Pd(i, j )

<

Pd(k, I) if P,*

<

P,.

A.6 Proof of Corollary 1 Because:

k2

.

n

>

kl

.

n, . m

>

k l . m ,

/ ~ . n - k a . m = k z . ( n - m ) > k l . ( n - m ) = k l . n - k i . m

then theorem 3.6 shows that there exists exactly 1 critical

probability in (0,l) for ( k l * m, ki 9 n)-IDS and

(k2

.

m, kz

.

n)-IDS.

Pd(4

j) =

Pd(k

0,

Q.E.D.

Calculate where the maximum of g(P,) is.

- ( n - m ) . P , + m . Q , = O ;

P, = m/n; and the maximum value of g(Ps) is g(m/n) =

1. Since P,

<

m/n, then, 0

<

g(P,)

<

1 when 0

<

P,

<

m/n. Because 0

<

g(P,)

<

1, then f ( P , )

<

0. exp [k

.

f ( P , ) ] -+ 0 as k -7' 00. Because, Therefore, then, Pd(k

.

m, k

.

n ) 0 as k --+ 00, for 0

<

P,

<

m/n. Q.

E. D.

A.8 Proof of Lemma 3

Lemma 1 shows that: Let

<

P,.

(10)

Let:

f(E)

=

log(g(Ps)).

Because 0

<

P,

<

1 and n 2 m , then g(P,)

>

0. Calculate where the maximum of g(P,) is.

-(n

-

m )

.

P,

+

7 7 1 . Q , = 0;

P,

= m / n ;

the maximum value of g(P,) is g ( m / n ) = 1. Hence,

o

<

g(P,)

<

1 when mln

<

P,. Because 0

<

g(P,)

<

1

,

then f(P,,)

<

0. Therefore, exp [k

.

f ( f \ ) ] -+ 0 as k -+ 00. Because, then, Hence, P d ( k . m , k

.

n ) 3 1 as k -+ 03. Q. E.

D.

Let

<

A,,

>

be any subsequence of

<

Ak

>.

If we can construct a subsequence

<

At,

>

of

<

A,,

>

such that

<

At,

>+

mln, then, by lemma 4, the theorem is proved. Corollary 1 asserts the existence & uniqueness of

Ak,

ie, Ak is unique in (0,l) such that Pd(m, n ) and Pd(k.m, k.n)

are equal at Ak. By assumption,

<

A,,

>

is a subsequence of

<

Ak

>,

so it corresponds to the subsequence,

<

Pd(Sk

m, s k

. ?

>

IO f )

Pd(k

.

m ,

k

.

n). Construct

<

At,

>

such that,

for all k. Consequently,

<

At,

>-+

mln as k --+ 00.

To begin with, choose tl = 2; then A2 E [0,1]. Define tk inductively. Let tk be defined for k = 1 , 2 , .

. .

,

z - 1. The following discussion is needed before

t,

is defined. Let,

L

=

Pd(m,

n ) and

L,,

= Pd(sk m , S k n ) ,

R = Pd(m, n ) and R,, =

Pd(sk

.

m , Sk + n ) ,

at P, =

-

z.

limkdW (L,, ) = 0 by theorem 3.7.

Therefore we can choose a subsequence

<

Uk

>

of

< S k

>

such that:

L,,

<

L , for all k ,

<

L,,

>

is strictly decreasing to 0.

limk+w (R,, ) = 1, by theorem 3.7.

Therefore we can choose a subsequence

<

Vk

>

of

<

uk

>

such that R,,

>

R for all k , and

<

R,,

>

is strictly increasing to 1.

L,,

<

L , and R,,

>

R, for all k.

Therefore, a t p - E l - E .

- n n . 2 ’

On the other hand,

Now consider Uk:

A,, E

[:

-

-,

-

+

-

,

for all k .

:

2

:

n?3

Geometrically, this can be understood easily; the Inter- mediate Value Theorem in calculus applies here. Let,

t;

s mink {Vk; u k

>

&-I}.

By induction, construct a subsequence

<

At,

>

of

<

Ak

>

such that,

< A t , >+m/n.

Hence, by lemma 4,

<

Ak

>-+

mln. Q.E.D.

As explained in section 3, just before theorem 3.9, P,” [ ( m , n ) , ( k . m, k . n ) ]

<

P,* [ ( m , n ) , ( t . m ,

t .

n)l,

if k

>

t.

The Cdf, Pd(m’,n’) of an (m’,n’)-IDS, is strictly monotonic increasing for P, E ( 0 , l ) ; therefore,

P,* [(t

.

m , t

.

n ) , (k

.

m , k

.

n ) ]

<

P,* [ ( m , n ) , ( k

.

m , k

.

n)]

< P,*

[ ( m , n), (t

.

m , t

.

n ) ] . Let, p ,

=

P,*[(t. m ,

t .

n ) , (k . m , k

.

n ) ] , Pb

=

Ps*[(m,n), ( k

.

m, k * n>l, p , e Pz[(m,n),

(t

.

m ,

t .

n ) ] . Pd(t. m, t

.

n )

<

Pd(m, n ) if

P,

<

p,, Pd(t. m , t

.

n )

<

Pd(k

.

m , k

.

n ) , if pa

<

P,.

(11)

472 IEEE TRANSACTIONS ON RELIABILITY, VOL. 46, NO. 4, 1997 DECEMBER

Because p ,

<

p c , Because pa

<

p b ,

[16] M.O. Rabin, “Efficient dispersal of information for security, load balancing, and fault tolerance”, J . A C M , vol 36,

1989 Apr, pp 335-348.

[17] A. Shamir, “HOW to share a secret”, Comm. A C M , vol22,

1979 Nov, pp 612-613.

P d ( t . m, t . n )

<

Pd(m, n ) , if

P,

I pb.

Pd(t. m, t . n )

<

Pd(k . m, k

.

n ) , if p b

5 P,.

Q.E.D.

R.EFER.ENCES

C. Asmuth, G.R. Rlakley, “Pooling splitting and restitut- ing information to overcome total failure of some channels of communication”, I E E E Proc. 1982 Symp. Securzty & Privacy, 1982, pp 156-169.

C. Asmuth, J. Bloom, “A modular approach to key safeguarding”, I E E E ’I3-ans. Information Theory, vol IT-29, num 2, 1983, pp 208-210.

A. Bestavros, “IDA-based redundant arrays of inexpen-

sive disks”, Proc. Farst Int ’I Conf. Parallel & Dzstributed Information Systems, 1991 Dec.

G.R. Blakley, “Safeguarding cryptographic keys”, Proc. NCC, vol 48, 1979, pp 313-317; AFlPS Press.

W.A. Burkhard, K.C. Claffy, T.J.E. Schwarz, “Perfor- mance of balanced disk array schemes”, llth IEEE Symp. Mass Storage Systems, 1991, pp 45-50.

W.A. Burkhard, J. Menon, “Disk array storage system reliability”, Proc 23’d I E E E Int ’1 Symp. Fault- Tolerant Computing, 1993, pp 432-441.

P. Chen, E. Lee, G. Gibson, et a2, “RAID: High- performance, reliable secondary storage”, A CM Comput-

zng Surveys, vol 26, num 2, 1994 Jun, pp 145-185. H. Chernoff, “A measure of asymptotic efficiency for tests

of a hypothesis based on the sum of observations”, Annals Mathematical Statzstzcs, vol 23, 1952, pp 493-507. D.E.R. Denning, Cryptography and Data Securzty, 1983; Addison- Wesley.

P. Erdo S , J. Spencer, Probabzlistic Methods zn Combana-

torics, 1974, pp 18; Academic Press.

R. G. Gallager, Informataon Theory and Reliable Commu- nzcatzon, 1968; John Wiley & Sons.

L. Gargano, A.A. Rescigno, U. Vaccaro, “Fault-tolerant hypercube broadcasting via information dispersal”, Net- works, vol 23, 1993, pp 271-282.

L. Gong, “Increasing availability and security of an authentication service”, I E E E J . Selected Areas zn Commu- nications, vol 11, 1993 Jun, pp 657-662.

Y.D. Lyuu, “Fast fault-tolerant parallel communication and online maintenance for hypercube using information dispersal”, Mathematzcal Systems Theory, vol 24, num 4,

Y.D. Lyuu, “Fast fault-tolerant parallel communication for de Bruijn and digit-exchange networks using information dispersal”, Networks, vol 23, 1993, pp 365-378. 1991, pp 273-294.

AUTHORS

Dr. Hung-Min Sun; Dep’t of Information Management; Chaoyang Univ. of Technology; Wufeng, Taichung, 413 TAI-

Internet (e-mad): hmsun@dscs.csie.nctu.edu.tw

Hung-Min Sun received his BS (1988) in Applied Math- ematics from National Chung-Hsing University, MS (1990) in Applied Mathematics from National Cheng-Kung University, and PhD (1995) in Computer Science and Information Engi- neering from National Chiao-Tung University. Since 1995 he has been with the Department of Information Management, Chaoyang University of Technology. His research interests include reliability theory, computer security, cryptography, and information theory.

WAN

-

R.O.C.

Dr. Shiuh-Pyng Shieh; Dep’t of Computer Science and Infor- mation Engineering; National Chiao Tung Univ; Hsinchu 30010

Internet (e-mail): ssp@csie.nctu.edu.tw

Shiuh-Pyng Shieh received the MS (1986) and PhD (1991) in Electrical Engineering from the University of Maryland, Col- lege Park. He is an Associate Professor with the Department of Computer Science and Information Engineering, National Chiao Tung University. From 1988 to 1991 he participated in the design & implementation of the B2 Secure XENIX for IBM, Federal Sector Division, Gaithersburg, Maryland, USA. He is the designer of the SNP (Secure Network Protocols). Since 1994 he has been a consultant for Computer & Com- munications Laboratory, Industrial Technology Research Insti- tute, TAIWAN - R.O.C. in network security and distributed operating systems. He is also a consultant for the National Security Bureau, TAIWAN

-

R.O.C. Dr. Shieh was on the or- ganizing committees of several conferences, such as Int’l Com- puter symp, and Int’l Conf. Parallel & Distributed Systems. He was the program chair’n of the Information Security Conf. (INFOSEC’97) and a program-committee member of the ACM Conf. Computer & Communications Security (CCCS’96). His

research interests include distributed operating systems, computer networks, and computer security.

TAIWAN

-

R.O.C.

Manuscript TR96-063 received 1996 May 6; Responsible editor: J.R. Dugan

Publisher Item Identifier S 0018-9529(97)09382-2