Edge-disjoint Undirected Spanning Trees on the Wrapped Butterfly Networks

(1)

Edge-disjoint Undirected Spanning Trees on the Wrapped Butterfly Networks

Tzu-Liang Kung, Tyne Liang

∗†

Department of Computer Science

National Chiao Tung University

Hsinchu, Taiwan 30050, R.O.C.

{tlkueng,tliang}@cs.nctu.edu.tw

Lih-Hsing Hsu

‡

Department of Computer Science

and Information Engineering

Providence University

Taichung, Taiwan 43301, R.O.C.

lhhsu@cs.pu.edu.tw

Abstract

The problem of finding the maximum number of edge-disjoint spanning trees arises from the need for developing efficient collective communication algorithms in distributed memory parallel computers. In this paper, we propose a formula for obtaining the maximum number of edge-disjoint undirected spanning trees on the wrapped butterfly network. The result can be applied to design efficient multicast rout-ing algorithms in wormhole-routed parallel systems.

Keywords: Interconnection network; Graph; Butterfly net-work; Spanning tree

1. Introduction

A multiprocessor/communication interconnection net-work is usually modeled as a graph, in which the vertices correspond to processors/nodes and the edges correspond to connections or communication links. Therefore we use the terms, graphs and networks, interchangeably. Among various kinds of popular network topologies, butterfly net-works are very suitable for VLSI implementation and par-allel computing. Recently, the wrapped butterfly graph has gained many researchers’ efforts for its nice topological properties [2, 4, 6, 8, 10–12].

Embedding one network onto another is an interesting subject because the portability of the guest network onto the host network would permit executing guest specified al-gorithms on the host with as little modification as possible. Embedding various topologies, such as rings, linear arrays, binary trees, etc., into the butterfly networks has been ad-dressed in research by [5, 11, 12]. In particular, the

prob-∗_{Corresponding author. Tel: 886-3-5131365. Fax: 886-3-5721490.} †_{This work was supported in part by the National Science Council of} the Republic of China under Contract NSC 96-2221-E-009-168-MY2.

‡_{This work was supported in part by the National Science Council of} the Republic of China under Contract NSC 97-2221-E-126-001-MYB.

lem of constructing edge-disjoint spanning trees in a net-work arises from the need for developing efficient collec-tive communication algorithms in distributed memory par-allel computers. Barden et al. [1] presented a brief compar-ison between two routing schemes, store-and-forward rout-ing [7] versus wormhole routrout-ing [9], and explained how and why edge-disjoint spanning trees are involved in these ap-plications. Not only did Touzene et al. [10] investigate how to embed edge-disjoint directed spanning trees on butterfly networks, but they also discussed the possible applications to communication algorithms. Since the proposed spanning trees are directed, their construction permits an edge (u, v) to be used in orientation hu, vi in one spanning tree and in orientation hv, ui in a second spanning tree. Such kind of applications are mainly based on the store-and-forward routing. Unlike the previous research, we turn our attention to undirected spanning trees, which can be applied to the wormhole routing. In [1], a recursive method was presented to construct bn

2c edge-disjoint undirected spanning trees on

an n-cube. In this paper, we give a formula for obtaining the maximum number of edge-disjoint undirected spanning trees on the wrapped butterfly network.

The rest of this paper is organized as follows. In Sec-tion 2, we introduce graph-theoretic terminologies and the definition of wrapped butterfly networks. Section 3 is de-voted to basic properties of the wrapped butterfly network. In Section 4, we show how to embed the maximum number of edge-disjoint undirected spanning trees onto the wrapped butterfly network. Finally, the concluding remarks are pre-sented in Section 5.

2. Preliminaries

In this paper, we concentrate on loopless undirected graphs. For the notations and graph-theoretic terminolo-gies, we follow the ones given by Bondy and Murty [3]. A graph G is a two-tuple (V, E), where V is a nonempty set and E is a subset of {(u, v) | (u, v) is an unordered

(2)

pair of V}. We say that V = V (G) is the vertex set and

E = E(G) is the edge set. Two vertices, u and v, are ad-jacent if (u, v) ∈ E. The number of vertices in a graph G, denoted by |V (G)|, is called the order of G; the

num-ber of edges, denoted by |E(G)|, is the size of G. The

de-gree of any vertex u in a graph G, denoted by degG(u),

is the number of edges incident with u. The maximum and minimum degrees among the vertex set are denoted by ∆(G) and δ(G), respectively. A graph G is k-regular if ∆(G) = δ(G) = k.

A graph H is a subgraph of a graph G if V (H) ⊆ V (G) and E(H) ⊆ E(G). Let S be a nonempty subset of vertices of a graph G. The subgraph induced by S is the subgraph of

G with the vertex set S and the edge set consisting of those

edges that join two vertices in S. Analogously, the subgraph

generated by a nonempty set F ⊆ E(G) is the subgraph of G with the edge set F and the vertex set consisting of those

vertices incident to at least one edge of F . If X is a subset of edges of graph G, then G − X is the spanning subgraph of G obtained by deleting the edges of X from E(G). Two graphs, G1and G2, are isomorphic if there exists a bijection

µ from V (G1) onto V (G2) such that (u, v) ∈ E(G1) if and

only if (µ(u), µ(v)) ∈ E(G2). This bijection µ is called an

isomorphism.

A path P of length k from vertex x to vertex y in a graph

G is a sequence of distinct vertices hv1, v2, . . . , vk+1i such

that v1 = x, vk+1 = y, and (vi, vi+1) ∈ E(G) for every

1 ≤ i ≤ k if k ≥ 1. We also write P as hx, P, yi to em-phasize its beginning and ending vertices. A path of length 0, consisting of a single vertex x, is denoted by hxi. Let u and v be vertices in a graph G. We say that u is connected to v if G contains a path between u and v. The graph G itself is connected if u is connected to v for every pair u, v of vertices of G. A subgraph H of graph G is a component of G if H is a maximal connected subgraph of G. A cycle is a path with at least three vertices such that the first vertex is adjacent to the last one. In order to emphasize the ver-tex order on a cycle, a cycle C of length k is represented by hv1, v2, . . . , vk, v1i. A tree is a connected graph without

cycles. A spanning tree of a graph G is a spanning sub-graph of G that is a tree. Let T be a tree rooted at vertex

r. The height of T , denoted by height(T ), is the length of

the longest path among all the paths from root r to any other vertices of T . The following theorem characterizes a tree. Theorem 1. [3] Let G be a graph. Then G is a tree if and

only if G is connected and |E(G)| = |V (G)| − 1.

Let Zn = {0, 1, . . . , n − 1} denote the set of integers

modulo n. The n-dimensional k-ary wrapped butterfly

net-work (or butterfly netnet-work for short), denoted by BF (k, n),

is a graph with vertex set Zn× Znk. Each of the n × kn

ver-tices is labeled by a two-tuple h`, a0. . . an−1i with a level

` ∈ Znand an n-digit radix-k string a0. . . an−1∈ Znk. The

edge set of BF (k, n) can be defined in terms of the follow-ing 2k generators, fiand fi−1with i ∈ Zk:

fi(h`, a0. . . an−1i)

= h(` + 1)mod n, a₀. . . a_`−1a(i)_` a_`+1. . . a_n−1i,

and

f_i−1(h`, a0. . . an−1i)

= h(` − 1)mod n, a₀. . . a_`−2a(−i)_`−1a_`. . . a_n−1i,

where a(i)_` ≡ a`+ i (mod k). By definition, BF (k, n) is

2k-regular. It should be noticed that BF (k, 2) is a multi-graph. The level of vertex h`, a0. . . an−1i is `. An edge

joining a level-` vertex and a level-(` + 1)mod n vertex is

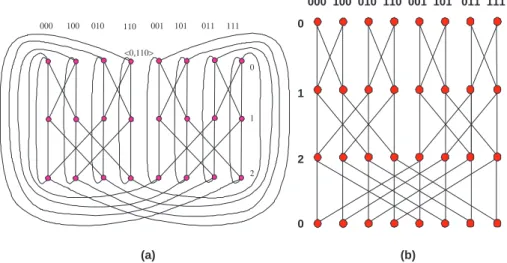
called a level-` edge. Figure 1(a) depicts BF (2, 3), and Figure 1(b) is an isomorphic structure of BF (2, 3) with the replication of level-0 vertices to ease visualization.

3. Fundamental properties of BF (k, n)

Suppose that k and n are two integers greater than or equal to two. For any ` ∈ Zn and i ∈ Zk, we use

BFi

`(k, n) to denote a subgraph of BF (k, n) induced by

{hh, a0. . . an−1i ∈ V (BF (k, n)) | a` = i}. It is

easy to see that BFi

`(k, n) is isomorphic to BF`j(k, n) for

any i, j ∈ Zk. Moreover, BF`i1(k, n) is isomorphic to

BFi

`2(k, n) for any `1, `2 ∈ Zn. Obviously, {BF i `(k, n) |

i ∈ Zk} forms a partition of BF (k, n). With this

obser-vation, Wong [12] proposed a stretching operation to obtain

BFi

`(k, n) from BF (k, n−1) when n ≥ 3. More precisely,

the stretching operation can be described as follows. Let i ∈ Zk and ` ∈ Zn for n ≥ 2. Furthermore, let Gn

denote the set of all subgraphs of BF (k, n). Suppose that

G ∈ Gn. We define the following subsets of V (BF (k, n +

1)) and E(BF (k, n + 1)):

V1 = {vih| 0 ≤ h < `, vh∈ V (G)},

V2 = {vih+1| ` < h ≤ n − 1, vh∈ V (G)},

V3 = {vi`| v`is incident to

a level-(` − 1)mod nedge in G},

V4 = {vi`+1| v`is incident to a level-` edge in G},

E1 = {(vhi, vh+1i ) | 0 ≤ h < `, (vh, uh+1) ∈ E(G)},

E2 = {(vh+1i , vh+2i ) | h ≥ `, (vh, uh+1) ∈ E(G)},

and

E3 = {(v`i, v`+1i ) | v`is incident to at least one

level-(` − 1)mod nedge and at least one

(3)

000 100 010 110 001 101 011 111 0 1 2 0 (b) (a) 000 100 010 110 001 101 011 111 0 1 2 <0,110>

Figure 1. (a) The structure of BF (2, 3); (b) BF (2, 3) with level-0 vertices replicated to ease visual-ization. where vh = hh, a0. . . a`−1a`. . . an−1i, uh = hh, b0. . . b`−1b`. . . bn−1i, vih = hh, a0. . . a`−1ia`. . . an−1i, and ui h = hh, b0. . . b`−1ib`. . . bn−1i.

Then the stretching function γi `: S n≥2Gn→ S n≥3Gn is defined by assigning γi

`(G) as the graph with vertex set

V1∪V2∪V3∪V4and with edge set E1∪E2∪E3. Obviously,

γi

` is well-defined and one-to-one. Furthermore, γ`i(G) ∈

Gn+1 if G ∈ Gn. It is easy to see that γ`i(BF (k, n)) =

BFi

`(k, n + 1). In particular, we have γ`i(P ) is a path in

BF (k, n + 1) if P is a path in BF (k, n).

In the next lemma, we use the following notations:

v` = h`, a0. . . an−1i and

v`i = h`, ia0. . . an−1i.

Lemma 1. Suppose that G is a connected spanning

sub-graph of BF (k, n) for k ≥ 2 and n ≥ 3. Let F0 = {v0∈ V (G) | v0is not incident to any

level-(n − 1) edge in G}, F1 = {v0∈ V (G) | v0is not incident to any

level-0 edge in G}. For i ∈ Zk, let Fi 0 = {v0i | v0∈ F0}, Fi 1 = {v1i | v0∈ F1}, and M = [ v0∈F/ 0∪F1 {(vi 0, v1i)}. Then F0∩ F1= ∅, F0i∩ F1i= ∅, F0i∪ F1i= V (BF0i(k, n + 1)) − V (γi 0(G)), and M ⊆ E(γ0i(G)).

4. Edge-disjoint spanning trees of BF (k, n)

A reasonable upper bound on the number of edge-disjoint undirected spanning trees in BF (k, n) is j |E(BF (k,n))| |V (BF (k,n))|−1 k = jn×kn+1 n×kn₋₁ k = k. In this section, we show that BF (k, n) contains exactly k edge-disjoint undirected spanning trees.

Lemma 2. Suppose n ≥ 2 and k ≥ 2. For every i ∈ Zk,

let si = h0, ini be a vertex of BF (k, n), and let Gi be a

subgraph of BF (k, n) generated by S_n−1 t=0 S (p0,...,pn)∈{(q0,...,qn)∈Zn+1k |qt=0} © (u, fpn(u)) | u = f0t◦ fpn−1◦ . . . ◦ fp0(si) ª . Then {Gi | i ∈ Zk} is a set of k spanning components

of BF (k, n) such thatSk−1_i=0 E(Gi) = E(BF (k, n)), and

E(Gi) ∩ E(Gj) = ∅ whenever i 6= j. Moreover, Ti =

Gi−

©¡

f₀−1(si), si

¢ª

is a spanning tree of BF (k, n) rooted at vertex si.

Proof. Assume that i ∈ Zk. It is clear that every

ver-tex of Gi is connected to si. Thus Gi is connected. To

see that Gi is a spanning component of BF (k, n), we

can decompose E(Gi) into the following disjoint subsets.

For any 0 ≤ j ≤ 2n − 2, let Fi,j = {(si, fp(si)) |

p ∈ Zk} if j = 0; Fi,j =

S

p∈Zk{(u, fp(u)) |

(4)

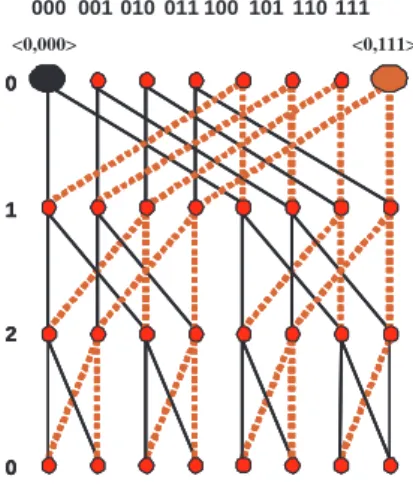
000 001 010 011 100 101 110 111 0 2 1 0 <0,000> 0 2 1 0 0 2 1 0 <0,111>

Figure 2. Two edge-disjoint undirected span-ning trees of BF (2, 3), rooted at h0, 000i and

h0, 111i, respectively. j ≤ n − 1; Fi,j = S (p0,p1,...,pn)∈X{(u, fpn(u)) | u = f₀j−n ◦ fpn−1 ◦ . . . ◦ fp0(si)} if n ≤ j ≤ 2n − 2, where X = {(q0, q1, . . . , qn) ∈ Zn+1k | qj−n = 0, (qj−n+1, . . . , qn−1) 6= (0, . . . , 0)}. Then we observe that E(Gi) = S2n−2

j=0 Fi,j and Fi,j∩ Fi0_,j0 = ∅ whenever

i 6= i0 _{or j 6= j}0_{. Thus, E(G}

i) ∩ E(Gi0) = ∅ if i 6= i0.

By counting, we have |E(Gi)| =

¯ ¯ ¯S2n−2_j=0 Fi,j ¯ ¯ ¯ = n × kn_. Since |E(BF (k, n))| = n × kn+1 ₌ Pk−1 t=0|E(Gt)|, we

obtainSk−1_t=0E(Gt) = E(BF (k, n)). Moreover, we have

|V (Gi)| = n × kn. Hence Gi is indeed a spanning

com-ponent of BF (k, n). It is easy to see that V (Ti) = V (Gi).

Therefore, we obtain |V (Ti)| = |V (Gi)| = n × kn and

|E(Ti)| = |E(Gi)| − 1 = n × kn− 1. By Theorem 1, Ti

turns out to be a spanning tree of BF (k, n) rooted at vertex si. Therefore the proof is completed.

Example 1. In Figure 2, we depict two edge-disjoint

span-ning trees of BF (2, 3), which are rooted at h0, 000i and h0, 111i, respectively.

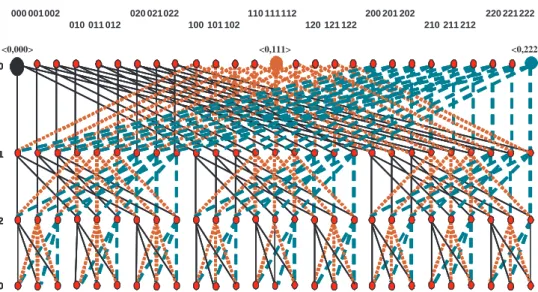
Example 2. In Figure 3, we depict three edge-disjoint

spanning trees of BF (3, 3), which are rooted at h0, 000i, h0, 111i, and h0, 222i, respectively.

Since BF (k, n) is vertex-transitive, we have the follow-ing corollary.

Corollary 1. Suppose that n, k ≥ 2. Let ` ∈ Zn

and a0. . . an−1 ∈ Znk. For any i ∈ Zk, let ri =

h`, a(i)₀ . . . a(i)_n−1i. Then there exist k edge-disjoint spanning

trees of BF (k, n) rooted at r1, . . . , rk, respectively.

Fur-thermore, each of these k edge-disjoint spanning trees has height 2n − 1.

Theorem 2. Let r be any vertex of BF (k, n) with k, n ≥ 2.

Then BF (k, n) contains k edge-disjoint undirected span-ning trees rooted at r, with k unused edges incident with r. One of these k spanning trees has height 2n + 1, and the other k − 1 spanning trees have height 2n.

Proof. Without loss of generality, we assume that r =

h0, 0n_{i. We partition BF (k, n) into {BF}i

0(k, n) | i ∈ Zk}.

For any j ∈ Zk, let Xj = {(h0, jwi, fq(h0, jwi)) |

w ∈ Zn−1

k \ {0n−1}, q ∈ Zk \ {0}} if j = 0

and Xj = {(h0, jwi, fq(h0, jwi)) | w ∈ Zn−1_k , q ∈

Zk \ {0}} ∪ {(r, fj(r))} otherwise. Moreover, for any

j ∈ Zk, let Yj = S t6=j{(h0, twi, h1, twi) | w ∈ Zn−1 k }} − S t6=j{(ft(r), f0−1(ft(r)))} if j = 0; Yj = {(fj(r), f0−1(fj(r)))} ∪ S t6=j{(h0, twi, h1, twi) | w ∈ Zn−1_k } otherwise.

Suppose that n = 2. We first construct k spanning components of BFi

0(k, 2) with i ∈ Zk. For every j ∈

Zk, let Γi,j be a subgraph of BF0i(k, 2) generated by

{(h0, iwi, h1, iwi) | w ∈ Zk} ∪ {(h1, iji, h0, ij(w)i) | w ∈

Zk}. Then we set Tp, with p ∈ Zk, to be the subgraph of

Obviously, {T0, . . . , Tk−1} is a set of edge-disjoint

undi-rected spanning trees of BF (k, 2) rooted at r. It is easy to see that the set of k unused edges is {(f−1

p (r), r) | p ∈ Zk}.

Suppose that n ≥ 3. First of all, we use Lemma 2 to construct k edge-disjoint components G0, . . . , Gk−1 of

BF (k, n − 1) such that Gj − {(f0−1(sj), sj)}, where

sj = h0, jn−1i, is a spanning tree of BF (k, n − 1)

rooted at sj. Since BF0i(k, n) = γ0i(BF (k, n − 1))

with i ∈ Zk, Lemma 1 ensures that V (BF0i(k, n)) −

V (γi

0(Gj)) = {h0, ixwi | x ∈ Zk − {j}, w ∈

Zn−2_k }. Hence, let Γi,j be a subgraph of BF0i(k, n)

generated by E(γi

0(Gj)) ∪ {(h0, iwi, h1, iwi) | w ∈

Zn−1_k } for j ∈ Zk. Similarly, we set Tp, with

p ∈ Zk, to be the subgraph of BF (k, n) generated by

³Sk−1 j=0E ¡ Γ(p+j) mod k,j ¢ ∪ Xp− Yp ´ −©¡f−1 p (r), r ¢ª . Then {T0, . . . , Tk−1} forms a set of edge-disjoint

undi-rected spanning trees of BF (k, n) rooted at r. Again, the set of k unused edges is {(f−1

p (r), r) | p ∈ Zk}.

Clearly, we have height(Tp) = 2n + 1 if p = 0 and

height(Tp) = 2n otherwise.

The proof is completed.

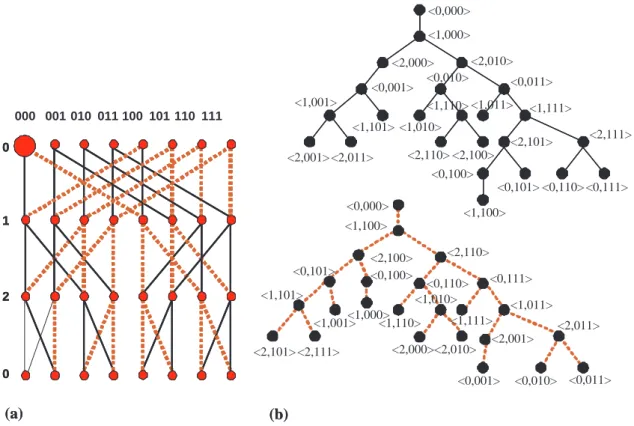
Example 3. In Figure 4, we depict two edge-disjoint

(5)

0 2 1 0 0 2 1 0 0 2 1 0 000 001002 010 011 012 020 021022 100 101 102 110 111112 120 121 122 200 201 202 210 211 212 220 221222 <0,000> <0,111> <0,222>

Figure 3. Three edge-disjoint undirected spanning trees of BF (3, 3), rooted at h0, 000i, h0, 111i, and

h0, 222i, respectively.

Figure 5, we illustrate three edge-disjoint undirected span-ning trees of BF (3, 3) rooted at h0, 000i.

5. Conclusion

In this paper, we show that every BF (k, n) contains k edge-disjoint rooted spanning trees whose heights do not exceed 2n + 1, provided k ≥ 2 and n ≥ 2. Our result has applications to multicast communication in wormhole-routed parallel systems.

References

[1] B. Barden, R. L. Hadas, J. Davis, and W. Williams, “On edge-disjoint spanning trees in hypercubes,”

In-formation Processing Letters vol. 70, pp. 13-16, 1999.

[2] J. C. Bermond, E. Darrot, O. Delmas, and S. Perennes, “Hamilton cycle decomposition of the Butterfly net-works,” Parallel Processing Letters vol. 8, pp. 371-385, 1998.

[3] J. A. Bondy and U. S. R. Murty, Graph Theory with

Applications, third ed., North Holland, New York,

1980.

[4] A. W. Fu and S. C. Chau, “Cyclic-cubes: a new family of interconnection networks of even fixed-degrees,”

IEEE Transactions on Parallel and Distributed Sys-tems vol. 9, pp. 1253-1998, 1998.

[5] A. K. Gupta and S. E. Hambrusch, “Embedding complete binary trees into butterfly networks,” IEEE

Transactions on Computers vol. 40, pp. 853-863,

1991.

[6] C. N. Hung, J. J. Wang, T. Y. Sung, and L. H. Hsu, “On the isomorphism between cyclic-cubes and wrapped butterfly networks,” IEEE Transactions on Parallel

and Distributed Systems vol. 11, p. 864, 2000.

[7] S. L. Johnsson and C. T. Ho, “Optimum broadcast-ing and personalized communication in hypercubes,”

IEEE Transactions on Computers vol. 38, pp.

1249-1268, 1989.

[8] F. T. Leighton, Introduction to Parallel Algorithms

and Architecture: Arrays · Trees · Hypercubes,

Mor-gan Kaufman, Los Altos, CA, 1992.

[9] L. Ni and P. McKinley, “A survey of wormhole routing techniques in direct networks,” IEEE Transactions on

Computers vol. 26, pp. 62-76, 1993.

[10] A. Touzene, K. Day, and B. Monien, “Edges-disjoint spanning trees for the generalized butterfly networks and their applications,” Journal of Parallel Distributed

Computing vol. 65, pp. 1384-1396, 2005.

[11] C. H. Tsai, T. Liang, L. H. Hsu, and M. Y. Lin, “Cycle embedding in faulty wrapped butterfly graphs,”

Net-works vol. 42, pp. 85-96, 2003.

[12] S. A. Wong, “Hamilton cycles and paths in butterfly graphs,” Networks vol. 26, pp. 145-150, 1995.

(6)

<0,000> (a) (b) 000 (a) (b) <1,000> <2,000> <2,010> <0,001> <1,001> <2,001> <2,011> <1,101> <0,010> _<0,011> <1,010> <1,110> <1,011> <1,111> <2,110> <2,100> <2,101> <2,111> <0,100> <1,100> <0,101> <0,110> <0,111> <0,000> <1,100> <2,100> <2,110> <0,101> _<0,100> <0,110> <0,111> <1,101> <1,001> <2,101> <2,111> <1,000> <1,110> <1,010> <1,111> <1,011> <2,000><2,010> <2,001> <2,011> <0,001> <0,010> <0,011> 0 2 1 0 0 2 1 0 0 2 1 0 001 010 011 100 101 110 111

Figure 4. Two edge-disjoint undirected spanning trees of BF (2, 3) rooted at h0, 000i.

000 0 2 1 0 0 2 1 0 001 002 010 011 012 020 021 022 100 101 102 110 111 112 120 121 122 200 201 202 210 211 212 220 221 222