注意:
允許學生個人、非營利性的圖書館或公立學校合理使用
本基金會網站所提供之各項試題及其解答。可直接下載
而不須申請。
重版、系統地複製或大量重製這些資料的任何部分,必
須獲得財團法人臺北市九章數學教育基金會的授權許
可。
申請此項授權請電郵
ccmp@seed.net.tw
Notice:
Individual students, nonprofit libraries, or schools are
permitted to make fair use of the papers and its
solutions. Republication, systematic copying, or
multiple reproduction of any part of this material is
permitted only under license from the Chiuchang
Mathematics Foundation.
Requests for such permission should be made by
e-mailing Mr. Wen-Hsien SUN
ccmp@seed.net.tw
2015 UPPER PRIMARY DIVISION FIRST ROUND PAPER
Time allowed:75 minutes
INSTRUCTION AND INFORMATION
GENERAL
1. Do not open the booklet until told to do so by your teacher.
2. No calculators, slide rules, log tables, math stencils, mobile phones or other
calculating aids are permitted. Scribbling paper, graph paper, ruler and compasses are permitted, but are not essential.
3. Diagrams are NOT drawn to scale. They are intended only as aids.
4. There are 20 multiple-choice questions, each with 5 choices. Choose the most reasonable answer. The last 5 questions require whole number answers between 000 and 999 inclusive. The questions generally get harder as you work through the paper. There is no penalty for an incorrect response.
5. This is a mathematics assessment, not a test; do not expect to answer all questions. 6. Read the instructions on the answer sheet carefully. Ensure your name, school
name and school year are filled in. It is your responsibility that the Answer Sheet is correctly coded.
7. When your teacher gives the signal, begin working on the problems.
THE ANSWER SHEET
1. Use only pencils.
2. Record your answers on the reverse side of the Answer Sheet (not on the question paper) by FULLY filling in the circles which correspond to your choices.
3. Your Answer Sheet will be read by a machine. The machine will see all markings even if they are in the wrong places. So please be careful not to doodle or write anything extra on the Answer Sheet. If you want to change an answer or remove any marks, use a plastic eraser and be sure to remove all marks and smudges.
INTEGRITY OF THE COMPETITION
The IMAS reserves the right to re-examine students before deciding whether to grant official status to their scores.
I
2015 UPPER PRIMARY DIVISION FIRST ROUND PAPER
Questions 1-10, 3 marks each
1. Which of the following expression is incorrect?
(A) 29 92 (2 9 )(92) (B) 47 74 (47)(74) (C)36 63 (3 6)(63) (D)56 65 (5 6)(65) (E)38 83 (3 8)(83)
2. Each of P, Q and R writes down an integer greater than 2015. When 2013 is subtracted from P’s number, 2014 is subtracted from Q’s number and 2015 is subtracted from R’s number, the product of the differences is 88407. Which of the following statements is correct?
(A)P’s and Q’s numbers are odd and R’s is even. (B)Q’s and R’s numbers are odd and P’s is even. (C)R’s and P’s numbers are odd and Q’s is even. (D)All three numbers are odd.
(E)Q’s number is odd and R’s and P’s numbers are even. 3. Which of the following figures has area closest to 1?
(A) (B) (C)
(D) (E)
4. The numerator of a fraction is reduced by 25% and the denominator is increased by 25%. By which of the following numbers can we multiply the original fraction to obtain the new fraction?
(A)1 2 (B) 1 4 (C) 3 4 (D) 3 5 (E)1 7 3 3 5 11 10 11 10 3 2 3 5 1 2 1 2 3 2 3 2
5. Sixteen points are arranged in a 3 cm by 3 cm formation. Four of them are removed, leaving behind twelve points as shown in the diagram. If we choose three of these twelve points as vertices of a triangle, what is the largest possible area of this triangle, in cm2 ?
(A)9 (B)9
2 (C)3 (D)2 (E)
3 2
6. From one-third of a positive integer, one-quarter of the next integer is subtracted. If the difference is 2, what is the sum of the two integers?
(A)31 (B)45 (C)55 (D)79 (E)103
7. The diagram below is the seating plan of a cinema. How many blocks of three adjacent seats are unshaded, not counting those in the first row?
1 2 3 4 5 6 7 8 9 10 11 12 (A)15 (B)16 (C)17 (D)18 (E)19
8. In an amusement park, each ride on the Bumper Cars costs 10 dollars, each ride on the Pirate Boat costs 15 dollars and each ride on the Roller Coaster costs 20 dollars. If Waldo spends 110 dollars in total on at least one ride of each kind, how many times has he taken a ride on the Roller Coaster?
(A)1 (B)2 (C)3 (D)4 (E)5
UP 2
Optional Seating Sold Seating
9. The first term of a sequence is 2. Each subsequent term is the remainder when 3 times the preceding term is divided by 5. Thus the second term is 1, the
remainder when 3 2 6 is divided by 5. How many of the first 2015 terms of
this sequence are equal to 1?
(A)403 (B)504 (C)672 (D)1008 (E)2014
10. A cubic box of side length 15 cm has two holes. One of them is 5 cm above and 5 cm to the left of the bottom right corner of the front face. The other is 5 cm below and 5 cm to the left of the top right corner of the right face. The size of the holes and the thickness of the box are negligible. If the box is filled with water and one of its faces rests on a horizontal surface, some water will leak out through the holes. What is the maximum amount, in cm3, of water that can remain inside the box?
(A)1000 (B)1125 (C)1500 (D)2250 (E)3375
Questions 11-20, 4 marks each
11. How many prime numbers less than 50 is 1 more than the product of two distinct prime numbers each less than 50?
(A)2 (B)3 (C)4 (D)5 (E)6
12. Goldie has two identical gold coins and Sylvia has three identical silver coins. The total weight of Goldie’s coins is equal to the total weight of Sylvia’s coins. If they trade one coin with each other, then the total weight of Goldie’s coins is 12 grams less than the total weight of Sylvia’s coins. What is the weight, in grams, of each gold coin?
(A)12 (B)15 (C)18 (D)21 (E)24
13. Jasmine tea sells for 320 dollars per kg while Oolong tea sells for 480 dollars per kg. A mixture consisting of 3 parts of Jasmine tea to 5 parts of Oolong tea sells for 450 dollars per kg. What is the maximum amount, in dollars, for which 10 kg of each of Jasmine tea and Oolong tea may be sold?
(A)8000 (B)8080 (C)8400 (D)8480 (E)9000 UP 3 5cm 5cm 5cm 5cm 15cm
14. Which of the following boxes has a net as shown in the diagram below?
(A) (B) (C) (D) (E)
15. The greatest common divisor of a certain positive integer and 315 is 3, and the least common multiple of the same integer and 45 is 360. What is this integer?
(A)12 (B)24 (C)30 (D)36 (E)48
16. After the fourth test, Kenny’s average mark rises by 5 points, but after the fifth test, it drops by 9 points. If his total score in the last two tests is 122 points, how many points does he score in the last test?
(A)91 (B)71 (C)61 (D)41 (E)31
17. Two paths are to be constructed in a garden 5 m by 5 m and three plans have been submitted. If the amount of space not taken up by the paths is to be as large as possible, which of the following statements is correct?
Plan I Plan II Plan III (A)The non-path area in Plan I is the largest.
(B)The non-path area in Plan II is the largest. (C)The non-path area in Plan III is the largest.
(D)The non-path areas in all three plans are the same. (E)The non-path areas in Plan I and Plan III are the same.
UP 4 1m 1m 5m 5m 1m 1m 1m 1m
18. City B is between City A and City C. William is riding a bike from B to C, a distance of 16 km. After he has gone 6 km, Mary begins to drive a car at 60 km per hour from A to C. If William continues onward, he will reach C at the same time as Mary. If he turns back, he will reach B at the same time as Mary. What is his riding speed, in km per hour?
(A)15 (B)16 (C)18 (D)20 (E)24
19. The eight symbols 2, 0, 1, 5, I, M, A and S are to be arranged in a row. The digits must precede the letters, and 0 cannot be in the first place. How many such arrangements are there?
(A)100 (B)232 (C)400 (D)432 (E)576
20. A hotel has 11 rooms and each staff member has keys to 7 different rooms. For each room, at least two staff members must hold its key. What is the minimum number of staff members the hotel must have?
(A)3 (B)4 (C)5 (D)6 (E)7
Questions 21-25, 6 marks each
21. If the first digit after the decimal point of a number is 4 or less, the number is rounded down, but if it is 5 or more, the number is rounded up. When 4 times a positive integer is divided by 100, the result after rounding is 18. When 9 times the same integer is divided by 100, the result after rounding is 42. What is this integer?
22. The sum of the three digits of a positive integer is 13. When this integer is subtracted from the one obtained by writing its digits in reverse order, the difference is 297. What is the maximum value of this integer?
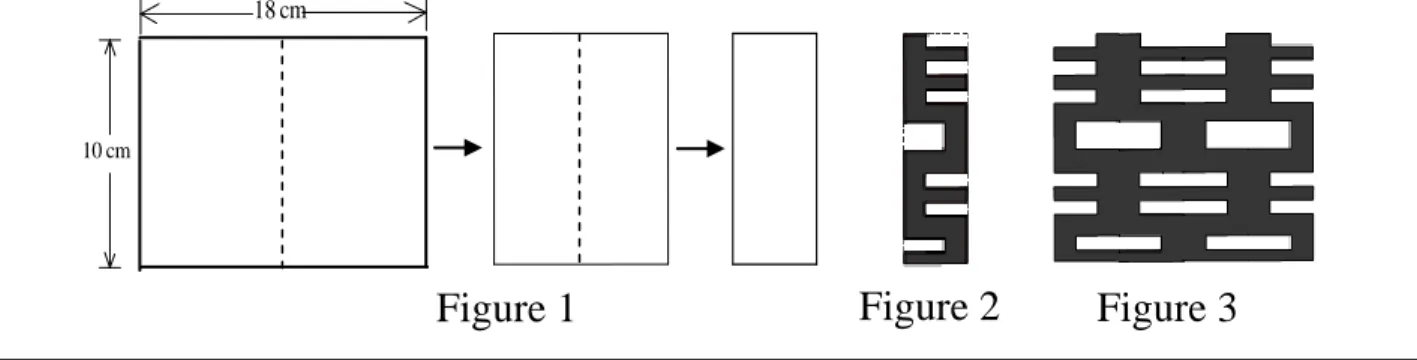
23. A 10 cm by 18 cm piece of paper is folded twice into a 10 cm by 4.5 cm stack of thickness 4, as shown in Figure 1. Eight 1 cm by 3 cm holes, two of which are adjacent, are cut from the stack, as shown in Figure 2. When the stack is unfolded, as shown in Figure 3, what is the area, in cm2, of this piece of punctured paper?
UP 5
18 cm
10 cm
24. The diagram shows a 5 by 5 chessboard and an L-shaped piece which covers exactly 4 squares of the chessboard. It may be rotated or reflected. In how many ways can be it placed on the chessboard covering exactly 4 squares?
25. In an election between three candidates, they are supported respectively by 10, 35 and 15 of the first 60 voters. 40 more votes are to be cast, each for one of the three candidates. In how many ways can the candidate currently with 10 supporters become the uncontested winner?
*** UP 6