The Bipolar Analysis of a Single Sphere in an Electrolytic Cell

(1)

J. Electrochem. Soc., Vol. 138, No. 9, September 1991 9

8. K. A. Mauritz and C. L. Gray, Macromolecules, 16, 1279

(1983).

9. T. Asawa, J. Appl. Electrochem., 19, 566 (1989).

10. D . L . P e e t and J. H. Austin, P a p e r presented at the Chlorine Institute Meeting, Feb. 5, 1986; reprint available from the Du P o n t Company, Wilmington, DE.

11. M. Seko, S. Ogawa, H. Ono, and O. Suzuki, in "Ad- vances in the Chlor-Alkali and Chlorate Industry," M. M. Silver and E. M. Spore, Editors, PV 84-11, pp. 49-72, The E l e c t r o c h e m i c a l Society S o f t b o u n d Pro- ceedings Series, P e n n i n g t o n , N J (1984).

12. W. G. F. Grot, Abstract 894, p. 1258, The Electrochemi- cal Society E x t e n d e d Abstracts, Vol. 87-2, Honolulu, HI, Oct. 18-23 (1987).

13. H . L . Yeager, J . D . Malinsky, and R . L . Dotson, in "Transport Processes in E l e c t r o c h e m i c a l Systems," R . S . Yeo, T. Katan, and D.-T. Chin, Editors, PV 82-10, pp. 215-222, The E l e c t r o c h e m i c a l Society Soft- b o u n d P r o c e e d i n g s Series, Pennington, N J (1982). 14. H . L . Yeager and J. D. Malinsky, U.S. Pat. 4,545,863

(1985).

15. H. L. Yeager and J. D. Malinsky, in " C o u l o m b i c Inter- actions in Macromolecular Systems," A. Eisenberg and F . E . Bailey, Editors, ACS S y m p o s i u m Series

The Electrochemical Society, Inc.

2697

No. 302, Chap. 11, A m e r i c a n Chemical Society (1986).

16. L. I. Krishtalik, Soviet Electrochem., 15, 632 (1979). 17. A. M. Peers, Disc. Faraday Soc., 21, 124 (1956). 18. H. Reiss and I. Bassignana, J. Mem. Sci., 11, 219 (1982). 19. C. W. Carr and K. Sollner, J. Gen. Physiol., 28, 119

(1944).

20. F. Helfferich, " I o n E x c h a n g e , " p. 134, McGraw-Hill, Inc., N e w York (1961).

21. J. T. Keating, Du P o n t Company, U n p u b l i s h e d results. 22. O~ P. Romashin, M. Fioshin, R. Erenburg, E. Ryabov, V. Kubasov, and L. Krishtalik, Soviet Electrochem., 15, 553 (1979).

23. "Nation | 90209 P r o d u c t Bulletin," Du P o n t Company, P o l y m e r P r o d u c t s Department, Wilmington, DE (1988).

24. J . T . Keating, Du P o n t Company, Private c o m m u n i - cation.

25. S. Lengyel, J. Giber, G. Beke, and A. Vertes, Acta Chim. Hung. Acad. Sci., 39, 357 (1963).

26. V. P. Troshin and E. V. Zvyagina, Soviet Electrochem., 8, 1669 (1972).

27. D . A . L o w n and H. R. Thirsk, Trans. Faraday Soc., 67, 132 (1971).

28. I. N. M a k s i m o v a and V. F. Yushkevich, Russ. J. Phys. Chem., 37, 475 (1963).

The Bipolar Analysis of a Single Sphere in an Electrolytic Cell

**Shi-Chern Yen* and Ching-Yih Yao**

Department of Chemical Engineering, National Taiwan University, Taipei, Taiwan, China

A B S T R A C T

The bipolar b e h a v i o r of a single sphere in an electrolytic cell is investigated in this study. A m a t h e m a t i c a l m o d e l is proposed for two surface conditions: linear polarized kinetics and the Butler-Volmer kinetics. Analytical current and potential distributions are obtained for a reversible reaction and linear polarized kinetics. Semianalytical potential and current distributions for the Butler-Volmer kinetics are also obtained by the boundary collocation method. T h e current en- h a n c e m e n t factor is defined as the ratio of the bipolar current to the applied current, and its value is predicted theoretically for linear polarization. The effective conductivity of a dilute dispersion is also formulated and related to the first coefficient D1 of the series e x p r e s s i o n of the potential in a continuous medium. The influences of various parameters, including dimensionless potential drop, * , conductivity ratio of electrolyte to solid phase, a, ratio of e x c h a n g e current density to applied current, B, and transfer coefficients, (~a and ac, are respectively discussed. The suitability of a s s u m i n g linear polarized kinetics is also evaluated by c o m p a r i n g it with the Butler-Volmer kinetics.

When an electric potential is applied across an electro- c o n d u c t i v e object that is isolated b e t w e e n the two current feeders, bipolar behavior m a y occur at the surface of this object, and b o t h anodic and cathodic reactions may occur on one and the other side of its surface, respectively. Bipo- lar b e h a v i o r has b e e n discussed in m a n y fields, w h i c h in- clude the dissolution of nuclear fuel (1), oxide film thick- ness control (2), and organic synthesis (3, 4), etc. In recent years, bipolar particulate electrodes, including packed- bed, trickle-bed, and fluidized bed types, have been broadly investigated (5, 6). The bipolar behavior is also c o n c e r n e d with the charge-transfer m e c h a n i s m in fluidized bed electrodes (7, 8).

In the literature s o m e theoretical models were de- v e l o p e d to predict the dispersion c o n d u c t i v i t y (9-11) or energy c o n s u m p t i o n (1, 4) in particulate bipolar cells. But either constant c u r r e n t density or linear potential distribution on the electrode surface was a s s u m e d in earlier models. As a matter of fact, the current and potential distributions at the electrode surface are n o n u n i f o r m and d e p e n d e n t on the relative electric c o n d u c t i v i t y of the solid and electrolyte phases, the resistance of the electrochemical reactions occurring at the electrode surface, the applied electric field, and the mass transport of the reactants. I f the primary current distribution is considered, the resistance of the e l e c t r o c h e m i c a l reaction and the mass transfer limitation of the reactants can be neglected. The potential distribution of a spherical particle for a reversible reaction

* Electrochemical Society Active Member.

had b e e n solved analytically and was used to estimate the effective c o n d u c t i v i t y of dilute dispersions of spherical particles by Maxwell (11, 12). When the secondary current distribution is relevant, the m a s s 4 r a n s f e r limitation can also be ignored.

Due to the i m p o r t a n c e of the bipolar behavior in some electrolytic cells, f u n d a m e n t a l studies are necessary for a detailed u n d e r s t a n d i n g and for the proper design of bipolar cells. In this paper, a m a t h e m a t i c a l m o d e l for the bipolar behavior on a single sphere is proposed in which the primary and secondary current distributions are considered. The effects of particle size, applied electric field, and solid-phase c o n d u c t i v i t y on the bipolarity of the sphere can be d e d u c e d and estimated exactly according to this model. Analytical solutions have b e e n obtained for cases in w h i c h the e l e c t r o c h e m i c a l reaction is reversible and w h e n dealing with linear polarized kinetics, respectively. The semianalytical solution for the Butler-Volmer kinetics at the surface is also given by using the boundary collocation m e t h o d (13). The c o n s u m p t i o n of electric energy due to the presence of the single sphere in a linear potential field is also formulated. The effective conductivity of a dilute dispersion for linear polarized kinetics or the Butler-Volmer kinetics can be e s t i m a t e d from the con- s u m p t i o n of electrical energy.

Analysis

The schematic diagram of the p r o b l e m considered is de- picted in Fig. 1. T h e potentials in the solid sphere and the electrolyte are described as $~ and (b2, respectively. The

(2)

2698

d. Electrochem. Soc., Vol. 138, No. 9, September 1991 9 The

Electrochemical Society, Inc.

i=

. . .

~:2/~:,

=0.01

. . .

a reversible electroreaction at the surface

Fig. I. A single sphere in an electrical field.

a n d for t h e B u t l e r - V o l m e r e q u a t i o n

{ I

j = i 0 e x p a , . r 1 6 2 n F w h e r e E' is t h e N e r n s t p o t e n t i a l o f t h e reaction, i0 is t h e ex- c h a n g e c u r r e n t d e n s i t y , a~ a n d % are a n o d i c a n d c a t h o d i c t r a n s f e r coefficients, r e s p e c t i v e l y . O n e o f Eq. [5]-[7] represents t h e b o u n d a r y c o n d i t i o n , w h i c h is d e p e n d e n t on t h e r e v e r s i b i l i t y o f t h e e l e c t r o d e r e a c t i o n , a n d Eq. [3]-[4] are t h e o t h e r b o u n d a r y c o n d i t i o n s h o l d i n g for all t h r e e cases.

I n o r d e r to m a k e t h e g o v e r n i n g e q u a t i o n d i m e n s i o n l e s s , t h e f o l l o w i n g d i m e n s i o n l e s s v a r i a b l e s a n d p a r a m e t e r s are d e f i n e d

6,

6~

6o

r

= V '

02 =V'

r -V'

c h a r g e b a l a n c e e q u a t i o n s h o u l d b e satisfied in e a c h phase, a n d i t c a n b e r e p r e s e n t e d b y L a p l a c e ' s e q u a t i o n w i t h s p h e r i c a l c o o r d i n a t e s as f o l l o w s V26I = 0 [1] in w h i c h V262 : 0 [2]

'

- - - - r 2 + - s i n 0 r 2 Or r a sinO OO B e c a u s e o n l y t h e p r i m a r y a n d s e c o n d a r y c u r r e n t distributions are c o n s i d e r e d , t h e m a s s b a l a n c e e q u a t i o n of t h e re- a c t a n t is n o t i n v o l v e d , a n d o n l y o n e e l e c t r o c h e m i c a l reac- t i o n is a s s u m e d to t a k e p l a c e at t h e s p h e r i c a l particle. T h e n t h e b o u n d a r y c o n d i t i o n s a r e e x p r e s s e d as follows: (i) A n e l e c t r i c a l field is a p p l i e d , a n d t h e p o t e n t i a l d i s t r i b u t i o n far f r o m t h e p a r t i c l e s h o u l d m a t c h t h e l i n e a r p o t e n t i a l field; thus, w h e n r --, 62 = - - - r cos0 + 60 [3] K2 w h e r e i= is t h e a p p l i e d c u r r e n t d e n s i t y far f r o m t h e electrode, K2 is t h e e l e c t r i c c o n d u c t i v i t y o f t h e electrolyte, a n d 60 is t h e r e f e r e n c e p o t e n t i a l far f r o m t h e s p h e r e at t h e p l a n e of z = O. (ii) A t t h e c e n t e r o f t h e s p h e r e (r = 0), 61 is finite. (iii) A t t h e i n t e r f a c e b e t w e e n t h e p a r t i c l e a n d t h e e l e c t r o l y t e (r = R), t h e c u r r e n t d e n s i t i e s f r o m t h e t w o p h a s e s s h o u l d b e equal, d u e to t h e flux c o n t i n u i t y . T h u s , at r = R 061 a 6 2 K , - = K 2 - [4] or or w h e r e K1 is t h e e l e c t r i c c o n d u c t i v i t y o f t h e p a r t i c l e a n d R is t h e r a d i u s of t h e s p h e r e . (iv) T h e last b o u n d a r y c o n d i t i o n is c o n c e r n e d w i t h t h e k i n e t i c s t h a t i n v o l v e s t h e e l e c t r o c h e m - ical r e a c t i o n at t h e s p h e r i c a l s u r f a c e (r = R). T h e electro- c h e m i c a l r e a c t i o n is c o n s i d e r e d as o n e of t h e f o l l o w i n g t h r e e cases, a r e v e r s i b l e r e a c t i o n , l i n e a r p o l a r i z e d kinetics, a n d k i n e t i c s d e s c r i b e d b y t h e B u t l e r - V o l m e r e q u a t i o n . T h e c a s e of B u t l e r - V o l m e r k i n e t i c s is r e g a r d e d as a g e n e r a l c a s e for an e l e c t r o d e r e a c t i o n . T h e e l e c t r o d e k i n e t i c s s h o u l d m a t c h t h e e l e c t r i c c u r r e n t at t h e i n t e r f a c e b e t w e e n t h e p a r t i c l e a n d t h e e l e c t r o l y t e . T h e r e f o r e , at r = R, for a re- v e r s i b l e r e a c t i o n 6 1 - - 6 2 = E ' [5] for l i n e a r p o l a r i z e d k i n e t i c s

(

n/_~) - K2 a62 [6] j = i0 (4h - r E') = Or r=R a n d E ' T E = -:-:, ~ - [8] v R K2 io n F = - - , ~ = -:--, t , = V [9] K 1 t~ .~)T w h e r e V = i | 2. T h e p a r a m e t e r ~ r e p r e s e n t s t h e r e l a t i v e e l e c t r i c c o n d u c t i v i t y o f t h e e l e c t r o l y t e to t h e solid electrode, a n d i f a --~ =, t h e s p h e r e c a n b e c o n s i d e r e d as insu- lated; i f a ~ 0, t h e p o t e n t i a l in t h e s p h e r e c a n b e r e g a r d e d as u n i f o r m . T h e p a r a m e t e r 13 is t h e ratio o f e x c h a n g e cur- r e n t d e n s i t y to t h e a p p l i e d c u r r e n t d e n s i t y ; l a r g e r 13 m e a n s t h a t t h e e l e c t r o c h e m i c a l r e a c t i o n t e n d s to a p p r o a c h c o m - p l e t e r e v e r s i b i l i t y . S m a l l e r !3 i n d i c a t e s t h a t t h e e x c h a n g e c u r r e n t d e n s i t y is so r e l a t i v e l y s m a l l t h a t t h e e l e c t r o d e re- a c t i o n t e n d s to b e m o r e irreversible. V is a d i m e n s i o n a l pa- r a m e t e r w h i c h r e p r e s e n t s t h e p o t e n t i a l d r o p s a c r o s s t h e d i s t a n c e of t h e s p h e r e ' s radius, a n d q, is its d i m e n s i o n l e s s p a r a m e t e r . S o t h e g o v e r n i n g e q u a t i o n s a n d b o u n d a r y c o n d i t i o n s can b e e x p r e s s e d in d i m e n s i o n l e s s f o r m as follows V 2 ~ t = 0 [ 1 0 ] V2~P2 = 0 [11] in w h i c h 1 V2 = ~ 0--~ ~ + ~2 sinO oO " T h e d i m e n s i o n l e s s b o u n d a r y c o n d i t i o n s are a t ~ = 0, at ~--~ | 9 1 is finite [12] @2 = - ~ cosO + q5o [13] a t e = 1, 00Pl

06

for a r e v e r s i b l e r e a c t i o n a t ~ = 1, 002 - a [ 1 4 ]

0~

q)t - O2 = E [ 1 5 a ] for l i n e a r p o l a r i z a t i o n f o r ~ = 1, 002

0~

for t h e B u t l e r - V o l m e r k i n e t i c s - - - - ~ I J ( ( l ) l -- ~:)2 -- E ) [ 1 5 b ]

(3)

d. Electrochem. Soc.,

Vol. 138, No. 9, September 1991 9 The Electrochemical Society, Inc. 2699

a t e = 1,

3 0 2

- 13{exp[aa~I'( dp' - ~2 - E)]

- exp[-OtcqffcPl - ~2 - E)]} T h e g e n e r a l s o l u t i o n s for Eq. [10] a n d [11] are

O, = ~ [ A . ~ " P . ( c o s 0 ) + B,,~-I"+i~P.(cos0)] n=0 [16a] 02

= ~ [Cn~npn(COSO) + D . ~ - ~

n=O [16b] w h i c h are t h e Z o n a l H a r m o n i c s (14). T h e f u n c t i o n P,, is a L e g e n d r e p o l y n o m i a l o f d e g r e e n, a n d t h e c o e f f i c i e n t s A,,, B,~, C~, a n d D~ a r e to b e d e t e r m i n e d a c c o r d i n g to t h e b o u n d a r y c o n d i t i o n s . S u b s t i t u t i n g Eq. [12]-[14] into Eq. [16a, b] g i v e s t h e f o l l o w i n g e q u a t i o n s

@,

= ~ A.~"P,,(cos0) r = r = (P0 - ~ cos0 + ~ Dn~-('+~>P,,(cos0) [17b] in w h i c h A0 a n d {D,,} are u n k n o w n , a n d by u s e of c u r r e n t c o n t i n u i t y , {An} for n -> 1 c a n b e r e l a t e d to AI = - a(1 + 2D1) A , = - ~ ( ~ n - ~ ) D n , f o r n - > 2 [18] T h e n t h e s o l u t i o n s for v a r i o u s s u r f a c e c o n d i t i o n s c a n b e o b t a i n e d r e s p e c t i v e l y f r o m Eq. [17a, b] a n d Eq. [15a, b, c].

A n a l y t i c a l solution f o r linear p o l a r i z a t i o n . - - T h e p o t e n -

tial d i s t r i b u t i o n in e a c h p h a s e for t h e c a s e o f l i n e a r polarization, c a n b e o b t a i n e d b y s u b s t i t u t i n g Eq. [15b] into Eq. [17a, b] 3a ~Pl = ~o + E ~ cos0 [19a] 1 + 2 ~ + 2~/

l - a - ~ /

c o s 0 9 2 = cP0 - ~ c o s 0 + [ 1 9 b ] 1 + 2 a + 2 ~ ~2 in w h i c h ~/= 1/13~t '. E q u a t i o n s [19a, b] a r e i d e n t i c a l to t h o s e o b t a i n e d b y M a x w e l l (11), as t h e e l e c t r o d e r e a c t i o n ap- p r o a c h e s c o m p l e t e r e v e r s i b i l i t y , ~---> 0. It s h o u l d b e no- t i c e d t h a t t h e s p h e r e still has a n i n f l u e n c e on t h e p o t e n t i a l d i s t r i b u t i o n e v e n in t h e c a s e o f a = 1, a n d this is c a u s e d by t h e r e s i s t a n c e o f t h e e l e c t r o c h e m i c a l r e a c t i o n at t h e surface. T h e c u r r e n t d i s t r i b u t i o n at t h e s u r f a c e of t h e s p h e r e for t h e l i n e a r p o l a r i z e d k i n e t i c s c a n be d e r i v e d f r o m t h e p o t e n t i a l d i s t r i b u t i o n a n d e x p r e s s e d as in 3 i| 1 + 2 a + 2 ~ cos0 Solutions f o r the B u t l e r - V o l m e r k i n e t i c s . - - T h e p o t e n t i a l d i s t r i b u t i o n s for t h e t w o cases m e n t i o n e d p r e v i o u s l y c a n b e s o l v e d in a n a l y t i c a l form. But, for t h e c a s e of con- s i d e r i n g t h e B u t l e r - V o l m e r k i n e t i c s , t h e coefficients A0 a n d D , in Eq. [17a, b] a n d [18] m a y n o t b e s o l u b l e analytically d u e to t h e n o n l i n e a r i t y o f t h e b o u n d a r y c o n d i t i o n in Eq. [15c]. T h e b o u n d a r y c o l l o c a t i o n m e t h o d is s u g g e s t e d for o b t a i n i n g t h e s e m i a n a l y t i c a l s o l u t i o n s in this case. S u b s t i t u t i n g Eq. [17b] i n t o Eq. [15c] g i v e s

•

+ 1 ) D ~ P n ( c o s 0 ) = ~ { e x p [ a a ~ ( d P i - dP2 - E)]

(

n

n = l

- exp[-ac~U(qh - ~2 - E)]}GI - cos0

B y s e l e c t i n g N points, {0i}, at t h e b o u n d a r y to satisfy t h e a b o v e e q u a t i o n , a set o f n o n l i n e a r a l g e b r a i c e q u a t i o n s for D~ c a n b e o b t a i n e d a n d e x p r e s s e d as N - I (n + 1)D~Pn(xi) = ~{exp[aa~}(xi] [15c] ,,_, - e x p [ - a c ~ ( x i ) ] } - xi i = 1 . . . . N [22] in w h i c h xi = cos0i, a n d 9 l(xi) = qbl - r - E = (A0 - dP0 - E) + (1 + a ) x i - ~ 1 + c~ D,,P,,(Xi) n = l n w h e r e (Ao - Oo - E) in t h e a b o v e e q u a t i o n is r e g a r d e d as an u n k n o w n in t h e c a l c u l a t i o n , a n d Ao c a n b e o b t a i n e d after (P0 a n d E are specified. T h e r e f o r e Eq. [22] c a n b e s o l v e d nu- m e r i c a l l y b y t h e N e w t o n - R a p h s o n m e t h o d , a n d t h e N col- l o c a t i o n p o i n t s are c h o s e n w i t h e q u a l d i v i s i o n for 0, in a [17a] r a n g e of 0 to ~r. C o n v e r g e n c e is r e a c h e d w h e n N is large e n o u g h to m a k e t h e c o n s e c u t i v e e r r o r less t h a n l0 -6. T h e c u r r e n t d i s t r i b u t i o n at t h e s u r f a c e o f t h e s p h e r e for t h e B u t l e r - V o l m e r k i n e t i c s is g i v e n b y in N- 1 - cos0 + ~ (1 + n)D.P.(cosO) [23] i . . . . 1

T h e r e in c a n b e c a l c u l a t e d b y Eq. [23] if t h e set of D . has b e e n f i g u r e d o u t b y s o l v i n g Eq. [22].

Results and Discussion

T h e s o l u t i o n s for all t h r e e cases satisfy t h e f o l l o w i n g in- t e g r a l c o n s t r a i n t (13) a u t o m a t i c a l l y

f

fsphere i,flA = 0 a n d t h u s t h e a n o d i c a n d c a t h o d i c c u r r e n t s are b a l a n c e d . I n c i t e d l i t e r a t u r e (5) t h e i n t e g r a l c o n s t r a i n t is an e x t r a c o n d i - tion, w h i c h has b e e n u s e d to d e t e r m i n e t h e p o t e n t i a l in t h e solid p h a s e , w h e r e a u n i f o r m p o t e n t i a l in t h e solid p h a s e is a s s u m e d . C u r r e n t e n h a n c e m e n t f a c t o r . - - T h e c u r r e n t e n h a n c e -

m e n t factor, fE, is d e f i n e d as t h e ratio o f t h e c u r r e n t p a s s i n g t h r o u g h t h e s p h e r e to t h e c u r r e n t p a s s i n g t h r o u g h t h e s a m e c r o s s - s e c t i o n a r e a w i t h o u t it. So it c a n be e x p r e s s e d a s I fE - . [24] z| 2 in w h i c h fc [ r -./2 2

I = 2~r i,,R 2 sin0 dO ~=2rr | i,,R

athode \ d0

[20] sin0 dO, for s y m m e t r i c eases, ~a = ~c) W h e n fE > 1, t h e s p h e r e is c u r r e n t a t t r a c t i v e , i.e., t h e cur- r e n t p a s s i n g t h r o u g h t h e s p h e r e is i n c r e a s e d d u e to its p r e s e n c e . T h e e n h a n c e m e n t f a c t o r for a r e v e r s i b l e reaction, ~/= 0, is g i v e n b y Eq. [24] a n d [20] as 3 fE - [25] l + 2 a It is o b v i o u s t h a t t h e m a x i m u m f~ is 3, w h e n a ~ 0. T h e en- h a n c e m e n t f a c t o r fE iS s m a l l e r t h a n 1 for a > 1. T h e s p h e r e is r e g a r d e d as an i n s u l a t o r as f~ o 0, for ~ o oo. W i t h o u t c o n s i d e r i n g t h e r e a c t i o n r e s i s t a n c e , t h e c u r r e n t p a s s i n g t h r o u g h t h e s p h e r e is d e t e r m i n e d b y t h e r e l a t i v e electric c o n d u c t i v i t y b e t w e e n t h e solid a n d e l e c t r o l y t e p h a s e s [21] only.

(4)

2 7 0 0

J. Electrochem. Soc.,

V o l . 138, N o . 9, S e p t e m b e r 1991 9 T h e E l e c t r o c h e m i c a l Society, Inc.

T h e c u r r e n t e n h a n c e m e n t f a c t o r for l i n e a r p o l a r i z e d ki- n e t i c s is also o b t a i n e d b y s u b s t i t u t i n g Eq. [20] into [24]

3 1 f~ - ; ~t - [26] 1 + 2~ + 2~/ 6'1 ~" E q u a t i o n [26] is t h e s a m e as Eq. [25] i f ~ / ~ 0, w h i c h corre- s p o n d s to a r e v e r s i b l e r e a c t i o n . A s c a n b e s e e n in Eq. [26], t h e p a r a m e t e r ~ r e d u c e s t h e f~ v a l u e , b e c a u s e t h e resis- t a n c e of t h e i n t e r f a c i a l e l e c t r o d e r e a c t i o n h a s b e e n in- v o l v e d in t h i s case. T h e c r i t e r i o n for f s > 1 is g i v e n f r o m Eq. [26] b y ~/+ ~ < 1 [27] in w h i c h ~ a n d a r e p r e s e n t t h e r e l a t i v e r e s i s t a n c e s o f t h e e l e c t r o d e r e a c t i o n a n d e l e c t r i c c o n d u c t i o n in t h e solid p h a s e to e l e c t r i c c o n d u c t i o n in t h e e l e c t r o l y t e phase, re- s p e c t i v e l y . B e c a u s e t h e e l e c t r i c c u r r e n t will c h o o s e a p a t h w i t h s m a l l e r r e s i s t a n c e , t h e p a t h t h r o u g h t h e s p h e r e will b e f a v o r e d if t h e c o m b i n e d r e s i s t a n c e of t h e e l e c t r o d e reac- t i o n a n d e l e c t r i c c o n d u c t i o n in t h e s p h e r e is s m a l l e r t h a n t h a t in t h e electrolyte. T h e e n h a n c e m e n t f a c t o r for B u t l e r - V o l m e r k i n e t i c s c a n b e c a l c u l a t e d b y t h e f o l l o w i n g e q u a t i o n , after D , v a l u e s are o b t a i n e d N-] l + n f ~ = 2 ~ ~=~ 1 + 2n [P,-~(Xc) - P,+~(xr + 1 - x~ [28]

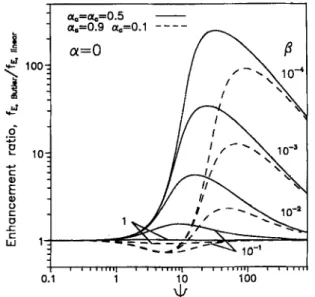
w h e r e xc = cosec, a n d 0c is t h e a n g l e o f t h e interfacial posi- t i o n w i t h i , = 0. 8r is c a l c u l a t e d b y s o l v i n g E q . [23] w i t h i~ = 0. F o r s y m m e t r i c a l t r a n s f e r coefficients ~ a n d ec, O~ is 90 ~ a n d t h e n x~ = 0. T h e e n h a n c e m e n t f a c t o r for t h e B u t l e r - V o l m e r k i n e t i c s is s h o w n in t h e f o l l o w i n g figures. T h e e f f e c t o f p a r a m e t e r q~ at v a r i o u s 13 on t h e e n h a n c e m e n t factor, fE, w i t h er = 0, is s h o w n in Fig. 2. It is o b s e r v e d t h a t f E is an i n c r e a s i n g func- t i o n of q~, a n d a l i m i t i n g v a l u e o f f E = 3 is o b t a i n e d if 9 is sufficiently large. T h e m a x i m u m v a l u e o f f E is t h e s a m e as t h a t f r o m t h e r e v e r s i b l e r e a c t i o n c o n d i t i o n , Eq. [25]. A s y m - m e t r i c a l oL a a n d ~ will d e c r e a s e fE, e s p e c i a l l y w h e n 13 is small. W h e n 13 is sufficiently large, t h e i n f l u e n c e of ~a a n d ec is d i m i n i s h e d . I n t h e c a s e o f s y m m e t r i c a l t r a n s f e r coefficients, ~ = a t = 0.5, b o t h a n o d i c a n d c a t h o d i c r e a c t i o n s h a v e t h e s a m e r e s i s t a n c e . B u t , if~o is less t h a n ~ , t h e resis- t a n c e of t h e c a t h o d i c r e a c t i o n is i n c r e a s e d so t h a t fE is de- creased. T h e p a r a m e t e r 13 is t h e ratio o f t h e e x c h a n g e cur- r e n t d e n s i t y i0 to t h e a p p l i e d c u r r e n t d e n s i t y i~; w h e n 13 is sufficiently large, t h e e l e c t r o d e r e a c t i o n will a p p r o a c h lin- e a r p o l a r i z e d or r e v e r s i b l e k i n e t i c s . I n t h e c a s e of l i n e a r po-

j

0 =.==o=O.S

3.0 ] = . . . ao=0.9 a:=0.1 /~ / / #

s~ 1

. ~ 1,0 10 -3

" 4

/

_1 /

_ . / . . / / j , ; ,

o . o = , . . . 0.1 1 10 100 a~ a==0.9 a==0.1 . . . . , ~ 1 o o l O -

.g

E lO

r " LU 1 -- -- ~_, ~-.-- ~ F ; . _ - , . . ~ 10_, i , i i i i ' i i I , i I I l l l l I i I i I I J H I I I i i i i 0.1 1 10 100

Fig. 3. The current enhancement foctor ratio of the Butler-Volmer ki- netics over the linear polarized kinetics.

larized k i n e t i c s , t h e effects o f a s y m m e t r i c a l t r a n s f e r coefficients will d i s a p p e a r , as s e e n in Eq. [t5b].

A c o m p a r i s o n o f f ~ b e t w e e n t h e B u t i e r - V o l m e r a n d lin- e a r p o l a r i z e d k i n e t i c s at v a r i o u s 13 a n d q~ is s h o w n in Fig. 3. W h e n t h e e n h a n c e m e n t ratio, fs.ButleJfmi ... is e q u a l to 1, t h e s a m e fE v a l u e is p r e d i c t e d b y e i t h e r t h e B u t l e r - V o l m e r k i n e t i c s or l i n e a r k i n e t i c s , a n d l i n e a r p o l a r i z e d k i n e t i c s is a s s u m e d r e a s o n a b l e in this situation. It is o b s e r v e d t h a t t h e e n h a n c e m e n t ratio is a p p r o x i m a t e l y e q u a l to 1 for < 1 o v e r t h e w h o l e r a n g e o f 13. W h e n q' is sufficiently large, t h e m a j o r r e s i s t a n c e will b e in t h e e l e c t r o l y t e so t h a t t h e e n h a n c e m e n t ratio o f t h e B u t l e r - V o l m e r k i n e t i c s o v e r t h e l i n e a r k i n e t i c s is e x p e c t e d to a p p r o a c h 1. T h e r e is a m a x i m u m o f t h e e n h a n c e m e n t ratio w h e n 9 is in t h e r a n g e o f 1-100. T h e e n h a n c e m e n t ratio is s m a l l e r as 13 is in- creased, a n d it is close to 1 for t h e w h o l e r a n g e o f ~ w i t h t3 = 1 as w e l l as oL a = 0L c. F o r a s y m m e t r i c a l t r a n s f e r coeffi-

c i e n t s (~a # ~c), t h e e n h a n c e m e n t ratio is a p p a r e n t l y re- d u c e d a n d a m i n i m u m v a l u e is also o b s e r v e d w h i l e 13 < 10 -z.

Current d i s t r i b u t i o n on the spherical s u r f a c e . - - T h e cur-

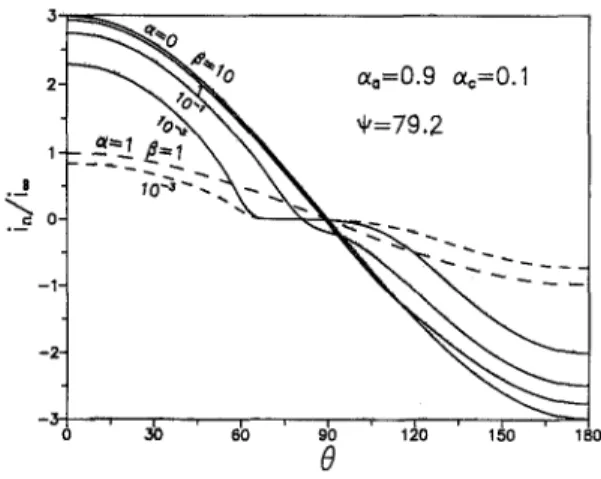
r e n t d i s t r i b u t i o n o n t h e s p h e r e w i t h c~a = ~c is s h o w n in Fig. 4. It is o b s e r v e d t h a t h i g h e r ~ gives h i g h e r b i p o l a r current, b u t t h e b i p o l a r c u r r e n t is d e c r e a s e d as ~ increases. N o n u n i f o r m c u r r e n t d i s t r i b u t i o n is o b t a i n e d , a n d t h e cur- r e n t d e n s i t y p a s s i n g t h r o u g h t h e s p h e r e m a y b e s m a l l e r t h a n i| at a p a r t of t h e surface, a l t h o u g h t h e fE is g r e a t e r t h a n t. T h e m a x i m u m c u r r e n t d e n s i t y o c c u r s w h e n e is e q u a l to 0 a n d 180 ~ a n d a z e r o c u r r e n t o c c u r s at e = 90 ~ W h e n ~3 = 10 -3, a n i n a c t i v e r e g i o n a p p e a r s a r o u n d 8 = 90% It s h o u l d b e n o t i c e d in Eq. [25] a n d [26] a n d E q . [20] t h a t t h e 3 ~ . . ~ . ~ = o #=Io -~ ._ ~ ' - J 0(==0.5, a~=0.5 -1- ,.1,=79.2 - 2 - - 3 _3b 9'0 do 1~o '~ "1 for Fig. 2. The effects of 9 on the enhancement factor, fE, at various I 3 Fig. 4. Current distribution at the electrode surface

(5)

J. Elevtrochem. Soc.,

Vol. 138, No. 9, S e p t e m b e r 1991 9 The Electrochemical Society, Inc. 2701

~ ~ 0 "

2 - ~ ~ ~o =0"9 ao =0"1

3b sb 9b so

8

Fig. 5. The same as Fig. 4 except mo = 0.9 and m~ = 0.1

1,4" 1'2 1.0 .._8 0.8 O.S 014 0'2 0.0 1 '0 0~,~=0.9 o~r I,'=79.2 ' \ ' ' , ~=1 .8=10 -~

~ j = l o ' - ' . . .

'.5

1 2 . ~ I 2. ~ I ~. S ' ~.5 I #. 0

~'=r/R

Fig. 7. The same as Fig. 6 except mo = 0.9 and m~ = 0.1.

m a g n i t u d e o f t h e m a x i m u m c u r r e n t d e n s i t y o c c u r r i n g at t h e s u r f a c e is e q u a l to its c u r r e n t e n h a n c e m e n t factor, fE, a n d t h e c u r r e n t v a r i a t i o n w i t h e is e q u a l to m u l t i p l y i n g fE b y cos0 directly, for t h e r e v e r s i b l e r e a c t i o n a n d t h e l i n e a r k i n e t i c s , r e s p e c t i v e l y . A l m o s t no c u r r e n t p a s s e s t h r o u g h t h e s p h e r e w h e n I ' is sufficiently small. T h e c u r r e n t distri- b u t i o n o n t h e s p h e r e w i t h a s y m m e t r i c a l t r a n s f e r coeffi- c i e n t s (m~ # me) is s h o w n in Fig. 5. T h e a s y m m e t r i c a l cur- r e n t d i s t r i b u t i o n is o b s e r v e d as 13 is d e c r e a s i n g , a n d t h e a r e a for t h e a n o d i c r e a c t i o n is s m a l l e r t h a n for t h e c a t h o d i c r e a c t i o n d u e to m~ > me. T h e i n a c t i v e r e g i o n still e x i s t s for 13 = 10 -3, b u t it g r a d u a l l y d i s a p p e a r s as 6 is increasing. W h e n 13 is s u f f i c i e n t l y large, a s y m m e t r i c a l d i s t r i b u t i o n c a n also b e o b s e r v e d , a n d t h e s a m e r e s u l t s are o b t a i n e d w i t h 13 < 1, w h e t h e r m a a n d e~ is s y m m e t r i c or not.

Current distribution at the plane o f z = & - - T h e c u r r e n t d i s t r i b u t i o n at t h e p l a n e of z = 0 has b e e n c a l c u l a t e d a n d is s h o w n in Fig. 6. W h e n ( >- 2.5, t h e p r e s e n c e o f t h e s p h e r i c a l p a r t i c l e offers a l m o s t n o influence. F o r t h e c a s e of m = 1 a n d 13 = 10, t h e p a r t i c l e has a b s o l u t e l y no e f f e c t on t h e electric field. T h i s is b e c a u s e for t h e c a s e of 13 = 10 a n d = 79.2, t h e r e s i s t a n c e o f t h e s u r f a c e r e a c t i o n c a n b e ne- g l e c t e d , a n d t h e r e s i s t a n c e of e l e c t r i c a l c o n d u c t i o n in b o t h t h e solid a n d t h e e l e c t r o l y t e p h a s e s is t h e s a m e for m = 1. Thus, a l i n e a r e l e c t r i c field is still m a i n t a i n e d a n d is n o t d i s t u r b e d b y t h e s p h e r e . T h e r e are t w o t y p i c a l k i n d s of curves. O n e is c u r r e n t - a t t r a c t i v e , in w h i c h fE is g r e a t e r t h a n 1, a n d t h e c u r r e n t gets s m a l l e r t h e c l o s e r o n e s gets to t h e p a r t i c l e surface; t h e o t h e r o n e is c u r r e n t - r e p u l s i v e , in w h i c h fE is less t h a n 1, a n d t h e c u r r e n t gets h i g h e r as o n e gets c l o s e r to t h e s p h e r e . It is n o t i c e d t h a t for s m a l l e r 6, t h e s p h e r e is m o r e r e p u l s i v e to c u r r e n t , o w i n g to t h e i n c r e a s e o f t h e r e s i s t a n c e o f t h e s u r f a c e r e a c t i o n . It is also o b s e r v e d s p e c i a l l y in Fig. 6 t h a t for m = 0 a n d 13 = 10 -3, c u r r e n t density has b e e n s l i g h t l y e n l a r g e d n e a r t h e s p h e r i c a l surface, a l t h o u g h f s is g r e a t e r t h a n 1 in this case. It c a n be ex- p l a i n e d b y c o m p a r i n g w i t h Fig. 4 t h a t t h e i n a c t i v e r e g i o n 1 . 4 - 1.2 1.0 8 0.8 0 . 6 - ~=0/~ ao=0.5, ao=0.5 / / / 0.4- / / / 0 . 2 - 0 . 0 L 0 /~=10 -3 . . . /~=10 1.~ ' 2 . b ' 2 . ~ ' 3 . b ' 3 . ~ ' , . 0

~=r/R

Fig. 6. Current distribution at the plane of z = 0 (0 = 90 ~ for Oto= m c = 0.5. o c c u r s n e a r t h e t o p o f t h e s p h e r e (0 = 90~ a n d t h e c u r r e n t is to b e r e p u l s e d n e a r t h e i n a c t i v e region, so t h a t t h e cur- r e n t b y p a s s e s t h e s p h e r e t h r o u g h t h e e l e c t r o l y t e phase. T h e c u r r e n t d i s t r i b u t i o n at p l a n e of z = 0 w i t h a s y m m e t r i - cal aa a n d m e is s h o w n in Fig. 7. T h e e f f e c t o f a s y m m e t r i c a l t r a n s f e r c o e f f i c i e n t s is d i m i n i s h e d as 13 increases, d u e to t h e a p p r o a c h o f l i n e a r p o l a r i z e d k i n e t i c s . C o m p a r i n g it w i t h t h e r e s u l t s f r o m s y m m e t r i c a l t r a n s f e r coefficients, t h e c u r r e n t p a s s i n g t h r o u g h t h e p l a n e o f z = 0 is higher, i.e., w h e r e m o r e c u r r e n t is r e p u l s e d b y t h e s p h e r e o w i n g to t h e h i g h e r r e a c t i o n r e s i s t a n c e p r o d u c e d b y t h e a s y m m e t r i c a l t r a n s f e r coefficients. As [3 is d e c r e a s e d , t h e c u r r e n t n e a r t h e e l e c t r o d e s u r f a c e is i n c r e a s e d ; for a = 1, c u r r e n t n e a r t h e s p h e r e is a l w a y s l a r g e r t h a n i , , w h e t h e r ~a a n d mc are s y m m e t r i c a l or not. It is also o b s e r v e d t h a t w h e n m = 0 a n d = 10 -3, t h e c u r r e n t b e c o m e s l a r g e r t h a n i| n e a r t h e s p h e r e , a l t h o u g h fE is g r e a t e r t h a n 1 in this case. As m e n - tioned, an i n a c t i v e r e g i o n o b s e r v e d at t h e e l e c t r o d e s u r f a c e a r o u n d 0 = 90 ~ m a y e x p l a i n t h i s p h e n o m e n o n .

Effective conductivity o f a dilute dispersion.--The differ- e n c e o f e l e c t r i c p o w e r c o n s u m p t i o n in t h e w h o l e d o m a i n b e t w e e n t h e p r e s e n c e o f a s i n g l e s p h e r e a n d its a b s e n c e in a l i n e a r p o t e n t i a l field is e x p r e s s e d as ~ p o w e r c o n s u m p t i o n } Q = ( i n s i d e t h e p a r t i c l e J + [ p o w e r c o n s u m p t i o n } + / p o w e r c o n s u m p t i o n } L o u t s i d e t h e p a r t i c l e ) [ at i n t e r f a c e ] _ I p o w e r c o n s u m p t i o n in t h e w h o l e d o m a i n / ( w i t h t h e s a m e c u r r e n t d e n s i t y ] A f t e r r a t h e r c o m p l i c a t e d m a t h e m a t i c a l o p e r a t i o n s w h i c h i n c l u d e a p p l y i n g t h e G a u s s d i v e r g e n c e t h e o r e m a n d G r e e n ' s t h e o r e m , t h e e n e r g y d i f f e r e n c e Q c a n be r e l a t e d to t h e first c o e f f i c i e n t D, of t h e series e x p r e s s i o n of t h e p o t e n - tial ~P2 in t h e c o n t i n u o u s m e d i u m ( 4 ~ R s Q = \ 3K~ i ~ ) . D ~ [29] F o r l i n e a r polarization, a c c o r d i n g to Eq. [17b] a n d [19b], t h e e n e r g y d i f f e r e n c e Q is ( 4~R3 i 2 t 1 -- ~ -- `/) [30] Q = \ 3K 2 ~// 1 + 2~ + 2-/ T h e e f f e c t i v e c o n d u c t i v i t y o f a d i l u t e d i s p e r s i o n c a n be r e l a t e d to t h e b i p o l a r a n a l y s i s o f a s i n g l e s p h e r e in a l i n e a r p o t e n t i a l field b y r e g a r d i n g t h e d i s p e r s i o n i t s e l f as an i m a g i n a r y s p h e r e of r a d i u s S w i t h an e f f e c t i v e c o n d u c t i v - ity Ke in a c o n t i n u o u s m e d i u m o f c o n d u c t i v i t y K2 a n d a re- v e r s i b l e e l e c t r o c h e m i c a l r e a c t i o n at interface. B y s e t t i n g t h e e n e r g y c o n s u m p t i o n d u e to t h e p r e s e n c e o f t h e imagi- n a r y s p h e r e o f r a d i u s S in t h e s a m e l i n e a r p o t e n t i a l field

(6)

2 7 0 2

J. Electrochem. Soc.,

V o l . 138, N o . 9, S e p t e m b e r 1991 9 T h e E l e c t r o c h e m i c a l Society, Inc. 1.0 0.5 D~

0.0

-0.5 10 -~ 10 s . . . . linear kinetics C~=0 - - Butler-Volmer kinetics

a

1

10 -1

10 -2

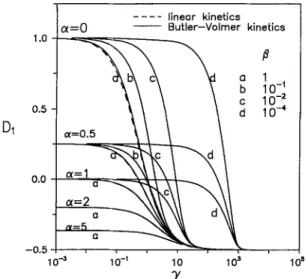
10-* 1 0 -1 1 0 1 0 ~ 7

Fig. 8. The first coefficient D 1 vs. the kinetic parameter ~ for various

c~ and 13.

equal to that obtained due to the presence of the spherical particle of radius R with c o n d u c t i v i t y KI, the following re- lation is obtained f r o m Eq. [29]

(

4~R3i2 ] . D 1 = ( 4~S3

,3K2 =/ \ 3K2 i~) "D,~ [31]

Conclusion

Analytical current and potential distributions have been obtained for a reversible reaction and a linear polarized kinetics, respectively. S e m i a n a l y t i c a | potential and current distributions for the Butler-Volmer kinetics are also obtained by the b o u n d a r y collocation method. By comparing the results b e t w e e n the Butler-Volmer kinetics and the linear polarized kinetics or reversible reaction, it is con- eluded that the surface reaction can be regarded as show- ing linear polarized kinetics for ~ - 1, and the linear kinetics is a good a s s u m p t i o n for 6 < 1, if 9 < 1. When ~ is sufficiently large, the major resistance will be in the electrolyte so that the e n h a n c e m e n t ratio of the Butler-Volmer kinetics over the linear kinetics will approach unity. F o r a s y m m e t r i c a l transfer coefficients (a~ ~ ~c), fE is reduced, e x c e p t that the linear polarized kinetics is approached. N o n u n i f o r m current distribution on the sphere is obtained, and its m a x i m u m v a l u e is at 0 = 0 or 180 ~ F o r the linear polarized kinetics, the current variation with 0 is the same as w o u l d be obtained by m u l t i p l y i n g fE by cos0 directly. F o r ~ ~ ~c, a s y m m e t r i c a l current distribution is obtained, and it b e c o m e s s y m m e t r i c a l w h e n the linear polarized kinetics is approached. The potential field in the electrolyte is disturbed by the sphere within a distance of 2.5 times the sphere's radius. The effective conductivity of dilute dispersions has also b e e n formulated from the results of the bipolar analysis of a single sphere in a linear potential field. It is related to the first coefficient Dt of the series e x p r e s s i o n of the potential r w h i c h is obtained analytically for linear polarization and numerically for the Butler-Volmer kinetics.

w h e r e

1 -- Ote K 2

DI~ = - - O~ e -- [32]

1 + 2(~'

K~

Let f be the v o l u m e fraction o f the dispersed phase, t h e n

By inserting Eq. [32] into Eq. [31] and using Eq. [33], the first coefficient D~ can be related to the effective conductivity Ke by the following e x p r e s s i o n

1 - o/. e KefK2 - 1

Dd ~ = D~ - - - - - - [34] l + 2 a ~ KJK2+2

Because the first coefficient D, of the series expression of the potential r is figured out analytically for linear polar- i z a t i o n or n u m e r i c a l l y for Butler-Volmer kinetics, the effective c o n d u c t i v i t y can be c o m p u t e d with the k n o w n vol- u m e fraction f of the dispersed phase. T h e first coefficient D~ vs. ~ for various ~ and [3 is shown in Fig. 8. As shown in Fig. 8, two a s y m p t o t i c values o f D~ are observed while ~ is approaching infinity as well as zero, respectively, in w h i c h the asymptotic D, can be calculated directly from the results of linear polarization. By rearranging Eq. [34], it can be c o n c l u d e d that the ratio KJK2 is greater than 1 if D1 > 0, and the p r e s e n c e of the dispersion is beneficial to electric c o n d u c t i o n in the electrolyte phase. On the contrary, for D, < 0, K~/K~ is smaller than 1, and the dispersion is an ob- stacle to electric c o n d u c t i o n in the electrolyte phase.

F o r linear polarization, Eq. [34] b e c o m e s

)

K~/K2- 1

1 - - a - - ~ /

f =

[35]

1 + 2 ~ + 2 ~ KJK 2 + 2

w h e r e ~ = K2/K1 and ~/ = 1/l~. As the electrochemical reaction approaches c o m p l e t e reversibility, ~ -~ 0; t h e n Eq. [35] is r e d u c e d to

Ke]K -- 1~ KJK2- 1

~ / f = K~/K2 +---~ [36] w h i c h is identical to that obtained by Maxwell (11, 12).

E f F io i= in j N n Q r R .4 Acknowledgment

This w o r k was s u p p o r t e d by the National Science Coun- cil, Taiwan, R e p u b l i c of China, u n d e r Contract No. NSC79- 0410-E002-60.

Manuscript s u b m i t t e d Dec. 3, 1990; revised m a n u s c r i p t received March 12, 1991.

National T a i w a n University assisted in meeting the pub- lication costs of this article.

L I S T OF S Y M B O L S English characters

Am, B~, C,,, D,, coefficients in Eq. [16a, b]

E' Nernst potential o f a reversible reaction, V

dimensionless Nernst potential, defined as E' /V

v o l u m e fraction of dispersion Faraday constant, 96,500 C/equiv. e x c h a n g e current density, A/m 2 applied current density, A/m 2

local current density at the surface of the sphere, A/m 2

local Faraday current density, expressed by Eq. [7]

n u m b e r of the collocation points selected n u m b e r of charge transfer in an electro- c h e m i c a l reaction

difference of p o w e r c o n s u m p t i o n arising from the presence of sphere, J/s

spatial variable in radial direction, m radius of the sphere, m

gas constant

S radius of an imaginary sphere, m

T temperature, K

V potential drop across h a l f t h e sphere,

i| V

xi local position at the spheric surface, defined as cos0i

xc the position w h e r e i,, = 0 at the spheric surface, defined as cOS0c

z spatial variable in the axial direction, m Greek characters

dimensionless parameter, K1/K~, defined by Eq. [9]

a~, ac anodic and cathodic transfer coefficients ~ dimensionless parameter, KJKI

(7)

J. Electrochem. Soc., Vol. 138, No. 9, September 1991 9 The Electrochemical Society, Inc.

2703

~q 0 0~ K! K2 K e

61

62

60

O~, 02, Oo q,

dimensionless parameter, idi| defined b y EQ. [9]

dimensionless parameter, 1 / ~

dimensionless surface overpotential, 01 - ~2 - E

spatial variable i n the circumferential direction, radian

the angle where iv, = 0 at the spheric surface, radian

the angle of the b o u n d a r y collocation points, radian

electric conductivity in solid phase, (~m) -z

electric conductivity in electrolyte phase, (~m) -~

effective electric eonductivity, (~m)- dimensionless radial position, r/R potential in solid phase, V potential in electrolyte phase, V

reference potential at the plane of z = 0 far from the sphere, V

dimensionless potential of 6L, 62, 60, defined by Eq. [8]

dimensionless parameter defined by Eq. [9]

R E F E R E N C E S

1. M. A. Hartland a n d A. J. M. Spencer, Trans. Inst. Chem. Eng., 41, 328 (1963).

2. P. R. N a d e b a u m a n d T. Z. Fahidy, Electrochim. Acta,

20, 715 (1975).

3. C. J. H. King, K. Lister, a n d R. E. Plimley, Trans. Inst. Chem. Eng., 53, 20 (1975).

4. F. Goodridge, C. J. H. King, a n d A. R. Wright, Electro- chim. Acta, 22, 347 (1977).

5. R. Alkire, This Journal, 120, 900 (1973).

6. K. Kusakable, S. Morooka, and Y. Kato, J. Chem. Eng. Jpn., 15, 45 (1982).

7. B. J. Sabacky a n d J. W. Evans, MetalL Trans., 8B, 5 (1977).

8. J. K. Lee, L. W. Shemilt, a n d H. S. Chun, J. Appl. Elec- trochem., 19, 877 (1989).

9. D. C. Eardley, D. Handley, a n d S. P. S. Andrew, Elec- trochim. Acta, 18, 839 (1973).

10. K. Kusakabe, S. Morooka, a n d Y. Kato, J. Chem. Eng. Jpn., 19, 43 (1986).

11. J. C. Maxwell, "Electricity a n d Magnetism," Vol. 1, 3rd ed., p. 8, Oxford (1892).

12. R. E. Meredith a n d C. W. Tobias, "Advances in Electro- chemistry a n d Electrochemical Engineering," Vol. 2, Chap. 2, J o h n Wiley a n d Sons, Inc., New York (1962).

13. M. J. G l u c k m a n , R. Pfeffer, and S. Weinbaum, J. Fluid Mech., 50, 705 (1971).

14. P. M. Morse a n d H. Feshbach, "Methods of Theoretical Physics," p. 124, McGraw-Hill Co., New York (1978). 15. P. S. F e d k i w a n d M. A. Bogard, This Journal, 135, 1726

(1988).

Experimental Approach to the Impedance

Spectroscopy Technique

G. Chiodelli

C.S.T.E.-C.N.R., Dipartimento di Chimica Fisica, Universita di Pavia, 27100 Pavia, Italy

P. Lupotto

S.E.A. Laboratoria, 13020 Pila, VC, Italy

ABSTRACT

The performances of commercially available frequency response analyzers, currently used in electrochemical impedance spectroscopy, have been improved by two methods. The first approach concerns the m a n a g e m e n t of the data acquisition and correction b y m e a n s of an interactive graphic program. Moreover, a new software is described, allowing the ex- p a n s i o n b y two orders of m a g n i t u d e the i m p e d a n c e range of the instrument. The second way consists in a homemade, high-impedance adaptor (10121~, 3 pF) with a guard circuit driver, that increases the sensitivity o f t h e analyzer. Thus, the electrical behavior of materials with high impedance m o d u l u s can be investigated.

A m o n g the various e x p e r i m e n t a l t e c h n i q u e s currently adopted in electrochemistry, i m p e d a n c e spectroscopy (IS) has proved to be a valuable research tool t h a n k s to its sensitivity a n d to the wide variety of possible applications, as it was foreseen by Bauerte (1) in his early work.

Three classes of i n s t r u m e n t s are principally used in electrochemical i m p e d a n c e spectroscopy: multifrequency bridges, lock-in amplifiers, a n d frequency response analyzers (FRA).

I n recent years, great efforts were devoted to data analysis, to conversion of i m p e d a n c e plots in m e a n i n g f u l infor- m a t i o n through suitable models of equivalent circuits (2, 3), to parameter extractions with n o n l i n e a r least squares fit (NLLF) programs (4, 5), a n d to graphic displays with different formalisms (6). I n particular, availability of more powerful personal computers has allowed the design of n e w software for routine analysis of data (4, 5, 7).

On the other side, there is a great need of e x p a n d i n g the i n p u t i m p e d a n c e of the commercial apparatus by means of an improved hardware system which can be defined as an " i m p e d a n c e adaptor" (7-9). A n interesting goal of this possible d e v e l o p m e n t is the characterization of low conductivity samples, viz. ceramic oxides based electrolytes (10-13) at t e m p e r a t u r e s lower t h a n 300~

I n this paper, a software program that manages the data acquisition a n d the interactive graphic display in real time is presented. In t h e section o n D a t a acquisition, treatment, a n d g r a p h i c display a flow-chart d i a g r a m will b e discussed. S e v e r a l routines for the correction of data f r o m the parasitic e l e m e n t effects are also illustrated. M o r e o v e r , a n e w device, the a b o v e m e n t i o n e d i m p e d a n c e a d a p t o r is described, a n d its circuit a n d applications in different fields are s h o w n .

Experimental

Theory o f the m e a s u r e m e n t s . - - A p e r t u r b a t i n g sinusoidal signal E = E0 sin (cot) at frequency F (co = 2~rF) is applied to the u n k n o w n sample, a n d the response is analyzed by a correlator in terms of the resulting current I = I0 sin (~ot + ~), where ~p represents the phase angle shift.

The corresponding complex impedance, obtained by varying the signal p u l s a t i o n co, is expressed by the dis- p l a c e m e n t of the vector ~ (co) with its parameters, the m o d u l u s Zo = Eo/Io and the phase angle ~ (polar coordinates) or with the real a n d imaginary values of the impedance (cartesian coordinates), as shown in Fig. 1.

As an example, in Fig. 2 a simple equivalent circuit of an electrochemical cell, a resistance in parallel with a capaci-