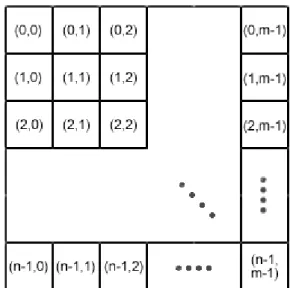
2 for an n ×m board used in this paper. The coordinates of the squares in the first row
全文
數據

相關文件
Write the following problem on the board: “What is the area of the largest rectangle that can be inscribed in a circle of radius 4?” Have one half of the class try to solve this
The function f (m, n) is introduced as the minimum number of lolis required in a loli field problem. We also obtained a detailed specific result of some numbers and the upper bound of
You are given the wavelength and total energy of a light pulse and asked to find the number of photons it
Reading Task 6: Genre Structure and Language Features. • Now let’s look at how language features (e.g. sentence patterns) are connected to the structure
Teachers may consider the school’s aims and conditions or even the language environment to select the most appropriate approach according to students’ need and ability; or develop
Now, nearly all of the current flows through wire S since it has a much lower resistance than the light bulb. The light bulb does not glow because the current flowing through it
Wang, Solving pseudomonotone variational inequalities and pseudocon- vex optimization problems using the projection neural network, IEEE Transactions on Neural Networks 17
volume suppressed mass: (TeV) 2 /M P ∼ 10 −4 eV → mm range can be experimentally tested for any number of extra dimensions - Light U(1) gauge bosons: no derivative couplings. =>