河川彎道中潛板系統最佳設置之研究

國立宜蘭大學土木工程學系 (研究所) 碩士論文

Department of Civil Engineering National Ilan University

Master Thesis

河川彎道中潛板系統最佳設置之研究

Optimal Configuration of a River Submerged Vane System

指導教授：歐 陽 慧 濤博士 Huei-Tau Ouyang Ph. D.

研究生：盧 志 晃 Chin-Huang Lu

中 華 民 國 九 十 五 年 六 月

摘要

潛沒式導流板系統是河川護岸工法的一種，其原理係利用一序列設置 在河川底床上的導流板，在彎曲渠道中產生反二次流，以消減河川二次流 之方式達到保護凹岸之效果。潛板系統之效果優劣與否與潛板之數量、尺 寸、設置位置等有關，其中潛板系統設置位置與成本較無直接關連，本研 究將針對此項進行最佳化分析，即是在現有資源下，將潛板系統之護岸效 果發揮至最大。

本研究使用定量流下之動量方程式與水流、沈滓之連續方程，求得河 川二次流產生之底床剪力，並以潛板理論推算潛板系統對河川底床造成之 剪力，將二者疊加後計算底床坡度，進而求得底床床形，並以此模式對潛 板系統設置位置進行最佳化分析，結果顯示，潛板系統最佳設置位置與河 川之曲寬比及寬深比有相當密切之關係，文中最後將潛板系統之最佳設置 位置依潛板數量、河川之曲寬比及寬深比展繪於圖，提供設計潛板系統時 的參考依據。

英文摘要

ABSTRACT

Submerged vane system is one technique for river bank protection.

By installing several flow training facilities on river bed, the secondary current responsible for the erosion at the bank is reduced. The performance of a submerged vane system is related to the vane size, flow condition, amount of vane and the configuration of the vane system upon all the factors that affect the function of a vane system, the vanes’ configuration is less cost-related. This thesis aims to study the optimal configuration of a vane system.

The bed shear stress induced by the secondary current in a bend flow is derived by using the continuity equation, momentum equation of the flow, and the continuity equation of the bed material. The vane-induced bed shear stress is obtained by using vane theory. The bed profile is determined by relating the bed shear stress and the bed slope. Optimal configuration of a vane system is investigated by utilizing the developed model. The results show that the optimal configuration of a vane system is closely related to the curvature-to-width ratio and width-to-depth ratio of the channel.

Several design charts associated with various flow and vane conditions are also provided for the design of a vane system.

河川彎道中潛板系統最佳設置之研究

本文目錄

摘要 ... I 英文摘要 ...II 本文目錄 ... III 表目錄 ... VI 圖目錄 ...VII 符號表 ... IX

第一章 緒 論 ...1

1-1 前言 ...1

1-2 文獻回顧 ... 2

1-2-1 彎道理論相關論文之回顧 ... 2

1-2-2 潛板理論相關論文之回顧 ... 3

1-3 研究目的 ...4

1-4 研究方法 ...4

1-5 本文結構... 4

第二章 潛板系統作用下之彎道床形 ...6

2-1 彎道理論 ...6

2-1-1 控制方程式 ... 6

2-1-2 尺度分析 ... 7

2-1-3 深度平均 ... 8

2-1-4 流速剖面描述 ... 9

2-1-5 沈滓推估 ... 13

2-1-6 完全發展之彎道流場 ... 14

2-1-7 方程式之無因次化 ... 15

2-2 潛板理論 ...16

2-2-1 單一潛板 ... 16

2-2-2 潛板系統 ... 19

2-2-3 凹岸邊界 ... 25

2-3 床形模式 ...28

第三章 彎道潛板系統數值模式 ...31

3-1 數值方法 ...31

3-2 模式參數設定 ...31

3-3 鏡像數量分析 ...33

3-3-1 垂直鏡像數量分析 ... 34

3-3-2 水平鏡像數量分析 ... 34

3-4 模式驗證 ...34

第四章 彎道潛板系統之設置最佳化流程 ...37

4-1 彎道潛板系統之最佳化目標... 37

4-2 彎道潛板系統之特性與最佳化程序... 38

第五章 結果與討論 ...41

5-1 模式參數對潛板系統最佳設置位置之影響 ...41

5-1-1 潛板設置角度 ... 42

5-1-2 潛板長度與水深之比 ... 42

5-1-3 潛板高度與水深之比 ... 43

5-1-4 沈滓福祿數 ... 44

5-1-5 彎道曲率半徑與河寬之比 ... 44

5-1-6 渠道寬度與水深之比 ... 45

5-1-7 潛板數量 ... 46

5-2 潛板系統最佳設置位置 ...47

5-3 潛板系統之效果與效率分析 ...49

5-3-1 潛板設置角度之影響 ... 50

5-3-2 沈滓福祿數之影響 ... 51

5-3-3 渠道寬深比之影響 ... 51

5-3-4 渠道曲寬比之影響 ... 52

5-3-5 潛板長深比之影響 ... 53

5-3-6 潛板高深比之影響 ... 53

第六章 結論與建議 ...55

6-2 建議 ...56 參考文獻 ...57

表目錄

表 3-1、IIHR動床試驗實測資料...59

圖目錄

圖 1-1、潛沒式導流板示意圖...60

圖 1-2、研究流程圖...61

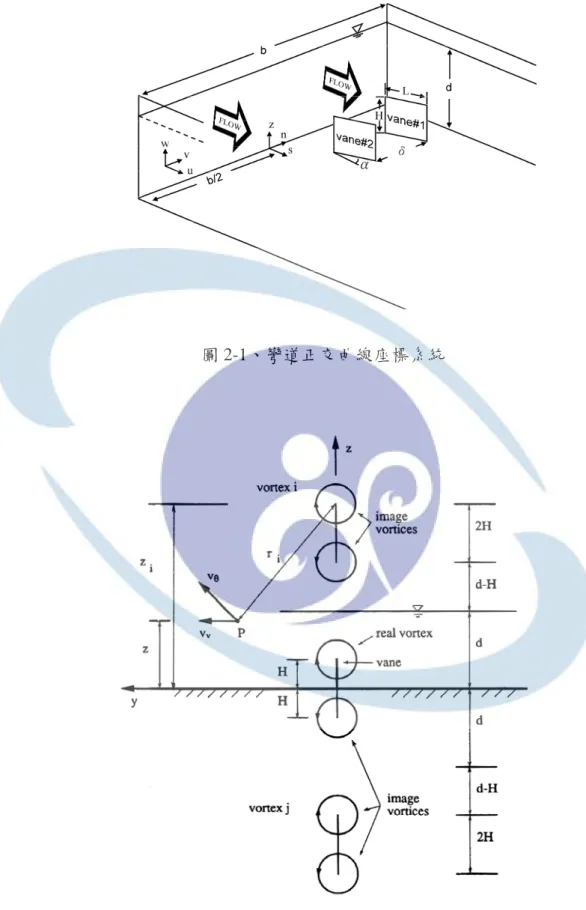
圖 2-1、彎道正交曲線座標系統...62

圖 2-2、潛板及其水面底床鏡像(摘自WANG,1991)... 62

圖 2-3、2 號板之尾跡渦流對 1 號板所產生之下沖流速...63

圖 2-4、2 號板之範束渦流對 1 號板所產生之下沖流速...63

圖 2-5、潛板實體與凹岸之鏡像示意圖...64

圖 3-1、垂直鏡像數量分析...65

圖 3-2、水平鏡像數量分析...65

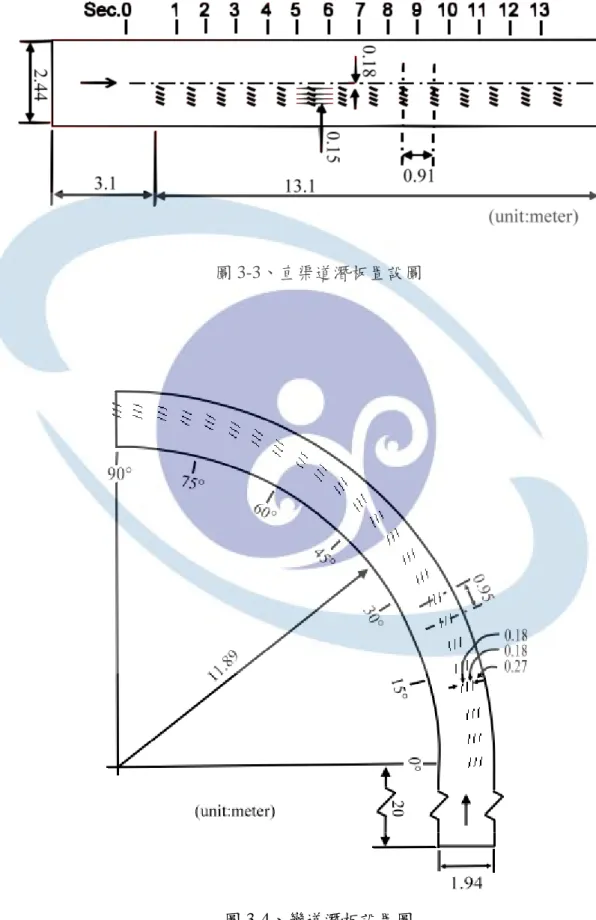
圖 3-3、直渠道潛板置設圖...66

圖 3-4、彎道潛板設置圖...66

圖 3-5、直渠道中 4 潛板系統引致之斷面床形...67

圖 3-6、彎導之斷面床形...67

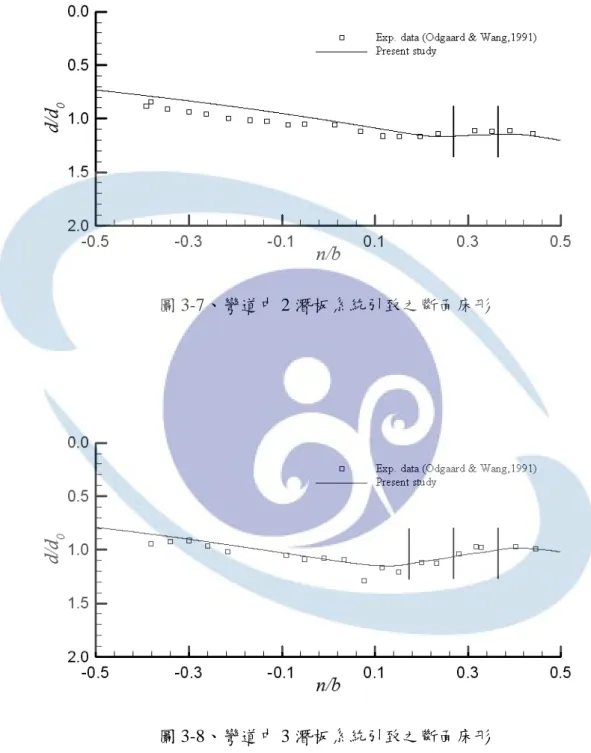
圖 3-7、彎道中 2 潛板系統引致之斷面床形...68

圖 3-8、彎道中 3 潛板系統引致之斷面床形...68

圖 4-1、潛板系統之最佳化流程圖...69

圖 5-1、不同α之單一潛板設置位置對凹岸水深之影響...70

圖 5-2、不同L/ d₀之單一潛板設置位置對凹岸水深之影響 ...70

圖 5-3、不同H / d₀之單一潛板設置位置對凹岸水深之影響 ...71

圖 5-4、不同F_p之單一潛板設置位置對凹岸水深之影響...71

圖 5-5、不同r_c/b之單一潛板設置位置對凹岸水深之影響 ...72

圖 5-6、不同b/ d₀之單一潛板設置位置對凹岸水深之影響...72

圖 5-7、潛板數量對潛板最佳位置之影響...74

圖 5-8(A)、單潛板系統最佳設置位置(b/ d₀=10.0) ... 75

圖 5-8(B)、雙潛板系統最佳設置位置(b/ d₀=10.0) ... 75

圖 5-8(C)、三潛板系統最佳設置位置(b/ d₀=10.0) ... 76

圖 5-8(D)、四潛板系統最佳設置位置(b/ d₀=10.0) ... 76

圖 5-9(A)、單潛板系統最佳設置位置(b/ d₀=20.0) ... 77

圖 5-9(B)、雙潛板系統最佳設置位置(b/ d₀=20.0) ... 77

圖 5-9(C)、三潛板系統最佳設置位置(b/ d₀=20.0) ... 78

圖 5-9(D)、四潛板系統最佳設置位置(b/ d₀=20.0) ... 78

圖 5-10(A)、單潛板系統最佳設置位置(b/ d₀=30.0) ... 79

圖 5-10(B)、雙潛板系統最佳設置位置(b/ d₀=30.0) ... 79

圖 5-10(C)、三潛板系統最佳設置位置(b/ d₀=30.0) ... 80

圖 5-10(D)、四潛板系統最佳設置位置(b/ d₀=30.0) ... 80

圖 5-11(A)、單潛板系統最佳設置位置(b/ d₀=40.0) ... 81

圖 5-11(B)、雙潛板系統最佳設置位置(b/ d₀=40.0) ... 81

圖 5-11(C)、三潛板系統最佳設置位置(b/ d₀=40.0) ... 82

圖 5-11(D)、四潛板系統最佳設置位置(b/ d₀=40.0) ... 82

圖 5-12(A)、單潛板系統最佳設置位置(b/ d₀=50.0) ... 83

圖 5-12(B)、雙潛板系統最佳設置位置(b/ d₀=50.0) ... 83

圖 5-12(C)、三潛板系統最佳設置位置(b/ d₀=50.0) ... 84

圖 5-12(D)、四潛板系統最佳設置位置(b/ d₀=50.0) ... 84

圖 5-13、各種潛板系統在不同設置角度時之效果與效率圖...85

圖 5-14、各種潛板系統在不同沈滓福祿數時之效果與效率圖...85

圖 5-15、各種潛板系統在不同寬深比時之效果與效率圖...87

圖 5-16、各種潛板系統在不同曲寬比之效果與效率圖...87

圖 5-17、各種潛板系統在不同長深比之效果與效率圖...88

圖 5-18、各種潛板系統在不同高深比之效果與效率圖...88

符號表

A~

：H~ ×L~單位化之單片潛板面積

B：與 Coulomb 動摩擦係數及底床升力及阻力比有關 b ：彎道平均河寬(m)

C ：Chezy 係數

C ：阻力係數 D

C ：升力係數 L

D：沈滓之中值粒徑(m) d ：水深(m)

d ：起始水深(0 m) d~

：d/ d₀

d ：河川二次流所產生之水深( m ) m

E：尺度因子

f ：Darcy-Weisbach 摩擦係數

F ：阻力 D

F ：升力 L

F ：沈滓福祿數 P

) , ,

(F_s F_n F_z ：分別為 s ， 及n z方向的應力項(N m²) g ：重力加速度(m s² )

) ,

(g_s g_n ：分別為 s 及 方向上每單位寬度的河床載體積流率(n m³ s) H ：潛板高度(m)

H ：起始潛板高度(0 m) H~

：H / d₀

k ： s 方向之水深平均流速與近底床流速之比值 L：潛板長度(m)

L~

：L/ d₀ l~

：最佳化過程之迭代步幅 m ：縱向流速剖面指數 N ：徑向潛板個數 p ：壓力( N )

r：彎道中任一點的曲率半徑(m)

r ：彎道中心線之曲率半徑( m ) c

r ：距漩渦中心之距離(d m) )

,

(r_i r_j ：P點距漩渦i及 j中心之距離(m)

S ： s 方向之水面坡降 s

S ： n 方向之水面報降 r

s ：沿主流方向之距離( m ) d

U ：潛板平均入流速度(m s)

u ：剪力速度 *

u ：平均主流流速(0 m s)

u： s 方向之水深平均流速(m s) u~ ：u / u₀

) , ,

(u v w ：在(s,n,z)方向之流速(m s) )

,

(u_b v_b ：分別為 與 方向之近底床流速(s n m s) v： 方向之水深平均流速(n m s)

'

vb：近底床之二次流強度 v ：漩渦切線速度(θ m s) v~ ：v/ u₀

w ：下沖流速(m s)

z ：底床高程( m ) b

z ：水面高程( m ) s

) ,

(z_i z_j ：河床面距漩渦i及 j中心之垂直距離(m) α：潛板之設置角度

Δ：沈滓之浸沒比重

δb：潛板至凹岸距離(m) δ^~b：δ_b/b

δn：潛板間之徑向距離( m )

ε ：渦流黏滯係數

Γ：範束渦流之環流量(m² s)

Γ ：翼中央處之環流量(c m² s) )

,

(τ_s τ_n ：分別為 s 及 方向之剪力(n N ) )

,

(τ_bs τ_bn ：分別為 s 及 方向之底床剪力(n N ) )

,

(τ_vs τ_vn ：分別為潛板產生之 s 及 n 方向底床剪力( N ) θ：臨界 Shields 剪力( N )

ρ：水體密度(kg m³)

ρs：沈滓密度(kg m³) λ：潛板交互作用因子

κ：von Karman 係數，約為 0.4 η：n / b

μ：潛板形狀因子

第一章 緒 論

1-1 前言

天然河川對河床及河岸材料有侵蝕、搬運與堆積之現象，此三種現象 皆與河川流場有關，河川流場對底床提供與流速相同方向之剪力，此剪力 若大於底床材料本身自重力與材料間之互制力時，材料將向合力方向位 移。河川之運移現象可分為縱向運移(河川中心線方向)與側向運移(垂直於 縱向與重力向)，縱向運移是材料從上游向下游移動，主要與河川縱向坡度 有關，若欲降低此向運移效果，可改變河床縱向坡度或設置消能設施；側 向運移是材料由河川一側向另一側移動，主要發生在河川彎道，彎道離心 力與流體黏性產生隨水深變化之側向速度；河岸在提供向心力時產生一水 壓力差，兩者作用下將產生一渦流，即河川二次流。就河川底床而言，將 有一向曲率中心之側向速度對底床材料進行運移，若欲降低此向運移效 果，可設置潛板系統或對岸邊築堤。

一直以來成本、效率、使用期限都是土木工程的主要考量，而在人類 利益為主要考量時，卻往往乎略了對生態環境的破壞。直到近年來長期累 積的傷害一一顯現，生態環境保護的觀念才被加以重視。站在河川生態環 境保護的觀點，於處理河川彎道所造成之凹岸侵蝕時，若以設置潛板系統 的方式加以改善，將是相當理想的作法。因其不須在河岸構築任何覆面或 大型的水工結構物，僅須在河川底床上設置潛沒式導流板(submerged vane,

圖 1-1)，即可減低河川二次流對河岸所造成的侵蝕，不但可以達到保護河 岸的效果，也可顧及生態環境與整體景觀。潛板系統效果之優劣與否，除 了潛板本身的形狀、大小、角度、數量，河川的速度與水深等因素外，另 一個重要的因素是潛板於河川中所在的位置。指出潛板若離凹岸越遠效果 越差，同時，若兩潛板距離過近則會相互影響，而無法達到原有的效果(Wang, 1991)，本文針對潛板間的交互作用現象進行研究，嘗試找出潛板系統沿一 河道徑向斷面的最佳設置位置。

1-2 文獻回顧

本節針對有關彎道理論與潛板理論之前人研究，分別作一簡要之回顧。

1-2-1 彎道理論相關論文之回顧

有關彎道的研究多在描述彎道流場、渠道床形及沈滓起動能力三個方 面的變化，在動床的情況下，此三者將會相互影響以維持平衡。Zimmermann and Kennedy (1978)於實驗室分別以不同曲率半徑、沈滓粒徑等參數，組合 成四十九組實驗，並以之分析水流及底床沈滓力平衡之關係，而求得彎曲 渠道底床徑向斜率。Odgaard (1981)以河床沈滓粒徑為主要參數，對彎曲渠 道計算其底床床形，並以實驗室及實際河川資料進行驗證，證明沈滓粒徑、

沈滓福祿數與彎曲渠道床形之關聯。Odgaard (1982)以美國 Sacramento 河之 實測資料，推算出彎道水深與深度平均後流速在徑向的關係式。Odgaard

佈。Odgaard (1986)指出彎曲渠道之床形與渠道寬深比、曲寬比、坡度及沈 滓福祿數有密切關聯，並以實驗室及現地資料驗證。Ikeda (1987)對沈滓粒 徑分佈與渠道床形之關係進行研究，並以實驗及實際資料驗證。

1-2-2 潛板理論相關論文之回顧

潛沒式導流板的理論與機翼理論甚為相關，機翼的理論分析可追朔到 1894 年，英國人 Lanchester 所提出之無限翼展機翼(infinite unitary group)升 力之環流量理論與渦旋理論。而在 1901~1910 年間，Kutta 和 Rukefusiji 分 別提出了翼型的環流量和升力理論，並建立升力理論的數學形式，建立了 二維機翼理論，而潛板理論則是將機翼理論應用於河川渠道中。Potapov (1951)最早將導流板應用於明渠中，並對設置潛板後之渠道流場加以研究。

Nicollet (1964)對潛板在穩定流場中所引發渦流之切線流速加以描述。

Odgaard (1983)以美國 Sacramento 河之潛板設置案例資料，對潛板產生之反 二次流效果進行研究。Odgaard (1984)以彎曲渠道完全發展模式，對渠道中 潛板所產生之效果，因主流方向距離增加之衰減進行研究，並以實驗室資 料驗證。Odgaard (1986)對設置角度為 及 、板高為 0.2 至 0.5 倍水深之 潛板，於直渠道中所造成之徑向流速及床形進行模擬，並以實驗資料證實。

Odgaard & Mosconi (1987)以美國 Nishnabotna 河於 1985 年夏天安裝之潛板 系統，對 1986 年春天之實測數據進行護岸能力之研究。Zijlstra (2003)以數 值模式與實驗，研究導流板對河川床形之影響。

10o 15^o

1-3 研究目的

在一般河川之河寬遠大於水深的特性下，單一潛板之影響範圍相當有 限。為增加其效果，通常會以數個潛板組合成潛板系統以增大其影響範圍，

並達到有效降低河川二次流之目的。影響潛板系統成效優劣的因素，除了 潛板本身的形狀、大小、角度、數量，河川的速度與水深外，另一個重要 的因素是潛板於河川中所在的位置。一般而言，為保護河川凹岸所設置之 潛板，其位置多會較靠近凹岸，以加強其效果。但若兩潛板距離過近則會 相互影響，無法達到原有之效率，當兩潛板距離為零時效果將等於單一潛 板(Wang, 1991)，本文之研究目的在發展一套理論模式以推估潛板間的交互 作用現象，並進而嘗試找出一潛板系統於一河川徑向斷面中之最佳設置位 置，使得該潛板系統能發揮最佳之保護河岸效果。

1-4 研究方法

本文以河川水流之三維動量方程式與水流及底床沈滓之連續方程式，

配合潛板理論中對尾跡渦流之速度描述方程式以推算在有潛板作用下之河 川底床之側向床形變化。並以潛板設置位置為變數，使凹岸水深達到最小 為最佳化目標，尋找最佳之潛板系統設置位置，研究流程如圖 1-2 所示。

1-5 本文結構

板系統數值模式、彎道潛板系統之最佳化流程、結果與討論以及結論與建 議等六章，以下為各章節之內容：

第一章 緒論

敘述本文的研究背景、研究目的，並回顧前人之研究，以進一步了解本研 究主題。

第二章 潛板系統作用下之彎道床形

針對彎道與潛板理論之基本假設與數學模式進行整理與推導。

第三章 彎道潛板系統數值模式

本章對本研究所使用之數值方法與彎道及潛板理論模式之結合方式加以敘 述，並對數值計算床形及實測床形進行比較與驗証。

第四章 彎道潛板系統之設置最佳化流程

對彎道潛板系統之特性加以分析，並建立適合於本研究之最佳化程序。

第五章 結果與討論

將對本研究中之重要參數加以探討，並展示潛板系統最佳化之成果。

第六章 結論與建議

總結全文的分析結果，並提出進一步研究之建議，以利後續研究之參考。

第二章 潛板系統作用下之彎道床形

2-1 彎道理論

當河川流經彎道時因離心力與底床剪應力的共同效應，而在徑向(radial direction)有二次流(secondary current)的現象發生，此二次流即為造成河川凹 岸淘刷及凸岸淤積的主要原因。本節將對此河川二次流之數學模式進行理 論的推導與整理。

文中採用彎道正交曲線座標系統，如圖 2-1 所示， 軸延河道中心線且 向下游為正，n軸垂直於 軸且向凹岸為正， 軸平行重力向且向上為正。

s

s z

2-1-1 控制方程式

河川彎道中的穩定流場控制方程式如下(Rozovskii,1957)

Fs

s P E r

uv z w u n v u s u E

u +

∂

− ∂

=

∂ + + ∂

∂ + ∂

∂

∂

ρ

1 (2-1)

Fn

n P r

u z w v n v v s v E

u +

∂

− ∂

=

∂ − + ∂

∂ + ∂

∂

∂

ρ

2 1

(2-2)

Fz

z g P

z w w n v w s w E

u +

∂

− ∂

−

∂ = + ∂

∂ + ∂

∂

∂

ρ

1 (2-3)

河川彎道中水流的質量守恆方程式為

) 0 ( 1

1 =

∂ +∂

∂ + ∂

∂

∂

z w n

rv r s u

E (2-4)

而彎道河床滓的守恆方程式則為

) 0 1 (

1 =

∂ + ∂

∂

∂

n rg r s g E

n

s (2-5)

上述諸式中

r：彎道中任一點的曲率半徑

：渠道中心線之曲率半徑 rc

E：尺度因子(1+n r_c ) P：壓力

ρ：水體之密度 g ：重力加速度

)：分別為 ,

,

(F_s F_n F_z s ， 及n z方向的應力項

：分別為 w

v

u ,, s ， 及n z方向的流速項

， ：分別為

gs g_n s 及 方向上每單位寬度的河床載體積流率 n

2-1-2 尺度分析

天然河川之特性為，河長遠大於河寬b ，河寬b 遠大於水深 ，主流流 速 u >>側向流速

d

v>>重力向流速w。前人的研究顯示在此種情況下，v 的大 小約略與u(d /b)相近，而w的大小則約略與u(d / r)或u(d /b)(d/r)相近 (Rozovskii,1957;Odgaard and Bergs,1988)。因此，上述方程式中，可將尺度

甚小的項次忽略不計，而 s 與 方向之剪力可化簡為 n

F_s z^s

∂

= ∂τ ρ

1 (2-6)

F_n zⁿ

∂

= ∂τ ρ

1 (2-7)

式中τ_s及τ_n分別為 s 與 方向之剪應力。 n (2-3)式則化簡成靜水壓分佈

1 =0

∂ + ∂

z g P

ρ ^(2-8)

同時，由於 方向為靜水壓分佈，z (2-1)及(2-2)式中的壓力項可分別用縱向水 面坡降S_s與徑向水面坡降S_r表示，如下式所示。

z E

gS r

uv z w u n v u s u E

u _{s s}

∂ + ∂

=

∂ + + ∂

∂ + ∂

∂

∂ τ

ρ

1 (2-9)

gS z r

u z w v n v v s v E

u _n

r ∂

+ ∂

=

∂ − + ∂

∂ + ∂

∂

∂ τ

ρ

2 1

(2-10)

2-1-3 深度平均

由於一般河川水流在 方向的變化遠小於 方向與 方向的變化，因此 通常採用深度平均加以簡化，將

z s n

(2-4)，(2-9)及(2-10)三式作水深方向之積 分，並輔以水面及底床之運動邊界條件(kinematic boundary condition)

=0

⎥⎦ =

⎢⎣ ⎤

⎡ −

∂ + ∂

∂

∂

zs

w z n v z s z E

u (2-11)

=0

⎥⎦ =

⎢⎣ ⎤

⎡ −

∂ + ∂

∂

∂

zb

w z n v z s z E

u (2-12)

上二式中z_s，z_b：分別為水面與底床高程 可得深度平均後之運動與連續方程式

) 0 ( ) (

1 + =

∂ +∂

∂

∂

r v d n

d v s

d u

E (2-13)

d E

gS r

v u n

d v v d s

d u u Ed r

v u n v u s u E

u _{s bs}

ρ

−τ

′ = + ′

∂

′

∂ ′

∂ +

′

∂ ′ +

∂ + + ∂

∂

∂ 1 ( ) 1 ( ) 2

(2-14)

gS d r

v v u u n

d v v d s

d v u Ed r

u s v v s v E

u bn

r ρ

−τ

′ =

− ′

′ + ′

∂

′

∂ ′

∂ +

′

∂ ′ +

∂ − + ∂

∂

∂ ² 1 ( ) 1 ( )

(2-15)

上述諸式中 v

u , ：分別為 s 與 方向之水深平均流速 n

：分別為 v

u′, ′ s 與 n 方向之流速與水深平均流速之差

bn bs τ

τ , ：分別為 s 與 方向之底床剪力 n

2-1-4 流速剖面描述

方程式(2-13)，(2-14)與(2-15)可描述 ，d u 及v的縱向與徑向變化。但 經深度平均後，此三式失去表現水深方向變化之能力，須加以適當流速剖

面分析。根據前人的研究，水流在縱向的速度剖面，可用冪次律加以描述，

(Zimmerman & Kennedy, 1978;Falcon & Kennedy, 1983)。

m

d u z m

u = m+1 ( )¹ (2-16)

上式中

：距底床高度 處之流速

u z

m：流速剖面指數

其中流速剖面指數m其可由下式求得

g C f

u

m =κ u =κ =κ

∗

8 (2-17)

上式中

f ：Darcy-Weisbach 摩擦係數

：Chezy 係數 C

κ：von Karman 係數，約為 0.4

：剪力速度(

u* τ_bs ρ )

此速度剖面已被証實可正確吻合量測數據。

徑 向 二 次 流 的 速 度 剖 面 ， 則 可 用 線 性 變 化 描 述 (Rozovskii, 1957;

Kikkawa et al., 1976; Odgaard, 1986) 2 ) (1 2 d

v z v

v = + _b′ − (2-18)

：近底床處 方向之流速與水深平均流速之差

v′b n

假設靠近底床之流速與剪力為同方向(Rozovskii, 1957)，則可得下列關係式

k u v v u

v _b

b b

bs

bn + ′

= τ =

τ

(2-19)

上式中

b：分別為

b v

u , s 與 方向之近底床流速 n

k ： s 方向之水深平均流速與近底床(距底床δ 處)流速之比值 δ 則可由下式估計(Rozovskii,1957)

g C d

κ δ = 442. −

ln (2-20)

剪力速度之定義如下

ρ τ_bs

u_* = (2-21)

將(2-21)代入(2-17)可得底床上 s 方向之剪力

2 2 2

m u

bs

τ = ρκ (2-22)

將(2-16)及(2-18)式代入(2-14)與(2-15)式後，化簡可得

d E

gS r

v u m n

d v u d m

s d u Ed m

m r

v u n v u s v E u

bs s b

b

ρ

−τ

′ =

− +

∂

∂ ′

− +

∂

∂ + +

∂ + + ∂

∂

∂

1 2 ) 2 (

) 1 2 (

1

) ( ) 2 (

1 ²

(2-23)

gS d r

v v r u m

m

n d v v d s

d v u Ed m

r u n v v s v E u

bn r b

b

b b b

ρ

−τ

′ =

− ′ + +

∂

′

∂ ′

∂ +

∂ ′ + +

∂ − + ∂

∂

∂

3 )

2 (

1

) (

3 ) 1 (

) 1 2 (

2 1

(2-24)

將(2-10)式寫成在水面之形式為

s n

r s

s s s s

z z gS z

r u n v v s v E u

=

∂ + ∂

=

∂ − + ∂

∂

∂ τ

ρ

2 1

(2-25)

上式中 m u u_s = m+1

b

s v v

v = − ′

z v

n ∂

= ρε ∂ τ

ε ：渦流黏滯係數； ^m

d z d z z m u

m ¹

* (1 )( )

1

− −

= + κ ε

將(2-25)式整理後可得

v m u

d m

k gS m r

u m m

n v v n

v v n v v s v s v E u m m

bn r

b b b

b

1 2 )

1 ( ) 2

( 1

) ( 2 ) 1 ) (

1 (

2 2

2 2

− + + +

+ =

−

∂

′

∂ ′

∂ +

∂ ′

∂ − + ∂

∂

∂ ′

∂ −

∂ +

κ ρ

τ ^(2-26)

將(2-26)式與(2-24)式相消可得

m uv d m

k

m k m r

v v n d d v v n

v v

n v v s

d v u Ed m

r u m

m

m m

s v E u m m s v E u m

bn b

b b

b b b

b b

b

1 2 )

1 (

) 1 ( 2

3 3

) ( 6 1

) ( ) ( )

1 2 (

1 )

2 (

2 6 2

1 1

2 2

2

2 2

− + +

+

= +

′

− ′

∂

′ ∂

− ′

∂

′

∂ ′ +

∂

∂ ′

∂ −

∂ ′ + +

+ +

− +

∂

∂ ′

− +

∂

∂

κ ρ

τ ^(2-27)

(2-13)，(2-23)及(2-27)三式，為深度平均後之水流質量守恆及 與 方向之運 動方程式。

s n

2-1-5 沈滓推估

(2-5)式中 方向之河床載體積流率 ，可用輸砂公式推估(Simons et al., 1977)

s g_s

uβ

K

g_s = _{s (2-28)}

上式中

β：指數參數，介於 2 到 4 之間

：底床沈滓性質係數 Ks

若考慮河床滓於底床上受力之平衡條件可得(Parker, 1985; Odgaard, 1980a)

n d B gD

g g

bs bs

bn

s n

∂

∂ + Δ

= τ

θρ τ

τ (2-29)

上式中

θ：臨界 Shields 剪應力參數

：沈滓浸沒比重，

Δ Δ =(ρ_s − ρ) ρ

ρs：沈滓密度 ρ：流體密度

D：沈滓中值粒徑

B：Coulomb 摩擦因子，建議採用B=4(Odgaard,1989)

2-1-6 完全發展之彎道流場

本研究係探討彎道中之流場已完全發展的情況，在此種情況下， =0

∂

∂ s 且 v =0，前述之控制方程式(2-23)及(2-27)式可分別化簡為

E gdS_s

bs

τ = ρ (2-30)

r d u m

k m m

m m

k

bn

2

2

2[2 ( 1)]

) 1 )(

1 2

( ρ

τ + +

+

− +

= (2-31)

將(2-28)式代入(2-5)式並加入上述環境條件 =0

∂

∂

s 後可得 ( ) 0

∂ =

∂ n rg_n

，其中

，因此可知完全發展時之側向河床載體積流率為零。將 rc

r

n = − g_n =0及

(2-22)式代入(2-29)式可得

gD bn

B u k

m dn

d

d τ

θ

ρ Δ

− ) =

( (2-32)

此式即為彎道二次流影響下徑向床形之斜率。

Chezy 公式在河寬 b 遠大於水深 d 之條件下可寫為下式

s

s d S

u RS

C u

0 0

0 ≈

= _(2-33)

將(2-17)、(2-22)及(2-23)三式代入(2-30)式中可得下式

0 2 2 0

Ed

u = du _(2-34)

2-1-7 方程式之無因次化

將渠道內之流速以 s 方向之平均流速 無因次化，水深以平均水深 無 因次化，徑向位置以河寬 b 無因次化後，

u0 d₀

(2-31)，(2-32)及(2-34)三式可改寫 為(Odgaard and Wang, 1991)

E u d

~ = ~ ^(2-35)

E d u A v_b

~ ~

~

− 1

′= _(2-36)

vb

d A d

d~ =− ~′

η 2 ^(2-37)

上述諸式中

/ 0

~ u u

u = u₀：s 方向之平均流速

/ 0

~ d d

d = d₀：平均水深

/ 0

~ v u v_b′ =

b

=n / η

rc

d m

k m

m

A_{1 2} m ₂ ⁰

)) 1 ( 2

(

) 1 )(

1 2 (

+ +

+

= + κ

0

2 d

b Bm

F

A k ^p

= Δ

θ κ

(2-37)式為水深在 方向變化，積分此式即可得彎道完全發展區之床形分 佈，如下式所示

n

2 2 1 2

1 [(1 ) 1]}

1

~ { − −

− +

+

= η

c c

r b b

A r A

d (2-38)

2-2 潛板理論

當潛板以一角度設置於流場中時，將會在下游流場中產生一尾跡渦 流，潛板即是利用此渦流消減河川中的二次流，尾跡渦流的強度與入流條 件、潛板尺寸、設置角度等參數皆相關，本節將對其中的關係進行理論推 導。

2-2-1 單一潛板

考慮一潛沒在水面下的導流板，當此導流板受到一沖擊角為α的水流 通過時，將在板身周圍產生一範束渦流，並在板尾處產生一尾跡渦流向下 游延伸，此尾跡渦流因流體黏性而逐漸擴散及衰減。在無邊界流場中，一 渦流所產生之切線速度為(Lamb,1932)

4 )]

exp(

1 2 [

2 d d d

s r U v r

ε π

θ = Γ − − (2-39)

上式中

：距漩渦中心之距離 rd

：沿主流方向之距離 sd

：範束渦流之環流量 Γ

U ：潛板平均入流速度

在福祿數(Froude Number)甚小時，可將水面與底床視為固定邊界(rigid boundary)，應用鏡像法(Method of images)以無限多個渦流模擬此二邊界的 效果，如圖 2-2 所示。流場中任一位置P(s,n,z)之 方向速度可利用重疊定 理(superposition)推得(Odgaard and Wang, 1991)

n

∑

∑

∞

=

+

∞

=

+

− − Γ −

−

− +

− Γ −

−

=

1

1 2 1

1 2

4 )]

exp(

1 2 [ ) 1 (

4 )]

exp(

1 2 [ ) 1 (

j dj

j dj dj

j

i di

i di di

i vn

r z r z

s U r

r z r z

s U v r

ε π

ε π

(2-40)

上式中

：潛板所產生之 方向流速

vvn n

, ：

rdi r_dj P點距渦流 及i j中心之距離 , ：河床面距渦流 及

zi z_j i j中心之垂直距離

根據 Kutta-Joukowskii 理論，環流量Γ與潛板之升力F_L間的關係如下

uH F_L

= ρ

Γ _(2-41)

將z =0與(2-41)式，代入(2-40)式中可得底床處因潛板所產生之 方向流速 如下

n

∑

=

+ − −

= −

1

2 1

4 )]

exp(

1 ) [ 1 (

j dj

j dj dj

j L

vnb r

r z s U r

uH v F

ε

πρ ^(2-42)

假設近底床流速與底床剪力為同一方向(Rozovskii,1957)，則潛板產生之 方 向近床流速所造成之 n 方向底床剪力

n

τvn為

k u

v u

v _vn

b vn

bs

vn = =

τ

τ (2-43)

假設 s 方向入流速度遵循冪次律，則潛板平均入流速度U 為

m H

m

d u H d dz

u z m m U H

1

0

1

) ( )

1 (

1 + =

=

∫

(2-22)、(2-42)及(2-44)三式代入(2-43)式中，可將潛板在 向方產生之底床剪 力

n

τvn寫成

v L

vn = F ⋅ f

τ _(2-45)

上式中

∑

=

+ − −

= −

1

2 1

2 2

4 )]

exp(

1 ) [ 1 (

j dj

j dj dj

j

a

v r

r z s U r

u u H m f k

ε π

κ (2-46)

依同原理，潛板在底床所產生之 s 方向剪力τ_vs可寫成 f

F ⋅

τ = _(2-47)

而升力F_L及阻力F_D可由下式求得(Odgaard & Mosconi, 1987)

∫

= _L ^H

L c L u dz

F 0

2

2

1 ρ (2-48)

∫

= _D ^H

D c L u dz

F 0

2

2

1 ρ (2-49)

上二式中

：潛板長 L

：升力係數，

CL

H C_L L

= + 1

2πα

：阻力係數，

CD ²

2 1

L

D C

H C L

= π

將流速以冪次律分佈代入(2-48)及(2-49)式中，則潛板之升力與阻力可寫為

m L

L d

H m

m u m HL C

F ²

2

2 ( )

) 2 (

) 1 ( 2

1

+

= ρ + _(2-50)

L L D

D F

C

F =C (2-51)

將(2-50)及(2-51)二式分別代入(2-45)和(2-47)二式中，即可求得潛板所產生 之 s 與 方向底床剪力。 n

2-2-2 潛板系統

前節的理論推導，是針對單一潛板在無其它潛板的干擾下的情況，但 對潛板系統而言，由於各潛板間的交互作用，導致各潛板的環流強度不一，

無法直接以前節公式推廣，須另行推導。

考慮一對沿河道斷面排列之潛板所組成的潛板系統，其中各潛板的編 號由凹岸向凸岸依序排列，如圖 2-1 所示，在交互作用的影響下，此二潛板 產生的環流量分別為

) (

) (

2 2 2

2

1 1 1

1

U LU w

U LU w

−

= Γ

−

= Γ

α π

α π

(2-52)

上式中

, ₂：分別為交互作用下 1 號及 2 號潛板所受到之下沖流速(downwash velocity)

w w1

：分別為 1 號及 2 號潛板之板前流速

2 1

1

,U U

1 號板所受到的下沖流速w 可依據其來源分解成如下分量

"

12 '

12 11

1 w w w

w = + + _(2-53)

上式中

：1 號板的尾跡渦流所產生之下沖流速 w11

：2 號板的尾跡渦流所產生之下沖流速

'

w12

：2 號板的範束渦流所產生之下沖流速

"

w12 '

w12的推導，須考慮 2 號板上一微小板高dh對 1 號板所產生之下沖流 速，如圖 2-3 所示

dh dh h d r dw h

v

) ( 4 ²

' 12

− Γ

= π ^(2-54)

上式中

：板高 h

：微小尾跡渦流中心到所影響潛板之中心距離 rv

) ：微小尾跡渦流之環流量，假設為橢圓形分佈 Γ(h

將(2-54)式對板高h積分可得

w H

4

12 2 1 ' 12

=σ Γ (2-55)

上式中

∫

= ¹

1 2 2 2

12

2 12

1 [( / ) ] 1

1 η

η η

δ

η

σ π d

H (2-56)

其中δ₁₂為 1 號板與 2 號板在 方向之間距。 n

由於一號板到一號板並無間距(δ₁₁=0)，將此條件代入(2-55)及(2-54)式，可 得σ₁¹¹=1，w₁₁可簡化為

w H 4

1 11

= Γ (2-57)

"

w12的推導，依機翼理論，可以一置於潛板 1/4 板長處的範束渦流對另 一潛板之 3/4 板長處所造成之流速加以推估，如圖 2-4 所示

2 12 12

" 2

12 2 r

w S

π

= Γ (2-58)

上式中

：2 號板的範束渦流中心至 1 號板 3/4 板長處的距離 r12

：2 號板的範束渦流中心在 1 號板的投影至 1 號板 3/4 板長處的距離 S12

將(2-57)式加以整理，可得w₁₂^" 的公式如下

12 2

" 2

12 σ

πL w Γ

= (2-59)

δ α δ

δ α σ

sin ) ( 4 ) ( 4 1

sin ) ( 2 1

12 12

12 12

2

L L

L + +

= + _(2-60)

2 號潛板的下沖流速w₂同樣可依其來源分解成下列分量：

"

21 '

21 22

2 w w w

w = + + (2-61)

上式中w₂₂及w₂₁^' 可由同理推得，僅須將上、下標之 1 與 2 互換即可。

"

w21亦可同理推得

21 2

" 1

21 σ

πL

w = Γ (2-62)

但由於兩潛板在板長方向並非對齊，因此σ₂^21與σ¹²₂ ^{並不相同，}σ₂^{21的公式如} 下

δ α δ

δ α σ

sin ) ( 4 ) ( 4 1

sin ) ( 2 1

2 21 21

21 21

2

L L

L

− +

= − _(2-63)

⎥⎦

⎢ ⎤

⎣

=⎡

⎥⎦

⎢ ⎤

⎣

⎡ Γ Γ

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

+ +

+ +

α π

α π π

σ π σ

σ π π σ

2 1

2 1 21

1 21 2

12 1 12 2

1 4 4

4 1 4

LU LU H

L H

L

H L H

L

(2-64)

上式之解即為各板在交互作用下的實際環流量。

為探討各板受到交互作用的影響，定義一潛板交互作用因子(interaction factor)如下

Γ0

= Γⁱ

λi _(2-65)

上式中

：各板在交互作用下之實際環流量 Γi

：單一潛板未受干擾之環流量，可由下式表示 Γ0

單一潛板未受干擾時，所產生之環流量可以下式表示 (Odgaard &

Mosconi,1987)

μ α π

2

0 1

= + Γ LU

(2-66)

式中μ為潛板形狀因子，當範束渦流為拋物線分佈時，μ =8H πL(Wang, 1991)

將(2-52)及(2-65)式代入(2-64)式，可改寫成

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡ +

= +

⎥⎦

⎢ ⎤

⎣

⎡

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

+ +

+ +

H L H L

H L H

L

H L H

L

1 4 1 4 1 4

4

4 1 4

2 1 21

1 21 2

12 1 12 2

π π λ

λ π

σ π σ

σ π π σ

(2-67)

求解上式，即可得潛板交互作用因子λ。

依此原理可將上述推導過程推廣至一含有N 片潛板之系統，(2-67)式可改寫 如下

∑

= +

=

N +

j

j ij

ij i N

H L H

L

1

1

2 , 1

1 4 4 )

(σ σ π λ π L _(2-68)

上式中σ₁具有對稱性，即σ₁^ij =σ₁^ji，但σ₂並不具有對稱性，須由下式決定

⎪⎪

⎪⎪

⎪⎪

⎪

⎩

⎪⎪

⎪⎪

⎪⎪

⎪

⎨

⎧

=

>

− +

−

<

+ +

+

=

j i

j i L

L L

j i L

L L

ij ij

ij ij ij

ij

ij

, 1

, sin

) ( 4 ) ( 4 1

sin ) ( 2 1

, sin

) ( 4 ) ( 4 1

sin ) ( 2 1

2 2

2

δ α δ

δ α δ α δ

δ α

σ _(2-69)

各潛板之交互作用求得後，潛板系統所產生的近床 方向流速及底床剪 力，可個別以單一潛板的模式計算後，分別以對應的交互作用因子修正，

再予以疊加計算而得。如下列式中所示。

n

∑

= ^N

i

i vn i

vn v

v

1

)

λ ( _(2-70)

∑

= ^N λ(F ) (f )

τ _(2-71)

∑

= ^N

i

i v i L i

vn F f

1

) ( ) λ(

τ _(2-72)

上式中

N ：潛板數目

2-2-3 凹岸邊界

自然河川之河寬 b遠大於水深 ，因此水面與底床的影響遠大於岸壁的 影響，在前人關於潛板的研究中多忽略不計，但本研究為潛板位置之最佳 化分析，在最佳化的過程中，亦可能出現潛板位置極為靠近岸壁的情況，

因此，須加一組潛板鏡像於凹岸的反對側，以模擬岸壁的影響，如圖 2-5 所示。圖中 1 號潛板為實體，1’號潛板則為 1 號潛板之鏡像。鏡像潛板之角 度方向與實體潛板相反，因此，鏡像潛板之設置角度為

d

− 。同(2-52)式之α 原理，可將實體及鏡像潛板上之環流量表示為

) (

) (

' 1 '

1

1 1

U LU w

U LU w

+

−

= Γ

−

= Γ

α π

α π

(2-73)

因實體及鏡像潛板之設置角度相反，使得二者之尾跡渦流旋轉方向也互為 反向，因此在潛板間設置角度相反時(2-56)式可改寫為

∫

−

=

= ¹

1 2 2 2

'

2 '

1 '

1 [( / ) ] 1

1 η

η η

δ

η σ π

σ d

ii H

i i

ii (2-74)

而兩反向設置角度潛板之範束渦流旋轉方向互為反向，同時無論其 方向之 間距為何，二者間之交互作用關係對等，因此在潛板間設置角度相反時(2-60) 與(2-63)式可合併改寫為

n

δ α δ

δ α σ

σ

sin ) ( 4 ) ( 4 1

sin ) ( 2 1

2 ' '

' '

2 ' 2

L L

L

ii ii

ii

i i ii

+ +

− −

=

= _(2-75)

同 2-2-2 節之推導，將(2-74)及(2-75)兩式代入(2-73)後，可得聯立方程 式系統：

⎥⎦

⎢ ⎤

⎣

⎡

= −

⎥⎦

⎢ ⎤

⎣

⎡ Γ

Γ

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

−

−

−

−

+ +

α π

α π π

σ π σ

σ π π σ

LU LU H

L H

L

H L H

L

' 1 1 1

' 1 1 1 ' 1 2

' 11 1 ' 11 2

1 4 4

4 1 4

(2-76)

將(2-65)式代入(2-76)式後，可將其改寫成下式

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡ +

= +

⎥⎦

⎢ ⎤

⎣

⎡

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

+ +

+ +

H L H L

H L H

L

H L H

L

1 4 1 4 1 4

4

4 1 4

' 1 1 1

' 1 1 1 ' 1 2

' 11 1 ' 11 2

π π λ

λ π

σ π σ

σ π π σ

(2-77)

考慮凹岸鏡像與實體潛板之相互影響後，可將(2-68)式擴展為

4 , 1 ) 4 )

( 4 )

((

4 , 1 ) 4 )

( 4 )

((

1

' '

' 1 ' ' 2 '

1 ' 2 1

' '

1 ' 2 1

2

H L H

L H

L

H L H

L H

L

N

j

j j

i j i j j

i j i N

j

j ij

ij j

ij ij

λ π σ π

σ π λ

σ σ

λ π σ π

σ π λ

σ σ

+

= +

+ +

+

= +

+ +

∑

∑

=

=

N i=1L

(2-78)