A new approach for handling classification problems based on fuzzy information gain measures

Abstract—In this paper, we present a new method for handling classification problems based on fuzzy information gain measures. First, we propose a fuzzy information gain measure of a feature with respect to a set of training instances.

Then, based on the proposed fuzzy information gain measure, we present an algorithm for constructing membership functions, calculating the class degree of each subset of training instances with respect to each class and calculating the fuzzy entropy of each subset of training instances, where each subset of training instances contains a part of the training instances whose values of a specific feature fall in the support of a specific fuzzy set of this feature. Finally, we propose an evaluating function for classifying testing instances. The proposed method can deal with both numeric and nominal features. It gets higher average classification accuracy rates than the existing methods.

I. INTRODUCTION

lassification techniques have been widely applied in many domains. Many kinds of classifiers have been proposed for dealing with classification problems, such as the rule-based method [2], [6], [8], [26], the instance-based method [9], the linear function method [10], the decision trees method [22], the C4.5 method [21], the artificial neural networks method (ANN) [17], the support vector machines (SVM) method [4], the sequential minimal optimization (SMO) method [20], the naive Bayes method [13], …, etc. A data set might have numeric or nominal features. Some classifiers may have high classification accuracy rates for numeric data and some other classifiers may have high classification accuracy rates for nominal data. If the chosen classifier can only deal with nominal features, the discretization of numeric features is necessary. If we can properly discretize each numeric feature into finite subsets, then we can increase the classification accuracy rates of classification systems [5].

In this paper, we present a new method for handling classification problems based on fuzzy information gain measures. First, we propose a fuzzy information gain measure of a feature with respect to a set of training instances. Then, based on the proposed fuzzy information gain measure, we present an algorithm for constructing membership functions,

This work was supported in part by the National Science Council, Republic of China, under Grant NSC 94-2213-E-011-005.

J.-D. Shie and S.-M. Chen are with the Department of Computer Science and Information Engineering, National Taiwan University of Science and Technology, Taipei 106, Taiwan, R.O.C. (e-mail: smchen@et.ntust.edu.tw).

calculating the class degree of each subset of training instances with respect to each class and calculating the fuzzy entropy of each subset of training instances, where each subset of training instances contains a part of the training instances whose values of a specific feature fall in the support of a specific fuzzy set of this feature. Finally, based on the constructed membership function of each fuzzy set of each feature, the obtained class degree of each subset of training instances with respect to each class and the obtained fuzzy entropy of each subset of training instances, we propose an evaluating function for classifying testing instances. The proposed method can deal with both numeric and nominal features. It gets higher average classification accuracy rates than the ones using the methods presented in [13], [20] and [21].

II. F

UZZY

I

NFORMATION

G

AIN

M

EASURES

Among the existing crisp logic based entropy measures, Shannon’s entropy measure [25] is the most popular one. It is used to estimate the average minimum number of bits needed to encode a string of symbols. The amount of information I(e) associated with a known element value e is defined as follows:

), ( log )

( e

₂

p e

I = − (1) where e∈E, E denotes a set of known element values, and p(e) denotes the probability of the occurrence of an element value e. The entropy measure H(E) of a set E of known element values is defined as follows:

), ( 1 ( ) log )

( E p e

₂

p e

H

ⁿ

i

∑

−

=

=

(2) where e∈E, n denotes the number of elements in E, and p(e) denotes the probability of the occurrence of an element value e.

In [22], Quinlan proposed an information gain measure based on Shannon’s entropy measure [25] for calculating the expected reduction in entropy caused by partitioning a set of training instances according to a specific feature. Assume that R denotes a set of training instances, C denotes a set of classes and f denotes a feature. The entropy H(R) of a set R of training instances is defined by:

), ) , ( ( log ) , ( )

( = − ∑

₂

∈C

c

p R c p R c

R

H (3)

where C denotes a set of classes and p(R, c) denotes the proportion of the training instances in R belonging to a class c.

A New Approach for Handling Classification Problems Based on Fuzzy Information Gain Measures

Jen-Da Shie and Shyi-Ming Chen, Senior Member, IEEE

C

July 16-21, 2006

The information gain Gain(R, f) [18], [22] of a feature f with respect to a set R of training instances is defined by:

, )) ( (

) ( ) ,

( = − ∑

( )

×

∈Values f

u ^u

u

H R

R R R

H f R

Gain (4)

where Values(f) denotes the set of all possible values for the feature f, R

u

denotes a subset of R whose feature f has the value u (i.e., R

u

= { r∈R | f(r) = u}), |R| denotes the number of instances contained in R, and |R

u

| denotes the number of instances contained in R

u

.

In [28], Zadeh defined a fuzzy entropy measure of a fuzzy set v, where a fuzzy set v is defined in the universe of discourse U and U ={u

1

, u

2,

…, u

n

} with respect to the probability distribution P = {p

1

, p

2

, …, p

n

}, shown as follows:

− ∑

=

=

n u p p

v H

i v i i i

1 ( ) log

)

( µ , (5) where μ

v

(u

i

) denotes the membership grade of u

i

belonging to the fuzzy set v, μ

v

(u

i

) ∈ [0, 1], p

_i

denotes the probability of u

i

, 1≤ i ≤ n, and n denotes the number of elements in the universe of discourse U.

In [14], Kosko proposed a fuzzy entropy measure of a fuzzy set based on the geometry of a hypercube. In [16], Luca et al. proposed four axioms for a fuzzy entropy measure and a fuzzy entropy measure of a fuzzy set. In [15], Lee et al.

proposed a fuzzy entropy measure of an interval.

In the following, we propose a definition of the fuzzy information gain measure of a feature with respect to a set of training instances. A feature can be described by several linguistic terms [29] and each linguistic term can be represented by a fuzzy set [27] characterized by a membership function. Assume that a set R of training instances is classified into a set C of classes and assume that a set V of fuzzy sets is defined in the feature f. Let μ

v

denote the membership function of the fuzzy set v, v ∈ V and let µ

_v

(x) denote the membership grade of value x belonging to the fuzzy set v. The support U

v

of a fuzzy set v denotes a subset of the universe of discourse U of a feature, where U

v

= {u |μ

v

(u)

> 0 and u ∈ U }. First, we review a class degree measure [7]

for calculating the degree of possibility of a subset of training instances belonging to a specific class whose values of a specific feature fall in the support of a specific fuzzy set, shown as follows:

Definition 2.1 [7]: The class degree CD

c

(v) of a subset R

v

of training instances belonging to a class c whose values of a feature f fall in the support U

v

of a fuzzy set v of the feature f, is defined by:

) , (

) ( )

( ∑

∑

=

∈

∈ X x

X x

x x v

CD

v

c v

c

µ

µ

(6) where X denotes the set of values of the feature f of the subset R

v

of training instances, X ⊂ U

_v

, X

c

denotes the set of values of the feature f of the subset R

v

of training instances belonging to the class c, c∈C, μ

_v

denotes the membership function of the

fuzzy set v, µ

v

(x) denotes the membership grade of value x belonging to the fuzzy set v, and µ

v

(x) ∈ [0, 1].

Then, based on the class degree measure [7] shown in Eq.

(6), we review a fuzzy entropy measure [7] for calculating the uncertainty about the class of a subset of training instances whose values of a specific feature fall in the support of a specific fuzzy set , shown as follows.

Definition 2.2 [7]: The fuzzy entropy FE(v) of a subset of training instances whose values of a feature f fall in the support U

v

of a fuzzy set v of the feature f is defined by:

, ) ( log ) ( )

( = ∑ −

₂

∈C

c

CD v CD v

v

FE

_{c c}

(7) where C denotes a set of classes and CD

c

(v) denotes the class degree of the subset of training instances belonging to a class c whose values of the feature f fall in the support U

v

of the fuzzy set v of the feature f.

Then, based on the fuzzy entropy measure [7] shown in Eq.

(7), we propose a fuzzy information gain measure for calculating the expected reduction in entropy caused by partitioning the set of training instances according to a specific feature, shown as follows.

Definition 2.3: The fuzzy information gain FIG(R, f) of a feature f with respect to a set R of training instances, is defined by:

, ) ( log

) ,

( = ∑ −

₂

− ∑

∈

∈C v V

c

s s FE v

n n n n f

R

FIG

^{c c v}

(8)

where n denotes the number of instances contained in R, n

c

denotes the number of instances which are contained in R and belonging to a class c, V denotes the fuzzy sets of the feature f, S denotes the summation of the membership grades of the values of the feature f of the set R of training instances belonging to each fuzzy set of the feature f, S

v

denotes the summation of the membership grades of the values of the feature f of the set R of training instances belonging to a fuzzy set v of the feature f, and FE(v) denotes the fuzzy entropy of a subset of training instances whose values of the feature f fall in the support U

v

of a fuzzy set v of the feature f.

In the following, we use an example to illustrate the proposed fuzzy information gain measure (i.e., Eqs. (6)-(8)).

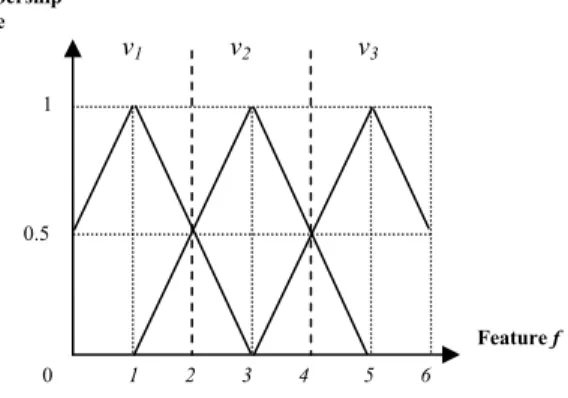
Assume that there is a set R of training instances with a feature f shown in Fig. 1 and assume that the corresponding fuzzy sets (i.e., v

1

, v

2

, and v

3

) of the feature f are shown in Fig.

2, where the symbols "+" and "-" denote the positive training instances and the negative training instances, respectively.

Table I shows the values of the feature f and their corresponding classes. Table II shows the supports of the fuzzy sets v

1

, v

2

and v

3

of the feature f, respectively.

Fig. 1. The distribution of the set of training instances with one feature.

0 1 2 3

Feature f

4 5 6

+

^－

+ +

^－

Fig. 2. The corresponding fuzzy sets of the feature f.

TABLE I

THE VALUES OF THE FEATURE f AND THEIR CORRESPONDING CLASSES The Value of the Featue f Classes

1 + 2 − 3 + 4 + 5 −

TABLE II

THE SUPPORTS OF THE FUZZY SETS v1, v2AND v3OF THE FEATURE f, RESPECTIVELY

Fuzzy Sets Supports of Fuzzy Sets v1 [0, 3]

v2 [1, 5]

v3 [3, 6]

Based on the proposed fuzzy information gain measure (i.e., Eqs. (6)-(8)), we can calculate the fuzzy information gain FIG(R, f) of the feature f with respect to the set R of training instances as follows:

(1) Calculate the fuzzy entropy of the subset R

1

of the training instances whose values of the feature f fall in the support of the fuzzy set v

1

of the feature f:

(i) Calculate the total membership grades of the subset R

1

of the training instances whose values of the feature f fall in the support of the fuzzy set v

1

of the feature f with respect to the positive class (+) and the negative class (−), respectively. Let X

+

be a set of values of the feature f of the subset R

1

of the training instances belonging to the positive class (+). Let X

−

be a set of values of the feature f of the subset R

1

of the training instances belonging to the negative class (−). From Fig. 1, we can see that X

+

= {1}

and X

−

= {2}. Then, we can get

. 5 . 0 ) (

, 1 ) (

1 1

∑ =

∈

=

∈ ∑

− +

X

x v

X

x v

x x µ µ

(ii) Based on Eq. (6), calculate the class degrees CD

+

(v

1

) and CD

−

(v

1

) of the subset R

1

of the training instances whose values of the feature f fall in the support of the fuzzy set v

1

of the feature f with respect to the positive class (+) and the negative class (−), respectively:

. 3333 . 0 )

(

, 6667 . 0 )

(

5 . 1

5 . 0 5 . 0 1

5 .

0 1.5

1 5 . 0 1

1

2 2

=

=

=

=

=

=

+ +

− +

v CD

v CD

(iii) Based on Eq. (7), the fuzzy entropy FE(v

1

) of the subset R

1

of the training instances whose values of the feature f fall in the support of the fuzzy set v

1

of the feature f is calculated as follows:

)) ( log ) ( ) ( log ) ( ( )

( v

₁

CD v

_{1 2}

CD v

₁

CD v

_{1 2}

CD v

₁

FE = −

_{+ +}

+

_{− −}

0.9182.

) 3333 . 0 log 3333 . 0 6667 . 0 log 6667 . 0

(

_{2 2}

≅

× +

×

−

=

(2) Calculate the fuzzy entropy of the subset R

2

of the training instances whose values of the feature f fall in the support of the fuzzy set v

2

of the feature f:

(i) Calculate the total membership grades of the subset R

2

of the training instances whose values of the feature f fall in the support of the fuzzy set v

2

of the feature f with respect to the positive class (+) and the negative class (−), respectively. Let X

+

be a set of values of the feature f of the subset R

2

of the training instances belonging to the positive class (+). Let X

−

be a set of values of the feature f of the subset R

2

of the training instances belonging to the negative class (−). From Fig. 1, we can see that X

+

= {3, 4}

and X

−

= {2}. Then, we can get

. 5 . 0 ) (

, 5 . 1 5 . 0 1 ) (

2 2

=

∈ ∑

= +

=

∈ ∑

− +

X

x v

X

x v

x x µ µ

(ii) Based on Eq. (6), calculate the class degrees CD

+

(v

2

) and CD

−

(v

2

) of the subset R

2

of the training instances whose values of the feature f fall in the support of the fuzzy set v

2

of the feature f with respect to the positive class (+) and the negative class (−), respectively:

. 25 . 0 )

(

, 75 . 0 )

(

2 5 . 0 5 . 0 5 . 1

5 . 0

2 5 . 1 5 . 0 5 . 1

5 . 1

2 2

=

=

=

=

=

=

+ +

− +

v CD

v CD

(iii) Based on Eq. (7), the fuzzy entropy FE(v

2

) of the subset R

2

of the training instances whose values of the feature f fall in the support of the fuzzy set v

2

of the feature f is calculated as follows:

)) ( log ) ( ) ( log ) ( ( )

( v

₂

CD v

_{2 2}

CD v

₂

CD v

_{2 2}

CD v

₂

FE = − + + + − −

0.8113.

) 25 . 0 log 25 . 0 75 . 0 log 75 . 0

(

_{2 2}

≅

× +

×

−

=

(3) Calculate the fuzzy entropy of the subset R

3

of the training instances whose values of the feature f fall in the support of the fuzzy set v

3

of the feature f:

(i) Calculate the total membership grades of the subset R

3

of the training instances whose values of the feature f fall in the support of the fuzzy set v

3

of the feature f with respect to the positive class (+) and the negative class (−), respectively. Let X

+

be a set of values of the feature f of the subset R

3

of the training instances belonging to the positive

Membership Grade

0 1 2 3

Feature f 1

0.5

4 5 6

v

₁

v

₂

v

₃

class (+). Let X

−

be a set of values of the feature f of the subset R

3

of the training instances belonging to the negative class (−). From Fig. 1, we can see that X

+

= {4}

and X

−

= {5}. Then, we can get

. 1 ) (

, 5 . 0 ) (

3 3

=

∈ ∑

∑ =

∈

− +

X

x v

X

x v

x x µ µ

(ii) Based on Eq. (6), calculate the class degrees CD

+

(v

3

) and CD

−

(v

3

) of the subset R

3

of the training instances whose values of the feature f fall in the support of the fuzzy set v

3

of the feature f with respect to the positive class (+) and the negative class (−), respectively:

. 6667 . 0 )

(

, 3333 . 0 )

(

5 . 1

1 1 5 . 0

1 1.5

5 . 0 1 5 . 0

5 . 0

3 3

≅

=

=

≅

=

=

+ +

− +

v CD

v CD

(iii) Based on Eq. (7), the fuzzy entropy FE(v

3

) of the subset R

3

of the training instances whose values of the feature f fall in the support of the fuzzy set v

3

of the feature f is calculated as follows:

)) ( log ) ( ) ( log ) ( ( )

( v

₃

CD v

_{3 2}

CD v

₃

CD v

_{3 2}

CD v

₃

FE = −

_{+ +}

+

_{− −}

0.9182.

) 6667 . 0 log 6667 . 0 3333 . 0 log 3333 . 0

(

_{2 2}

≅ − × + ×

=

(4) Based on Eq. (8), we can calculate the fuzzy information gain FIG(R, f) of the feature f with respect to the set R of training instances, shown as follows:

0.0577.

0.9812]

1.5) 2 1.5/(1.5

0.8113 1.5)

2 2/(1.5

0.9812 1.5)

2 [1.5/(1.5

- ] 2/5) log (-2/5 3/5) log [(-3/5 ) ,

(

_{2 2}

≅ + + + + + + + + × × × +

= f R FIG

III. T

HE

P

ROPOSED

M

ETHOD FOR

D

EALING WITH

C

LASSIFICATION

P

ROBLEMS

In this section, we propose a new method for dealing with classification problems based on fuzzy information gain measures. In the proposed method, the discretization of numeric features must be carried out by a preprocessing process. In this paper, we apply the k-means clustering algorithm [11] to generate k cluster centers and then to construct their corresponding membership functions to discretize a numeric feature, where the cluster centers are used as the centers of fuzzy sets. The fuzzy information gain of a feature with respect to a set of training instances increases when the number of fuzzy sets increases. However, to construct too many fuzzy sets of a numeric feature could cause the overfitting problem [24], reducing the classification accuracy rates for classifying testing instances. In this paper, we define a threshold value T to avoid the overfitting problem, where T ∈ [0, 1]. In the following, we present an algorithm for constructing the membership function of each fuzzy set of each feature, calculating the class degree of each subset of

training instances with respect to each class and calculating the fuzzy entropy of each subset of training instances, where each subset of training instances contains a part of the training instances whose values of a specific feature fall in the support of a specific fuzzy set of this feature. Assume that R denotes a set of training instances, C denotes a set of classes, c denotes a class of C, F denotes a set of features, F = {f

1

, f

2

, …, f

n

}, n denotes the number of features, and f

i

denotes the ith feature of F. The proposed algorithm for handling classification problems is now presented as follows:

Step 1: Initially, set i = 1.

Step 2: Set the number k of clusters to 2 and select the ith feature f

i

from F.

Step 3: Construct the membership functions of the feature f

i

. If f

i

is a nominal feature, then go to Step 3.1. Otherwise, go to Step 3.2;

Step 3.1: /* Construct the membership function of each fuzzy set of a nominal feature. Each value of the universe of discourse U of a nominal feature is regarded as a singleton fuzzy set, where U denotes the universe of discourse of the feature f

i

, U = {u

1

, u

2,

…, u

p

}, u

j

denotes the jth value of the universe of discourse of the feature f

i

, and p denotes the number of values of the universe of discourse of the feature f

i

. Each value u

j

of a nominal feature f

i

can be regarded as a fuzzy set, where

⎩ ⎨

⎧ ⁼

= otherwise u x

x if

^j

uj

0 ,

, ) 1

µ ( . For example, the

set of values of the feature “Sex” is {male, female}. When the value of the feature “Sex” is “male”, the membership grades are: µ

_male

(male ) = 1 and µ

_female

(male ) = 0.*/

for j = 1 to p do {

let

⎩ ⎨

⎧ ⁼

=

= otherwise

u x x if

x

^j

uj

vij

0 ,

, ) 1 ( )

( µ

µ

where v

ij

denotes the jth fuzzy set of the feature f

i

,

vij

µ denotes the membership function of the fuzzy set v

ij

, and (x )

vij

µ denotes the membership grade of value x belonging to the fuzzy set v

ij

};

go to Step 4.

Step 3.2: /* Construct the membership functions of a numeric feature. */

Apply the k-means clustering algorithm [11] for clustering the values of the feature f

i

of the set R of training instances into k clusters (i.e., [x

11

, x

12

], [x

21

, x

22

], …, and [x

_k1

, x

k2

]) to generate k cluster centers m

1

, m

2,

…, and m

k

;

for j = 1 to k do {

/* Use cluster center m

j

as the center of fuzzy set v

ij

to construct its membership function

vij

µ

as shown in Fig. 3,

where “U

min

” denotes the minimum value of the universe

of discourse of the feature f

i

, “U

max

” denotes the

maximum value of the universe of discourse of the feature f

i

, and the clusters centers of v

i1

, v

i2

, …, and v

ik

, are m

1

, m

2

, …, and m

k

, respectively. */

if j =1 then {

/* Construct the membership function of the fuzzy set v

i1

corresponding to the first cluster center m

1

, where U

min

denotes the minimum value of the universe of discourse of the feature f

i

, m

1

denotes the first cluster center, and m

2

denotes the second cluster center.*/

let

⎪ ⎪

⎩

⎪⎪ ⎨

⎧

≤

− <

− −

≤

≤

− ×

− −

=

otherwise m x m m if

m m x

m x U m if

U m x

x ₁

1 1

1 1 1

1 vi

, 0

, 1

, 5 . 0 1

)

( ₂

2

min min

µ

} else {

if j = k then {

/* Construct the membership function of the fuzzy set v

ik

corresponding to the kth cluster center m

k

, where U

max

denotes the maximum value of the universe of discourse of the feature f

i

, m

k

denotes the kth cluster center, m

k-1

denotes the left cluster center of m

k

. */

let

⎪ ⎪

⎩

⎪ ⎪

⎨

⎧

≤

<

− ×

− −

≤

− ≤

− − ₋

−

=

otherwise U x m m if

Ux mk

m x m m if

m m x

k k

k k k

k k

vik

x

, 0

, 5 . 0 1

1 , 1

max max

1

) µ (

} else

{

/* Construct the membership function of the fuzzy set v

ij

corresponding to the jth cluster center m

j

, where 1 < j < k, m

j

denotes the jth cluster center, m

j-1

denotes the left cluster center of m

j

, and m

j+1

denotes the right cluster center of m

j

. */

let

⎪ ⎪

⎩

⎪ ⎪

⎨

⎧

+ +

− −

≤

− <

− −

≤

− ≤

− −

=

otherwise m x m m if m

mj x

m x m m if m

m x

j j j

j

j j j

j j

vij

x

, 0

, 1

, 1

1 1 1 1

) µ (

} } }.

Step 4: Based on the constructed membership function of each fuzzy set v

ij

of a feature f

i

in Step 3, calculate the class degree CD

c

(v

ij

) of each subset R

ij

of the training instances with respect to each class by Eq. (6), where each subset R

ij

of

the training instances contains a part of the training instances whose values of the feature f

i

fall in the support of a fuzzy set v

ij

of the feature f

i

. Then, calculate the fuzzy entropy FE(v

ij

) of each subset R

ij

of the training instances by Eq. (7). Then, calculate the fuzzy information gain FIG(R, f

i

) of the feature f

i

with respect to the set R of training instances by Eq. (8).

Step 5: /* If feature f

i

is a numeric feature, determine whether to increase the number k of clusters or not. Let T denote a threshold value given by user, where T ∈ [0, 1], and I

value

denotes the increasing value of the fuzzy information gain of the feature f

i

with respect to the set R of training instances between the number of clusters equals to k-1 and the number of clusters equals to k.*/

if f

i

is a numeric feature then {

if k = 2 or I

value

≥ T then k = k + 1 and go to Step 3.2

else {

Use the membership functions constructed by the values of the feature f

i

clustered into k-1 clusters as the membership functions of the fuzzy sets of the feature f

i

; k = k - 1

} }.

Step 6: if i < n then i = i + 1 and go to Step 2. Otherwise, Stop.

Fig. 3. A numeric feature fi with fuzzy sets vi1, vi2, …, and vik.

Based on the constructed membership function of each fuzzy set of each feature, the obtained class degree of each subset of training instances with respect to each class, and the obtained fuzzy entropy of each subset of training instances, we propose an evaluating function for classifying testing instances. Giving weights to features is one kind of feature selection methods used in many existing methods [4], [10], [19], [20], [23], and it is more flexible than the methods in [1]

and [2] by omitting some features directly. Most of the methods [4], [10], [19], [20], [23] use static weights which are

v

i(k-1)

U

min

m

k-1

U

max

Membership Grade

v

i1

v

i2

v

ik

0

m

1

m

2

f

i

1

0.5

m

k

…

…

…

generated at the training time to classify testing instances. In the proposed method, weights of features for each testing instance are generated at testing time and each feature f

i

of a testing instance is assigned a dynamic weight w

i

, where w

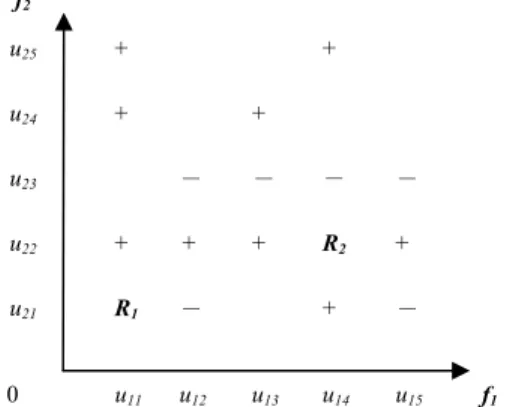
i

∈ [0, 1]. For example, assume that there is a set of instances, shown in Fig. 4, where the symbol "+" denotes the positive training instances, the symbol "-" denotes the negative training instances, and R

1

and R

2

denote two testing instances.

From Fig. 4, we can see that the feature f

1

is more important than the feature f

2

for the testing instance R

1

because the distribution of the training instances (i.e., the positive training instances "+" and the negative training instances "-") for the value u

11

of the feature f

1

has a smaller entropy than that of the distribution of the training instances for the value u

21

of the feature f

2

, but the feature f

2

is more important than the feature f

1

for the testing instance R

2

because the distribution of the training instances for the value u

22

of the feature f

2

has a smaller entropy than the distribution of the training instances for the value u

14

of the feature f

1

. In the proposed method, the weights of the features of the testing instances R

1

and R

2

will be generated according to the distribution of the training instances for the values of each feature of the testing instances R

1

and R

2

, respectively, where the weight of the feature f

2

will be smaller than the weight of the feature f

1

for the testing instance R

1

and the weight of the feature f

1

will be smaller than the weight of the feature f

2

for the testing instance R

2

.

Fig. 4. The distribution of the instances with two features and two classes.

In the following, we propose a method to generate dynamic weights of features for each testing instance, called the fuzzy entropy weight measure. Since the proposed fuzzy entropy weight measure is calculated based on estimating the uncertainty about the class of a testing instance according to each value of each feature of this testing instance, we use the fuzzy entropy measure [7] (i.e., Eq. (7)) to propose an estimated fuzzy entropy measure for calculating the uncertainty about the class of a testing instance according to the value of a specific feature of this testing instance.

Definition 3.1: The estimated fuzzy entropy EFE

f

(x) of a testing instance r according to the value x of a feature f of this testing instance is defined by:

)), ( ) ( ( )

( x x FE v

EFE

f v

f

=

v

∑

V

×

∈

µ (9)

where V

f

denotes the set of fuzzy sets of the feature f, µ

v

denotes the membership function of the fuzzy set v and is constructed at the training time, µ

v

(x) denotes the membership grade of value x belonging to a fuzzy set v, µ

v

(x) ∈ [0, 1] and FE(v) denotes the fuzzy entropy of the subset of training instances whose values of the feature f fall in the support of the fuzzy set v of the feature f and is obtained at the training time.

Then, based on the proposed estimated fuzzy entropy measure shown in Eq. (9), we propose a fuzzy entropy weight measure for generating the weights of features of a testing instance, described as follows. Assume that the probability of a testing instance belonging to a class is in a uniform distribution, where P(x) = 1/ n

c

, x∈X, X denotes a set of testing instances, P(x) denotes the probability density function of the set X of testing instances, and n

c

denotes the number of classes. In this case, the set X of testing instances has the maximum entropy [12]. Assume that the probability of a testing instance belonging to a class is in a uniform distribution, the definition of the proposed fuzzy entropy weight measure is as follows.

Definition 3.2: The fuzzy entropy weight FEW

f

(x) of a feature f of a testing instance r is defined by:

∑ × − −

−

−

= ×

∈F

g ^{c c c g g}

c f c c

f

n n n EFE x

x n EFE n n

x

FEW [ ( 1 log 1 ) ( )]

) ( 1 )

1 log ) (

(

2

2

, (10) where x denotes the value of a feature f of the testing instance r, EFE

f

(x) denotes the estimated fuzzy entropy of the testing instance r according to the value x of the feature f of the testing instance r, F denotes a set of features, n

c

denotes the number of classes, x

g

denotes the value of a feature g of the testing instance r, EFE

g

(x

g

) denotes the estimated fuzzy entropy of the testing instance r according to the value x

g

of a feature g of the testing instance r.

According to the definition of the proposed fuzzy entropy weight measure, the feature with a larger estimated fuzzy entropy value will have a lower fuzzy entropy weight and the one with a smaller estimated fuzzy entropy value will have a higher fuzzy entropy weight. In the following, based on the class degree measure [7] (i.e., Eq. (6)), we propose an

“estimated class degree measure” for calculating the degree of possibility of a testing instance belonging to a specific class according to the value of a specific feature of this testing instance.

Definition 3.3: The estimated class degree ECD

c

(x, f) of a testing instance r belonging to a class c according to the value x of a feature f of this testing instance is defined by:

)) ( ) ( ( ) ,

( x f x CD v

ECD

_c

f v

c

=

v

∑

V

×

∈

µ , (11) where V

f

denotes the fuzzy sets of the feature f, µ

v

denotes the membership function of the fuzzy set v and is constructed at the training time, µ

v

(x) denotes the membership grade of value x belonging to the fuzzy set v, µ

v

(x) ∈ [0, 1], and CD

_c

(v) denotes the class degree of the subset of training instances belonging to a class c whose values of the feature f fall in the

f1

u25

0 u11 u12 u13 u14 u15

u21

u22

u23

u24

+

+ +

－

+

+

－ R2

+ +

R1

－

－ － －

f2

+

+

support of the fuzzy set v of the feature f and is obtained at the training time.

Based on the proposed fuzzy entropy weight measure as shown in Eq. (10) and the proposed estimated class degree measure as shown in Eq. (11), we propose a “weighted estimated class degree measure” for calculating the possibility of a testing instance belonging to a specific class.

Definition 3.4: The weighted estimated class degree WECD

c

(r) of a testing instance r belonging to a class c is defined by:

), ) , ( ) ( ( )

( =

_∈

∑

,_∈

×

F f X

x f c

c

r FEW x ECD x f

WECD (12)

where F denotes a set of features, X denotes the set of values of the features of the testing instance r, FEW

f

(x) denotes the fuzzy entropy weight of a feature f of the testing instance r, and ECD

c

(x, f) denotes the estimated class degree of the testing instance r belonging to the class c according to the value x of a feature f of this testing instance.

Based on the proposed weighted estimated class degree measure shown in Eq. (12), the definition of the proposed evaluating function WECDC(r) for classifying a testing instance r is shown as follows:

Definition 3.5: The evaluating function WECDC(r) for classifying a testing instance r is defined by:

), ( max

arg )

( r WECD r

WECDC

_c

c∈C

= (13) where C denotes a set of classes, WECD

c

(r) denotes the weighted estimated class degree of the testing instance r belonging to a class c, and “

arg maxWECD_c(r)

c∈C

” returns such a class c, c∈C, which maximizes the function WECD

_c

(r).

In summary, the proposed evaluating function WECDC(r) for classifying a testing instance r to a class c can be calculated based on Definitions 3.1, 3.2, 3.3, 3.4 and 3.5, shown as follows:

{ }.

,

)) ( ) ( (

))]

( ) ( ( 1 )

1 log ( [

)) ( ) ( ( 1 )

1 log ( max

arg

2

)

2

(

_∈

∑

_∈

∈

∈

∑ ×

∈

∈

∑ × − − ∑ ×

×

∑ ×

−

−

×

=

∈

F f X

x vV

V

v

x CD

_c

v

Vf

v v

F

g c c c g v

f v

c c c

v FE n x

n n

v FE n x

n n C

c

r

WECDC µ

µ µ

(14)

IV. E

XPERIMENTAL

R

ESULTS

We have implemented the proposed method by using IBM Lotus Notes version 4.6 [32] on a Pentium 4 PC. In the following, we use six different kinds of UCI data sets [30] for comparing the average classification accuracy rate of the proposed method with three different kinds of classifiers (i.e., naive Bayes [13], C4.5 [21] and sequential minimal optimization (SMO) [20]). We summarize these data sets as follows:

(i) Iris data set: This data set has 150 instances which are classified into three classes. Each instance is described by four numeric features, which are (1) Sepal Length, (2) Sepal Width, (3) Petal Length and (4) Petal Width.

(ii) Breast Cancer data set: This data set contains 699 instances which are classified into two classes. Since 16 instances of the data set have missing values, we use 683 instances. Each sample is described by nine numeric features, which are (1) Clump Thickness, (2) Uniformity of Cell Size, (3) Uniformity of Cell Shape, (4) Marginal Adhesion, (5) Single Epithelial Cell Size, (6) Bare Nuclei, (7) Bland Chromatin, (8) Normal Nucleoli and (9) Mitoses.

(iii) Wine Recognition data set: This data set contains 178 instances which are classified into three classes. Each instance is described by thirteen numeric features, which are (1) Alcohol Content, (2) Malic Acid Content, (3) Ash Content, (4) Alcalinity of Ash, (5) Magnesium Content, (6) Total Phenols, (7) Flavanoids, (8) Nonflavanoids Phenols, (9) Proanthocyaninsm, (13) Color Intensity, (14) Hue, (15) OD280/OD315 of Diluted Wines and (16) Praline.

(iv) Glass Identification data set: This data set contains 214 instances which are classified into seven classes. Each sample is described by nine numeric features, which are (1) Refractive Index, (2) Sodium, (3) Magnesium, (4) Aluminum, (5) Silicon, (6) Potassium, (7) Calcium, (8) Barium and (9) Iron.

(v) Credit Approval data set: This data set has 690 instances which are classified into two classes. Since 37 instances of the data set have missing values, we use 653 instances. Each case represents an application for credit card facilities described by eight nominal features and six numeric features.

The original feature names have been changed to meaningless symbols (A1-A14) with the purpose of protecting the confidentiality of the data.

(vi) Balance Scale data set: This data set has 625 instances which are classified into three classes. Each sample is described by four numeric features which are (1) Left Weight, (2) Left Distance, (3) Right Weight and (4) Right Distance.

We used the proposed method and used these three different kinds of classifiers (i.e., naive Bayes [13], C4.5 [21]

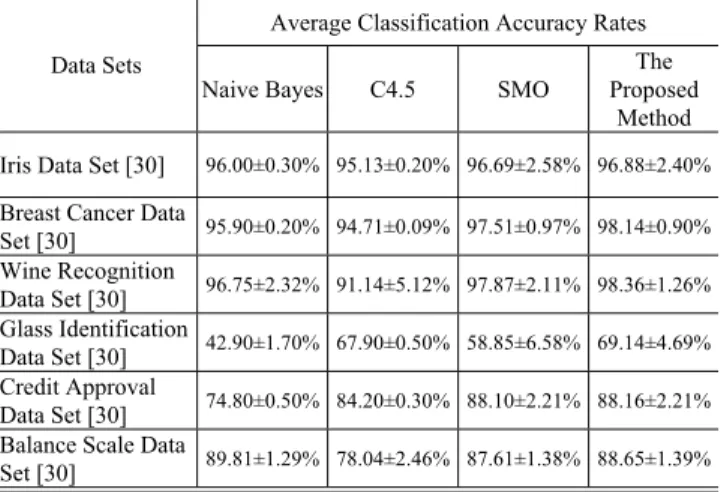
and sequential minimal optimization (SMO) [20]) to execute 200 times on each data set, respectively. Each time, we let 75% of the data set be the training instances and let the remaining instances be the testing instances. We make the experiments of these three classifiers (i.e., naive Bayes [13], C4.5 [21] and sequential minimal optimization (SMO) [20]) in the environment of the free software Weka [31] on a Pentium 4 PC. A comparison of the average classification accuracy rates for the different methods is shown in Table III.

From Table III, we can see that the proposed method gets

higher average classification accuracy rates than the naive

Bayes method [13], the C4.5 method [21] and the sequential

minimal optimization (SMO) method [20].

Table III

ACOMPARISON OF THE AVERAGE CLASSIFICATION ACCURACY RATES OF THE PROPOSED METHOD WITH THE DIFFERENT METHODS

Average Classification Accuracy Rates Data Sets

Naive Bayes C4.5 SMO

The Proposed

Method Iris Data Set [30] 96.00±0.30% 95.13±0.20% 96.69±2.58% 96.88±2.40%

Breast Cancer Data

Set [30] 95.90±0.20% 94.71±0.09% 97.51±0.97% 98.14±0.90%

Wine Recognition

Data Set [30] 96.75±2.32% 91.14±5.12% 97.87±2.11% 98.36±1.26%

Glass Identification

Data Set [30] 42.90±1.70% 67.90±0.50% 58.85±6.58% 69.14±4.69%

Credit Approval

Data Set [30] 74.80±0.50% 84.20±0.30% 88.10±2.21% 88.16±2.21%

Balance Scale Data

Set [30] 89.81±1.29% 78.04±2.46% 87.61±1.38% 88.65±1.39%

(Note: All results are reported as mean ± standard deviation computed from 200 independent trials.)

V. C

ONCLUSIONS

In this paper, we have presented a new method for handling classification problems based on fuzzy information gain measures. First, we propose a fuzzy information gain measure of a feature with respect to a set of training instances. Then, based on the proposed fuzzy information gain measure, we present an algorithm for constructing membership functions, calculating the class degree of each subset of training instances with respect to each class and calculating the fuzzy entropy of each subset of training instances, where each subset of training instances contains a part of the training instances whose values of a specific feature fall in the support of a specific fuzzy set of this feature. Finally, based on the constructed membership function of each fuzzy set of each feature, the obtained class degree of each subset of training instances with respect to each class and the obtained fuzzy entropy of each subset of training instances, we propose an evaluating function for classifying testing instances. The proposed method can deal with both numeric and nominal features. It gets higher average classification accuracy rates than the existing methods.

R

^EFERENCES

[1] P. W. Baim, “A method for attribute selection in inductive learning systems,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 10, no. 6, pp. 888-896, 1988.

[2] R. B. Banerji, “A language for the description of concepts,” General Systems, vol. 9, no. 1, pp. 135-141, 1964.

[3] R. Battiti, “Using mutual information for selecting features in supervised neural net learning,” IEEE Transactions on Neural Networks, vol. 5, no. 4, pp. 537-550, 1994.

[4] B. E. Boser, I. M. Guyon, and V. N. Vapnik, “A training algorithm for optimal margin classifiers,” Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, Pennsylvania, 1992, pp.144-152.

[5] J. Catlett, “On changing continuous attributes into ordered discretize attributes,” Proceedings of the Fifth European Working Session on Learning, Berlin, Germany, 1991, pp. 164-178.

[6] S. M. Chen and C. H. Chang, "A new method to construct membership functions and generate weighted fuzzy rules from training instances,"

Cybernetics and Systems: An International Journal, vol. 36, no. 4, pp.

397-414, 2005.

[7] S. M. Chen and J. D. Shie, “A new method for feature subset selection for handling classification problems,” Proceedings of the 2005 IEEE International Conference on Fuzzy Systems, Reno, Nevada, 2005, pp.

183-188.

[8] S. M. Chen and C. H. Yu, "A new method to generate fuzzy rules from training instances for handling classification problems," Cybernetics and Systems: An International Journal, vol. 34, no. 3, pp. 217-232, 2003.

[9] T. M. Cover and P. E. Hart, “Nearest Neighbor Pattern Classification,”

IEEE Transactions on Information Theory, vol. IT-13, no. 1, pp. 21-27, 1967.

[10] R. A. Fisher, “The use of multiple measurements in taxonomic problems,” Annals of Eugenics, vol. 7, no. 2, pp 179-188, 1936.

[11] J. A. Hartigan and M. A. Wong, “A k-means clustering algorithm,”

Journal of the Royal Statistical Society: Series C (Applied Statistics), vol. 28, no. 1, pp. 100-108, 1979.

[12] E. T. Jaynes, “Information theory and statistical mechanics,” Physical Review, vol. 106, no. 4, pp. 620-630, 1957.

[13] G. H. John and P. Langley, “Estimating continuous distributions in Bayesian classifiers,” Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence, Montreal, Canada, 1995, pp.

338-345.

[14] B. Kosko, “Fuzzy entropy and conditioning,” Information Sciences, vol.

40, no. 2, pp. 165-174, 1986.

[15] H. M. Lee, C. M. Chen, J. M. Chen, and Y. L. Jou,” An efficient fuzzy classifier with feature selection based on fuzzy entropy”, IEEE Transactions on Systems, Man and Cybernetics-Part B: Cybernetics, vol. 31, no. 3, pp. 426-432, 2001.

[16] A. D. Luca and S. Termini, “A definition of a non-probabilistic entropy in the setting of fuzzy set theory,” Information and Control, vol. 20, no.

4, pp. 301-312, 1972.

[17] W. S. McCulloch and W. Pitts, “A logical calculus of the ideas immanent in nervous activity,” Bulletin of Mathematical Biophysics, vol. 5, no. 1, pp. 115-133, 1943.

[18] T. M. Mitchell, Machine Learning, New York: McGraw-Hill, 1997.

[19] B. T. Ongkowijaya and Z. Xiaoyan, “A new weighted feature approach based on GA for speech recognition,” Proceedings of the 7th International Conference on Signal Processing, Istanbul, Turkey, 2004, pp. 663-666.

[20] J. C. Platt, “Using analytic QP and sparseness to speed training of support vector machines,” Proceedings of the Thirteenth Annual Conference on Neural Information Processing Systems,” Denver, Colorado, 1999, pp. 557-563.

[21] J. R. Quinlan, C4.5: Programs for Machine Learning, San Francisco:

Morgan Kaufmann, 1993.

[22] J. R. Quinlan, “Induction of decision trees,” Machine Learning, vol. 1, no. 1, pp. 81-106, 1986.

[23] V. E. Ramesh and M. N. Murty, “Off-line signature verification using genetically optimized weighted features,” Pattern Recognition, vol. 32, no. 1, pp. 217-233, 1999.

[24] C. Schaffer, “Overfitting avoidance as bias,” Machine Learning, vol. 10, no. 2, pp. 153-178, 1993.

[25] C. E. Shannon, “A mathematical theory of communication,” Bell System Technical Journal, vol. 27, no. 3, pp. 379-423, 1948.

[26] T. P. Wu and S. M. Chen, "A new method for constructing membership functions and fuzzy rules from training examples," IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, vol. 29, no. 1, pp. 25-40, 1999.

[27] L. A. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, pp. 338-353, 1965.

[28] L. A. Zadeh, “Probability measures of fuzzy events,” Journal of mathematical Analyses and Applications, vol. 23, no. 2, pp. 421-427, 1965.

[29] L. A. Zadeh, “The concept of linguistic variable and its application to approximate resoning-I,” Information Sciences, vol. 8, no. 3, pp.

199-245, 1975.

[30] UCI Repository of Machine Learning Databases and Domain Theories.

ftp://ftp.ics.uci.edu/pub/machine- learning-databases/.

[31] Weka (a free software), http://www.cs.waikato.ac.nz/ ml/weka/.

[32] IBM Lotus Notes, http://www-306.ibm.com/software/ lotus/.