有關對立圖形的探討 - 政大學術集成

全文

(1)國立政治大學應用數學系碩士學位論文. 政治大. 立有關對立圖形的探討. ‧ 國. 學. Some Problems on Opposition Graphs. ‧. n. er. io. sit. y. Nat. al. Ch. engchi. i n U. v. 碩士班學生：潘丞偉撰指導教授：張宜武博士中華民國 102 年 1 月 10 日.

(2) Contents. Abstract. ii. 中文摘要. iii. 1 Introduction. 1. 2 Definitions. 3. 3 Some Opposition Graphs. 立. 政治大. 7. R(T ) = ∅ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 8. 3.2. There Are Only One Vertex u in R . . . . . . . . . . . . . . . . . .. 11. 3.3. There Are Two Vertices u,v in R(T ) . . . . . . . . . . . . . . . . .. 16. 3.4. There Are More Than Two Vertices in R . . . . . . . . . . . . . . .. ‧. ‧ 國. 學. 3.1. sit. y. Nat. io. n. al. er. 4 Some Families of Opposition Graphs. i n U. v. 5 Open Problems and Further Directions of Studies References. 22. Ch. engchi. i. 24 28 29.

(3) Abstract In this thesis, we use the number of vertices with degree greater than or equal to 3 as a criterion for trees being opposition graphs. Finally, we prove some families of graphs such as Pn , Cn with n ≥ 3 and n = 4k, k ∈ N are opposition graphs and some families of graphs such as Tn , Cn with n ≥ 3 and n ̸= 4k, k ∈ N are not opposition graphs. keywords: Opposition Graphs.. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. ii. i n U. v.

(4) 中文摘要在這篇論文中，我們探討對立圖形的特性，並藉由度數大於等於三的點，判斷一樹是否為對立圖形，最後證明 Pn , Cn n ≥ 3 且 n = 4k, k ∈ N 家族的圖是對立圖形且 Tn , Cn n ≥ 3 且 n ̸= 4k, k ∈ N 家族的圖是對立圖形。關鍵詞：對立圖形. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. iii. i n U. v.

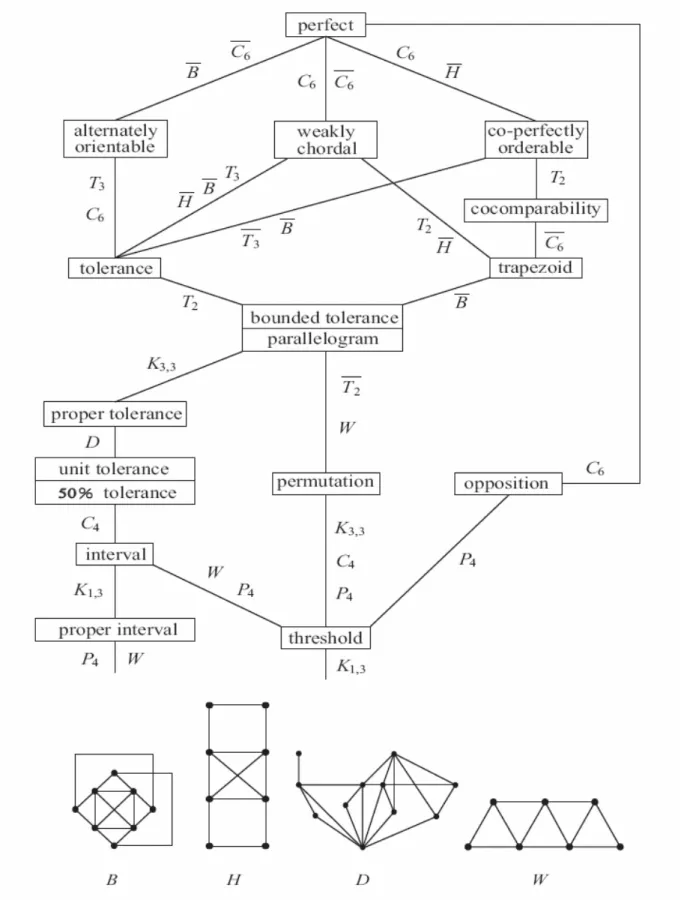
(5) 1. Introduction From the book [1], they introduce many containment relationships between. classes of graphs. In Figure 1, we can see the relations between opposition graphs and threshold graphs, and the relations between opposition graphs and perfect graphs. For example, P4 is an opposition graph but not a threshold graph; C6 is a perfect graph but not an opposition graph. Now we put our attention on the opposition graphs, we want to know what kind of graphs are opposition graphs. By [2] and [3], we define a graph G(V, E), where V = V (G) is the vertex set and E = E(G) is the edge set. Therefore, in chapter 2, we introduce some basic. 政治大. definitions and theorems. In chapter 3, we give a set R which is the set of vertices with degrees greater than or equal to 3. In section 3.1, we discuss the case when. 立. R is empty, then we create some ways to give an orientation to a path. In section. ‧ 國. 學. 3.2, we discuss the case that there is only one vertex in R, then we create a way to give an orientation to a rooted tree. In section 3.3, we discuss the case that there are two vertices in R. In section 3.4, we discuss that there are more than. ‧. two vertices in R, and find out the minimum obstruction for the class of opposition. y. Nat. graphs. In chapter 4, we prove some families of graphs such as Pn , Cn with n ≥ 3. sit. and n = 4k, k ∈ N are opposition graphs and some families of graphs such as Tn ,. al. n. some open problems and further directions of research.. Ch. engchi. 1. er. io. Cn with n ≥ 3 and n ̸= 4k, k ∈ N are not opposition graphs. Finally, we bring up. i n U. v.

(6) 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. i n U. v. Figure 1: A complete hierarchy of classes of perfect graphs.. 2.

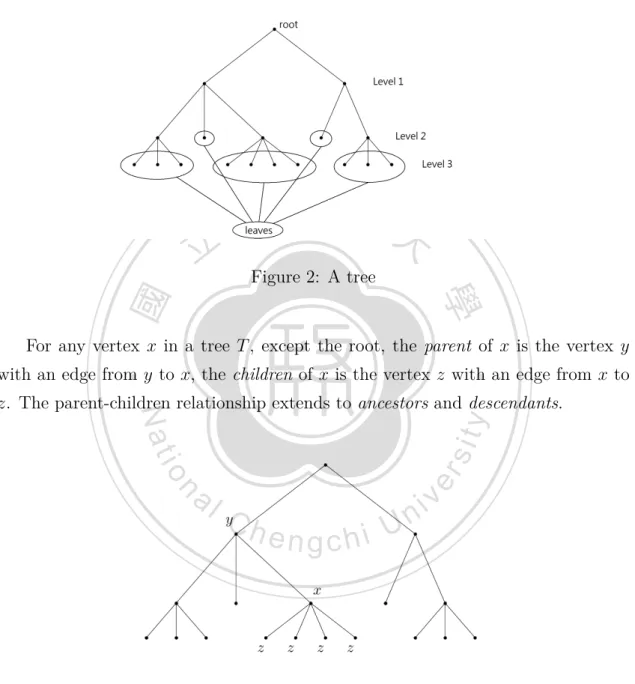
(7) 2. Definitions In this chapter, we mention some basic definitions about graphs and trees. For most of them, we follow [2] and [3]. A graph G is a triple consisting of a. vertex set V (G), an edge set E(G), and a relation that associates with each edge two vertices. Sometimes the edge are ordered pairs of vertices, called directed edges, the ordered pairs of vertices is called a direction. A directed graph or digraph G is a triple consisting of a vertex set V (G), an edge set E(G), and a function assigning each edge an ordered pair of vertices. The first vertex of the ordered pair is the tail of the edge, and the second is the head;. 政治大 head.An orientation of a graph G is a digraph D obtained from G by choosing an 立 orientation (u → v or v → u) for each edge uv ∈ G. together, they are the endpoints. We say that an edge is an edge from its tail to its. ‧ 國. 學. The degree of vertex v is the number of incident edges.. ‧. A subgraph of a graph G is a graph H such that V (H) ⊆ V (G) and E(H) ⊆ E(G) and the assignment of end points to edges in H is the same as in G. An induced. y. Nat. subgraph is a subgraph obtained by deleting a set of vertices. The complement G of. n. al. er. io. if and only if uv ̸∈ E(G).. sit. a simple graph G is the simple graph with vertex set V (G) defined by uv ∈ E(G). i n U. v. A path P is a simple graph whose vertices can be ordered so that two vertices. Ch. engchi. are adjacent if and only if they are consecutive in the list. A path with n vertices is call Pn . A cycle C is a graph with an equal number of vertices and edges whose vertices can be placed around a circle so that two vertices are adjacent if and only if they appear consecutively along the circle. A cycle with n vertices is call Cn . A graph with no cycle is acyclic. If G is a u, v-path, then the distance from u to v, written d(u, v), is the least length of u, v-path. A graph G is connected if it has a u, v-path whenever u, v ∈ V (G). A tree is a connected acyclic graph. One can define a tree as a graph with a designated vertex called a root such that there is a unique path from the root to any other vertex in the tree. If a tree is unoriented, then any vertex can be the root.. 3.

(8) A leaf is a vertex of degree 1. The level number of a vertex x in a tree T is the length from the root u to x. The height of a tree is the length of the longest path form root, equivalently, the largest level number of any vertex.. 立. 政治大 Figure 2: A tree. ‧ 國. 學. For any vertex x in a tree T , except the root, the parent of x is the vertex y. ‧. with an edge from y to x, the children of x is the vertex z with an edge from x to. n. al. er. io. sit. y. Nat. z. The parent-children relationship extends to ancestors and descendants.. Ch. engchi. i n U. v. Figure 3: y is the parent of x; z are the children of x; y is an ancestor of z; z are the descendants of y.. 4.

(9) Note the difference between “maximal” and “maximum”. As adjectives, maximum means “maximum-sized”, and maximal means “no larger one contains this one”. Example 2.1. In Figure 4, the path v1 − v2 − v3 − v4 is a maximum path and a maximal path. The path v1 − v2 − v5 is a maximal path but not a maximum path.. 學. ‧ 國. 立. 政治大 Figure 4:. ‧. Definition 2.2. A graph G is called an opposition graph if we can give an orienta-. Nat. sit. y. tion of its edge such that in every induced P4 , the two end edges both either point. io. n. al. er. inwards or outwards.. i n U. v. We know that if G is an opposition graph, then every induced P4 must be shown as Figure 5. Ch. engchi. Figure 5: An orientation. 5.

(10) Example 2.3. The graph C8 is an opposition graph shown as Figure 6.. Figure 6: The graph C8 is an opposition graph.. 政治大. Example 2.4. In the graph C5 , we can give an orientation for C5 . If the direction for the edge v1 v2 is v1 → v2 , we must have the following directions: v4 → v3 , v5 →. 立. v1 , v3 → v2 , then there are no direction for the edge v4 v5 . Similar for the direction. ‧. ‧ 國. as Figure 7.. 學. for the edge v1 v2 is v2 → v1 . Hence, the graph C5 is not an opposition graph shown. n. er. io. sit. y. Nat. al. Ch. engchi. i n U. v. Figure 7: The graph C5 is not an opposition graph.. Definition 2.5. A graph G is called a threshold graph if it does not contain a P4 , C4 , and C4 as induced subgraphs. Proposition 2.6. If a graph G is a threshold graph, then G is an opposition graph. Proof. If G is a threshold graph, then G has no induced P4 . Hence, G is an opposition graph.. 6.

(11) 3. Some Opposition Graphs In this chapter, we will discuss relations between opposition graphs and trees.. Let T be a tree. Let R(T ) = {x ∈ v(T ) | deg(x) > 3}, we have the following four cases : Case 1 R(T ) = ∅. Case 2 There is only one vertex u in R(T ). Case 3 There are two vertices u,v in R(T ).. 政治大. Case 4 There are more than two vertices in R(T ).. 立. For a tree T , we will show that T is an opposition graph if and only if any two. ‧ 國. 學. vertices in R(T ) have even distance. We also find the minimal obstruction for trees as opposition graphs.. ‧. n. er. io. sit. y. Nat. al. Ch. engchi. 7. i n U. v.

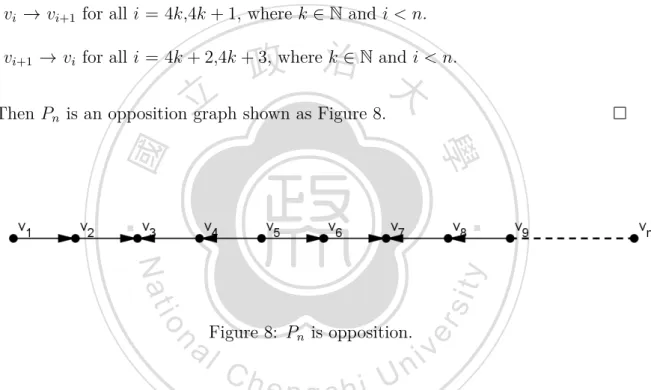
(12) 3.1. R(T ) = ∅ In this section, we discuss the case R(T ) = ∅. Every vertex in the tree T has. only degree 1 or 2, so T is a path Pn . Theorem 3.1. The path Pn is an opposition graph. Proof. Let v1 ,v2 ,..., vn be the vertices of Pn . We can give an orientation of Pn as follows : vi → vi+1 for all i = 4k,4k + 1, where k ∈ N and i < n.. 政治大. vi+1 → vi for all i = 4k + 2,4k + 3, where k ∈ N and i < n.. 立. Then Pn is an opposition graph shown as Figure 8.. ‧. ‧ 國. 學 er. io. sit. y. Nat. n. a lFigure 8: P is opposition. i v n Ch U e n graph. c h iThe orientation of G which satisfy Definition 3.2. Let G be an opposition g n. the definition of opposition graphs is called the oppositional orientation. Theorem 3.3. There are only four oppositional orientations of Pn :. Proof. Let v1 ,v2 ,...,vn be the vertices of Pn . Case 1 If the direction between v1 and v2 is v1 → v2 , then we must have the following directions: vi → vi+1 for all i = 4k + 1, where k ∈ N and i < n.. 8.

(13) vi+1 → vi for all i = 4k + 3, where k ∈ N and i < n. Then we have two subcases: subcase 1 The direction between v2 and v3 is v2 → v3 , then we have the following directions: vi → vi+1 for all i = 4k + 2, where k ∈ N and i < n. vi+1 → vi for all i = 4k + 4, where k ∈ N and i < n. subcase 2 The direction between v2 and v3 is v3 → v2 , then we have the following directions: vi → vi+1 for all i = 4k + 4, where k ∈ N and i < n.. 政治大. vi+1 → vi for all i = 4k + 2, where k ∈ N and i < n.. 立. Case 2 If the direction between v1 and v2 is v2 → v1 , then we must have the. ‧ 國. 學. following directions:. vi → vi+1 for all i = 4k + 3, where k ∈ N and i < n.. sit. y. Nat. Then we have two subcases:. ‧. vi+1 → vi for all i = 4k + 1, where k ∈ N and i < n.. er. io. subcase 1 The direction between v2 and v3 is v3 → v2 , then we have the following directions:. n. al. Ch. i n U. v. vi → vi+1 for all i = 4k + 4, where k ∈ N and i < n.. engchi. vi+1 → vi for all i = 4k + 2, where k ∈ N and i < n. subcase 2 The direction between v2 and v3 is v2 → v3 , then we have the following directions: vi → vi+1 for all i = 4k + 2, where k ∈ N and i < n. vi+1 → vi for all i = 4k + 4, where k ∈ N and i < n.. 9.

(14) Theorem 3.3 told us that there are only four oppositional orientations D1 , D2 , D3 and D4 for a path. We can choose any one of these four oppositional orientations to give an orientation for a path.. 立. 政治大. ‧ 國. 學 Figure 9: the orientation of Pn .. ‧. n. er. io. sit. y. Nat. al. Ch. engchi. 10. i n U. v.

(15) 3.2. There Are Only One Vertex u in R If there is only one vertex u in R(T ), then T must be the tree shown as Figure 10,. we call it sunshine graph. We will discuss whether T is an opposition graph.. 立. 政治大. ‧. ‧ 國. 學 y er. io. sit. Nat. Figure 10: Sunshine graph.. Theorem 3.4. If T is a sunshine graph, then T is an opposition graph.. n. al. Ch. engchi. i n U. v. Proof. Let u ∈ R(T ) be the root of T . We can give an orientation for the edges of T as follows :. Level i → level i + 1 for all i = 4k, 4k + 1, where k ∈ N and i < l, l is the height of T . Level i + 1 → level i for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T . Then T is an opposition graph shown as Figure 11.. 11.

(16) 立. 政治大. ‧ 國. 學 ‧. Figure 11: Sunshine graph is an opposition graph.. y. Nat. sit. Theorem 3.5. For a sunshine graph T . Let u be the root of T . If there are at. er. al. n. sunshine graph T .. io. least two vertices in level 2, then there are only two oppositional orientations for a. Ch. engchi. i n U. v. Proof. Let T be a sunshine graph. Let u ∈ R(T ) be the root of the tree T . There are n paths from u to leaves Q1 , Q2 ,...,Qn . By Theorem 3.3, there are only four oppositional orientations for a path. case 1 If the orientation of Q1 is D1 , then the orientation of Q2 ,...,Qn must be D1 . Hence, the orientation of T is level i → level i + 1 for all i = 4k, 4k + 1 and level i + 1 → level i for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T . case 2 If the orientation of Q1 is D2 , then the orientation of Q2 ,...,Qn must be D2 . Hence, the orientation of T is level i + 1 → level i for all i = 4k, 4k + 1, and. 12.

(17) level i → level i + 1 for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T . Suppose the vertices of level 1 in Q1 , Q2 , Q3 are v11 , v12 , v13 , and suppose the vertices of level 2 in Q1 , Q2 , are v21 , v22 . case 3 If the orientation of Q1 is D3 , then the directions of T must be v12 → u, v12 → v22 , v13 → u. Hence, the orientation of the path v13 uv12 v22 gives us a contradiction. case 4 If the orientation of Q1 is D4 , then the directions of T must be u → v12 , v22 → v12 , u → v13 . Hence, the orientation of the path v13 uv12 v22 gives us a contradiction.. 立. 政治大. So there are only two oppositional orientations for a sunshine graph T .. ‧ 國. 學. By Theorem 3.5, we can give another orientation of edges of T as follows :. ‧. Level i ← level i + 1 for all i = 4k, 4k + 1, where k ∈ N and i < l, l is the height. sit. y. Nat. of T .. io. height of T .. n. al. er. Level i + 1 ← level i for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the. Ch. engchi. Then T is an opposition graph shown as Figure. i n 12. U. v. Corollary 3.6. For a sunshine graph T . Let u be the root of T . If there are at least two vertices in level 2, then the orientation of T must be given as follows: Level i → level i + 1 for all i = 4k, 4k + 1, where k ∈ N and i < l, l is the height of T . Level i + 1 → level i for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T .. Proof. By Theorem 3.5, there are two orientations for T , these two orientations are symmetric, so we can use case1 to give the orientation for T .. 13.

(18) 立. 政治大. ‧ 國. 學. Figure 12: An sunshine graph is an opposition graph.. ‧. Theorem 3.7. For a tree T . Let u be the root of T . If there are at least two vertices in level two and T is opposition, then the orientation of T must be given as follows:. y. Nat. n. al. er. io. of T .. sit. Level i → level i + 1 for all i = 4k, 4k + 1, where k ∈ N and i < l, l is the height. i n U. v. Level i + 1 → level i for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T .. Ch. engchi. Proof. Let T be a tree. Suppose R(T ) = {u, u1 , u2 ...un }. There is a maximal subtree T1 containing u which is a sunshine graph. Then T can be decomposed into T1 and some paths Q1 , Q2 , ..., Qk with one of endpoints in R(T ). Because T1 is a sunshine graph, the orientation is given by Corollary 3.6. Now we add all paths Qi into T1 . Suppose uj is an endpoint of Qi . Then uuj union Qi is a path, the orientation of this path is given by case 1 of Theorem 3.3. Hence, the orientation of T must be given as follows: Level i → level i + 1 for all i = 4k, 4k + 1, where k ∈ N and i < l, l is the height of T .. 14.

(19) Level i + 1 → level i for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T .. Now, by Theorem 3.7, when we want to determine if a tree T is an opposition graph, we can give the orientation by only one way: Let u ∈ R(T ) be the root. Level i → level i + 1 for all i = 4k, 4k + 1 and level i + 1 → level i for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T . When the orientation is given as above, if some induced P4 doesn’t satisfy the definition of opposition graphs, then T is not an opposition graph.. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 15. i n U. v.

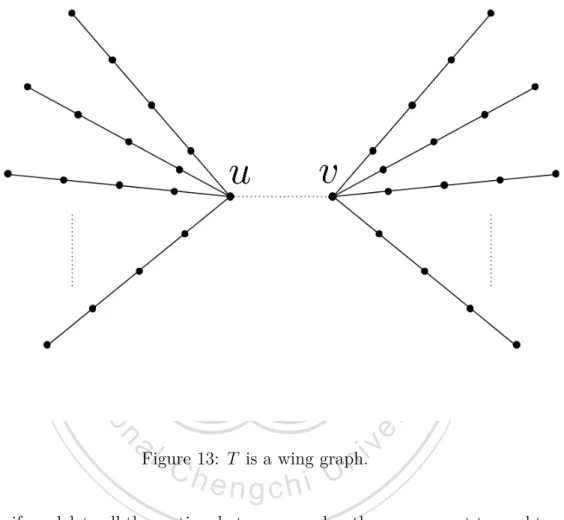
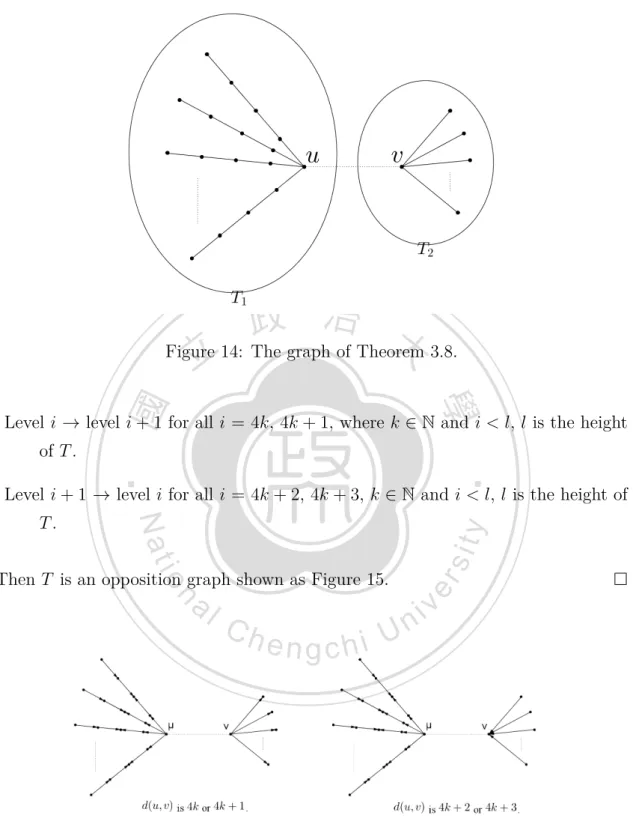
(20) 3.3. There Are Two Vertices u,v in R(T ) If there are exactly two vertices u and v in R(T ), then T must be the tree shown. as Figure 13, we call it wing graph. We will discuss whether T is an opposition graph.. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. i n U. Figure 13: T is a wing graph.. engchi. v. Now, if we delete all the vertices between u and v, then we can get two subtrees containing u and v, we call them T1 and T2 . Observably, the degrees of u and v are greater than or equal to 2. The trees T1 and T2 are paths or sunshine graphs because the degrees of every vertices are less than 3 except u and v. Theorem 3.8. Let T be a tree with exactly two vertices u, v in R(T ). Let T1 and T2 be the subtrees from deleting the vertices between u and v. If at least one of T1 and T2 does not contain P4 , then T is an opposition graph. Proof. Suppose T2 does not contain P4 and v is in T2 . Let u be the root of the tree T. We can give an orientation of edges of T as follows :. 16.

(21) 政治大 Figure 14: The graph of Theorem 3.8. 立. ‧ 國. 學. Level i → level i + 1 for all i = 4k, 4k + 1, where k ∈ N and i < l, l is the height of T .. ‧. Level i + 1 → level i for all i = 4k + 2, 4k + 3, k ∈ N and i < l, l is the height of. n. al. Ch. engchi. er. io. Then T is an opposition graph shown as Figure 15.. sit. y. Nat. T.. i n U. v. Figure 15: The orientation of Theorem 3.8.. 17.

(22) Theorem 3.9. Let T be a tree and v ∈ R(T ). There are n paths Q1 , Q2 ,...,Qn with endpoint v. Let v11 ∈ Q1 , v12 ∈ Q2 ,...,v1n ∈ Qn be the vertices whose distance from v is 1. Let v21 ∈ Q1 , v22 ∈ Q2 ,...,v2n ∈ Qn be some vertices whose distance from v is 2. If T is an opposition graph, then the directions of the edges uv1i and v1i v2i must be as follows: Case 1 The directions are v → v1i for all i = 1, ..., n and v1i → v2i for all i = 1, ..., n. Case 2 The directions are v1i → v for all i = 1, ..., n and v2i → v1i for all i = 1, ..., n.. 政治大 Proof. T is a tree. Let u ∈ R(T ) be the root of T . Suppose the path Q is between 立 u and v. By Theorem 3.7, we give an orientation for T , there are two cases in the 1. ‧ 國. 學. edge between v11 and v21 :. ‧. Case 1 If we give the direction v11 → v21 , then the directions of the edges uv1i and v1i v2i is v → v1i for all i = 2, ..., n, v1i → v2i for some i = 2, ..., n, and v →. sit. y. Nat. v11 .. er. io. Case 2 If we give the direction v21 → v11 , then the directions of the edges uv1i and v1i v2i is v1i → v for all i = 2, ..., n, v2i → v1i for some i = 2, ..., n, and v11 →. al. n. v.. Ch. engchi. i n U. v. So there are only two cases for the directions of the edges uv1i and v1i v2i .. Figure 16: The orientation of Theorem 3.9.. 18.

(23) Theorem 3.9 can give us a way to determine if T is an opposition graph. For a tree T , by Theorem 3.7, we can give an orientation, then the orientation of every vertex u in R(T ) must satisfy Theorem 3.9. If the orientation of any vertex u in R(T ) doesn’t satisfy Theorem 3.9, then T is not an opposition graph. Then we will discuss that both T1 and T2 contain P4 . We have the following two cases : Case 1 If dist(u,v) is odd. Case 2 If dist(u,v) is even.. 治政大u and v. If both T T be the subtrees from deleting the vertices between 立odd, then T is not an opposition graph. contain P and dist(u,v) is. Theorem 3.10. Let T be a tree with exactly two vertices u, v in R(T ). Let T1 and 2. 1. and T2. 4. ‧ 國. 學. Proof. Suppose u is in T1 and v is in T2 . Let u be the root of the tree T . We can give an orientation of edges of T by Corollary 3.7. Then the orientation of T is. ‧. shown as Figure 17. The orientation of T2 doesn’t satisfy Theorem 3.9, so T is not. sit. y. Nat. an opposition graph.. al. er. io. Theorem 3.11. Let T be a tree with exactly two vertices u, v in R(T ). Let T1 and. n. T2 be the subtrees from deleting the vertices between u and v. If both T1 and T2. Ch. i n U. v. contain P4 and dist(u,v) is even, then T is an opposition graph.. engchi. Proof. Let u be the root of the tree T . We can give an orientation of edges of T by Corollary 3.7. Then the orientation of T is shown as Figure 18, so T is an opposition graph.. 19.

(24) 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. i n U. v. Figure 17: The orientation of Theorem 3.10.. 20.

(25) 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. i n U. v. Figure 18: The orientation of Theorem 3.11.. 21.

(26) 3.4. There Are More Than Two Vertices in R. Theorem 3.12. Let T be a tree. Let R(T ) = {v1 , v2 , ..., vn } be the set of vertices in T whose degree is greater than or equal to 3. If d(vi , vi+1 ) is even for all i = 1, ..., n, then T is an opposition graph. Proof. We use the induction on R(T ) to prove the statement. Let T be a tree and R(T ) = {v1 , v2 ...vn } be the set of vertices in T which degree is greater than or equal to 3. Basic step Suppose n=2. By Theorem 3.11, T is an opposition graph.. 政治大 dist(v(i, v ) ≤ dist(v , v ) for all i < j. Let T be the subtree of T whose 立 vertex set V (T ) are v and all of its descendant. Let T be the subtree of T. Induction step Suppose n > 2. Let v1 be the root of the tree T . Suppose 1. j. n. 1. n. ′. n. ‧ 國. T ′ is an opposition graph by induction hypothesis.. 學. whose vertex set V (T ′ ) are {vn } ∪ V (T ) − V (Tn ). Now, |R(T ′ )| = n − 1, so. ‧. Let v1 be the root of T ′ . We can give an orientation to T ′ :. Nat. Level i → level i + 1 for all i = 4k, 4k + 1, where k ∈ N and i < l, l is the. sit. y. height of T ′ .. er. io. Level i + 1 → level i for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T ′ .. al. n. v i n C h for T and add UT to T . Let v Then we give the orientation engchi n. n. ′. n. be the root of. Tn . There are two cases in Tn :. case 1 If d(v1 , vn ) = 4k, then level i → level i + 1 for all i = 4k, 4k + 1 and level i + 1 → level i for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T . case 2 If d(v1 , vn ) = 4k + 2, then level i + 1 → level i for all i = 4k, 4k + 1 and level i → level i + 1 for all i = 4k + 2, 4k + 3, where k ∈ N and i < l, l is the height of T . Hence, T is an opposition graph for n > 2.. 22.

(27) Definition 3.13. Let the path u1 u2 u3 u4 and v1 v2 v3 v4 be two P4 . We add an odd path between u2 and v2 , the graph is called H graph shown as Figure 19.. 立. 政治大. ‧ 國. 學 Figure 19: H graph.. ‧ sit. y. Nat. Theorem 3.14. If T be an H graph, then T is a minimal obstruction for the class. io. er. of opposition graphs.. al. n. v i n C3.4, than or equal to 3, by Theorem h eT nis gancopposition i U graph. If we remove u , the h path u u u is a P , then by Theorem 3.8, T is an opposition graph. Similar for Proof. If we remove u1 , then there is only one vertex v2 which degree is greater 4. 1 2 3. 3. the vertices v1 and v4 .. 23.

(28) 4. Some Families of Opposition Graphs. Theorem 4.1. If P is an induced P4 in G, then P is an induced P4 in G. Proof. If the path abcd is an induced P4 in G, then cadb is an induced P4 in G Corollary 4.2. P is an induced P4 in G if and only if P is an induced P4 in G. Proof. P is an induced P4 in G, by Theorem 4.1, P is an induced P4 in G. P is an induced P4 in G, by Lemma 4.1, P is an induced P4 in G If the path vi vi+1 vi+2 vi+3 is an induced P4 in Pn , then the path vi+2 vi vi+3 vi+1 is an induced P4 in P n. 立. 政治大. y. ‧. ‧ 國. 學. Nat. n. Ch. engchi. er. io. al. Theorem 4.3. Pn is an opposition graph.. sit. Figure 20:. i n U. v. Proof. Let Pn be v1 , v2 , v3 ,...,vn . We give an orientation for Pn as following : vk+2 → vk for all k is even. vi → vj for all i < j. Then we can check the orientation for all induced P4 in Pn : Case 1 If n < 4, then Pn has no P4 , so Pn is an opposition graph. Case 2 If n ≥ 4, by Corollary 4.2, P is a P4 in Pn if and only if P is a P4 in Pn . Suppose the path vi vi+1 vi+2 vi+3 is an induced P4 in Pn , then the path vi+2 vi vi+3 vi+1 is an induced P4 in P n , the orientation is as follows : 24.

(29) Figure 21:. If i is odd, then the orientation is vi+2 ←vi →vi+3 →vi+1 , shown as Figure 21. 政治大 If i is even, then the 立orientation is v →v →v ←v (a).. i+2. i. i+1 ,. i+3. shown as Figure 21. (b).. ‧ 國. 學. So Pn is an opposition graph.. ‧ y. Nat. er. io. al. sit. Theorem 4.4. T2 is not an opposition graph.. n. Proof. T2 is expressed in Figure 22, there are six P4 in T2 : a2 a1 ob1 , a2 a1 oc1 , b2 b1 oa1 ,. Ch. i n U. v. b2 b1 oc1 , c2 c1 oa1 , c2 c1 ob1 . By Theorem 4.2, there are six P4 in T 2 : a1 b1 a2 o, a1 c1 a2 o,. engchi. b1 a1 b2 o, b1 c1 b2 o, c1 a1 c2 o, c1 b1 c2 o. We can suppose the direction of the edge a1 b1 is a1 → b1 , then we have the following direction : o → a2 , a1 → c1 , c2 → o, b1 → c1 , b2 → o, then the P4 b1 a1 b2 o gives us a contradictory. Similar for the direction b1 → a1 . So T2 is not an opposition graph. Corollary 4.5. Tn is not an opposition graph for all n > 1. Proof. Because Ti ⊆ Tj for all i < j, so T i ⊆ T j for all i < j. By Theorem 4.4, T2 is not an opposition graph, so Tn is not an opposition graph for all n > 1. Theorem 4.6. The graphs Cn is an opposition graph if and only if n = 4k or n = 3.. 25.

(30) 立. 政治大 Figure 22: T 2. ‧ 國. 學. Proof. The graphs C3 and C4 don’t have an induced P4 , so C3 and C4 are opposition graphs. Let v1 , v2 , v3 , ..., vn be the vertices of Cn . Deleting the edge vn v1 , the graph. ‧. sit. Nat. vi → vi+1 for all i = 4k, 4k + 1, where k ∈ N and i < n.. y. is a path Pn . By Theorem 3.3, we can give an orientation as follows :. er. io. vi+1 → vi for all i = 4k + 2, 4k + 3, where k ∈ N and i < n.. al. n. v i n case 1 If n = 4k where k ∈ N, of the edge v v C hthen the orientation U i e h n Hence, C is an opposition graph. g c. n 1. is v1 → vn .. n. case 2 If n = 4k + 1 where k ∈ N, then the path v4k−1 v4k v4k+1 v1 is an induced P4 , the orientation of the edge v4k+1 v1 is v4k+1 → v1 . The induced P4 v4k+1 v1 v2 v3 gives us a contradictory, so Cn is not an opposition graph. case 3 If n = 4k + 2 where k ∈ N, then the path v4k v4k+1 v4k+2 v1 is an induced P4 , the orientation of the edge v4k+2 v1 is v4k+2 → v1 . The induced P4 v4k+2 v1 v2 v3 gives us a contradictory, so Cn is not an opposition graph. case 4 If n = 4k + 3 where k ∈ N, then the path v4k+1 v4k+2 v4k+3 v1 is an induced P4 , the orientation of the edge v4k+3 v1 is v1 → v4k+3 . The induced P4 v4k+2 v4k+3 v1 v2 gives us a contradictory, so Cn is not an opposition graph. 26.

(31) Hence, Cn is an opposition graph if and only if n = 4k or n = 3.. Figure 23:. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 27. i n U. v.

(32) 5. Open Problems and Further Directions of Studies In this article, we prove some graphs are opposition graphs. In a tree T , R is. the set of vertices with degree greater than or equal to 3, if every distance of any two vertices is even, then T is an opposition graph. In a cycle Cn , if n = 4k for all k is integer, then Cn is an opposition graph. There are still some open problems for future studies: 1. In Chapter 3, we have known some classes of trees are opposition graphs. Furthermore,. 治政 being opposition graphs. 大立 b. We would like to find out the necessary and sufficient conditions of any a. We would like to find out the necessary and sufficient conditions of trees. ‧ 國. 學. graph being an opposition graph.. 2. In the Figure 1, we know that P4 is an opposition graph but not a threshold. ‧. graph; C6 is a perfect graph but not an opposition graph. Furthermore,. y. Nat. a. We would like to find out the relation between opposition graphs and. io. sit. perfect graphs.. n. al. er. b. We would like to find out the relation between opposition graphs and the other graphs.. Ch. engchi. 28. i n U. v.

(33) References [1] A. N. Trenk, Tolerance Graphs, Cambridge Univ Pr, 2004. [2] A. Tucker, Applied Combinatorics, Wiley, 2006. [3] D. B. West, Introduction to Graph Theory, Prentice Hall, 2001.. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 29. i n U. v.

(34)