Fault Diameter of the Cayley Graphs Based on the Alternating Group

全文

(1)FAULT DIAMETER OF THE CAYLEY GRAPHS BASED ON THE ALTERNATING GROUP Chin-Tsai Lin Department of Information Management, Da-Yeh University Taiwan, Republic of China. ctlin@mail.dyu.edu.tw Abstract The paper computes the exact fault diameter of the Cayley graphs based on the alternating group. The fault diameter of a graph is the maximum diameter achieved when we delete from the original graph any set of nodes that is smaller than its node connectivity. Based on the algebraic properties of the generators, we show that the fault diameter is the original diameter plus one. Keywords: Interconnection networks, Cayley graphs, alternating group, fault diameter. 1. INTRODUCTION Group graphs provide a rich framework for the design of the topology of interconnection networks. Famous network topologies such as hypercube[4], star graphs[1], etc. are all able to be modeled as Cayley graphs[2]. Alternating group graphs[8], introduced by Jwo, Lakshmivarahan and Dhall, are Cayley graphs based on the alternating groups. They have shown that alternating group graphs are edge symmetry, 2-transitive, Hamiltonian and strongly hierarchical. They also describe algorithms for embedding of a class of multidimensional grids with unit expansion and dilation three and embedding of a variety of cycles with unit dilation. The simulations of greedy routing on hypercubes, star graphs and alternating group graph have been evaluated. It shows that alternating group graphs offer the best performance with respect to delay time and maximum queue length. The alternating group graphs are defined as follows. Let <n>={1, 2, …, n}, p = p1p2…pn, pi∈<n> and pi≠pj for i ≠ j, where pi denotes the element at position i for 1 ≤ i ≤ n. That is, p is a permutation of <n>. The permutation p can also be represented by its cycle structure as p = c1c2…cke1e2…el, where ci is a cycle of length |ci| ≥ 2 for 1 ≤ i ≤ k and ei is k. an invariant for 1 ≤ i ≤ l. Thus, n = ∑ i =1 |ci| + l. For convenience, the set of all invariants may be omitted in the cycle representation of p. For example, the cycle. structure of permutation 132546 is (23)(45)(1)(6), where (1) and (6) are invariants and may be omitted. Let ζ(p) denote the number of inversions in p. The parity of p is ζ defined as η(p) = (-1) (p) . A permutation is called even or odd depending on its parity being +1 or –1. Thus, 132546 is an even permutation. Let Sn be the symmetric group, i.e., Sn contains all the permutations of n elements. The alternating group An contains the set of all even permutations of Sn, where |An| = n!/2. Let gi+ = (1 2 i), gi- = (1 i 2) and Ω = {gi+ | 3≤ i ≤ n}∪{gi-|3≤ i ≤n}. It is well known that Ω is a generator set for An. Definition 1. An alternating group graph of dimension n, AGn = (Vn, En), is defined as Vn = An, the set of all even permutations of <n> and En = {(p, q) | p, q ∈ An, q= p⋅ h, for h ∈ Ω}, where "⋅" is the usual binary combination operator defined as f ⋅ g(x) = f (g(x)). An important parameter for graphs is their fault tolerance and fault diameter. The fault tolerance of a graph is defined as the maximum number of nodes that can be removed from it provided that the remaining graph is still connected. Hence, the fault tolerance of a graph is defined to be one less than its connectivity. By the theorems proved in [5], the connectivity of the alternating group graphs is optimal, i.e., equal to the degree. Fault diameter d f of the graph G with fault tolerance f is defined as the maximum diameter of any graph obtained from G by deleting at most f nodes. If an interconnection network is to be used as a multicomputer communication medium, it is very important that its fault diameter is close to its normal diameter. A family of graphs {Gn} is defined to be strongly resilient if the fault diameter dn f of any member of the family Gn is at most dn + k, where dn is the normal diameter of Gn and k is a constant independent of n. We will show that for the alternating group graphs, the fault diameter is the original diameter plus one..

(2) 2. BACKGROUND The n dimensional alternating group graph AGn is a regular graph with degree 2(n-2), |Vn| = n!/2, |En| = (n-2) × n!/2, diameter dn = 3 × (n-2)/2, and the connectivity is 2(n-2). Alternating group graphs have a highly recursive structure. AGn is made up of n copies of AGn-1. An understanding of the routing algorithm is essential for our development. Let s, d ∈ An. By definition, (s, d) ∈ En if and only if d = s⋅ h, h∈Ω. By extending the notion of an edge in AGn, the path from s to d can be represented by a sequence of generators: Path(s, d) = h1 ⋅ h2 ⋅⋅⋅ ht, that is, d = s ⋅ h1 ⋅ h2 ⋅⋅⋅ ht, where hi ∈ Ω for 1≤ i ≤ t. By group theory, we have I = d -1⋅ s ⋅ h1 ⋅ h2 ⋅⋅⋅ ht. Let p = d -1⋅ s. Then the properties of path from s to d can be analyzed by considering the path from p to I. So we can focus how to route from p to I only, and the routing is equivalent to sorting a permutation. Consider what is changed by a routing step on gi+ and gi-, 3≤ i ≤n. Clear, they rotate the three symbols at position 1, 2 and i with different directions. gi+ p1 p2 …pi …pn → p2 pi …p1 …pn gip1 p2 …pi …pn → pi p1 …p2 …pn As shown in the above figure, gi+ moves the symbol at position i to position 2, the symbol at position 2 to position 1, and the symbol at position 1 to position i; while gi- moves the symbol at position i to position 1, the symbol at position 1 to position 2, and the symbol at position 2 to position i. Obviously, gi+gi+ = gi-, gi-gi= gi+ and (gi+)-1 = gi-, 3 ≤ i ≤ n. To find the shortest path from p to I is to optimally sort the set of symbols in p using the basic rotations. (We say symbol i is sorted if it is at position i.) Notice that there is no need to sort symbol 1 and 2, they will be automatically sorted after sorting symbol 3, 4, …, n because it should be an even permutation. The shortest path routing algorithm from p = p1p2…pn to I may be described as follows: Let p' be the first node on the shortest path from p to I. Then, (1) p' = p⋅ gi+ or p' = p⋅ gi- for some i, where i is a noninvariant if p1, p2 ∈{1, 2}; (2) p' = p⋅ gi+, where i= p1 if p1 ∉{1, 2}; (3) p' = p⋅ gi-, where i= p2 if p2 ∉{1, 2}. Repeat the above process until the path reaches the node I.. As an example, let p = 14523 = (2 4)(5 3). A shortest path from p to I is as follows: 14523 g4- 21543 g3+ 15243 g5- 31245 g3+ 12345. Let Dp denote the length measured in terms of the number of edges in the shortest path from p to I. We have the following lemma [8]. Lemma 2. If p = c1c2…cke1e2…el ∈ An, then Dp = n+k-l if p1 = 1 and p2 = 2 = n+k-l-3 if p1 = 2 and p2 = 1 = n+k-l-2 if p1 ≠ 1 and p2 = 2 = n+k-l-2 if p1 = 1 and p2 ≠ 2 = n+k-l-3 if 1, 2∈ci for some i and | ci | ≥ 3 = n+k-l-4 if 1∈ci and 2∈cj, i≠j. The result of routing is obtained in the form of a product of generators. Since the product of two generators of alternating group graphs is not commutative, there is no trivial rule for finding alternative paths of the same length. However, like star graphs [6], rules for finding the alternative paths in an alternating group graph can be based on the concepts of “ordinary” and “barrel” products of generators. Ordinary and barrel products are basic parts of any shortest path that can be manipulated in order to obtain alternative paths. The whole analysis relies on the mapping of each generator to the corresponding movement of symbols. Therefore, the complex product can be tracked as a set of movements of symbols. Let σ(i) denote the sign + if i is even, or the sign - if i is odd. Definition 3. The initial product is the product of the following form: for some integer l, h1σ(l)h2σ(l+1) ⋅⋅⋅hnσ(l+n-1). Definition 4. The ordinary product is any product that is an arbitrary permutation of an arbitrary subset of k distinct-index generators with alternating signs from the initial product. Definition 5. The barrel product of generator is obtained when the first generator of an ordinary product is appended at the end of that product with alternating signs, i.e., the product of the following form: h1σ(i)h2σ(i+1) ⋅⋅⋅hnσ(i+n-1) h1σ(i+n). The properties of the barrel product are exposed in the following lemma and its corollaries. Lemma 6. For AGn, the following holds. (Inverting signs) g3+g4- ⋅⋅⋅ gn-2σ(n-3)gn-1σ(n-2)gnσ(n-1)g3σ(n) = g3-g4+ ⋅⋅⋅ gn-2σ(n-2)gn-1σ(n-1)gnσ(n)g3σ(n+1)..

(3) Lemma 7. For AGn, the following holds. (Rotation) g3+g4- ⋅⋅⋅ gn-2σ(n-3)gn-1σ(n-2)gnσ(n-1)g3σ(n) = g4-g5+ ⋅⋅⋅ gn-1σ(n-4)gnσ(n-3)g3σ(n-2)g4σ(n-1) …. =gn-1σ(n-2)gnσ(n-1)g3σ(n)g4σ(n+1)⋅⋅⋅gn-3σ(2n-6)gn-2σ(2n-5)gn-1σ(2n-4). Corollary 8. For AGn, let t1, t2, …, tm be distinct integers in <n>-{1, 2}. Then, gt1+gt2- ⋅⋅⋅ gtmσ(m-1)gt1σ(m). = gt1-gt2+ ⋅⋅⋅ gtmσ(m)gt1σ(m+1) σ(m-2). σ(m-1). σ(m). = gt2+ ⋅⋅⋅ gtm gt1 gt2 =… = gtm+gt1- ⋅⋅⋅ gtm-1σ(m-1)gtmσ(m). That is, Lemmas 6 and 7 hold when an arbitrary ordinary product is substituted for the ordinary part of barrel product. A barrel product of k distinct-index generators can be represented in 2k different ways, all preserving the same cyclic ordering of generators. Definition 9. Let ∏ = h1σ(l)h2σ(l+1) ⋅⋅⋅ hmσ(l+m-1) be an ordinary or barrel product. The invert-sign product ∏- of ∏ is h1σ(l+1)h2σ(l+2)⋅⋅⋅hmσ(l+m). The positive-sign product ∏+ of ∏ is ∏ itself. The following two lemmas introduce the law of commutativity between the ordinary and barrel subproducts of generators. Lemma 10. For AGn, let t1, t2, …, tm be distinct integers in <n>-{1, 2}. Then, gt1+gt2-⋅⋅⋅gtjσ(j-1)gt1σ(j) gtj+1σ(j+1)gtj+2σ(j+2) ⋅⋅⋅ gtmσ(m)gt j+1σ(m+1) = gtj +1+gtj+2- ⋅⋅⋅ gtmσ(m–j-1)gt j+1σ(m–j ) gt1σ(m–j +1)gt2σ(m–j +2) ⋅⋅⋅ gtjσ(m)gt1σ(m+1). =gt1+ gt2-⋅⋅⋅gtiσ(i-1) gtj+1σ(i) gtj+2σ(i+1) ⋅⋅⋅ gtmσ(i+m-j-1) gtj+1σ(i+m–j) gti+1σ(i+m–j+1) ⋅⋅⋅ gtjσ(m)gt1σ(m+1).. Lemma 11. For AGn, let t1, t2, …, tm be distinct integers in <n>-{1, 2}. Then, gt1+gt2-⋅⋅⋅ gtjσ(j-1) gtj+1σ(j+1)gtj+2σ(j+2) ⋅⋅⋅ gtmσ(m)gtj+1σ(m+1) = gt1+ gt2- ⋅⋅⋅ gtiσ(i-1) gtj+1σ(i)gtj+2σ(i+1)⋅⋅⋅gtmσ(i+m-j-1)gtj+1σ(i+m–j) gti+1σ(i+m–j+1) ⋅⋅⋅ gtjσ(m). = gtj+1σ(l)gtj+2σ(l+1)⋅⋅⋅gtmσ(l+m-j-1)gtj+1σ(l+m–j) gt1σ(m–j+1) gt2σ(m–j+2) ⋅⋅⋅ gtjσ(m).. When commuting with a barrel product that contains odd number of generators, the ordinary product should turn to. its invert-signed product. The following example will illustrate the nesting of subproducts. ∏o = g3+g4-g3+g5+g6= g5-g6+g3+g4-g3+ = g5-g6+g3-g4+g3= g5-g3-g4+g3-g6= g5-g3+g4-g3+g6-. Definition 12. The coupled ordinary product is a concatenation of two ordinary products such that all the generators are of distinct-index and their boundary is of the same sign, not alternating signs. For example, g3+g4-g5-g6+ is a coupled ordinary product. Lemma 13. Let ∏1 and ∏2 are two ordinary products. Suppose that ∏1∏2 is a coupled ordinary product. Then,. ∏1∏2=∏2σ(l) ∏1σ(m), where l and m are the numbers of generators contained in ∏1 and ∏2, respectively. Definition 14. The generalized ordinary product is either an ordinary product or a coupled ordinary product.. Corollary 15. If some product of generators in AGn, consists of k products of distinct sets of generators ∏o =∏1⋅∏2⋅⋅⋅∏i⋅⋅⋅∏k and if at most one of these products is a generalized ordinary one while all other products are of barrel type, then the ordering of products ∏i in the overall product ∏o is arbitrary except that the signs of the generalized ordinary one may be obligated to invert. Theorem 16. Every product of arbitrary number of generators in AGn can be reduced to product of k ≥ 1 subproducts of distinct sets of generators ∏m =∏1⋅∏2⋅⋅⋅∏i⋅⋅⋅∏k in which at most one subproduct is a generalized ordinary one and all others are of barrel type. Product ∏m cannot be further reduced, therefore it has the form of “minimal” product of generators. Without loss of generality, we let ∏1 be the generalized ordinary subproduct if it exists. Product ∏m will be referred to as minimal product and it actually represents the routing function in AGn. The diameter of AGn corresponds to the minimal product with the maximal number of generators. Since barrel product has the property of repeating the first generator, the maximal.

(4) length of the minimal product corresponds to the maximal number of barrel products in it. Lemma 17. The maximal number k of subproducts in a minimal product from Theorem 16 is (n-2)/2.. 3. FAULT DIAMETER Let us consider two nodes A and B in AGn and some shortest paths ∏AB between A and B. Suppose ∏AB =∏1⋅∏2⋅⋅⋅∏i⋅⋅⋅∏k, which has determined subsets of generators and their relative ordering for each ∏i. In case no adjacent nodes or channels has failed, the message is free to leave the node along the first generator of the ordinary subpaths (with a proper sign), or along any of the generator that belongs to any barrel subpath from ∏AB, without increasing the length of the path. Now, suppose that 2(n-2)–1 nodes that are adjacent to A have failed, and that the connection with the rest of the network is only along the channel corresponding to generator goσ(l), 3 ≤ o ≤ n and l∈N. In other words, the message is forced to leave the node A only along the channel goσ(l). Obviously, this tends to increase the path length between A and B. As a result or analysis, we shall compute worst cases of path lengthening, i.e., the fault diameter of AGn. We distinguish the following cases: (1) goσ(l) or goσ(l+1) is a generator contained in ∏AB. Then we have the following five subcases. (1.a) One of the barrel subproducts contains goσ(l) or σ(l+1) go . According to cummutativity of subproducts in the “minimal” product (shortest path), this subproduct can be put at the beginning of the path. Then according to the known features of barrel products, this subproduct can be transformed to its equivalent have goσ(l) at the beginning and at the end (with proper sign). Hence, a message can leave the node along goσ(l) without increasing the length of the path. Let us consider for example, path ∏AB = g3+g4-g5+g6-g5+ and goσ(l) = g6-. This path can be transformed in the following way: ∏AB= g3+g4- g5+g6-g5+ = g5+g6-g5+ g3-g4+ = g6-g5+ g6- g3-g4+. (1.b) goσ(l) is at the beginning of the ordinary subpath. In this case, ordinary subpath can be placed at the beginning of the path, and message can again leave the node without lengthening the path. According to Lemma 13, we always assume that goσ(l) or goσ(l+1) is at the first ordinary subproduct of the generalized ordinary one without loss of generality.. (1.c) goσ(l+1) is at the beginning of the ordinary subpath. In this case the original shortest path must be lengthened and transformed, keeping that the permutation that maps A to B is not changed. This can be achieved by using the inverting property of generators: If the ordinary product contains only one generator, ∏′AB = ∏1⋅∏2⋅⋅⋅∏k. = goσ(l)[coup.][barr.1][barr.2] ⋅⋅⋅[barr.k-1]. = goσ(l+1)goσ(l+1)[coup.][barr.1][barr.2] ⋅⋅⋅[barr.k-1] =goσ(l+1)[barr.1]goσ(l+m+1)[coup.]σ(m)[barr.2]⋅⋅⋅[barr.k-1], where m is the number of generators in the barrel product [barr.1]. Therefore, the length of ∏ÁB is no more than that of ∏AB plus one. In that case, the maximal length of ∏AB is dn, n ≥ 5. Thus, the maximal length of ∏′AB is dn+1. It is trivial if there is no couple or barrel product: ∏ÁB = goσ(l+1)goσ(l+1). For example, ∏AB = g3+g5+g6-g5+ and goσ(l) = g3-. Then, ∏′AB = g3-g3-g5+g6-g5+ = g3-g5+g6-g5+g3+. If there is only the couple product, ∏′AB =goσ(l+1) goσ(l+1)[coup.]. =goσ(l+1) goσ(l+1) [guσ(l) coup.′] =goσ(l+1) goσ(l+1) guσ(l+1) guσ(l+1) [coup.′] =goσ(l+1) guσ(l) goσ(l) guσ(l+1) [coup.′],. where guσ(l) is the first generators in the couple product [coup.]. Therefore, the length of ∏ÁB is no more than that of ∏AB plus two. In that case, the maximal length of ∏AB is n-2, n ≥ 4. The maximal length of ∏′AB is n. For example, ∏AB = g3+g5+g6- and goσ(l) = g3-. Then, ∏′AB = g3-g3-g5+g6= g3-g3-g5-g5-g6= g3-g5+g3+g5-g6-. Otherwise, ∏′AB = ∏1⋅∏2⋅⋅⋅∏k. =[goσ(l) ord.][coup.][barr1][barr2] ⋅⋅⋅[barr.k-1] =[goσ(l) ord.] goσ(l+m+1) goσ(l+m) [coup.] [barr.1] [barr.2] ⋅⋅⋅ [barr.k-1] =goσ(l+1)ord.-goσ(l+m)goσ(l+m)[coup.][barr1][barr2]⋅⋅⋅[barrk-1] = goσ(l+1) ord.-goσ(l+m+1)[coup.][barr.1][barr.2] ⋅⋅⋅[barr.k-1], where m is the number of generators in the ordinary product [ord.]. Therefore, the length of ∏′AB is no more than that of ∏AB plus one. The maximal length of ∏′AB.

(5) is dn, n ≥ 4. The maximal length of ∏′AB is dn + 1. For example, ∏AB = g3+g4-g5+g6-g5+ and goσ(l) = g3-. Then, ∏ÁB = g3+g4-g3+g3-g5+g6-g5+ = g3-g4+g3-g3-g5+g6-g5+ = g3-g4+g3+g5+g6-g5+. (1.d) goσ(l) is contained in the ordinary subpath but not at the first position. The original shortest path must be lengthened and transformed. ∏′AB=[ord.′goσ(l)ord.″][coup.][barr.1][barr.2]⋅⋅⋅[barr.k-1] =goσ(l+m) goσ(l+m+1) ord.′ goσ(l) ord.″ [coup.] [barr.1] [barr.2]⋅⋅⋅[barr.k-1], where m is the number of generators in the ordinary product ord.′. The enclosed subproduct is now of barrel type. If m is even, goσ(l+m) = goσ(l) and the enclosed subproduct can be rotated into form that begins with some generator from ord.′. Therefore, the length of ∏′AB is no more than that of ∏AB plus two. In that case, the maximal length of ∏AB is 3+3(n-5)/2, n ≥ 5. The maximal length of ∏′AB is 5+3(n-5)/2 = 2+3(n-3)/2. If m is odd, we can invert the sign of the enclosed subproduct as follows. ∏′AB= goσ(l+m) goσ(l+m) ord.′- goσ(l+1) ord.″ [coup.] [barr.1] [barr.2] ⋅⋅⋅ [barr.k-1] = goσ(l) ord.′- goσ(l+1) ord.″ [coup.] [barr.1] [barr.2] ⋅⋅⋅ [barr.k-1]. Therefore, the length of ∏′AB is no more than that of ∏AB plus one. In that case, the maximal length of ∏AB is 2+3(n-4)/2, n ≥ 4. The maximal length of ∏′AB is 3+3(n-4)/2 = 3(n-2)/2 = dn. (1.e) goσ(l+1) is contained in the ordinary subpath but not at the first position. We can treat this case almost the same way to (1.d). σ(l+1). ∏′AB=[ord.′go. ord.″][coup.][barr.1][barr.2]⋅⋅⋅[barr.k-1]. = goσ(l+m+1) goσ(l+m+2)ord.′goσ(l+1) ord.″ [coup.] [barr.1] [barr.2]⋅⋅⋅[barr.k-1], where m is the number of generators in the ordinary product ord.′. The enclosed subproduct is now of barrel type. If m is odd, goσ(l+m+1)=goσ(l) and the enclosed subproduct can be rotated into form that begins with some generator from ord.′. Therefore, the length of ∏′AB is no more than that of ∏AB plus two. In that case, the maximal length of ∏AB is 2+3(n-4)/2, n ≥ 4. The maximal. length of ∏′AB is 4+3(n-4)/2 =1+3(n-2)/2 = dn+1. If m is even, we can invert the sign of the enclosed subproduct as follows. ∏′AB = goσ(l+m+1) goσ(l+m+1) ord.′- goσ(l) ord.″ [coup.][barr.1] [barr.2] ⋅⋅⋅ [barr.k-1] = goσ(l) ord.′- goσ(l) ord.″ [coup.] [barr.1] [barr.2] ⋅⋅⋅ [barr.k-1]. Therefore, the length of ∏′AB is no more than that of ∏AB plus one. In that case, the maximal length of ∏AB is 3+3(n-5)/2, n ≥ 5. The maximal length of ∏′AB is thus 4+3(n-5)/2 = 1+3(n-3)/2. (2) Neither goσ(l) nor goσ(l+1) is a generator contained in ∏AB. Then we have two different cases. (2.a) If ∏AB conatins at least one barrel subproduct. (It may optionally contain ordinary subproduct but this does not affect the analysis). In that case we again use inverting property of generators to lengthen the path without changing the mapping between A and B. ∏′AB = goσ(l) goσ(l+1) [ord. ][coup.][barr.]. Since goσ(l+1) is not contained in subproducts in ∏AB, one barrel product can be nested between goσ(l) goσ(l+1) and ∏′AB is given the following form: ∏′AB = goσ(l) goσ(l+1)[ord.][barr.][coup.] σ(m) = goσ(l) goσ(l+1) [barr.][ord.] σ(m)[coup.] σ(m) = goσ(l) [barr.] goσ(m+l+1) [ord.] σ(m) [coup.] σ(m), where m is the number of generators in the barrel product [barr.]. The maximal length of ∏′AB is dn-1+2. This value is also a candidate for fault diameter since dn-1+2 ≥ dn. For example, ∏AB = g3+g5+g6-g5+ and goσ(l) = g4-. Then, ∏′AB is obtained in the following way: ∏′AB = g4-g4+g3+g5+g6-g5+ = g4-g4+ g5+g6-g5+ g3= g4- g5+g6-g5+ g4-g3-. (2.b) If ∏AB contains only a generalized ordinary subproduct. In that case we must append a pair of goσ(l) and goσ(l+1) at the beginning and at the end of ∏AB in order to form a barrel product. If the number of generators in the ordinary product is odd, ∏′AB = goσ(l+1) goσ(l) [ord.] goσ(l) goσ(l+1) [coup.] = goσ(l+1) goσ(l+1) [ord.]- goσ(l+1) goσ(l+1) [coup.] = goσ(l) [ord.]- goσ(l) [coup.]..

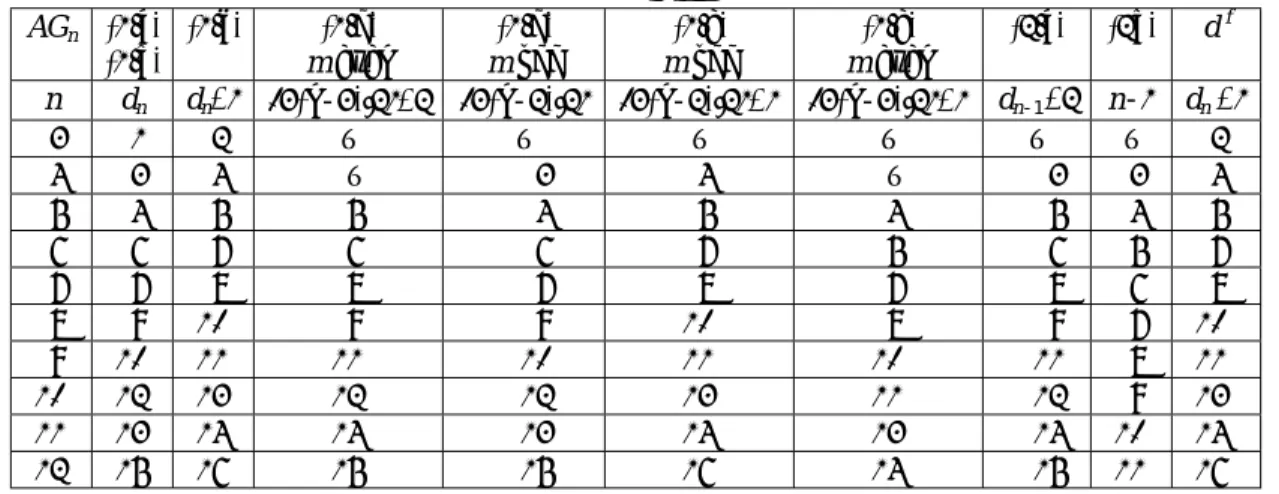
(6) If the number of generators in the ordinary subproduct is even, ∏′AB = goσ(l+1) goσ(l) [ord.] goσ(l+1) goσ(l) [coup.] = goσ(l+1) goσ(l+1) [ord.]- goσ(l) goσ(l) [coup.] = goσ(l) [ord.]- goσ(l+1) [coup.]. Evidently, this path transformation increases its length by 2. The maximum length of ∏′AB is n-3+2=n-1.. 4. CONCLUDING REMARKS Since dn is not a linear function of n, it seems convenient to determine the fault diameter by representing the candidates in tabular form, as shown in Table 1. From f. Table 1, we can conclude that d n =dn+1 for AGn, i.e., the fault diameter of the alternating graphs is optimal.. 5. REFERENCES [1] S. B. Akers, D. Harel, and B. Krishnamurthy, “The star graph: An attractive alternative to the n-cube”, Proceedings of the International Conference on Parallel Processing, 1987, pp. 393-400. [2] S. B. Akers and B. Krishnamurthy, “Group graphs as interconnection networks”, Proceedings of the 14th. International Conference on Fault Tolerant Computing, 1984, pp. 422-427. [3] Béla Bollobás, Extremal graph theory, Academic Press Inc., 1978. [4] S. P. Dandamudi, “On hypercube-based hierarchical interconnection network design”, Journal of Parallel and Distributed Computing, Vol. 12, No. 3, 1991, pp. 283-289. [5] Y. O. Hamidoune, “The connectivity of hierarchical Cayley digraphs”, Discrete Applied Mathematics, Vol. 37/38, 1992, pp. 275-280. [6] Z. Jovanović and J. Mišić, “Fault tolerance of the star graph interconnection network”, Information Processing Letters, Vol.49, 1994, pp. 145-150. [7] J.-S. Jwo, S. Lakshmivarahan, and S. K. Dhall, “Characterization of node disjoint (parallel) paths in star graphs”, Proceedings of the 5th International Parallel Processing Symposium, April 1991, pp. 404-409. [8] J.-S. Jwo, S. Lakshmivarahan, and S. K. Dhall, “A new class of interconnection networks based on the alternating group”, Networks, Vol.23, No.4, July 1993, pp. 315-326. [9] M. S. Krishnamoorthy and B. Krishnamurthy, “Fault diameter of interconnection networks”, Comput. Math. Applic., Vol.13, No. 5/6, 1987, pp. 577-582. [10] S. Latifi, “On the fault-diameter of the star graph”, Information Processing Letters, Vol. 46, 1993, pp. 145-150. [11] Y. Rouskov and P. K. Srimani, “Fault diameter of star graphs”, Information Processing Letters, Vol. 48, 1993, pp. 243-251.. Table 1. The maximum lengths of ∏′AB and the fault diameters d f. (1.d) AGn (1.a) (1.c) (1.b) m even n dn dn+1 3(n-3)/2+2 3 1 2 – 4 3 4 – 5 4 5 5 6 6 7 6 7 7 8 8 8 9 10 9 9 10 11 11 10 12 13 12 11 13 14 14 12 15 16 15. (1.d) m odd 3(n-2)/2 – 3 4 6 7 9 10 12 13 15. (1.e) (1.e) (2.a) (2b) df m odd m even 3(n-2)/2+1 3(n-3)/2+1 dn-1+2 n-1 dn +1 – – – – 2 4 – 3 3 4 5 4 5 4 5 7 5 6 5 7 8 7 8 6 8 10 8 9 7 10 11 10 11 8 11 13 11 12 9 13 14 13 14 10 14 16 14 15 11 16.

(7)