On the Super Spanning Properties of Binary Wrapped
Butterfly Graphs
Tz-Liang Kueng
∗Tyne Liang
Jimmy J.M. Tan
†Department of Computer Science
National Chiao Tung University
{tlkueng, tliang, jmtan}@cs.nctu.edu.tw
Lih-Hsing Hsu
Department of Computer Science and
Information Engineering, Providence University
lhhsu@pu.edu.tw
Abstract
A k-container Ck(u, v) of a graph G is a set of k
internally vertex-disjoint paths joining vertices u and
v. It becomes a k∗-container if every vertex of G is
passed by a certain path of Ck(u, v). A graph G is
said to be k∗-connected if there exists a k∗-container
between any two vertices of G. A graph G with connectivity κ is super spanning connected if it is i∗-connected for every 1 ≤ i ≤ κ. A bipartite graph
G is k∗-laceable if there exists a k∗-container between
any two vertices u and v from different partite sets of G. A bipartite graph G with connectivity κ is super spanning laceable if it is i∗-laceable for all
1 ≤ i ≤ κ. In this paper, we show the n-dimensional binary wrapped butterfly graph is super spanning connected (resp. super spanning laceable) if n is odd (resp. even).
Keywords: Container; Butterfly graph;
Hamil-tonian connected; Hamiltonian laceable; Super
spanning connected; Super spanning laceable
1
Introduction
A multiprocessor/communication interconnection network is usually represented by a graph, in which the vertices correspond to processors and the edges correspond to connections or communication links. Hence, we use the terms, graphs and networks, inter-changeably. Among various kinds of network topolo-gies, the wrapped butterfly network is very suitable for VLSI implementation and parallel computing and thus its topological properties have been widely dis-cussed in [1, 4–7, 11, 12, 14]. For example, embedding of rings, linear arrays, and binary trees into a butter-fly network was addressed in literature [5, 6, 12, 14].
∗Corresponding author.
†This work was supported in part by the National Science
Council of the Republic of China under Contract NSC 96-2221-E-009-137-MY3.
Throughout this paper, we concentrate on
loop-less undirected graphs. For the graph
defi-nitions and notations we follow the ones
de-fined in [2]. A graph G consists of a finite
nonempty set V (G) and a subset E(G) of {(u, v) | (u, v) is an unordered pair of V (G)}. The set V (G) is called the vertex set of G and E(G) is called the edge set. Two vertices u and v of G are adjacent if (u, v) ∈ E(G). A graph H is a subgraph of G if V (H) ⊆ V (G) and E(H) ⊆ E(G). Let S be a nonempty subset of V (G). The subgraph induced by S is the subgraph of G with its vertex set S and with its edge set which consists of those edges joining any two vertices in S. We use G − S to denote the sub-graph of G induced by V (G) − S. Analogously, the subgraph generated by a nonempty subset F ⊆ E(G) is the subgraph of G with its edge set F and with its vertex set consisting of those vertices of G incident with at least one edge of F . We use G − F to denote the subgraph of G with vertex set V (G) and edge set E(G) − F .
A path P of length k joining vertex x to vertex y in a graph G is a sequence of distinct vertices
hv1, v2, . . . , vk+1i such that x = v1, y = vk+1, and
(vi, vi+1) ∈ E(G) for every 1 ≤ i ≤ k. For
con-venience, we write P as hv1, . . . , vi, Q, vj, . . . , vk+1i
where Q = hvi, vi+1, . . . , vji. Note that we allow Q
to be a path of length zero. For i ≥ 1, the i-th vertex of P is denoted by P (i); i.e., P (i) = vi. Moreover,
we use P−1 to denote the path hv
k+1, vk, . . . , v1i. Let V (P ) = {v1, v2, . . . , vk+1} and I(P ) = V (P ) −
{v1, vk+1}. A set of k paths P1, . . . , Pk are internally
vertex-disjoint (or disjoint for short) if I(Pi)∩I(Pj) =
φ for any i 6= j. A cycle is a path with at least three vertices such that the last vertex is adjacent to the first one. For clarity, a cycle of length k is represented by hv1, v2, . . . , vk, v1i. A path of a graph G is a hamil-tonian path if it spans G. A graph G is hamilhamil-tonian connected if there exists a hamiltonian path joining any two distinct vertices of G. Similarly, a hamilto-nian cycle of a graph G is a cycle that traverses every
vertex of G exactly once. A graph is hamiltonian if it has a hamiltonian cycle.
The degree of a vertex u in G is the number of edges incident to u. A graph G is k-regular if all its vertices have the same degree k. The connectivity of a graph G, denoted by κ(G), is the minimum num-ber of vertices whose removal leaves the remaining graph disconnected or trivial. A k-container Ck(u, v)
of G between vertices u and v is a set of k internally vertex-disjoint paths joining u and v. Suppose that κ(G) = k. It follows from Menger’s theorem [9] that there exists a k-container of G between any two dis-tinct vertices. In this paper, a k-container Ck(u, v) is
a k∗-container if it contains all vertices of G. A graph
G is k∗-connected if there exists a k∗-container
be-tween any two distinct vertices. In particular, G is 1∗
-connected if and only if it is hamiltonian--connected. Moreover, G is 2∗-connected if it is hamiltonian. The
spanning connectivity of a graph G, κ∗(G), is defined
as the largest integer m such that G is i∗-connected
for all 1 ≤ i ≤ m. A graph G is super spanning
connected if κ∗(G) = κ(G). Recently, a number of
networks had been shown to be super spanning con-nected [8, 13].
A graph G is bipartite if its vertex set can be parti-tioned into two disjoint subsets V0 and V1 such that every edge joins a vertex of V0 and a vertex of V1. A bipartite graph is k∗-laceable if there exists a k∗
-container between any two vertices from different par-tite sets. Note that a 1∗-laceable graph is also known
as a hamiltonian-laceable graph [10] and a bipartite graph is 2∗-laceable if and only if it is hamiltonian.
Similarly, the spanning laceability of a hamiltonian laceable graph G, κ∗
L(G), is the largest integer m such
that G is i∗-laceable for every 1 ≤ i ≤ m. A bipartite
graph G is super spanning laceable if κ∗
L(G) = κ(G).
Likewise, a number of networks had been shown to be super spanning laceable [3, 8].
Let Zn= {0, 1, . . . , n−1} denote the set of integers
modulo n. The n-dimensional binary wrapped butter-fly network (or butterbutter-fly network for short) BF (n) is a graph with Zn × Zn2 as vertex set. Each vertex is labeled by a two-tuple h`, a0. . . an−1i with a level
` ∈ Zn and an n-digit binary string a0. . . an−1 ∈
Zn
2. A level-` vertex h`, a0. . . a`. . . an−1i is
adja-cent to two vertices, h(` + 1)mod n, a0. . . a`. . . an−1i and h(` − 1)mod n, a0. . . a`−1. . . an−1i, by straight edges, and is adjacent to another two vertices,
h(` + 1)mod n, a0. . . a`−1a`a`+1. . . an−1i and h(` −
1)mod n, a0. . . a`−2a`−1a`. . . an−1i, by cross edges.
More formally, the edges of BF (n) can be defined in terms of four generators g, g−1, f , and f−1 as
follows: g(h`, a0. . . an−1i) = h(` + 1)mod n, a0. . . an−1i, g−1(h`, a 0. . . an−1i) = h(` − 1)mod n, a0. . . an−1i, f (h`, a0. . . a`. . . an−1i) = h(` + 1)mod n, a0. . . a`. . . an−1i, and f−1(h`, a 0. . . a`−1. . . an−1i = h(` − 1)mod n, a0. . . a`−1. . . an−1i
where a`≡ a`+ 1 (mod 2). Throughout this paper,
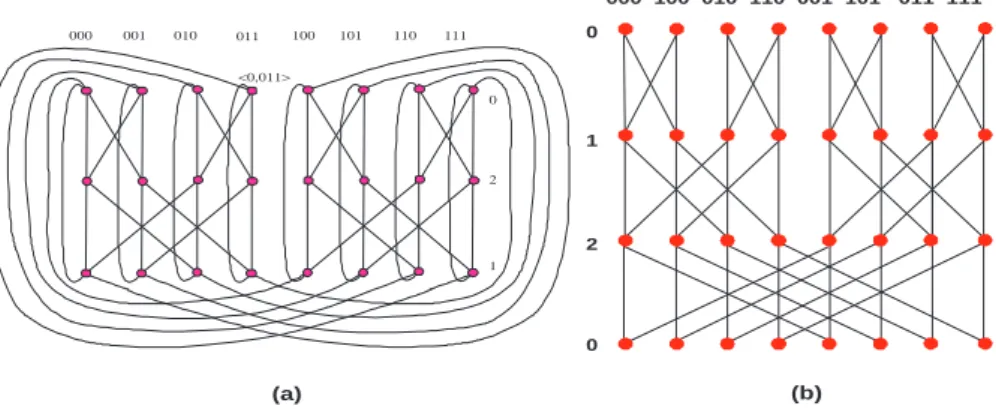
a level-` edge of BF (n) is an edge that joins a level-` vertex and a level-(` + 1)mod n vertex. To avoid the degenerate case, we assume n ≥ 3 throughout this paper. So BF (n) is 4-regular. Moreover, BF (n) is bipartite if and only if n is even. Figure 1(a) depicts the structure of BF (3) and Figure 1(b) is the iso-morphic structure of BF (3) with level-0 replication for easy visualization.
According to [14], BF (n) is 1∗-connected and 2∗
-connected (resp. 1∗-laceable and 2∗-laceable) if n is
odd (resp. even). In this paper, we show that BF (n) is 3∗-connected and 4∗-connected (resp. 3∗-laceable
and 4∗-laceable) if n is odd (resp. even). The rest
of the paper is organized as follows. Section 2 in-troduces the nearly recursive construction of BF (n), which was proposed by Wong [14]. Section 3 provides the useful lemmas to prove the main results. Since the proof of the main theorem is rather long, it is broken into several lemmas in Section 4 and Section 5. For the sake of clarity, the detailed proofs of sev-eral lemmas are described in Appendix. Finally, the future work is discussed in Section 6.
2
Nearly recursive
construc-tion of BF (n)
Let n ≥ 3. For any ` ∈ Zn and i ∈ Z2, we use
BFi
`(n) to denote the subgraph of BF (n) induced
by {hh, a0. . . an−1i | h ∈ Zn, a` = i}. Obviously, BFi `1(n) is isomorphic to BF j `2(n) for any i, j ∈ Z2 and `1, `2 ∈ Zn. Moreover, {BF`i(n) | i ∈ Z2}
forms a partition of BF (n). With such observation, Wong [14] proposed a stretching operation to obtain
BFi
`(n) from BF (n − 1). More precisely, the
stretch-ing operation can be described as follows. Assume
that ` ∈ Zn and i ∈ Z2. Let =n be the set of all
subgraphs of BF (n) and let G ∈ =n. We define the
following subsets of V (BF (n+1)) and E(BF (n+1)):
V1 = {vhi | 0 ≤ h < `, vh∈ V (G)}, V2 = {vh+1i | ` < h ≤ n − 1, vh∈ V (G)}, V3 = {v`i| v`is incident with
a level-(` − 1)mod nedge in G}, V4 = {v`+1i | v`is incident with
a level-` edge in G},
E1 = {(vhi, vih+1) | 0 ≤ h < `, (vh, uh+1) ∈ E(G)}, E2 = {(vh+1i , vh+2i ) | ` ≤ h ≤ n − 1, (vh, uh+1) ∈ E(G)},
and
E3 = {(v`i, vi`+1) | v`is incident with at least one
level-(` − 1)mod nedge and at least one
000 100 010 110 001 101 011 111 0 1 2 0 (b) (a) 000 001 010 011 100 101 110 111 0 2 1 <0,011>
Figure 1: (a) The structure of BF (3); (b) BF (3) with level-0 replicated to ease visualization.
where vh = hh, a0. . . a`−1a`. . . an−1i, uh = hh, b0. . . b`−1b`. . . bn−1i, vhi = hh, a0. . . a`−1ia`. . . an−1i, and ui h = hh, b0. . . b`−1ib`. . . bn−1i.
Then we define the function γi
` :
S
n≥3=n →
S
n≥4=n by assigning γ`i(G) as the graph with the
vertex set V1∪V2∪V3∪V4and the edge set E1∪E2∪E3. One may find that γi
` is well-defined and one-to-one.
Furthermore, γi
`(G) ∈ =n+1if G ∈ =n. In particular, γi
`(BF (n)) = BF`i(n + 1). Moreover, γ`i(P ) is a path
in BF (n + 1) if P is a path in BF (n).
In fact, BF (n) can be further partitioned.
As-sume that 1 ≤ m ≤ n, i1, . . . , im ∈ Z2, and
`1, . . . , `m ∈ Zn such that `1 < . . . < `m.
We use BFi1,...,im
`1,...,`m(n) to denote the subgraph of
BF (n) induced by {hh, a0. . . an−1i | h ∈ Zn, a`j =
ij for 1 ≤ j ≤ m}. So, {BF`i11,...,`,...,imm(n) | i1, . . . , im ∈
Z2, `1, . . . , `m ∈ Zn, `1 < . . . < `m} forms a
par-tition of BF (n). To avoid the complicated case
caused by modular arithmetic, we restrict our atten-tion on 1 ≤ m ≤ n − 1, 0 ≤ `1 < . . . < `m, and
`j < n − m + j − 1 for each 1 ≤ j ≤ m. Then the
following lemmas can be easily derived.
Lemma 1. Suppose that i1, . . . , im ∈ Z2 and
`1, . . . , `m are integers such that 0 ≤ `1 < . . . < `m
and `j < n − m + j − 1 for each 1 ≤ j ≤ m. Then
BFi1,...,im `1,...,`m(n) = γim `m◦ . . . ◦ γ i3 `3(BF i1,i2 `1,`2(3)) if m = n − 1, γim `m◦ . . . ◦ γ i2 `2(BF i1 `1(3)) if m = n − 2, γim `m◦ . . . ◦ γ i1 `1(BF (n − m)) otherwise. In the next lemma, we let
v = h`, a0. . . an−1i,
vij` = h`, a0. . . a`−1ija`. . . an−1i,
vij`+1 = h` + 1, a0. . . a`−1ija`. . . an−1i, and vij`+2 = h` + 2, a0. . . a`−1ija`. . . an−1i.
Lemma 2. Let n ≥ 3. Assume that 0 ≤ ` ≤ n − 1, Γ ∈ =n, and G is a connected spanning subgraph of
Γ. For any i, j ∈ Z2, let
F0 = {v | v is not incident with any
level-(` − 1)mod n edge in G},
F1 = {v | v is not incident with any
level-` edge in G}, F0 = [ v∈F0 {v`ij, v`+1ij }, F1 = [ v∈F1 {v`+1ij , v`+2ij }, X0 = [ v∈F0 {(v`ij, v`+1ij )}, X1 = [ v∈F1 {(v`+1ij , vij`+2)}, M0 = [ v∈G−(F0∪F1) n (v`ij, v`+1ij ) o , and M1 = [ v∈G−(F0∪F1) {(vij`+1, v`+2ij )}.
Then F0∩ F1= φ and F0∩ F1= φ. Thus, F0∪ F1=
V (γ`+1j ◦ γi
`(Γ)) − V (γ`+1j ◦ γi`(G)) can be represented
asSmk=1{uk, g(uk) | uk∈ V (γ`+1j ◦ γi`(Γ))} with some
m ≥ 1 such that {uk | 1 ≤ k ≤ m} ∩ {g(uk) | 1 ≤ k ≤
m} = φ. Moreover, M0∪ M1⊆ E(γ`+1j ◦ γ`i(G)) and
X0∪ X1=
Sm
k=1{(uk, g(uk)) | uk ∈ V (γ`+1j ◦ γ`i(Γ))}
is a set of edges with no shared endpoints.
Lemma 3. Assume n ≥ 3 and k ≥ 1. Suppose
that {P1, . . . , Pk} is a k-container of BF (n) between
two vertices x and y with the following conditions:
(i) V (BF (n)) −Ski=1V (Pi) =
Sm
i=1{ui, g(ui) | ui ∈
V (BF (n))} with some m ≥ 1 such that {ui | 1 ≤
i ≤ m} ∩ {g(ui) | 1 ≤ i ≤ m} = φ, and (ii)
Sm
i=1{(f (ui), g−1◦ f (ui)) ⊆
Sk
i=1E(Pi). Then there
exists a k∗-container of BF (n) between x and y.
Proof. Let A = Smi=1 {(ui, g(ui))} ∪
Sm
i=1
{(ui, f (ui))} ∪
Sm
i=1{(g(ui), f−1 ◦ g(ui))} and
³Sk
i=1E(Pi)
´
= φ. Then ³³Ski=1E(Pi)
´ ∪ A
´ − B forms a k∗-container of BF (n) between x and y.
Let G be a subgraph of BF (n) and let C be a cycle of G. Then C is an `-scheduled cycle with respect to G if every level-` vertex of G is incident with a level-(`−
1)mod nedge and a level-` edge in C. Furthermore, C
is a totally scheduled cycle of G if it is an `-scheduled cycle of G for all ` ∈ Zn. Obviously, γ`i(C) with
i ∈ {0, 1} is a totally scheduled cycle of γi
`(G) if C is
a totally scheduled cycle of G.
Theorem 1. [14] Assume n ≥ 3. Then BF (n) is
1∗-connected if n is odd, and BF (n) is 1∗-laceable
otherwise.
Theorem 2. [14] Assume n ≥ 3. Every BF (n) has a totally scheduled hamiltonian cycle. Thus, BF (n)
is 2∗-connected
By stretching operation, we have the following lemma and corollary.
Lemma 4. Let n ≥ 3. Assume that 0 ≤ ` ≤ n − 2
and i, j ∈ Z2. Then there exists a totally scheduled
hamiltonian cycle of BF`,`+1i,j (n).
Corollary 1. Assume that n ≥ 4 and i, j, p, q ∈ Z2. Then there exists a totally scheduled hamiltonian
cy-cle of BF0,1,2,3i,j,p,q(n), including all straight edges of level
0, level 1, level 2, and level 3 in BF0,1,2,3i,j,p,q(n).
3
Basic properties of BF (n)
A path P of BF (n) is `-scheduled if every level-` ver-tex of I(P ) is incident with a level-(` − 1)mod n edge and a level-` edge on P . A path P of BF (n) is weakly `-scheduled if at least one level-` vertex of I(P ) is in-cident with a level-(` − 1)mod nedge and a level-` edge on P .
Lemma 5. Let n ≥ 3. Assume i, j ∈ Z2 and
0 ≤ ` ≤ n − 3. Suppose that s is any level-(` + 1)
ver-tex of BF`,`+1i,j (n) and d is any level-(` + 2) vertex of
BF`,`+1i,j (n). When n = 3, there exists a 0-scheduled
hamiltonian path P3 of BF0,1i,j(3) joining s to d with
P3(2) = g−1(s). When n ≥ 4, there exists an
`-scheduled hamiltonian path Pn of BF`,`+1i,j (n) joining
s to d such that Pn is weakly (` + 2)-scheduled with
Pn(2) = g−1(s). In particular, Pn(n × 2n−2− 2) = g−2(d) and P
n(n × 2n−2− 1) = g−1(d) for n ≥ 3 if d 6= g(s).
Proof. Omitted.
In terms of the symmetry of BF (n), we have the following corollary.
Corollary 2. Let n ≥ 3. Assume i, j ∈ Z2 and
0 ≤ ` ≤ n − 3. Suppose that s is any level-(` + 1)
vertex of BF`,`+1i,j (n) and d is any level-` vertex of
BF`,`+1i,j (n). When n = 3, there exists a 2-scheduled
hamiltonian path P3of BF`,`+1i,j (n) joining s to d with
H(2) = g(s). When n ≥ 4, there exists an (` +
2)-scheduled hamiltonian path Pn of BF`,`+1i,j (n) joining
s to d such that Pnis weakly `-scheduled with Pn(2) =
g(s). In particular, Pn(n × 2n−2− 2) = g2(d) and
Pn(n × 2n−2− 1) = g(d) for n ≥ 3 if d 6= g−1(s).
Lemma 6. Assume that n ≥ 3. For any x ∈ Zn
2,
let Fx = {hh, xi | h ∈ Zn}. Then there is a totally
scheduled hamiltonian cycle in BF (n) − Fx.
Proof. Without loss of generality, we assume x =
0n. Then we prove this lemma by induction on n.
The induction basis is a totally scheduled hamiltonian cycle of BF (3) − {h0, 000i, h1, 000i, h2, 000i}, listed in Table 1.
Now we suppose that the statement holds for BF (n − 1) with n ≥ 4 and partition BF (n) into
{BF0
0(n), BF01(n)}. Thus, Fx ⊂ V (BF00(n)). Let F0
x = {hh, 0n−1i | h ∈ Zn−1}. By induction
hypoth-esis, there exists a totally scheduled hamiltonian cy-cle C0 of BF (n − 1) − F0
x. By Theorem 2, there
exists a totally scheduled cycle C1 of BF (n − 1).
Since BF0
0(n) − Fx = γ00(BF (n − 1) − Fx0) and
BF1
0(n) = γ01(BF (n − 1)), then γ00(C0) and γ01(C1) are totally scheduled hamiltonian cycles of BF0
0(n) − Fx and BF01(n), respectively. Let C be the sub-graph of BF (n) generated by E(γ0
0(C0)) ∪ E(γ01(C1))
∪ { (h0, 01n−1i, h1, 1ni), (h0, 1ni, h1, 01n−1i)} − {
(h0, 01n−1i, h1, 01n−1i), (h0, 1ni, h1, 1ni)}. Then C is
a totally scheduled hamiltonian cycle of BF (n) − Fx.
Lemma 7. Assume i, j ∈ Z2, n is an odd
in-teger greater than or equal to 3, and x ∈ Zn−2
2 .
Let uh = hh, ijxi for any h ∈ Zn. Then the
following statements are true: (i) There exists a
hamiltonian cycle in BF0,1i,j(n) − {u1}; (ii) there
ex-ists a 0-scheduled hamiltonian cycle in BF0,1i,j(n) −
{u0, u1, un−1}; (iii) there exists a 0-scheduled
hamil-tonian cycle in BF0,1i,j(n) − {u0, u1, u2}.
Proof. By Lemma 6, there is a totally scheduled hamiltonian cycle Cf in BF (n) − {uh | h ∈ Zn}.
With regard to each statement, we construct a cycle as follows:
Let C1 be the subgraph of BF0,1i,j(n)
gener-ated by (E(Cf) ∪ {(u2t, u(2t+1)mod n) | 1 ≤ t ≤
bn
2c} ∪ {(u2t, f (u2t)) | 1 ≤ t ≤ bn2c} ∪
{(u(2t+1)mod n, f−1(u(2t+1)mod n)) | 1 ≤ t ≤ bn2c}) −
{(f (u2t), f−1(u
(2t+1)mod n)) | 1 ≤ t ≤ bn2c}. Then C1
is a hamiltonian cycle in BF0,1i,j(n) − {u1}.
Let C2 be the subgraph of BF0,1i,j(n) generated
by (E(Cf) ∪ {(u2t, u2t+1) | 1 ≤ t ≤ bn2c − 1} ∪ {(u2t, f (u2t)) | 1 ≤ t ≤ bn 2c − 1} ∪ {(u2t+1, f−1(u2t+1)) | 1 ≤ t ≤ bn2c − 1}) − {(f (u2t), f−1(u2t+1)) | 1 ≤ t ≤ bn 2c − 1}. Then C2
forms a 0-scheduled hamiltonian cycle in BF0,1i,j(n) − {u0, u1, un−1}.
Let C3 be the subgraph of BF0,1i,j(n) generated
Table 1: A totally scheduled hamiltonian cycle of BF (3) − {h0, 000i, h1, 000i, h2, 000i} as induction basis. hh0, 100i, h1, 100i, h2, 110i, h0, 111i, h1, 011i, h2, 011i, h0, 011i, h1, 111i, h2, 101i, h0, 101i, h1, 001i,
h2, 001i, h0, 001i, h1, 101i, h2, 111i, h0, 110i, h1, 010i, h2, 010i, h0, 010i, h1, 110i, h2, 100i, h0, 100ii
{(u2t−1, f (u2t−1)) | 2 ≤ t ≤ bn2c} ∪ {(u2t, f−1(u2t)) |
2 ≤ t ≤ bn2c}) − {(f (u2t−1), f−1(u2t)) | 2 ≤ t ≤
bn
2c}. Then C3 is a 0-scheduled hamiltonian cycle in
BF0,1i,j(n) − {u0, u1, u2}.
Lemma 8. Assume that n is an odd integer greater than or equal to 3. Let s and d be two distinct level-0 vertices of BF (n). Then there exists a hamiltonian path of BF (n) joining s to d such that s is incident with a (n−1) edge and d is incident with a level-0 edge.
Proof. Without loss of generality, we assume s =
h0, 0ni and d = h0, ijxi with some i, j ∈ Z
2 and
x ∈ Zn−2
2 . Then we construct the desired
hamilto-nian path of BF (n) by induction on n. The induction bases depend upon the hamiltonian paths of BF (3) joining h0, 000i to the other level-0 vertices, enumer-ated in Table 2. Then we suppose that the statement holds for BF (n − 2) with n ≥ 5 and partition BF (n) into {BF0,1p,q(n) | p, q ∈ Z2}.
Case 1: Suppose that x = 0n−2. Let t =
h0, yi be a level-0 vertex of BF (n − 2) other than
s0 = h0, 0n−2i. By induction hypothesis, there
is a hamiltonian path Q of BF (n − 2) joining s0
to t such that s0 is incident with a level-(n − 3)
edge and t is incident with a level-0 edge.
Fur-thermore, let upqh = hh, pq0n−2i and tpq
h = hh, pqyi
for any p, q ∈ Z2 and h ∈ {0, 1, 2}. Since
BF0,10,0(n) = γ0
1◦ γ00(BF (n − 2)), γ10◦ γ00(Q) is a path of BF0,10,0(n) joining s = u000 to t002 . By Corollary
2, there is a 2-scheduled hamiltonian path Hij =
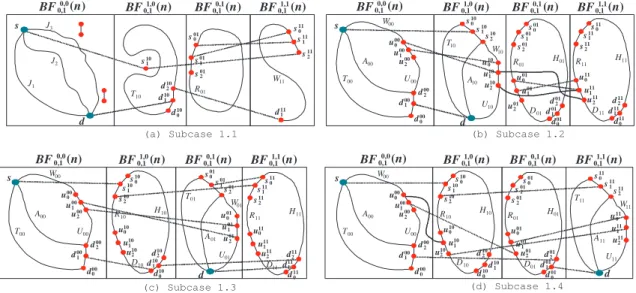
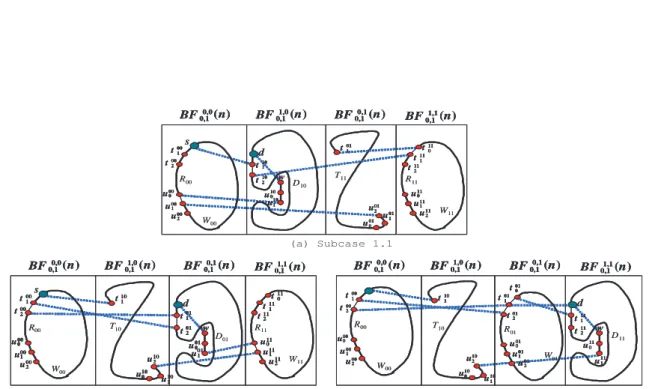
htij1, Pij, uij2, uij1, uij0i of BF0,1i,j(n) joining tij1 to uij0. By Lemma 4, there is a totally scheduled hamiltonian cycle Cpq = htpq 0 , tpq1 , tpq2 , Dpq, upq0 , upq1 , upq2 , Rpq, tpq0 i of BF0,1p,q(n) for pq ∈ Z2 2− {00, ij}. Subcase 1.1: If ij = 10, d = u10 0 . Then J = h s, γ0 1◦ γ00(Q), t002 , t001 , t000 , t101 , P10, u102 , u111 , u010 , D−101, t01 2 , t011 , t010 , R−101, u012 , u011 , u110 , D−111, t112 , t111 , t110 , R−111, u11 2 , u101 ,d i is a path of BF (n) joining s to d. See Figure 2(a) for illustration.
Subcase 1.2: If ij = 01, d = u01 0 . Then J = h s, γ0 1◦ γ00(Q), t002 , t011 , P01, u012 , u011 , u110 , D11−1, t112 , t111 , t11 0 , R11−1, u112 , u101 , u100 , D−110, t102 , t101 , t100 , R−110, u102 , u11
1 , d i joins s to d. See Figure 2(b). Subcase 1.3: If ij = 11, d = u11 0 . Then J = h s, γ0 1◦ γ00(Q), t002 , t011 , t012 , D01, u010 , u011 , u012 , R01, t010 , t11 1 , P11, u112 , u101 , u100 , D10−1, t102 , t101 , t100 , R−110, u100 , u11
1 , di joins s to d. See Figure 2(c).
Case 2: Suppose that x 6= 0n−2. By induction
hy-pothesis, there is a hamiltonian path Q of BF (n − 2) joining s0 = h0, 0n−2i to d0 = h0, xi such that s0is
in-cident with a level-(n−3) edge and d0is incident with
a level-0 edge. Furthermore, let spqh = hh, pq0n−2i
and dpqh = hh, pqxi for any p, q ∈ Z2, h ∈ {0, 1, 2}. Obviously, γ0
1 ◦ γ00(Q) joins s000 = s to d002 . By Lemma 4, there is a totally scheduled hamiltonian cycle Cpq = hdpq
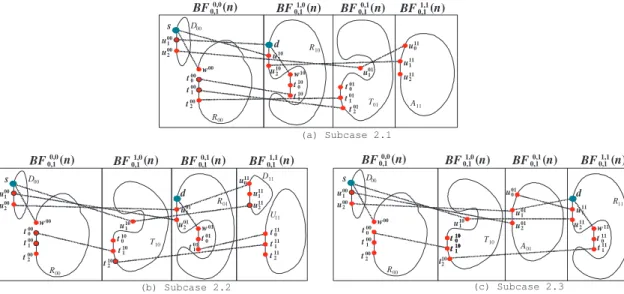
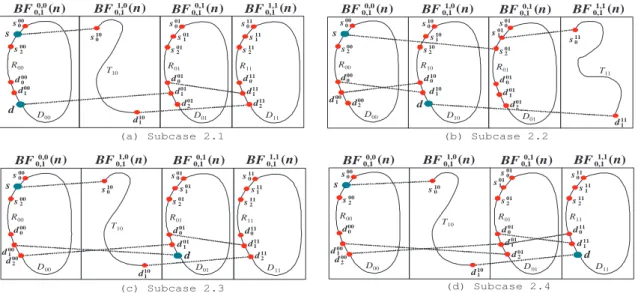
0 , dpq1 , dpq2 , Rpq, dpq0 i of BF0,1p,q(n) for any p, q ∈ Z2. By Corollary 2, there is a hamiltonian path Tij = hsij 1, Wij, dij2, dij1, di of BF0,1i,j(n) joining sij1 to d. Subcase 2.1: If ij = 00, d = d00 0 . Then J = hs, γ0 1◦ γ00(Q), d002 , d001 , d100 , R−110, d102 , d111 , d010 , R−101, d012 , d01
1 , d110 , R−111, d112 , d101 , di joins s to d. See Figure 3(a).
Subcase 2.2: If ij = 10, d = d10
0 . By Lemma 5,
there is a hamiltonian path L11 = h d11
1 , D11, s110 , s11 1 , s112 i of BF0,11,1(n) joining d111 to s112 . Then J = hs, γ0 1◦ γ00(Q), d002 , d011 , d012 , R01, d010 , d111 , D11, s110 , s11
1 , s112 , s101 , W10, d102 , d101 , di joins s to d. See Figure 3(b).
Subcase 2.3: If ij = 01, d = d01
0 . By Corollary
2, there is a hamiltonian path S11 = h d11
1 , U11, s112 , s11 1 , s110 i of BF0,11,1(n). Then J = hs, γ10◦ γ00(Q), d002 , d00 1 , d000 , d101 , d100 , R10−1, d102 , d111 , U11, s112 , s111 , s110 , s01
1 , W01, d012 , d011 , di joins s to d. See Figure 3(c) for illustration.
Subcase 2.4: If ij = 11, d = d11
0 . By Corollary
2, there is a hamiltonian path S01 = h d01
1 , U01, s012 , s01 1 , s010 i of BF0,10,1(n). Then J = hs, γ10◦ γ00(Q), d002 , d01 1 , U01, s012 , s011 , s010 , s111 , W11, d112 , d101 , d100 , R−110, d10
2 , d111 , di joins s to d. See Figure 3(d).
Note that J is a 1-container of BF (n) joining s to
d. By Lemma 2, V (BF (n)) − V (J) = V (BF0,10,0(n)) −
V (γ0
1◦γ00(Q)) =
Sm
i=1{ui, g(ui)} for some m ≥ 1 with
{ui| 1 ≤ i ≤ m} ∩ {g(ui) | 1 ≤ i ≤ m} = φ.
Further-more,Smi=1{(f (ui), g−1◦f (ui))} ⊆ E(J). By Lemma
3, there exists a 1∗-container of BF (n) joining s to d. Thus, the requirements are all satisfied.
4
3
∗-containers of BF (n)
Based on the symmetry of BF (n), only the containers between two vertices at the same level and the con-tainers between two vertices of odd level differences are concerned.
Assume that ` ∈ Zn for n ≥ 3. A
sub-graph G of BF (n) is `-designed if G spans BF (n) and every level-` vertex of G is incident with at least one level-(` − 1)mod n edge and at least one level-` edge. Obviously, γ`+1j ◦ γi
`(G) spans γ`+1j ◦ γi
`(BF (n)) = BF`,`+1i,j (n + 2) if G is `-designed. Let
s = h`, a0a1. . . an−1i and d = h`, b0b1. . . bn−1i be two
distinct level-` vertices of BF (n). Since BF (n) is vertex-transitive, we define the automorphism µs,d=
µn−1◦ . . . ◦ µ1◦ µ0 over V (BF (n)) where for 0 ≤ i ≤
Table 2: Hamiltonian paths of BF (3) as the induction bases.
d A hamiltonian path of BF (3) from h0, 000i to d with the desired property
h0, 100i hh0, 000i, h2, 001i, h1, 001i, h0, 101i, h2, 101i, h1, 111i, h0, 011i, h2, 011i, h1, 011i, h0, 111i, h2, 111i, h1, 101i, h0, 001i, h2, 000i, h1, 010i, h0, 110i, h2, 110i, h1, 100i, h2, 100i, h1, 110i, h0, 010i, h2, 010i, h1, 000i, h0, 100ii h0, 010i hh0, 000i, h2, 001i, h1, 001i, h0, 101i, h2, 101i, h1, 111i, h0, 011i, h2, 011i, h1, 011i, h0, 111i, h2, 111i, h1, 101i,
h0, 001i, h2, 000i, h1, 000i, h2, 010i, h1, 010i, h0, 110i, h2, 110i, h1, 100i, h0, 100i, h2, 100i, h1, 110i, h0, 010ii h0, 110i hh0, 000i, h2, 001i, h1, 001i, h0, 101i, h2, 101i, h1, 111i, h0, 011i, h2, 011i, h1, 011i, h0, 111i, h2, 111i, h1, 101i,
h0, 001i, h2, 000i, h1, 000i, h0, 100i, h2, 100i, h1, 100i, h2, 110i, h1, 110i, h0, 010i, h2, 010i, h1, 010i, h0, 110ii h0, 001i hh0, 000i, h2, 001i, h1, 001i, h0, 101i, h2, 100i, h1, 110i, h0, 010i, h2, 010i, h1, 000i, h2, 000i, h1, 010i, h0, 110i,
h2, 110i, h1, 100i, h0, 100i, h2, 101i, h1, 111i, h0, 011i, h2, 011i, h1, 011i, h0, 111i, h2, 111i, h1, 101i, h0, 001ii h0, 101i hh0, 000i, h2, 001i, h1, 001i, h0, 001i, h2, 000i, h1, 000i, h2, 010i, h1, 010i, h0, 110i, h2, 110i, h1, 100i, h0, 100i,
h2, 100i, h1, 110i, h0, 010i, h2, 011i, h0, 011i, h1, 011i, h0, 111i, h2, 111i, h1, 111i, h2, 101i, h1, 101i, h0, 101ii h0, 011i hh0, 000i, h2, 001i, h0, 001i, h1, 101i, h2, 101i, h0, 100i, h1, 100i, h2, 110i, h0, 110i, h1, 010i, h2, 000i, h1, 000i,
h2, 010i, h0, 010i, h1, 110i, h2, 100i, h0, 101i, h1, 001i, h2, 011i, h1, 011i, h0, 111i, h2, 111i, h1, 111i, h0, 011ii h0, 111i hh0, 000i, h2, 001i, h0, 001i, h1, 101i, h2, 111i, h1, 111i, h2, 101i, h0, 100i, h1, 100i, h2, 110i, h0, 110i, h1, 010i,
h2, 000i, h1, 000i, h2, 010i, h0, 010i, h1, 110i, h2, 100i, h0, 101i, h1, 001i, h2, 011i, h0, 011i, h1, 011i, h0, 111ii
0 0 o (Q) 1 0 (a) Subcase 1.1 (c) Subcase 1.3 (b) Subcase 1.2 s d d P01 d P11 u1 00 u2 00 t0 00 t1 00 t2 00 u1 10 u2 10 P10 t1 10 u0 01 u1 01 u2 01 R01 D01 t0 01 t1 01 t2 01 BF0,0 0,1(n) BF0,11,0(n) BF0,10,1(n) BF0,11,1(n) BF0,0 0,1(n) BF0,11,0(n) BF 0,1 0,1(n) BF 1,1 0,1(n) u0 11 u1 11 u2 11 R11 D11 t0 11 t1 11 t2 11 u0 11 u1 11 u2 11 R11 D11 t0 11 t1 11 t2 11 u0 10 u1 10 u2 10 R10 D10 t0 10 t1 10 t2 10 u2 01 u1 01 t1 01 BF0,0 0,1(n) BF 1,0 0,1(n) BF 0,1 0,1(n) BF 1,1 0,1(n) 0 0 o (Q) 1 0 s u1 00 u2 00 t0 00 t1 00 t2 00 0 0 o (Q) 1 0 s u1 00 u2 00 t0 00 t1 00 t2 00 u0 10 u1 10 u2 10 R10 D10 t0 10 t1 10 t2 10 u0 01 u1 01 u2 01 R01 D01 t0 01 t1 01 t2 01 u1 11 u2 11 t1 11
Figure 2: Illustrations for Case 1 of Lemma 8.
(b) Subcase 2.2 (c) Subcase 2.3 (d) Subcase 2.4 (a) Subcase 2.1 s d d1 00 d2 00 s1 00 s2 00 R10 BF0,0 0,1(n) BF0,11,0(n) BF 0,1 0,1(n) BF 1,1 0,1(n) d2 10 d1 10 d0 10 d0 01 d1 01 d2 01 R01 d0 11 d1 11 d2 11 s s1 00 s2 00 d1 00 d2 00 d0 00 BF0,0 0,1(n) BF 1,0 0,1(n) BF 0,1 0,1(n) BF 1,1 0,1(n) W10 D11 d d1 10 d2 10 s1 10 d0 01 d1 01 d2 01 R01 R11 d1 11 s1 11 s2 11 s0 11 s d1 00 d2 00 s1 00 s2 00 d0 00 BF0,0 0,1(n) BF0,11,0(n) BF 0,1 0,1(n) BF 1,1 0,1(n) R10 d2 10 d1 10 d0 10 d W01 d1 01 d2 01 s1 01 U11 s1 11 s2 11 s0 11 d1 11 BF0,0 0,1(n) BF0,11,0(n) BF0,10,1(n) BF0,11,1(n) s s1 00 s2 00 d1 00 d2 00 d0 00 R10 d2 10 d1 10 d0 10 U01 s1 01 s2 01 s0 01 d1 01 W11 d d1 11 d2 11 s1 11 0 0 o (Q) 1 0 0 0 o (Q) 1 0 0 0 o (Q) 1 0 0 0 o (Q) 1 0
otherwise. For any path joining s to d, say P = hs =
v0, v1, ..., vk = di with some k ≥ 1, we further define
µs,d(P ) = hd = µs,d(v0), µs,d(v1), ..., µs,d(vk) = si.
For the sake of clarity, the proofs of the following lemmas are described in Appendix.
Lemma 9. Assume that n is an odd integer greater
than or equal to 3 and also that ` ∈ Zn. Let s and d
be two distinct vertices at level ` of BF (n). Then
there exists a 3∗-container {P
1, P2, P3} of BF (n)
joining s to d such that the following requirements
are all satisfied: (i) both P2 and P3 begin with
level-` edges, (ii) only one path of {P1, P2, P3} ends up
with a level-` edge, (iii) at least one of P2 and P3 is
weakly `-scheduled, (iv) there are two vertices v1, v2
of I(P2) ∪ I(P3) so that µs,d(v1) = v2 and each
of {v1, v2} is incident with a level-(` − 1)mod n edge
and a level-` edge, and (v) the subgraph generated by
E(P1) ∪ E(P2) ∪ E(P3) is `-designed.
Lemma 10. For n ≥ 3, assume that `s and `d are
two integers of Zn such that `d− `s = 1. Let s be
any level-`s vertex of BF (n) and d be any level-`d
vertex of BF (n). Then there exists a 3∗-container
{P1, P2, P3} of BF (n) joining s to d such that the
following requirements are satisfied: (i) only P1 ends
up with a level-`dedge, (ii) (s, g(s)) ∈ E(P2)∪E(P3),
(iii) at least one of P2and P3is weakly `d-scheduled,
and (iv) the subgraph generated by E(P1) ∪ E(P2) ∪
E(P3) is `d-designed.
Lemma 11. Let s be any level-0 vertex of BF (4) and d be any level-3 vertex of BF (4). Then there exists
a 3∗-container {P
1, P2, P3} of BF (4) joining s to d
such that the following requirements are satisfied: (i)
only P1 ends up with a level-3 edge, (ii) P2 or P3 is
weakly 3-scheduled, and (iii) the subgraph generated
by E(P1) ∪ E(P2) ∪ E(P3) is 3-designed.
Lemma 12. For n ≥ 5, assume that `s and `d are
two integers of Zn such that `d − `s is odd between
3 and n − 1. Let s be any level-`s vertex of BF (n)
and d be any level-`d vertex of BF (n). Then there
exists a 3∗-container {P
1, P2, P3} of BF (n) joining s
to d such that the following requirements are satisfied:
(i) only P1 ends up with a level-`d edge, (ii) at least
one of P2 and P3 is weakly `d-scheduled, and (iii)
the subgraph generated by E(P1) ∪ E(P2) ∪ E(P3) is
`d-designed.
By Lemma 9, Lemma 10, Lemma 11, and Lemma 12, we derive the following result.
Theorem 3. Let n ≥ 3. Then BF (n) is 3∗
-connected if n is odd and is 3∗-laceable otherwise.
5
4
∗-containers of BF (n)
By Lemma 9 and the automorphism µs,d defined
above, we have the following corollary.
Corollary 3. Assume that n is an odd integer greater
than or equal to 3 and also that ` ∈ Zn. Let s and d
be two distinct level-` vertices of BF (n). By Lemma
9, there is a 3∗-containers {P
1, P2, P3} where P1
be-gins with a level-(` − 1)mod n edge. Then Ω = {Q1 =
(µs,d(P1))−1, Q2= (µs,d(P2))−1, Q3 = (µs,d(P3))−1}
is also a 3∗-container of BF (n) joining s to d with
the following conditions: (i) only one path of Ω begins
with a level-` edge, (ii) only Q1 ends up with a
level-(` − 1)mod nedge, (iii) at least one path of {Q2, Q3} is weakly `-scheduled, (iv) there are two level-` vertices
v1, v2 of (I(P2) ∪ I(P3)) ∩ (I(Q2) ∪ I(Q3)) such that
µs,d(v1) = v2 and each of v1 and v2 is incident with
a level-(` − 1)mod n edge and a level-` edge, and (v)
the subgraph generated by E(Q1) ∪ E(Q2) ∪ E(Q3) is
`-designed.
With Lemma 9 and Corollary 3, we have the follow-ing proposition. The proof is described in Appendix. Proposition 1. Assume that n is an odd integer
greater than or equal to 3 and also that ` ∈ Zn. Let s
and d be two distinct level-` vertices of BF (n). Then
there is a 3∗-container of BF (n) between s and d such
that each of {s, d} is incident with only one level-` edge.
Lemma 13. Assume that n is an odd integer greater than or equal to 3. Let s and d be two distinct vertices
at the same level of BF (n). Then there exists a 4∗
-container of BF (n) between s and d.
Proof. Without loss of generality, we assume that
s = h0, 0ni and d = h0, ijxi with some i, j ∈ Z
2 and x ∈ Zn−2
2 . The desired 4∗-containers of BF (3) are enumerated in Table 3. When n ≥ 5, BF (n) is partitioned into {BF0,1p,q(n) | p, q ∈ Z2}.
Case 1: Suppose that x 6= 0n−2. Let spq
h =
hh, pq0n−2i for any p, q ∈ Z
2and h ∈ {0, 1, 2}. Then we have to consider the following subcases.
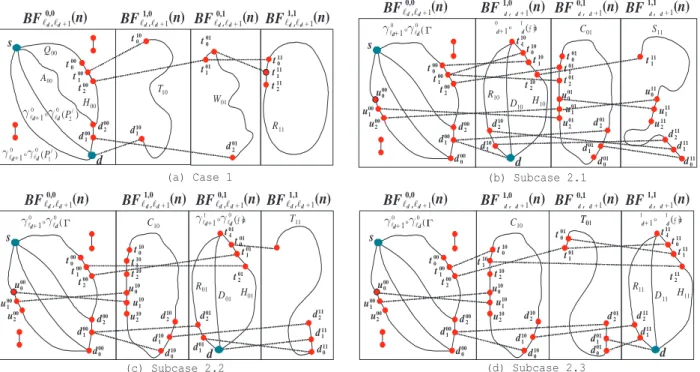
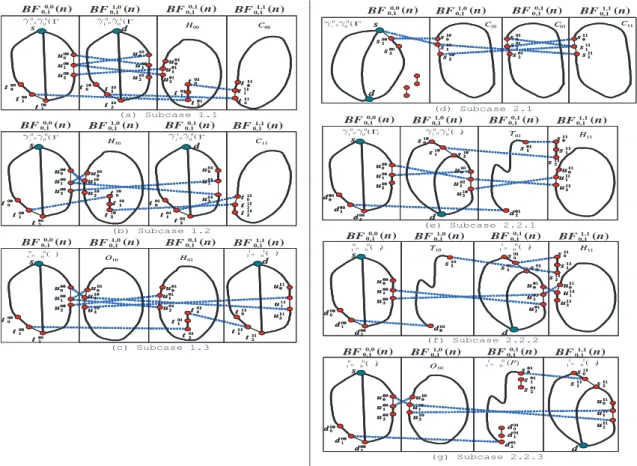
Subcase 1.1: Assume that ij = 00. By Propo-sition 1, we build a 3∗-container {P
1, P2, P3} of
BF (n − 2) joining s0 = h0, 0n−2i to d0 = h0, xi.
Let Γ be the subgraph of BF (n − 2) generated
by E(P1) ∪ E(P2) ∪ E(P3). Since BF0,10,0(n) =
γ0
1 ◦ γ00(BF (n − 2)), γ10 ◦ γ00(Γ) consists of three disjoint paths {J1, J2, J3} of BF0,10,0(n) joining s to
d. By Lemma 4, there is a totally scheduled
hamiltonian cycle C01 = hs01
0 , s011 , s012 , R01, s010 i of BF0,10,1(n). By Lemma 7, there is a hamiltonian cy-cle C10= hd10
0 , d101 , d102 , T10, d100 i of BF0,11,0(n) − {s101 }.
By Lemma 5, there is a hamiltonian path P11 =
hs11
2 , s111 , s110 , W11, d111 i of BF0,11,1(n). Then, let J4 =
hs, s10
1 , s112 , s111 , s010 , R−101, s012 , s011 , s110 , W11, d111 , d10
2 , T10, d100 , d101 , di, and thus {J1, J2, J3, J4} is a 4-container of BF (n) joining s to d. See Figure 4(a) for illustration. By Lemma 2, V (BF (n)) − S4i=1V (Ji) = V (BF0,10,0(n)) − V (γ0 1 ◦ γ00(Γ)) = Sm j=1{uj, g(uj)} for
some m ≥ 1 with {uj| 1 ≤ j ≤ m} ∩ {g(uj) | 1 ≤ j ≤
m} = φ. Moreover, Smj=1{(f (uj), g−1 ◦ f (uj))} ⊆
S4
i=1E(Ji). Thus, by Lemma 3, there is a 4∗
Table 3: 4∗-containers of BF (3) joining h0, 000i to the other level-0 vertices.
d 4∗-container {J1, J2, J3, J4} joining h0, 000i to d.
h0, 100i J1 = hh0, 000i, h1, 000i, h0, 100ii J2 = hh0, 000i, h1, 100i, h0, 100ii
J3 = hh0, 000i, h2, 000i, h1, 010i, h2, 010i, h0, 010i, h1, 110i, h2, 100i, h0, 100ii
J4 = hh0, 000i, h2, 001i, h0, 001i, h1, 001i, h0, 101i, h1, 101i, h2, 111i, h0, 110i, h2, 110i, h0, 111i, h1, 011i, h2, 011i, h0, 011i, h1, 111i, h2, 101i, h0, 100ii h0, 010i J1 = hh0, 000i, h1, 000i, h2, 010i, h0, 010ii
J2 = hh0, 000i, h1, 100i, h0, 100i, h2, 100i, h1, 110i, h0, 010ii J3 = hh0, 000i, h2, 000i, h1, 010i, h0, 010ii
J4 = hh0, 000i, h2, 001i, h1, 001i, h0, 001i, h1, 101i, h0, 101i, h2, 101i, h1, 111i, h2, 111i, h0, 110i, h2, 110i, h0, 111i, h1, 011i, h0, 011i, h2, 011i, h0, 010ii h0, 110i J1 = hh0, 000i, h1, 000i, h2, 010i, h0, 010i, h2, 011i, h0, 011i, h1, 011i, h0, 111i, h2, 110i, h0, 110ii
J2 = hh0, 000i, h1, 100i, h0, 100i, h2, 100i, h1, 110i, h0, 110ii J3 = hh0, 000i, h2, 000i, h1, 010i, h0, 110ii
J4 = hh0, 000i, h2, 001i, h1, 001i, h0, 001i, h1, 101i, h0, 101i, h2, 101i, h1, 111i, h2, 111i, h0, 110ii h0, 001i J1 = hh0, 000i, h1, 000i, h2, 010i, h1, 010i, h0, 010i, h2, 011i, h1, 001i, h0, 001ii
J2 = hh0, 000i, h1, 100i, h0, 100i, h2, 100i, h0, 101i, h2, 101i, h1, 111i, h0, 011i, h1, 011i, h0, 111i, h2, 110i, h1, 110i, h0, 110i, h2, 111i, h1, 101i, h0, 001ii J3 = hh0, 000i, h2, 000i, h0, 001ii
J4 = hh0, 000i, h2, 001i, h0, 001ii
h0, 101i J1 = hh0, 000i, h1, 000i, h2, 010i, h0, 011i, h2, 011i, h1, 011i, h0, 111i, h1, 111i, h2, 101i, h0, 101ii J2 = hh0, 000i, h1, 100i, h0, 100i, h2, 100i, h0, 101ii
J3 = hh0, 000i, h2, 000i, h1, 010i, h0, 010i, h1, 110i, h2, 110i, h0, 110i, h2, 111i, h1, 101i, h0, 101ii J4 = hh0, 000i, h2, 001i, h0, 001i, h1, 001i, h0, 101ii
h0, 011i J1 = hh0, 000i, h1, 000i, h2, 010i, h0, 011ii
J2 = hh0, 000i, h1, 100i, h2, 100i, h0, 100i, h2, 101i, h0, 101i, h1, 101i, h2, 111i, h1, 111i, h0, 011ii J3 = hh0, 000i, h2, 000i, h1, 010i, h0, 010i, h1, 110i, h0, 110i, h2, 110i, h0, 111i, h1, 111i, h0, 011ii J4 = hh0, 000i, h2, 001i, h0, 001i, h1, 001i, h2, 011i, h0, 011ii
h0, 111i J1 = hh0, 000i, h1, 000i, h2, 010i, h1, 010i, h0, 110i, h1, 110i, h0, 010i, h2, 011i, h0, 011i, h1, 111i, h0, 111ii J2 = hh0, 000i, h1, 100i, h2, 110i, h0, 111ii
J3 = hh0, 000i, h2, 000i, h0, 001i, h1, 001i, h0, 101i, h2, 100i, h0, 100i, h2, 101i, h1, 101i, h2, 111i, h0, 111ii J4 = hh0, 000i, h2, 001i, h1, 011i, h0, 111ii
(a) Subcase 1.1 (c) Subcase 1.3 (b) Subcase 1.2 (d) Subcase 1.4 s d J1 T10 J2 J3 R01 W11 s d T00 U00 W00 T10 U10 W10 R01 D01 H01 BF0,0 0,1(n) BF 1,0 0,1(n) BF 0,1 0,1(n) BF 1,1 0,1(n) s110 d210 d110 d010 s201 s101 s001 d111 s011 s111 s2 11 BF0,0 0,1(n) BF 1,0 0,1(n) BF 0,1 0,1(n) BF 1,1 0,1(n) A00 d200 d100 d000 u000 u100 u200 A10 s0 10 s110 s210 u010 u110 u2 10 s001 s101 s201 d101 d001 d2 01 u001 u101 u201 R11 D11 H11 s011 s111 s211 d111 d011 d211 u011 u111 u211 BF0,0 0,1(n) BF0,11,0(n) BF0,10,1(n) BF0,11,1(n) s T00 U00 W00 A00 d200 d100 d000 u000 u100 u200 d T01 U01 W01 A01 s001 s101 s201 u001 u101 u201 R11 D11 H11 s011 s111 s2 11 d1 11 d011 d211 u011 u111 u211 R10 D10 H10 s0 10 s110 s210 d110 d010 d210 u010 u110 u210 s T00 U00 W00 A00 d200 d100 d000 u000 u100 u2 00 BF0,0 0,1(n) BF0,11,0(n) BF0,10,1(n) BF0,11,1(n) d T11 U11 W11 A11 s011 s111 s211 u0 11 u111 u211 R10 D10 H10 s0 10 s110 s210 d110 d010 d210 u010 u110 u210 R01 D01 H01 s001 s101 s2 01 d1 01 d001 d201 u001 u101 u201
Subcase 1.2: Assume that ij = 10. By Lemma 9, there is a 3∗-container {P1, P
2, P3} of BF (n−2)
join-ing s0= h0, 0n−2i to d0 = h0, xi such that only P1
be-gins with a level-(n−3) edge. By Corollary 3, there is another 3∗-container {Q
1, Q2, Q3} of BF (n − 2)
join-ing s0to d0such that only Q1ends up with a level-(n−
3) edge. Moreover, (I(P2) ∪ I(P3)) ∩ (I(Q2) ∪ I(Q3)) contains a level-0 vertex u incident with a level-0 edge and a level-(n − 3) edge. We set u = h0, yi with some
y ∈ Zn−2
2 − {0n−2, x}. Further, we set upqh = hh, pqyi
and dpqh = hh, pqxi for any p, q ∈ Z2and h ∈ {0, 1, 2}.
Let Γ1 be the subgraph of BF (n − 2) generated by
E(Q1) ∪ E(Q2) ∪ E(Q3). By Corollary 3, Γ1 is
0-designed with respect to BF (n−2). Thus, γ0
1◦γ00(Γ1) spans BF0,10,0(n) and consists of three disjoint paths
{D00
1 , D200, D300} joining s to d002 . Accordingly, we
have D00
1 = hs, T00, d000 , d001 , d002 i where T00 joins s to d00
0 . Moreover, D002 and D003 form a cycle which can be written as hs, W00, u00
0 , u001 , u002 , U00, d002 , A00, si. Suppose that Γ2is the subgraph of BF (n − 2) gen-erated by E(P1) ∪ E(P2) ∪ E(P3). By Lemma 9, Γ2 is 0-designed with respect to BF (n − 2). Hence, γ1j◦ γi
0(Γ2) spans BF0,1i,j(n) and consists of three dis-joint paths {Dij1, Dij2, Dij3} between sij2 and d. Ac-cordingly, we write Dij1 = hsij2, sij1, sij0, Tij, di where Tij joins sij0 to d. Moreover, Dij2 and Dij3 form a cycle which can be written as h sij2, Wij, uij0, uij1, uij2, Uij, d, Aij, sij2 i. By Lemma 4, there is a to-tally scheduled hamiltonian cycle Cpq = h spq
0 , s pq 1 , spq2 , Rpq, upq0 , u pq 1 , u pq 2 , Dpq, dpq0 , d pq 1 , d pq 2 , Hpq, spq0 i of BF0,1p,q(n) for pq ∈ Z2
2− {00, ij}. Then we
cre-ate a 4∗-container {J1, J 2, J3, J4} of BF (n), in which J1= hs, T00, d000 , d001 , di, J2= hs, A−100, d002 , U00−1, u002 , u00 1 , u100 , W10−1, s102 , A−110, di, J3= hs, W00, u000 , u101 , u11 2 , D11, d110 , d111 , d112 , H11, s110 , s111 , s112 , R11, u110 , u01 1 , u012 , D01, d010 , d011 , d012 , H01, s010 , s011 , s012 , R01, u01
0 , u111 , u102 , U10, di, and J4= hs, s101 , s100 , T10, di. See Figure 4(b).
Subcase 1.3: Assume that ij = 01.
Sim-ilar to Subcase 1.2, we create a 4∗-container
{J1, J2, J3, J4} of BF (n), in which J1= hs, T00, d000 , d00 1 , d100 , D−110, u102 , u101 , u100 , R−110, s102 , s111 , s112 , R11, u11 0 , u111 , u112 , D11, d110 , d111 , di, J2 = hs, A−100, d002 , U00−1, u00 2 , u011 , u010 , W01−1, s012 , A−101, di, J3= hs, W00, u00
0 , u001 , u012 , U01, di, and J4 = hs, s101 , s100 , H10−1, d10
2 , d101 , d112 , H11, s110 , s011 , s010 , T01, di. See Figure 4(c).
Subcase 1.4: Assume that ij = 11.
Sim-ilar to Subcase 1.2, we create a 4∗-container
{J1, J2, J3, J4} of BF (n), in which J1= hs, T00, d000 , d00 1 , d012 , H01, s010 , s011 , s012 , R01, u010 , u011 , u110 , W11−1, s11 2 , A−111, di, J2 = hs, A−100, d002 , U00−1, u002 , u001 , u012 , D01, d01 0 , d011 , di, J3 = hs, W00, u000 , u101 , u100 , R−110, s10 2 , s111 , s110 , T11, di, and J4= hs, s110, s100 , H10−1, d102 , d10
1 , d100 , D10−1, u102 , u111 , u112 , U11, di. See Figure 4(d).
Case 2: Suppose that x = 0n−2. Let tpq
h =
hh, pq0n−31i, upq
h = hh, pq0n−2i, and wpq =
hn − 1, pq0n−31i for any p, q ∈ Z2 and h ∈
{0, 1, 2}. Obviously, s = u00
0 , d = uij0, and
{(s, w00), (d, wij)} ⊂ E(BF (n)). Suppose that
C00
0 = hs, u001 , u002 , D00, si is a cycle of length n,
in which D00 = hu00
2 , g(u002 ), . . . , gn−3(u002 )i. By
Lemma 6, there is a totally scheduled hamiltonian cy-cle C00
1 = hw00, t000 , t001 , t002 , R00, w00i of BF0,10,0(n) −
V (C00
0 ). By Lemma 7, there is a hamiltonian
cy-cle hd, uij1, uij2, Rij, di of BF0,1i,j(n)−{wij, uij0, uij1} and for pq ∈ Z2
2− {00, ij}, there is a hamiltonian cycle
Opq= htpq 0 , t pq 1 , t pq 2 , Tpq, tpq0 i of BF p,q 0,1(n) − {u pq 1 }. By
Lemma 4, there is a totally scheduled hamiltonian cy-cle hupq0 , upq1 , upq2 , Apq, upq0 i of BF0,1p,q(n) for any p, q.
Subcase 2.1: Assume that ij = 10. We create a 4∗-container {J
1, J2, J3, J4} of BF (n), in which J1=
hs, u10
1 , di, J2 = hs, u001 , di, J3 = hs, D00−1, u002 , u011 , u11
0 , A11, u112 , u111 , u102 , R10, di, and J4 = hs, w00,
R−1
00, t002 , t011 , t010 , T01−1, t201, t001 , t000 , t101 , t100 , w10, di. See Figure 5(a).
Subcase 2.2: Assume that ij = 01. Let
Q11
0 = hu110 , u111 , u112 , D11, u110 i be a cycle of length
n, in which D11 = hu112 , g(u112 ), . . . , gn−3(u112 )i. By
Lemma 6, there is a totally scheduled hamiltonian cycle Q11
1 = ht110 , t111 , t211, U11, t110 i of BF0,11,1(n) −
V (Q11
0 ). Then we build a 4∗-container {J1, J2, J3, J4} of BF (n), in which J1= hs, u101 , u112 , D11, u110 , u111 , di, J2 = hs, u001 , u012 , R01, di, J3 = hs, D00−1, u002 , u011 , di, and J4= hs, w00, R−1
00, t002 , t001 , t000 , t101 , t100 , T10−1, t102 , t11
1 , t112 , U11, t110 , t011 , t010 , w01, di. See Figure 5(b). Subcase 2.3: Assume that ij = 11. We create a 4∗-container {J1, J 2, J3, J4} of BF (n), in which J1= hs, u10 1 , u112 , R11, di, J2= hs, u001 , u012 , A01, u010 , u111 , di, J3 = hs, D−100, u002 , u011 , di, and J4 = hs, w00, R−100, t00 2 , t001 , t000 , t101 , t100 , T10−1, t102 , t111 , t110 , w11, di. See Figure 5(c).
Lemma 14. For n ≥ 3, assume that `s and `d are
integers of Zn such that 1 ≤ `d− `s ≤ n − 1. Let s
be any level-`s vertex of BF (n) and d be any
level-`d vertex of BF (n). Then there is a 4∗-container
Ω of BF (n) joining s to d such that the following requirements are satisfied: (i) at least one path of Ω,
ending with a level-(`d − 1)mod n edge, is weakly `d
-scheduled, and (ii) at least one path of Ω, ending up
with a level-`d edge, is weakly `d-scheduled.
Proof. Without loss of generality, we assume `s= 0
such that s = h0, 0ni and d = h`
d, x1ijx2i with
some 1 ≤ `d ≤ n − 1, i, j ∈ Z2, x1 ∈ Z`2d, and
x2 ∈ Zn−2−`2 d. We prove this lemma by induction
on n. Note that we only construct the desired
con-tainer for 1 ≤ `d ≤ bn/2c. By symmetry of BF (n),
the required container for bn/2c + 1 ≤ `d ≤ n − 1
can be easily derived. Moreover, only odd `d will be
concerned when n is even. The induction bases, de-pending on n ∈ {3, 4}, can be checked by a computer program. As the induction hypothesis, we suppose the statement holds for BF (n − 2) with n ≥ 5. Then we partition BF (n) into {BF`p,q
d,`d+1(n) | p, q ∈ Z2}.
By the induction hypothesis, there is a 4∗-container
{P0
1, P20, P30, P40} of BF (n − 2) joining s0 = h0, 0n−2i
to d0 = h`
d, x1x2i such that (1) P10 is weakly `d