Transform Domain Approach for Sequence Design
and Its Applications
Lung-Sheng Tsai, Student Member, IEEE, and Yu T. Su, Member, IEEE
Abstract—Many communication and radar systems necessi-tate the use of sequences with desired autocorrelation (AC) and cross-correlation (CC) properties. This paper presents a system-atic method based on the transform domain characterization of the AC and CC constraints to generate new families of sequences that meet the requirements. We demonstrate that some existing families can easily be generated by our approach. Our approach, however, renders new families of sequences with less constraints. The proposed approach is elementary and can easily be extended to synthesize two-dimensional arrays or even higher dimensional waveforms that possess the desired multidimensional correlation properties. A preamble structure based on our new sequence family is suggested and performance of frequency offset and channel estimation algorithms for a multiantenna orthogonal frequency-division multiplexing (OFDM) system that uses such a preamble is given.
Index Terms—Autocorrelation (AC), cross-correlation (CC), or-thogonal waveform design, polyphase sequence.
I. INTRODUCTION
S
ETS OF periodic sequences with good correlation proper-ties are desired in many communication and radar applica-tions. In a communication system, such sequences are used ei-ther in the preamble such that a receiver can easily perform pilot-assisted synchronization and/or channel estimation or as the sig-nature codes for a spread spectrum multiple access network.Oftentimes, we hope to have a family of sequences whose au-tocorrelation (AC) function has a single peak at the zero delay and whose cross-correlation (CC) values are identically zero at all delays. Such sequences can be used to avoid or minimize: 1) the interference from other users or other antennas if multiple transmit antennas were in place and 2) self-interference [e.g., in-tersymbol interference (ISI)] due to multiple propagation paths. Practical considerations also require that the sequence length be arbitrary and the family size be as large as possible, while main-taining the desired AC and CC properties.
Unfortunately, such an optimal family of sequences does exist for one cannot have both the ideal AC and CC. In fact, the Manuscript received October 4, 2004; revised June 1, 2005. This work is supported in part by the National Science Council of Taiwan under Grant 92-2213-E-009-050, and in part by the MediaTek Research Center, National Chiao Tung University. This paper was presented in part at the IEEE Interna-tional Conference on Communications, Seoul, Korea, May 16–20 , 2005.
L. S. Tsai was with the Department of Communications Engineering, National Chiao Tung University, Hsinchu 30056, Taiwan. He is now with the Graduate Institute of Communications Engineering, National Taiwan University, Taipei 10617, Taiwan (e-mail: longson@ieee.org).
Y. T. Su is with the Department of Communications Engineering, National Chiao Tung University, Hsinchu 30056, Taiwan (e-mail: ytsu@mail.nctu.edu.tw).
Digital Object Identifier 10.1109/JSAC.2005.858888
bounds on CC and AC of sequences discussed in [1] indicate that there is a tradeoff between AC and CC when designing se-quences. An alternate design approach is to either give up one of the desired correlation properties which has less impact on the system performance or to loosen the requirements and grant certain degree of nonzero correlations. For example, since the AC at time-lags (delays) larger than the transmission channel’s maximum multipath delay do not contribute to self-interference, we might just require zero AC values at those nonzero lags less than the maximum delay, allowing arbitrary AC values outside the range of concern. The families of PS sequences [2] do have similar suboptimal correlation properties but its length is lim-ited to squares of integers.
Recently, Park et al. [3] proposed a sequence generation method based on perfect reconstruction quadrature mirror filter banks. The sequences produced by this method have zero AC and CC at some delays; the remaining nonzero correlation values are in general lower than those of the well-known Gold sequences. However, their AC and CC are defined as the real parts of the conventional complex AC and CC functions and the length of
the sequences must be of the form .
Tropp et al. [4] formulated the sequence design problem as an inverse singular value problem. But they considered symbol-syn-chronous code-division multiple-access (CDMA) systems, thus, require zero CC at periodic delays only.
In this paper, we present a transform domain approach for generating families of sequences whose periodic AC functions have nonzero values only at some subperiodic delays and whose periodic CC functions are identically zero. Although the PS sequences have similar correlation properties, our approach for constructing the desired sequences is elementary and simpler. It transforms the correlation requirements into transform domain identities, imposes almost no constraint on the sequence duration and, moreover, can be used to generate a large number of families. Our approach also has the benefit of interpreting the so-called modulatable orthogonal sequences [5] from the frequency (transform) domain’s viewpoint.
The rest of this paper is organized as follows. In Section II, we derive the basic transform domain requirements on AC and CC. Section III presents the main theorem and a systematic trans-form domain process for constructing families of sequences with the desired correlation properties. Section IV provides a transform domain derivation of the class of modulatable orthog-onal sequences. We then proceed to show that the class of PS sequences can be easily generated by our method (Section V). A transform domain approach for constructing multidimensional arrays with desired AC and CC is presented in Section VI. A preamble structure for multiple-input–multiple-output (MIMO) 0733-8716/$20.00 © 2006 IEEE
orthogonal frequency-division multiplexing (OFDM) wideband local area network (WLAN) systems is suggested in Section VII in which related frequency and channel estimator performance is also provided. Finally, we give some concluding remarks in Section VIII.
II. DEFINITIONS ANDFUNDAMENTALPROPERTIES Let denote a set of complex-valued sequences of period
, i.e., for every sequence , , for
all , being the set of integers.
Definition 1: The periodic CC function of two period-
se-quences , is defined by
(1) The periodic AC function for the sequence is just
. We assume that for all , then
it is obvious that and for all ,
.
To facilitate the subsequent discourse, we need some more definitions; some of them are adopted from [2] for convenience of reference.
Definition 2: The discrete Fourier transform (DFT) matrix with index is given by
(2)
where is a natural number, , ,
and .
Definition 3: The diagonalized matrix associated with the sequence is defined as
(3)
Definition 4: A period- sequence is called an
or-thogonal sequence if its AC satisfies
(4)
where is the Kronecker delta function and .
It is periodic orthogonal with period if
(5) where divides .
Definition 5: A family of period- sequences is called near-optimal if all its member sequences are periodic or-thogonal and each pair has zero CC, i.e., for
(6)
where .
Definition 6: A set of -dimensional vectors is said to be an orthogonal tone set if , , where is the support of the vector . The set is complete if , i.e., if is a partition of the set . If the set has only two vectors , we say they are an orthogonal tone pair.
Definition 7: Let be the delay operator that cyclicly shifts the components of a vector to the right by one place and
-denote the operator that shifts the components of a vector to the right cyclicly by places.
Definition 8: The -fold expander converts a
length-sequence into a length- sequence by
if
otherwise (7) is referred to as the expanding rate, while is a rate-ex-panding mapping [6].
For convenience of reference we list the following well known property concerning the last definition.
Property 1: is an -period
exten-sion of , i.e., , , and
is an -period extension of , where modulo .
We shall refer to an -dimensional vector and its periodic extension interchangeably, making no distinction be-tween an -dimensional vector and its periodic extension when there is no danger of confusing. The -point DFT of , (or
), is called its spectral vector (representation).
We also need the following fundamental lemma and its corol-laries in our subsequent discourse.
Lemma 1: The DFT of the periodic CC function
of two period- sequences, and , is equal to , where and are the DFTs of and , respectively.
This lemma is well known and has appeared in the literature in various forms; e.g., see [10] and [11]. It follows immediately that.
Corollary 1: The AC function is equivalent to
and .
Hence, a sequence is orthogonal, i.e., , iff is a constant for all .
Corollary 2: The periodic CC of the two sequences , is identically zero iff their DFT’s satisfy
, .
Corollary 3: Members of the set of sequences , , have zero CC if their spectral representa-tions form a set of orthogonal tones. Moreover, the “combined” sequence has impulse-like AC (i.e., orthogonal) if is a complete set of orthogonal tones and is a constant for all .
III. FREQUENCY-DOMAINSYNTHESIS
A. Main Theorem
Based on the transform domain characterization of the AC and CC correlation functions, we now present a theorem that
suggests a frequency-domain approach for generating
near-op-timal families of sequences.
Lemma 2: Let be a set of
pe-riod- sequences, where and denote the -point
DFT of by , then is a near-optimal
family if
(8) where is the DFT of a length- perfect AC sequence.
Proof: Let be the -point DFT of the AC func-tion of . Then
(9) The establishment of the perfect CC property is straightforward since the spectral vectors form a complete set of orthogonal tones.
Substituting (8) into (9), we obtain
(10)
If is a period- sequence with
per-fect AC function, then
(11) Therefore, for
otherwise (12) and according to Property 1, the AC function of is the -pe-riod extension of that of , i.e.,
(13)
The other ’s for are simply
frequency-shifted versions of , i.e.,
(14) The frequency-shifting operation induces a phase rotation in the time-domain
(15) i.e., the AC function has a nonzero value only when . is referred to as the generating sequence of since its spectrum determines those of all members of .
In proving the above lemma, we make use of the facts that has constant modulus and the spectral vectors form a complete set of orthogonal tones to derive the near-optimal AC and CC properties. It can easily be generalized to the following.
Theorem 1: Let , be -dimensional vectors, not necessarily distinct and define the
-dimen-sional vectors, . Then, the sequences,
, , have zero CC and
the corresponding AC functions in one period are -period extensions of those of . Furthermore, if
are constant modulus vectors, then the family is near-optimal.
B. Synthesis Process
The construction procedure suggested by Lemma 2 requires that a sequence with constant modulus spectrum (or perfect AC) be found to begin with. There are many such sequences for use as the generating sequence. In fact, Corollary 1 tells us that a perfect AC sequence can be generated by specifying a con-stant modulus spectral sequence and there are practically infinite many such sequences. Practical consideration, however, prefers to use a sequence whose components are drawn from a finite constellation such as phase-shift keying (PSK) or quadrature amplitude modulation (QAM). One known candidate sequence is the Frank–Zadoff–Chu (FZC) sequences [7], [8]—a class of unity-modulus polyphase sequences with impulse-like periodic AC functions.
Theorem 1 also suggests that if we let ,
be the spectral vectors of -sequences (not necessarily distinct) of period , then we can generate a family with zero CC and AC function the same as a periodic extension of that of . We summarize the synthesis procedure and the major attributes of the resulting sequences as follows.
(S.1) Given an orthogonal sequence of period and let be the corresponding spectral sequence of constant modulus. Rate-expanding by -fold and taking -point inverse discrete Fourier trans-form (IDFT) on the cyclic-shifted versions
, , we obtain a
near-optimal family of length- sequences.
(S.2) The generating sequence determines the AC function in one period, and the CC properties between sequences are determined by their DFTs.
(S.3) A member sequence will consists of complex numbers with unity magnitude if is an FZC sequence (see Example 1 below) or a polyphase sequence gener-ated by the method suggested in Lemma 3. We can also achieve the same result by selecting an -sequence as the generating sequence. However, in most cases an fast Fourier transform (FFT)-like transform for a sequence with period is not as fast as the conventional FFT on sequences with a period of powers of 2 [11].
Example 1: To generate two near-optimal sequences
of length 12, one has to choose a perfect AC sequence first. Let an FZC sequence of length 6 be chosen and pick which is relative prime to . According to the generating method in [8], the elements of the FZC
sequence would be , where .
Following the above synthesizing procedure, we obtain
two orthogonal polyphase sequences ,
, 1, where
and . It can
easily be proved that the AC functions of them are
for ,
and the CC function is identically zero for all . IV. CLASS OFORTHOGONALSEQUENCES
Although a sequence with perfect AC can be immediately obtained by taking IDFT on a vector of constant modulus, it
is always preferred that the components of the sequence be-long to a small set of special symbols. A method to construct a class of polyphase sequences that have perfect AC was pro-posed in [5]. This section provides a transform domain approach and interpretation for generating the same sequences and their generalizations.
For a set of basic symbols located on the circle of radius
in the complex plane and , we
define the basic orthogonal sequence matrix of size as
(16)
Note that for the case , ,
. As the factor does not af-fect the AC property, it will be omitted in the remaining discussion. Consider the sequence
(17) where denotes the (column vectors) stacking operator. Without loss of generality, we take the case , as an example and let , then
(18)
where , , and .
The th column vector of the matrix is equal to the -point IDFT of . Since there is only one nonzero component in and all the components in have unit magnitude, the components of must have identical magnitude.
Employing a procedure similar to (8), we first expand the time-domain vectors by threefold, and then cyclic-shift the rate-expanded vectors to obtain the set of orthog-onal tones
(19) The -point DFT of is the -period extension of , while that of is a linearly phase-shifted -period extension of . Define the new vector
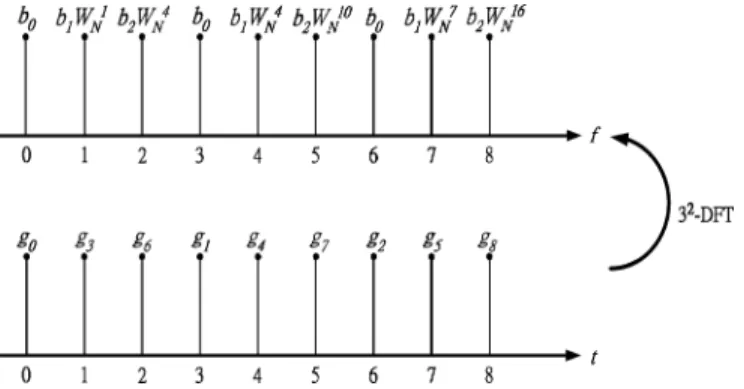
(20) The -point DFT of is a constant modulus vector (see Fig. 1) and, according to Corollary 1, has the perfect AC property, irrespective of the linear phase rotation induced by the time-shifting operation. The reason why we obtain a constant modulus spectrum is obviously due to the fact that is a set of orthogonal tones which resulted from the tone-orthogonality of the set . Generalizing the above argument, we can easily verify.
Lemma 3: Let , where is an
matrix whose column vectors
Fig. 1. Generating a sequence with perfect periodic AC property. All time and spectral components are of the same magnitude.
have constant modulus components, i.e., , and , and form a complete set of orthogonal tones. Then
is an orthogonal sequence of period . Moreover, if each has only one nonzero unit-modulus component, then is a polyphase sequence.
Note that considering of (20) not as components of but as individual transform domain vectors, Corollary
3 then implies that the sequences do form a near-optimal family.
Extending to the cases now, we first note that
, where ,
which is the case that . Taking -point IDFT on , we obtain the vector
. In general, the th column of , can be written as
(21) where
(22)
is a phase-rotated version of , for . Hence, we have
(23) The above relation implies that the parameter determines the order of the frequency-domain index cyclic-shifting. As long as form a complete set of orthogonal tones, the sequence will preserve the perfect periodic AC property. On the other hand, if such that the sequence
has perfect AC, then we can find a column-permuted matrix
of the diagonal matrix such that
. We, thus, claim the following generalization of the results reported in [5].
Theorem 2: Let , where is an ma-trix whose column vectors form a complete set of orthog-onal tones. Then, is an orthogonal sequence of period
iff .
Proof: We shall start with the special case , then proceed to prove the general case using (23) directly.
1) , , where
is the support of the th column vector of the matrix .
For if , then
(24)
The assumption then implies that
divides and so . Therefore, we must have .
2) .
Let and , then .
It can easily be established that
,
, . But
implies that and .
Hence, . The equivalence class
under mod addition has ele-ments and there are different equivalence classes.
For the general case that the matrix is composed of column vectors that form a complete set of orthogonal tones, we can treat each column vector as the sum of vectors having only one nonzero component so that , where is the support of the vector . Obviously, we have . Following a similar argument in proving for the special case , we conclude that is an orthogonal sequence of period iff
.
The following example checks a special case of this theorem; other examples can be found in [9].
Example 2: Consider the case, , ,
, and . In this case, we have
. The basic orthogonal sequence matrix is . Taking DFT on column vectors of and using the resulting frequency-domain vectors as the column vectors of , we then obtain
(25)
It can be proved that the AC function of the sequence
is .
As ’s are selected from the unit circle, the generated se-quence will be composed of complex numbers with the same magnitude. Fig. 1 plots an example in which the entries of the se-quence have the same magnitude in both time and frequency do-mains. As mentioned before, a sequence has perfect AC function if all of its frequency components have the same magnitude. The
time-frequency duality property of Fourier transform pairs then implies that if one exchanges the roles of the “time-domain” sequence and the “frequency-domain” sequence, the AC prop-erty can still be maintained. This propprop-erty is shared by the se-quence generated here and the FZC sese-quences, therefore, (8) can be modified as
otherwise (26)
This sequence generation procedure is a much simpler than but equivalent to that of the PS sequences.
V. GENERATION OF THEPS SEQUENCES
The so-called PS sequences [2] is also a near-optimal family that consists of polyphase sequences of period , where . The value determines the period of the AC function of the member PS sequences. We now provide a trans-form domain derivation of the PS sequences and their AC and CC properties. The derivation is much simpler and more instruc-tive than that given in [2].
Let the basic orthogonal sequence of length [5] be generated by (16) with and , i.e.,
(27) Again, following a process similar to (8), we first rate-ex-pand the basic orthogonal sequence with a rate of , and then use the cyclic-shifted versions , of the rate-expanded vector as column
vectors of the matrix
(28) Since is a complete set of orthogonal tones, their time-domain representations must have zero CC. The
column vectors of the
matrix
(29) form a near-optimal family whose member sequences are called
PS sequences. As is a -fold-expanded version of a constant modulus vector, the AC function of a PS sequence is
(30) A careful examination of the above construction procedure re-veals that it is the same as that suggested by Lemma 2 except for: 1) the choice of the generating sequence and its period and 2) instead of using the Fourier transform of a perfect AC sequence , a perfect AC sequence is used for rate-ex-panding and cyclic-shifting. Despite 2), we obtain a near-op-timal family since happens to be a constant modulus se-quence. Replacing by any other perfect AC -phase se-quence of the same period, we obtain another set of PS-like sequences. Note, however, that our proposed construction im-poses no constraint on the period of the sequences except that it cannot be a prime. For example, one cannot generate PS se-quences having AC function of period 38; since , for any natural numbers and .
VI. MULTIDIMENSIONALARRAYS
Like the one-dimensional (1-D) case, two-dimensional (2-D) arrays that possess some desired AC or CC properties are useful in sonar/radar and communication applications. Similarly, higher dimensional array signals are needed in some multidimensional search and detection applications. In this section, we extend the method we developed for 1-D sequences to two or higher dimensions arrays.
A. Preliminary
For convenience of reference, we follow the notations and definitions used by [10].
Definition 9: Let an array sequence be denoted by
(31)
The 2-D periodic AC function between two array sequences and having the same dimensions is defined as
(32)
Definition 10: An array is called a perfect array if its periodic
AC function satisfies
(33)
where .
There are many published works on the syntheses of perfect arrays; one of them is based on [10]
Theorem 3: (Folding method.) Let be an orthogonal se-quence of length . Then, the array defined by (34)
is perfect if .
B. Generation of New 2-D Arrays
Our approach for generating a family of 2-D arrays consists of three steps.
Step 1) Applying the folding method to the FZC sequence or any other orthogonal sequence of length ,
where , we obtain an
perfect array . Denote the 2-D DFT of this perfect array by , i.e.,
(35) Step 2) Using the as the basic building spectral array, we construct 2-D spectral arrays ,
, , and ,
according to
otherwise
(36) This assignment rule is illustrated in Fig. 2.
Fig. 2. (a) ConstructingF (U; V ) from the 2-D DFT of the basis array. (b) Composite spectral representations ofF (U; V ); different symbols are used to represent the nonzero positions of different spectral arrays (K = 2, K = 2, N = 4, and N = 5).
Step 3) Taking the 2-D IDFT on , we obtain
an array sequence of dimension
, where the 2-D IDFT is defined by
(37)
The elements of the array are in the form of , where if is even
if is odd
(38) and ’s are integers. The new array sequences possess some desired properties similar to those in the 1-D case. It can be easily proved that
(39) The AC function is periodic in both argu-ments—the period in is , while the period in is . Moreover, the periodic CC function between any two arrays of ’s is zero and the number of the member arrays in the
family is .
Example 3: Suppose we have a perfect array of dimension
already and want to generate neoptimal
ar-rays of dimension with , ,
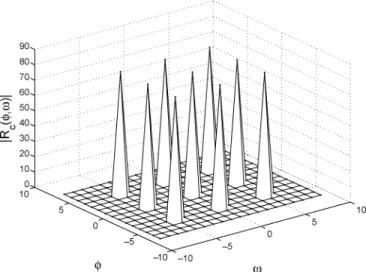
and . Applying the folding method to the FZC sequence of length 20, we immediately have a 4 5 perfect array. By following steps 2–3, we obtain near-op-timal arrays. The magnitude of the AC function for these arrays, , , is periodic in both and and is plotted in Fig. 3, where the period along is 4, while the period along is 5.
C. Extension to Multidimensional Arrays
It is straightforward to extend the above concept to higher di-mensional arrays. One of the key steps in generalizing the tech-nique presented in the previous subsection for synthesizing 2-D arrays is to find a 2-D perfect array. Similarly, to construct a
Fig. 3. MagnitudejR j of the 2-D periodic AC function associated with the proposed array. (K = 2, K = 2, N = 4, and N = 5).
family of multidimensional arrays with the near-optimal prop-erty, one has to have a perfect multidimensional array (i.e., one whose multidimensional AC function is nonzero only at the origin) to begin with. This task is made easier by noting that
Corollary 1 can be extended to higher dimensional domains.
Define the -dimensional DFT of an array
of dimension by
(40) Then, we have as follows.
Corollary 4: An array is perfect if is a constant for all .
In Theorem 3, we mention a method to construct a perfect 2-D array from an orthogonal sequence. It can be shown that this method does satisfy the above corollary for .
Given an perfect array of dimension
, we generate a family of multidimensional arrays by a three-step procedure similar to that of Section VI-B.
(C.1) Taking -dimensional DFT on this basis (perfect) array.
(C.2) Let be arrays to
be generated and denote the corresponding
-dimen-sional DFT’s by ,
i.e.,
(41)
where . Then,
is constructed according to the assignment rule otherwise (42)
where defines the support (nonzero posi-tions) in transform domain for the th newly-generated array. The distribution of is a multidimensional generalization of that of Fig. 2(b); for a given , they are equally spaced along all axes.
(C.3) Taking -dimensional IDFT on
(43) We then obtain an array sequence of dimension . It can be proved that the CC function between any two array sequences so generated is identically zero.
VII. PREAMBLE DESIGN FORMULTIANTENNA OFDM SYSTEMS
Applications of the near-optimal family of sequences to CDMA or similar systems are well known [2]. This section provides another application example of such sequences in designing preambles for multiantenna OFDM systems. Note that, as mentioned in (S.3), we can generate finite-constellation polyphase sequences in both domains, hence, at least in the preamble part, the peak-to-average power ratio is not a concern. We assume that the OFDM guard interval is of length and is larger than the maximum delay spread of the channel of con-cern. For such a bounded maximum delay spread scenario, we use the proposed near-optimal polyphase family, choosing a se-quence length such that the unwanted AC peak values occurs at delays larger than . Using members of a near-optimal family with period as preamble sequences, where is the number of transmit antennas, we then have all the self in-terference due to multipath propagation eliminated. For applica-tions to IEEE 802.11a-compatible multiantenna OFDM systems with transmit antennas, we can use a family of near-optimal sequences with period 64 or 32 to replace the two long training symbols of the 802.11a standard.
In our simulation, we use an exponentially decayed Rayleigh-fading channel with the impulse response given by
. and are independent zero-mean complex Gaussian random variables with the same variance ,
where , is the sampling period, and
is the maximum delay spread. Table I summarizes system and sequence parameters used in our simulation. We also assume that channels between different transmit and receive antennas are independent.
A. Frequency Synchronization
Moose [12] proposed a correlation-based technique that uses two consecutive identical pilot symbols to estimate CFO. Schmidl and Cox (SC) [13] suggested a differentially encoded preamble and applied the correlation metric to obtain both integer and fractional parts of CFO. Subsequent techniques use multiple identical or differentially encoded pilots with a smaller
TABLE I
SOMESYSTEM ANDSEQUENCEPARAMETERSUSED INSIMULATION
Fig. 4. Effect of the channel delay spread on the CFO estimator’s MSEE performance; 2Txs and 1 Rx with frequency offset= 0:3 subcarrier spacings.
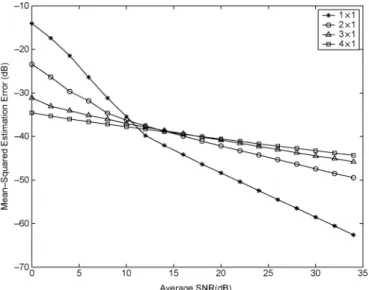
Fig. 5. Effect of the transmit antenna numbers on the MSEE performance of the SC frequency estimator; CFO = 0:3 subcarrier spacings and r.m.s. channel delay spread= 50 ns.
symbol period to increase the estimation range of CFO (see [14] and the references therein). For the multiple antenna systems with two identical pilots, the correlation metric of [12] is still applicable. A proper weighted version would give the optimal estimate, however. In Figs. 4 and 5, we respectively examine the influences of the channel’s delay spread and the number of transmit antennas on the mean-squared estimation error (MSEE) performance of the SC estimate. We notice that the estimator is insensitive to the r.m.s. delay spread of the channel except for low average SNRs, where a larger delay spread helps reducing MSEE, if the maximum channel delay spread does not exceed the length of the guard interval. In Fig. 5, for fairness of comparison, we assume that the total transmit power is fixed.
These performance curves indicate that there is a threshold (around 11.5 dB) beyond which the noncoherent combining loss associated with the SC frequency estimate outweighs the corresponding diversity combining gain.
B. Channel Estimation
With the use of members of a near-optimal family as pilot sequences, the receiving end of a MIMO system can separate the signals originated from different transmit antennas. Hence, one can easily modify any pilot-assisted, correlation-based channel estimator designed for conventional single antenna systems to serve as a MIMO channel estimator. The structure of the proposed pilot sequences, however, allows a very simple least-squares (LS) channel estimator to achieve the optimal performance. We give a sketch of the proof for a 2 1 system in the following paragraph. Extension to the general MIMO systems is straightforward [15].
Let be the received data
vector and denote the transmit pilot vector from the th antenna
by . Assuming perfect frame
timing and frequency offset compensation, we have, for a 2 1 system
(44) where is the channel impulse response vector associated with the th transmit antenna and
..
. ... ... (45)
Notice that for since cyclic prefix
is added. It can be shown that if is a zero-mean complex white Gaussian vector, the corresponding MSEE of the LS channel
estimator is lower-bounded by
(46) where is the energy of the polyphase pilot vector. The lower bound is achieved by a pilot vector that satisfies and the minimum MSEE is independent of the channel response. It is clear that our pilot sequences satisfy this criterion with and the LS estimator can be further simplified to , which means it is to be derived from a simple matched filtering.
As the two long training symbols associated with each an-tenna contain two periods of the corresponding pilot sequence, an improved channel estimator can be obtained by
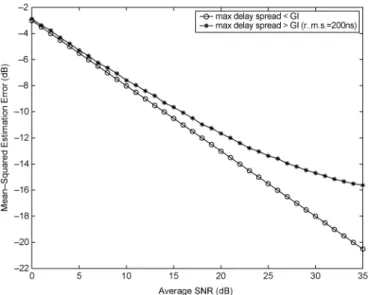
(47) The minimum MSEE is guaranteed so long as the channel memory is less the guard interval, irrespective of the true channel response. When the channel memory is longer than the guard interval, the performance deteriorates accordingly. Nevertheless, it is highly likely that the strengths for those paths
Fig. 6. MS channel estimation error performance for channels with different memory lengths; guard interval width= 16 samples.
whose relative delays are larger than the guard interval are very small. Fig. 6 compares the per-channel MSEE performance for both cases.
VIII. CONCLUSION
We have presented systematic methods for generating 1-D se-quences and multidimensional arrays with near-optimal AC and CC properties. The well-known fact that the AC and CC func-tions are closely related to the DFTs of the desired sequences en-able our approach to render a natural interpretation, a much sim-pler derivation and a generalization of the orthogonal sequences proposed in [5]. We also show that the class of PS sequences [2] is a special family within the sequence families generated by our new synthesis method. Our approach is elementary and it is be-lieved that our approach can provide an avenue for discovering new sequences with other desired properties.
These families of sequences or arrays have many interesting applications. We present application examples for frequency synchronization and channel estimation in MIMO-OFDM sys-tems. Numerical simulation indicates that, as the preamble se-quences used possess the desired properties, both estimators yield excellent performance.
REFERENCES
[1] D. V. Sarwate, “Bounds on cross correlation and autocorrelation of se-quences,” IEEE Trans. Inf. Theory, vol. IT-25, pp. 720–724, Nov. 1979. [2] S. I. Park, S. R. Park, I. Song, and N. Suehiro, “Multiple-access interfer-ence reduction for QS-CDMA systems with a novel class of polyphase sequences,” IEEE Trans. Inf. Theory, vol. 46, no. 4, pp. 1448–1458, Jul. 2000.
[3] S. R. Park, I. Song, and H. Kwon, “DS/CDMA signature sequences based on PR-QMF banks,” IEEE Trans. Signal Process., vol. 50, pp. 3043–3054, Dec. 2002.
[4] J. A. Tropp, I. S. Dhillon, and R. W. Heath, “Finite-step algorithms for constructing optimal CDMA signature sequences,” IEEE Trans. Inf.
Theory, vol. 50, no. 11, pp. 2916–2921, Nov. 2004.
[5] N. Suehiro and M. Hatori, “Modulatable orthogonal sequences and their application to SSMA systems,” IEEE Trans. Inf. Theory, vol. 34, no. 1, pp. 93–100, Jan. 1988.
[6] P. P. Vaidyanathan, Multirate Systems and Filter Banks. Englewood Cliffs, NJ: Prentice-Hall, 1993.
[7] R. L. Frank and S. Zadoff, “Phase shift codes with good periodic corre-lation properties,” IEEE Trans. Inf. Theory, vol. IT-8, pp. 381–382, Oct. 1962.
[8] D. C. Chu, “Polyphase codes with good periodic correlation properties,”
IEEE Trans. Inf. Theory, vol. IT-18, no. 4, pp. 531–532, Jul. 1972.
[9] L.-S. Tsai, “Transform domain approach for sequence design and its applications to MIMO-OFDM systems,” M.S. thesis, Dept. Commun. Eng., National Chiao Tung Univ., Hsinchu, Taiwan, Jun. 2004. [10] P. Z. Fan and M. Darnell, Sequence Design for Communications
Appli-cations. London, U.K.: Research Studies Press, 1996.
[11] J. H. McClellan and C. R. Rader, Number Theory in Digital Signal
Pro-cessing. Englewood Cliffs, NJ: Prentice-Hall, 1979.
[12] P. H. Moose, “A technique for orthogonal frequency division multi-plexing frequency offset correction,” IEEE Trans. Commun., vol. 42, no. 10, pp. 2908–2914, Oct. 1994.
[13] T. M. Schmidl and D. C. Cox, “Robust frequency and timing syn-chronization for OFDM,” IEEE Trans. Commun., vol. 45, no. 12, pp. 1613–1621, Dec. 1997.
[14] J. H. Yu and Y. T. Su, “Pilot-assisted maximum likelihood frequency-offset estimation for OFDM systems,” IEEE Trans. Commun., vol. 52, no. 11, pp. 1997–2008, Nov. 2004.
[15] C. Fragouli, N. Al-Dhahir, and W. Turin, “Training-based channel es-timation for multiple-antenna broadband transmissions,” IEEE Trans.
Wireless Commun., vol. 2, no. 2, pp. 384–391, Mar. 2003.
Lung-Sheng Tsai (S’05) was born in Tainan,
Taiwan, 1980. He received the B.S. degree in electrical engineering from the National Tsing Hua University, Hsinchu, Taiwan, in 2002, and the M.S. degree in communications engineering from National Chiao Tung University, Hsinchu, Taiwan, in 2004. He is currently working towards the Ph.D. degree in the Graduate Institute of Communication Engineering, National Taiwan University, Taipei, Taiwan.
His current research interests include wireless communications, communication sequences design, and scheduling in mul-tiuser systems.
Yu T. Su (S’81–M’83) received the Ph.D. degree
in electrical engineering from the University of Southern California, Los Angeles, in 1983.
From 1983 to 1989, he was with LinCom Corpora-tion, Los Angeles, CA, where he was a Corporate Sci-entist involved in the design of various measurement and digital satellite communication systems. Since September 1989, he has been with the National Chiao Tung University, Hsinchu, Taiwan, where he is As-sociative Dean of the College of Electrical and Com-puter Engineering and was the Head of the Commu-nications Engineering Department from 2001 and 2003. He is also affiliated with the Microelectronic and Information Systems Research Center, National Chiao Tung University and served as a Deputy Director from 1997 to 2000. His main research interests include communication theory and statistical signal processing.