A systolic algorithm for solving dense linear systems

P e r g a m o n

Computers Math. Applic. Vol. 32, No. 12, pp. 77-91, 1996 Copyright©1996 Elsevier Science Ltd Printed in Great Britain. All rights reserved 0898-1221/96 $15.00 -t- 0.00 PII: S0898-1221 (96)00208-8

A Systolic Algorithm for Solving

D e n s e Linear Systems

CHAU-JY LIN

Department of Applied Mathematics, National Chiao-Tung University Hsinchu, 30050, Taiwan, R.O.C.

cj lin~math, nctu. edu. t w

(Received and accepted M a y 1996)

A b s t r a c t - - F o r an arbitrary n x n matrix A and an n × 1 column vector b, we present a systolic algorithm to solve the dense linear equations A x = b. An important consideration is that the pivot row can be changed during the execution of our systolic algorithm. The computational model consists of n linear systolic arrays. For 1 < i < n, the ith linear array is responsible to eliminate the ith

unknown variable xi of x. This algorithm requires 4n time steps to solve the linear system. The elapsed time unit within a time step is independent of the problem size n. Since the structure of a PE is simple and the same type PE executes the identical instructions, it is very suitable for VLSI implementation. The design process and correctness proof axe considered in detail. Moreover, this algorithm can detect whether A is singular or not.

K e y w o r d s - - P a x a l l e l computer, Linear array, Systolis algorithm, Dense linear system.

1. I N T R O D U C T I O N

P a r a l l e l c o m p u t e r s have b e e n used to solve m a n y p r o b l e m s in t h e fields of sciences a n d engi- n e e r i n g . Systolic a r r a y is o n e of parallel c o m p u t e r s . A n a l g o r i t h m which c a n be e x e c u t e d o n a systolic a r r a y is called a s y s t o l i c a l g o r i t h m . T h e systolic a r r a y has b e e n w i d e l y used t o solve v a r i o u s p r o b l e m s b e c a u s e of its r e g u l a r s t r u c t u r e , simple i n t e r c o n n e c t i o n , a n d feasibility for VLSI i m p l e m e n t a t i o n [1-5]. Some useful discussions of systolic a r r a y s a n d systolic a l g o r i t h m s c a n be referred to t h e p a p e r s in [6-8].

G i v e n a n a r b i t r a r y n × n m a t r i x A = ( a i j ) a n d a n n × 1 c o l u m n vector b = (b~), t h e s o l u t i o n of t h e l i n e a r s y s t e m A x = b is one of m a j o r p r o b l e m s i n c o m p u t a t i o n a l a n d a p p l i e d m a t h e m a t i c s . For s o l v i n g A x = b, u n d e r t h e e l e m e n t a r y row o p e r a t i o n o n A, a s e q u e n t i a l a l g o r i t h m is always r e q u i r e d t o find a n i th pivot row such t h a t t h i s row possesses t h e largest a b s o l u t e v a l u e a m o n g t h e i th c o l u m n of A. T h i s p a r t i a l p i v o t i n g m e t h o d is n o t easy to be a c c o m p l i s h e d w i t h i n a p a r a l l e l a l g o r i t h m . T h u s , m a n y parallel a l g o r i t h m s t o solve A x = b r e q u i r e some a s s u m p t i o n s , such as A is n o n s i n g u l a r t h a t t h e d i a g o n a l e n t r i e s of A are nonzero, a n d t h a t t h e p r o b l e m r e l a t i n g to p i v o t i n g is n o t c o n s i d e r e d [9-15].

W h e n A is a n o n s i n g u l a r m a t r i x , t h e L U d e c o m p o s i t i o n is a v e r y useful m e t h o d to solve A x = b. T h i s m e t h o d o b t a i n s a t r i a n g u l a r m a t r i x from A followed by t h e back s u b s t i t u t i o n . T h a t is, t h e s o l u t i o n of A x = b comes from t h e s o l u t i o n s of two t r i a n g u l a r s y s t e m s L y = b This work was supported by the National Science Council, Taiwan, R.O.C., under the contract number: NSC 84-2121-M009-012.

Typeset by Jth~S-TF_ ~ 77

78 c.-J. LIN

and U x = y. However, it is possible t h a t there exist m a n y nonsingular matrices in which the L U decomposition is not easy to do. For example, a zero will a p p e a r in the diagonal of A

when the L U decomposition is in progress. In this article, without any assumption on the given

m a t r i x A, we present a systolic algorithm to obtain the solution of A x = b. Under our m e t h o d , an existing pivot row can be replaced by a new pivot row during the execution of the e l e m e n t a r y row operation on A. If A is a singular matrix, t h e n we can find a row or a column such t h a t it has all zero entries.

T h e c o m p u t a t i o n a l model used to solve A x = b is a two-dimensional systolic a r r a y which consists of n linear systolic arrays. Each linear array is designed by the same consideration. Thus, these n linear arrays have similar structure and execute identical instructions. E v e r y linear a r r a y has n equations as input d a t a and also has n equations as o u t p u t data. For 1 < i < n, the ith linear a r r a y is responsible to eliminate the i th unknown variable xi of x. This ith linear a r r a y deletes (n - 1) coefficients of xi and remains the value of 1 as the coefficient of xi in the last equation. B u t this coefficient 1 of xi is not involved into the work of the following (n - i) linear systolic arrays which are used to eliminate the unknown variables x k for i + 1 < k < n, respectively. Hence, when we perform the instructions on the ith linear array, the unknown variables xl for 1 < l < i - 1 are all ignored. This design consideration implies t h a t the back

substitution which is followed the L U decomposition is unnecessary in our systolic algorithm.

2. A N O V E R V I E W O F S Y S T O L I C A R R A Y

A systolic array consists of m a n y simple structure P E s (processing elements) such t h a t the same t y p e P E executes the same instructions. Each P E only can communicate d a t a with its neighboring PEs. Suppose t h a t PE1 and PE2 are two P E s in a systolic array. If it is necessary to transfer d a t a from PE1 to PE2, then there exists a communication link, say ~-link, joining PE1 to PE2. T h e d a t a sending out by PE1 on ~-link is denoted as ~out of PE1. T h e d a t a receiving by PE2 from ~-link is denoted as ~in of PE2. This ~-link is also considered as an o u t p u t link of PE1 and an input link of PE2.

In a systolic array, a t i m e s t e p is considered as an enough large elapsed t i m e unit such t h a t all P E s can p e r f o r m the following three tasks.

(c~) T h e P E reads d a t a from its input links.

(~) T h e P E executes the designed algorithm exactly once loop. (V) T h e P E sends out d a t a to its o u t p u t links.

In our algorithm, the elapsed t i m e unit within a time step is independent of the problem size n. If a ~-link from PE1 to PE2 has a delay symbol ~D, then the ~out sending out by PE1 at a t i m e step t will be the ~in of PE2 at the time step t + $. In our systolic array, each link has only one delay, t h a t is, ~ -- 1. Thus, we omit the delay symbol in our systolic array. T h e condition of

~ 0 means t h a t the behavior of d a t a broadcasting is not allowed within our systolic array. 3 . T H E D E S I G N C O N S I D E R A T I O N

O F A L I N E A R S Y S T O L I C A R R A Y

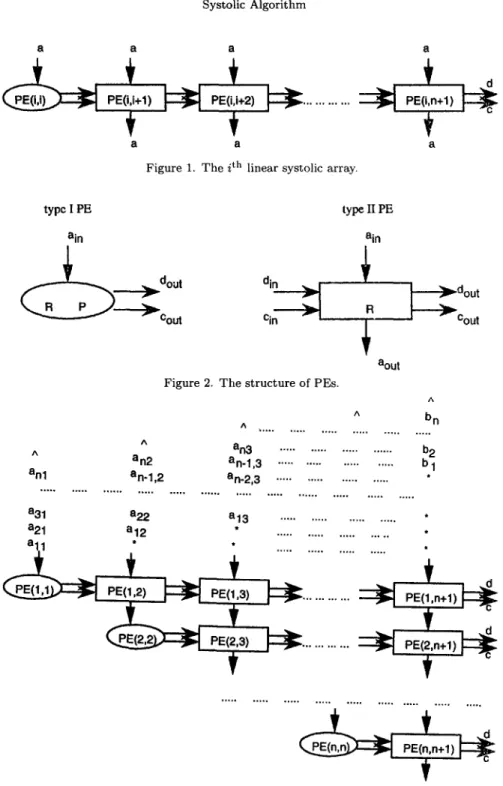
For a fixed integer i such t h a t 1 <: i <: n, we design the ith linear systolic array to eliminate t h e ith unknown variable xi of x. T h e ith linear array consists of (n - i + 2) P E s and three c o m m u n i c a t i o n links with names a-link, d-link, and c-link. See Figure 1. These P E s are indexed as P E ( i , j ) for i < j _< n + 1. T h e d-link and c-link are used to send d a t a from P E ( i , j ) to P E ( i , j + 1). T h e input a-link of P E ( i , j ) is used to receive d a t a from the (i - 1) th linear array. T h e o u t p u t a-link of P E ( i , j ) is used to send d a t a to the (i ÷ 1) th linear array.

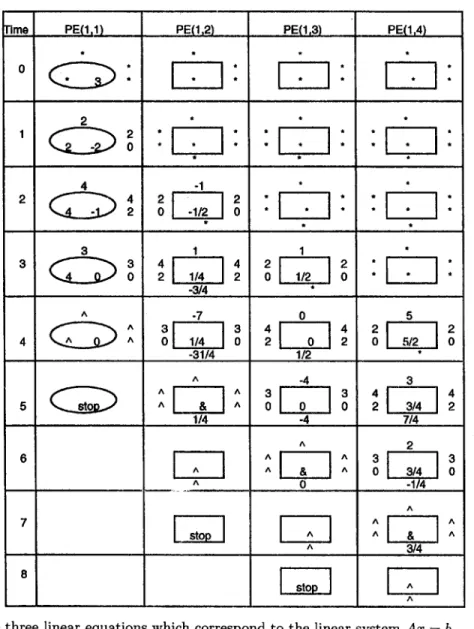
We classify our P E s into two types. T h e PE(i, i) is in the t y p e I and the remaining P E s are in the t y p e II. T h e structures of P E s are depicted in Figure 2. Each P E contains a register R. T h e t y p e I P E has a more register P. T h e PE(i, i) is responsible to find a pivot row. W h e n a pivot row had found, the t y p e II P E s u p d a t e the entries of another rows.

8 a

PE(i,i+l)

a

PE(i,i+2)

Figure 1. The ith linear systolic array.

d PE(i,n+l) ~ c a typc I PE ain Cin ~Yl

Figure 2. T h e structure of PEs.

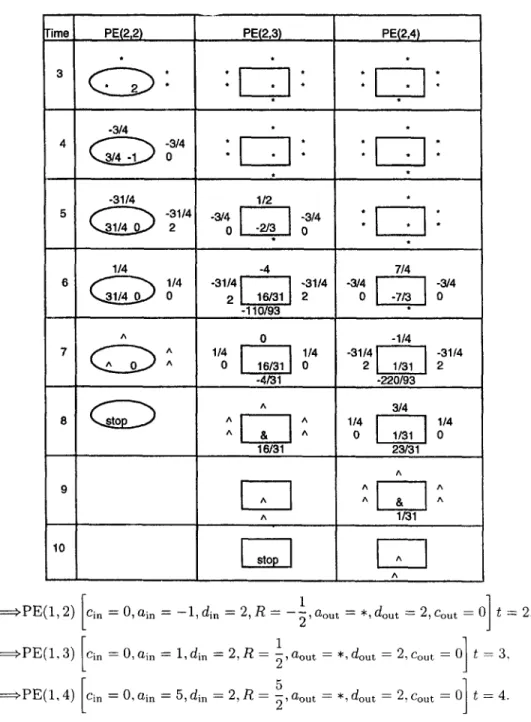
type II PE ain aout A ^ b n A ^ an3 ^ . . . b 2 an2 an-l,3 . . . b 1 an1 a n - l , 2 an-2,3 . . . *

a31 a22 a13 . . . •

a21 a12 * . . . •

~

dout Cout

_ t

t

t

t

Figure 3. T h e two-dimensional systolic array.

From the above discussion, we o b t a n n linear systolic arrays. These n linear arrays are con-

nected to form a two-dimensional array as shown in Figure 3, where the k th column of A will be

arranged to meet PE(1, k) for 1 < k < n and the column b will be arranged to meet PE(1, n ÷ 1). We use the symbols " * " and ... to m e a n a waiting and a stopping signal, respectively.

Let [A (°) , b (°)] be the n × ( n ÷ 1) augmented m a t r i x by adjoining b to A. At the beginning of our algorithm, the m a t r i x [A (°), b (°)] is the input values of the a-links on the first linear array. T h e o u t p u t data, except the symbol " *," which comes from the a-links of the i t h linear array will be formed and denoted as the m a t r i x [A (0, b(0]. According to the order of the values a p p e a r i n g on the o u t p u t a-links of the i t h linear array, the row indexes in [A (i) , b (0] are numbered sequentially as i + 1, i ÷ 2 . . . n, 1 , 2 , . . . , / . T h a t is, the first a o u t of P E ( i , j ) has the row index (i + 1) in

80 C.-J. LIN

[A(i),b (~)] and the last aout of P E ( i , j ) has the row index i in [A(i),b(0]. Of couse, this m a t r i x [A (i), b (i)] will be the input data of the (i + 1) th linear array.

Note t h a t the matrix [A (i), b (i)] is an n × (n - i -}- 1) matrix since PE(i, i) has no o u t p u t a-link. T h e absence of o u t p u t a-link in PE(i, i) causes the ith unknown variable xi to be deleted. T h e solution of A x = b will appear on the aout of P E ( n , n + 1) which is on the n th linear array.

In our systolic array, the d-link is only used to carry the ain of PE(i, i) to PE(i, j ) , for all j > i. T h e major work of the c-link is to indicate whether a new pivot row is found or not. At the initial state, we assign ( n - i + 1) to the register P of PE(i, i). When the first pivot row is found, we reset P as 1 - P. This value of 1 - P indicates how many remaining rows will be tested as a pivot row. T h e register R of PE(i, j ) contains an entry of the current pivot row. At the initial state, we set the symbol " * " into the register R of all P E ( i , j ) .

4 . T H E I N S T R U C T I O N S O F P E S

For 1 < i < n and i < j _< n + 1, we will present the major instructions of P E ( i , j ) . All PEs perform their instructions until the signal ... appears on their input a-links. First, we consider the work of type I PE.

(1) T h e main purpose of PE(i, i) is to find the first pivot row by detecting its first nonzero

value of ain. Once PE(i, i) has found its first pivot row, PE(i, i) performs the following

three tasks.

((~) P E ( i , i ) sets its P = 1 - P.

(~) P E ( i , i ) assigns lain], the absolute value of ain, into its R. (V) P E ( i , i ) sends ain to its d-link.

(2) If PE(i, i) has its P > 0 and ain ---- 0, then P E ( i , i ) is still on the state of finding the first pivot row. T h a t is, the first pivot row is not appeared until now. In this case, PE(i, i) decreases one from P and PE(i, i) continues its search of the first pivot row. At any time step, once P E ( i , i ) has its ain ~ 0, P E ( i , i ) sets its Cout ---- 1 in order to detect whether there exists a zero row in the matrix A (i-1). T h e existence of a zero row in A (i-l) causes the singularity of A.

(3) If there exists no pivot row, we obtain P = 0 and R -- * in PE(i, i). T h a t is, the first column of A (i-1) will be appeared as a zero column. In this case, PE(i, i) announces t h a t A is a singular matrix by sending the message of its Cout = 3.

(4) After PE(i, i) had found a pivot row and PE(i, i) has its P < 0, if PE(i, i) has ain ~ 0 again, then PE(i, i) tries to replace the existing pivot row. When lainl > R, the action of exchanging two pivot rows will be performed. This exchanged message is transferred by a value of 2 on the c-link.

Now we consider the major work of the type II PE. These PEs will be used to modify the entries of [A (i-1), b (~-1)] into the entries of the matrix [A (i), b(i)].

(5) P E ( i , j ) always sends its din to dour.

(6) If PE(i, j ) knows t h a t PE(i, i) had found its first pivot row, then PE(i, j ) assigns the value of a i n / d i n t o its R. At this same time step, PE(i, j ) sends out the symbol " * " to its aout. (7) If PE(i, j ) has its Cin = 0 and R ¢ *, then PE(i, j ) modifies the value of its ain into the

value of its aout.

(8) When P E ( i , j ) has its cin = 1, P E ( i , j ) detects whether its ain = 0. If ain -~ 0, then P E ( i , j ) passes its cin to Cout- Otherwise, if ain ¢ 0, P E ( i , j ) sets its Cout = 0. This work detects whether there exists a zero row in A (i-1). When PE(i, n) has its Cout = 1, we know t h a t A is a singular matrix because of a zero row in the matrix A (i-1).

(9) If P E ( i , j ) has its Cin -- 2, then the action of exchanging two pivot rows is performed. The PE(i, j ) retrieves the content of R to be modified into its aout and PE(i, j ) stores the new pivot entry a i n / d i n into its register R.

Systolic Algorithm 81 resets R as a special s y m b o l "&" i n order t o s e n d t h e signal " ^ " t o its aout a t t h e n e x t t i m e step.

5. T H E S Y S T O L I C

A L G O R I T H M

F i r s t of all, we define n i n e procedures. T h e first five p r o c e d u r e s are used i n t h e t y p e I P E . T h e last four p r o c e d u r e s are used for t h e t y p e II P E .

p r o c e d u r e t e s t i n g - f i r s t - p i v o t i f P - - 1 t h e n s e n d i n g - s i n g u l a r - m a t r i x e l s e s e a r c h i n g - f i r s t - p i v o t . p r o c e d u r e s e n d i n g - s i n g u l a r - m a t r i x - Cout -- 3; R = ^ . p r o c e d u r e s e a r c h i n g - f i r s t - p i v o t =_ P = P - 1; Cout -- 1. p r o c e d u r e f i n d i n g - f i r s t - p i v o t -- P = 1 - P ; R = laini; Cout = 0. p r o c e d u r e t r y i n g - n e w - p i v o t =- P = P + I ;

i f lainl > R t h e n ( R = lainl; Cout -- 2} e l s e ( i f a i n = 0 t h e n Cout = 1 e l s e Cout = 0.} p r o c e d u r e s e n d i n g - l a s t - e l e m e n t -- aout ~- R; R --- ~ .

p r o c e d u r e e x c h a n g i n g - t w o - p i v o t s - aout = R - a i n / d i n ; R : a i n / d i n . p r o c e d u r e m o d i f y i n g - a - l i n k -

i f R -- • t h e n s t o r i n g - f i r s t - p i v o t e l s e aout = ain - R * din.

p r o c e d u r e s t o r i n g - f i r s t - p i v o t - i f din ~ 0 t h e n ( R -- a i n / d i n ; aout -- *} e l s e aout -- ale. ALGORITHM. L I N E A R - S O L V E R (A, b, n ) -

I n i t i a l s t a t e :

For l < i < n a n d i < j < _ ( n + l ) , we set R = . in all PEs. S e t P = n - i + l i n P E ( i , i ) . T h e e n t r y ai,3 of A m e e t s P E ( 1 , j ) a t t h e t i m e step t -- j + i - 1. T h e e n t r y bi of b m e e t s P E ( 1 , n + 1) at t h e t i m e step t -- n ÷ i. A s t o p p i n g signal " ^ " will m e e t P E ( 1 , j ) a t t h e t i m e step t -- n + j . All t h e r e m a i n i n g links are d e n o t e d b y t h e s y m b o l "* "

E x e c u t i v e s t a t e : r e p e a t / * d o p a r a l l e l f o r a l l P E s o f t y p e I . * / dnut ~ ain; i f ain ~- * t h e n (Cout = *; b r e a k } ; i f a i n - - ^ t h e n ( R -- ^ ; Cou t ---- ^ ; b r e a k }; i f P = 0 t h e n Cout = 0; i f P < 0 t h e n t r y i n g - n e w - p i v o t ; if P > 0 t h e n { i f a i n ---- 0 t h e n t e s t i n g - f i r s t - p i v o t e l s e f i n d i n g - f i r s t - p i v o t } ; / , d o p a r a l l e l f o r a l l P E s o f t y p e I I . * / dout -- din;

i f ( C i n ~ - 1 a n d ain ~ 0) t h e n Cout = 0 e l s e Cout = t i n ;

i f ain : * t h e n (aout --- *; b r e a k ; } i f ( R = & o r ci, = 3) t h e n ( R = ^ ; a o u t ---- ^ ; b r e a k ; } i f a i n : ^ t h e n ( s e n d i n g - l a s t - e l e m e n t ; b r e a k ; } i f Cin = 2 t h e n e x c h a n g i n g - t w o - p i v o t s ; i f (Cin = 0 o r Cin = 1) t h e n m o d i f y i n g - a - l i n k ; u n t i l R = ^.

6. A N I L L U S T R A T I V E

E X A M P L E

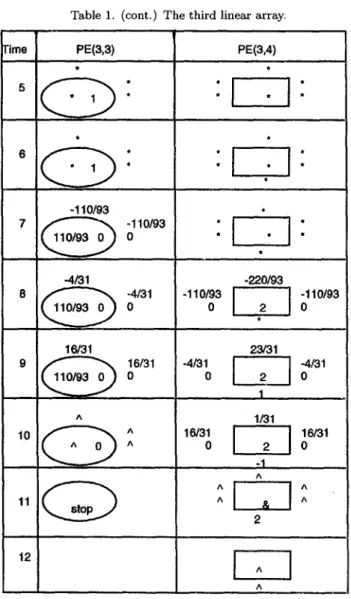
We give a n e x a m p l e w i t h 0 - 7 - 4 2

82 c.-J. LIN t o i l l u s t r a t e o u r a l g o r i t h m as s h o w n in T a b l e 1. T h e r e l a t e d v a l u e s o f T a b l e 1 a r e c o r r e s p o n d i n g t o t h e p o s i t i o n s o f links a n d r e g i s t e r s as s h o w n in F i g u r e s 1 a n d 2, w h e r e t h e a r r o w s a r e o m i t t e d . I n w h a t follows, we use t h e n o t a t i o n " P E ( i , j ) [ a ; , = 2, R -- 3 , . . . It = 4" t o i n d i c a t e t h a t P E ( i , j ) h a s its ain -- 2, R -- 3, a n d so o n a t t h e t i m e s t e p t = 4. T h e s y m b o l "S1 ==~ $2" m e a n s t h a t t h e s t a t e m e n t S1 i m p l i e s t h e s t a t e m e n t $2.

Table 1. An illustrative for n = 3 (the first linear array).

Time PE(1,1) PE(1,2) PE(1,3) PE(1,4)

* = t

{ - {

{ - {

{ - {

0 ~' ,t * • t • t ~ * 2 * * t • t 4 - 1 * t t t 3 1 1 *

~ C i:)0 ~ ~ V ~

~ V ~

: V ~ :

-3/4 ^ -7 0 5

4 ~^^

~1-~-I ~o 4[ o-1'2 o~1-~. ~o

-31/4 1/2 ^ -4 3 ^ A 3 4 5 ~ A [ & ' ~ ^ 3 I ~ O 1 0 2 F ~ ' - - - I 4 2 "114 -4 7/4 ^ 2

°

I-:--I

^^I-71 ^^ o~ I-~13o

^ 0 -1/4 A

V:~

[ ~

_^

^^~1 ^^

_3/4 A T h e r e a r e t h r e e l i n e a r e q u a t i o n s w h i c h c o r r e s p o n d t o t h e l i n e a r s y s t e m A x = b. 2Xl - x2 + x3 -- 5, (1) 4 x l + z2 = 3, (2) 3 x l - 7 x 2 - 4x3 = 2. (3) I n T a b l e 1, t h r e e l i n e a r s y s t o l i c a r r a y s a r e c o n s i d e r e d in t h e following t h r e e cases, r e s p e c t i v e l y . CASE ( a ) . O n t h e first l i n e a r a r r a y , since P E ( 1 , 1 ) [ a i n = 2, P = 3]t = 1, t h e e q u a t i o n (1) is a p i v o t row. F r o m t h e p r o c e d u r e s f i n d i n g - f i r s t - p i v o t a n d s t o r i n g - f i r s t - p i v o t , we h a v e

Systolic Algorithm

Table 1. (cont.) The second linear array.

83

rime

PE(2,2}

PE(2,3)

.

:-1

10

.3/4

•

< E b

-3"

0

"

*

. - 7

*

.31/4

1/2

0

3114 -3/4 ~

-

3

/

0

4

2

0

1/4

-4

~

1/4

.31/4r~-~ .3114

0

2 l ,olo, i 2

.110/93

^

0

( ~ )

^^

1/4 ~

1 1 4 0 0

-4/31

^ E l

^

A ^

16/31

A

PE(2,4}

.

t

.-i-

•

.7.

=

: I - ]

7/4

-3/40 ~ ' ~

0"3/4

-1/4

- 3 1 / 4 [ ~

2"31/4

-220193

3/4

1140 [ ~

01/4

23/31

A

^ ~ - ~ ^

A A

1/31

A

===~PE(1,2) Icin =O, ain = - l , d i n = 2, R = - 2 , a o u t = * , d o u t = 2, Cout =O] t = 2,

==~PE(1,3) [Cin = O, ain = l,din = 2, R = ~,aout = .,dout = 2, Cout = Ol t = 3~

===aPE(I,4) [Cin = O, ain = 5, din = 2, R = 5,aout = *,dout = N, cout = Ol t = 4.

F r o m e q u a t i o n (2), we have P E ( 1 , 1 ) [ P = - 2 , ain = 4, R = 2It - 2. B y t h e e x e c u t i o n s of

trying-new-pivot a n d t h e fact lain[ ::> R, t h e m e s s a g e of e x c h a n g i n g two p i v o t rows m u s t be c a r r i e d t o P E ( 1 , j ) for j > 1. T h u s , b y t h e a s s i g n m e n t of aou t = R - a i n / d i n w i t h i n t h e p r o c e d u r e

exchanging-two-pivots, we o b t a i n

P E ( 1 , 1 ) [ R = 4, dout = 4, Cout = 2] t : 2,

- - - ~ P E ( 1 , 2 ) din = 4, Cin = 2, ain = 1,aout = - ~ , R = ~ , d o u t = 4, Cout = 2 t = 3,

----~PE(1,3) [din = 4, cin = 2, ain -= O, aout = l , R = O, dout = 4, Cout = 2] t = 4, ==aPE(I,4) [din = 4, Cin = 2, ain = 3, aout = 7 , R = 3,dout = 4, Cout = 2] t = 5.

84 C.-J. LIN

Table 1. (cont.) The third linear array. Time 5

PE(3,3)

PE(3,4)

! 7 -110/93 -110/93 0

1

,t

I

1

I

* . t 10

11

-4/31

-4/31

0 16/31 16/31 0 A A

-220/93

"110/93 I

0

2

I "110/93

0

23/31

-4/310

~ - ~ 0-4/31 1 1/31 16/31 16/31

o lo

:1 A

I - 1

A A 2 12

F 1

A

T h e a b o v e t h r e e v a l u e s of aou t f o r m t h e first r o w o f [A(1),b (1)] w i t h r o w i n d e x 2. F o r e q u a -

t i o n (3), b y t h e p r o c e d u r e trying-new-pivot w i t h ]ainl -- 3 < R a n d t h e e x e c u t i o n of t h e a s s i g n m e n t

aout -- a i . - R * din w i t h i n t h e p r o c e d u r e modifying-a-link, we h a v e

P E ( 1 , 1) [ P -- - 1 , ain = 3, R = 4, dou t -- 3, Cout = 0] t -- 3,

- - - - * P E ( 1 , 2 ) ain = - 7 , din = 3, cin = O,R = 1 , a o u t = - - ~ - , out 3, eout = 0 t = 4,

= ~ P E ( 1 , 3) [ain -- - 4 ,

din = 3, tin --- 0, R -= 0, aout --=- - 4 , dout = 3, tout -- 0] t = 5,

[ 3 1 ]

= = ~ P E ( 1 , 4 ) ai~ = 2, din = 3, ei~ = O , R = ~ , a o u t = - ~ , d o u t = 3,¢out = 0 t = 6.

T h e a b o v e t h r e e v a l u e s of aout f o r m t h e s e c o n d r o w of [A (1), b (1)] w i t h r o w i n d e x 3. F r o m t h e

i n i t i a l s t a t e o f o u r a l g o r i t h m , we h a v e PE(1,j)[ain = ^ ]t = j + 3 for 1 _< j < 4. H e n c e , P E ( 1 , 1)

s t o p s i t s e x e c u t i o n a t t = 4. F r o m t h e p r o c e d u r e sending-last-element, we h a v e

P E ( 1 , 2) ain -~ , aout -~ "~, R = & t = 5, P E ( 1 , 3) [ain -- , aout -- 0, R = &] t = 6,

a n d

3

Systolic Algorithm 85

__3

4 [A(1) b(1)] = 31 ' 4 1 which corresponds to t h e linear s y s t e m of

T h e above t h r e e values of aout form the third row of [A (1), b (1)] with 1 as its row index. T h e n we have P E ( 1 , j ) [ a o u t = , R = ^ I t = j + 4 for 2 <_ j <_ 4. Thus, these t h r e e P E s stop their executions. F r o m t h e above executions, we o b t a i n 1 7 1 - 4 - ~ , 3

0

3

7 - x 2 - 4 x 3 = - ~ , ( 5 ) x l + x2 = - . (6) 4

CASE (~). On the second linear systolic array, [A (1), b (1)] is the input d a t a on the input a-links of P E ( 2 , j ) for 2 _< j <_ 4. F r o m e q u a t i o n (4) and e E ( 1 , 2 ) [ a o u t = - 3 / 4 ] t = 3, we have

P E ( 2 , 2 ) ain - 4 ' 4 '

[

3

1

2

3

]

===~PE(2, 3) Cin = 0, din -~ - ~ , ain --- 2 ' R = - ~ , aout ~- *, dout -- - 3 ' Cout -- 0 t = 5,

[

]

---~ P E ( 3 , 4 ) c i . = 0, din =

-3,ai.

= 3 , R = - g , a o u t = * , d o u t = - - ~ , C o u t = 0 t = 6.

F r o m e q u a t i o n (5) and t h e p r o c e d u r e exchanging-two-pivots with lainl > R, we have

[

31,R

= ,dout = --~-,Cout = 2, P = 0 t = 5,

]

P E ( 2 , 2 ) ain - 4

31

II0

16

31

]

= 2, din ---- - - ~ - , a i n -- - 4 , aout - , R -- ~ - , d o u t -- - - T , Cout --- 2 t -- 6, - - 2 , din = - ~ - , a i n = - ~ , a o u t - - , R = ~-~, out = - Cout = 2 t = 7. values of aou t form the first row of [A (2), b (2)] with row index 3. F r o m equa- ~ P E ( 2 , 3) [CAn :===~PE(2, 4) [Cin T h e above two tion (6), we have BE(2, 2) ==~PE(2, 3) ==*-PE(3, 4) 1 31 1 ] ain ---- 4 ' R - - - 4 ' d°ut : 4 ' C ° u t - - 0 t - - 6 ,

[ _{CAn : O, din ---- 1, ain ---- 0, R : ~ , aout ---- - ~ - ,} 16 4 d _{out : 4 ' C ° u t :} 1 ₀ 1 _{t : 7,}

CAn = 0, din ---- 1 , ain = 4 ' ~ - , aout ---- ~ - , out : 4 ' tout : 0 t : 8.

T h e above two values of aout form the second row o f [A(2),b (2)] with row index 1. Now

PE(1,2)[aout -- ^ ]t -- 6 implies PE(2, 2)[al, -- ^ ]t = 7. In t h e same way, we have B E ( l , 3 ) [ a o u t = ^ ] t = 7 and B E ( l , 4 ) [ a o u t = ^ ] t = 8 ,

[

]

[

]

86 C.-J. LIN

T h e s e two values of aout f o r m t h e t h i r d row of [A (2), b (2)] w i t h row index 2. step, P E ( 2 , j ) s t o p s its execution.

Until now, we have t h e m a t r i x

110 31

1_6

31 which c o r r e s p o n d s t o t h e linear s y s t e m of 220 23 31 ' 1 3 1 A f t e r this t i m e - x 3 - - 9 3 ' ( 7 ) x l - z 3 = ~ , ( 8 )

1

z ~ + z 3 = - - . ( 9 ) 31

CASE ( ~ ) . We consider t h e o p e r a t i o n s on t h e t h i r d linear array. E q u a t i o n (7) is a p i v o t row.

Hence, it implies

[ 110 110 . 110 ]

B E ( 3 , 3 ) a i n - - - - - ~ - , R - - - ~ , d o u t - - - ~ , C o u t = 0 , P = 0 t = 7 ,

[

110

_1 0

]

= = ~ P E ( 3 , 4) Cin = 0 , din - 93 ' ain -- - , R = 2, aout = *dout = 93 ' Cout = 0 t = 8.

F r o m e q u a t i o n (8), we have

P E ( 3 , 3 ) a i . = - ~ - , d o u t = - 3 i - ' P = 0, Cout = 0 t = 8,

~ P E ( 3 , 4 ) Cin = 0 , d i n =

-~,R

= 2, a ~ , = ~ - i - , a o u t = 1 , d o u r = - g i - , e o u t = 0 t = 9.

T h i s o u t p u t o f aout = 1 forms t h e first row of [A (3), b (3)] w i t h row index 1. N o t e t h a t in this last linear array, t h e m a t r i x A (a) is e m p t y . F r o m e q u a t i o n (9), we have

[ 16 ~

16 p = O , c o u t = O l t = 9 '

P E ( 3 , 3) ain = ~ ' , R = ' d°ut = 3 1 '

[

10

]

~ P E ( 3 , 4 ) Cin = 0, di, =

-~,ai, =

, R

= 2, aout = - 1 , d o u t = ~-~,Cout = 0 t = 10. T h i s aout = - 1 is t h e o n l y e n t r y in t h e second row of

[A(a),b (3)]

w i t h row index 2. Since

P E ( 2 , 3 ) h a s i t s a o u t = ^ a t t = 9, w e h a v e P E ( a , a ) [ a i n = ~

,R

= ^ ]t = 10. A t t h i s s a m e t i m e

step, P E ( 3 , 3) s t o p s its execution. Also we have P E ( 2 , 4)[aout = ^ ]t = 10 which implies t h e result of P E ( 3 , 4 ) [ a i n -- ^ ,aout - - 2, R -- &]t = 11.

T h i s aout -- 2 is in t h e t h i r d row of [A (3), b (3)] w i t h row index 3. Finally, we have P E ( 3 , 4) h a s its R = ^ , aout ---- ^ a t t ---- 12, a n d thus, all P E s s t o p t h e i r executions. T h e solution of

Ax = b

is in t h e m a t r i x [A (3), b (3)] which c o r r e s p o n d s t o t h e linear e q u a t i o n s o f Xl -- 1, x2 -- - 1 , a n d

X3~2.

7. T H E C O R R E C T N E S S

P R O O F

F r o m t h e p r o c e d u r e

sending-first-pivot,

we k n o w t h a t w h e n t h e first pivot row is found b y P E ( i , i), t h e t y p e I I P E ( i , j ) sends o u t a s y m b o l " * " t o its aout. T h e s e s y m b o l s " * " which are g e n e r a t e d b y t h e i t h linear a r r a y will p r o p a g a t e t o t h e P E s of t h e following k t h linear a r r a y for

k > i. T h e s e s y n b o l s " * " a n d t h e waiting s y m b o l " * " given in t h e initial s t a t e of o u r a l g o r i t h m will cause s o m e P E s t o be idle.

LEMMA 1. O n t h e i TM linear a r r a y , w h e n we ignore t h e " * " d u e to t h e initiM s t a t e , b u t we i n c l u d e t h e " * " g e n e r a t e d b y t h e p r e v i o u s l i n e a r array, t h e first e n t r y on t h e i n p u t a - B n k o f P E ( i , j ) a p p e a r s a t t h e t i m e s t e p t = i + j - 1.

P a O O F . F r o m t h e i n i t i a l s t a t e , for 1 _< j _< n, we o b t a i n P E ( 1 , j ) [ a i n = ul,Jl c-(°)~` = j . A l s o we have

P E ( 1 , n + 1)fain = b~°)]t = n + 1. Since t h e r e is one t i m e d e l a y on e a c h a - l i n k , b y i n d u c t i o n on t h e i n t e g e r i, P E ( i , j ) h a s an e n t r y on its a - l i n k a t t h e t i m e s t e p t = j + i - 1 for i <_ j _<

n + l . l

LEMMA 2. On t h e i TM linear array, i f we h a v e t h e e n t r y a(ki~ 1) = 0, for a11 i < k < n, t h e n P E ( i , i)

s e n d o u t i t s Cout = 3 before t h e t i m e s t e p t = n + 2i - 2.

PROOF. B y t h e p r o c e d u r e testing-first-pivot, we know t h a t t h e case of all _(i-1) ak,i = 0 will b e

d e t e c t e d b y P E ( i , i ) on t h e i th l i n e a r array. F r o m L e m m a 1, P E ( i , i ) h a s its first e n t r y on its A i - i )

i n p u t a - l i n k a t t = 2i - 1. Since ui, i is t h e first e n t r y of t h e first c o l u m n of A (~-i) a n d t h e r e

a r e a t m o s t (i - 1) s y m b o l s " * " g e n e r a t e d f r o m t h e p r e v i o u s (i - 1) l i n e a r a r r a y s , P E ( i , i) h a s

_ ( i - 1 )

t h e e n t r y (ti# o n its i n p u t a - l i n k b e f o r e t h e t i m e s t e p t = 2i - 1 + (i - 1) = 3i - 2. T h u s ,

h(i-1)

P E ( i , i) h a s its ain ---- an, i b e f o r e t = (3i - 2) + (n - i) = n + 2i - 2. A t t h i s t i m e s t e p , P E ( i , i)

has P = 1 a n d ai~ = 0. T h e p r o c e d u r e s e n d i n g - s i n g u l a r - m a t r i x i m p l i e s t h a t P E ( i , i) s e n d s its

corn = 3 t o i n d i c a t e t h e s i n g u l a r i t y of A. |

LEMMA 3. D u r i n g t h e e x e c u t i o n on t h e i th l i n e a r a r r a y , i f t h e r e e x i s t s a n i n t e g e r k, for i < k < n ~(~-i)

s u c h t h a t t h e e n t r i e s ~k,j = O, for all i <_ j <_ n, t h e n P E ( i , n) has its Cout = 1 before t h e t i m e s t e p t = n + k + i - 2.

PROOF. B y L e m m a 1, t h e first e n t r y ain of P E ( i , i) a p p e a r s a t t = 2 i - 1. Since t h e first ( k - i + 1) rows of [A ( i - 1 ) , b (i-1)] are i n d e x e d s e q u e n t i a l l y from i to k, a n d t h e r e a r e a t m o s t ( i - 1) s y m b o l s " * " g e n e r a t e d b y t h e p r e v i o u s (i - 1) l i n e a r a r r a y s , t h e e n t r y a2i~ -1) will m e e t P E ( i , i) b e f o r e t h e

~(~-i)

t i m e s t e p t = 2i - 1 + (k - i) + (i - 1) = 2i + k - 2. B y uk# = 0, P E ( i , i) h a s its Cout = 1 b y t h e

e x e c u t i o n o f p r o c e d u r e searching-first-pivot o r t h e p r o c e d u r e t r y i n g - n e w - p i v o t . T h u s , we have

PE(i, i) fain

= 0, Cou t = 1] t ~ 2 i + k - 2,

[

(~-~)

]

= = * P E ( i , i + 1) Cin = 1,ain = 0 = ak,i+l,Cou t = 1 t <_ 2i + k - 1,

~ P E ( i , n ) [Cin = 1, a i n = 0 , Cout = 1 ] t < 2 i + k - 2 + ( n - i ) = n + k + i - 2.

T h e Cout = 1 on P E ( i , n ) i n d i c a t e s t h a t A (i-1) h a s a zero row. T h e r e f o r e , A is a s i n g u l a r m a t r i x . F r o m L e m m a s 2 a n d 3, we k n o w t h a t if t h e r e e x i s t s a n i n t e g e r i such t h a t P E ( i , n) h a s its Co,t = 1 o r Cout = 3, t h e n A is s i n g u l a r . I n t h e following t h r e e l e m m a s , we a s s u m e t h a t A is n o n s i n g u l a r .

LEMMA 4. T h e t y p e I P E ( i , i) s t o p s its e x e c u t i o n a t t h e t i m e s t e p t = n + 3i - 2 a n d t h e

t y p e H P E ( i , j ) s t o p s its e x e c u t i o n a t t h e t i m e s t e p t = n + 2 i + ] - 1. T h a t is, we h a v e P E ( i , i ) [ R = ° It = n + 3i - 2 and P E ( i , j ) [ R = ^ , aout = ~ }t = n + 2i + j - 1, for 1 < i < n and i < j < n + l . PROOF. B y i n d u c t i o n on i. B a s i s : F o r z = 1. F r o m t h e i n i t i a l s t a t e , we have a(°) ] P E ( 1 , 1 ) a i , = 1 , 1 ] t = 1 , a(0) ] = = * P E ( 1 , 1) a i n =- 1,n] t ---- n , = = * P E ( 1 , 1 ) fain = ' , R = ^ ] t = n + 1.

8 8 C . - J . LIN

F r o m t h e initial s t a t e , we k n o w t h a t the e n t r y of t h e first row of [A (°), b (°)] m e e t s P E ( 1 , j ) a t t h e t i m e s t e p t - - j + i - 1. Since each c o l u m n in [A(°),b (°)] has n entries, we have

= n + j - 1, a ( ° ) . ] P E ( 1 , j ) ain = n,3] t = ~ P E ( 1 , j ) [ai, = ^ , R = & I t - - n + j , = = ~ P E ( 1 , j ) [ R = ^ , a o u t = ^It = n + j + 1. T h u s , it is t r u e for i -- 1.

A s s u m p t i o n : For i -- k, it is true. T h u s , we have B E ( k , k ) [R = ^ I t = n + 3 k - 2, a n d P E ( k , j ) [R : ^ , a o u t : ^ I t : n + 2 k ÷ j - 1, I n d u c t i o n : For i = k + 1. F r o m t h e a b o v e a s s u m p t i o n w i t h j = k + 1, we have f o r j > k ÷ l . P E ( k , k + 1) [aout = ^ ] t = n ÷ 2k + (k ÷ 1) - 1 = n ÷ 3k, ===~PE(k + 1, k ÷ 1) [ a i n - - ^] t ---- n ÷ 3k + 1 = n + 3(k + 1) - 2, = = ~ P E ( k + 1, k + 1) [R = ^ I t = n + 3(k + 1) - 2. F r o m t h e a b o v e a s s u m p t i o n w i t h j > k + 1, we have P E ( k , j ) [R = ^ I t -- n + 2k + j - 1, = = ~ P E ( k , j ) [aout ----^ ] t ---- n + 2k + j - 1,

.~PE(k + 1, j ) lain = ^ , R = &] t = n + 2k + j,

===~PE(k + 1, j ) [R = ^, aout = ^ ] t ---- n + 2k + j + 1 = n + 2(k + 1) + j - 1.

T h u s , i = k + 1 is true. Therefore, t h e l e m m a is p r o v e d b y induction. |

LEMMA 5. T h e t i m e c o m p l e x i t y o f o u r s y s t o l i c a l g o r i t h m is 4 n .

PROOF. L e t i = n a n d j = n + l , in L e m m a 4. We have P E ( n , n + l ) [ R = ^ ]t = n + 2 i + j - 1 = 4 n . T h u s , P E ( n , n + 1) s t o p s its e x e c u t i o n a t t h e t i m e s t e p t = 4n. | LEMMA 6. T h e i t h //near a r r a y p r o d u c e s the values

O#aout

t o f o r m the m a t r i x [A (i), b (i)] w h i c h c o r r e s p o n d s t o t h e / / n e a r s y s t e m o [

(~) . a ( i ) ~ (i) h(i)

a i + l , i + l X i + l T i + 1 , i + 2 ~ i + 2 ÷ • . • ÷ a z + l , n X n = V i + l ,

(i) - a (i) a (i) x = b (~)

a i + 2 , ~ + l X i + l ' ~ i + 2 , i - ~ 2 X i + 2 ÷ "" " ÷ i + 2 , n n i ~ - 2 ,

a(i) _{n , i + l} x _{i + 1} -F ^(i) _{t~n,iq- 2} x _i-t-2 + _{" ' "} + a (i) x _{n , n n =} b (i) _{n ,}

- - a (i) x + ~(i) x + + (i) b~i),

X l --r 1 , i + 1 i + 1 t ~ l , i + 2 i + 2 " "" a l , n X n =

(i) _ h!~)

_ (i) a (i) X " ÷ + a i , n X n - z " X i t a i , i + l X i + l -{- i , i + 2 z + 2 " " "

B a s i s : For i -- 1.

F r o m t h e initial state, t h e m a t r i x [A, b] = [A (°), b (°)] is assigned to t h e input a-links of P E ( 1 , j ) , 1 < j < (n + 1). T h u s , we have P E ( 1 , 1)[ain _{_ _ ~} "(°)1÷ _{~ k , l J ~ ~---} k for 1 < k < n..

S u p p o s e t h a t _(0) is t h e first nonzero value m e e t i n g P E ( 1 , 1) at t h e t i m e step t = u. Since _~u,1

P E ( 1 , 1 ) [ P = n]t = 1, t h e p r o c e d u r e testing-first-pivot causes t h e searching-first-pivot to be

e x e c u t e d for ( u - 1) times. T h u s , we have P E ( 1 , 1 ) [ P = n - u + 1]t = u - 1. A t the next

t i m e step, we have P E ( 1 , 1)[ain ¢ 0]t = u. F r o m t h e execution of finding-first-pivot, we have

B E ( 1 , 1 ) [ P = - n + u]t = u.

F r o m t h e t i m e step t = 1 t o t h e t i m e step t = u - 1, P E ( 1 , 1) sets its Cout = 1 a n d dour = 0. T h i s causes t h e t y p e II P E ( 1 , j ) assigning its ain to its aout by t h e assignment of aout = ain within

t h e p r o c e d u r e storing-first-pivot u n d e r t h e condition of din = 0. T h a t is, for 2 <_ j < (n + 1),

P E ( 1 , j ) carries t h e first (u - 1) rows of [A (°), b(°)], u n d e r deleting the first c o l u m n of A (°), to form t h e first (u - 1) rows of [A(1),b(1)]. T h e s e (u - 1) rows in [A(1),b (1)] are n u m b e r e d as t h e row indexes from 2 to u.

Since t h e u TM row of [A (°), b (°)] is the first pivot row found by P E ( 1 , 1), we o b t a i n din ¢ 0 on

P E ( 1 , j ) for 2 < j _< (n + 1). F r o m t h e p r o c e d u r e storing-first-pivot, we have

[a o

]

P E ( 1 , j ) R = ~ i n , a O u t = * t = u + j - 1 , for 2 _< j <_ (n + l).

F r o m t h e time step t = u + 1 to t = n, P E ( 1 , 1) sends t h e message to indicate w h e t h e r t h e a c t i o n of e x c h a n g i n g pivot row occurs or not. This implies t h a t t h e t y p e II P E ( 1 , j ) modifies t h e

last ( n - u ) rows of [A (°), b (°)] to form t h e rows of [A (1), b (1)] with t h e row indexes from u + 1 to n.

Until now, we o b t a i n (n - 1) rows in [A 0), b(1)]. T h e s e (n - 1) rows of [A (1), b (1)] c o r r e s p o n d to (n - 1) linear e q u a t i o n s such t h a t all t h e coefficients of Xl are deleted.

A t t h e time step t = n + 1, P E ( 1 , 1 ) receives t h e s t o o p i n g signal ain = ^ • So PE(1,1) stops its execution. Similarly, we have P E ( 1 , j ) [ a i n = ^ It = n + j , for 2 _< j < (n + 1). T h e p r o c e d u r e

sending-last-element causes P E ( 1 , j ) t o assign the c o n t e n t of R t o aout to form t h e last row of [A (1), b(1)]. T h i s last row has its index 1 a n d it corresponds t o a linear e q u a t i o n such t h a t its coefficient of t h e u n k n o w n xl is 1. Therefore, t h e case of i = 1 is true.

A s s u m p t i o n : Suppose t h a t this l e m m a is t r u e for i = k.

I n d u c t i o n : For i = k + 1.

Since t h e values on t h e o u t p u t a-links of the k TM linear a r r a y form t h e m a t r i x [A (k), b(k)], this

m a t r i x is t h e i n p u t of a-links of t h e (k + 1) th linear array. B y L e m m a 1, we know t h a t t h e first

e n t r y g e n e r a t e d by t h e k TM linear a r r a y meets P E ( k + 1, k + 1) at t = 2k + 1.

For k + 1 < r < n, let ~(k) _~r,k-I-1 m e e t P E ( k + 1, k + 1) at t h e time step t = t~. Since there are k

s y m b o l s " * " g e n e r a t e d b y t h e previous k linear arrays, t h e tr has to satisfy t h e c o n d i t i o n of

2k + 1 < tr < n + 2k. Suppose t h a t .(k) is t h e first n o n z e r o value m e e t i n g P E ( k + 1, k + 1) at

- - - - ~ v , k + l

(k)

the t i m e step t = tv, for k + l < v < n. T h a t is, we have as,k+ 1 = 0, for s satisfing k + l < s < v - 1 .

Hence, from t h e t i m e step t = t~ + j - k - 1 to t = t~ + j + v - 2 k - 2, t h e t y p e II P E ( k + 1 , j ) carries t h e first (v - k - 1) rows of [A (k), b(k)], u n d e r deleting the first c o l u m n in A (k), to form

t h e first (v - k - 1) rows of [A(k+l),b(k+l)] with t h e row indexes from k + 2 to v.

Since t h e first pivot row of [A (k), b (k)] is found by P E ( k + 1, k + 1) at t = t~ by Ak) _{Uv,k+ 1 ¢ O,} w e

have P E ( k + 1 , j ) [ R =

ain/din,aout

- * ] t = tv + j - k - 1, for k + 2 ___ j _< n + 1. After sending

a o u t --- * , P E ( k + 1, j ) modifies t h e following (n - v + k) rows of [A (k) , b (k)] t o form t h e (n - v + k)

rows of [A(k+l),b (k+l)] w i t h row indexes as v + 1, v + 2 . . . . , n - 1, n, 1, 2, . . . , k - 2, k - 1, k.

A t t h e initial state, we set P E ( i , i ) [ P = n - i + 1It = 0. Thus, on t h e (k + 1 ) t h linear array,

t h e r e are o n l y t h e first (n - k) rows of [A (k),b (k)] t o be d e t e c t e d as a pivot row. T h e last k

rows of [A(k),b(k)], with row index l for 1 < l < k, c o r r e s p o n d to t h e k linear e q u a t i o n s w i t h

90 C.-J. L:N

equations are not involved into the work for detecting a pivot row. Since the pivot row on the (k + 1) th linear array does not contain the unknowns xl for 1 < l < k, the assignment of aout ---- ain -- R * din cannot influence the coefficients of xl. Thus, the coefficient of xz preserves as 1 under the executions of the (k + 1) th linear array. From L e m m a 4, for k + 2 < j < n + 1, we have

P E ( k , k + l)[aout = ^ ] t = n + 3k and P E ( k , j ) [ a o u t = ^ ] t = n + 2k + j - 1 ,

~ P E ( k + l , k + l)[ain = ^ , R = ^ ] t = n + 3k + l,

and

P E ( k + 1 , j ) l a i n = ^ ,aout = R , R = &] = n + 2k + j .

These (n - k) values of aout form the last row of [A (k+l), b (k+l)] with row index k + 1. This last row corresponds to a linear equation with the coefficient 1 on the unknown Xk+l. At the next t i m e step, we have P E ( k + 1 , j ) [ R = ^ ,aout ---- ^ It = n + 2k + j + 1. T h e case of i = k + 1 is

true. Therefore, this l e m m a is proved by induction. |

THEOREM. T h e systolic algorithm L I N E A R - S O L V E R ( A, b, n) is correct to solve the dense linear

s y s t e m A x = b within 4n t i m e steps.

PROOF. From the results of L e m m a s 5 and 6 the following concludes. |

8 . C O N C L U S I O N S

We present a systolic algorithm to solve the linear systems A x = b. An i m p o r t a n t feature in our algorithm is t h a t , during the elementary row operation on A, the action of exchanging two pivot rows can performed. Since we need to preserve the coefficient of xz, for 1 < l < (i - 1), within a linear equation during the execution of the i th linear systolic array, the e l e m e n t a r y row o p e r a t i o n on the i th linear array has to be accomplished by the way of R j - c * Ri, where R j is the row to be modified, c is a scale value, and Ri is the current pivot row. This requirement is achieved by the assignment of aout = ain - R * din within the procedure modifying-a-link.

This algorithm can be used to solve the linear systems A X = B for X , B being n × m matrices. In this case, the algorithm requires (4n + m - 1) t i m e steps. W h e n B is an n by n identity m a t r i x and A is nonsingular, the solution is the inverse m a t r i x of A. Moreover, it seems t h a t the absolute value of the d e t e r m i n a n t of A is the product of R in PE(i, i) for 1 < i < n.

_(i-:)

During the execution of our algorithm, if we have ~,~ ~ 0, for all 1 < i _< n and the action of exchanging pivot row does not occur, then our algorithm has the same work as the L U decomposition to do. In this case, the c-link is redundant. In fact, the m a j o r purpose of c-link is used to carry the message of exchanging pivot row. However, note t h a t the L U decomposition only obtains the u p p e r triangular m a t r i x of A, but our algorithm solves the linear s y s t e m A x = b. We hope t h a t this m e t h o d of designing a systolic algorithm can be applied to solve some N P - c o m p l e t e problems, such as the knapsack and travel-salesman problems.

R E F E R E N C E S

1. C.J. Lin, Generating subsets on a systolic array, Computers Math. Applie. 21 (1/2), 103-109, (1991). 2. C.J. Lin, A systolic algorithm for dynamic programming, Computers Math. Applic. 2T (1), 1-10, (1994). 3. J.A. Mchugh, Algorithmic Graph Theory, Prentice-Hall International, (1990).

4. M. Zubair, Efficient systolic algorithm for find bridges in a connected graph, Parallel Computing 6, 57-61, (1988).

5. S.H. Zak and K. Hwang, Polynomial division on systolic arrays, IEEE Trans. on Computers 34 (6), 577-578, (1985).

6. L. Convay a n d C. Mead, Introduction to VLSI System, Addison-Wesley, Reading, MA, (1980). 7. D.J. Evans, Systolic algorithms, Intern. J. Computer Math. 25, 155-172, (1988).

9. E.A. Ahmed, Solution of dense linear systems on a n optimal systolic architecture, Computer ~A Elect. Engng. 13 (3/4), 177-193, (1987).

10. J.R. Gilbert, Parallel symbolic factorization of sparse linear systems, Parallel Computing 14, 151-162, (1990). 11. C.K. Koc and R.M. Piedra, A parallel algorithm for exact solution of linear equations, In International

Conference on Parallel Processing III, pp. 1-8, (1991).

12. R. Melham, Parallel Gauss-Jordan elimination for solution of dense linear systems, Parallel Computing 4, 339-343, (1987).

13. P.I. Piskoulijski, Error analysis of parallel algorithm for the solution of a tridiagonal toeplitz linear system of equations, Parallel Computing 18, 431-438, (1992),

14. M.K. Sridhar, R. Srinath and K. Parthasaxsthy, On the direct parallel solution of system of linear equations: New algorithms and systolic structures, Information Sciences 43, 25-53, (1987).

15. O. W i n g and W. Huang, A computation model of parallel solution of linear equations, I E E E Trans. on Comput. C - 2 9 , 632-638, (1980).