On the (2,2) Visual Multi-Secret Sharing Schemes

全文

(1)On the (2,2) Visual Multi-Secret Sharing Schemes K.Y. Chen, W.P. Wu and C.S. Laih Department of Electrical Engineering, National Cheng Kung University, Tainan Taiwan, Roc. ccbruce@crypto.ee.ncku.edu.tw, trot@crypto.ee.ncku.edu.tw and laihcs@eembox.ncku.edu.tw Abstract The concept of visual secret sharing (VSS) scheme was first proposed by Noar and Shamir in 1994. This is a technique to divide a secret image into several meaningless images, called shadows, such that certain qualified subsets of shadows can recover the secret image by “eyes”. The main characteristic of VSS schemes is that its decoding process can be perceived directly by the human visual system without the knowledge of cryptography and cryptographic computations. It possesses a special meaning and effect that “the secret codes are visible”. In this paper, we propose a new Visual Multi-Secret Sharing (VMSS) scheme. The main difference between VMSS scheme and traditional Visual Secret Sharing (VSS) scheme is that it is allowed to hide more than one secret in VMSS while VSS can hide only one secret. We give an optimal generating codebook of (2,2) VMSS scheme and discuss the security of the proposed scheme. The characteristic of the (2,2) VMSS scheme is to conceal two secret messages (P1 and P2) on two shadows such that P1 is recovered by stacking together the two shadows. However, P2 is recovered by reversing one of the two shadows.. 1. Introduction Visual secret sharing (VSS) scheme brought up by Naor and Shamir [11] in 1994 is established on the concept of secret sharing scheme. The key concept of VSS scheme is that the original shared secret is image (printed text, handwritten notes, pictures, etc.), and the decoder for the VSS scheme is “eyes” of human being, i.e., the shared secret is perceived directly by the human visual system without the knowledge of cryptography and cryptographic computations. For more concise description, we assume a secret image P is encoded into shared images called shadows Ti, i = 1,2…, such that certain qualified subsets of shadows can recover the secret image by “eyes”. The decoder by “eyes” consists of xeroxing the shares onto transparencies, and then stacking them. After stacking, the secret image P is revealed without any calculation.. However, stacking unqualified subsets of shadows does not reveal any information about P. After the concept of VSS scheme was proposed, there are many research institutes have plunged into studying, such as [2-4, 8-10, 15-16, 19-21]. Some important ideas have been considered in the following literatures.. .. In 1994, Naor and Shamir [11] first considered the VSS scheme and proposed a solution of 2-outof-n scheme.. .. And then, Ateniese et al. gave an efficient solution [1] for general access structures.. .. Droste [6] considered the problem that sharing more than one secret image among a set of participants. A construction was given to obtain VSS schemes in which different subsets of transparencies reveal different secret images.. .. In [12], an alternative reconstruction method for VSS schemes was studied. This method provides a higher contrast in the reconstructed image for 2out-of-n schemes, but cannot be applied to the kout-of-n schemes.. .. Advanced VSS scheme to share colored images were given in [14], [18] and [23].. .. The bounds and contrast in VSS scheme were discussed in [5], [7] and [18].. .. The authentication and identification using VSS scheme were studied in [13] and [22]. In this paper, we propose a new Visual Multi-Secret Sharing (VMSS) scheme. The main difference between VMSS and traditional VSS scheme is that it is allowed to hide more than one secret with the same qualified subset of shadows in VMSS while VSS can hide only one secret. This paper was organized as follows. We review the basic concept and characteristics of VSS schemes in section 2. Then, we will propose our (2,2) VMSS scheme in section 3. The codebooks of generating (2,2) VMSS scheme and their security analysis are also given. The characteristic of the proposed (2,2) VMSS scheme is to conceal two secret messages P1 and P2 on two shadows such that P1 can be recovered by stacking together the two shadows and then P2 can be recovered by reversing one of the two shadows. The experimental results and conclusion.

(2) are given in section 4 and 5, respectively.. 2. The Review of VSS Schemes In the VSS scheme, we assume the secret is an image which is consisted of black and white pixels. Each original pixel is transformed into m subpixels on n modified shares shown for each transparency (shadow). Each share in a shadow is a collection of m black and white subpixels, which are printed very closely so that the human visual system averages their individual black/white contributions. We symbolize the resulting structure by a n × m Boolean matrix S = [sij], where sij = 1 if and only if the jth subpixel in the ith transparency is black. When transparencies i1, i2,...ir are stacked together in a way which properly aligns the subpixels, we see a combined share whose black subpixels are represented by the Boolean “or” of rows i1, i2,...ir in S. The gray level of this combined share is proportional to the Hamming weight of the “or”ed mvector V. For some fixed threshold 1 ≤ d ≤ m and relative difference α > 0, if H(V) ≥ d, this gray level is interpreted by the users’ visual system as black. And if H(V) ≤ d - αm, the result is interpreted as white. A solution to k out of n visual secret sharing scheme can be shown as two collections of n × m Boolean matrices C0 and C1. When sharing a white pixel, the dealer randomly choose one row of the Boolean matrix C0 to a relative share. On the other hand, he selects one row of the Boolean matrix C1 for sharing a black pixel. The chosen matrix defined the gray level of the m subpixels in every one of the n shares. The solution is valid if it can meet the following three conditions[11]: 1. For any S in C0, the “or” V of any k of the n shares satisfies H(V) ≤ d - αm. 2. For any S in C1, the “or” V of any k of the n shares satisfies H(V) ≥ d. 3. For any q shares and q < k, the “or” V of q of the shares satisfies H(V) = const. It means that we cannot distinguish whether the pixel is black or white. With the illustration given above, the important parameters of a VSS scheme are:. .. m is the number of subpixels generated from a pixel in a share. This represented the loss in the resolution from the original picture to shared one. From the viewpoint of efficiency, we would like m to be as small as possible.. .. α is the relative difference in weight between combined shares that come from a white pixel and a black pixel in the original picture. From the contrast point of view, we would like α to be as large as possible.. Figure 1. The basic (k, n) model of VSS scheme The foremost two conditions are called contrast and the third condition is called security. In other words, by the third condition, we cannot get any information about the share secret if we do not have more than k shares. The basic model of (k, n) VSS schemes is shown in Figure 1.. 3. The proposed (2,2) VMSS Scheme The traditional (2,2) VSS scheme we discussed divides a secret message P into two shadows, T1 and T2. If we got only one shadow, we cannot obtain any information about P. However, we observe that the rectangular shadows are transparent and dual-face. It means that there are two combinations in two shadows T1 and T2, i.e., one is to stacking T1 and T2 together and the other is to reverse one of T1 and T2 and then stack them together. Thus, the basic concept of our VMSS scheme is to hide more than one secrets in the shadows such that the same qualified subset of shadows can reveal the secrets and the revealed secrets are relied on the position of the shadows. Due to the page limitation, we only discuss the (2,2) VMSS scheme in this paper. Note that it is allowed to hide two secrets in two shadows in our (2,2) VMSS scheme and it is possible to hide 2k-1 secrets in (k,n) VMSS schemes.. 3.1 Codebook Generating As far as we know, all the proposed (2,2) VSS schemes [1,2] can only conceal a secret message in two shadows, and the size of each shadow extends fourth as much as of the original secret message. In order to conceal more messages in the same size of transparency, we propose the way as follows. Considering two secret messages, P1 and P2, the scheme shares them into two shadows, T1 and T2. When T1 and T2 stacked together, P 1 is recovered. By reversing T1 and covering it on T2, then P 2 is recovered. Because of the need of reversing T1, we have to consider the symmetric two points (top and down) of a.

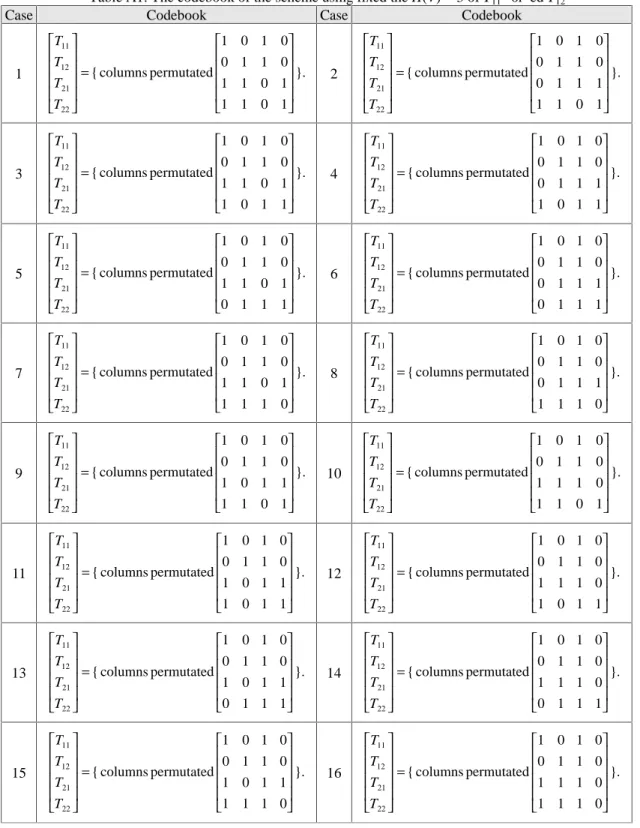
(3) message simultaneously in the codebook construction. The number of messages we want to conceal are two, so we have to consider four points simultaneously.. Figure 2. The pixels of two original secret messages As shown in Figure 2, suppose that there are two messages, P 1 and P 2. The symmetric two pixels of P 1 are P 11 and P 12. The symmetric two pixels of P 2 are P 21 and P 22. After calculating, two shadows are generated, T1 and T2. The share in T1 is composed of two black and two white subpixels so its Hamming weight is 2. And the share in T2 is composed of three black and a white subpixels so its Hamming weight is 3. The symmetric two shares of T1 are T11 and T12. The symmetric two shares of T2 are T21 and T22. The relationship between the shadow and its shares is shown in Figure 3.. corresponding pixels in secrets P1 and P2 be {P11, P12, P21, P22}={B, W, W, B} which is the case 7 in Table 1. If we fix the Hamming weight of T11 “or”ed T12 to be 3, then from T11    the case 7 of codebook in Table A1, we have that T12  T21    T22  1 0 1 0  are the columns permutated from 0 1 1 0 . The 1 1 0 1    1 1 1 0  subpixels of stacked shadows are shown in Figure 4.. Figure 4. An example of the VMSS scheme (case 7). 3.2 Security Analysis Figure 3. The subpixels of four shares in two shadows When T1 and T2 are stacked, if the Hamming weight of T1 “or”ed T2 is 4 then it means black while it means white if the Hamming weight is 3. For we need to consider four pixels at a time and for each pixel has changes of black and white, the number of the cases needed to consider are sixteen. Let P11, P 12, P 21 and P 22 ∈ {W, B}, the sixteen cases (1 ~ 16) are shown in Table 1. Table 1.The cases of the VMSS scheme 1 1 1 1 Case 1 2 3 4 5 6 7 8 9 0 1 2 3 P11 B B B B B B B B W W W W W P12 B B B B W W W W B B B B W P 21 B B W W B B W W B B W W B P 22 B W B W B W B W B W B W B. 1 4 W W B W. 1 5 W W W B. 1 6 W W W W. We design this scheme by two ways. First, we fix the Hamming weight of T11 “or”ed T12 to be 3 and the codebook is shown in Table A1 in Appendix. Second, we fix the Hamming weight of T21 “or”ed T22 to be 4 and design the codebook as shown in Table A2 in Appendix. Here, we give an example of this scheme. Let the. Due to the fact that the hiding secrets in our (2,2) VMSS schemes are two times of (2,2) VSS schemes. It is possible that one secret will be revealed some information when another secret and one shadow are given (Note that there is no pixel expansion in our schemes). It means that the proposed (2,2) VMSS scheme can not satisfy the perfect secrecy. However, it satisfies perfect secrecy for the two secrets P1 and P2 independently, when only one shadow T1 or T2 is given. Now, we make the security analysis for our (2,2) VMSS scheme as follows. In order to generate our codebook, we must fix the Hamming weight of T11 “or”ed T12 (T21 “or”ed T22) and generate the code of T21 and T22 (T11 and T12). What value will the Hamming weight of T21 “or”ed T22 (T21 “or”ed T22) be? It is an interesting question for us to discuss. Some tables as follows are listed to discuss this question. In Table 2, we fix the Hamming weight of T11 “or”ed T12 to be 3 and analyze the Hamming weight of T21 “or”ed T22. Table 2. Fix H(V) = 3 for T11 “or”ed T12 to analysis H(V) of T21 “or”ed T22 Case 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 H(V) 3 4 4 4 4 3 4 4 4 4 3 4 4 4 4 3 In Table 2, we find there are four special cases that may affect the security of the (2,2) VMSS scheme. We list.

(4) them as below.. . . . .. Case 01: {P11, P12, P21, P22} = {B, B, B, B}. Case 06: {P11, P12, P21, P22} = {B, W, B, W}. Case 11: {P11, P12, P21, P22} = {W, B, W, B}.. Case 16: {P11, P12, P21, P22} = {W, W, W, W}. It means that these cases can be identified by observing one shadow, i.e., T11 and T12 in T1. Although it still can not guess the secrets P1 and P2, it can not achieve perfect secrecy theoretically. In Table 3, we fix the Hamming weight of T21 “or”ed T22 to be 4 and analyze the Hamming weight of T11 “or”ed T12.. (a) The shadow T1. Table 3. Fix H(V) = 4 for T21 “or”ed T22 to analysis H(V) of T11 “or”ed T12 (I) Case 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 H(V) 2 3 3 4 3 4 2 3 3 2 4 3 4 3 3 2. (b) The shadow T2. We change four codes (case 4, case 7, case 10 and case 13) shown in Table A2 in Appendix, and hope to improve our scheme. The change is shown in Table A3 in Appendix. Those are the same to the codebook of fixing the Hamming weight of T11 “or”ed T12 to be 3. Hamming weight of T11 “or”ed T12 is changed by code alteration is listed as follows.. (c) T1 and T2 stacked together. Table 4. Fix H(V) = 4 for T21 “or”ed T22 to analysis H(V) of T11 “or”ed T12 (II) Case 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 H(V) 2 3 3 3 3 4 3 3 3 3 4 3 4 3 3 2 All codebooks that can be used in our scheme are considered in Table A1, A2 and A3 in Appendix. After we gather statistical data, total 28 different codebooks can be used to generate this scheme as shown in Table A4 which can be grouped into 16 cases. In a moment, we will compare our different methods used to generate the visual secret sharing schemes. The different kinds of conditions to analyze the security of (2,2) VMSS scheme and the comparison with the (2,2) VSS scheme are shown in Table A5.. 4. Experimental Results Let us see an example for this scheme. Two secret images, P1 and P2, share into two shadows T1 and T2. The shadows T1 and T2 are generated by the first method, i.e., the Hamming weight of Ti1 “or”ed Ti2 is 3 for i=1 and 2. When T1 and T2 stack together, the P1 is revealed. While T1 is inverted to T1’ and then we pile T1’ with T2, the P2 is appeared. They are shown in Figure 5.. (d) T1’ and T2 stacked together Figure 5. The example of VMSS scheme. 5. Conclusion In this paper, the concept of hiding more than multiple secrets in the same qualified subset of shadows in VSS schemes is proposed. We call it Visual Multi-Secret Sharing (VMSS) schemes. Two methods of constructing (2,2) VMSS scheme with concealing two secrets are given. The experimental results are also given. From our security analysis, it is impossible to design a (2,2) VMSS scheme satisfying perfect secrecy for two secrets due to the generating codebook is related to the two secrets, i.e., given one shadow the probability to guess 4 corresponding pixels in P1 and P2 is higher than 1/16. Nevertheless, it is possible to design a (2,2) VMSS scheme satisfying perfect secret for only one secret as.

(5) traditional (2,2) schemes. Nevertheless, The proposed VMSS schemes has the advantage to hide more secrets with the same size of shadows.. References [1]. [2]. [3] [4]. [5]. [6]. [7]. [8]. [9]. [10]. [11]. [12]. [13]. G. Ateniese, C. Blundo, A. De Santis and D.R. Stinson, “Visual Cryptography for General Access Structures,” Information and Computation, Vol. 129, No. 2, 1996, pp. 86-106. G. Ateniese, C. Blundo, A. De Santis and D.R. Stinson, “Constructions and Bounds for Visual Cryptography,” in Proceedings of the 23rd International Colloquium on Automata, Languages and Programming. Lecture Notes in Computer Science, No. 1099, Springer-Verlag, 1996, pp. 416-428. G.R. Blakley, “Safeguarding Cryptographic Keys,” AFIPS conference proceedings, Vol. 48, 1979, pp. 313-317. C. Blundo, P. D’ Arco, A. De Santis and D.R. Stinson, “Contrast Optimal Threshold Visual Cryptography Scheme,” to appear in the SIAM Journal on Discrete Mathematics. C. Blundo, A. De Santis and D.R. Stinson, “On the Contrast in Visual Cryptography Schemes,” Journal of Cryptology, Vol. 12, 1999, pp. 261-289. S. Droste, “New Results on Visual Cryptography,” Advances in Cryptography -EUROCRYPT’96, Lecture Notes in Computer Science No. 1109, Springer-Verlag, 1996, pp. 401-415. T. Hofmeister, M. Krause and H.U. Simon, “ContrastOptimal k out of n Secret Sharing Schemes in Visual Cryptography,” in COCOON ’97, Lecture Notes in Computer Science No. 1276, Springer-Verlag, 1997. T. Katoh and H. Imai, “Some Visual Secret Sharing Schemes and their Size,” Proceedings of International Conferences on Cryptology and information Security, 1996, pp.41-47. K. Kobara and H. Imai, “Limiting the Visible Space Visual Secret Sharing Schemes and Their Application to Human Identification,” Advances in Cryptology ASIACRYPT ’96, Lecture Notes in Computer Science, No. 1163, Springer-Verlag, 1996, pp. 185-195. C.S. Laih, “Threshold Scheme,” in Proc. of the first conference on Information Security, Chiayi, Dec., 1990, pp.107-145. M. Naor and A. Shamir, “Visual Cryptography”, Advances in Cryptology -EUROCRYPT’94, Lecture Notes in Computer Science No. 950, pp.1-12, Springer-Verlag, 1995. M. Naor and A. Shamir, “Visual Cryptography II: Improving the Contrast via the Cover Base,” in Proc. of Security protocols: international workshop 1996, Lecture Notes in Computer Science No. 1189, Springer-Verlag, 1997, pp. 69-74. Available as ftp://theory.lcs.mit.edu/pub /tcryptol/96-07.ps. M. Naor and B. Pinkas, “Visual Authentication and Identification,” Advances in Cryptology-CRYPT’97, Lecture Notes in Computer Science No. 1294, SpringerVerlag, 1997, pp. 322-336. Available as http://philby.ucsd.edu/ cryptolib/1997.html. [14] V. Rijmen and B. Preneel, “Efficient Colour Visual Encryption or ‘Shared Colors of Benetton’,” presented at EUROCRYPT’96 Rump Session. Available as http://www.iacr.org/conferences/ec96/ rump/preneel.ps. [15] A. De Santis, “On Visual Cryptography Schemes,” Information Theory Workshop, 1998, pp. 154 –155. [16] A. Shamir, “How to Share a Secret,” Commun. of the ACM, Vol. 22,1979, pp. 612-613. [17] D.R. Stinson, “An Introduction to Visual Cryptography,” presented at Public Key Solutions ’97, Toronto, April 2830, 1997. Available as http://bibd.unl.edu/~stinson/ VKSPKS.ps. [18] E.R. Verheul and H.C.A. Van Tilborg, “Constructions and Properties of k out of n Visual Secret Sharing Schemes,” Designs, Codes and Cryptography, Vol. 11, No. 2, May, 1997, pp. 179-196. [19] D.R. Stinson, “Visual Cryptography and Threshold Schemes,” IEEE Potentials, Vol. 18, Feb.-Mar. 1999, pp. 13-16. [20] C.N. Yang, The Application of Coding Techniques to Cryptography, Ph. D Dissertation, Department of Electrical Engineering National Cheng Kung University, Tainan, Taiwan, R.O.C., Dec. 1997, Chapter 6. [21] C.N. Yang and C.S. Laih, “New (K, K) Visual Secret Sharing Schemes Using Hierarchical Structure Technique,” Workshop on Cryptology and Information Security, ICS’98, pp. 148-154. [22] C.N. Yang, Y.B. Yeh and C.S. Laih, “A Dynamic Password Visual Authentication Scheme through Internet,” International Telecommunications Symposium (ITS ‘98), Vol. III, Taipei, Taiwan, 1998, pp. 163-167. [23] C.N. Yang and C.S. Laih, “New Colored Visual Secret Sharing Schemes,” Designs, Codes and Cryptography, Vol. 20, No. 3, July 2000, pp. 325-336. [24] Y.B. Yeh, On the Applications and Implementation of Network Security Based on Visual Secret Sharing, Thesis for Master of Science, Department of Electrical Engineering National Cheng Kung University, Tainan, Taiwan, R. O. C., June 1998, Chapter 3..

(6) Appendix Case. Table A1. The codebook of the scheme using fixed the H(V) = 3 of T11 “or”ed T12 Codebook Case Codebook. 1. T11  1 T    12  = { columns permutated 0 T21  1    1 T22 . 0 1 0 1 1 0 }. 1 0 1  1 0 1. 3. T11  1  T   12  = { columns permutated 0 T21  1    T 1  22 . 0 1 0 1 1 0 }. 1 0 1  0 1 1. 5. T11  1 T    12  = { columns permutated 0 T21  1    0 T22 . 0 1 0 1 1 0 }. 1 0 1  1 1 1. 7. T11  1 T    12  = { columns permutated 0 T21  1    1 T22 . 0 1 0 1 1 0 }. 1 0 1  1 1 0. 9. T11  1 T    12  = { columns permutated 0 T21  1    T 1  22 . 0 1 0 1 1 0 }. 0 1 1  1 0 1. 11. T11  1 T    12  = { columns permutated 0 T21  1    1 T22 . 0 1 0 1 1 0 }. 0 1 1  0 1 1. 13. T11  1 T    12  = { columns permutated 0 T21  1    T 0  22 . 0 1 0 1 1 0 }. 0 1 1  1 1 1. 15. T11  1 T    12  = { columns permutated 0 T21  1    T 1  22 . 0 1 0 1 1 0 }. 0 1 1  1 1 0. 2. T11  1 T    12  = { columns permutated 0 T21  0    1 T22 . 0 1 0 1 1 0 }. 1 1 1  1 0 1. 4. T11  1  T   12  = { columns permutated 0 T21  0    T 1  22 . 0 1 0 1 1 0 }. 1 1 1  0 1 1. 6. T11  1 T    12  = { columns permutated 0 T21  0    0 T22 . 0 1 0 1 1 0 }. 1 1 1  1 1 1. 8. T11  1 T    12  = { columns permutated 0 T21  0    1 T22 . 0 1 0 1 1 0 }. 1 1 1  1 1 0. 10. T11  1 T    12  = { columns permutated 0 T21  1    T 1  22 . 0 1 0 1 1 0 }. 1 1 0  1 0 1. 12. T11  1 T    12  = { columns permutated 0 T21  1    1 T22 . 0 1 0 1 1 0 }. 1 1 0  0 1 1. 14. T11  1 T    12  = { columns permutated 0 T21  1    T 0  22 . 0 1 0 1 1 0 }. 1 1 0  1 1 1. 16. T11  1 T    12  = { columns permutated 0 T21  1    T 1  22 . 0 1 0 1 1 0 }. 1 1 0  1 1 0.

(7) Case. Table A2. The codebook of the scheme using fixed the H(V) = 4 of T21 “or”ed T22 Codebook Case Codebook. 1. T11  1  T   12  = { columns permutated 1 T21  0    1 T22 . 0 0 1 0 0 1 }. 1 1 1  1 1 0. 2. T11  1  T   12  = { columns permutated 0 T21  0    1 T22 . 0 0 1 0 1 1 }. 1 1 1  1 1 0. 3. T11  1 T    12  = { columns permutated 1 T21  0    1 T22 . 1 0 0 0 0 1 }. 1 1 1  1 1 0. 4. T11  1 T    12  = { columns permutated 0 T21  0    1 T22 . 1 0 0 0 1 1 }. 1 1 1  1 1 0. 5. T11  1 T    12  = { columns permutated 1 T21  0    T 1  22 . 0 0 1 1 0 0 }. 1 1 1  1 1 0. 6. T11  1 T    12  = { columns permutated 0 T21  0    T 1  22 . 0 0 1 1 1 0 }. 1 1 1  1 1 0. 7. T11  1 T    12  = { columns permutated 1 T21  0    1 T22 . 1 0 0 1 0 0 }. 1 1 1  1 1 0. 8. T11  1 T    12  = { columns permutated 0 T21  0    1 T22 . 1 0 0 1 1 0 }. 1 1 1  1 1 0. T11  0 T    12  = { columns permutated 1 T21  0    T 1  22 . 0 1 1 0 0 1 }. 10 1 1 1  1 1 0. T11  0 T    12  = { columns permutated 0 T21  0    T 1  22 . 0 1 1 0 1 1 }. 1 1 1  1 1 0. 9. T11  0 T  1 12    = { columns permutated 11 T21  0    1 T22 . 1 1 0 0 0 1 }. 12 1 1 1  1 1 0. T11  0 T    12  = { columns permutated 0 T21  0    1 T22 . 1 1 0 0 1 1 }. 1 1 1  1 1 0. T11  0 T  1 12 13   = { columns permutated  T21  0    1 T22 . 0 1 1 1 0 0 }. 14 1 1 1  1 1 0. T11  0 T    12  = { columns permutated 0 T21  0    1 T22 . 0 1 1 1 1 0 }. 1 1 1  1 1 0. T11  0 T    12  = { columns permutated 1 T21  0    T 1  22 . 1 1 0 1 0 0 }. 16 1 1 1  1 1 0. T11  0 T    12  = { columns permutated 0 T21  0    T 1  22 . 1 1 0 1 1 0 }. 1 1 1  1 1 0. 15.

(8) Table A3. The result of changing codes by fix H(V) = 4 for T21 “or”ed T22 Codebook Case Codebook T11  T11  1 1 0 0 1 T  0 1 0 1 T   12  }. 7  12  = { columns permutated 1 4   = { columns permutated  T21  T21  0 1 1 1 0        1 1 1 0 T T   1  22   22  T11  T11  0 0 1 1 0 0 1 0 1  T  T  12  }. 13  12  = { columns permutated 1 10   = { columns permutated  T21  T21  0 1 1 1 0        1 1 1 0 1 T22  T22 . Case. 1 0 0 0 1 0 }. 1 1 1  1 1 0 0 1 1 0 1 0 }. 1 1 1  1 1 0. Table A4.The distribution of different codebook in 16 cases Case (H(T1), H(T2))* Case (H(T1), H(T2)). 1 (2, 4) (3, 3) (2, 3) 9 (3, 4). 2. 3. 4. 5. (3, 4). (3, 4). (4, 4) (3, 4). (3, 4). 12. 13. (3, 4). (4, 4) (3, 4). 10. 11 (4, 4) (3, 3) (2, 4) (3, 4) (4, 3). 6 7 (4, 4) (3, 3) (2, 4) (3, 4) (4, 3) 14 15 (3, 4). (3, 4). 8 (3, 4) 16 (2, 4) (3, 3) (2, 3). * H(T1) (or H(T2)) represents that the Hamming weight of T11 “or”ed T12 (or T21 “or”ed T22). Table A5. The security analysis of (2,2) VMSS schemes Conditions. Cases. VMSS scheme VMSS scheme VMSS scheme (Fix the H(V) = 3 of (Fix the H(V) = 4 of (Change previous T11 “or”ed T12) T21 “or”ed T22) codebook). Normal case. 1/12. 1/8. 1/12. Special case. 1/4. 1/4. 1/2. Normal case. 1/4. 1/4. 1/4. Special case. 1/4. 1/4. 1/2. Normal case. 1/4. 1/4. 1/4. Special case. 1/4. 1/2. 1/2. Normal case. 1/4. 1/4. 1/4. Special case. 1/2. 1/4. 1/2. Guess P1 or P2 independently (1pixel). Normal case. 1/2. 1/2. 1/2. Special case. 1/2. 1/2. 1/2. Guess P1 or P2 (2 pixels(P11, P12) or (P21, P22)). Normal case. 1/3. 1/2. 1/3. Special case. 1. 1. 1. Guess P1 or P2 independently (1pixel). Normal case. 1/2. 1/2. 1/2. Special case. 1. 1. 1. Guess P1 and P2 (4 pixels). Unknown P1 and P2. Guess P1 or P2 independently (2 pixels, (P11, P12) or (P21, P22)) Guess P1 or P2 relationship (2 pixels, (P11, P22) or (P12, P12)) Guess P1 or P2 relationship (2 pixels, (P11, P21) or (P12, P22)). VSS scheme (get the no weak shadow) 1/16. 1/4. 1/4. 1/4. 1/2. Known P1 or P2. 1/4. 1/2.

(9)