Frequency-domain interpolation-based channel estimation in pilot-aided OFDM systems

Frequency-Domain Interpolation-Based Channel

Estimation

in

Pilot-Aided OFDM Systems

Pei-Yun

Tsai

and Tzi-Dar Chiueh Graduate Institute of Electronics Engineering

and Department of Electrical Engineering National Taiwan University, Taipei, Taiwan, 10617.

Abstract-In this paper, we propose a novel freqneucy- domain interpolation algorithm for channel estimation in comb-type pilot-aided orthogonal frequency-division multiplex- ing (OFDM) systems. There exist two major types of pilot- aided OFDM channel estimation methods: time-domain and frequency-domain. We show that these two estimation meth-

ods have mathematical equivalence. The performance of these channel estimators mainly depends on how the channel impulse mponse (CIR) is reconstructed from frequency-domain channel mponse sample at the pilot suh-carriers. By closely examining timedomain CIR characteristics, we propose a new frequency- domain interpolation-based algorithm that can overcome the limitation of conventional frequency-domain algorithms. Mean- while, this new algorithm has the advantages of less latency and computation complexity when compared to time-domain approaches. Simulation results show that the proposed algorithm outperforms frequency-domain interpolation-based and time- domain algorithms in most cases.

I. INTRODUCTION

OFDM has attracted considerable attention since last decade, mainly because its substantial advantages in high- rate transmission over frequency-selective fading channels. By dividing

a

wide-band frequency-selective-fading channel into a large number of narrow-band flat-fading sub-channels, OFDM systems can easily compensate adverse channel ef- fects by a simple one-tap frequency-domain equalizer. More- over, with a cyclic prefix, inter-symbol interference can be mitigated and the mutually-overlapped spectra improve the spectrum efficiency. These features facilitate the adoption of OFDM in communications standards, such as digital au- dio broadcasting (DAB), digital video broadcasting-terresua1 (DVB-T), and IEEE 802.11dg wireless LAN.

In OFDM technology, high-rate transmission is achieved by using higher-order constellations. Robust coherent detection of such OFDM signals calls for accurate channel estimation. To this end, pilot sub-caniers are often interlaced with data sub-carriers. The comb-type pilot insertion has been shown to be suitable for channel estimation in fast fading channels [I]. Various comb-type pilot-aided channel estimation schemes for OFDM systems have been proposed. Among them, there are two major types: time-domain windowing and frequency- domain interpolation.

In the time-domain windowing algorithms, a time-domain CIR is obtained by first inverse Fourier transforming the

frequency-domain channel response at the pilot sub-carriers. In this case, the number of pilot sub-caniers M must be greater than the normalized maximum excess delay, i.e.,

A4

>

T,,,~& [21, where T ~ , , , and

I",

represent the maxi- mum excess delay and the sample time. Thereafter, different windowing techniques are applied to the contaminated time- domain CIR in order to reduce noise and aliasing effect. In

[ 3 ] , the CIR is directly cut off below a threshold. Similarly, Minn [4] and Fukuhara [ 5 ] keep only the more significant samples in the CIR. Garacia [6l gathers A,f samples in the CIR. Yang [2] utilizes all the CIR samples and applies

minimum mean squared error (MMSE) weighting.

In the frequency-domain interpolation algorithms, linear in- terpolation of the responses at the pilot sub-caniers has been proposed to estimate the frequency-domain channel response for all sub-caniers [7]. In

[SI,

a second-order interpolation technique has been shown to outperform linear interpolation. Coleri [ 11 uses a low pass filter and spline cubic interpolation. Usually, in frequency-domain interpolation techniques, pilot sub-caniers over-sample the channel frequency response in the frequency domain by at least a factor

of

two, i.e., &I

2

2rmaZ/Ts

VI.

We can see that these two types of channel estimation algorithms developed along different directions. In the time- domain windowing algorithms, researchers have tried to in- crease estimation accuracy by weighting the time-domain CIR samples. In the frequency-domain interpolation algorithms, higher-order polynomials are adopted to approximate the ideal sinc interpolation regardless of the CIR characteris- tics. Nevertheless, these two types of algorithms have their own limitations. In the time-domain windowing algorithms, although discrete Fourier transform

(DFT)

can be imple- mented by fast Fourier transform (FIT) algorithms, buffers

are needed for temporary data storage. Moreover, F l T and IFFT operations amount to overhead in latency as well as complexity, which is non-existent in the frequency-domain interpolation algorithms. On the other hand, in order to get acceptable performance, the conventional frequency-domain interpolation algorithms need more pilot sub-caniers, which reduce transmission efficiency.

In this paper, we first show correspondence between these two types of channel estimation algorithms. Then, we propose

AwGN&

4 2"

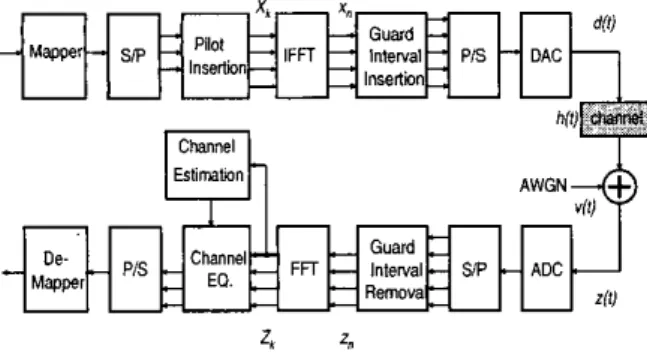
Fig. 1. Baseband block d i a g m of B typical pilot-aided OFDM system.

a novel frequency-domain interpolation-based channel esti- mation algorithm that can efficiently extract pilot sub-carrier information as the time-domain methods. Furthermore, the proposed technique strikes a balance between noise suppres- sion, aliasing removal, and CIR preservation by effectively shifting the time window and using a new interpolation function.

The paper is organized as follows. In Section 11, the description of the comb-type pilot-aided OFDM system is given. Section 111 illustrates the correspondence between time-domain windowing and frequency-domain interpolation. The proposed frequency-domain interpolation function is presented in Section IV. Simulation results and comparisons

are given in Section V. Section VI concludes this paper. 11. SYSTEM DESCRIPTION

Fig. 1 shows a typical block diagram of an OFDM system based on pilot-aided channel estimation. The IFFT block transforms frequency-domain data, X k . on the k-th subcarrier into time-domain samples 2, as

k = - - N I Z + l

(1)

where N is the number of total sub-carriers. In order to deal with inter-symbol interference (ISI), a cyclic prefix of Ny samples is inserted at the beginning of every symbol. The comb-type pilot allocation is shown in Fig. 2. Assume

that A4 pilot sub-carriers are uniformly distributed in a total of iV sub-carriers. The pilot sub-canier spacing is D = N f M , where D is an integer. Note that in addition to N ,

transmission sub-carriers, there are reserved sub-carriers used

as guard bands on both ends of the specuum. Among the Nu transmission sub-carriers, there are

11.1,

pilot sub-carriers for channel estimation.

At the receiver, the baseband signal is first sampled to obtain z,. With the cyclic prefix removed, 2, is sent to the

0 0 0 Q 0

0

0

4

+

frequency

N

0

Guard band Pilot subcarriers 0 Data subcarriers Fig. 2. Pilot sub-c-ers allocation.

FFT

block for transformation to the frequency domain: N-1

z,

= z , , e-327+h7, k = - N / Z

+

1,. ,

.

,

N / 2 . ( 2 )

n=0

Assume that the duration of the cyclic prefix is long enough so that there is no IS1 and that the down-conversion is accurate enough so that there is no inter-carrier interference (ICI). Then the frequency-domain received baseband data z k is given by

zk

= X k H k

+

v k , (3)

where H k is the channel response on the k-th sub-carrier and V, is the noise term. The frequency-domain channel response is given by

Hk

= h , . e - j 2 n G , (4)

where h,- and T~ denote the gain and delay of the r-th path

and the CIR has the form of h ( t ) =

E,

h , ( t ) .

6 ( t

- T J t ) ) . From the received frequency-domain data on the pilot sub-carriers, the channel response on those sub-carriers can be computed as H,,,, = Z,DfX,,,D, m = -A4,/2

+

1 , .

.

.

,At,

f2. Henceforth, the channel response on all data sub-caniers can be estimated, and the received data are equalized by the channel estimation, H k

" z k H k

X k = 7 ,

k =

- N U / 2 f 1 , . . . , O , . . . ,N,,/2. ( 5 )

111. TIME-DOMAIN WINDOWING AND FREQUENCY-DOMAIN INTERPOLATION

In time-domain channel estimation algorithms, A<-point inverse Fourier transform is applied to the AI pilot sub-c+er channel responses to reconsmct the time-domain CIR, h,:

Due to the sub-sampling in the frequency domain,

Ln

is a folded version of the original CIR with a period of A4 samples. We can usually avoid aliasing by setting A4

> Ny

since CIR energy mainly appears in the first N g taps.

Usually, a time-domain window is applied on the pen- odic AI-sample CIR. Let us denote this window by w =

[w-b w-b+1 .., W L - b - 1 l T , where L is the window width

and b controls its starting position. After windowing, the esti- mates of the frequency-domain channel response are obtained by Fourier transforming the weighted and zero-padded CIR

as

L-b-1

n=-b

(7) where

<.>

denotes modulo

M .

The equation above can be ipterpreted as interpolation in the frequency domain using

H,D

as base points and interpolation coefficients 1471 where

n=-b

Similarly, in a frequency-domain interpolation algorithm, a corresponding time-domain window can be derived. For a set of J-tap interpolation coefficients, W k , the windowing vector is given by

J D / 2

R' -

-

I{7k,&2"nk/'Y, (9)

k = - J D / 2 + 1

" - D

The fact that these two types of operations are closely related offers a possibility of mapping between these two types of algorithms. Therefore, one can design a channel estimation algorithm that has advantages from both the frequency- domain algorithms and the time-domain algorithms.

IV. NEW FREQUENCY-DOMAIN INTERPOLATION FOR

CHANNEL ESTIMATION

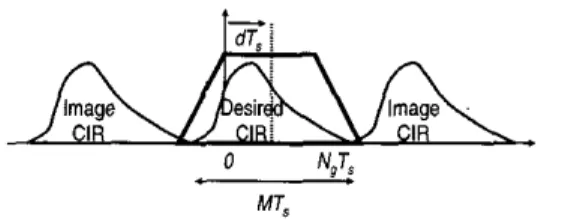
The inverse Fourier transform of M pilot sub-canier frequency-domain responses generates a periodic time- domain signal with a period of

MTS,

as shown in Fig. 3. If the OFDM symbol boundary acquisition is accurate, the first pulse of the CIR will he at the origin and the remaining impulse response appears in the guard interval [O,N,T,].

However, energy leakage occurs in the uniformly T,-spaced CIR due to the non-T,-spaced channel delay T~ [IO]. There-

fore there exist pre-cursor as well as post-cursor in the reconstructed CIR. A time-domain window is used to preserve the major portion of the CIR and at the same time reject the aliased components. It is clear from Fig. 3 that the window must be shifted to the right instead of centering at the origin

as the conventional polynomial interpolators in F q (9). Note that shifting the window in the time domain is equivalent to rotating the phase of the interpolation coefficients in the frequency domain.

MT,

Fig. 3. Periodic CIR in the time domain

Usually, the magnitude of the time-domain CIR decays gradually to the right. The time-domain CIR reconstructed by the samples of the frequency-domain channel response is corrupted by noise and aliasing effect. The weighting window must be flat over the duration where CIR is strong so that it is not distorted [ l l ] . On the two edges of the window, the weighting should be smaller in order to suppress noise and aliasing effect. Moreover, smooth weighting in the time domain entails fast-decaying magnitude in the frequency- domain interpolation coefficients, and thus fewer of them are needed.

In light of the above considerations, we choose the raised- cosine function as the frequency-domain interpolation coeffi-

cients and set

where

p

is the roll-off factor; d is the time shift and it is decided by the worst-case channel delay spread. Note that in a short delay-spread channel, the estimation error is insensitive to d since the major podon of the CIR will be covered by the window with a wide range of d.

V. SIMULATION RESULTS AND COMPARISONS In order to show the effectiveness of the proposed raised-

cosine-based frequency-domain channel estimation algorithm, we conduct simulation

on

some practical scenarios. In the simulation. we use the typical urban channel model given in [12], which has 20 paths and a maximum excess delay of 24.28 samples at a sampling rate of 11.52 MHz. There are 1024 sub-carriers with 29 pilot sub-carriers evenly insetted for channel estimation. The guard interval has

a

length of 26

samples.

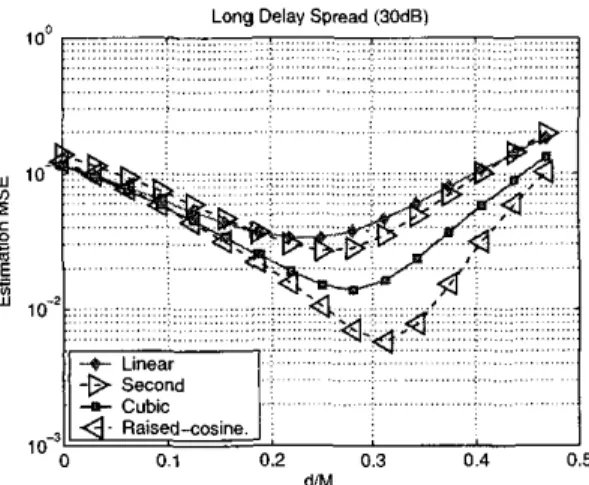
Fig. 4 demonstrates the improvement in channel esti- mation accuracy if we consider the time shift effect by incorporating a phase rotation term in several frequency- domain interpolation-based algorithms. Since the time- domain weighting window derived from the polynomial interpolators' coefficients has wide and non-flat mainlobe

[13], aliasing is unavoidable. So the CIR will be distorted, yielding larger estimation error. We can also see the proposed raised-cosine interpolator is by far the best frequency-domain interpolation-based channel estimator in terms of estimation accuracy. In addition, note that for each algorithm, the ermr

Long Delay Spread (3068) lo

r-

I

_{: I : : : :}

_...

---

'

-

7

~ . . . : . . . . . j . . .

]

. . . . ~ . . . b . . .

4

1

...

;.-?@-q

. . . .- E .i . . . -&- Cubic ~ . Raised-cosine. : 0.1 0.2 0.3 0.4 0.5 diM

Long Delay Spread

too 10 a Y m to SNR h g . 4.

in frequency-domain interpolation-based channel estimation.

Improvement in estimtioh accumcy if the time shift is considered Fig. 6.

channel with long delay spread.

Bit error rate performance using different channel estimators in B

Long Delay Spread

100 Lu to-' 0) I 5 E c ... .- I i o - 2 5 t o 15 20 25 30 SNR Fig. 5.

long delay spread.

Estimation ermr of different channel estimators in a channel with

decreases as the time shift increases, and after reaching a minimum, the error starts to rise again.

Fig. 5 illustrates the performance of several channel estima- tors under different levels of SNR. RC-6 and RC-8 denote the proposed frequency-domain interpolation channel estimation algorithm using 6-tap and 8-tap raised-cosine coefficients, respectively. We then apply such estimated channel response to a frequency-domain equalizer in a 16-QAM sub-canier

data receiver. The resulting hit error rates versus S N R are depicted in Fig. 6. From these two figures, we see that in the case of channels with long delay spread, the proposed algorithm is significantly better than all other frequency- domain algorithms and most of the time-domain algorithms. Computational complexity and memory requirement are also important issues in the choice of channel estimators .

The time-domain windowing estimators require A$ log, AT

+

IV log, N complex multiplications and Af

+

N - 2 complex buffers for radix-4 FFTnFFT and 2A2 real multiplications for windowing by w in the time domain. The entries in

w are pre-computed and stored thus occupy

M

buffers. Due to the latency of 2N - 1 samples caused by IFFT

and

FFT,

21%'" complex data must be also buffered. For

the proposed frequency-domain J-tap interpolation channel estimator (shown in Fig. 7). we need ZNu J

+

4fi-u real multiplications and 25 real data buffers and (D - l)J real buffers for the real coefficients. Since the latency of the frequency-domain interpolation is much reduced to JD/Z-1, only J ( D

-

1)/2 complex data buffers are necessary.

As the FFI size increases, the overhead in the buffers and multiplications increases rapidly if a time-domain windowing channel estimator is implemented. The numbers of multipli- cations and of buffers needed by the time-domain channel estimators and the frequency-domain estimators for different

FFT

size are plotted in Fig. 8. Note that a 6-tap frequency- domain interpolation estimator is used for comparison. For the proposed estimator, the reduction in computational com- plexity is evident, especially when the number of sub-caniers is large.

VI. CONCLUSION

In this paper, we examined the time-domain and frequency- domain chaMel estimation algorithms in the comb-type pilot- aided OFDM systems. We showed that there exists correspon- dence between these two types of channel estimators. We then proposed to include a phase rotation term in the frequency- domain interpolation to account for the equivalent time shift for better CIR window location. In addition, the proposed raised-cosine interpolation coefficients not only have good attenuation on noise and aliasing but also preserve most CIR information and provide very good estimation accuracy. The

Fig. 7.

channel estimator.

Block diagram of the proposed frequency-domain interpolation

Complexity comparison 106 1 os .-

E

2 10‘

a

1 o3 1 O2 1 o2 1 0’ 10‘ No. of subcamen Fig. 8.

estimton: F.D.: frequency-domain estimators.

Channel estimtor complexity versus FFI size. T.D.: time-donuin

complexity of the proposed frequency-domain interpolation

is

shown to be less than all time-domain channel estimators in almost all FFT sizes. With its low hardware complexity and accurate estimation performance, the raised-cosine frequency- domain interpolation channel estimator will find many appli- cations in

OFDM

communication systems.

REFERENCES

[I] S. Cole”, M. Ergen, A. h r i and A. BahaLThannel estimation techniques based on pilot arrangement in OFDM systems,” IEEE

tronsoction on Bmodcasrirrg, vol. 48. “0.3, pp. 223-229, Sep. 2002.

[21 B. Yang, 2. Cao and K. B. LetaieF, “Analysis of low-complexity

windowed DIT-based MMSE channel estimator For OFDM systems:’

IEEE rmrzucrion on Cornmunicarions, Vol. 49, No. 11, pp.1977-1987, Nov. 2001.

[31 Y Zhaa and A. Huang, “A novel channel estimation method for OFDM mobile communication system based on pilot signals und transform dormin processing,” in Pmc. of I997 IEEE 47rh Vehicular Technology Conferenre. Vol. 3, May 1997, pp. 2089-2093.

[4] H. Minn. V. K. Bhargava “An investigation into time-domain approach for OFDM channel estimation,” IEEE Transactions on Broodcarring,

Vol. 46, Issue 4, pp. 240-248. Dec. 2ooO.

[SI T. Fukuhara. H. Yuan, Y. Takeuchi and H. Kobayashi. “A novel channel estimation method far OFDM tnnsmission technique under fast time-vkmt fading channel,” in Pmc. sf2W3 IEEE 57th Vehicular

Technology Confemnce, 2003.

I61

[91

1101

M. J. Femander-Getino Garcia J. M. Paez-Borrallo and S. Z z o , “DFT based channel estimation in 2D-pilot-symbol-aided OFDM wireless systems,” in Pmc. of 2001 IEEE 53th Vehicular Technology Conference.

Vol. 2 . 2001, pp. 810-814.

J. Rime and M. Renfors, “Pilot spacing in orthogonal frequency division multiplexing system on pncticvl channels:‘ IEEE Transoetion

on Consrrmer Elecrroics, vol. 42, no. 4, pp. 959-962. Nov. 1996. M. H. Hsieh and C . H. Wei, “Channel estimation for OFDM Systems based on comb-type pilot mangemem in frequency selective fading channels:’ IEEE Traonsncrion on Coasumer Elecrmio, vol. 44. no. I, pp. 217-225, Feb. 1998.

Y. Hoeher. S. Kaiser and P. Robenson.“Two dimensional pilot-symbol- aided channel estimation by Wiener Rltefing.” in IEEE I!ttenwtior,ol Corfeference on Acoustics. Speech, orrd Sigrwl Processing, vol. 3, 1997. pp. 1845-1848.

J. -J van de Beek, 0. Edfors, M. Sandell. S. K. Wilsoh and P. 0. Borjesson. “On channel estinmtion in OFDhl systems:’ in Proc. of

1995 IEEE 45th Vehicular Techaology Con/crence. Vol. 2, Jul. 1995,

pp. 815-819.

H. Tang. I(. Y Lau and R. W. Brodersen.”Interpolai~”-based m i m u m lkelihwd channel estimation using OFDM pilot symbols:’ in IEEE

Global T~lecornmuaicntior2s Corference. vol. 2. 2002, pp. 186i-1864.

3GPP Technique Specification Group (TSG) RAN WG4: Deployment Aspects. TR 25.943 v2.1.0 (2001-061.

L. Emp. F. M. Gardner and R. A. Harris.”lntelpolatian i~ Digital Modems-Pan II: implementation and perfommce,” in IEEE Trans-

ncrion O I I cornmueicoriorzs. vol. 41. no. 6. pp. 998-1008. Jun. 1993.