On Multilevel Coded MPSK for the Rayleigh Fading Channel

(1)

On Multilevel Coded MPSK for the

Rayleigh Fading Channel

Ruey-Yi Wei and Mao-Chao Lin

Abstract—This paper presents a new upperbound on the

pair-wise error probability of MPSK sequences for the Rayleigh fading channel when channel state information (CSI) is unavailable. This bound is derived by adding weight factors in computing symbol metrics. Simulation results show that the weight factors which optimize the upperbound likely optimize the error rate as well. Multilevel coded MPSK schemes for the Rayleigh fading channel are also devised. Results show that the added weight factors improve the error performances of these schemes in the case that CSI is unavailable.

Index Terms— Coded modulation, fading channel, multilevel

coding.

I. INTRODUCTION

C

ODED modulation [1] is a bandwidth-efficient technique that can provide reliable data transmission with high spectral efficiency. For a coded modulation system applied to the additive white Gaussian noise (AWGN) channel, max-imizing its minimum-squared Euclidean distance (MSED) [1] is highly desired. For a coded MPSK system applied to the Rayleigh fading channel, MSED is not the major factor which affects the error performance. By deriving upperbounds on the pairwise error probability of MPSK sequences for the Rayleigh fading channel, Divsalar and Simon [2], [3] showed that maximizing both minimum symbol distance (MSD) and minimum product distance (MPD) is highly desired, regardless of whether or not channel state information (CSI) is available. In this paper, we derive a new upperbound on the pairwise error probability for the Rayleigh fading channel without CSI by adding weight factors in calculating the symbol metrics. The channel considered herein is the frequency nonselective slow Rayleigh fading channel with perfect phase tracking. Infinite interleaving depth is assumed such that the effect of fading on a signal is independent of the fading on other signals. Weight factors that optimize the upperbound are derived. Simulation results obtained from several examples show that the weight factors which optimize the upperbound appear to be the best choices in lowering the error rates.

Coded modulation for the fading channel has been exten-sively studied [2]–[16]. In particular, coded modulation based on multilevel coding has attracted a lot of attention [11]–[16]. The basic idea of multilevel coding [17] is to partition a signal

Manuscript received August 22, 1996; revised July 11, 1998. This work was supported by the National Science Council, Taiwan, R.O.C., under NSC Grant 85-2213-E-002-012.

The authors are with the Department of Electrical Engineering, National Taiwan University, Taipei 106, Taiwan, R.O.C.

Publisher Item Identifier S 0018-9545(99)01048-8.

set into several levels and to separately encode each level (or a combination of certain levels) with a proper component code. Either a block code or a convolutional code can be used as a component code. If all the component codes are block codes of identical lengths, the associated coded MPSK can be regarded as a multilevel block-coded modulation (BCM) scheme [13]. A variation of multilevel BCM can be designed by using block codes of different lengths as component codes [14]. If all the component codes are convolutional codes, the associated coded MPSK can be regarded as a multilevel trellis-coded modulation (TCM) scheme [15]. A mixed design for which some component codes are block codes and some component codes are convolutional codes can be found in [13] and [16]. Under a similar coding rate and decoding complexity, using convolutional codes as component codes generally yields bet-ter error performances than using block codes. However, the disadvantage of using convolutional codes as component codes is its long decoding delay, which is due to the required trun-cation length in the Viterbi decoding for convolutional codes. In [18], a multilevel coded modulation scheme called BCM with interblock memory (BCMIM) was designed for the AWGN channel to increase the coding rate without decreasing MSED as compared to the associated multilevel BCM. In this paper, we modify the design of BCMIM for MPSK so that the coding rate can be increased without decreasing MSD and MPD. When CSI is available, the modified BCMIM scheme yields a satisfactory error performance for the Rayleigh fading channel. When CSI is unavailable, the error performance of the modified BCMIM scheme for the Rayleigh fading channel is not as good as expected if conventional symbol metrics are used. However, adding proper weight factors to the symbol metrics can improve the error performance. The optimal choice for the weight factor is a value proportional to the inverse of the level Euclidean distance in each level. The advantage of BCMIM over BCM is demonstrated by comparing several examples based on their coding rates, error performances, and decoding complexities.

II. ANUPPERBOUND ON THE PAIRWISEERROR

PROBABILITY OFMPSK SEQUENCES WITHIDEAL CSI This section briefly reviews an upperbound on the pairwise error probability of MPSK sequences with ideal CSI for the Rayleigh fading channel derived by Divsalar and Simon [2], [3].

Let be a transmitted coded MPSK

symbol sequence of length where denotes the

trans-mitted symbol at time Let be the

(2)

corresponding received sequence. The th received symbol is given by

(1) where is a zero-mean complex Gaussian variable with variance and is a normalized random variable with Rayleigh distribution having the following probability density function:

(2) Assume that the fading gain sequence is

The pairwise error probability of choosing instead of is

(3) where denotes the metric of which is used in the decoding trellis.

We set which is the

maximum-likelihood metric, since is Gaussian distributed. Applying Chernoff bound to (3) yields

(4) where denotes an arbitrary nonnegative real number and represents the set of all for which

The parameter which optimizes the upperbound in (4) is With this we have

(5)

where is the ratio of symbol energy to noise spectral density. It can be shown that

(6) if is a random variable with Rayleigh distribution. With this, inequality (5) yields

(7)

For reasonably large values, inequality (7) can be approximated by

(8)

The right-hand side of inequality (8) suggests that in de-signing a coded MPSK system with ideal CSI, an MSD (i.e., minimum Hamming distance) and an MPD are highly desired. Such a design criterion differs from that of the coded modulation for the AWGN channel which requires a large MSED.

III. UPPERBOUNDS ON THE PAIRWISE ERROR

PROBABILITY FORMPSK SEQUENCES WITHOUT CSI When CSI is absent and the fading gain sequence is the pairwise error probability of selecting instead of is

(9)

Conventionally, is set to be [2], [3]. This metric is not the maximum-likelihood metric. Herein, we

propose setting where is a weight

factor. Applying the Chernoff bound to (9) leads to

(10) Inequality (10) can be rewritten as

(11) where denotes the complex conjugate of and represents the real part of Assume that Then, it can be easily shown that

(12) It can also be shown that

(13) Then, inequality (11) can be expressed as

(14)

where Normalizing the Chernoff parameter (replacing by ) and substituting for in (14) yield

(15) Under the assumption of infinite interleaving, the pairwise error probability is

(16) where and are identical and mutually independent for and denotes the probability density function of

(3)

Assume that each is a random variable with Rayleigh distribution. With a procedure resembling that used in [2] and [3], we have

(17) where

(18) and is the complementary error function.

Since can be approximated by

(19) for large then (17) can be approximated by

(20)

where denotes the cardinality of

The value of which optimizes the upperbound in (20) is (21)

Substituting (21) into (20) yields

(22)

By setting for each inequality (22) becomes the upperbound derived in [3], which is

(23)

The upperbound in (23) can be improved by selecting which optimizes the right-hand side of (22) for each

The arithmetic-mean–geometric-mean inequality implies

(24)

which further implies

(25)

where the equality holds if and only if is proportional to for each Based on this fact, the tightest case of the upperbound in (22) can be expressed as

(26)

Note that, the upperbound without CSI given in (26) is inferior to the upperbound with CSI given in (8) by a factor of

A simple example is used herein to demonstrate that the proposed upperbound in (26) is better than the upperbound in (23).

Example 1: Consider two 8PSK sequences, i.e.,

and such that

and The ratio of optimal weight factors is

Fig. 1 presents the simulation results of pairwise error probabilities and the upperbounds given in (8), (23), and (26), respectively.

Although we have shown that to minimize the upperbound of pairwise error probability, the optimal weight factor is proportional to the inverse of we are unable to theoretically prove that to minimize the pairwise error probability

also requires that is proportional to the inverse of However, simulation results in Fig. 1 indicate that setting to be proportional to the inverse of is likely the best choice. Hence, we recommend the following: “for decoding in the Rayleigh fading channel without CSI, the best weight factor at the th position may be proportional to the inverse of the Euclidean distance between the two associated symbols.”

IV. SEVERAL CODED MPSK SYSTEMS FOR THE RAYLEIGH FADING CHANNEL

In this section, we design several coded MPSK systems which are suitable for the Rayleigh fading channel. For the convenience of presentation, we restrict M to be eight. How-ever, all the designs can be easily extended to

where is a positive integer.

Consider an 8PSK signal constellation as given in [1], in which each signal point is labeled by where and By successive two-way partitions of 8PSK signal set, the intrasubset squared Euclidean distances are

(4)

Fig. 1. Prfxxx ! ^xg for 8PSK sequences given in Example 1. (A) Upper-bound (8). (B) UpperUpper-bound (23). (C) UpperUpper-bound (26). (D) Simulation results with CSI. (E) Simulation results without CSI usingw1: w2: w3= 1 : 1 : 1:

(F) Simulation results without CSI usingw1: w2: w3= 1 : 0:54 : 0:38:

and , respectively [1],

where is a constant. Let be

a sequence of the transmitted 8PSK signals. A conventional multilevel coding system is designed in such a manner that is a codeword of a binary code is a codeword of a binary code and is a codeword of a binary code Herein, represents the code used for coding level where Assume that is an binary block code with generator matrix where Then we have a multilevel BCM scheme for which each block consists of 8PSK signal points and the coding rate is bits per 8PSK signal point. Such a multilevel BCM scheme can be easily decoded by a three-stage decoding, where at the th stage of decoding, a trellis for is used.

The important parameters which affect the error perfor-mance of a coded MPSK system for the Rayleigh fading channel are MSD, MPD and where is the number of neighbors at a symbol distance of and at a product distance of According to the upperbounds in (8) and (26), MSD is the most important parameter for high signal-to-noise ratio (SNR). Hence, it is natural to set and to be the same code, so that a large MSD can be achieved [15].

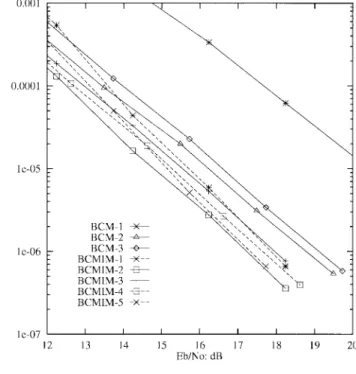
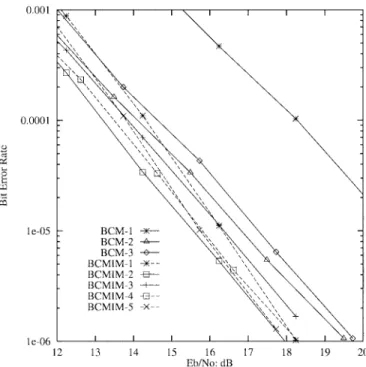
Example 2 (BCM-1): Let be a (8, 4, 4) binary code. Then, we have a BCM scheme with coding rate of 12/8 bits per symbol. The parameters MSD, MPD, and (MSD, MPD) are 4, , and 224, respectively. Sim-ulation results for the Rayleigh fading channel with CSI and without CSI which are obtained from a three-stage decoding are given in Figs. 2–4, respectively. In Fig. 3, weight factors are not used, and in Fig. 4 optimal weight factors are used. The ratio of optimal weight factors for levels and is

Fig. 2. Simulation results with CSI.

Fig. 3. Simulation results without CSI usingw_a: w_b: w_c= 1 : 1 : 1:

In each stage of the three-stage decoding, a four-state trellis for the (8, 4, 4) binary code is needed.

For BCM-1, the error performance is unsatisfactory, since its MPD is not sufficiently large. One way to increase MPD is to decrease the code rate of as given in Example 3.

Example 3 (BCM-2): Substitute in BCM-1 with a (8, 1, 8) code. Then, the coding rate is reduced to 9/8 bits per symbol. The parameters MSD, MPD, and (MSD, MPD) are 4, , and 224, respectively. Simulation results in Figs. 2–4 show the improvement of the bit error rate (BER).

(5)

Fig. 4. Simulation results without CSI usingw_a:w_b:w_c= 1 : 0:54 : 0:38.

The error performance of BCM-2 is improved with the price of lower coding rate. The coding rate can be increased without decreasing MSD and MPD by using longer block codes.

Example 4 (BCM-3): Let be a (16, 5, 8) binary code and be a (16, 11, 4) binary code. The coding rate is 27/16 bits per symbol. The parameters MSD, MPD, and (MSD, MPD) are 4, , and 2240, respectively. Simulation results are presented in Figs. 2–4. In the three-stage decoding, eight-state trellises for and , respectively are needed.

For all the three BCM examples, the decoding results without CSI are independent of the weight factors. This phe-nomenon can be accounted for as follows. In the first stage of decoding, the squared Euclidean distance (SED) between any two symbols of the same position is either 0.586E or 0. Hence, in the first stage of decoding, there is only one weight factor However, the usage of only one weight factor is equivalent to not using any weight factor. The circumstances for the second and third decoding stages are similar.

BCM-3 has been discussed in [13] and [14]. Compared to BCM-2, the advantage of BCM-3 is its bandwidth effi-ciency. In addition to the increased trellis complexity, the error performance of BCM-3 is worse than that of BCM-2. The poor error performance of BCM-3 is attributed to its large number of nearest neighbors. In the following, we introduce a coded modulation scheme which can provide satisfactory error performance with increased coding rate.

A scheme called BCM with interblock memory (BCMIM) [18] was proposed in 1994, which is obtained by adding interblock memory to the BCM so as to increase the coding rate without decreasing the MSED. The original BCMIM [18] was designed for the AWGN channel. For the Rayleigh fading channel, the coding rate must be increased without sacrificing the MSD and MPD. Hence, further consideration is necessary.

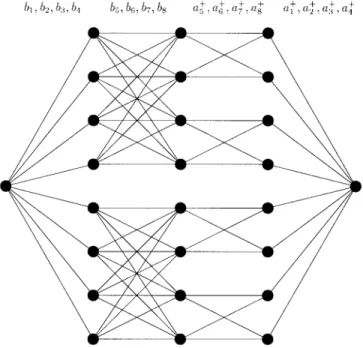
Fig. 5. Coding configuration of BCMIM with interblock memory between levels a and b:

Let represent a

block of 8PSK signal points and

represent the following block. These two adjacent blocks are combined to be called a superblock. For a BCM scheme, we have

and where

is the generator matrix of the binary block code and is a -bit message for For a BCMIM scheme with interblock memory between levels and it is designed such that

(27) where is a -bit message

(28)

is the generator matrix of a binary code and and are both matrices. Also, coding for level is obtained by Fig. 5 illustrates the coding configuration. In this manner, the coding rate is bits per 8PSK signal point. If we switch the roles of the “ ”and “ ” symbols in the above coding design, then we have a BCMIM scheme with interblock memory between levels and Obviously, an interblock memory between levels and can be provided in a similar way.

Consider the case for which the interblock memory is provided between levels and Let the MSD and MPD of the original BCM be and respectively. Let denote the binary block code with

generator matrix where

is the transpose of a matrix Let

and be distinct messages which are

encoded into and

respectively. Consider the following conditions.

1) Assume that Then, the MSD and MPD between the associated superblocks are equal to and

(6)

2) Assume that Then, the MSD and MPD between the associated superblocks are

(29) and

(30) respectively.

Herein, we require either (A) and

or (B) In this manner, MSD and MPD of the con-structed BCMIM are still and , respectively. Moreover, of the BCMIM is the same as that of the original BCM. Hence, BER of the BCMIM will be close to that of the original BCM at the same

Then, BCMIM has a lower BER than BCM at the same as attributed to the smaller bandwidth required by BCMIM, where denotes the energy of each signal point, represents the energy of each message bit and is the one-sided power spectral density of AWGN. The decoding of this BCMIM can be implemented by a two-stage decoding, where in the first stage of decoding, a trellis for is used and in the second stage of decoding, a trellis for is used.

BCMIM, for which interblock memory is provided between other levels, can be similarly designed.

The following examples show specific designs of BCMIM for the Rayleigh fading channel. Simulation results with CSI are given in Fig. 2. Simulation results without CSI and not using any weight factor are given in Fig. 3. Simulation results without CSI and using optimum weight factors are given in Fig. 4.

Example 5 (BCMIM-1): For this BCMIM,

and are (8, 1, 8), (8, 4, 4), (8, 4, 4), (8, 4, 4), and (8, 7, 2) binary linear codes, respectively. The coding rate is 12/8 bits per signal point. In the two-stage decoding, an eight-state trellis for the (16, 8, 4) binary code as shown in Fig. 6 and a four-state trellis for are needed. Each branch on the left half part of the trellis shown in Fig. 6 represents a coset of a (4, 1, 4) binary code.

and are (8, 1, 8), (8, 4, 4), (8, 4, 4), (8, 4, 4), and (8, 7, 2) binary linear codes, respectively. The coding rate is 12/8 bits per signal point. In the two-stage decoding, an eight-state trellis for the (16, 8, 4) binary code and a four-state trellis for

are needed.

and are (8, 1, 8), (8, 4, 4), (8, 4, 4), (8, 7, 2), and (8, 7, 2) binary linear codes, respectively. The coding rate is 12/8 bits per signal point. In the two-stage decoding, an eight-state trellis for the (16, 11, 4) binary code and a one-state trellis for are needed.

According to simulation results in Fig. 2, for which perfect CSI is available, the error performance of any of the three BCMIM examples is better than that of either 1 or BCM-2. Among the three BCMIM examples, BCMIM-2 which provides interblock memory between levels and is the best. This phenomenon can be accounted for by more closely examining the distance properties of these BCMIM examples,

Fig. 6. The decoding trellis of (16, 8, 4) binary codeC:

even though MSD and MPD of these BCMIM are all identical.

In case that we have and

and for BCMIM-1;

and and for

BCMIM-2; and and

for BCMIM-3. Since is more important than for high SNR, we can expect that BCMIM-2 which also has the smallest is the best. Although is larger and is smaller, BCMIM-1 is better than BCMIM-3 for high SNR, as attributed to the larger

According to Figs. 3 and 4, for all the three BCMIM examples, the usage of weight factors can improve the error performance. Herein, we use BCMIM-2 as an example for explanation. In the first stage of decoding for BCMIM-2, the SED between any two symbols in the first eight positions is either 4E or 0 and the SED between any two symbols in the last eight positions is either 0.586E or 0. In decoding this stage, the optimal ratio of weight factors is

Compared with BCM-2, the coding rate of BCMIM-2 is increased from 9/8 to 12/8, and the error rate is lowered. The price is that the decoding complexity for decoding BCMIM-2 is about twice of that for BCM-BCMIM-2. In the following, we slightly lower the coding rate of BCMIM-2 to more clearly demonstrate the merits of BCMIM over BCM.

and are (8, 1, 8), (8, 4, 4), (8, 4, 4), (8, 3, 4), and (8, 6, 2) binary linear codes, respectively. The coding rate is 11/8 bits per signal point. In the two-stage decoding, a four-state trellis for the (16, 7, 4) binary code and a four-state trellis for are needed. The decoding complexity of BCMIM-4 is nearly the same as that of BCM-2. However, simulation results in Figs. 2 and 4 indicate that BCMIM-4 has a higher coding rate and lower BER than BCM-2.

(7)

The coding rate of BCMIM-1 is lower than that of BCM-3. However, the error rate of BCMIM-1 is lower than that of BCM-3. Moreover, the decoding complexity for BCMIM-1 is roughly two thirds of BCM-3. We may modify BCMIM-1 to show the advantage of BCMIM over BCM.

and are the same as BCMIM-1. Code is the (16, 11, 4) binary code. Notably, at level , a binary code of length 16 is used to replace two independent binary codes of length 8. We may consider BCMIM-5 as a slight variation of BCMIM. The coding rate is 27/16 bits per signal point. In the two-stage decoding, an eight-state trellis for the (16, 8, 4) binary code and an eight-state trellis for are needed. Compared with BCM-3, BCMIM-5 has the same coding rate and similar decoding complexity. However, simulation results in Figs. 2 and 4 demonstrate that, for BER BCMIM-5 is better than BCM-3 by about 1.8 dB regardless of whether or not CSI is available.

V. CONCLUSION

By introducing weight factors to symbol metrics, we have derived a new upperbound on the pairwise error probability of MPSK sequences for the Rayleigh fading channel when CSI is unavailable. In simulation, the weight factors significantly lower the pairwise probability. Since each weight factor de-pends on the Euclidean distance between two symbols of the same position in two symbol sequences, the weight factors can only be calculated in multilevel coded modulation systems. However, in a conventional multilevel coded modulation sys-tem, each decoding stage involves only one coding level and hence there is only one weight factor in each decoding stage. Thus, assigning weight factors to different coding levels be-comes meaningless. In this paper, we have designed BCMIM systems for the fading channel. For designing a BCM system, increasing the coding rate without sacrificing MSD and MPD entails using block codes of longer length as component codes. This generally increases the number of nearest neighbors and hence increases its BER. BCMIM provides an interesting alter-native. Notably, interblock memory in a BCMIM scheme can increase the coding rate without sacrificing MPD, MSD, and the number of nearest neighbors. In a certain decoding stage for a BCMIM system, two coding levels are involved. Hence, for a BCMIM system, assigning different weight factors to different coding levels do affect the decoding performance, thereby implying lowering of the error rate. Examples pre-sented demonstrate the detailed criterion in designing appro-priate BCMIM for the Rayleigh fading channel. Furthermore, BCMIM and BCM are compared with respect to their error performances, decoding complexities and coding rates.

ACKNOWLEDGMENT

The authors wish to thank the anonymous reviewers and Dr. J.-Y. Wang for their comments and valuable suggestions.

REFERENCES

[1] G. Ungerboeck, “Channel coding with multilevel/phase signals,” IEEE

Trans. Inform. Theory, vol. IT-28, pp. 55–67, Jan. 1982.

[2] D. Divsalar and M. K. Simon, “Trellis coded modulation for 4800–9600 bits/s transmission over a fading satellite channel,” IEEE J. Select. Areas

Commun., vol. SAC-5, pp. 162–175, Feb. 1987.

[3] , “The design of trellis coded MPSK for fading channels: Perfor-mance criteria,” IEEE Trans. Commun., vol. 36, pp. 1004–1012, Sept. 1988.

[4] , “The design of trellis coded MPSK for fading channels: Set partitioning for optimum code design,” IEEE Trans. Commun., vol. 36, pp. 1013–1021, Sept. 1988.

[5] C. Schlegel and D. J. Costello, Jr., “Bandwidth efficient coding for fading channels: Code construction and performance analysis,” IEEE J.

Select. Areas Commun, vol. 7, pp. 1356–1368, Dec. 1989.

[6] J. Du, B. Vucetic, and L. Zhang, “Construction of new MPSK trellis codes for fading channels,” IEEE Trans. Commun., vol. 43, pp. 776–784, Feb./Mar./Apr. 1995.

[7] F. Gagnon and D. Haccoun, “Coding and modulation schemes for slow fading channels, ” IEEE Trans. Commun., vol. 43, pp. 858–868, Feb./Mar./Apr. 1995.

[8] E. J. Leonardo, L. Zhang, and B. Vucetic, “Multidimensional M-PSK trellis codes for fading channels,” IEEE Trans. Inform. Theory, vol. 42, pp. 1093–1108, July 1996.

[9] B. D. Jelicic and S. Roy, “Cutoff rates for coordinate interleaved QAM over Rayleigh fading channels,” IEEE Trans. Commun., vol. 44, pp. 1231–1233, Oct. 1996.

[10] S. A. Al-Semari and T. E. Fuja, “I-Q TCM: Reliable communication over the Rayleigh fading channel close to the cutoff rate,” IEEE Trans.

Inform. Theory, vol. 43, pp. 250–262, Jan. 1997.

[11] S. Rajpal, D. Rhee, and S. Lin “Multidimensional trellis coded phase modulation using a multilevel concatenation approach—Part II: Codes for the AWGN and fading channels,” IEEE Trans. Commun., vol. 45, pp. 177–186, Feb. 1997.

[12] E. Zehavi, “8-PSK trellis codes for a Rayleigh channel,” IEEE Trans.

Commun., vol. 40, pp. 873–884, May 1992.

[13] D. J. Rhee, S. Rajpal, and S. Lin “Some block- and trellis-coded modulations for the Rayleigh fading channel,” IEEE Trans. Commun., vol. 44, pp. 34–42, Jan. 1996.

[14] L. Zhang and B. Vucetic, “Multilevel block codes for Rayleigh fading channels,” IEEE Trans. Commun., vol. 43, pp. 24–31, Jan. 1995. [15] N. Seshadri and C.-E. W. Sundberg, “Multilevel trellis coded

modula-tions for the Rayleigh fading channel,” IEEE Trans. Commun., vol. 41, pp. 1300–1310, Sept. 1993.

[16] J. Wu and S. Lin, “Multilevel trellis MPSK modulation codes for the Rayleigh fading channel,” IEEE Trans. Commun., vol. 41, pp. 1311–1318, Sept. 1993.

[17] H. Imai and S. Hirakawa, “A new multilevel coding method using error correcting codes,” IEEE Trans. Inform. Theory, vol. IT-23, pp. 371–376, May 1977.

[18] M. C. Lin and S. C. Ma, “A coded modulation scheme with interblock memory,” IEEE Trans. Commun., vol. 42, pp. 911–916, Feb./Mar./Apr. 1994.

Ruey-Yi Wei was born in Miaoli, Taiwan, R.O.C., in 1971. He received the B.S. degree in electronics engineering from National Chiao Tung University, Taiwan, in 1993 and the Ph.D. degree in electrical engineering from National Taiwan University, Tai-wan, in 1998.

Since 1998, he has been with Telmax Technology Corporation, Taipei, Taiwan. His research interests are error control coding, coded modulation, nonco-herent detection, and modems.

Mao-Chao Lin was born in Taipei, Taiwan, R.O.C., on December 24, 1954. He received the B.S. and M.S. degrees in electrical engineering from Na-tional Taiwan University, Taiwan, in 1977 and 1979, respectively, and the Ph.D. degree in electrical en-gineering from the University of Hawaii, Manoa, in 1986.

From 1979 to 1982, he was an Assistant Sci-entist at the Chung-Shan Institute of Science and Technology, Lung-Tan, Taiwan. He is currently with the Department of Electrical Engineering, National Taiwan University, Taipei, as a Professor. His research interest is in the area of coding theory.