An Automatic Method for Selecting the Parameter of the Normalized Kernel Function to Support Vector Machines

An Automatic Method for Selecting the Parameter of

the Normalized Kernel Function to Support Vector Machines

CHENG-HSUAN LI1_{, HSIN-HUA HO}2_{, YU-LUNG LIU}3_{, CHIN-TENG LIN}1_, BOR-CHEN KUO+_{AND JIN-SHIUH TAUR}2

1_{Institute of Electrical Control Engineering}

National Chiao Tung University Hsinchu, 300 Taiwan

2_{Department of Electrical Engineering}

National Chung Hsing University Taichung, 402 Taiwan

3_{Department of Computer Science and Information Engineering}

Asia University Taichung, 413 Taiwan

+_{Graduate Institute of Educational Measurement and Statistics}

National Taichung University of Education Taichung, 403 Taiwan

Soft-margin support vector machine (SVM) is one of the most powerful techniques for supervised classification. However, the performances of SVMs are based on choosing the proper kernel functions or proper parameters of a kernel function. It is extremely time consuming by applying the k-fold cross-validation (CV) to choose the almost best pa-rameter. Nevertheless, the searching range and fineness of the grid method should be de-termined in advance. In this paper, an automatic method for selecting the parameter of the normalized kernel function is proposed. In the experimental results, it costs very little time than k-fold cross-validation for selecting the parameter by our proposed method. Moreover, the corresponding soft-margin SVMs can obtain more accurate or at least equal performance than the soft-margin SVMs by applying k-fold cross-validation to determine the parameters.

Keywords: soft-margin support vector machine, SVM, kernel method, optimal kernel,

normalized kernel, k-fold cross-validation

1. INTRODUCTION

In the recent years, soft-margin support vector machines (SVMs) are widely and successfully used in several remote sensing studies. In many studies, they performed more accurately than other classifiers or performed at least equally well [1-6], since soft- margin SVMs have three properties [3]:

1. They can handle large input spaces efficiently. 2. They are robust for dealing with noisy samples. 3. They can produce sparse solutions.

Received January 24, 2011; revised August 18, 2011; accepted August 30, 2011. Communicated by Irwin King.

However, the performances of soft-margin SVMs are based on choosing the proper kernel functions. For a given kernel function with some parameters, one can adjust the parameters to find different feature mappings which map samples from original space to a kernel induced feature spaces. Hence, the parameters play an important role by apply-ing the soft-margin SVM or in the kernel method. How to determine the proper parame-ters of a kernel function is an import issue. Recently, some studies use a data-dependent kernel based on some basic kernel [16], e.g., the Radial Basis Function (RBF) kernel, and use the optimization procedure to find the combination coefficients. However, it still needs to determine the basic kernel parameters, e.g., the width in RBF kernel or the de-gree of the polynomial kernel. In generally, a “grid-search” on parameters, the parame-ters of kernel functions and the penalty parameter C which controls the magnitudes of the slack variables, of soft-margin SVMs with the k-fold cross-validation (CV) is used for choosing the parameters and prevents the over fitting problem [6, 7]. Nevertheless, it is time consuming. Furthermore, before doing a grid-search, a better region and fineness on the grid should be pre-determined.

In this paper, we will propose an automatic method for selecting the parameters of the normalized kernel function such as the RBF kernel function. The experimental results indicate that the searching efficiency is much improved and the corresponding perform-ance is almost as good as the soft-margin SVM with the k-fold cross-validation.

The rest of the paper is organized as follows. The reviews of kernel method and SVM are introduced in section 2. The proposed search method will be introduced in sec-tion 3. The experiments on hyperspectral image data sets and UCI data sets are designed to evaluate the performances of the proposed method in section 4 and the experimental results are also reported in this section. Section 5 contains comments and conclusions.

2. REVIEWS OF KERNEL METHOD AND SOFT-MARGIN SUPPORT VECTOR MACHINES

2.1 Kernel Method

It is easier for classification if pixels are more sparsely distributed. Generally speak-ing, samples with high dimensionality, the number of spectral bands, potentially have better class separability. The strategy of kernel method is to embed the data from original space Rd _{into a feature space H, a Hilbert space with higher dimensionality, where more}

effective hyperplanes for classification are expected to exist in this space than in the original space. From this, we can compute the inner product of samples in the feature space directly from the original data items using a kernel function. This is based on the fact that any kernel function κ: Rd _{× R}d _{→ R satisfying the characterization of kernels [1],}

can be stated formally in the following theorem:

Theorem 1 Characterization of kernels. A function κ: Rd _{× R}d _{→ R which is either}

continuous or has a finite domain, can be decomposed κ(x, z) = <φ(x), φ(z)>, where x, z ∈ Rd_,

into a feature map φ into a Hilbert space H applied to both its arguments followed by the evaluation of the inner product in H if and only if it is a symmetric function for which the matrices K = [κ(xi, xj)]1≤i,j≤N formed by restriction to any finite subset {x1, …, xN} of

the space Rd _{are positive semi-definite, i.e., having no negative eigenvalues.}

The following are some popular kernels. • Linear kernel:

κ(x, z) = <x, z>, (1)

• Polynomial kernel:

κ(x, z, r) = (<x, z> + 1)r_{, r ∈ Z}+_{, (2)}

• Gaussian Radial Basis Function kernel (RBF kernel): 2 2 ( , , ) exp , (0, ), 2 x z x z κ σ σ σ ⎛ ₋ ⎞ ⎜ ⎟ = − ∈ ∞ ⎜ ⎟ ⎝ ⎠ (3) where x and z are the samples in Rd_{. Moreover, r and σ are the parameters which should}

be pre-determined of polynomial kernel and RBF kernel, respectively.

It is worth stressing here that the size of the kernel matrix is N × N and contains in each position Kij the information of distance among all possible pixel pairs (xi and xj)

measured with a suitable kernel function κ fulfilling the characterization of kernels and if we use the linear kernel, then the feature mapping φ is an identity map, that is, φ is linear. Otherwise, the feature mapping can be nonlinear. One important idea for using kernel method is without knowing the nonlinear mapping explicitly [15].

2.2 Normalized Kernel Function Kernel

In this paper, a normalized kernel function [1] is used. Given a based kernel func-tion κ, e.g., the RBF kernel or the polynomial kernel, with a parameter β, the corre-sponding normalized kernel is defined as

( , , ) ( , , ) . ( , , ) ( , , ) x z x z x x z z κ β κ β κ β κ β = (4)

One can observe that RBF kernel is a good example of a normalized kernel with a parameter β which is equal to σ, the width in the RBF kernel. Moreover, the norms of samples in the feature space are all one, since ( , , ) 1κ x x β = for all x ∈ Rd_{. This means}

that the samples in the feature space are on the surface of a hypersphere. Therefore, the magnitudes of distances of samples in H are of the same order of magnitudes of the an-gles of samples in H, and the similarity, the cosine values of anan-gles between samples can be determined by the normalized kernel function value. Furthermore, different value of the parameter β indicates that different corresponding mapping φ, and, hence, the

corre-sponding feature space H is also adopted. Based on this property, we propose an auto-matic method for determining which value of the parameter β is the best for discrimina-tion.

2.3 Soft-Margin Support Vector Machines

Soft-margin SVM is to find a hyperplane in the feature space, a Hilbert space H, in the middle of the most separated margins between two classes, and this hyperplane can be applied for classifying the new testing samples [1-7]. Let {xi}Ni=1 and {yi}Ni=1 be a set

of training samples and the corresponding label set, respectively. The soft-margin SVM algorithm is performed by the following constrained minimization optimal problem:

, ₁ 1 min , 2 i N T i wξ w w C+

∑

where w is a vector normal to the hyperplane in H, b is a constant such that b/||w|| repre-sents the distance of hyperplane from the origin, ξi’s are slack variables to control the

training errors, and C ∈ R+ _{− {0} is a penalty parameter that permits to tune the}

gener-alization capability.

In general, an equivalent dual representation by using the Lagrange optimization is used to find the optimizer. The corresponding dual Lagrange function is defined as:

1 1 1 1 max ( , ), 2 i N N N i i j i j i j i i j y y x x α

∑

∑∑

∑

Once αi are determined, any new test pattern z ∈ Rd is associated with a forecasting

label yz, 1 = sgn(N ( , ) + ) z i i i i y yα κ x z b =

∑

where b is chosen so that

1 ( , ) 1, N j i i i j i y yα κ x x b − ⎛ ⎞ + = ⎜ ⎟ ⎝

∑

for any xj with 0 < αj < C.

There are two parameters, β and C, for soft-margin SVMs with the normalized ker-nel function. Which are the best for a given problem is unknown beforehand. To identify good β and C so that the classifier can accurately predict unknown samples is the main goal. A “grid-search” on β and C of soft-margin SVMs with the k-fold cross-validation (CV) is often used and prevents the overfitting problem [6, 7]. However, this approach is extremely time-consuming, especially for the large training data set situation or the high-

dimensional dataset situation. Moreover, the range and fineness of the grid could also affect the quality of the selected parameter value. Hence, in the next section, an auto- matic way for determining the value of β is proposed for solving this parameter selection problem.

3. PROPOSED METHOD: AUTOMATIC PARAMETER SELECTION METHOD

Suppose Ωi is the set of training samples in class i, i = 1, 2, …, L. There are two

important properties of the normalized kernel function: (1) κ( , , ) 1,x x_{i i} β = ∀i = 1, …, n,

i.e., the norm of every sample in the feature space is 1, and (2) − 1 ≤ κ( , , ) 1x x_{i j} β ≤ , ∀i, j = 1, …, n, i.e., the cosine value of two training samples xi and xj in the feature space can

be computed by κ( ,x x_{i j}, )β and it determines the similarity between these two samples. Based on the above two observations and the concepts, two properties are desired and described as follows: (1) The samples in the same class should be mapped into the same area in the feature space and (2) the samples in the different classes should be mapped into the different areas. We want to find a proper parameter β such that

(1) κ( , , )x z β ≈ 1, if x, z ∈ Ωi, i = 1, …, L and

(2) κ( , , )x z β ≈ − 1, if x ∈ Ωi, z = Ωj, i ≠ j.

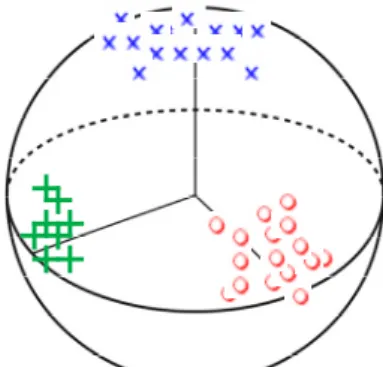
We use RBF kernel to illustrate these properties. If the parameter σ is close to 0, then the corresponding kernel function values are all close to 0, the lower bound of the RBF kernel function. This means that all samples in a feature space are all approximately mutually perpendicular. When σ increases, the values of the RBF kernel function with respect to the samples which are closer by applying the Euclidean distance in the original space increase fast. As σ is close to infinity, the corresponding kernel function values are all close to 1. So the samples in the feature space are close to a fixed point. Fig. 1 shows the image of the ideal distribution in the ideal feature space.

Fig. 1. The ideal distribution in the desirous feature space.

the mean of values applied by the normal kernel function on the samples in the same class: 2 1 1 1 ( ) ( , , ), i i L L i x z i i x z ω β κ β = ∈Ω ∈Ω = = Ω

∑ ∑ ∑

∑

where |Ωi| is the number of training samples in class i. The parameter β should be

deter-mined such that ω(β) closes to 1. Second one is the mean of values applied by the nor-malized kernel function on the samples in the different classes:

1 1 1 1 1 ( ) ( , , ).

| | | |

∑∑ ∑ ∑

∑ ∑

So β should be determined also such that b(β) closes to − 1. Hence, the optimal β * _{can be}

obtained by solving the following optimization problem:

min ( ) (1J ( )) (1 b( )) 2 ( ) b( ).

β β ≡ −ω β + + β = −ω β + β (11)

The time complexity for computing J(β) is O(N 2_{d) which depends on the number of}

training samples N and the dimensionality d.

Note that if κ( , , )x z β is differentiable, e.g., the based kernel is RBF kernel

func-tion, with respect to β, the gradient descent method [10],

1= ( ), > 0, 1, 2,

n n n J n n n

β ₊ β − ∇γ β γ = … (12)

is used to solve the proposed optimization problem, where

( _n) ( _n) ( _n), J β b β ω β β β ∂ ∂ ∇ = − ∂ ∂ (13)

and γn is the step size at the nth iteration.

Otherwise, if the parameter β is discrete, e.g., the based kernel is polynomial kernel, then we can find the best β * _{such that}

*_{= arg min{ ( )J = 1, 2, , }s} β

β β β … (14)

where s is an integer and should be pre-determined.

The general steps of the proposed method to the soft-margin SVM can be listed as follows.

Step 1: Find the best parameter β * _{such that}

min ( ) (1J ( )) (1 b( )) 2 ( ) b( ).

Step 2: Use the k-fold cross-validation (CV) to find the proper parameter C of the soft-

margin SVM by applying the normalized kernel function ( , , )κ x x β with β*.

4. EXPERIMENTS

In this section, the experiments in order to investigate the multiclass classification performances of the soft-margin SVMs with the normalized kernel function by applying our proposed method (OP) and the selected parameters the 5-fold cross-validation (CV) in experiments 1 and 2. Both the parameters C by applying OP and CV to the soft-margin SVMs should still be selected via 5-fold cross-validation. The polynomial kernel func-tion and the RBF kernel funcfunc-tion are used for as the based kernels. This study employs two measures of classification accuracy to investigate classifier performance: (1) overall classification accuracy (the percentage of the correctly classified samples for all classes) and (2) overall kappa coefficient (the percentage of the kappa coefficient for all classes).

4.1 Experiment 1

Two real data sets are applied to compare the performances in the experiment 1. They are the Indian Pine Site image, a mixed forest/agricultural site in Indiana, and the Washington, DC Mall hyperspectral image [11] as an urban site. The first one of these data sets was gathered by a sensor known as the Airborne Visible/Infrared Imaging Spec-trometer (AVIRIS). The Indian Pine Site image, mounted from an aircraft flown at 65000 ft altitude and operated by the NASA/Jet Propulsion Laboratory, with the size of 145 × 145 pixels has 220 spectral bands measuring approximately 20 m across on the ground. Since the size of samples in some classes are too small to retain enough disjoint samples for training and testing, only eight classes, Cornmin, Corn-notill, Soybean-clean, Grass/ Pasture, Soybeans-min, Hay-windrowed, Soybeans-notill, and Woods, were selected for the experiments.

The other dataset, Washington, DC Mall from an urban area, is a Hyperspectral Digital Imagery Collection Experiment airborne hyperspectral data flight line over the Washington, DC Mall. Two hundred and ten bands were collected in the 0.4-2.4 m re-gion of the visible and infrared spectrum. Some water-absorption channels are discarded, resulting in 191 channels [11]. There are seven information classes, roofs, roads, trails, grass, trees, water, and shadows, in the data set.

In this experiment, for investigating the influences of training sample sizes to the dimension, three distinct cases, |Ωi| = 20 < n < d (case 1), |Ωi| = 40 < d < n (case 2), and d

< |Ωi| = 300 < n (case 3), will be discussed. The case 1 is a so called ill-posed

classifica-tion situaclassifica-tion, which means data dimensionality exceeds the total number of independent training samples in every class. Moreover, the case 2 is a so called poorly-posed classi-fication situation, which means data dimensionality is greater than or comparable to the number of (independent) per-class representative training samples, but smaller than the total number of representative samples. In case 3, there are enough independent training samples. The MultiSpec [11] was used to select training and testing samples. In the In-dian Pine Site dataset, all samples in the image are used as the testing samples to compute the validation measures, overall accuracies and overall kappa accuracies. In the

Wash-ington, DC Mall dataset, 100 testing samples per class, in our experiments which is the same method in [11-13].

If the RBF kernel is the based kernel, then the best β by applying CV is found in the given sets {27_{, 2}8_{, …, 2}16_{} and {2}15_{, 2}16_{, …, 2}24_{} in Indian Pine Site and Washington, DC}

Mall data sets, respectively. The parameters C by applying OP and CV in these two data sets should be selected on the set {20_{, 2}1_{, …, 2}15_{}. If polynomial kernel is the based}

ker-nel, then the best β by applying CV is found in the given set {1, 2, …, 32}.

The shape of the function J(β) by using the Indian Pine Site dataset and the RBF kernel as the based kernel in case 1 is shown in Fig. 2. The horizontal and vertical axes are the values of the parameter β and the corresponding J(β), respectively. This graph indicates that J(β) has only one minimum value which is the desired selected value of σ in the proposed method. Fig. 3 shows the accuracies and kappa accuracies of testing samples and all samples in the Indian Pine Site Image at different β by applying soft- margin SVMs with a fixed C in case 1.

0 2000 4000 6000 8000 10000 12000 14000 16000 18000 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 β J( β ) β vs. J(β)

Fig. 2. The optimizer locates in the range [3500, 4000].

β β

β β

Fig. 3. There are accuracies and kappa accuracies of testing samples and all samples in the Indian Pine Site Image at different β by applying soft-margin SVMs with a fixed C in the case 1. The near optimal performances occur in the rage [3500, 4500].

One can note that the minimum of J(β) in Fig. 2 locates in the range [3500, 4000] and the near optimal overall and kappa accuracies of testing samples and all samples in the Indian Pine Site Image by applying SVMs with a fixed C occur in the rage [3500, 4500]. These two figures show that the proposed method obtains a proper parameter which the overall classification accuracy and kappa accuracy are near the best.

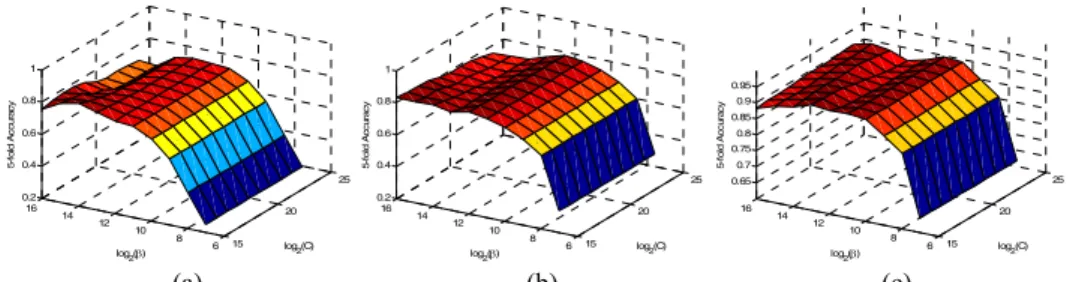
Moreover, Fig. 4 shows the 5-fold accuracies of training samples in three cases. The more are training samples, the smoother are the surfaces. Moreover, Fig. 5 shows the “β versus J(β)” in three cases. The optimizers (also in the range [3500, 4000]) are similar among three cases. However, the optimizers obtained from k-fold cross-validation (Fig. 4) are very different among three cases, since it depends on the random partitions. Hence, the proposed method could find a more suitable parameter than k-fold cross-validation, especially in the small sample size. From Fig. 4, we observe that the tendency near the optimizer is similar in every case. Therefore, it is reasonable to seek the optimal parame-ter β and then seek the parameparame-ter C which is following [16].

15 20 25 6 8 10 12 14 16 0.2 0.4 0.6 0.8 1 log_2(C) log₂₍β) 5-fo ld A ccu ra cy 15 20 25 6 8 10 12 14 16 0.2 0.4 0.6 0.8 1 log_2(C) log₂₍β) 5-fo ld A ccu ra cy 15 20 25 6 8 10 12 14 16 0.65 0.7 0.75 0.8 0.85 0.9 0.95 log_2(C) log₂₍β) 5-fo ld A cc ur ac y (a) (b) (c)

Fig. 4. (a), (b), and (c) are the 5-fold accuracies of training samples in cases 1, 2, and 3, respectively.

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 β J( β) β vs. J(β) 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 β J( β) β vs. J(β) 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 β J( β) β vs. J(β) (a) (b) (c) Fig. 5. (a), (b), and (c) are the “β versus J(β)” in cases 1, 2, and 3, respectively.

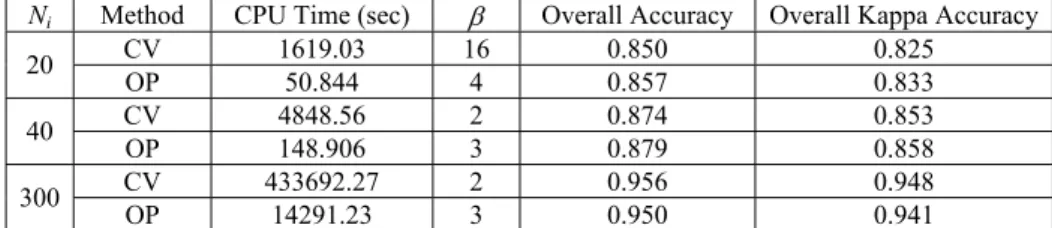
Tables 1 and 2 are the overall and kappa accuracies in Indian Pine Site dataset and Washington, DC dataset by applying RBF kernel as the based kernel function, respec-tively. Tables 3 and 4 are the overall and kappa accuracies in Indian Pine Site dataset and Washington, DC dataset by applying polynomial kernel as the based kernel function, re-spectively. One can find that the cost of time for proposed method is much less than the 5-fold cross-validation on both two datasets. Moreover, the classification results show that the soft-margin SVMs by using OP to find the parameter can obtain more accurate in the small sample size. By the way, the optimal values by OP in three cases are similar. So we can use small number of samples to approximate the optimal value.

Table 1. Overall and kappa accuracies in the Indian Pine Site dataset (the based kernel is the RBF kernel).

Ni Method CPU Time (sec) β Overall Accuracy Overall Kappa Accuracy

CV 197.50 8192 0.749 0.712 20 OP 21.22 3622.80 0.768 0.733 CV 531.25 8192 0.811 0.781 40 OP 58.78 3615.36 0.831 0.804 CV 22859.95 4096 0.928 0.915 300 OP 2416.61 3795.66 0.928 0.916

Table 2. Overall and kappa accuracies in the Washington, DC Mall dataset (the based kernel is the RBF kernel).

Ni Method CPU Time (sec) β Overall Accuracy Overall Kappa Accuracy

CV 91.56 524288 0.826 0.80 20 _{OP 9.91 178600.96 0.844 0.82} CV 249.64 131072 0.886 0.87 40 _{OP 27.91 177898.80 0.881 0.86} CV 14191.69 2097152 0.961 0.96 300 _{OP 1474.45 182370.06 0.951 0.94}

Table 3. Overall and kappa accuracies in the Indian Pine Site dataset (the based kernel is the polynomial kernel).

Ni Method CPU Time (sec) β Overall Accuracy Overall Kappa Accuracy

CV 1020.14 31 0.753 0.716 20 _{OP 42.20 32 0.754 0.717} CV 4138.03 32 0.806 0.777 40 OP 170.66 32 0.806 0.777 CV 295986.27 32 0.918 0.904 300 OP 12159.09 32 0.918 0.904

Table 4. Overall and kappa accuracies in the Washington, DC Mall dataset (the based kernel is the polynomial kernel).

Ni Method CPU Time (sec) β Overall Accuracy Overall Kappa Accuracy

CV 1619.03 16 0.850 0.825 20 OP 50.844 4 0.857 0.833 CV 4848.56 2 0.874 0.853 40 OP 148.906 3 0.879 0.858 CV 433692.27 2 0.956 0.948 300 OP 14291.23 3 0.950 0.941

After comparing Tables 1-4, we can find that, in some case, the performance by us-ing the polynomial kernel as the based kernel is better than by usus-ing the RBF kernel as the based kernel. For example, in Table 4, the overall accuracy of the Washington, DC Mall dataset with OP in case 1 is 0.857. But the overall accuracy of the Washington, DC Mall dataset with OP in case 1 in Table 2 is 0.844. Hence, in upcoming research, we can extend our proposed method based on the composite kernel, i.e., a combination of the

RBF kernels and the polynomial kernels, to combine the advantages of these two basic kernel functions for classification.

4.2 Experiment 2

The four real data sets, “Ionosphere,” “Monk1,” “Pima,” and “Iris” are described in Table 5. These data sets are available from the FTP server of the UCI [23] data reposi-tory. Similar to the experiment 1, the RBF kernel and the polynomial kernel are used as the based kernels. The grid-search ranges by applying CV method are also showed in Table 5. The columns β = σ and β = γ indicate the based kernel functions are the RBF kernel and the polynomial kernel, respectively. Again, the parameters C by applying OP and CV in these data sets should be selected on the sets which show in the last column of Table 5.

Table 5. Descriptions of three real data sets and the corresponding sets for CV (# of FEs means the number of features).

Dataset Classes # of Samples # of FEs β = σ β = γ C

Ionosphere 2 351 34 {2−5, 2−4, …, 214_{} {1, 2, …, 7} {2}−30_{, 2}−29_{, …, 2}30_} Monk1 2 432 6 {2−3, 2−2, …, 25_{} {1, 2, …, 30} {2}0_{, 2}1_{, …, 2}10_}

Pima 2 768 8 {2−8, 2−7, …, 28_{} {1, 2, …, 26} {2}0_{, 2}1_{, …, 2}10_} Iris 3 150 4 {2−8, 2−7, …, 210_{} {1, 2, …, 100} {2}0_{, 2}1_{, …, 2}20_} Table 6. Overall and kappa accuracies in UCI data sets (the based kernel is the RBF

kernel).

Dataset Method CPU Time (sec) β Overall Accuracy Overall Kappa Accuracy

CV 32.22 2 0.980 0.931 Ionosphere OP 2.53 1.94 0.980 0.931 CV 11.81 1 0.884 0.769 Monk1 OP 1.48 1.66 0.894 0.787 CV 318.88 128 0.755 0.489 Pima OP 25.02 73.83 0.786 0.557 CV 34.80 0.5 0.973 0.960 Iris OP 2.48 1.45 0.987 0.980

Table 7. Overall and kappa accuracies in UCI data sets (the based kernel is the polyno-mial kernel).

Dataset Method CPU Time (sec) β Overall Accuracy Overall Kappa Accuracy

CV 95.83 7 0.960 0.869 Ionosphere OP 13.46 3 0.980 0.931 CV 60.56 22 0.857 0.713 Monk1 OP 1.90 11 0.887 0.773 CV 2159.78 2 0.734 0.454 Pima OP 65.86 5 0.729 0.439 CV 556.02 11 0.987 0.980 Iris OP 5.69 51 0.987 0.980

From Tables 6 and 7, the proposed method OP spends much less time than CV. Moreover, the accuracies by applying OP are higher than or similar to the accuracies by applying CV.

5. CONCLUSION

In this paper, an automatic method for selecting the parameter of the normalized kernel was proposed, and we have compared it and the k-fold cross-validation experi-mentally. The experiments of two hyperspectral images and four UCI data sets show that the time cost of the proposed method is much less than the k-fold cross-validation. How-ever, the classification performance by applying the soft-margin SVM with our proposed method is higher than or similar to that with the k-fold cross-validation. Furthermore, we will try to develop the framework to other kernel functions and apply the proposed method to kernel-based feature extraction methods, e.g., generalized discriminant analy-sis [14] and kernel nonparametric weighted feature extraction [15].

ACKNOWLEDGMENT

The authors would like to thank Prof. Landgrebe for providing the Indian Pine Site and the Washington DC Mall data sets.

REFERENCES

1. S. T. John and C. Nello, Kernel Methods for Pattern Analysis, Cambridge University Press, Cambridge, 2004.

2. F. Melgani and L. Bruzzone, “Classification of hyperspectral remote sensing images with support vector machines,” IEEE Transactions on Geoscience and Remote Sen-

sing, Vol. 42, 2004, pp. 1778-1790.

3. G. Camps-Valls and L. Bruzzone, “Kernel-based methods for hyperspectral image classification,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 43, 2005, pp. 1351-1362.

4. G. Camps-Valls, L. Gomez-Chova, J. Munoz-Mari, J. L. Rojo-Alvarez, and M. Mar-tinez-Ramon, “Kernel-based framework for multitemporal and multisource remote sensing data classification and change detection,” IEEE Transactions on Geoscience

and Remote Sensing, Vol. 46, 2008, pp. 1822-1835.

5. G. Camps-Valls and L. Bruzzone, Kernel Methods for Remote Sensing Data

Analy-sis, John Wiley and Sons, Ltd., London, 2009.

6. G. Camps-Valls, L. Gómez-Chova, J. Calpe, E. Soria, J. D. Martín, L. Alonso, and J. Moreno, “Robust support vector method for hyperspectral data classification and knowledge discovery,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 42, 2004, pp. 1530-1542.

7. C. C. Chang and C. J. Lin, “LIBSVM: A library for support vector machines,” 2001, http://www.csie.ntu.edu.tw/~cjlin/libsvm.

em-pirical feature space,” IEEE Transactions on Neural Networks, Vol. 16, 2005, pp. 460-474.

9. B. Chen, H. Liu, and Z. Bao, “Optimizing the data-dependent kernel under a unified kernel optimization framework,” Pattern Recognition, Vol. 41, 2007, pp. 2107-2119. 10. E. K. P. Chong and S. H. Zak, An Introduction to Optimization, 3rd ed., John Wiley

and Sons, Inc., New York, 2008.

11. D. A. Landgrebe, Signal Theory Methods in Multispectral Remote Sensing, Wiley, Hoboken, New Jersey, 2003.

12. J. A. Benediktsson, J. A. Palmason, and J. R. Sveinsson, “Classification of hyper-spectral data from urban areas based on extended morphological profiles,” IEEE

Transactions on Geoscience and Remote Sensing, Vol. 43, 2005, pp. 480-491.

13. B. S. Sebastiano and M. Gabriele, “Extraction of spectral channels from hyperspec-tral images for classification purposes,” IEEE Transactions on Geoscience and

Re-mote Sensing, Vol. 45, 2007, pp. 484-495.

14. G. Baudat and F. Anouar, “Generalized discriminant analysis using a kernel ap-proach,” Neural Computation, Vol. 12, 2000, pp. 2385-2404.

15. B. C. Kuo, C. H. Li, and J. M. Yang, “Kernel nonparametric weighted feature ex-traction for hyperspectral image classification,” IEEE Transactions on Geoscience

and Remote Sensing, Vol. 47, 2009, pp. 1139-1155.

16. K. P. Wu and S. D. Wang, “Choosing the kernel parameters for support vector ma-chines by theinter-cluster,” Pattern Recognition, Vol. 42, 2009, pp. 710-717.

Cheng-Hsuan Li (李政軒) received the B.S. and M.S.

de-grees from National Chung Hsing University, Taichung, Taiwan, in 2001 and 2003, respectively. He is currently working toward the Ph.D. degree in Institute of Electrical Control Engineering, National Chiao Tung University, Hsinchu, Taiwan. He is cur-rently a research assistant with the Graduate Institute of Educa-tional Measurement and Statistics, NaEduca-tional Taichung University of Education, Taichung. His research interests include pattern recognition and machine learning.

Hsin-Hua Ho (何省華) received the B.S. degree from

Na-tional Chung Hsing University, Taichung, Taiwan, in 2002, and the M.S. degree from National Taichung University of Educa-tion, Taichung, Taiwan in 2006. He is currently working toward the Ph.D. degree in Department of Electrical Engineer, National Chung Hsing University, Taichung, Taiwan. Her research in-terests include pattern recognition and machine learning.

Yu-Lung Liu (劉育隆) received the B.S. degrees from St.

John’s University, Taipei Campus, Taiwan, in 2005, and M.S. degree from School of Graduate Institute of Educational Meas-urement and Statistics, National Taichung University, in 2007. He is currently a Ph.D. candidate in the Computer Science and Information Engineering at the Asia University, Taiwan. His re-search interests are computerized adaptive testing, control item- exposure, U-learning, Bayesian network and machine learning.

Chin-Teng Lin (林進燈) received the B.S. degree from the National Chiao Tung University (NCTU), Hsinchu, Taiwan, in 1986, and the Ph.D. degree in Electrical Engineering from Purdue University, West Lafayette, IN, in 1992. He is currently the Chair Professor of Electrical and Computer Engineering at NCTU. His research interests include biologically inspired information sys-tems. He has authored or coauthored more than 120 journal pa-pers in the areas of neural networks, fuzzy systems, multimedia hardware/software, and cognitive neuroengineering, including ap-proximately 74 IEEE journal papers.

Bor-Chen Kuo (郭伯臣) received the B.S. degree in Mathe- matics Education and the M.S. degree in Statistics and Assess-ment from National Taichung Teachers College, Taichung, Tai-wan, in 1993 and 1996, respectively, and the Ph.D. degree in Electrical Engineering from Purdue University, West Lafayette, IN, in 2001. From 2002 to 2005, he was an Associate Professor with National Taichung University of Education, Taichung, where he is currently a Professor and the Director of the Graduate Insti-tute of Educational Measurement and Statistics. His research in-terests include pattern recognition, feature extraction and classi-fication of high-dimensional data, computerized adaptive testing, and nonparametric functional estimation. Dr. Kuo is a member of the Chinese Association of Psychological Testing AdCom and the Editor of the Journal of Educational Measurement and Statistics, Taiwan. He was the recipient of an Outstanding and Excellence Research Award from the Taiwan Education and Research Society in 2009.

Jin-Shiuh Taur (陶金旭) received the B.S. and M.S. degrees

in Electrical Engineering from the National Taiwan University, Taipei, Taiwan, in 1987 and 1989, respectively, and the Ph.D. de-gree in Electrical Engineering from Princeton University, Prince-ton, NJ, in 1993. He was a member of the Technical Staff with Siemens Corporate Research, Inc. He is currently a Professor with the National Chung Hsing University, Taichung, Taiwan. His re-search interests include neural networks, pattern recognition, computer vision, and fuzzy-logic systems. Dr. Taur was the reci- pient of the 1996 IEEE Signal Processing Society’s Best Paper Award.