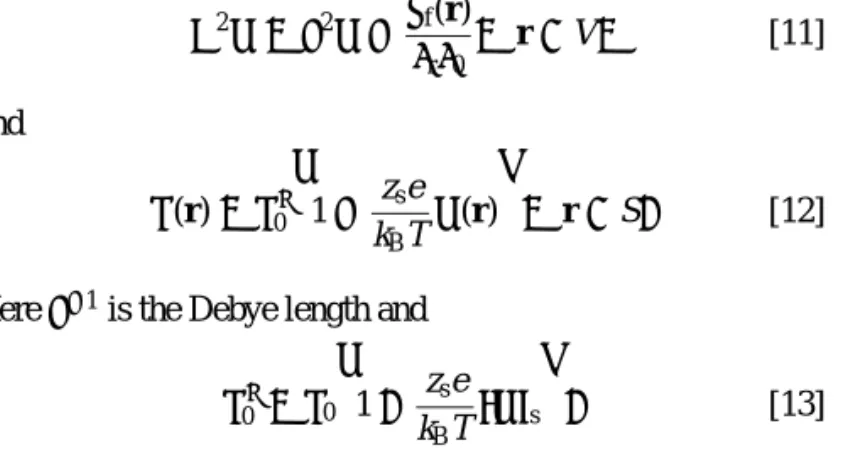The Electrostatic Interaction of a Charged Particle with a Surface:
The Effect of Surface Charge Rearrangement
Heng-Kwong Tsao∗,1and Yu-Jane Sheng†
∗Department of Chemical Engineering, National Central University, Chung-li, Taiwan 320, Republic of China; and †Department
of Chemical Engineering, National Taiwan University, Taipei, Taiwan 106, Republic of China
Received June 5, 2000; accepted September 28, 2000
In this paper we investigate the electric interaction between a charged particle and a surface in which the charged ions are capa-ble of moving in response to the electric potential disturbance caused by the approach of the charged particle. Such surfaces include ionic surfactants distributed in air-water interface and charged lipids in bilayer membranes. On the basis of the mean field theory, the free energy of the system, which includes the electrostatic internal energy and the entropy of the mobile ions and surface ions, can be written down. The surface charge-potential relation is then de-rived by the calculus of variation. When the potential disturbance is small enough, a linear charge regulation model is obtained. The interaction energy associated with a long rod parallel to the inter-face is studied and an analytical expression is obtained. When a rod approaches an oppositely charged surface, the interaction can change from attraction to repulsion, depending on the ratio of the characteristic regulation length to the Debye length. At low surface charge density, the surface behaves as under the condition of con-stant charge density and acts as that of concon-stant potential for high enough charge density. °C2001 Academic Press
Key Words: free energy; Poisson-Boltzman equation; surface ions
rearrangement; charge regulation.
1. INTRODUCTION
The electrostatic interactions between a charged particle and a charged surface have been an important subject of both experi-mental and theoretical investigations due to their practical appli-cations in a variety of fields, such as protein adsorption and the adhesion of DNA to substrates. Kaplan et al. have investigated the interaction between a charged sphere and a charged planar wall under condition of constant surface potential (1, 2). When both surfaces are maintained at constant surface charge density, Stahlberg et al. calculated the electrostatic interaction energy by solving the linearized Poisson-Boltzmann equation (3). For an ion-penetrable sphere interacting with an ion-impenetrable plate, an exact expression of the electrostatic interaction energy has been given by Ohshima and Kondo for both the constant surface potential and the constant surface charge density cases (4).
1To whom correspondence should be addressed.
Nonspherical colloidal particles are also plentiful in nature and industrial applications. A large class of macromolecules, which are not flexible, is assumed to have a rod-like shape. For instance, some polynucleotides or polypeptides form a helix structure that can be considered as a rigid rod. Recently, appli-cations involving DNA strands and charged surfaces, such as prokaryotic DNA replication, to gene therapy, and even DNA chip technology, have raised an interest in understanding the interactions between charged rods and charged surfaces. In con-trast to spherical particles, little attention has been focused on the electrostatic interactions of nonspherical particles with a charged surface (5–7).
When a charged particle approaches a charged surface, the plane may maintain constant surface potential or constant sur-face charge density during interactions (8). In between these two limits, the surface charge density can be regulated by the dissoci-ation of the counterions, i.e., the potential determining ions. The electric field distrubance due to the approach of the charged par-ticle influences the local degree of dissociation on the interface and therefore alters the surface charge distribution. Although the charges on a solid plane often originate from dissociation of counterions or adsorption of ions, some charged surfaces, such as air-water interfaces and biomembranes, contain the surface ions that are mobile in the two-dimensional plane. For such sur-faces, consequently, the approach of a charged particle can also induce the redistribution of charges at the interface. The total charges at the surface, however, are still maintained the same.
The calculation of the double-layer interaction between a charged particle and a charged surface is a problem of con-siderable intricacy. Though theoretical progress has been made by the statistical mechanical theories, such as Brownian dy-namics simulations (6, 7), the mean-field descriptions, such as the Poisson-Boltzmann equation (5), are also useful tools be-cause of their concise forms. For a surface capable of charge regulation, the latter approach is particularly advantageous. In conventional charge-regulation models, such as the two-site dis-sociation model, the charge-potential relations can be obtained directly from the law of mass action (9–12). However, for a sur-face in which the charges can rearrange themselves, the sursur-face charge-potential relation is not known and must be determined by minimization of the free energy of the system.
124 0021-9797/01 $35.00
Copyright°C2001 by Academic Press All rights of reproduction in any form reserved.
In this paper, we consider a surface in which the charged ions are capable of moving in response to the electric potential dis-turbance due to the approach of a charged particle. On the basis of the mean-field description, we write down the free energy of the system, which contains the electrostatic internal energy, the bulk entropy of the mobile ions, and the two-dimensional en-tropy of the surface ions. The Poisson-Boltzmann equation and the surface charge-potential relation are then derived through minimization of the free energy by the calculus of variation. The electrostatic interactions of a long rod with a surface are then considered under the Debye-H¨uckel approximation.
2. FREE ENERGY AND CHARGE REGULATION A system consists of charged ion-impenetrable surfaces (S) and charged particles immersed in z+: z−electrolyte solutions (V ). The charges on the particles are regarded as fixed charges. When the charged particle approaches the surface, the surface ions can move and rearrange themselves in response to the elec-tric potential disturbance.
The free energy of the system F contains the electrostatic internal energy contribution Ueland the entropic contribution −T Sel,
F = Uel− T Sel. [1]
Within the mean-field approximation, the total free energy can be expressed in terms of the local electric potentialψ(r), the concentrations of the mobile ions c±(r), the distribution of fixed chargesρf(r), and the surface charge densityσ (r). Assume that the electrolyte is a dilute, ideal solution with uniform dielectric properties. In addition, the surface ions also behave ideally. As a result, Uel= − εrε0 2 Z V |∇ψ|2dr3+ Z V [z+ec+(r)+ z−ec−(r) + ρf(r)]ψ(r) dr3+ Z S σ(r)ψ(r) dr2, [2] and −T Sel= kBT Z V {c+[ln(c+v0)− 1] + c−[ln(c−v0)− 1]} dr3 + kBT Z S σ zse · ln µ σ zse a0 ¶ − 1 ¸ dr2, [3]
wherev0and a0are the volume per mobile ion and the area per charged molecule composing the surface.εrandε0are, respec-tively, the relative permittivity of the electrolyte solutions and the permittivity of a vacuum. kBT denotes the thermal energy, e is the electron charge, and zsis the valency of surface ions. The first term in Eq. [2] is the self-energy of the electic field (13). The next two terms are the electrostatic energy associated with the mobile ions and fixed charges in V and surface ions at S. In
Eq. [3] the first term represents the entropies of the mobile ions, whereas the second term is the entropy associated with the ions at the surfaces.
The thermodynamic equilibrium state corresponds to the min-imum of the total free energy subject to the constraints of elec-troneutrality in the system and the conservation of surface ions. That is, Z V (z+c++ z−c−)e dr3+ Z S σ dr2 = 0, [4] and Z S σ(r) dr2= σ0 Z S dr2. [5]
Using the method of Lagrangian multiplier, the variation of the total free energy with respect toψ, c±, and σ yields a set of equations which describe the equilibrium state of the system.
δF/δψ = 0 gives Z V [εrε0∇2ψ + z+ec++ z−ec−+ ρf] dr3 + Z S [σ + εrε0∇ψ · n] dr2= 0.
The Poisson equation and the boundary condition at S are then obtained,
∇2ψ = −z+ec+(r)+ z−ec−(r)+ ρf(r)
εrε0 , r ∈ V, [6]
εrε0∇ψ · n = −σ(r), r ∈ S. [7]
δF/δc± = 0 produces the Boltzmann distribution, c±= cbexp · −z±e kBT ψ(r) ¸ , r ∈ V. [8]
The surface charge distribution due to surface ions rearrange-ment follows the conditionδF/δσ = 0. The Lagrangian multi-plier can be evaluated by Eq. [5] and the result is also Boltzmann-like, σ (r) = σ0 exp£−zse kBTψ ¤® s exp · −zse kBT ψ(r) ¸ , r ∈ S, [9]
where cb is the bulk concentration of the mobile ions andh·i denotes the area average at S,
hAi = R S A(r) dr 2 R Sdr 2 . [10]
In the Debye-H¨uckel limit, Eqs. [8] and [9] can be linearized. As a result, we are left with the linearized Poisson-Boltzmann
equation and the linearized surface charge-potential relation, ∇2ψ = κ2ψ −ρf(r) εrε0 , r ∈ V, [11] and σ(r) = σ∗ 0 · 1− zse kBT ψ(r) ¸ , r ∈ S. [12] Hereκ−1is the Debye length and
σ∗ 0 = σ0 · 1+ zse kBThψis ¸ . [13]
After obtaining the electric field,σ0∗andhψiscan be determined in a self-consistent way. If the surface area is large compared to the charged particle,hψisis weakly dependent on the distance between the charged particle and the charged plane. Note that in order to fulfill the conditionσ (r)/σ0> 0 everywhere, as illus-trated in Eq. [9], zsehψis/kBT > −1. Equation [12] indicates that the behavior of the surface is similar to that of a surface ca-pable of linear charge regulation due to counterion dissociation. Now we return to the free energy calculation. Using the di-vergence theorem and Eq. [8], Uelin Eq. [2] can be simplified furthermore. Uel= 1 2 Z V ρf(R)ψ dr3+ 1 2 Z S σ ψ dr2 + O · kBT Z V cb µ z±eψ kBT ¶2 dr3 ¸ . [14a]
Similarly, substituting Eqs. [8] and [9] into Eq. [3] gives −T Sel= − Z S σψ dr2+ kBT Z S σ zse · ln µ σ∗ 0a0 zse ¶ − 1 ¸ dr2 + O · kBT Z V cb µ z±eψ kBT ¶2 dr3 ¸ . [14b]
For a given distribution of fixed charges, such as rod- and ring-like particles, the variation of the free energy with the separation from the center of fixed charges to charged surfaces, R, is inde-pendent of the self-energy. Note thatσ0∗is separation-dependent. Using Eqs. [5] and [12] forσ, the free energy can be expressed as
F (R)= 1 2 Z V ρf(R)ψ dr3− 1 2σ ∗ 0 Z S ψ dr2+ Z S σ0hψisdr2 + O ·µ eψ kBT ¶2¸ + constant, [15]
where the constant denotes the separation-independent terms. This result differs from that of a charged surface, which can be linearly regulated by counterion dissociation (9–12). Equation [14b] indicates that the leading order contribution to the entropy
comes from that associated with surface ions rearrangement under the condition of eψ/kBT ¿ 1.
3. A CHARGED ROD PARALLEL TO THE INTERFACE Now we apply the above results to the interaction between a rod-like particle and the charged interface. The length of the rod
L is large and the diameter d is small compared to the Debye
lengthκ−1, i.e., d¿ κ−1¿ L. Consequently, the charged rod can be treated as a line of point charges. It is positioned along the plane, i.e., perpendicular to the z-axis as shown in Fig. 1. The line charge density isα and the electric potential in the system is low enough so that the Debye-H¨uckel approximation is valid. The surface potential-charge relation in Eq. [12] is the same as that associated with a linear charge-regulation surface due to counterion dissociation (10, 11). Thus the distribution of the electric potential can be solved by the same method (14). Be-cause the superposition principle can be used in the Debye-H¨uckel limit, this problem can be reduced to that associated with a fixed point ion carrying charge q at position Q, i.e.,
ρf(r)= qδ(Q). The electric potential at P can be written as the sum of three contributions
ψ(P) = ψp+ ψq+ ψq∗, [16]
whereψp andψq are, respectively, the unperturbed potentials
caused by the surface and the fixed charge in the absence of interactions. The last termψq∗ can be considered as the
poten-tial produced by the image point with charge q∗, which must satisfy the charge-potential relation on the surface Eq. [12]. The solutions are given by
ψp= kBT/zse 1+ κλ exp(−κz), [17] ψq = q 4πεrε0 exp(−κ ˜s) ˜s , [18] and ψq∗ = − qκ 4πεrε0 Z ∞ 1 µ 1− κλ · η 1+ κλ · η ¶ J0 ׳pη2− 1 · κr´exp[−ηκ(R + z)] dη, [19]
FIG. 1. Schematic representation of the system containing a long rod of length L at a separation R from the charged surface. s is the distance measured from the center of the rod.
where ˜s= |P − Q| and λ = εrε0kBT/σ0∗zse represents the char-acteristic regulation length. The solution ofψq∗ is obtained by
the method of separation of variables (14). Equations [17]–[19] are the results for a fixed point charge and can be generalized to any string-like particle straightforward.
Now we use the results [17]–[19] to calculate the mean sur-face potentialhψisand to determineσ0∗andλ as a charged rod approaches the surface:
hψis=kBT/zse 1+ κλ + αL S λ exp(−κ R) εrε0(1+ κλ) . [20]
Obviously, the second term is small if the surface area S is large enough or the rod is far away from the surface, i.e.,κ R À 1. The criterion will be given later. Since the regulation lengthλ is inversely proportional toσ0∗, which in turn depends onhψis, it can be decided from Eq. [20] so that
σ∗ 0 = σ0 µ 1+ 1 1+ κλ ¶ , [21a] and κλ = √ 1+ 432+ 1 23 − 1. [21b]
Here the dimensionless charge density is defined as 3 =
σ0zse/κεrε0kBT . As3 → ∞, κλ ≈ 1/23 → 0. On the other hand, as3 → 0, κλ ≈ 1/3 → ∞.
We can also calculate the interaction energy for a rod parallel to a charged surface by substituting Eqs. [17]–[19] into Eq. [15]. The electrostatic interaction energy W is defined as the differ-ence between the free energy at separation R and infinity, i.e.,
W (R)= F(R) − F(∞). According to Eq. [15], the interaction
energy W can be written as W = Wp+ Wr. Here Wpis the inter-action energy associated with the surface, in which the surface ions can rearrange themselves, and it comes from the potential produced by the charged rod and its image,
Wp = − 1 2σ ∗ 0 Z L/2 −L/2 ·Z ∞ 0 (ψq+ ψq∗)z=02πr dr ¸ α ds + Z S σ0hψisdr2 = −1 2 σ0 κεrε0 κλ(2 + κλ) (1+ κλ)2 (αL)e −κ R + σ0 κεrε0 κλ (1+ κλ)(αL)e −κ R. [22]
Wr is the interaction energy associated with the rod and is due to the potential produced by the plane and the image,
Wr= 1 2 Z L/2 −L/2ψpα ds + 1 2 Z L/2 −L/2 ·Z L/2 −L/2ψq ∗ds ¸ α ds0, [23] TABLE 1
The Coefficients bkin Eq. [24] for the Interaction Energy of a Long Rod Parallel to a Charged Surface
k bk(a) 1 √2 2 1 1+a 2 − √ 2 8 1+5a (1+a)2 3 √ 2 64 3+14a+43a2 (1+a)3 4 − √ 2 256 5+27a+71a2+177a3 (1+a)4 5 √ 2 4096
35+220a+642a2+1276a3+2867a4 (1+a)5
where s and s0 are, respectively, the distances measured from the center of the rod and its image.
The first term in Eq. [23] can be evaluated from Eq. [17] and the result cancels the contribution from the first term in Eq. [22]. To carry out the second integration in Eq. [23] analytically, we assume that the rod is infinitely long, i.e., integrating with respect to s from−∞ to ∞. The error due to the end effects would be
O(κ L)−1small. 1 2 Z L/2 −L/2 ·Z ∞ −∞ψq ∗ds ¸ α ds0= 1 2 (αL)2κ 4πεrε0 × ( K0(2κ R) − 2 ∞ X i=1 bi(κλ) exp(−2κ R) (2κ R)i−12 0 µ i−1 2 ¶) . [24]
The integration is performed in the appendix and the coefficients
bi are given in Table 1. Equation [24] behaves like K0(2κ R) asκλ → ∞ and −K0(2κ R) as κλ → 0. The infinite series in Eq. [24] converges very slowly and the convergence rate can be greatly improved by adopting the Shank transform.
With Eqs. [22], [23], and [24], the interaction energy is then given by W∗(κ R; κλ, Ä) = W (£ κ R) (αL)2κ 4πεrε0 ¤ = Ä1+ κλκλ e−κ R+1 2 ( K0(2κ R) − 2X∞ i=1 bi(κλ) exp(−2κ R) (2κ R)i−12 0 µ i−1 2 ¶) , [25]
whereÄ = 4πσ0/κ2(αL). The dimensionless interaction en-ergy varies with the dimensionless groups:Ä, κλ (or 3), and
κ R. Note that Eq. [25] reduces to the result of constant surface
charge densityσ0 if κλ → ∞ and to that of constant surface potentialψ0= (σ0/κεrε0)[κλ/(1 + κλ)] if κλ → 0.
4. RESULTS AND DISCUSSION
The air-water interface and the biomembrane are often in-volved with the surface ions that are mobile in the two-dimensional plane. The effect of surface ions rearrangement due
to the approach of charged particles on the electrostatic interac-tion is studied. Under circumstances like strong dissociainterac-tion, the charges of the particle can be regarded as fixed during interac-tions. By minimizing the free energy of the system, the surface charge-potential relation is obtained in addition to the Poisson-Boltzmann equation. The free energy includes the electrostatic internal energy, the bulk entropy of the mobile ions, and the two-dimensional entropy of the surface charges.
As a charged particle approaches, the local surface charge density may be adjusted by several ways. In the conventional charge regulation models, such as single-site and two-site dis-sociation models (8), the surface charge density is regulated by the chemical equilibrium taking place on the surface. In these models, the positions of reactive sites are usually fixed at sur-faces. For a single-site model, such as A H→ A−+ H+, the surface charge A−is produced if a counterion H+is dissociated from the neutral species A H . The equilibrium constant is given by K = [A−][H+]/[AH]. The surface charge-potential relation follows σ(r) = σt 1+ [H+]bexp ¡zseψ kBT ¢± K, [26]
whereσt is the total surface charge associated with complete dissociation and [H+]bis the bulk proton concentration.
In the present study, there is no chemical reaction occurring and the electrostatic interaction is regulated by the local rear-rangement of the surface charges. Equation (9) shows that the surface charge density follows a Boltzmann distribution with respect to the surface potential. The differences between con-ventional charge regulation models and the present model can be seen by comparing Eqs. [9] with [26]. For strong dissocia-tion, i.e., [H+]/K ¿ 1, Eq. [26] indicates that the surface charge density is essentially constantσt. However, when [H+]/K À 1, Eq. [26] can reduce to a form similar to Eq. [9]. As a conse-quence, both models should have similar behavior in the weak dissociation limit.
When the electric potential is low enough, all the charge-regulation models can be linearized to give the same form,
σ(r) = σ∗
0 − Cψ with C ≥ 0. For the case of surface charge re-arrangement, C/σ0∗= zse/kBT . Moreover,σ0∗ depends on the separation of the charged particle from the interface R because of the variation ofhψis with R as shown in Eq. [13]. Under certain circumstances,hψis can be regarded as a constant and the evaluation ofσ0∗is thus simplified. If the charged particle is a long rod, the criterion of takingσ0∗to be independent of R is obtained by comparing the two terms in Eq. [20]
SÀ zse(αL)
κεrε0kBT
κλe−κ R.
The result indicates that the assumption is valid if the interfacial area S is large enough. When the particle is far away (e−κ R ¿ 1) or the mean charge density is high enough (κλ ¿ 1 or 3 À 1), this simplification is also reasonable.
DNA or polyelectrolytes, such as poly(diallyldimethylammo-nium) chloride (PDDA), are often modeled as a rigid, charged rod. Under the Debye-H¨uckel approximation, the interaction en-ergy for a long rod parallel to the charged interface is calculated and given in Eq. [25] forκ L À 1 and κd ¿ 1. The interaction energy is found to consist of two terms. The first term is as-sociated with the direct interaction between the charge surface and the rod. It is proportional to the product of the unperturbed surface charge density σ0 and the total charge carried by the rodαL. However, a correction related to the characteristic reg-ulation lengthκλ must be made. Furthermore, it decays expo-nentially with the distanceκ R. The second term is associated with the rod and its image. The dielectric behind the surface is polarized by the charged rod. The electric field produced by the induced dipoles in the dielectric is represented by the image of the rod. As a result, it is proportional to the square of the to-tal charge associated with the rod and decays approximately as exp(−2κ R)/√2κ R.
In a 1–1 electrolyte solution of 1–10 mM, the Debye length is aboutκ−1≈ 3–10 nm. A charged rod with diameter d <∼ 1 nm and length L >∼ 50 nm satisfies the condition κd ¿ 1 and
κ L À 1 approximately. If the line charge density ranges from α = 0.2 to 1 e/nm, then αL = 10–50 e for L = 50 nm. A
PDDA polymer may be represented by these parameters (7). As illustrated in Eq. [25], the dimensionless interaction energy is determined by the dimensionless groups: Ä, κλ, and κ R. The interaction energy is scaled by (αL)2κ/(4πεrε0), which is about 7 kBT forαL = 10 e and k−1= 10 nm at 298 K. With
σ0 = 0.005 C/m2andκ−1= 3 nm, the characteristic charge ra-tioÄ = 4πσ0κ−2/(αL) ranges about from ±0.3 to ±2 and the dimensionless regulation lengthλ/κ−1may be as large as 20 for
αL = 50 e and Ä = ±0.2. The distance R is also scaled by κ−1.
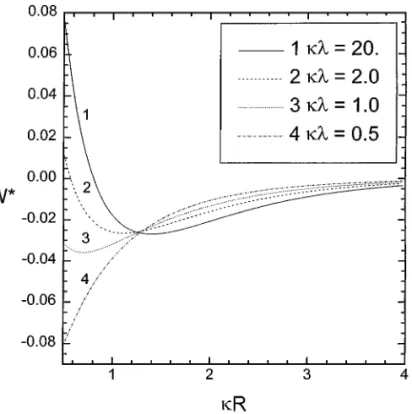
Since the rod is regarded as a line charge in the present anal-ysis, the condition RÀ d must be satisfied to have consistent results. The dimensionless separationκ R = 0.5 for κ−1= 3 nm corresponds to R = 1.5 nm, which is in the margin of validity. Therefore,κ R begins from 0.5 instead of 0.0 in Figs. 2 and 3.
Figure 2 shows the variation of the dimensionless interaction energy W∗ with the dimensionless separationκ R for various values ofκλ at Ä = −0.2. Though Ä < 0 denotes that the rod and the surface are oppositely charged, the interaction can vary from attraction to repulsion asκ R decreases. When the separa-tion is large enough, the direct-interacsepara-tion term dominates and thus the interaction is attractive. Asκ R → 0, the image-related contribution, i.e., the 2κ R-term, becomes important and depends on the ratio of the characteristic regulation length to the Debye length,κλ. When κλ À 1, the surface behaves like under the condition of constant surface charge density. As a result, the re-pulsion eventually dominates with decreasing the separation. On the contrary, the surface acts like under the condition of constant surface potential forκλ → 0 and the image-related contribution enhances the attraction. The separation at which the interaction force becomes zero is increased with increasingκλ. In other words, the charge regulation results in an increase of attraction asκλ decreases.
FIG. 2. The variation of the dimensionless interaction energy W∗with the dimensionless separationκ R for various values of κλ at Ä = −0.2.
For a given electrolyte concentration, the regulation length increases with decreasing the average surface charge density according to Eq. [21]. As a consequence, the surface behaves like that of constant charge density for low charge density and functions as that of constant potential if the charge density is
FIG. 3. The variation of the dimensionless interaction energy W∗with the dimensionless separationκ R for Ä = ±0.5 and ±2 at κλ = 4.
high. For κλ ¿ 1, the Debye-H¨uckel approximation may be invalid because3 → ∞ as κλ → 0. The nonlinear form for both the Poisson-Boltzmann equation [6] and the surface charge-potential relation [9] should be adopted. Nevertheless, we expect that the linearized equations can still furnish us with detailed insight and reveal important features of the problem.
Regardless of the sign ofÄ, the image-related term always gives the same contributions for a given value ofκλ. As a re-sult, the interaction energy behaves asymmetrically for ±Ä. Figure 3 depicts the comparison between the interaction energy ofÄ = ±0.5 and ±2. Since the image-related term is positive forκλ = 4, the rearrangement of surface ions tends to reduce the attraction and to enhance the repulsion between the charged rod and the interface. However, the situation can be reversed if
κλ is small enough. Note that the image-related term becomes
dominant at short separationκ R < 1. When the salt concentra-tion is high enough, the size of the rod can play an equally important role and the interaction may differ from our pre-diction.
In this study, the surface ions are restricted to move in the two-dimensional plane and the total charges are maintained constant during interactions. Nevertheless, the surface ions, such as ionic surfactants, may be in thermodynamic equilibrium with those in the bulk solution. Thus, an electric potential disturbance on the surface can also lead to a redistribution of these ions between the surface and the bulk. In that case, the free energy should include contributions of ionic surfactants in the bulk. A similar approach can be employed to determine the surface charge-potential re-lation. However, the Lagrangian multiplier must be determined by the conservation of total surfactants. If the charge species is essentially insoluble in water, such as charged lipid, then our analysis is valid.
SYMBOLS α line charge density (C/m)
δ Dirac function
ε permittivity (C2/J· m)
κ Debye-H¨uckel parameter (m−1)
λ characteristic regulation length (m)
ρ fixed charge density (C/m3)
σ surface charge density (C/m2)
ψ electric potential (J/C) 0 Gamma function
3 dimensionless surface charge density Ä characteristic charge ratio of surface to rod
c concentration of mobile ions (#/m3)
d diameter of rods (m)
e fundamental charge, 1.6× 10−19C
z valency of ions
K modified Bessel function
L length of rods (m)
R rod-surface separation (m)
APPENDIX We perform the integration of Eq. [24], 1 2 Z L/2 −L/2 ·Z ∞ −∞ψq ∗dr ¸ α dr0 = −(αL)2κ 4πεrε0 Z ∞ 1 µ −1 + 2 1+ κλ · η ¶ exp(−η · 2κ R) p η2− 1 dη = α2L 4πεrε0 · K0(2κ R) − 2 Z ∞ 1 · 1 (1+ κλ · η)pη2− 1 ¸ × e−η·2κ Rdη¸ [A1]
where we have used the relationsR0∞J0(br ) dr = b−1 and K0 is the modified Bessel function.
By expanding the preexponential part of the integrand in the last integration in Eq. [A1] aboutη − 1, one has
1 1+ κλ · η 1 p η2− 1 = ∞ X k=1 bk(κλ)(η − 1)k− 3 2. [A2]
Then the integration can be carried out Z ∞ 1 exp(−η · 2κ R) (1+ κλ · η)pη2− 1dη =X∞ k=1 bk(κλ) Z ∞ 1 (η − 1)k−32e−η·2κ Rdη =X∞ k=1 bk(κλ) exp(−2κ R) (2κ R)k−12 0 µ k−1 2 ¶ , [A3]
where we have used the relation Z ∞ 1 (η − 1)ν2e−η·2κ Rdη = exp(−2κ R) (2κ R)1+ν2 0 µ 1+ν 2 ¶ , ν = −1, 1, 3, . . . . [A4]
Some of the coefficients bk are listed in Table 1. Note that bk(α) → 0 as a → ∞ and Eq. [A3] becomes 0. On the other
hand, one has the asymptotic expression of K0(2κ R) from Eq. [A3] asκλ = 0.
ACKNOWLEDGMENT
This research is supported by National Council of Science of Taiwan under Grant NSC 90-2214-E-008-012.
REFERENCES
1. Kaplan, F. S., Solomak, T. B., and Brosov, K. N., Kolloid. Zh. 51, 867 (1989).
2. Kaplan, F. S., Solomak, T. B., and Brosov, K. N., Kolloid. Zh. 51, 1100 (1989).
3. Stahlberg, J., Appelgren, U., and J¨onsson, B., J. Colloid Interface Sci. 176, 397 (1995).
4. Ohshima, H., and Kondo, T., J. Colloid Interface Sci. 157, 504 (1993). 5. Tsao, H.-K., J. Colloid Interface Sci. 202, 527 (1998).
6. Mashl, R. J., and Gronbech-Jensen, N., J. Chem. Phys. 109, 4617 (1998). 7. Mashl, R. J., Gronbech-Jensen, N., Fitzsimmons, M. R., L¨utt, M., and Li,
D., J. Chem. Phys. 110, 2219 (1999).
8. Hunter, R. J., “Foundations of Colloid Science.” Oxford, New York, 1992. 9. Healy, T. W., Chan, D., and White, L. R., Pure Appl. Chem. 52, 1207 (1980). 10. Chan, D. Y. C., and Mitchell, D. J., J. Colloid Interface Sci. 95, 193
(1983).
11. Carnie, S. L., and Chan, D. Y. C., J. Colloid Interface Sci. 161, 260 (1993). 12. Tsao, H.-K., and Sheng, Y.-J., Langmuir 14, 6793 (1998).
13. Borukhov, I., and Andelman, D., Phys. Rev. Lett. 79, 435 (1997). 14. Tsao, H.-K., Langmuir 16, 7200 (2000).