A modified BFKL equation with Q dependence

CHINESE JOURNAL OF PHYSICS VOL. 37, NO. 3 JUNE 1999

A Modified BFKL Equation With Q Dependence

Jyh-Liong Lim’ and Hsiang-nan Li2

1 Department of Electrophysics, Nationai Chiao- Tung University, Hsinchu, Taiwan 300, R.O.C.

2Department of Physics, National Cheng-Kung University, Tainan, Taiwan 701, R.O. C.

(Received September 17, 1998)

We propose a modified Balitsky-Fadin-Kuraev-Lipatov (BFKL) equation for the summation of large ln(l/z), I being the Bjorken variable, which contains an extra dependence on the momentum transfer Q compared to the conventional BFKL equation. This Q dependence comes from the phase space constraint for soft real gluon emissions in the derivation of the BFKL kernel. The modified equation gives a slower rise of the gluon distribution function with l/z for smaller Q, such that the predictions for the structure functions Fz,~(x, Q2) involved in deep inelastic scattering match the HERA data. These results are similar to those obtained from the Ciafaloni-Catani-Fiorani-Marchesini equation, which embodies both the In Q and ln( l/r) summations. The reason that the conventional BFKL equation can not be applied to the low Q (soft pomeron dominant) region is given.

PACS. 12.38.B~ - Perturbative calculations.

PACS. 12.38.C~ - Summation of perturbation theory.

I. Introduction

The deep inelastic scattering (DIS) experiments performed at HERA [l] have stimu-lated many intensive discussions on the behavior of the structure function F,(z, Q”) at small Bjorken variable z for various values of the momentum transfer Q. One of the important subjects is to explain the data of F2 using the known evolution equations. In the low 2 region with ln(l/z) >> lnQ, the appropriate tool is the Balitsky-Fadin-Kuraev-Lipatov (BFKL) equation [2] which sums large ln( l/r) in the gluon distribution function to all orders. Since the BFKL equation does not depend on the momentum transfer explicitly, its predictions for the gluon distribution function and for F2 exhibit a weak Q dependence. However, the HERA data show that the rise of F2 at small 2 varies with Q in a more sensitive way: The ascent is rapid for large Q, which is attributed to hard (or BFKL) pomeron contributions. The slow ascent at low Q, which can not be explained by the BFKL equation, is interpreted as the consequence of soft pomeron exchanges.

To understand the Q-dependent rise of the gluon distribution function and of the structure function, the Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) equation [3] for the 1nQ summation should be included somehow. One may resort to the DGLAP equation directly, because the relevant splitting function P,, 0; l/z also gives an increase 271 @ 1999 THE PHYSICAL SOCIETY OF THE REPUBLIC OF CHIKA

272

A MODIFIED BFKL EQUATION WITH Q DEPENDENCE VOL. 37

at small 5. However, the DGLAP

rise is

milder, and a steep nonperturbative input of the

gluon distribution function

at

low Q must be adopted. An alternative is the pT-factorization

theorem [4], which has been

shown to

be equivalent to the collinear (mass) factorization,

the framework on

which the

DGLAP equation is based. By including the next-to-leading

ln(~/~)

from singlet quark contributions, the rise becomes faster, and

a flat input is

pro-posed [5]. The double scaling tendency exhibited by the predictions from the DGLAP equation with the next-to-leading logarithms taken into account and by the data of FZ has been explored

[6].

T he conclusion also favors a flat nonperturbative input. The above investigations imply that the structure function at low Q is dominated by soft pomeron contributions, and the large-Q behavior is the result of the DGLAP evolution.

Another possibility is the Ciafaloni-Catani-Fiorani-Marchesini (CCFM) equation [7], which embodies the BFKL equation for small 2: (and intermediate Q) and the DGLAP equation for large Q (and intermediate z). To derive the CCFM equation, the angular ordering of rung gluons in ladder diagrams is assumed, which can be regarded as a com-bination of the rapidity ordering for the BFKL equation and the transverse momentum ordering for the DGLAP equation. The CCFM equation has been studied in details in [8]. It is found that the resultant gluon distribution function shows the desired Q dependence, and the predictions for F2 are in agreement with the HERA data. This equation, though considering only the gluon contributions, predicts a steeper rise than the DGLAP equation does, since the running coupling constant involved in the splitting function is evaluated at the gluon transverse momentum, instead of at Q.

The above analyses, though consistent with the data, did not address the issue why the BFKL equation can not be applied to DIS in the low Q region, where it is supposed to be more appropriate because of ln(l/z) > lnQ. In this paper we shall derive the BFKL equation in an alternative way from the viewpoint of the Collins-Soper-Sterman resumma-tion technique [9]. By truncating the loop momenta of real gluons at Q in the evaluaresumma-tion of the evolution kernel, a modified equation is obtained. Since real gluon emissions are responsible for the BFKL rise, the rise is rendered slower at smaller Q, where the phase space for real gluon emissions is more restricted. We argue that this is a plausible reason the conventional BFKL equation, overestimating real gluon contributions, fails in the low Q region. The modified equation is simpler than the CCFM equation, and explains the HERA data of the structure functions F,,L well.

In Sect. II we derive the Q-dependent BFKL equation using the resummation tech-nique, and show that it approaches the conventional one as the cutoff of the loop momenta is removed. In Sect. III the evolution of the gluon distribution function in 5 predicted by the

modified BFKL equation is compared with those by the DGLAP

equation, the conven-tional BFKL equation, and the CCFM equation. The modified BFKL equation is solved numerically, and the results of the gluon distribution function and of the structure functions

Fz,L

are presented in Sect. IV. Section V is the conclusioin, and the Appendix contains the details of the involved calculations.

II. Formalism

In [lo, 111 we have proposed a unified derivation of the known evolution equations that sums various large logarithms based on the resummation technique [9], such as the

VOL. 37 JYH-LIONG LIM AND HSIANG-NAN LI 273 DGLAP, BFKL, CCFM, and Gribov-Levin-Ryskin (GLR) equation [12]. The GLR equa-tion includes the annihilaequa-tion effect of two gluons into one gluon in the region with Q and l/z being simultaneously large. Briefly speaking, the resummation technique relates the derivative of a parton distribution function to a new function involving a special vertex [9,13]. The new function is then expressed as a factorization formula involving the subdi-agram containing the special vertex and the original distribution function. Evaluating the subdiagram according to some specific ordering of radiative gluons, the derivative of the distribution function turns into the corresponding evolution equation. The complexity of the conventional derivation of the evolution equations is thus greatly reduced.

In this section we apply the above formalism to DIS of a proton with light-like m o m e n t u m P” = P+&‘+ in the small z limit, where z = -q2/(2P . q) = Q2/(2P . q) is the Bjorken variable, q being the momentum of the photon. The unintegrated gluon distribution function F(z, J+), describing the probability of a gluon carrying a longitudinal momentum fraction z and transverse momentum pr, is defined by

x(pIF,‘(Y-,YT>F”+(o)IP)

)

in the axial gauge n . A = A+ = 0, n = &‘- being a vector on the light cone. The ket

IP) denotes the incoming proton, and Fz is the field tensor. Averages over the spin and color are understood. To implement the resummation technique, we allow n to vary away from the light cone (n2 # 0) first. It will be shown that the BFKL kernel turns out to be n-independent. After deriving the evolution equation, n is brought back to the light cone, and the definition of the gluon distribution function coincides with the standard one [14]. That is, the arbitrary vector n appears only at the intermediate stage of the derivation and as an auxiliary tool of the resummation technique.

Though F at z --+ 0 does not depend on Pt explicitly as shown later, it varies with

P+ through the momentum fraction implicitly, which is proportional’ to (P+)-l. Hence, the derivative P+dF/dP+ can be written as

P+ -&F(s, PT) = -z;F(s, PT)

Because of the scale invariance of F in n, as indicated by the gluon propagator, (-i/Z2)NP”(I), with

F must depend on P via the ratio (P . n)“/n”. We then have the chain rule relating

P+d/dP+ to d/dn [9.13],

P+ d-F=-- n2 d

dP+ -v,-F,v. n dn@

(4)

vup = SP+ being a vector along P. The operator d/dn, applying to the gluon propagator gives

274 A MODIFIED BFKL EQUATION WITH Q DEPENDENCE VOL. 37

(5)

The loop momentum 1” (1”‘

) contracts with the vertex the d.iRerentiated gluon attaches,

which is then replaced by a special vertex

6, =

n2vp

v.nn.1’

(6)

This special vertex can be read off from the combination of Eqs. (4) and (5).

The contraction of 1” hints the application of the Ward identities [lo, 111,

(7)

for the quark-gluon vertex, and

I”

-iN=“(

k

+ Z)

r

--W’(k) =

4

-ii’F

(

k)

-iP’(k + I)

(k + I)”

lrvx k2

k2 -

_(k+Z)2

’

₁

for the triple-gluon vertex l?,,yx. The Ward identity for the four-gluon vertex,

(8)

I?

_px”,‘y

0: fabefcde(9h9po - 9xc79pY) + faccfbde(9Ap9”b - 9Xc79,“>

(9)

i-f

adefcbet9A"9pv

-

9Ap9cw)

,

is simpler. The sum of the four contractions from If, I;, Z3y, and 2: to the four-gluon vertex

vanishes: The contractions from 1: and I$ to the first term of T$$, cancel each other.

because the first term is antisyrnmetric with respect to the interchange of the indices X and

p. Similar cancellation occurs between the contractions from 1; and 1:. The contractions

from 1: and /3y and from 1; and 1: to the second term cancel separately. The contractions

from 1: and 1: and from I$ and 1; to the third term also cancel separately.

Summing the diag&ns with different differentiated gluons, those embedding the

special vertices cancel by pairs, leaving the one where the special vertex moves to the outer

end of the parton line [9]. We obtain the formula,

-S-&P*) = 2~(VJ?-)

, (10)

described by Fig. l(a), where the new function E contains one special vertex represented

by a square. The coefficient 2 comes from the equality of the new functions with the special

vertex on either of the two parton lines. Note that Eq. (10) is an exact consequence of the

Ward identities without approximation [9]. An approximation will be introduced, when E

is related to F by factorizing out the subdiagram containing the special vertex, such that

Eq. (10) reduces to a differential equation of

F.

It is known that factorization holds in the leading regions. The leading regions of

the loop momentum

1

flowing through the special vertex are soft and hard, since the factor

VOL. 37 JYH-LIONG LIM AND HSIANG-NAN LI 275 l/n . I with n2 # 0 in Eq. (6) suppresses collinear divergences [9]. For soft and hard 1, the subdiagram containing the special vertex is factorized according to Figs. l(b) and l(c), respectively. Fig. l(b) collects the soft divergences of the subdiagram by eikonahzing the gluon propagator, which will be explained below. We extract the color factor from the relation fabc fbdc = -ArcGad, the indices a,

b, .

. . being indicated in Fig. l(b), and NC = 3 the

number of colors. The corresponding factorization formula is written as

where iN, comes from the product of the overall coefficient -i in Eq. (8) and the color, factor -NC extracted above, g is the coupling constant, and the triple-gluon vertex for vanishing Z is given by

(b)

FIG. 1. (a) The derivative -xdF/dx in axial gauge. (b) The soft structure and (c) the ultraviolet structure of the O((rS) subdiagram containing the special vertex.

G

VOL. 37 JYH-LIONG LIM AND HSIANG-NAN LI 277

stated before, and the transverse degrees of freedom of a parton must be taken into account,

leading to the pr-factorization theorem [4]. The n dependence residing in Fig. l(c) then

disappears with the vanishing of Eq. (15).

If neglecting the contribution from Fig. l(c), i.e., adopting E = pS, Eq. (10) becomes

dF(x, PT)

d~(llx)

=

&s(PT)

J

$

T

[F(?

IPT t

lT1)

-

%$ -

~%%pT)]

,

(16)

which is exactly the BFKL equation adopted in [8]. Note that the BFKL equation has been

written in various forms. The above form, though different from that appearing in [2], is

simpler. The argument of 6, has been set to the natural scale PT. It is then understood

that the subdiagram containing the special vertex plays the role of the evolution kernel.

Obviously, the BFKL kernel is gauge invariant. After deriving the evolution equation, we

make the vector np approach 6p-, and the definition of F returns to the standard one [14].

A careful examination reveals that it is not proper to extend the loop momentum

I+

of a real gluon to infinity when deriving Eq. (14), since the behavior of F(x + 1+/P+),

vanishing at the large momentum fraction, should introduce an upper bound of 1+. To

obtain a more reasonable evolution kernel, we propose to truncate If at some scale, and

a plausible choice of this scale is of order Q. The cutoff of Z+ introduces a n dependence.

However, this n dependence can be absorbed into the cutoff, which will be regarded as a

fitting parameter and be determined by the data of F2 (for some value of Q). Then the

gauge dependence does not appear explicitly in the modified evolution equation. It can be

verified that the predictions are insensitive to the cutoff, and a good choice of the cutoff is

Q/(~v), where v is the gauge factor appearing in Eq. (15). Performing the integration over

l- and 1+, Eq. (14) becomes

(17)

x [F(x, IPT t 1~1, Q> - ~VP; - %)F(x, PT,

Q>l ,

where the Q dependence of F from the constraint of phase space for the real gluon emission

has been indicated. With this modification, the real gluon has smaller phase space at lower

Q.

We derive the modified BFKL equation

dFh

PT,

Q> =

& (pT>

dln(l/x)

’ s$[F(x, IPT f 1~1,

Q) -

B(P$ - %%PT,

Q>l

;lT F(X, IPT + h\,Q) (18)

-h(PT-) 71.

_J

_{l;+Q2 '}

where the first and last terms correspond to the lower and upper bounds of 1+, respectively.

Obviously, Eq. (18) approaches the conventional equation (16) in the Q -t 00 limit. The

first term on the right-hand side of Eq.

(18)

is responsible for the rise of F at small x, and

the last term acts to moderate the rise

[ll].

We then expect that the ascent of F is slower at

VOL. 37 JYH-LIONG LIM AND HSIANG-NAN LI 281

IV. Numerical results

We solve both the modified and conventional BFKL equations numerically following

the repetation method proposed in

[8]

by starting with a “flat” gluon distribution function

[8,151,

F(‘)(z,p~)

=.A-N,(l-

s)5exp(-p$/Qi)

,

with Q. =

1

GeV. The active flavor number nf in the running coupling constant Q, is

set to 4. The normalization constant N, will be determined by the data of the structure

function F2 (2, QZ) at some Q , and then employed to make predictions for other

Q .

We solve

Eqs. (16) and (18) with F(‘) in Eq. (35) inserted into their right-hand sides. Substitute the

obtained solution of F into the right-hand sides of Eqs.

(16)

and (IS), and solve them again.

Repeat this procedure until a limit solution of F is reached. In the numerical analysis we

introduce a lower bound pr > 1 GeV to avoid the infrared divergence in b,(pr) from the pr

diffusion at small z. The CCFM equation is also solved in a similar way with the driving

term F(O),

F(Ok

PT, Q>

=

$&

exp(-&lQi)

/’

Ge(Q

-

ZpT) 0

~&vs(~:PT,PT)

d(

1 -Z/Z)5

dln(a/z) '

(36)

with reduces to F(‘), when the functions 6’ and ANs are set to unity.

The expressions of the structure functions Fz,L, according to the pr-factorization

theorem [4], are given by

F&Q’) =

1’ f

1” %

I

H~(~/J,PT,Q)F(~,PT,Q) i- $(d2),

(37)

p, and p: being the upper bounds of pr which will be specified later. The hard scattering

subamplitudes H2,L denote the contributions from the quark box diagrams in Fig. 2, where

both the incoming photon and gluon are off shell by q2 = -Q2 and p2 = -p$, respectively,

P = (~p+,o,pT) b eing the parton momentum and t the momentum fraction. They are

written as

H2 = e;“Cz

lr

Z2 +

(1 - z)” - 2z(l - 2z$ + 2z2&

Q" Q4

1

(39)

VOL. 37 JYH-LIONG LIM AND HSIANG-NAN LI 283 If pT is large, the gluon coming out of the proton will be highly off-shell, and can not be regarded as a parton. It is easy to observe that the terms in the braces of H2 approaches the splitting function

P,,(r) =

C[z2 •t

(1- z)“]

(43)

in the pr -+ 0 limit.

We evaluate Eq. (37) for Q2 = 15 GeV2 with F(J,pr, Q) obtained from the modified BFKL equation, and then determine the normalization constant as Arg = 3.29 from the data fitting. When Q2 varies, we adjust N, such that zg has a fixed normalization Jer xgdx. F2 for Q2 = 8.5,12, 25, and 50 GeV2 are then computed, and results along with the HERA data [l] are displayed in Fig. 3. It is obvious that our predictions agree with the data well. The curves have a slower rise at smaller Q, which is the consequence of the phase space constraint for real gluon emissions. For comparision, we show the results from the’ conventional BFKL equation, and from the CCFM equation. The former are almost Q-independent, and close to those from the modified BFKL equation only at large Q2 = 50 GeV2. Therefore, their match with the data is not very satisfactory, especially in the low Q region. The latter, also consistent with the data, are similar to those from the modified BFKL equation as expected.

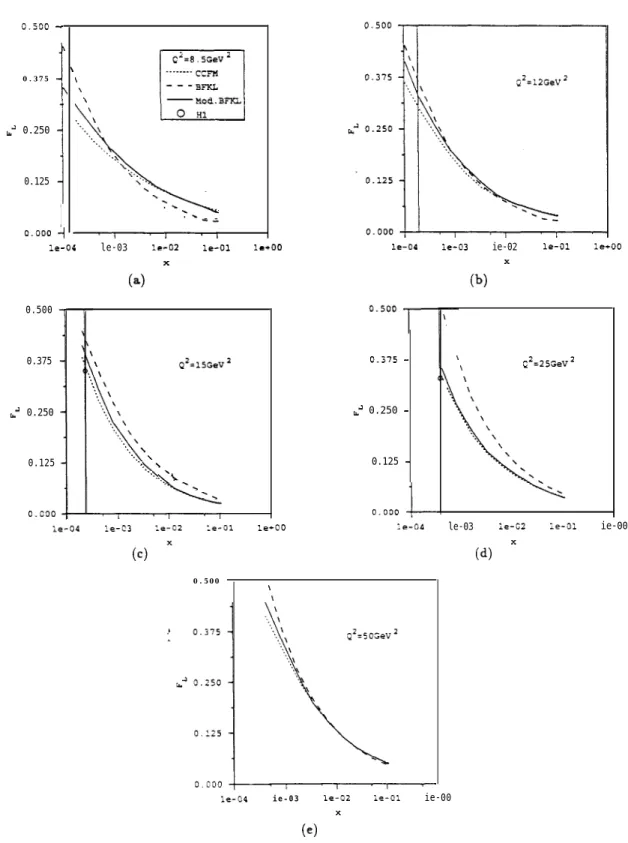
The normalization constants N, for F2 are then employed to evaluate the structure function FL(z, Q”) using Eq. (38) for the corresponding Q. The predictions for Q2 = 8.5, 12, 15,25, and 50 GeV’ are presented in Fig. 4, which behave in a similar way to F2(z, Q”), but are smaller in magnitude. Note that the uncertainty of the experimental data [16] shown in Fig. 4 is still large: The vertical lines adjacent to x = 10m4 for Q” = 8.5 and 1 2 GeV2 represent the error bars. The central values slightly above 0.5 are outside of the plot range. Hence, it is not difficult to explain the current data. To draw a concrete conclusion, more precise data are necessary.

The gluon density xg is defined by the integral of the unintegrated gluon distribution function over pr [8],

xg(x,Q2) =

1”

~F(x>PT,

Q)

.

₍₄₄₎

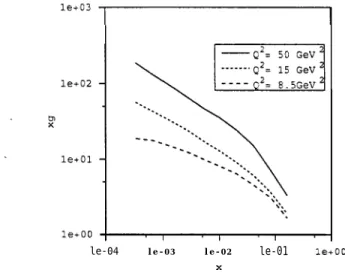
The dependnece of zg on x for Q 2 = 8.5, 15, and 50 GeV2 derived from the modified BFKL equation is displayed in Fig. 5. If letting the parameter X characterize the behavior of xg N x-x at small 5, we find the values X M 0.3 for Q2 = 8.5 GeV2 and X % 0.4 for Q2 = 50 GeV2. T he former is consistent with that obtained from a phenomenological fit to the HERA data [17]. The latter is close to that from solving the conventional BFKL equation numerically [ 181, i.e., from hard pomeron contributions. As explained before, the smaller X at lower Q is due to the more restricted phase space for real gluon emissions. The flat gluon density corresponding to soft pomeron exchanges can then be understood following this vein.

284

2.0

I.5

Lm 1.0

0.5

A iMODIFIED BFKL EQUATION WITH Q DEPENDENCE

pi_-\ - - - BFKL

1

.‘Y

-Mod.SFKL A‘. \

L

-... -\ \ -. ‘. _..__ -. -.-._ 2.0 1.5 &- 1.0 0.5 0.0 j I I

I

FIG. 3. VOL. 37 0.0 -j

le-04 1e-03 ie-02 1e-01 let00 :e-04 1e-03 :e-C2 le-01 ;e*oo

x

(4

I.5 L- 1.0 0.5 x

(b)

0.0 / _{/ /}

:e-C3 le-02 le-01 .??*OO x

Cd)

1

The dependence of F2 on x for Q2 = 8.5, 12, 15. 25! and 50 GeV’ derived from the modified BFKL equation, the conventional BFKL equation, and the CCFM equation. The HERA data [I] are also shown.

VOL. 37 JYH-LIONG LLI AND HSIANG-NAN LI 285 0.500 -0 . 3 7 5

1

I

LJ 0.250 0.125 i

1

0.000 4 &a. 5Gev2 -....-.. CCFn \ \ --_BFKL \ -HOCl.BFIU \ \

II

0 Hl ., \_{. . . .} '__{'_} '. "\ \

‘-..:

'x.. ;.. \ \ . . . . -1e-04 L \ \ 0.500 0.375 hJ 0.250 0.125 o.coo

le-03 1e-02 1e-01 lc+OO 1e-04 1e-03 ie-02 1e-01 1e+oo

x x

(4

(b)

\ Q2=15GeV2 c\ : ’_: 1 ‘. ’ : \ ‘. ’ ‘,., \ ‘. 1 \ ‘.., \ ‘_ x .. \. . ‘. . ...’ L -. -. 0.275 k= 0.250 0.125 -0.000

c

le-C3 le-02 :e-01 1e+oo :e-04

0 . 5 0 0

\ \

\

\ C2=25GeV2

le-04 i e - 0 3 1e-02 le-Cl ie-00 x

(e)

le-03 ie-C2 :e-01 ie-00

Cd) x

FIG. 4. The dependence of FL on 3: for Q 2 = 8.5, 12, 15, 25, and 50 GeV2 derived from the modified BFKL equation, the conventional BFKL equation, and the CCFM equation. The HERA data [16] are also shown.

286 A MODIFIED BFKL EQUATION WITH Q DEPENDENCE VOL. 37

le-04 le-03 le-02 le-01 le+OO

x

FIG. 5. The dependence of xg on x derived from the modified BFKL equation.

V. Conclusion

In this paper we have studied in details the modified BFKL equation proposed from the viewpoint of the resummation technique. This equation possesses a

Q

dependence from the constraint of the phase space for soft real &on emissions. It gives rise to the desired behaviors in z and in

Q

of the gluon distribution function and the structure functions

F2,L,

which are consistent with the HERA data. The predictions are close to those from the CCFM equation, whose Q dependence is, however, due to the lnQ summation. The rise of the gluon density at small z predicted by the modified BFKL equation is steeper than that by the DGLAP equation, and is more sensitive to the variation of Q compared to that by the conventional BFKL equation. We have also explained why the conventional BFKL equation overestimates the real gluon contributions and thus the rise of the structure functions in the low Q region. Real gluons, responsible for the BFKL rise, in fact should have more restricted phase space at smaller Q.

This work demonstrates the simplicity and success of the resummation technique in the study of the DIS structure functions at small z. However, the power-law rise of the structure functions predicted by either the conventional or modified BFKL equation violates the unitarity bound [19]. A further application of our formalism to the issue of the unitarity of the BFKL evolution is referred to [20].

Acknowledgments

This work was supported by the National Science Council of Republic of China under the Grant No. NSC87-2112-M-006-018.

VOL. 37 JYH-LIONG LIM AND HSIANG-NAN LI 2 8 9

Q

1 PO = -2[ &(I - z +

zp2/Q2) '

Q

P3 = -

1 +2q2/Q2

2J Jz(l- zt~p~/Q~)&t4~~p~/Q~ '

Because of P2 = 0, it is easy to obtain the transverse components

pT =

p&

1

t2 1 + 4z2p2/Q2 ’

(59)

It will be found that all the contributions from Fig. 2 to PpP”W,, can be expressed in terms of the invariant,

P.k = P,k, - P3kocos8 - PTk,,sin8cos4, ₍₆₀₎ with Q2 1+ 2zp2/Q2 Wo = G J1-t 4z2p2/Q2

'

(61)

PTQ &(l- ztzp2/Q2)

PTko = -2x

,/l +

4z2p2/Q2 ’

C#J being the azimuthal angle of the momentum k. Following a similar procedure, we derive the squared amplitudes from Figs. 2(a), 2(b) and 2(c),

(PfiPv@w)a

= &re;a,C$ 2(P. k)2 - -P.k

Q2

1

,

Z (P’P”ti&&Jb = (P~PVti~“),y * u) ) (P”P”W,Jc = -Bne;u,C; i2(Q2 + p")(P . k)” -$ [Q2+p2-$AcosB P.k

1

-

Acod) fp2 ₇

respectively, with A = Jl + 4z2p2/Q2. T he complete expression is given by

290 A MODIFIED BFKL EQUATION WITH Q DEPENDENCE VOL. 37

To extract the hard scattering subamplitudes, we integrate Eqs. (56) and (62) over

phase space. For -gPVI@,,, which is independnet of the azimuthal angle 4, the integral is

written as

1 1 H2 =

--2n

(2n)4 Jd4k’d4kb4(p + q - k - Ic’)

x2T6+(k2)27r6+(k’2)z(-g~vw~y) ,

1 = 32??z- / d cost’z(-g”“tiJ .

(64)

Substituting Eq. (56) into

Eq.

(64) and integrating it over cos 8, we obtain Eq. (39), where

the relation p2 = -& has been inserted. For another contraction PPW,,, which depends

on 4, the integral is given by

HL =

&

J

4x2

d cosBd~2rQzP”P”tipv .

After a tedious calculation, we obtain Eqs. (40) and (41).

References

111

121

[31

[41

151

161

[71

LB1

[91

1101

1111

[=I

PI

[I41

[l jl

(65)

ZEUS Collaboration, M. Derrick Ahmed et al., Nucl. Phys. B439, E. A. Kuraev, L. N. Lipatov and Balitskii and L. N. Lipatov, Sov. JETP 63, 904 (1986).

et al., Z. Phys. C65, 379 (1995); Hl Collaboration, T. 471 (1995).

V. S. Fadin, Sov. Phys. JETP 45, 199 (1977); Ya. Ya. J. Nucl. Phys. 28, 822 (1978); L. N. Lipatov, Sov. Phys. V. N. Gribov and L. N. Lipatov, Sov. J. Nucl. Phys. 15, 428 (1972); G. Altarelli and G. Parisi, Nucl. Phys. B126, 298 (1977); Yu.L. Dokshitzer, Sov. Phys. JETP 46, 641 (1977). T. Jaroszewicz, Acta. Phys. Pol. Bll, 965 (1980); S. Catani, M. Ciafaloni, and F. Hautmann, Phys. Lett. B242, 97 (1990); Nucl. Phys. B366, 657 (1991); S. Catani and F. Hautmann, Nucl. Phys. B427, 475 (1994).

R. K. Ellis, F. Hautmann, and B. R. Webber, Phys. Lett. B348, 582 (1995). R. D. Bail and S. Forte, Phys. Lett. B335, 77 (1994); 336, 77 (1994).

M. Ciafaloni, Nucl. Phys. B296, 49 (1988); S. Catani, F. Fiorani, and G. Marchesini, Phys. Lett. B234, 339 (1990); Nucl. Phys. B336, 18 (1990); G. Marchesini, Nucl. Phys. B445, 49 (1995).

J. Kwiecinski, -4. D. Martin, and P.J. Sutton, Phys. Rev. D52, 1445 (1995); 53, 6094 (1996). J. C. Collins and D. E. Soper, Nucl. Phys. B193, 381 (1981).

H-n. Li, Phys. Lett. B405, 347 (1997).

H-n. Li, Phys. Lett. B416, 192 (1998); Chin. J. Phys. 37, 8 (1999).

L. V. Gribov, E. M. Levin and M. G. Ryskin, Nucl. Phys. B188, 555 (1981); Phys. Rep. 100, 1 (1983).

H-n. Li, Phys. Rev. D55, 105 (1997). H-n. Li, Report No. hep-ph/9803202.

P. D. B. Collins and F. Gault, Phys. Lett. BI12, 255 (1982); A. Donnachie and P. V. Landshoff, Nucl. Phys. B244, 322 (1984); Nucl. Phys. B267, 690 (1986).

VOL. 37 JYH-LIONG LIM AND HSIANG-NAN LI 291 [16] Hl Collaboration, Report No. ISSN 0418-9833; A. De Roeck, presented at the International

Symposium on QCD Corrections and New Physics, Hiroshima, Japan, 1997.

[17] A. D. Martin, R. G. Roberts, and W. J. Stirling, Phys. Rev. D50, 6734 (1994); Phys. Lett. B354, 155 (1995).

[lS] A. J. A sk ew, et al., Phys. Rev. D49, 4402 (1994); J. R. Forshaw, R. G. Roberts, and R. S. Thorne, Phys. Lett. B356, 79 (1995).

[19] P. D. B. Collins and E. J. Squires, Regge Poles in Particle Physics, Springer Tracts in Modern Physics,’ Vol. 45 (Springer-Verlag, Berlin, 1968).