On the complexity of the k-chain subgraph cover problem

ELSEVIER Theoretical Computer Science 205 ( 1998) 85-98

Theoretical Computer Science

On the complexity of the k-chain subgraph cover problem

a Department qf‘ Infirmation Munagemmt, Miny Hsin Institute of’ Technology und Commerce, Hsin-Chu, Toi\vun. ROC

b Department qf’ Computer Science and Information Engineering, Nutionul Taiwan Unitirrsity, Tuipei, Taibvan, ROC

‘Institute qf Infirmution Science. Academia Sinicu. Nunkany. Tuipei, Tuivvmn. ROC Received February 1993; revised April 1995

Communicated by M.S. Paterson

Abstract

The k-chain subgraph cover problem asks if the edge set of a given bipartite graph G is the union of the edge sets of k chain graphs, where each chain graph is a subgraph of G. Although the X--chain subgraph cover problem is known to be NP-complete for the class of bipartite graphs, it is still unknown whether this problem is NP-complete or polynomial-time solvable for subclasses of bipartite graphs. In this paper, we answer this question partially by showing that this problem for an important subclass of bipartite graphs, termed convex bipartite graphs, belongs to not only the class P, but also the class NC. More specifically, we show that the k-chain subgraph cover problem on the convex bipartite graph can be solved in 0(m2) time sequentially or O(log*n) time in parallel using 0(m3) processors on the CRCW PRAM, where n and m denote the number of vertices and edges, respectively. @ 1998-Elsevier Science B.V. All rights reserved

Keywords: Bipartite graph; Comparability graph; Convex bipartite graph; NC class; P class; Parallel random access machine

1. Introduction

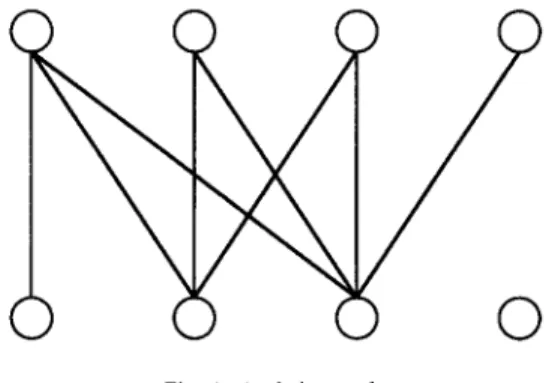
In this paper, we study a problem concerning bipartite graphs and chain graphs. A bipartite graph G = (S, T, E) is a chain graph if each pair of edges either share an end vertex or are connected by an edge (see Fig. 1). A chain graph is also called a non- separable bipartite graph [lo]. The k-chain s&graph couer problem [18] asks if the edge set of a given bipartite graph G is the union of the edge sets of k chain graphs, where each chain graph is a subgraph of G. This problem has a close relation to the

* Corresponding author. Fax: (886)-(2)-3628167; e-mail: ghchen@csie.ntu.edu.tw.

0304-3975/98/$19.00 @ 1998 ~ Elsevier Science B.V. All rights reserved PII SO304-3975(97)00036-4

86 C.-W. Yu et al. I Theoretical Computer Science 205 (1998) 85-98

Fig. 1. A chain graph.

partial order dimension problem [ 181. This problem is known to be NP-complete for k > 3 and polynomial-time solvable for k = 2 [ 181.

Recently, Ma and Spinrad [16] presented an O(n2) time algorithm for the 2-chain subgraph cover problem. Moreover, they showed that many problems can be reduced to the k-chain subgraph cover problem. Among those, there is a problem called the biorder dimension problem [7]. This problem arises from applications in social science, where multidimensional scaling is called for. There is a problem, named the union biorder dimension k problem [7], related to the biorder dimension problem. This problem asks whether a given bipartite partially ordered set can be covered by k biorders. It is exactly the k-chain subgraph cover problem interpreted in another context.

Although the k-chain subgraph cover problem which is defined on bipartite graphs is NP-complete, it is still unknown whether this problem is NP-complete or polynomial- time solvable for subclasses of bipartite graphs. In this paper, we answer this question partially by showing that this problem for an important subclass of bipartite graphs, termed convex bipartite graphs (explained below), belongs to not only the class P, but also the class NC (Nick’s Class [ 111). Previously, Cozzens and Leibowitz [7] have proposed a polynomial-time algorithm to solve the union biorder dimension k problem on the bipartite posets whose underlying graphs do not contain any induced 3k2 (three independent edges). This subclass of bipartite graphs and the convex bipartite graphs do not contain each other.

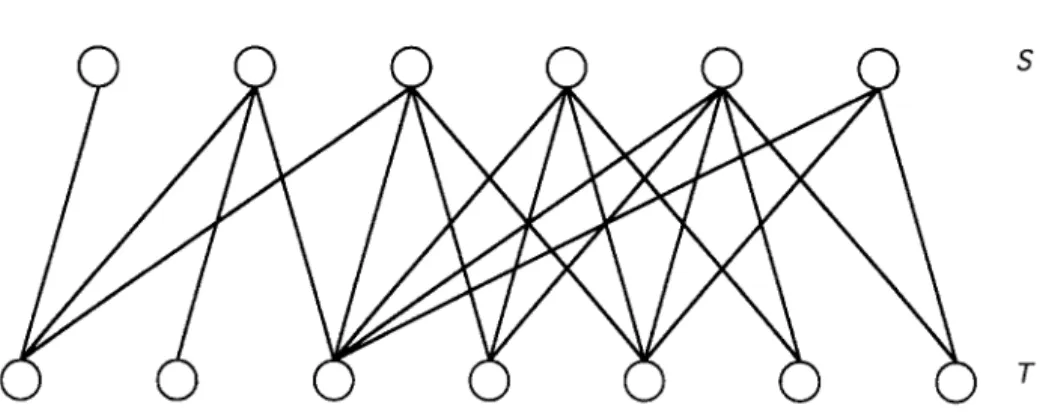
For a bipartite graph G = (S, T, E), an ordering on S (or T) has the adjacency prop- erty if for each vertex u E T (or S), N(v) contains consecutive vertices in the ordering. A bipartite graph G = (S, T,E) is called a conuex bipartite graph [15] if there is an ordering of S or T which has the adjacency property (see Fig. 2). In [13], Glover showed a practically important application of the convex bipartite graph in industry. In [ 151, Lipski and Preparata solved the maximum matching problem on the convex bipartite graph in O(jS] + ITI) t ime. Dekel and Sahni [9] designed an efficient parallel algorithm to obtain maximum matchings in convex bipartite graphs. Their algorithms can be used to obtain parallel algorithms for several scheduling problems. Damaschke et al. [8] showed that many domination problems are polynomial-time solvable in con- vex bipartite graphs. Recently, Chen and Yesha [5] devised a parallel algorithm for

C-W. Yu et al. I Theoretical Computer Science 205 (1998) 85-98

T

Fig. 2. A convex bipartite graph which S has the adjacency property.

recognizing the consecutive l’s property. This algorithm can be applied to recognize a convex bipartite graph in O(log2n) time using O(n3) processors.

In order to solve the k-chain subgraph cover problem on convex bipartite graphs, we show that it can be reduced to the coloring problem on comparability graphs, to be defined below. The reduction is detailed in Section 3. The resulting algorithm and complexity analysis are shown in Section 4. In the next section, we introduce some notations and definitions that are used throughout this paper.

2. Notations and definitions

For each vertex x in G = (S, T,E), we define N(x) = {y 1 xy E E}, which is called the neighborhood of x. Given a graph G = (V, E), the induced subgraph of G by V’ c V, which is denoted by Gvt, is the subgraph of G whose vertex set is V’ and whose edge set contains those edges in E having both end vertices in V’. We say that two edges xy, wz of G are independent of each other if vertices x, y, w,z are distinct and G{,Y,,,Z) contains only two edges xy and wz. A bipartite graph is a chain graph if it does not contain any pair of independent edges. Equivalently, G = (S, T, E) is a chain graph if and only if N(u) C N(v) or N(u) &N(u) holds for any pair of vertices U, u E S (or T) [17].

A partially ordered set (P, <) is a set of transitive and irreflexive binary relations on P. For a given (P, <), we can construct a directed graph GYP,<) as follows: the vertex set of Gcp, < ) is P, and there exists an arc from a to b in Gcp, < ) if and only if a< b holds. The underlying graph of a directed graph is an undirected graph having the same vertex set, but replacing each arc with an edge having the same end vertices. A graph G is called a comparability graph if there exists a partially ordered set (P, < ) such that G is the underlying graph of G (p, < ) [ 121. Moreover, the directed graph GCp, <) is called a transitive orientation of G. We define x(G) as the minimum number of colors needed to color the vertices of G so that adjacent vertices are assigned different colors. An independent set in a graph G is a subset of vertices of G such that no two vertices in this subset are adjacent.

88 C.-W Yu et al. I Theoretical Computer Science 205 (1998) 85-98

3. Reductions

For a bipartite graph G, we use ch(G) to denote the smallest k so that G is k chain subgraphs coverable. Since ch(Gr U G2 U . . . U G,) = ch( G1) + ch(G2) + . . . + ch(G,) if Gl,Gz,,.., G, are connected components of G, we assume the input graph G is connected.

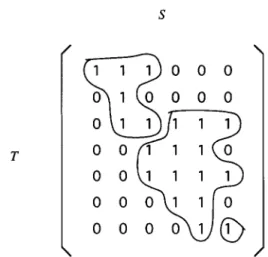
Let G = (S, r, E) be a convex bipartite graph such that S = {st ,s2,. . . ,sk} has the adjacency property. That is, the vertices adjacent to each t in T have consecutive indices in S. Let min(t) denote the minimum i such that si is adjacent to t. We sort T into tl,tz,..., t[ such that i <j if min(ti) < min(ti). Then, an adjacency matrix M of G is constructed as follows: M[i, j] = 1 if and only if ti and sj are adjacent. M is called a canonical adjacency matrix of G, which plays an important role in decomposing the edge set of G. An example is shown in Fig. 3. As usual, the element with the smallest row and column indices is located at the upper-left corner of a matrix. An induced submatrix in M is a matrix with elements {M[i,j] 1 i E R, j E C}, where R is a set of row indices and C is a set of column indices. From the definition, a bipartite graph G is a chain graph if and only if there are no induced submatrix

in the adjacency matrix of G. For a particular adjacency matrix, a pair of edges are called an CI pair if they induce the former submatrix, and a /I pair if they induce the latter submatrix.

As a consequence of the adjacency property of the convex bipartite graph, the fol- lowing lemma results.

T 111000

73

2

Fig. 3. The corresponding canonical adjacency matrix of Fig. 2 and the resulting partition generated by the greedy decomposition algorithm.

C.-W Yu et al. I Theoretical Computer Science 205 (1998) X5-98 89

Lemma 1. Let G be a convex bipartite graph. Then any canonical adjacency matrix does not contain any of the following induced submatrices:

[ 1 0 1 ] and

[ 1

,

It follows that there is no /I pair in M.

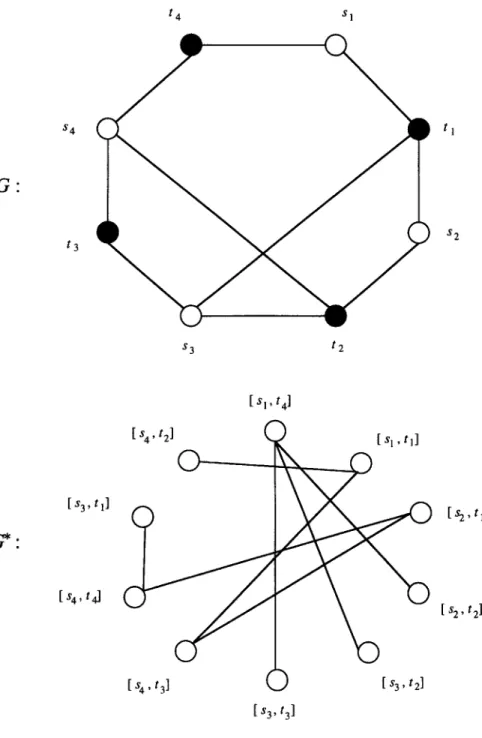
Then we construct G” = (V*, E*) from G = (S, T,E) such that V* = E and two ver- tices in V” are adjacent if and only if the two edges in G are independent. It is not difficult to see that the edge set of every chain subgraph of G induces an independent set of G*, but the reverse is not always true. For example, let us consider the bipartite graph G=(S, T,E) shown in Fig. 4, where S={sr,s~,s~,s~} and T= {tl,tz,t3,t4}. Al- though the edge subset E’ = (($1, tl ), (SZ, t2), (~3, tx), (SJ, td)} induces an independent set of G*, no subgraph of G whose edge set contains E’ can be a chain graph. However, when G is restricted to a convex bipartite graph, we will show that there exists a special decomposition of the edge set of G (i.e. the vertex set of G*) such that each edge subset of G can be extended to a chain subgraph of G.

Theorem 2. G* is a comparability graph if G is a convex bipartite graph.

Proof. Let A4 be a canonical adjacency matrix of G. The 1’s in A4 represent the vertices in G*. Since each pair of independent edges in G induce the submatrix

1 0 [ 0 1

1

in M by Lemma 1, we orient the edge from u to v as (u, v) if the entry representing u in M has smaller column and row indices than the entry representing u in M. Suppose there is a violation to the transitivity, i.e. after the orientation we have (u, t’) and (v, w) but no (u, w). The submatrix of M- induced by u, v, and w has the form

uox

[

1

0 u 0 .

Y 0 w

Since (u, w) does not exist, either x = 1 or y = 1 results in a forbidden Lemma 1, which is a contradiction. 0

submatrix of

Since the edges of a chain subgraph of G induce an independent set in G*, we have x(G*) <c/r(G). By a greedy algorithm (shown below), we can decompose the vertices of G* into k independent sets. Therefore, we derive a k-coloring of G*. Since G* is a comparability graph and the ordering (adopted by the greedy algorithm) of the vertices is actually a perfect ordering [3] on G* (a topological sort of the transitively oriented graph), the greedy algorithm yields an optimal coloring [3, 141. If each of

C-W Yu et al. I Theoretical Computer Science 205 (1998) 85-98

G:

t1

C.-W. Yu et al. I Theoretical Computer Science 205 (1998) 85-98 91

the k color classes can be extended into an independent set (in G* ) which forms a chain subgraph of G, then x( G* ) 3 ch( G). Consequently, we have x( G* ) = ch( G). The greedy decomposition algorithm is shown as follows.

Greedy Decomposition Algorithm.

Input: A canonical adjacency matrix M of a convex bipartite graph G = (X, Y,E). Output: A partition of E (the l’s in M) into Si,

Sl,

.

not contain an induced CY pair. begin scanned : = 0; k := 0; while scanned< 1 E 1 do begin k:=k+l Sk := 8;

for i:= 1 to IYI do for j := 1 to IX I do

if M[i, j] = 1 and Xjyi combining with each edge in Sk does not induce an CI pair

then begin end. end add Xjyi to Sk ; M[i, j] := 0; scanned:= scanned+1 end

We call each Si (1 Qi < k) a greedy independent set. It is worthwhile to note that there is no c( pair in each greedy independent set, but there might exist some /I pairs, which prevent a greedy independent set in G* from becoming a chain subgraph of G. For example, refer to Fig. 3 where a p pair can be found in the second greedy inde- pendent set Sz.

Our approach to overcoming these obstacles is that for each fi pair M[x, y],M[w,z] (X <w is assumed) in Si, add M[x,z],M[x,z + 11,. . . ,M[x, y - l] into Si. We use S,! to denote the set of these newly added elements, and we say that the B pair M[x, y],M[w,z] introduce M[x,z],M[x,z + 11,. . . , M[x, y - l] into Si. Since M[x, z] = 1 (otherwise, M[x,z],M[x, y], and M[w,z] form a forbidden submatrix), we do destroy this /I pair. We claim that no new c( or /3 pair will be generated by this operation. The remaining work of this section is to prove that for 16 i <k (= x(G)), the edge set Si U S; forms a chain subgraph.

In subsequent discussions we assume that G is a convex bipartite graph and Si , Sl, . . . , Sk are the output of the greedy decomposition algorithm. Moreover, we use M[Si] to

92 C.-W Yu et al. I Theoretical Computer Science 205 (1998) 85-98

denote the smallest induced submatrix of A4 that contains &. The submatrix M[Si] contains l’s in the entries specified by Si, and O’s otherwise. For example, M[&] with respect to Fig. 3 contains 13 1 ‘s. Note that the two entries at the left-up comer and the right-bottom corner of M[&] are O’s, although they are l’s in M. We say that M[i,_j] << M[k, I] if i 6 k and j 6 1 (M[i,j] is scanned before M[k, 1] in the greedy decomposition algorithm). Next we show some properties of Si and Si U Sir. In our subsequent proofs, a lot of discussions are made on the relative positions of elements of a canonical adjacency matrix M. We shall use lines, if necessary, to indicate elements with the same row or column indices. To avoid tediousness, some boundary and/or trivial cases are left to the readers.

Lemma 3. There is no induced submatrix [ 1 0 l] contained in each M[S,].

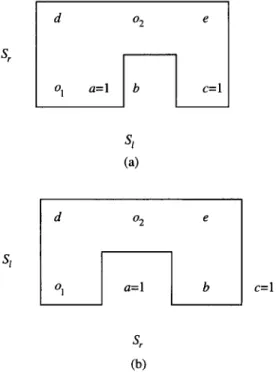
Proof. It is sufficient to prove that the greedy decomposition algorithm selects consec- utive l’s for each row of M. Conversely, we suppose it is not true. Consider the [ 1 0 l] ( = [a b c]) submatrix in some M[S,.]. Since [l 0 l] is forbidden in A4 by Lemma 1, we have b = 1 initially in M and b $ A’,. Without loss of generality, we assume b E SI.

If 1 >r (refer to Fig. 5(a)), there exists d = 1 ES, such that b and d form an c1 pair. Then we have 01 = 02 =0 in M. Since d E S, and c E S,, d and c do not form an E pair, and we have e = 1 in M. Thus there is a forbidden submatrix [d, 02, e], which is a contradiction.

Similarly there is a forbidden submatrix [d,oz,e] when 1 <r (refer to Fig. 5(b)). 0

sr

s,

r

Sl

(a)

1

I

C.-W Yu et 01. I Theoretid Computer Science 205 (1998) 85-98 93

x

Ol y

b

Fig. 6. The proof of Lemma 5.

Lemma 4. There is no induced submatrix [ 1 0 l] contained in each M[S, U S:].

Proof. Note that the set S: contains l’s distributed over one or more rows. These l’s are consecutive if they belong to the same row. Moreover, in each row there is a 1 (in Si) next to the rightmost 1 (in S:). Hence M[Si U $1 does not contain [l 0 I] as an induced submatrix. 0

Lemma 5. Suppose y E Si and z ES,. If y KZ, then i<j.

Proof. Suppose i > j. There exists an x E Sj such that x and y form an cx pair. Refer to Fig. 6, and we have or = 02 = 0. Since x and z are in S,, either a or c is 1. Then either {x, 02, a} or {o 1, y, c} forms a forbidden submatrix in A4, which is a contradiction. 0 Lemma 6. rf’x << y < z and x, z E S,, then y E Si.

Proof. Suppose y E Sj. Since x < y <z, by Lemma 5 we have i < j d i. Hence, j=i. 0

To prove the edge set Si U S,! forms a chain subgraph, it is then sufficient to prove that there are no new c( pairs and /I pairs in S, US:, which can be assured by subsequent lemmas.

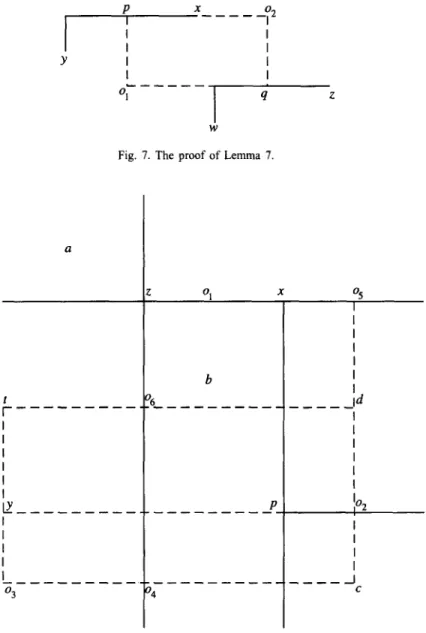
Lemma 7. There are no induced CI pairs in S,! - S;.

Proof. Suppose p,q E S: - S,, and they form an x pair in Si U S:. Without loss of generality, we assume p << q. Moreover let the b pair x, y introduce p, and the /I pair z, w introduce q (refer to Fig. 7), where x, y,z, w E Si. We note that according to the property of consecutive 1 ‘s, x cannot be on the right of 02 (=O). Thus we have x << q <z. Since x,z E S,, by Lemma 6 we have q E Si, which is a contradiction. 0 Lemma 8. There are no induced LY pairs between Si and S,! - Si.

Proof. Suppose z E S: - S,, w E Si, and they form an a pair in Si U S,!. Moreover, let the fi pair x, y introduce z. Refer to Fig. 8. We consider all possible positions of w,

94 C.-W. Yu et al. I Theoretical Computer Science 205 (1998) 85-98 i_____[

Y I I

I I

uF---4

Fig. 7. The proof of Lemma 7.

a I I I P_______________ I I I I I _--- 03 04 - I P I ---- 102 l --- 5

Fig. 8. The proof of Lemma 8.

relative to z. Since z and w form an c( pair, there are four possible positions of w, i.e. a, b, c, and d.

We claim w # a. Otherwise there is a contradiction because by Lemma 6 a <z <x and a,xESi imply ZEST. Also we claim w#b. Otherwise [z,oi,x] (=[l 0 11) forms a forbidden submatrix in M[S, U $1.

Next, we claim w # c. The reason is as follows. If w = c, we have 04 = 05 = 0 in M[Si U S{]. We then consider the possible values of p in M. If p = 1, by Lemma 6 p belongs to Si because x << p < c. Then x and y do not form a fl pair in Si, which

C.-W. Yu et al. I Theoretical Computer Science 205 (1998) 85-98 95

Fig. 9. The proof of Lemma 9

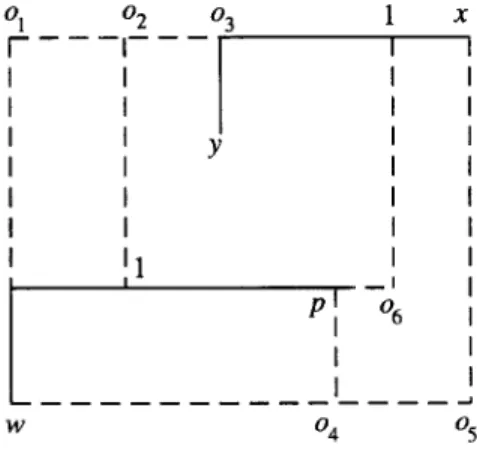
is a contradiction. If p = 0, we have 02 = 0 according to the property of consecutive 1’s. Moreover, we have 03 = 0 in M[Si U S:], because otherwise [o~,o~,c] (=[l 0 11) forms a forbidden submatrix in M[Si U S:]. Since 03 = 02 = 0 in M[Si U S:], y and c (=w) form an CY pair in Si, which is a contradiction.

Last, we claim w # d. Conversely, we suppose w = d. Since z and d form an CI pair in Si U $, we have 06 $! Si U s,! and by Lemma 6 t 6 Si because t < 06 < d and d E Si. Besides, since x and y form a fl pair in Si, we have p $ Si and by Lemma 6 02 4 Si because y < p < 02. Hence, y and d form a p pair in Si, and according to our process of eliminating j pairs, we have 06 E Si US,!, which is a contradiction.

Since all four cases lead to contradictions, the lemma follows. 0 Lemma 9. There are no new p pairs generated in S,! - Si.

Proof. Suppose there is a new /I pair (the two l’s in Fig. 9) generated in Si - Si. Then 02 = 0 in M[Si US,!]. Let the two l’s be introduced by two p pairs x, y and p, w (refer to Fig. 9), respectively. Since x,y, p, and w are all in Si, we have 03 = 04 =0 in M[Si]. Then we have 01 = 05 = 0 in M[Si]. Otherwise either [oi,o3,x] or [w,o4,05] forms the forbidden submatrix [l 0 11. Note that 04 is on the left of 05 because if p has a greater column index than x, then 06 E S,! and the new fi pair would not exist. It is implied (from 01 = 05 = 0) that x and w form a B pair in Si, and they introduce 02 = 1 into Si U 5’:. This contradicts our assumption about 02. 0

Lemma 10. There are no new fi pairs generated between Si and S,! - Si.

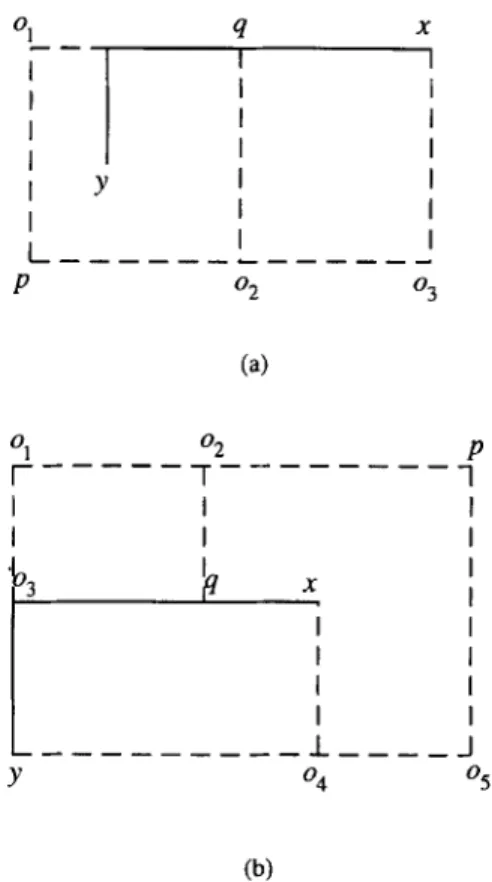
Proof. Suppose there is a new /3 pair p,q, where p E Si and q ES,! - Si. Also q is assumed to be introduced by the j3 pair x, y. The subsequent discussion is made according to the relative positions of p and q.

96 C.-W. Yu et al. I Theoretical Computer Science 205 (1998) 85-98

O1

r ---

:---T

.k3

Fig. 10. The proof of Lemma 10. (a) q has a greater column index than p. (b) p has a greater column index than q.

Case I: q has a greater column index than p (refer to Fig. 10(a)).

We have 01 = 02 =0 in M[Si U $1. If 03 $!Si, then p and x form a p pair in Si, and they introduce 01 (=l) into 5’i U Si, which is a contradiction. If 03 ES;, then [p, o2,03]= [ 1 0 l] forms a forbidden submatrix.

Case 2: p has a greater column index than q (refer to Fig. IO(b)).

We have 02 = 0 in M[Si U $1. Since 03 = 04 = 0 in M[Si], we have 01 = 05 = 0 in M[S;]. Otherwise, either [ol, 02, p] or [y, 04, OS] forms the forbidden submatrix [ 1 0 11. Hence, y and p form a /I pair in Si, and consequently 02 = 1 E Si U S;. This implies that p and q do not form a p pair in Sj U S:, which is a contradiction. 0

Thus far we have proved by Lemmas 7-10 that no new independent edge in G (an c( pair or a /3 pair in M) would be generated by adding S:, 1 d i <k. Therefore, each edge set Si Us:, 1 <i<x(G*), forms a chain subgraph. Summarizing the discussion of this section, we obtain the main result of this paper as stated below.

C-W. Yu et al. I Theoretid Computer Science 205 (199X) 85-98 91

4. Algorithm and complexity analysis

According to Theorem 11, the k-chain subgraph cover problem on the convex bi- partite graph can be solved by the following algorithm.

Input: A convex bipartite graph G = (X, Y, E).

Output: Find minimum number of chain subgraphs of G that can cover G. Step 1: Determine an ordering of X having the adjacency property.

Strp 2: Generate the canonical adjacency matrix A4 of G by sorting Y. Step 3: Construct G* and its transitive orientation from M.

Step 4: Partition E into Si, S,, . . . ,& by coloring vertices of G*.

Step 5: Determine St US{, & U Si, . . , Sk U SL, and generate k chain subgraphs from them.

Let n and m denote the numbers of vertices and edges, respectively, in G. The complexity of the algorithm is analyzed as follows. Step 1 can be completed in O(m) sequential time by Booth and Lueker’s work [l]. If Chen and Yesha’s algorithm [5] is applied, Step 1 can be completed in 0(log2 n) parallel time using 0(n3) processors on the CRCW PRAM.

Step 2 can be done by (1) computing all min(yi)‘s, (2) sorting Y according to min(y;)‘s, and (3) constructing A4 from sorted Y. Substep ( 1) takes O(m) sequential time or O(logn) parallel time using O(n’/logn) processors on the EREW PRAM [l I]. Substep (2) takes O(n logn) sequential time or O(logn) parallel time using O(n) processors on the EREW PRAM [6]. It is quite easy to complete substep (3) in O(n2) sequential time or 0( 1) parallel time using O(n2) processors on the EREW PRAM. So totally Step 2 takes 0(n2) sequential time or O(logn) parallel time using O(n2/logn) processors on the EREW PRAM.

Step 3 can be done in 0(m2) sequential time or 0( 1) parallel time using 0(m2) processors on the CREW PRAM. Step 4 can be completed in O(m2) sequential time [ 141 or O(log n) parallel time using O(m3 ) processors on the CREW PRAM [4]. With the aid of Lemma 4, Step 5 can be completed in O(m*) sequential time or O(logn) parallel time using O(m2) processors on the CREW PRAM.

To sum up, the execution of the algorithm needs 0(m2) time sequentially or 0(log2 n) time in parallel using O(m3) processors on the CRCW PRAM.

Theorem 12. The k-chain subgraph cover problem on the convex bipartite graph can be solved in 0(m2) time sequentially or O(log2 n) time in parallel using 0(m3) proces- sors on the CRCW PRAM, where n and m denote the numbers of’ vertices and edges, respectively. Besides, if the answer is “‘yes”, the k-chain subgraphs can be constructed Izlith the same time complexity and processor complexity.

Corollary 13. The k-chain subgraph cover problem on the convex bipartite graph belongs to not only the class P, but also the class NC.

98 C.-W. Yu et al. I Theoretical Computer Science 205 (1998) 85-98

5. Conclusion and open problems

The containment relationships for some subclasses of bipartite graphs are known as follows [2]: bipartite permutation graphs c doubly convex bipartite graphs c convex bipartite graphs c chordal bipartite graphs C perfect elimination bipartite graphs c bi- partite graphs. The k-chain subgraph cover problem has been proved to be NP-complete for the bipartite graph. In this paper we further show that it belongs to the class P (also in the class NC) for the convex bipartite graph. The immediate open problem resulting from this paper is to decide whether the k-chain subgraph cover problem is solvable in polynomial time for chordal bipartite graphs.

References

[l] KS. Booth, G.S. Lueker, Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms, J. Comput. System Sci. 13 (1976) 335-379.

[2] A. Brandstadt, J. Spinrad, L. Stewart, Bipartite permutation graphs are bipartite tolerance graphs, Congr. Numer. 58 (1987) 165-174.

[3] V. Chvatal, Perfectly ordered graphs, Ann. Discrete Math. 21 (1984) 63-65.

[4] L. Chen, Logarithmic time NC algorithms for comparability graphs and circle graphs, Lecture Notes in Computer Science: Advances in Computing and Information, vol. 497, 1991, pp. 383-394.

[5] L. Chen, Y. Yesha, Parallel recognition of the consecutive ones property with applications, J. Algorithms 12 (1991) 375-392.

[6] R. Cole, Parallel merge sort, SIAM J. Comput. 17 (1988) 770-785.

[7] M.B. Cozzens, R. Leibowitz, Multidimensional scaling and threshold graphs, J. Math. Psychol. 31 (1987) 179-191.

[8] P. Damaschke, H. Muller, D. Kratsch, Domination in convex and chordal bipartite graphs, Inform. Process. Lett. 36 (1990) 231-236.

[9] E. Dekel, S. Sahni, A parallel matching algorithm for convex bipartite graphs and application for scheduling, J. Parallel Distrb. Comput. 1 (1991) 185-205.

[JO] G. Ding, Covering the edges with consecutive sets, J. Graph Theory 15 (5) (1991) 559-562. [ 1 l] A. Gibbons, W. Rytter, Efficient Parallel Algorithms, Cambridge University Press, Cambridge, 1988. [12] P.C. Gilmore, A.J. Hoffman, A characterization of comparability graphs and of interval graphs, Can.

J. Math. 16 (1964) 539-548.

[13] F. Glover, Maximum matching in a convex bipartite graph, Naval Res. Logist. Quart, 14 (1967) 313-316.

[14] M.C. Golumbic, Algorithmic Graph Theory and Perfect Graphs, Academic Press, New York, 1981. [15] J.W. Lipski, F.P. Preparata, Efficient algorithms for finding maximum matching in convex bipartite

graphs and related problems, Acta Inform. 15 (198 1) 329- 346.

[16] T. Ma, J. Spinrad, On the 2-chain subgraph cover and related problems, J. Algorithms 17 (1994) 25 l-268.

[ 171 M. Yannakakis, Node-deletion problems on bipartite graphs, SIAM J. Algebraic Discrete Methods 10 (2) (1981) 310-327.

[18] M. Yannakakis, The complexity of the partial order dimension problem, SIAM J. Algebraic Discrete Methods 3 (1982) 351-358.