The Electric Conductivity of Dilute Suspensions of Charged Porous Spheres

(1)

ARTICLE NO.CS975021

The Electric Conductivity of Dilute Suspensions

of Charged Porous Spheres

Yung C. Liu and Huan J. Keh1

Department of Chemical Engineering, National Taiwan University, Taipei 106-17, Taiwan, Republic of China

Received March 4, 1997; accepted June 2, 1997

potential but also the local ionic densities and fluid velocity. The effective electric conductivity of a dilute suspension of poly- _{That is, one must first solve a set of coupled electrokinetic} electrolyte molecules or charged flocs in an electrolyte solution is

equations to obtain the distributions of electric potential, analytically studied. The model used for the particles is a porous

ionic concentrations and fluid velocity in the electrolyte solu-sphere in which the density of hydrodynamic frictional segments,

tion, and then compute the average electric current and con-and therefore also that of the fixed charges, is constant. The

equa-ductivity in the suspension. tions which govern the electrochemical potential distributions of

Theoretical studies on the effective electric conductivity ionic species and the fluid flow field inside and outside a porous

of a suspension of impermeable charged spheres have been particle migrating in an unbounded solution are linearized

assum-made by Saville ( 1 ) and O’Brien ( 2 ) , assuming that the ing that the system is only slightly distorted from equilibrium.

Using a perturbation method, these linearized equations are solved particles and their electric double layers occupy only a small for a porous sphere in a uniform applied electric field with the _{fraction of the total volume. Approximate formulas for the} density of the fixed charges as the small perturbation parameter. _{conductivity were obtained using a perturbation method for} An analytical expression for the effective conductivity of a dilute _{particles with low z potential immersed in a symmetric} elec-suspension of identical charged porous spheres is obtained from

trolyte correct to O ( z2

) . Their results have some discrepanc-the average electric current density calculated using discrepanc-the solution

ies with the experimental data reported by Watillon and of electrochemical potential distributions of the ions. The result

Stone-Masui ( 3 ) , who measured the surface conductances demonstrates that the presence of the fixed charges in the porous

of a number of monodisperse polystyrene latices over a range particles can lead to an augmented or a diminished electric

con-of particle volume fractions. Later, Saville ( 4 ) considered ductivity of the suspension relative to that of a corresponding

the effects of added counterions produced by the particle suspension of uncharged porous particles, depending on the

char-charging procedure and of nonspecific adsorption which al-acteristics of the electrolyte solution and the suspending particles.

When the anionic and cationic diffusion coefficients of a symmet- ters the concentrations of ions in the solution outside the ric electrolyte are the same, the correction for the effect of the _{double layers, and obtained better agreement between} theo-fixed charges of the particles on the electric conductivity of the _{ries and experiments.}

suspension is proportional to the square of the fixed charge density. _{The basic equations governing the electric conductivity}

q 1997 Academic Press _{of a dilute suspension of colloidal particles also describe the}

Key Words: polyelectrolyte particles; porous spheres; electric

electrophoretic phenomena. O’Brien ( 5 ) derived the analyti-conductivity; dilute suspensions.

cal formulas for the electrophoretic mobility and the electric conductivity of a dilute suspension of dielectric spheres with thin but polarized double layers in a general electrolyte solu-1. INTRODUCTION

tion. Using a similar analysis, O’Brien and Ward ( 6 ) also determined the electrophoretic mobility and the effective When an electric field is applied to charged colloidal

parti-conductivity of a dilute suspension of randomly oriented cles suspended in an electrolyte solution, the particles and

spheroids with thin polarized diffuse layers at the particle the surrounding ions are driven to migrate. As a

conse-surfaces. On the other hand, approximate analytical expres-quence, the fluid is dragged to flow by the motion of the

sions for the electrophoretic mobility and the conductivity particles and the ions, and there is an electric current through

of dilute suspensions of colloidal spheres in symmetric elec-the suspension to produce. To determine elec-the current density

trolytes were obtained by Ohshima et al. ( 7 ) . These expres-distribution and transport properties such as the electric

con-sions are correct to order ( ka )01

, where k is the Debye – ductivity, it is necessary to find out not only the local electric

Huckel parameter ( defined by Eq. [ 34 ] ) and a is the particle radius. When the zeta potential of the particles is small, their

1

To whom correspondence should be addressed. reduced result is in agreement with O’Brien’s ( 2 ) .

(2)

In most practical applications, the electric conductivity of cles is given as an integral over a large surface enclosing a single particle and its adjacent double layer, and the a suspension is known from direct measurement and then

the zeta potential of dielectric particles in the suspension effective conductivity of the suspension is related to the electrochemical potential energies of the ionic species. can be calculated. Similarly, one can also measure the

elec-trophoretic mobility of a particle in order to get the zeta In Section 3, we present the fundamental electrokinetic equations and boundary conditions which govern the elec-potential. O’Brien and Perrins ( 8 ) derived a formula for the

electric conductivity of a porous plug composed of closely trochemical potential distributions, the electrostatic poten-tial profile, and the fluid flow field inside and outside a packed spheres and compared it with the conductivity data

for dilute and concentrated dispersions of monodisperse porous particle migrating in an unbounded solution when a constant electric field is applied. These basic equations polystyrene particles reported by van der Put and

Bijster-bosch ( 9 ) . They found significant differences between the are linearized assuming that the ionic concentrations, the electric potential, and therefore the electrochemical poten-zeta potentials evaluated from measurements of the electric

conductivity and of the electrophoretic mobility. Similar dif- tials have only slight deviations from equilibrium due to the imposed field. The axisymmetric electrophoretic mo-ferences were also found by another work ( 10 ) in which the

conductivities and electrophoretic mobilities of polystyrene tion of a charged porous sphere in an unbounded electro-lyte solution is considered in Section 4. Using the Debye – latex systems were measured. On the other hand, Stigter

( 11 ) developed a theory based on the concepts used to de- Huckel approximation, we first get the solution of the equilibrium electric potential distribution. Then the linear-scribe the conductivity of strong electrolyte solutions, in

which the specific conductance of the suspension was com- ized electrokinetic equations are transformed into a set of differential equations by using a regular perturbation puted by summing the individual contributions of the

parti-cle – ion interactions expressed in terms of equivalent con- method with the density of the fixed charges inside the porous particle as the small perturbation parameter. The ductances. The differences between the kinetic charges

cal-culated from electrophoresis and from conductance in this perturbed electrochemical potentials of ions and the fluid velocity are determined by solving this set of differential theory were found to be small and within the errors of the

experiments and the theoretical models ( 12 ) . equations subject to the appropriate boundary conditions. An analytical expression for the electric conductivity of A theoretical investigation of the electrokinetic

phenom-ena of charged porous particles was first performed by Her- a dilute suspension of identical charged porous spheres is obtained. Finally, in Section 5, typical numerical results mans and Fujita ( 13, 14 ) . They derived formulas for the

electrophoretic mobility of a porous sphere by introducing for the effects of the fixed charges of porous spheres on the effective conductivity of the suspension are presented. the Brinkman equation for the internal flow field of the

parti-cle and assuming that the electric double layer remains

spherically symmetric in the presence of the applied electric _{2. AVERAGE CURRENT DENSITY IN A SUSPENSION} field. The effect of the distortion of the counterion atmo- _{OF CHARGED PARTICLES}

sphere around a nearly free-drained polyelectrolyte coil un-der an applied electric field was examined theoretically by

We consider a dilute suspension of identical charged parti-Imai and Iwasa ( 15 ) , and their numerical results agree well

cles immersed in a solution containing M ionic species. The with the experimental data ( 16 ) . Recently, analytical

expres-particles may be either porous or impermeable to the fluid. sions were derived by Liu and Keh ( 17 ) for the

sedimenta-It is assumed that the suspension is statistically homogeneous tion velocity and potential in a dilute suspension of charged

and all effects of its boundaries are ignored. When the iso-porous spheres under the situation that the electric potentials

tropic suspension is subjected to a uniform applied electric are low. However, the effects of particle charges on the

field E_`, one has effective conductivity of a suspension of porous particles

have not yet been theoretically investigated.

In this work, we study analytically the effective

conduc-E`Å 0 1

V

*

V

Ç_{cd x ,} _[1]

tivity of a suspension of charged porous particles. The density of charged segments of each porous particle is assumed to be uniform, but no assumption is made as to

where c( x ) is the electric potential at position x and V the thickness of the electric double layer relative to the

denotes a sufficiently large volume of the suspension. There dimension of the particle. The suspension is sufficiently

is a resulting volume-averaged current density, which is col-dilute that the suspended particles occupy only a small

linear with E`, defined by

fraction of the total volume of the suspension and the double layer surrounding each particle does not overlap

with the others. In Section 2, the average electric current _»_i_{… Å} 1

V

*

V

i d x , [ 2 ]

(3)

parti-where i ( x ) is the current density distribution. The effective of concentration of species m , electric potential, and electro-chemical potential energy of species m , respectively, and electric conductivity L of the suspension can be assigned

by the linear relation dnm, dc, and dmmare the small perturbations to the

equilib-rium state ( in which no external field is applied ) . The equi-librium concentration of any species is related to the

equilib-»_i_{… Å}_LE_`_. _{[ 3 ]}

rium potential by the Boltzmann distribution, Since the measured electric field and current density are

equal to E` and »i…, respectively, Eq. [ 3 ] reduces to the

n( eq )

m Ån`mexp

S

0

zme c( eq )

kT

D

, [ 8 ]

usual experimental definition of conductivity, provided that the suspension is everywhere homogeneous.

The current density i can be written as

where n`mis the constant bulk concentration of type-m ions.

The perturbation quantity dmmis linearly related to the others

i Å

∑

M

mÅ1

zmeJm, [ 4 ] by

where Jm( x ) and zmare the number flux distribution and the dm_mÅ_kT dnm

n( eq )

m

/zmedc. [ 9 ]

valence of species m , respectively, and e is the charge of a proton. If the solution is dilute, the flux Jmis given by

Substituting Eqs. [ 5 ] – [ 9 ] into Eq. [ 4 ] , using the fact thatÇ_m( eq )

m Å0 , and neglecting products of the small

quanti-Jm Ånmu0nm

Dm

kT

Ç_m_m_, _{[ 5 ]}

ties u , dnm, and dmm, one has

with the electrochemical potential energy field of the mth

i Å

∑

M mÅ1 zmen ( eq ) m

S

u0 Dm kT Ç_dm_m

D

_. _{[10 ]} species mm( x ) defined as ( 7 ) mmÅm0m/kT ln nm/zme c. [ 6 ]

Far from any particle ( beyond the double layer ) , n( eq )

m r

n`mand Eq. [10 ] becomes

Here, u ( x ) is the fluid velocity field; nm( x ) is the

concentra-tion distribuconcentra-tion of species m ; Dmis the diffusion coefficient

of species m which is assumed to be constant both inside and _i_{r 0}

_∑

M mÅ1 zmeDm

S

Çdnm/ zmen`m kT Ç_dc

D

_. _[11]

outside the particles if they are porous; k is the Boltzmann constant; T is the absolute temperature; and m0

mis a constant.

The first term on the right-hand side of Eq. [ 5 ] represents By adding and subtracting the current density given by the the convection of the ionic species by the fluid and the above equation in the integrand of Eq. [ 2 ] , one obtains second term denotes the diffusion and electrically induced

migration of the ions.

»_i_{… Å 0}

∑

M mÅ1 zmeDm V

*

V

S

Ç_dn_m_/zmen ` m kT Ç_dc

D

_{d x}

The linear relation [ 3 ] between the volume-average cur-rent density and the electric field for a suspension will be exact in the limit as E` r 0 . To calculate the effective

/ 1 V

*

V

F

i/

∑

M mÅ1 zmeDm

S

Çdnm/ zmen`m kT Çdc

DG

d x .

conductivity of the suspension we may assume that the inten-sity of the applied electric field is not high, and hence that

the electric double layer surrounding each particle is only [12 ]

slightly distorted from equilibrium by the application of the

field. Therefore, the concentration distribution of each ionic _{In a statistically homogeneous suspension, the volume} species and the electric potential distribution have small de- _{average of}_Ç_dn

mis zero. According to the definition of Eq.

viations from equilibrium, and one can write _{[1] the first term on the right-hand side of Eq. [12 ] equals} L`E`, where nmÅn ( eq ) m /dnm, [ 7a ] cÅc( eq ) /dc, [ 7b ] L`Å

∑

M mÅ1 z2 me 2 n`mDm kT , [13 ] mmÅm( eq )m /dmm, [ 7c ] where n( eq )

(4)

in the absence of the particles. The integral in the second all species, which do not react with one another, in the steady state requires that

term on the right-hand side of Eq. [12 ] can be calculated by first considering for a single particle as if the others were

absent and then multiplying the result by the particle number _{Ç r}

JmÅ0, m Å1, 2, . . . , M . [16 ]

N in the volume V, since the integrand vanishes beyond the

double layers surrounding the particles and the suspension

Here, the species fluxes Jmare defined by Eq. [ 5 ] taking u

is assumed to be sufficiently dilute that the double layers do

as the fluid velocity relative to the particle. not overlap with one another. Also, the volume integral can

We assume that the Reynolds number for the fluid motion be transformed into a surface integral over a spherical

bound-is very small, so the inertial effect on the fluid momentum ary of infinite radius containing the single particle at its

balance can be neglected. The fluid flow is governed by the center. With this arrangement, the second term becomes

modified Stokes equations,

N V

*

rr`

S

nrir /

∑

M mÅ1 zmen`mDm kT dmmn

D

dS _hÇ2 u0h ( x ) f uÅ Çp/

∑

M mÅ1 zmenmÇc, [17 ] Å 0 N V

∑

M mÅ1 zmen`mDm kT

*

rr ` ( nrÇ_dm_m_r ₀_dm_m_{n ) dS ,} _{Ç r} uÅ0, [18 ] [14 ]

where h is the viscosity of the fluid; f is the friction coeffi-cient inside the porous particle per unit volume of the fluid; where r is the position vector relative to the particle center,

p ( x ) is the dynamic pressure distribution; and h ( x ) is a unit r Å ÉrÉ, and n is the unit vector outwardly normal to the

step function which equals unity if x is inside the particle, surface of the boundary. To obtain Eq. [14 ] , the requirement

and zero otherwise. In Eq. [17 ] , h and f are assumed to be of the conservation of electric charge (Çri Å 0 ) and Eq.

constant. Note that f can be expressed as 6phasNs, where [11] have been used. Therefore, the average current density

Ns and as are the number density and the Stokes radius, given by Eq. [12 ] can be expressed as

respectively, of the particle segments.

The electric potential c and the space charge density are

»_i_{… Å}_L`_E_` ₀ N

V

∑

M

mÅ1

zmen`mDm

kT related by Poisson’s equation:

1

*

rr ` ( rÇ_dm_mr_n0dm_m_{n ) dS .} _{[15 ]} _Ç2 c Å 04p e [

∑

M mÅ1 zmenm/h ( x ) Q ] . [19 ]

The determination of dmm in the above equation is

con-Here, Q is the fixed charge density inside the porous particle cerned with the solution of a set of basic electrokinetic

equa-and eÅ 4pe0er, where er is the relative permittivity of the tions for the electrolyte around a single particle. These

elec-electrolyte solution, which is assumed to be the same inside trokinetic equations for the case of a charged porous particle

and outside the particle, and e0 is the permittivity of free are described in the next section and their analytical solution

space. Experimental data for layers of poly ( methacrylic for a charged porous sphere with low fixed charge density

acid ) , poly ( 4-vinylpyridine ) ( 18 ) , and poly ( N-isopropyla-is presented in Section 4. From thN-isopropyla-is solution we shall derive

crylamide ) ( 19 ) on the surfaces of polymer particles indicate the effective conductivity of a dilute suspension of identical

that the magnitude of Q ranges from very low to as high as porous spheres.

9 1 106 C /m3

, depending on the temperature, pH value, and ionic strength of the electrolyte solution.

3. BASIC ELECTROKINETIC EQUATIONS FOR

If the strength of the imposed electric field is weak, the A CHARGED POROUS PARTICLE

deviations in the ionic concentrations and electric poten-IN AN ELECTRIC FIELD

tial from equilibrium are so slight that Eqs. [16 ] and [17 ] can be linearized. It has been found that the perturbed In this section we consider a charged porous particle ( such _{electrochemical potential energies dm}

mand the fluid

veloc-as a polyelectrolyte molecule or an aggregate of fine particles _{ity u satisfy the following set of electrokinetic equations} bearing surface charges ) of arbitrary shape in an unbounded _{( 5, 7 ) :}

liquid solution containing M ionic species when a constant electric field E` is applied. In this solvent-permeable and

ion-penetrable particle, idealized charged segments are as- _n( eq )

m Ç2dmm/ Çn( eq )m rÇdmmÅ

kT Dm

Ç_n( eq )

m ru , [ 20 ]

(5)

cr 0E_`rx . [ 27c ] hÇ2_{Ç 1} u0h ( x ) fÇ 1uÅ

∑

M mÅ1 Ç_n( eq ) m 1 Çdmm. [ 21]

Here, mE is the electrophoretic mobility of the charged Substituting Eq. [ 8 ] into Eqs. [ 20 ] and [ 21] , one has porous particle, and its expression for a porous sphere will be given in the next section. Because the equilibrium electric potential and concentration of type-m ions in the

Ç2_dm mÅ zme kT

S

Ç_c( eq )_rÇ_dm m0 kT Dm Ç_c( eq )_r

u

D

, [ 22 ] _{bulk solution have been set equal to zero and n}`

m,

respec-tively, from Eqs. [ 7 ] , [ 9 ] , [ 27b ] , and [ 27c ] one obtains

Ç2

Ç 1u0h ( x ) l2

Ç 1uÅ the following condition for dmm at large distances from

the particle: 01 h

∑

M mÅ1

F

zmen`m kT exp

S

0 zme c( eq ) kT

D

Ç_c( eq )_{1 Ç}_dm m

G

, [ 23 ] dmmr 0zmeE`r_{x .} _{[ 28 ]} where lÅ( f / h )1 / 2

, and the solution of c( eq )

for the case

Equations [17 ] , [18 ] , and [ 27a ] take a reference frame that of a charged porous sphere will be given in the following

the porous particle is at rest and the velocity of the fluid at section. Note that the reciprocal of the parameter l is the

infinity is the particle velocity in the opposite direction. shielding length characterizing the extent of flow

penetra-tion inside the porous particle. For some model porous

4. SOLUTION FOR THE EFFECTIVE CONDUCTIVITY particles made of steel wool ( in glycerin – water solution )

OF A DILUTE SUSPENSION OF CHARGED ( 20 ) and plastic foam slab ( in silicon oil ) ( 21 ) ,

experi-POROUS SPHERES mental values of 1 / l can be as large as 0.4 mm, while in

the charged or uncharged temperature-sensitive poly (

N-We now consider a charged porous sphere of radius a isopropylacrylamide ) hydrogel layers on latex particles

immersed into an unbounded electrolyte solution under a in electrolyte solutions, values of 1 / l were found to be

uniform applied electric field E`. The electrophoretic

veloc-about 1 – 50 nm ( 19 ) .

ity of the particle is mEE`ez, where ez is the unit vector in

The conditions inside the particle are

the axial direction and E`Å ÉE`É_{. The origin of the spherical}

coordinate system ( r , u, f ) is taken to be the center of the dmmand u are finite. [ 24 ]

particle.

We first seek the solution of c( eq )

which appears in the The boundary conditions at the surface of the particle ( S{

)

governing equations [ 22 ] and [ 23 ] for a charged porous are

sphere. Substituting the Boltzmann distribution, Eq. [ 8 ] , into Poisson’s equation [19 ] at equilibrium, one can get the dmmÉS/ÅdmmÉS0, [ 25a ] _{equilibrium Poisson – Boltzmann equation,}

Ç_dm_mÉ_S/Å Çdm mÉS0, [ 25b ] uÉ_S/ ÅuÉ_S0, [ 25c ] _Ç2_c( eq )_{Å 0}4p e nr_sÉ_S/ Ånr_sÉ_S0. [ 25d ] 1

F

∑

M mÅ1 zmen`mexp

S

0 zme c( eq ) kT

D

/h ( r ) Q

G

, [ 29 ]

Here, s is the hydrodynamic stress of the fluid given by

s Å 0pI/h[Ç_u_/₍Ç_{u )}T

] , [ 26 ] where h ( r ) equals unity if rõa and is zero if rúa .

The appropriate boundary conditions for the equilibrium potential are

where I is the unit dyadic. Equations [ 25a ] and [ 25b ] indi-cate that the concentration and flux of species m and the

potential and electric field must be continuous at the particle _c( eq )_É

r Å0is finite, [ 30a ]

surface. Equations [ 25c ] and [ 25d ] are the continuity

re-c( eq )

É_{r Åa}/Å c( eq )É_{r Åa}0, [ 30b ] quirement of the fluid velocity and stress tensor.

The conditions far from the particle are _dc( eq ) dr

Z

r Åa/ Å dc ( eq ) dr

Z

r Åa0 , [ 30c ] uÅ 0mEE`, [ 27a ] nm rn`m, [ 27b ] c( eq )Érr ` r0. [ 30d ]

(6)

The solution to Eq. [ 29 ] satisfying the above boundary con- equations [ 22 ] and [ 23 ] and the boundary conditions [ 24 ] , [ 25 ] , [ 27a ] , and [ 28 ] , and equating like powers of QV on ditions is

both sides of the respective equations, we obtain a set of differential equations and boundary conditions for each set c( eq )

Åceq1_QU /_{O ( QU}2

) . [ 31]

of the functions mm j, uj, and mEjwith j Å1, 2, . . . .

After collecting the O ( QV ) terms in the procedure of this Here,

regular perturbation, one obtains the following equations:

QUÅ 4peQ ek2 kT, [ 32 ] Ç2mm 1Å 0 z2 me2E` kT

Ç_ceq1rÇ_{( r cos u ) ,} _{[ 36a ]} Ç2

Ç 1u10h ( r ) l 2

Ç 1u1 which is the nondimensional charge density of the porous

sphere, and ( 13 ) Å 1 h

∑

M mÅ1 z2 me 2 n`mE` kT Ç_ceq1_{1 Ç}_{( r cos u ) .} _{[ 36b ]} ceq1( r )Å kT e

F

10( ka/1 ) e 0 kasinh ( kr ) kr

G

, if rõa ,

The boundary conditions for mm 1and u1are

[ 33a ]

rÅ0: mm 1and u1are finite; [ 37a ]

ceq1( r )Å kT

e [ ka cosh ( ka )0sinh ( ka ) ] e0 kr

kr , if rúa , r Åa : mm 1and u1are continuous, [ 37b ]

Ç_m_{m 1} _{and n}rs₁are continuous; [ 37c ]

[ 33b ]

r r `: mm 1are zero, [ 37d ]

where k is the reciprocal of the Debye screening length,

u1r 0mE1E`ez. [ 37e ]

defined by

The solutions for mm 1 and the r and u components of u1

subject to Eqs. [ 37 ] are kÅ

S

4pe 2 ekT

∑

M mÅ1 z2 mn`m

D

1 / 2 . [ 34 ] mm 1ÅE`Fm( r ) cos u; [ 38 ] Note that c( eq )

is a function of r only. Expression [ 31] for

u1rÅE`Fu( r ) cos u, [ 39a ]

c( eq )

as a power series in the fixed charge density of the porous sphere up to O ( QV ) is the equilibrium solution for

u1uÅ 0E` 1 2r d dr[ r 2 Fu( r ) ] sin u, [ 39b ]

the linearized Poisson – Boltzmann equation that is valid for small values of the electric potential ( the Debye – Huckel approximation ) . That is, the charge density Q of the porous

with particle must be small enough for the potential to remain small.

To solve the small quantities dmm, u , and mEfor the case

Fm( r ) Åz2mea

F

0 1 3 r a/

S

1/ 1 ka

D

e 0 ka a( kr ) ( kr )2

G

, of small parameter QV , these variables can be written as

perturbation expansions in powers of QV ,

if rõa , [ 40a ] dmmÅ 0zmeE`r cos u/ mm 1QU /mm 2QU 2/ rrr, [ 35a ] Fm( r ) Åz2mea

F

0 1 3

S

a r

D

2 / a( ka ) ka kr/1 ( kr )2 e 0 kr

G

, uÅu1QU /u2QU 2/ rrr, [ 35b ] if rúa ; [ 40b ] mEÅmE1QU /mE2QU 2_{/ rrr} , [ 35c ] Fu( r ) Å 0 ekT 4phe

HS

k l

D

2 /2 ( ka /1 ) e0 ka k 2 l2 0k2 where the functions mm j, uj, and mEj, with j Å 1, 2, . . . ,

are independent of QV . The zeroth-order terms of u and mE disappear because an uncharged particle will not move by

1

F

a( ka ) a( la ) 0 a( kr ) a( lr )

G

a( lr ) ( kr )3

J

, if rõa , [ 41a ] applying an electric field. Substituting the expansions given

by Eq. [ 35 ] and c( eq )

D

dceq1 dr dr

G

cos u, [ 45 ] 0( ka/1 ) e0 ka] 1 ( kr )3, if rúa , [ 41b ]

where functions Fm( r ) and Fu( r ) are given by Eqs. [ 40 ]

and [ 41] . Note that mm 2 takes the same forms both in the

2 ka ( 1/e02k a )01/e02k a la coth ( la )01 01/e 02k a

GJ

. [ 43 ] _{Here, ep}_{is the porosity of each particle; w}_Å_{N ( 4 / 3 ) pa}3 ( 1

0ep) /V is the true volume fraction of the porous particles; Here, the fact that the sum of the hydrodynamic frictional

L1 Å( M mÅ1z3mn`mDm (M mÅ1z 2 mn`mDm 1 ( ka )2 [ 47 ] force and electric force exerted on the porous sphere must

be zero has been used to determine mE1. Equation [ 43 ] for the electrophoretic mobility of a charged porous sphere at

for a general electrolyte; and low electric potential is the same as that obtained by

Her-mans and Fujita ( 13 ) . This formula was also derived by

Ohshima ( 22 ) who considered the electrophoresis of a soft L1Åz ( D/0D0)

D// D0

1

( ka )2, [ 48a ] spherical particle which tends to a charged porous sphere in

the absence of the particle core.

L2Å 0 ek 2 T2 2ph( D//D0) e 2A0 z 2 B [ 48b ] Among the O ( QV2

) terms in the perturbation procedure, the only distribution we need in the following calculations

is the electrochemical potential energy mm 2. If the solution _{for a symmetric electrolyte ( M}_Å _{2, z}

/ Å 0z0Å z , n`/ Å

contains only a symmetrically charged, binary electrolyte _n`

0Ån`, L`Å( D//D0) z2e2n`/ kT , where subscripts/

the equation governing mm 2is _and ₀ _{refer to the cation and anion, respectively ) . In}

Eq. [ 48b ] , Ç2_m m 2Å zme kT Ç_ceq1r

S

Çm_{m 1}0 kT Dm u1

D

. [ 44 ] _A_Å 1 ( la )2 ( ka )2/ 2/ka ( ka )8 [ a( ka ) ] 2 e02k a 0

S

k 2 l2 0k2

D

( 1/ka )2 ( ka )8 e 02k a [ a( ka ) sinh ( ka ) The boundary conditions for mm 2 are also given by Eq.

[ 37 ] with the subscript 1 of mm 1being replaced by 2. For

a general electrolyte there is an extra term on the right-hand side of Eq. [ 44 ] involving the O ( QV 2

) correction to 0sinh2 ( ka )/( ka )2 ]/ 2l 2_k2 ( l2 0k2 )2 ( 1/ka )2 ( ka )8 the equilibrium potential as expressed by Eq. [ 31] . This

extra term considerably complicates the problem. So we

1a( ka ) e02k a

FS

l

Note that Eq. [ 46 ] is correct to order w, ( ka )2

QV and ( ka )4

QV 2

are independent of k or n`, and the result of the

QV 2

term is limited to a symmetric electrolyte. As ex- 1

S

k

l

D

/ 1 4

F

4 ( ka )40 3 ( ka )5

GS

k l

D

2 . [ 53 ] pected, the electric conductivity of a suspension of

un-charged porous particles penetrable to electrolyte ions is

When la! 1 and ka is moderate, parameter A becomes the same as that in the absence of the particles ( LÅL`

if Q Å 0 ) . The coefficient L1 of the QV term, which is independent of the shielding parameter l, is proportional

A É 1 ( la )2 ( ka )2/ 2/ka ( ka )8 [ a( ka ) ] 2 e02k a

to ( ka )02, and disappears for a symmetric electrolyte when the diffusivities of the cation and anion take the same value. As to the coefficient L2of the QV 2

term for a

/( 1 /ka )

2

( ka )8 [ a( ka ) sinh ( ka ) symmetric electrolyte, the first term of the right-hand side

of Eq. [ 48b ] ( which depends on parameters ka and la )

0sinh2

( ka )/( ka )2 ] e02k a

. [ 54 ]

represents the effect due to the convection of the fluid, while the second term ( which is a function of ka only )

denotes the effect due to the deviations of the electro- When both la and ka are much smaller than unity, A reduces chemical potential distributions from their combined to

equilibrium and applied values. It is understood that the result given by Eqs. [ 46 ] – [ 49 ] is only valid with the requirements that w! 1 and ka[ ( 10 ep) / w]1 / 3_@

1. AÉ 1 ( la )2 ( ka )2/ 1 15

F

4 ( ka )20 5 ka

G

. [ 55 ] When ka!1 and la is moderate, parameters A and B in

Eq. [ 49 ] have the approximate forms

5. RESULTS AND DISCUSSION

A É1 9

F

2/ 3 ( la )2/ 2 sinh ( la ) a( la )

G

1 ( ka )20 1

3ka, [ 50a ] For an aqueous solution of KCl in which the cation and anion mobilities are nearly equal, the coefficient L1 of the QV term in Eq. [ 46 ] is small in magnitude and equal

B É 1 36ka0 1 35. [ 50b ] t o 00 . 0 17 ( k a) 0 2 (c a l cu l a te d u si n g th e v al u e s o f ek2 T2

/ 4phDmz2me2for ions at room temperature listed in Ref.

( 23 ) ) . For other electrolytes in which the ionic mobilities are very different, the magnitude of L1can be quite large; When ka@ 1 and la is still moderate, A and B become

e.g., L1 Å 00.206 ( ka )02

for NaCl and L1Å0.672 ( ka )02

for HClO4. Note that the value of electric conductivity of a suspension of charged porous particles ( L ) can be smaller or larger than that of the suspension when the porous

parti-A É 1

( la )2

( ka )2/ 1

2 ( ka )5, [ 51a ]

cles are uncharged or in the absence of the particles ( L`) , depending on the signs of L1and Q . Also, the influence of

B É 1

24

F

4 ( ka )40

9

( ka )5

G

. [ 51b ] the presence of the charged particles on the electric conduc-tivity of a suspension is reduced if the concentration of the electrolyte is increased ( i.e., k is increased ) assuming all When both ka and la are large compared with unity, Eq. other conditions are constant.

The parameters A and B in association with the coefficient [ 49a ] reduces to

(9)

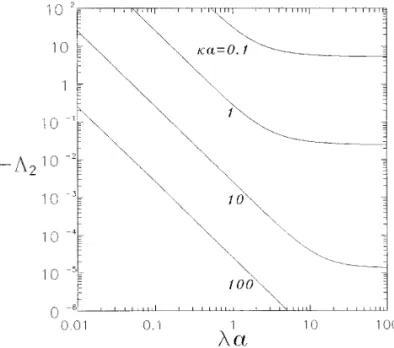
FIG. 3. Plot of the coefficient L2in Eq. [ 46 ] for the effective

conductiv-ity of a dilute suspension of identical charged porous spheres in an aqueous FIG. 1. Plot of the parameter A given by Eq. [ 49a ] for the coefficient

L2 versus ka at fixed values of la . The dotted curve is plotted for the solution of KCl versus ka at fixed values of la .

parameter B given by Eq. [ 49b ] .

01 when ka!1 and04 when ka@1, as required by Eqs. [ 50b ] and [ 51b ] . Likewise, Fig. 2 illustrates that the slope L2by Eq. [ 48b ] can be evaluated for given values of

parame-ters ka and la using Eq. [ 49 ] with the aid of a basic hand of each curve for A with constant ka equals02 when la! 1 and 0 when la@ 1, consistent with Eqs. [ 54 ] and [ 53 ] . calculator, and their results are plotted in Figs. 1 and 2

logarithmically. Figure 1 indicates that both A and B decrease Note that the situation of Bú A is possible only when la

@1 and ka) 3. monotonically with increasing ka for a given value of la ,

and Fig. 2 shows that A is a monotonic decreasing function Figures 3 and 4 show plots of the coefficient L2of the

QV 2

term in Eq. [ 46 ] as a function of parameters ka and of la for a fixed value of ka . It can be seen in Fig. 1 that

the slope of each curve for A with a constant value of la la in an aqueous solution of KCl where the value of ek2

T2

/ 2ph( D// D0) z2e2Å 0.2585 ( 23 ) is used in the

equals02 when ka ! 1 and when ka @ 1, in accordance

with Eqs. [ 50a ] and [ 51a ] , and that the slope of B equals calculations. As is the case for parameters A and B , the

FIG. 4. Plot of the coefficient L2for a KCl electrolyte versus la at

fixed values of ka . FIG. 2. Plot of the parameter A versus la at fixed values of ka .

(10)

magnitude of L2 also decreases monotonically with the APPENDIX: NOMENCLATURE increase of ka or la , the other parameter being kept

con-stant. Comparing Figs. 3 and 4 with Figs. 1 and 2, one a Radius of a porous sphere ( m)

can find that L2 is dominated by parameter A if laõ 5 A , B Parameters defined by Eqs. [ 48b ] , [ 49 ]

or if ka õ 1, and L2is dominated by parameter B if la D/, D0 Diffusion coefficients of cation and anion,

respec-@ 1 and kaú 3. tively ( m2

rs01)

Dm Diffusion coefficient of type-m ions ( m

2

rs01)

e Protonic charge ( C ) 6. CONCLUDING REMARKS

E`, E` Applied electric field ( Vr_m01₎

f Friction coefficient within the porous particle per The effective electric conductivity of a dilute suspen- _{unit volume of fluid ( kg}r_m03r_s01₎

sion of charged porous particles in an electrolyte solution _F_m _{Function defined by Eq. [ 40 ] ( C}r_m)

is analytically studied in this work. Each porous particle _F_u _{Function defined by Eq. [ 41] ( m}2_r

s01r_V01₎

is treated as a solvent-permeable and ion-penetrable ob- _h _{Unit step function}

ject in which fixed-charged groups and frictional seg- _i _{Electric current density ( A}r_m02₎

ments are distributed at uniform densities. The electric _J_m _{Number flux of type-m ions ( s}01

r_m02₎

double layer surrounding each particle is assumed not to k The Boltzmann constant ( 1.38 110023

JrK01)

overlap with the others. The average electric current den- n Unit normal vector outwardly to a surface sity passing through the suspension is given by Eq. [15 ] n` Bulk concentration of a symmetric electro-as an integral over a large spherical surface surrounding lyte ( m03

)

a single particle plus its double layer and is related to the nm Concentration of type-m ions ( m

03

)

electrochemical potential energies of the electrolyte ions. Equilibrium concentration of type-m ions ( m03

)

n( eq )

m

Solving the linearized electrokinetic equations applicable Bulk concentration of type-m ions ( m03

)

n`m

to the system of an isolated porous sphere by a regular _N _{Number of the particles in volume V of a} suspen-perturbation method, we have derived the electrochemical _sion

potential distributions of ionic species and the fluid veloc- _p _{Pressure distribution of the fluid ( N}rm02)

ity field under the application of a uniform electric field. _Q _{Fixed charge density inside the porous} par-An analytical expression, Eq. [ 46 ] , is obtained as a power _{ticle ( C}rm03)

series in the fixed charge density of the particles up to _Q_V _Å_{4peQ / ek}2

kT O ( QV 2

) for the electric conductivity of a dilute suspension _r _{Position vector relative to the center of a particle}

of identical charged porous spheres. _{( m)}

It is worth repeating that Eq. [ 46 ] with Eqs. [ 47 ] and _r _{Radial spherical coordinate ( m)} [ 48 ] is obtained on the basis of the Debye – Huckel approxi- _T _{Absolute temperature ( K )} mation for the equilibrium potential distribution around a _u _{Fluid velocity ( m}r_s01₎

porous sphere. A similar formula for the electric conductivity _u₁ _{Fluid velocity of the order Q}_{V (m}r_s01₎

of a dilute suspension of identical impermeable spheres with _u_1r_{, u1u} _{The r and u components of fluid velocity u1} low z potential was shown to give a good approximation _{( m}r_s01₎

for the case of reasonably high z potential ( with an error of _V _{A sufficiently large volume of the dilute} suspen-about 5% in a KCl solution and less than 2% in a HClO4 _{sion ( m}3

)

solution for the case of ze / kT Å 02 ) ( 2 ) . Therefore, our _x _{Position vector in the suspension ( m)} results might be used tentatively for the situation of reason- _z _{Valence of a symmetric electrolyte} ably high electric potentials. On the other hand, the decay _z_m _{Valence of type-m ions}

of the density distributions of frictional segments and fixed

charges in the porous particle with the distance from the _{Greek Letters} particle center has not been considered in our calculations.

In order to see whether our theory can be reasonably ex- a Function defined by Eq. [ 42 ]

dnm Perturbed concentration of type-m ions relative to

tended to the higher values of electric potential or to the

nonuniform density distributions of segments and fixed equilibrium ( m03

)

dmm Perturbed electrochemical potential energy of

charges, we propose to obtain a numerical solution of the

electrokinetic differential equations with no assumption on type-m ions relative to equilibrium ( J ) dc Perturbed potential relative to equilibrium ( V ) the magnitude of electric potential allowing the use of

arbi-trary distributions of charge and fluid drag components in e Å4pe0er ( C2_r J01_r

m01

)

e0 Permittivity of a vacuum ( 8.854 1 10012

the porous particle and compare it with the approximate

solution. C2_r

(11)

ep Porosity of a porous particle REFERENCES er Dielectric constant of the fluid

h Fluid viscosity ( kgr_m01r_s01₎

1. Saville, D. A., J. Colloid Interface Sci. 71, 477 ( 1979 ) . u, f Angular spherical coordinates _{2. O’Brien, R. W., J. Colloid Interface Sci. 81, 234 ( 1981 ) .} k The Debye – Huckel parameter ( m01

) 3. Watillon, A., and Stone-Masui, J., J. Electroanal. Chem. 37, 143 ( 1972 ) .

l Å( f / h )1 / 2 ( m01)

4. Saville, D. A., J. Colloid Interface Sci. 91, 34 ( 1983 ) . L Electric conductivity of the suspension

5. O’Brien, R. W., J. Colloid Interface Sci. 92, 204 ( 1983 ) . ( V01r_m01₎

6. O’Brien, R. W., and Ward, D. N., J. Colloid Interface Sci. 121, 402 L1, L2 Coefficients defined by Eqs. [ 46 ] – [ 48 ] _{( 1988 ) .}

L` Electric conductivity of the bulk electrolyte solu- 7. Ohshima, H., Healy, T. W., and White, L. R., J. Chem. Soc., Faraday

Trans. 2 79, 1613 ( 1983 ) .

tion ( V01

rm01)

8. O’Brien, R. W., and Perrins, W. T., J. Colloid Interface Sci. 99, 20 mE Electrophoretic mobility of a charged porous

par-( 1984 ) . ticle ( m2

rs01rV01)

9. van der Put, A. G., and Bijsterbosch, B. H., J. Colloid Interface Sci. mE1 Electrophoretic mobility of a charged porous par- _{75, 512 ( 1980 ) .}

ticle of the order QV (m2

rs01rV01) _{10. Zukoski, C. F., and Saville, D. A., J. Colloid Interface Sci. 107, 322} ( 1985 ) .

mm Electrochemical potential energy of type-m

11. Stigter, D., J. Phys. Chem. 83, 1663 ( 1979 ) . ions ( J )

12. Stigter, D., J. Phys. Chem. 83, 1670 ( 1979 ) . mm 1 Electrochemical potential energy of type-m ions

13. Hermans, J. J., and Fujita, H., Proc. Akad. Amsterdam B 58, 182

of the order QV (J) _{( 1955 ) .}

mm 2 Electrochemical potential energy of type-m ions _{14. Hermans, J. J., J. Polymer Sci. 18, 527 ( 1955 ) .}

of the order QV 2

( J ) 15. Imai, N., and Iwasa, K., Israel J. Chem. 11, 223 ( 1973 ) .

16. Noda, I., Nagasawa, M., and Ota, M., J. Amer. Chem. Soc. 86, 5075 Equilibrium electrochemical potential energy of

m( eq )

m

( 1964 ) . type-m ions ( J )

17. Liu, Y. C., and Keh, H. J., 1996. [ Paper presented at Electrokinetic

s Hydrodynamic stress ( Nr_m02₎

Phenomena ’96, Rome ] s1 Hydrodynamic stress of the order QV (Nrm

02

) _{18. Aoyanagi, O., Muramatsu, N., Ohshima, H., and Kondo, T., J. Colloid} w True volume fraction of the porous particles Interface Sci. 162, 222 ( 1994 ) .

19. Makino, K., Yamamoto, S., Fujimoto, K., Kawaguchi, H., and Ohs-c Electrical potential of the solution ( V )

hima, H., J. Colloid Interface Sci. 166, 251 ( 1994 ) . c( eq )

Equilibrium electrical potential of the solution (V)

20. Matsumoto, K., and Suganuma, A., Chem. Eng. Sci. 32, 445 ceq1 Function defined by Eq. [ 34 ] ( V )

( 1977 ) .

21. Masliyah, J. H., and Polikar, M., Can. J. Chem. Eng. 58, 299 ( 1980 ) .

ACKNOWLEDGMENT

22. Ohshima, H., J. Colloid Interface Sci. 163, 474 ( 1994 ) .

23. van de Ven, T. G. M., ‘‘Colloidal Hydrodynamics,’’ p. 86. Academic This research was supported by the National Science Council of the