The Fading Number of a Multiple-Access
Rician Fading Channel
Gu-Rong Lin and Stefan M. Moser, Senior Member, IEEE
Abstract—The sum-rate capacity of a noncoherent memoryless
multiple-access Rician fading channel is investigated under three different categories of power constraints: individual per user peak-power constraints, individual per user average-peak-power constraints, or a global power-sharing average-power constraint. Upper and lower bounds on the sum-rate capacity are derived, and it is shown that at high signal-to-noise ratio the sum-rate capacity only grows double-logarithmically in the available power. The asymptotic be-havior of capacity is then analyzed in detail and the exact asymp-totic expansion is derived including its second term, the so-called
fading number. It is shown that the fading number is identical to the
fading number of the single-user Rician fading channel that is ob-tained when only the user seeing the best channel is transmitting and all other users are switched off at all times. This pessimistic result holds independently of the type of power constraint that is imposed.
Index Terms—Channel capacity, escaping to infinity, fading
number, high signal-to-noise ratio (SNR), multiple-access channel (MAC), multiple-input single-output (MISO), multiple users, noncoherent detection, Rician fading, sum-rate capacity.
I. INTRODUCTION
I
N a noncoherent fading channel where neither transmitter nor receiver know the fading realization, it has been shown in [1] that the capacity at high signal-to-noise ratio (SNR) behaves fundamentally differently from the usual asymptotics seen in Gaussian channels or in coherent fading channels: instead of a logarithmic growth in the SNR, the capacity only grows double-logarithmically. To be precise, if the fading process is stationary, ergodic, and has a finite differential en-tropy rate and a finite expected second moment, then we have(1) Manuscript received February 24, 2010; revised October 29, 2010; accepted February 07, 2011. Date of current version July 29, 2011. This work was sup-ported in part by the Industrial Technology Research Institute (ITRI), Zhudong, Taiwan, under Contracts G1-98006 and 99-EC-17-A-05-01-0626; in part by the National Science Council (NSC) under Grants NSC 96-2221-E-009-012-MY3 and NSC 99-2628-E-009-002-MY3; and in part by the MediaTek Research Center, National Chiao Tung University. The material in this paper was presented in part at the IEEE Information Theory Workshop (ITW), Taormina, Sicily, Italy, October 2009.
G.-R. Lin was with the Department of Electrical Engineering, National Chiao Tung University (NCTU), Hsinchu, Taiwan. He is now with Hon-Hai Precision Ind. Co., Ltd., Taiwan.
S. M. Moser is with the Department of Electrical Engineering, National Chiao Tung University (NCTU), Hsinchu, Taiwan.
Communicated by M. Skoglund, Associate Editor for Communications. Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Digital Object Identifier 10.1109/TIT.2011.2158470
where denotes terms that tend to zero as the SNR tends to infinity; and where is a constant independent of the SNR that is called fading number. The value of depends on the exact specifications of the fading law and has been derived for the case of a general memoryless fading process in [1], [2] and for the case of a general stationary, ergodic and regular fading process in [1], [3], [4].
The present work is a first step towards generalizing the setup to a multiple-user situation. Concretely, we include transmit-ters, each having a certain number of antennas and trying to communicate to a common receiver with only one antenna. The fading law is assumed to be memoryless both over time and space and Gaussian distributed with line-of-sight (LOS) compo-nents. We will propose upper and lower bounds on the sum-rate capacity of this channel and derive the exact asymptotic expan-sion of the sum-rate capacity for the SNR tending to infinity.
The remainder of this paper is structured as follows. After some short remarks about notation we will introduce the mul-tiple-access (MAC) Rician fading channel and three different power constraints in Section II. In Section III we will derive upper and lower bounds on the sum-rate capacity of this model that are valid for all SNR. In Sections IV and V the asymptotic behavior of the sum-rate capacity will be analyzed and stated ex-actly. The proof of the main result can be found in Section VI. We conclude in Section VII.
We try to clearly distinguish random and constant quantities: while random quantities are denoted by capital Roman letters, constants are typeset in small Romans or the Greek alphabet. To distinguish numbers from vectors, vectors are in bold face, e.g., denotes a random vector and its realization, while is a random variable and its realization. There are a few excep-tions to this rule: matrices are denoted by capital letters, but of a different font, e.g., stands for capacity; for the available power; denotes the mutual information functional; and is a cumulative distribution function (CDF) of the channel input. The superscript refers to the transpose operation of vectors and matrices. We use to denote the Euclidean norm of vectors. Sets are set in calligraphic font , and denotes the comple-ment set. All rates specified in this paper are in nats per channel use, i.e., denotes the natural logarithmic function.
II. CHANNELMODEL ANDPOWERCONSTRAINTS We consider a multiple-access channel with transmitters (users) and one receiver. The signals transmitted by the users are assumed to be independent. The receiver is assumed to have only one antenna, whereas each user has some number of transmit antennas, , which yields a total number of
antennas at the transmitter side of .
All channels between one of the transmit antennas and the receiver antenna are assumed to be memoryless and indepen-dent Rician fading channels, i.e., the fading is complex Gaussian distributed with variance 1 and some mean (line-of-sight com-ponent) . To simplify our notation and because we as-sume all channels to be IID over time, we restrain ourselves from using time indices.
So the channel output can be written as
(2)
Here denotes the input vector for the antennas
of user ; the components of the random vector
de-scribe Rician fading and are assumed
to be independent ; and
denotes additive, zero-mean, circularly symmetric
Gaussian noise, independent from the fading .
We assume a noncoherent situation, i.e., neither transmit-ters nor receiver have knowledge of the current fading realiza-tion, they only know the fading distributions.1Note that we do
not restrict the receiver and/or transmitters to try to gain such knowledge. Any power or bandwidth used for such estimation schemes, however, are taken into account for the capacity anal-ysis and are not given for free as in a coherent setup. Neither will it be possible for the receiver to gain perfect channel knowledge. We do not allow cooperation between the users, i.e., we as-sume that the input vectors of the different users are statistically independent:
(3) We also mention for completeness that the users’ input vectors are assumed to be independent from fading and noise.
For simplicity of notation, we will sometimes collect all LOS vectors into one -vector
(4) the fading vectors into one fading vector of length
(5) and the input vectors of all users into one -vector
(6) In the given setup we can consider several possible constraints on the power. We will analyze three different scenarios:
• Peak-Power Constraint: At every time-step, every user is allowed to use a power of at most
(7)
for some fixed number .
1Note that the constant line-of-sight (LOS) vectorsd are part of the
distri-butions and are, therefore, known everywhere.
• Average-Power Constraint: Averaged over the length of a codeword, every user is allowed to use a power of at most
(8)
for some fixed number .
• Power-Sharing Average-Power Constraint: Averaged over the length of a codeword all users together are al-lowed to use a power of at most
(9)
for some fixed number .
Note that if for all , we have the special case where all users have an equal power available. Also note that in (7) and (8) we have normalized the power to the number of users . This might be strange from an engineering point of view; however, in regard of our freedom to choose , it is irrelevant, and it simplifies our analysis because we can easily connect the power-sharing average-power constraint with the other two constraints. Indeed, if we define to be the average of the constants , i.e.,
(10)
then the three constraints are in order of strictness: the peak-power constraint is the most stringent of the three constraints in the sense that if (7) is satisfied for all , then the other two constraints are also satisfied; and the average-power constraint is the second most stringent in the sense that if (8) is satisfied for all , then also the power-sharing average-power constraint (9) is satisfied. In the remainder of this paper we will always assume that (10) holds.
It is worth mentioning that the slackest constraint, i.e., the power-sharing average-power constraint, implicitly allows a form of cooperation: while the users are still assumed to be statistically independent, we do allow cooperation concerning power distribution. This is not very realistic, however, we include it anyway because it will help in deriving bounds on the sum-rate capacity. As a matter of fact, it will turn out that the asymptotic sum-rate capacity is unchanged irrespective of which constraint is assumed.
The sum-rate capacity of the channel (2) is given by
(11)
where the supremum is over the set of all probability distri-butions of the input vectors such that the users are statisti-cally independent of each other (3), and such that one particular power constraint (7), (8), or (9) is satisfied.
III. NONASYMPTOTICBOUNDS ON THESUM-RATECAPACITY
A. Relationship Between MAC and MISO
We derive an upper and a lower bound on the sum-rate ca-pacity (11) by properly changing the setup to a single-user situ-ation.
Firstly, we upper-bound by dropping the indepen-dence-constraint (3), i.e., allowing full cooperation among all users. Moreover, we choose the most relaxed power constraint (9)
(12)
(13)
Here, denotes the (single-user) capacity of the
multiple-input single-output (MISO) Rician fading channel with transmitter antennas (and one receiver antenna)
(14) (where , and are defined in (4), (5), and (6), respectively) under the average-power constraint
(15) On the other hand, obviously the sum rate cannot be smaller than the single-user rate that can be achieved if all but one user are switched off, assuming the most stringent type of power con-straint (7), and assuming the minimal amount of power among all users, i.e., for an arbitrary
(16) (17)
(18)
Here, denotes the (single-user) capacity of the
MISO Rician fading channel with transmitter antennas (and one receiver antenna)
(19) under the peak-power constraint
(20) and we define
(21)
Hence, we have the following first important result.
Theorem 1: The sum-rate capacity (11) of the
multiple-ac-cess Rician fading channel (2) under one of the three power con-straints (7), (8), or (9) is bounded as follows:
(22)
B. Bounds on Capacity of MISO Rician Fading Channel
In order to be able to derive more explicit bounds on the MAC sum-rate capacity, we make a small detour and develop some bounds on the MISO Rician fading channel. We start with an upper bound, which is a generalization of a bound from [1], based on a dual expression of mutual information.
Proposition 2: The capacity of the MISO Rician fading
channel (14) under an average-power constraint (15) is upper-bounded as follows:
(23) where denotes the exponential integral function
(24)
and where denotes Euler’s constant.
Proof: This is a generalization of an upper bound on the
single-input single-output Rician fading channel presented in [1, (166)]. It relies on a duality-based upper bound on the mutual information [1, (25)]. The details are omitted.
In order to be able to apply any lower bound on the MISO Rician fading channel to Theorem 1, we need to consider a peak-power constraint instead of an average-power constraint. We will derive two different lower bounds. The first bound re-lies on an input chosen such that the logarithm of its magnitude
is uniformly distributed in the interval for
some constant .
The second lower bound is based on a binary input
(25)
with and (independent of )
being uniform between 0 and . The induced
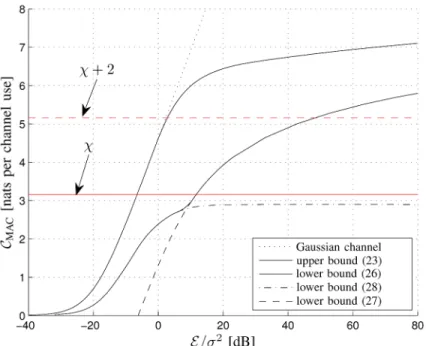
Fig. 1. Nonasymptotic bounds (22) on the sum-rate of a two-user multiple-access Rician fading channel. The dotted line shows the capacity of an additive Gaussian noise channel with equivalent received SNR. The red horizontal line corresponds to the fading number as derived in Section V, and the dashed red line is the approximate threshold + 2 nats between the efficient low-SNR and the highly inefficient high-SNR behavior.
Proposition 3: The capacity of the MISO Rician fading channel (19) under a peak-power constraint (20) is lower-bounded as follows: – (26) where (27) and (28) with (29) Here, denotes the modified Bessel function of order zero, and is defined in (24).
Proof: The derivation of the first bound is based on [1,
Lemma 4.9] and is related to [1, Corollary 4.20]. The second bound uses the binary input (25) and computes the resulting mutual information. The details are omitted.
C. Discussion
Proposition 2 and 3 can be applied directly to Theorem 1 to get bounds on the sum-rate capacity. Fig. 1 depicts an example with two users , each of them having the same power
constraint, i.e., . The LOS components are
assumed to be and , such that .
Note that the exact choice of the vectors and including their dimensions and is irrelevant for the given bounds. The LOS components influence the expressions only via their magnitudes.
We clearly see that there exist two distinct regimes: for SNR values below around 10 dB (or a rate of about nats) the sum-rate capacity grows logarithmically in the SNR, while above the threshold the growth changes dramatically and be-comes very slowly growing. We will show in the next section that this high-SNR growth is double-logarithmic.
We conclude that one should not use this channel at high SNR, and we ask for more insight about this threshold be-tween the efficient low-SNR regime and the highly inefficient high-SNR regime. As described in [4, Sec. I.B] it turns out that an asymptotic capacity analysis is the clue to such an investigation. This might seem strange at first sight as we just have concluded that we are not interested in this channel at high SNR. However, it is important to realize that around the threshold, the sum-rate capacity is dominated by the second (constant) term of the asymptotic high-SNR expansion of the sum-rate capacity (and not by the double-logarithmic term!).
Indeed, we note that nats for
dB dB and, therefore, conclude that as a rule of
thumb, the threshold will be around nats.
Hence, in deriving the asymptotic expansion of capacity one gains important understanding of the behavior of the channel at a reasonable and finite SNR. In the remainder of this paper we
will investigate the asymptotic behavior of the sum-rate capacity and in particular compute its exact asymptotic expansion.
IV. ASYMPTOTICSUM-RATECAPACITY
We will now consider the asymptotic case, i.e., the situation when the available power tends to infinity. We know that for the MISO Rician fading case2[1, Theorem 4.27]
(30) where denotes terms that tend to zero as tends to infinity and where is a constant denoted MISO fading number. Note that the value of is independent of whether we have assumed an average-power or a peak-power constraint and is given by [1, Corollary 4.28]
(31) where is defined in (24) and where denotes the LOS vector of the MISO Rician fading channel.
We further note that for any constant factor
(32) i.e., the double-logarithmic growth is not influenced by the fac-tors or in Theorem 1. Therefore, we directly get from (22), (30), and (32) the following result.
Corollary 4: The sum-rate capacity (11) of the
multiple-ac-cess Rician fading channel (2) under any one of the three power constraints (7), (8), or (9), and irrespective of the values of , grows double-logarithmically in the power at high power
(33) We next step out to analyze the second term of the high-SNR expansion of the sum-rate capacity: the MAC fading number.
Definition 5: The MAC fading number is defined as
(34)
A priori depends on the type of power constraint (7), (8), or (9) that is imposed on the input. However, it will turn out that the value of the MAC fading number is identical for all three cases. We, therefore, take the liberty to use a slightly sloppy notation that does not specify the used power constraint.
From (22), (30), and (32) we realize that
(35)
2Note that forE " 1; log 1 + log 1 + = log log + o(1).
or explicitly (by (31))
(36) where we remind the reader that is the LOS vector of user
and is the stacked LOS vector of all users.
Using the monotonicity of we now
define such that
(37) From (36), we know that
(38) In the remainder we will derive the exact value of .
We would like to point out that in [5] it has been proven that
for the two-user case with (and with
) the upper bound in (38) cannot be achieved, i.e., (39) with strict inequality.
V. MAINRESULT: THEMAC FADINGNUMBER
Theorem 6: Consider a multiple-access Rician fading
channel as defined in (2). Then, irrespective of which power constraint (7), (8), or (9) is imposed on the input and irre-spective of the values of , the MAC fading number
(34) is given by
(40) with
(41) This shows that the lower bound in (38) is tight, which is a rather pessimistic result. It means that if the magnitude of the LOS vector of one user is strictly larger than the LOS vectors of the other users, then the asymptotic sum-rate capacity can only be achieved if all but this strongest user are switched off at all times. If there are several users with LOS vectors of identical largest magnitude, the sum-rate capacity can also be achieved by time sharing among those best users.
Note that the result holds even if we allow for power sharing among the users.
VI. PROOF OFMAINRESULT
The proof of Theorem 6 consists of two parts. The first part is given already in Section IV: it is shown in (38) that
is a lower bound to . Note that this lower bound can be achieved using an input that satisfies the strictest constraint, i.e., the peak-power constraint (7).
The second part will be to prove that also is an upper bound to . We will prove this under the assumption of the slackest constraint, i.e., the power-sharing average-power constraint (9). Since the peak-power constraint (7) and the av-erage-power constraint (8) are more stringent than the power-sharing average-power constraint (9), the result will follow.
Before we start with the actual derivation of this upper bound, we need to generalize a concept that has been introduced in [1] and [3].
Proposition 7 (Input Distributions That Escape to Infinity):
Let be a family of joint input distributions of the multiple-access Rician fading channel (2), parametrized by the available power , satisfying the power-sharing average-power constraint (9), and satisfying
(42) where denotes the mutual information between input and output of this channel induced by the input distribution .
Then at least one user’s input distribution must escape to
in-finity, i.e., for any fixed
(43)
Proof: This theorem has been proven in [3, Theorem 8]
for the single-user case. It can be generalized to multiple users using the fact that a MAC can be upper-bounded by a MISO channel. The details are omitted.
To put it in an engineering way, Proposition 7 says that in the limit when the available power tends to infinity, at least one user must use a coding scheme where every used symbol uses infinite energy. Or in other words, if all users use one or more symbols with finite energy, the asymptotic growth rate of the sum-rate capacity cannot be achieved.
Definition 8: We define to be the set of families of joint input distributions of all users such that the users are indepen-dent (3), such that the power-sharing average-power constraint (9) is satisfied, and such that the input distribution of at least one user escapes to infinity when the available power tends to infinity (43), i.e.,
(44) We are now ready for the derivation of an upper bound on the MAC fading number. The following bound is derived from a duality-based bound on mutual information.
Lemma 9: The MAC fading number (34) is upper-bounded
as follows:
(45)
Proof: The proof is related to the derivation of Proposition
2, taking into account the definition of the MAC fading number (Definition 5). The details are omitted.
Noting that is a monotonically
increasing function and using our definition of in (37), we hence conclude that
(46) We would like to point out that without the constraint (43) the right-hand side (RHS) of (46) actually equals to , i.e., to the RHS of (38), from which we already know that it is (at least in some cases) strictly loose. So we see that the presented generalization of the concept of input distributions that escape to infinity (Proposition 7) is crucial to this proof.
We now continue as follows:
(47)
(48)
(49)
where in (48) we split the supremum into many separate suprema, and where (49) follows from the Cauchy-Schwarz inequality
(50) We next upper-bound the first term in (49) as follows:
(51) (52) (53) (54)
where we have defined the vector and the matrix
(55) The equality (53) follows from the Rayleigh–Ritz Theorem [6, Theorem 4.2.2].
To address the remaining terms in (49) we note that by defini-tion of in (44) at least one user’s input must escape to infinity. Without loss of generality assume that is among them. Then we can separate the remaining terms in (49) into two kinds
(56) and
(57) Our proof is concluded once we can show that
(58) (59)
for .
We start with (58) and note that by dropping some terms in the denominator we have
(60) Next, we define
(61)
and recall that if then by our assumption that
user 1 escapes to infinity. Note further that
(62)
and that is monotonically decreasing if .
Therefore, for an arbitrary choice of , we define the set as (63) and bound (64) (65) (66) Here in the first inequality (64) we define as the set of all input distributions of the first user that escape to infinity, and take the supremum over all without any constraint on the average power and no dependence on . The last inequality (66) then follows from splitting the inner integration into two parts and from the fact that the supremum of a sum is always upper-bounded by the sum of the suprema.
Next, let’s look at the first term in (66) and use (62)
(67)
(68)
(69)
(70) (71) Here, (67) follows from (62); the subsequent inequality (68) fol-lows by taking the supremum into the first integral which can only enlarge the expression; in (69) we exchange limit and in-tegration which needs justification: define
(72) (73) (74) and then note that
(75) i.e., is independent of and integrable. Thus, by the Dominated Convergence Theorem [7] we are allowed to swap limit and integration.
Finally, (71) follows from Proposition 7 because escapes to infinity.
Continuing with (66), we now have
(76) (77) (78) (79) (80) (81) for any if we choose large enough. Here (77) follows
because is monotonically decreasing if .
Since is arbitrary, we obtain
(82) This proves (58).
To prove (59), we again drop some terms in the denominator
(83) We once more use definition (61) and note that
(84)
and that is monotonically decreasing.
For an arbitrary choice of , we use the set from (63) to derive
(85)
(86)
(87)
Here in (85) we define as the set of all input distributions such that the first user escapes to infinity, and take the supremum over all joint distributions of and without any restric-tion on the average power. In the subsequent inequality (86) we apply (84) to replace by . In the last inequality we split the inner integration into two parts using (63).
For the first term in (87), we have
(88) (89) where (89) follows from a derivation analogous to (67)–(71).
The second term in (87) can be bounded as follows:
(90) (91) (92) for any if we choose large enough. Here in the first in-equality we use that is monotonically decreasing. Since is arbitrary, this proves (59) and concludes the proof.
VII. CONCLUSION
In this paper we have derived a new upper and lower bound on the sum-rate capacity of a noncoherent memoryless multiple-ac-cess Rician fading channel with transmitters (with a different number of antennas each) and one receiver (with only one an-tenna). We have shown that while the sum-rate capacity at low SNR behaves normally with a logarithmic growth in the avail-able power, at high SNR it is highly power-inefficient and only grows double-logarithmically. It is, therefore, advisable not to operate such a channel at high SNR. These bounds rely on novel bounds on the capacity of a single-user MISO Rician fading channel that are valid for any SNR.
In a second step we then derived the exact asymptotic high-SNR expansion of the sum-rate capacity, which has the form
(93) In Section III-C we have argued that such an analysis is of prac-tical importance because it allows us to gain insights on the threshold between the two SNR-regimes.
We have shown that this asymptotic sum-rate capacity is limited by the asymptotic capacity of the user seeing the best channel and can only be achieved if all users with a channel that
is strictly worse than the best channel are always switched off and cannot communicate. Note that this should not be confused with the idea of time sharing where at any given time only one user is allowed to communicate. In the presented setup, as long as the channel model does not change, the best user will remain the best user, i.e., all other users can never communicate.3
This seems at first sight very similar to a result by Knopp and Humblet [8]–[10], who showed that the strategy of one user at a time also is optimal for the MAC with full channel state infor-mation both at the transmitter and receiver side.4However, we
would like to point out that in this setup, each user can transmit regularly and has a strictly nonzero average communication rate, while in the channel model considered here, it turns out that optimally most users have a zero transmission rate. So these two results are not properly comparable.
We remark further that from the fact that the sum-rate ca-pacity is achieved in a corner where only one user has positive rate, one can deduce that the asymptotic capacity region has the shape of an -dimensional simplex.
In the analysis of the channel we have allowed for many dif-ferent types of power constraints. We grouped them into three categories: an individual peak-power constraint for each user, an individual average-power constraint for each user, and a com-bined power-sharing average-power constraint among all users. The power-sharing constraint does not make sense in a practical setup as it requires the users to share a common battery, while their signals still are restricted to be independent. However, the inclusion of this case helps with the analysis. Moreover, it turns out that the pessimistic results described above even hold if we allow for such power sharing.
Within a category of constraints, we do allow for different power settings for different users as long as the constraints scale linearly (see the constants and in (7)–(9)). It would be pos-sible to extend the shown results to situations where the power constraints among the different user differ exponentially, i.e., if every user is allowed to use a power of at most
for some . In this case, however, will influence the MAC fading number5via an additive term . This then
means that in the evaluation of the MAC fading number (40) not only is important, but also this additive term has to be taken into account.
While in this paper we have restricted the channel model to be memoryless, a generalization to a fading process with memory is possible. Again, one has to be careful as the memory will influence the MAC fading number and thereby affect the search for the best channel.
3The only exception is if there are several users having the same best channel.
In this case these equivalent best users can use time sharing to alternatively communicate.
4In [8] a continuous-time system is considered and it is shown that if the
trans-mitter and receiver have full knowledge of the fading, then it is best if the users are assigned separate frequency and time slots corresponding to best fading re-alizations (orthogonal signaling).
5The double-logarithmic term in the asymptotic expansion will remain
un-changed.
An important clue to the derivations is a generalization of the concept of input distributions that escape to infinity. Note that while we have stated this concept here specifically for the multiple-access Rician fading channel at hand, it can be further extended to more general multiple-user channels.
ACKNOWLEDGMENT
Many fruitful discussions with Amos Lapidoth are gratefully acknowledged. The authors are also indebted to the anonymous reviewers for their inspiring comments.
REFERENCES
[1] A. Lapidoth and S. M. Moser, “Capacity bounds via duality with ap-plications to multiple-antenna systems on flat fading channels,” IEEE
Trans. Inf. Theory, vol. 49, no. 10, pp. 2426–2467, Oct. 2003.
[2] S. M. Moser, “The fading number of memoryless multiple-input mul-tiple-output fading channels,” IEEE Trans. Inf. Theory, vol. 53, no. 7, pp. 2652–2666, Jul. 2007.
[3] A. Lapidoth and S. M. Moser, “The fading number of single-input mul-tiple-output fading channels with memory,” IEEE Trans. Inf. Theory, vol. 52, no. 2, pp. 437–453, Feb. 2006.
[4] S. M. Moser, “The fading number of multiple-input multiple-output fading channels with memory,” IEEE Trans. Inf. Theory, vol. 55, no. 6, pp. 2716–2755, Jun. 2009.
[5] A. Lapidoth and S. M. Moser, “On the Ricean fading multi-access channel,” presented at the Winter School Cod. and Inf. Theory, Monte Verità, Ascona, Switzerland, Feb. 24–27, 2003.
[6] R. A. Horn and C. R. Johnson, Matrix Analysis. Cambridge, U.K.: Cambridge Univ. Press, 1985.
[7] H. A. Priestley, Introduction to Integration. Oxford, U.K.: Oxford Univ. Press, 1997.
[8] R. Knopp and P. A. Humblet, Institut Eurecom, France, Multiuser Di-versity, Tech. Rep. EURECOM+607, Jan. 1997.
[9] R. Knopp and P. A. Humblet, “Information capacity and power con-trol in single-cell multiuser communications,” in Proc. IEEE Int. Conf.
Comm., Seattle, WA, Jun. 18–22, 1995, pp. 331–335.
[10] R. Knopp and P. A. Humblet, “Multiple-accessing over frequency-se-lective fading channels,” in Proc. IEEE Int. Symp. Pers., Indoor and
Mob. Radio Commun., Toronto, ON, Canada, Sep. 27–29, 1995, pp.
1326–1330.
Gu-Rong Lin was born in Taiwan. He received a Bachelor’s degree in
com-munication engineering in 2006 and a Master’s degree in comcom-munication engi-neering in 2009, both from National Chiao Tung University (NCTU), Hsinchu, Taiwan.
During 2007 to 2009, he was a member of the Information Theory Laboratory advised by Dr. Stefan Moser. He studied information theory, and focused on the field of channel capacity. His research interests include information theory, digital communications and wireless communications.
Since 2010, Gu-Rong Lin has been a communication software engineer with Hon-Hai Precision Industry.
Stefan M. Moser (S’01–M’05–SM’10) was born in Switzerland. He received
the diploma (M.Sc.) in electrical engineering (with distinction) in 1999, the M.Sc. degree in industrial management (M.B.A.) in 2003, and the Ph.D. de-gree (Dr. sc. techn.) in the field of information theory in 2004, all from ETH Zurich, Switzerland.
During 1999 to 2003, he was a Research and Teaching Assistant, and from 2004 to 2005, he was a Senior Research Assistant with the Signal and Informa-tion Processing Laboratory, ETH Zurich. Since 2005, he has been an Assistant Professor, and since 2008, an Associate Professor with the Department of Elec-trical Engineering, National Chiao Tung University (NCTU), Hsinchu, Taiwan. His research interests are in information theory and digital communications.
Dr. Moser received the Best Paper Award for Young Scholars by the IEEE Communications Society Taipei and Tainan Chapters and the IEEE Information Theory Society Taipei Chapter in 2009, the National Chiao Tung University Outstanding Researchers Award in 2007, 2008, and 2009, the National Chiao Tung University Excellent Teaching Award and the National Chiao Tung Uni-versity Outstanding Mentoring Award both in 2007, the Willi Studer Award of ETH in 1999, the ETH Medal for an excellent diploma thesis in 1999, and the Sandoz (Novartis) Basler Maturandenpreis in 1993.