保險公司殖利率曲線變動風險的免疫策略

行政院國家科學委員會專題研究計畫 成果報告

保險公司殖利率曲線變動風險的免疫策略

研究成果報告(精簡版)

計 畫 類 別 ： 個別型

計 畫 編 號 ： NSC 95-2416-H-002-043-

執 行 期 間 ： 95 年 08 月 01 日至 96 年 10 月 31 日

執 行 單 位 ： 國立臺灣大學財務金融學系暨研究所

計 畫 主 持 人 ： 曾郁仁

計畫參與人員： 博士班研究生-兼任助理：張永郎、蔡英哲、鐘正皇

報 告 附 件 ： 出席國際會議研究心得報告及發表論文

處 理 方 式 ： 本計畫可公開查詢

中 華 民 國 96 年 10 月 23 日

行政院國家科學委員會專題研究計畫成果報告

計畫編號：NSC 95-2416-H-002-043

執行期限：95 年 8 月 1 日至 96 年 10 月 31 日

主持人：曾郁仁教授 國立台灣大學財務金融學系暨研究所

計畫參與人員：研究生助理 張永郎

研究生助理 蔡英哲

研究生助理 鐘正皇

國立台灣大學財務金融學系暨研究所

中文摘要

本篇文章首先展示傳統的利率變動免

疫策略並無法排除殖利率曲線變動的風

險，本文進而提出目標規劃法來控制殖利

率曲線變動的風險。在和傳統(Tzeng et al.,

2000)的利率變動免疫策略所用的方法比

較之後，本文證明目標規劃法在盈餘管理

上非常顯著地降低了殖利率曲線變動的風

險。

關鍵字: 資產負債管理,免疫策略,殖利率曲

線變動

Abstract

This paper first demonstrates that the

immunization strategy proposed by the

traditional immunization strategy fails to

protect the surplus of an insurance company

against yield curve shift risks. Using goal

programming, we propose a new method of

immunization. The results of our simulation

show that, compared to the traditional

immunization strategy (Tzeng et al., 2000),

the goal programming proposed in this paper

can significantly reduce the risks of yield

curve shifts against an insurance company’s

surplus.

Key words: asset and liability management,

immunization strategy, yield curve shift.

Introduction

The early literature (Grove, 1974; Bierwag,

1987; and Reitano, 1991 and 1992)

recommended that insurance companies can

set the duration of assets equal to the

asset/liability ratio times the duration of

liabilities to immunize the interest-rate risk

against an insurance company’s surplus.

However, most of the research since has

shared a common assumption that the shift of

the yield curve is parallel. To recognize the

non-parallel shifts of the curve, (Tzeng, et al.,

2000) extended the traditional immunization

strategy to the case where interest rates

follow a stochastic process. However, their

strategy immunizes only the risk of a shift of

the current interest rate; and this shift has

almost no impact on the long-term yield,

since they assumed that the underlined

stochastic process of the interest rates is

unchanged. Thus, (Tzeng et al., 2000)’s

strategy can be applied to only a limited set

of non-parallel yield curve shifts.

(Reitano, 1996) proposed a

mean-variance approach to immunize an

insurer’s surplus against a stochastic shift of

the yield curve. While this idea is intriguing,

in practice it may be difficult to find the

required information for implementing this

strategy. To calculate the mean and variance

of the insurer’s surplus under a stochastic

yield curve shift, (Reitano, 1996) assumed

that the insurance company knows the

distribution of this shift. However, it be

unrealistic to assume that this information is

known in real practice.

In this paper, we intend to propose an

immunization strategy against unknown yield

curve shifts. Unlike (Reitano, 1996), we

assume that insurance companies do not

know the distribution of the stochastic yield

curve shift. The mechanism of our method

relies on the insurance company forming a

strategy to immunize parameter changes

characterized by the yield curve. (Wang and

Tzeng, 2003) proposed a method for an

insurance company to immunize the

parameter risks of the stochastic process.

However, the change of the stochastic

process is unobservable. Likewise, the

parameter changes in the stochastic process

are unobservable. Unlike (Wang and Tzeng,

2003) focus on unobservable parameter

changes in the stochastic process, our paper

focuses on the shift of the yield curve, which

is generally observable by the insurance

companies.

Thus, we first demonstrate that (Tzeng

et al., 2000)’s strategy cannot immunize the

risk of a general yield curve shift.

Furthermore, unlike (Tzeng et al., 2000)’s

focus on the current interest rate change

under a stochastic process, we follow

(Reitano, 1996)’s idea of coping directly

with the shift of the yield curve. We then

propose a goal-programming algorithm to

form the strategy against parameter changes

of the yield curve. The results of our

simulation show that, compared to (Tzeng et

al., 2000), the goal programming proposed in

this paper can significantly reduce the yield

curve shift risks against an insurance

company’s surplus.

Model

Assume that the yield curve function

)

(i

r

is as follows,

)

(

i

c

c

i

c

i

c

i

c

i

c

i

r

=

+

+

+

+

+

,

(1)

where i is the maturity period and

n

i

=

1

,...,

, )

r

(i

is the yield rate of i maturity

period, and

c ,

,

,

c

,

,

and

c

are the parameters.

____________________________________

1 _{The setting of the yield curve function is just for the}

sake of simplicity. Many models are proposed to sketch the yield curve function, e.g., (McCulloch, 1975), (Vasicek and Fong, 1982), (Nelson and Siegel,

Assume that

CI

(i

)

and )

CO

(i

are the

cash inflows and outflows of an insurance

company at i maturity period. Thus, as

evaluated by the net present value, the assets

and liabilities of an insurance company are

then equal to

∑

=

i

P

i

CI

A

)

(

)

(

∑

=

i

P

i

CO

L

)

(

)

(

(2)

where )

P

(

i

)

=

exp(

−

r

(

i

)

i

, as a discount

factor. Let S denote an insurance company’s

surplus, and S is then equal to

L A

S = −

(3)

We characterize movement of the yield

curve shift as parameter changes in Equation

(1). To immunize the risks of the yield curve

shifting under an insurance company’s

surplus management, we propose the goal

programming method as follows,

) ( min i CI

d

s.t

,

,

,

,

,

,

,

,

,...,

1

,

)

(

)

(

))

(

)

(

(

n

j

K

j

P

i

P

i

CO

i

CI

=

≥

−

∑

and

.

,...,

1

,

0

)

(

i

i

n

CI

≥

=

(4)

where d is the minimum distance of the

surplus change between the goal and the final

outcome of insurance company—i.e., the risk

position the insurance company has to bear

;

0

c

w ,

w ,

w ,

w ,

w , and

w are the

weights of the parameter risks; and

K is the

insurance company’s minimum cash flow

holding at

j maturity period.

The first six constraints in Equation (4)

control the impact on the surplus of each

parameter change. It should be noted that

insurance companies can set a smaller weight

for any parameter if they are more concerned

about a specific parameter change. Following

(Tzeng et al., 2000), we assume that an

insurance company may need to fulfill the

minimum solvency margins and may have

borrowing constraints. The last two

constraints in Equation (4) represent the

solvency and borrowing constraints for

insurance companies.

Conclusion

In this paper, we proposed to use goal

programming to form an immunization

strategy against risks of yield curve shifts.

The method in our paper could be easier to

implement in real practice than that in

(Reitano, 1996) because it copes with

observable changes of the yield curve and

requires no information about the distribution

of stochastic yield curve shifts. Moreover,

the results of our simulation show that,

compared to (Tzeng et al., 2000), the goal

programming proposed in this paper can

significantly reduce risks of yield curve shifts

against an insurance company’s surplus.

References

Bierwag, Gerald O., 1987, Duration Analysis:

Managing Interest Rate Risk, Cambridge,

MA: Ballinger Publishing Company.

immunize the yield curve shift risks---i.e., minimize the maximum surplus change of the insurance company while the parameters changed.

Cox, J. C., Ingersoll, J. E., and S. A. Ross,

1985, A Theory of the Term Structure of

Interest Rates, Econometrica, 53: 385-407.

Grove, M.A., 1974, On Duration and

Optimal Maturity Structure of the Balance

Sheet, Bell Journal of Economics and

Management Sciences, 5:696-709.

Heath, D. C., Jarrow, R. A. , and A. Morton,

1992, Bond Pricing and the Term Structure

of Interest Rates: A New Methodology for

Contingent Claims Valuation, Econometrica,

60:77-105.

Ho, T. S. and S. B. Lee, 1986, Term

Structure Movements and Pricing Interest

Rate Contingent Claims, The Journal of

Finance, 41:1011-29.

McCulloch, J., 1975, The Tax-Adjusted

Yield Curve, Journal of Finance,

30:811–830.

Nelson, C., and A. Siegel, 1987,

Parsimonious Modelling of Yield Curves,

Journal of Business, 60:473-489.

Reitano, R. R., 1991, Non-Parallel Yield

Curve Shifts and Spread Leverage, The

Journal of Portfolio Management, 82-87.

---, 1992, Non-Parallel Yield Curve Shifts

and Immunization, The Journal of Portfolio

Management, 36-43.

---, 1996, Non-Parallel Yield Curve Shifts

and Stochastic Immunization, The Journal of

Portfolio Management, 71-78.

Svensson, L.,1994, Estimating and

Interpreting Forward Interest Rates: Sweden

1992-1994, International Monentary Fund,

Working Paper no. 114.

Tzeng, L.Y., Wang, J. L., and J. Soo, 2000,

Surplus Management Under a Stochastic

Process, Journal of Risk and Insurance,

67:451-62.

Vasicek, O., 1977, An Equilibrium

Characterization of the Term Structure, The

Journal of Financial Economics, 5:177-88.

Vasicek, O. and H. Fong, 1982, Term

Structure Modelling Using Exponential

Splines, Journal of Finance, 37:339-356.

Wang, J. L. and L.Y. Tzeng, 2003, Parameter

Risks of Surplus Management Under a

Stochastic Process, Journal of Financial

Studies, 11:95-115.

計劃成果自評:

此計劃之成果已刊登於保險專刊，詳

細資料如下：

2007，何憲章、曾郁仁、張永郎，“保險

公司對殖利率曲線移動的免疫策略”，保

險專刊，23 卷, 1 期。

行政院國家科學委員會補助專題研究計畫成果報告

※※※※※※※※※※※※※※※※※※※※※※※※※※

※ ※

※

（

保險公司對殖利率曲線移動的免疫策略

） ※

※ ※

※※※※※※※※※※※※※※※※※※※※※※※※※※

計畫類別：√ 個別型計畫 □整合型計畫

計畫編號：NSC 95－2416－H－002－043

執行期間：

95 年 8 月 1 日至 96 年 10 月 31 日

計畫主持人：曾 郁 仁 教授

共同主持人：

計畫參與人員：研究生助理 張永郎

研究生助理 蔡英哲

研究生助理 鐘正皇

本成果報告包括以下應繳交之附件：

□赴國外出差或研習心得報告一份

□赴大陸地區出差或研習心得報告一份

■出席國際學術會議心得報告及發表之論文各一份

□國際合作研究計畫國外研究報告書一份

執行單位：國立台灣大學財務金融學系暨研究所

中 華 民 國

96 年 10 月 22 日

行政院國家科學委員會補助國內專家學者出席國際學術會議報告

96 年 5 月 8 日

報告人姓名

曾郁仁

服務機構

_及職稱

台灣大學財務金融系

教授

時間

會議

地點

2007/04/20~2007/04/22

美國賓州州立大學

本會核定

補助文號

NSC 95-2416-H-002-043

會議

名稱

(中文) 2007 風險理論研討會

(英文)

2007 Risk Theory Seminar

發表

論文

題目

(中文) 保險市場的隱藏後悔及優勢選擇

(英文) Hidden Regret and Advantageous Selection in Insurance

Markets

報告內容應包括下列各項：

一、參加會議經過

Risk Theory Seminar 是學術界關於風險與保險研究精英色彩相當濃

厚的會議。Risk Theory Seminar 一年舉辦一次，今年四月二十日到四月

二十二日在美國賓州州立大學舉行。此次會議共有有 10 篇論文發表，包括

許多國際知名學者的論文。

二、與會心得

個人於會議中發表一篇論文，個人的論文從從與會學者處得到很實質

的幫助。最重要的是個人透過此次會議與多位國際重要學者交換研究心得

並商討合作計畫。

三、攜回資料名稱及內容

個人出席此次論文發表會，我同時帶回許多進行中的研究論文，這些

論文包括許多進行中關於風險與保險的尖端研究，我也非常願意與國內其

他學者分享這些資料。

附

件

三

Hidden Regret and Advantageous Selection

in Insurance Markets

∗

Rachel J. Huang

Ming Chuan University

Alexander Muermann

University of Pennsylvania

Larry Y. Tzeng

National Taiwan University

March 16, 2007

Abstract

We examine insurance markets in which there are two types of customers: those who regret suboptimal decisions and those who don’t. In this setting, we characterize the equilibria under hidden information about the type of customers and hidden action. We show that both pooling and separating equilibria can exist. Furthermore, there exist separating equilibria that predict a positive correlation between the amount of insurance coverage and risk type, as in the standard economic models of adverse selection, but there also exist separating equilibria that predict a negative correlation between the amount of insurance coverage and risk type, i.e. advantageous selection.

∗_{Muermann gratefully acknowledges financial support of the National Institutes of Health - National Institute on}

Aging, Grant number P30 AG12836, the Boettner Center for Pensions and Retirement Security at the University of Pennsylvania, and National Institutes of Health — National Institute of Child Health and Development Population Research Infrastructure Program R24 HD-044964, all at the University of Pennsylvania.

1

Introduction

The markets for annuities, long-term care insurance, and Medigap insurance have become increas-ingly important for societies whose population is aging, as e.g. in the US and Europe. Surprisincreas-ingly, the demand for these insurance products is very low (see e.g. Mitchell, et al., 1999, Brown and Finkelstein, 2004) which might put a huge burden on future generations. Whether public or private insurance provision is more efficient depends on the underlying inefficiencies in these markets, a large part of which is due to asymmetric information. Interestingly, those markets exhibit contrast-ing characteristics with respect to the relation between insurance coverage and risk type.

Rothschild and Stiglitz (1976) show in their classical adverse selection model in insurance mar-kets that, in equilibrium—if it exists—lower risk individuals self-select into contracts which offer lower insurance coverage. The model thus predicts a positive correlation between the amount of insurance coverage and claim frequency. Similarly, economic models of moral hazard predict this positive relation: individuals with higher insurance coverage reduce their investments in risk-mitigating measures and thereby are of higher risk type. The empirical evidence, however, of the relation between insurance coverage and claim frequency, is mixed. In the markets for acute care health insurance and annuities the empirical evidence is consistent with the prediction of adverse selection and moral hazard models (see e.g. Cutler and Zeckhauser, 2000, Mitchell, et al., 1999, Finkelstein and Porteba, 2004). In contrast, a negative relationship between insurance coverage and claim frequency exists in the markets for term-life insurance, long-term care, and Medigap insurance (see e.g. Cawley and Philipson, 1999, Finkelstein and McGarry, 2006, Fang, et al., 2006). de Meza and Webb (2001) argue that a negative relationship between insurance coverage and risk type—which they term advantageous selection—can be explained by hidden heterogeneity of viduals’ degree of risk aversion. They show that there exist equilibria in which high risk-averse indi-viduals both purchase more insurance coverage and invest more in risk-mitigating measure—thereby becoming lower risk types—than less risk-averse individuals. The empirical evidence, however, on the sign of the negative relationship between degree of risk aversion and risk type is mixed.

Finkel-stein and McGarry (2006) find evidence in the long-term care insurance market that is consistent with advantageous selection, i.e. more risk averse individuals are more likely to purchase long-term care insurance and less likely to enter a nursing home. In contrast, Cohen and Einav (2006) and Fang, et al. (2006) find the opposite in automobile and Medigap insurance: risk type is positively correlated with risk aversion.

In this paper, we propose hidden heterogeneity in degrees of anticipatory regret as an alternative reason for a negative relationship between insurance coverage and risk type. Regret is interpreted as the anticipated disutility incurred from an ex-ante choice that turns out to be ex-post suboptimal and individuals make their decision by trading off the maximization of expected utility of wealth against the minimization of expected disutility from anticipated regret. The latter is modeled as a second attribute to the utility function that depends on the difference in utilities of wealth levels derived from the foregone best alternative and derived from the actual choice.

Our intuition suggests that individuals who consider ante a disutility associated with ex-post regret, i.e. with having foregone a better alternative, might both purchase less insurance coverage under actuarially fair prices and invest less in risk-mitigating measures than individuals who do not consider regret. We examine the existence and type of equilibria when insurers can neither observe this preference heterogeneity nor investment behavior in risk-mitigating measures. We are particularly interested in deriving conditions under which separating equilibria exist that are consistent with advantageous selection. The interesting and challenging feature of anticipatory regret is that foregone alternatives, and thus the menu of insurance contracts offered, impact individual welfare which could imply the existence of pooling equilibria.

Regret theory was initially developed by Bell (1982) and Loomes and Sugden (1982) and has been shown in both the theoretical and experimental literature to explain individual behavior. More recently, the impact of regret on decision making has been examined in different scenarios. Braun and Muermann (2004) and Muermann, et al. (2006) show that regret moves individuals away from extreme decisions, i.e. regret leads to more (less) insurance coverage if insurance is relatively expensive (cheap) and, similarly, regret leads financial investors to buy more (less) risky

stocks if the equity risk premium is relatively high (low). In a dynamic setting, Muermann and Volkman (2006) show that anticipatory regret and pride can cause investors to sell winning stocks and hold on to losing stocks, i.e. it can explain behavior that is consistent with the disposition effect. Regret preferences have also been applied to asset pricing and portfolio choice in an Arrow-Debreu economy (Gollier and Salanié 2006), to currency hedging (Michenaud and Solnik 2006), and to first price auctions (Filiz and Ozbay 2006).

In this paper, we contribute to the literature above by considering the equilibrium effects under asymmetric information in a market in which both types of investors coexist, those that consider anticipated regret in their decision-making, and those that do not.

In the following section, we introduce the model and derive properties of indifference curves as those will be used for our graphical analysis of equilibria in Section 3. In Section 4 we derive comparative statics of model parameters with respect to the existence and type of equilibria. We conclude in Section 5.

2

Model Approach

The model will focus on two types of individuals: those that regret suboptimal decisions, type R individuals, and those that do not, type N individuals. Let λ be the fraction of type R individuals in the population. Both types are endowed with initial wealth w and face a potential loss of size

L with initial probability p0. Individuals can invest in self-protection at a disutility fi ∈ {0, F },

i = N, R, to reduce the probability of a loss from p (0) = p0 to p (F ) = pF < p0. Type N individuals

maximize expected utility with respect to an increasing, concave utility function u (·). For type R individuals, we follow Bell (1982) and Loomes and Sugden (1982) by implementing the following two-attribute utility function to incorporate regret in preferences

Type R individuals thus maximize expected utility with respect to the utility function uR(·).1

The first attribute is the utility derived from the final level of wealth, W , and is thus equivalent to the utility of type N individuals. The second attribute accounts for the fact that the individual considers regret in his decision-making. Regret depends on the difference between the utility of

wealth, Wmax, the individual could have obtained with the foregone best alternative (FBA) and

the utility of actual final wealth, W . The function g (·) measures the disutility incurred from regret and we assume that g (·) is increasing and convex with g (0) = 0. This assumption is supported in the literature (Thaler, 1980, Kahneman and Tversky, 1982) and has recently found experimental support by Bleichrodt et al., 2006.

Insurers are risk-neutral and offer insurance contracts which are specified by the amount of insurance coverage, I, and the premium rate, c, per dollar of coverage. We assume that there is asymmetric information about both preferences and actions. That is, whether or not a specific individual regrets his decision and whether or not he invests in risk-mitigating measures is pri-vate information to the individual. The insurer only knows the distribution of the two types of individuals, N and R, in the population; that is, the insurer knows the parameter λ.

2.1

Investing in self-protection

The gains in expected utility for type i individuals, ∆i(I, c), i = N, R, from investing in

self-protection under an insurance contract (I, c) is

∆N(I, c) = (p0− pF) (u (w − cI) − u (w − L + (1 − c) I)) − F (2)

1

This two-attribute utility function is consistent with the axiomatic foundation of regret developed by Sugden (1993) and Quiggin (1994).

for type N individuals and

∆R(I, c) = ∆N(I, c) − pFg (u (WLmax) − u (w − L + (1 − c) I) + F )

+p0g (u (WLmax) − u (w − L + (1 − c) I))

− (1 − pF) g (u (WN Lmax) − u (w − cI) + F ) + (1 − p0) g (u (WN Lmax) − u (w − cI))

(3)

where W_Lmax and W_{N L}max are the wealth levels under the FBA in the Loss and No-Loss state,

re-spectively. As investing in self-protection only has ex-ante value to the insured, it is never opti-mal from an ex-post point of view to have invested in self-protection. In the No-Loss state, the FBA is thus to not have invested in self-protection and to not have bought insurance coverage, i.e.

W_{N L}max= w. In the Loss state, the FBA is to have bought the contract with the highest net coverage

(1 − ˜c) ˜I = arg max(I,c)(1 − c) I amongst the set of contracts offered, i.e. WLmax= w −L+(1 − ˜c) ˜I.

Let X = ³

˜ I, ˜c

´

denote the insurance contract with the highest net insurance coverage amongst the set of contracts offered. Therefore

∆R(I, c) = ∆N(I, c) − pFg ³ u³_{w − L + (1 − ˜c) ˜}I´_{− u (w − L + (1 − c) I) + F}´ +p0g ³ u³_{w − L + (1 − ˜c) ˜}I´_{− u (w − L + (1 − c) I)}´ − (1 − pF) g (u (w) − u (w − cI) + F ) + (1 − p0) g (u (w) − u (w − cI)) . (4)

The gains from investing in self-protection is larger for the type N individuals if the cost of

investing in self-protection, F , is high enough. More precisely, (4) implies that ∆N(I, c) > ∆R(I, c)

if and only if F satisfies the following inequality

pFg ³ u³_{w − L + (1 − ˜c) ˜}I´_{− u (w − L + (1 − c) I) + F}´_{+ (1 − p}F) g (u (w) − u (w − cI) + F ) > p0g ³ u ³ w − L + (1 − ˜c) ˜I ´ − u (w − L + (1 − c) I) ´ + (1 − p0) g (u (w) − u (w − cI)) . (5)

To demonstrate the existence of equilibria in which there exists a negative relation between insurance coverage and risk type, i.e. advantageous selection, we assume that the cost of investing in self-protection, F , is high enough such that type R individuals will not find it optimal to invest

in self-protection under any contract, i.e. we assume a level of F such that ∆R(I, c) < 0 for all I

and c with pF ≤ c ≤ p0.

2.2

Demand for insurance

Braun and Muermann (2004) have shown that type R individuals “hedge their bets” by avoiding extreme decisions. That is, type R individuals purchase more (less) insurance coverage than type N individuals if it is optimal for type N individuals to purchase very little (a lot of) insurance coverage. This implies that type R individuals value insurance coverage relatively more (less) than type N individuals if an insurance contract offers very little (a lot of) coverage.

2.3

Graphical analysis

We will use diagrams to analyze the existence of equilibria. In all diagrams, the x-axis represents

the individuals’ level of final wealth in the No-Loss state, WN L = w −cI, whereas the y-axis denotes

the individuals’ level of final wealth in the Loss state, WL = w − L + (1 − c) I. The individuals’

endowment point is (w − L, w) and labeled A. PF, ¯P, and P0 denote the actuarially fair pricing

lines with respect to the premium rates c = pF,c = ¯p = λpF + (1 − λ) p0, and c = p0, respectively.

Type N individuals. The levels of expected utility for type N individuals investing and not

investing in self-protection under contract (I, c) are

EUN(I, c, F ) = pFu (WL) − (1 − pF) u (WN L) − F

and

The slope of type N individuals’ indifference curve are dWL dWN L|EUN(I,c,F )= − 1 − pF pF u0(WN L) u0_(WL) and dWL dWN L|EUN(I,c,0) = − 1 − p0 p0 u0(WN L) u0_(WL) .

The slope of the locus of contracts under which type N individuals are indifferent between

investing and not investing in self-protection, i.e. for which ∆N(I, c) = 0, is given by

dWL dWN L|∆N(I,c)=0 = u 0_(W N L) u0_(WL) .

The line of those contracts is thus increasing and below the 45◦ _{line as 0 <} dWL

dWN L|∆N(I,c)=0 < 1.

Furthermore, for any premium rate c there exists a unique level of coverage ¯I (c) < L such that

∆N

¡_¯

I (c) , c¢ = 0. Since ∂∆N(I,c)

∂WL < 0 we conclude that it is optimal for types N individuals

to not invest in self-protection under all contracts that are above the line of contracts for which

∆N

¡_¯

I (c) , c¢= 0. For all contracts below this line, it is optimal for type N individuals to invest in

self-protection. Note, that for all contracts with ∆N

¡_¯

I (c) , c¢ = 0, indifference curves are kinked

with a steeper slope below than above as ¯ ¯ ¯ ¯ dWL dWN L|EUN(I,c,F ) ¯ ¯ ¯ ¯ > ¯ ¯ ¯ ¯ dWL dWN L|EUN(I,c,0) ¯ ¯ ¯ ¯ .

Type R individuals. The level of expected utility of type R individuals not investing in

self-protection under contract (I, c) is

EUR(I, c, 0) = EUN(I, c, 0)−p0g

³

u³_{w − L + (1 − ˜c) ˜}I´_{− u (W}L)

´

Note that the expected utility of type R individuals and therefore the shape of the indifference

curves depends upon the contract X =³I, ˜˜ c´that offers the highest net insurance coverage. The

slope of type R individuals’ indifference curve is

dWL dWN L|EUR(I,c,0)= − 1 − p0 p0 u0_{(WN L)} u0_(WL) 1 + g0_{(u (w) − u (WN L))} 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ < 0. (6)

The second derivative of type R individuals’ indifference curve is given by

d2WL dW2 N L |EUR(I,c,0) = − µ dWL dWN L|EUR(I,c,0) ¶2 u00(WL) u0_(WL) − 1 − p0 p0 u00(WN L) u0_(WL) 1 + g0_{(u (w) − u (W}N L)) 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ + µ dWL dWN L|EUR(I,c,0) ¶2 u0(WL) g00³u³_{w − L + (1 − ˜c) ˜}I´_{− u (W}L) ´ 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ +1 − p0 p0 (u0(WN L))2 u0_(WL) g00_{(u (w) − u (W}N L)) 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ > 0.

Type R individuals’ indifference curve are thus also both decreasing and convex.

Comparison of indifference curves between types. We next compare the slopes of the

indifference curves of type R and type N individuals with contracts under which type N individuals invest in self-protection. The indifference curve of type R individuals are flatter than the one of type N individuals if and only if

1 − p0 p0 1 + g0_{(u (w) − u (W}N L)) 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ ≤ 1 − pF pF . (7)

At the endowment point A = (w − L, w) condition (7) is satisfied and the indifference

increasing the amount of coverage I at the same premium rate c on the left-hand side of condition (7) is ∂ ∂I ⎛ ⎝ 1 + g0(u (w) − u (WN L)) 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ ⎞ ⎠ = cu0(WN L) g00(u (w) − u (WN L)) 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ +(1 − c) u 0_(W L) g00 ³ u³_{w − L + (1 − ˜c) ˜}I´_{− u (W}L) ´ (1 + g0_{(u (w) − u (W}N L))) ³ 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´´2 > 0.

This implies that, for a given premium rate c and contract X = ³I, ˜˜ c´, condition (7) can only

switch once at the unique level of insurance coverage ˆI = ˆI (c, X). We thus conclude that for

low levels of coverage the indifference curve of type R individuals are flatter than the one of type N individuals whereas for high levels of coverage the indifference curve of type R individuals can be steeper than the one of type N individuals. This is consistent with the result of Braun and Muermann (2004) who show that type R individuals value insurance coverage relatively more (less) than type N individuals if an insurance contract offers very little (a lot of) coverage. Valuing insurance coverage relatively more (less) implies a flatter (steeper) indifference curve.

At the level I = ˆI (c, X), the indifference curves or type R and type N individuals have the

same slope, i.e. condition (7) is satisfied with equality which implies

d2WL dW_{N L}2 |EUR(I,c,0) = d 2_W L dW2 N L |EUN(I,c,F )+ µ dWL dWN L|EUR(I,c,0) ¶2 u0(WL) g00 ³ u ³ w − L + (1 − ˜c) ˜I ´ − u (WL) ´ 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ +1 − p0 p0 (u0(WN L))2 u0_(WL) g00_{(u (w) − u (W}N L)) 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ d2WL

The indifference curve of type R individuals at I = ˆI (c, X) are thus more convex than the one of type N individuals for all premium rates c and contracts X.

Changing the foregone best alternative. An interesting feature of regret is that preferences

depend upon foregone alternatives. In particular, insurance companies can change preferences of

type R individuals by offering a contract X with higher net insurance coverage (1 − ˜c) ˜I. The

impact of increasing net insurance coverage of the foregone best alternative on the slope of the indifference curve of R types is

∂ ∂ (1 − ˜c) ˜I µ dWL dWN L|EUR(I,c,0) ¶ = − ∂ ∂ (1 − ˜c) ˜I ⎛ ⎝ 1 + g0(u (w) − u (WN L)) 1 + g0³_u³_{w − L + (1 − ˜c) ˜I}´_{− u (WL)}´ ⎞ ⎠ > 0.

This implies that the indifference curves of types R individuals become flatter at any contract (I, c). The intuition is that increasing net insurance coverage of the foregone best alternative increases the regret in the Loss-state and thereby makes coverage relatively more valuable to type R individuals. This implies that offering a contract with a higher net insurance coverage increases the level of

coverage I = ˆI (c, X) at which condition (7) switches.

3

Equilibrium Analysis

We have shown that type R individuals might be both less willing to invest in self-protection and prefer less insurance coverage than type N individuals. These results suggests that there can be equilibria in which there exists a negative relation between insurance coverage and risk type, i.e. advantageous selection. We consider the following game between insurers and individuals:

Stage 1 Insurers make binding offers of insurance contracts specifying coverage I and premium

rate c.

Stage 2 Individuals choose either a contract from the set of contracts offered or no contract. If

Stage 3 Individuals choose whether or not to invest in self-protection.

We will consider the existence and type of pure-strategy, subgame-perfect Nash equilibria. As examined above, regret introduces two interesting features. First, types R individuals value insurance relatively more (less) than type N individuals if the level of coverage offered is small (large). Second, the foregone best alternative and thus the expected utility of type R individuals depends on the set of contracts offered. An insurance company could thus strategically offer two contracts: one contract, contract X, is only offered to change the expected utility of type R individuals and the other contract serves the purpose of attracting customers given the shift in preferences of type R individuals. We can restrict our strategies to those where the “preference-shifting” contract X offers a higher net coverage than the other contracts offered as only then type R preferences shift. In our equilibrium analysis, we thus have to carefully examine those strategies.

3.1

Pooling equilibria

In this section, we examine the existence of pooling equilibria as a function of the level of coverage offered and via graphical analysis. The main result of this section is that, contrary to Rothschild and Stiglitz (1976) and de Meza and Webb (2001), a pooling equilibrium can exist. As defined

above, contract ( ˆI (¯p, X) , ¯p) denotes the contract with premium rate ¯p under which the indifference

curve of type R individuals have the same slope than the one of type R individuals and contract ¡_¯

I (¯p) , ¯p¢denotes the contract with premium rate ¯p under which type N individuals are indifferent

between investing and not investing in self-protection, i.e. ∆N

¡_¯

I (¯p) , ¯p¢ = 0. As shown above,

both contracts are unique.

Proposition 1 Suppose that the cost of investing in self-protection, F , is high enough such that

∆R(I, c) < 0 for all I and c with pF ≤ c ≤ p0.

2. If ˆI (¯p, X) < ¯I (¯p) for X = (L, c0) where c0 is implicitly defined by EUN

¡_¯

I (¯p) , ¯p, F¢ =

EUN(L, c0, 0), then the contract

¡_¯

I (¯p) , ¯p¢is the unique pooling equilibrium if and only if

(a) EUR¡I (¯¯ p) , ¯p, 0¢> EUR(I, p0, 0) for all I

(b) EUN

¡_¯

I (¯p) , ¯p, F¢> EUN(I, ¯p, F ) for all I that satisfy EUR(I, ¯p, 0) > EUR

¡_¯

I (¯p) , ¯p, 0¢

(c) EUN

¡_¯

I (¯p) , ¯p, F¢> EUN(I, p0, 0) for all I with ∆N(I, p0) < 0

Proof. First note that no pooling equilibrium exists under which neither type R nor type N invest

in self-protection. Type N individuals prefer full coverage and type R individuals prefer partial

coverage as shown in Braun and Muermann (2004), i.e. for any pooling contract (I, p0) there exist

a contract to which either type R or type N individuals deviate. We can thus restrict our analysis to all contracts (I, ¯_{p) with I ≤ ¯}I (¯p).

1. Suppose ˆI (¯p, X) > ¯I (¯p) for some contract X. This implies for any pooling contract B = (I, ¯p)

we must have I < ˆI (¯p, X). We have shown above that for all I < ˆI (¯p, X) the indifference

curve of type R individuals are flatter than the one of type N individuals, i.e. (7) is satisfied (see Figure 1). This implies that no pooling equilibrium exist under those contracts as a contract with slightly less coverage and a potentially different premium rate (contract D in Figure 1) attracts type N individuals but not type R individuals. Note that contract D does not change preferences of type R individuals as it offers lower net indemnity than contract

B. The intuition behind this result is that for low levels of coverage I < ˆI (¯p, X) type R

individuals value insurance coverage relatively more than type N individuals and can thus not be attracted by such contracts. This is equivalent to the proof in Rothschild and Stiglitz (1976) who show that under any pooling contract there exist contracts that attract low-risk types but not high-risk types as high-risk types value insurance coverage relatively more. Suppose ˆI (¯p, X) = ¯I (¯p). Contract B = ( ˆI (¯p, X) , ¯p) in Figure 2 cannot be a pooling

equilib-rium as the indifference curve of type R individuals at I = ˆI (¯p, X) are more convex than the

and a potentially different premium rate which attracts type N individuals but not type R individuals (contract D in Figure 2). Again, contract D does not change preferences of type R individuals as it offers lower net indemnity than contract B.

2. Suppose ˆI (¯p, X) < ¯I (¯p) with X = (L, c0) where c0 is defined as above. Contract X (see

Figure 5) is the contract with the highest net insurance coverage such that neither type R nor

type N individuals will prefer X over ¡I (¯¯ p) , ¯p¢. As argued above, any contract B = (I, ¯p)

with I < ˆI (¯p, X) cannot be a pooling equilibrium. Equivalently to above, the contract

B = ( ˆI (¯p, X) , ¯p) is also not a pooling equilibrium (see Figure 3).

For any contract B = (I, ¯p) with ˆI (¯p, X) < I < ¯I (¯p), the indifference curve of type R indi-viduals is steeper than the one of type N indiindi-viduals, i.e. type N indiindi-viduals value insurance coverage relatively more than type R individuals (see Figure 4). A contract offering slightly more coverage and a potentially different premium rate (contract D in Figure 4) attracts type N individuals but not type R individuals. Note, however, that the introduction of con-tract D does not change the preferences of type R individuals as concon-tract X offers higher

net insurance coverage than contract D. Thus, no pooling equilibria B = (I, ¯p) exist with

ˆ

I (¯_{p, X) ≤ I < ¯}I (¯p).

Now let’s examine contract B = ¡I (¯¯ p) , ¯p¢ (see Figure 5). Since ˆI (¯p, X) < ¯I (¯p), the indif-ference curve of type R individuals is steeper at B than the one of type N individuals. This

implies that there does not exist any contract (I, c) with ∆N(I, c) > 0 that attracts type N

individuals but not type R individuals. Condition 2a implies that any contract (I, c) with

∆N(I, c) < 0 must offer a rate c < p0 to attract type N individuals and thereby make

neg-ative profits. Condition 2b ensures that no other contract (I, ¯p) on the price line ¯Pattracts

both types of individuals. Last, condition 2c implies that no contract (I, p0) on the price line

P0 attracts type R individuals. Therefore, B = ¡I (¯¯ p) , ¯p¢constitutes a pooling equilibrium

In the pooling equilibrium, type R individuals value insurance coverage relatively less than type R individuals, i.e. the amount of insurance coverage must be relatively high. Offering less coverage would be relatively more attractive to type R individuals and, under the conditions above, yield negative expected profits. Offering more coverage would induce type N individuals to not invest in self-protection and also imply negative expected profits.

3.2

Separating equilibria

In this section, we examine the existence and type of separating equilibria. We assume that each contract offered and chosen by individuals must earn non-negative expected profits. We thus do not allow for cross-subsidization between types as it is examined, for example, in Miyazaki (1977) and Crocker and Snow (1985).

Under the assumption that type R individuals do not invest in self-protection, the contract

chosen by type R individuals in equilibrium is priced at the rate c = p0 and offers the optimal

amount of coverage I_R∗ = I_R∗(p0, X), given contract X that offers the highest net insurance

cover-age. Let us denote this contract by R = (I_R∗ (X) , p0). As shown by Braun and Muermann (2004)

that the optimal amount of coverage at a fair rate is less than full coverage, i.e. I_R∗ (p0, X) < L for

all X. As optimal amount of coverage depends on contract X, three contracts might be offered in separating equilibria: contract N and R chosen by types N and R individuals, respectively, and the “preference-changing”contract X which is not chosen by any type of individual. In equilib-rium, contract X must offer the highest net insurance coverage such that neither type chooses the

contract. If a contract X0 with lower net insurance coverage and thus R (X0) = (I_R∗(p0, X0) , p0) is

offered then offering contract X with higher net insurance coverage than X0 together with contract

R (X) = (I_R∗(p0, X) , p0) attracts type R individuals as the optimal amount of insurance coverage

is increasing in the net insurance coverage of the foregone best alternative in the Loss-state. In the following proposition we show that there exists a separating equilibrium under which both types do not invest in self-protection and both types receive the optimal amount of coverage

Proposition 2 Suppose that the cost of investing in self-protection, F , is high enough such that

∆R(I, c) < 0 for all I and c with pF ≤ c ≤ p0. Then the two contracts N = (L, p0) and R =

(I_R∗ (p0, X) , p0) constitute a separating equilibrium if and only if EUN(L, p0, 0) > EUN(I, ¯p, F ) for

all I ≤ ¯I (¯p) that satisfy EUR(I, ¯p, 0) ≥ EUR(I_R∗ (p0, X) , p0, 0).

Proof. Figure 6 illustrates the equilibrium. In this scenario, the “preference-changing”contract

X with the highest net insurance coverage coincides with contract N . The additional condition outlined in the proposition assures that no pooling contract can attract both types of individuals while making zero expected profits.

In the separating equilibrium outlined above, both types of individuals do not invest in self-protection but purchase different amounts of insurance coverage. The empirical prediction under this scenario is thus that both types are of identical risk-type and that type R individuals purchase less insurance coverage than type N individuals. The equilibrium contracts only separate different preference type individuals rather than risk type as in Rothschild and Stiglitz (1976). Note that the premium rates for both types are the same. Thus, this type of equilibrium predicts that the premium rate and coverage will be insignificant related in empirical studies.

3.2.1 Advantageous selection

In the following proposition, we show that there exist and characterize separating equilibria that predict a negative relationship between insurance coverage and risk type, i.e. advantageous

selec-tion. As above, we denote the amount of coverage ¯I = ¯I (c) under which type N individuals are

indifferent between investing and not investing in self-protection, i.e. under which ∆N

¡_¯

I (c) , c¢= 0.

Proposition 3 Suppose that the cost of investing in self-protection, F , is high enough such that

∆R(I, c) < 0 for all I and c with pF ≤ c ≤ p0. Then the three contracts N , R, and X constitute

a separating equilibrium with advantageous selection if and only if under one of the following two scenarios:

(a) c satisfies EUN ¡_¯ I (pF) , pF, F ¢ = EUN(L, c, 0) and c ≥ p0 (b) EUR(IR∗ (p0, X) , p0, 0) ≥ EUR ¡_¯ I (pF) , pF, 0 ¢ 2. N =¡I (c¯ N) , cN ¢ , X = (L, c), and R = (I_R∗(p0, X) , p0) where (a) cN satisfies EUN ¡_¯ I (cN) , cN, F ¢ = EUR(I_R∗ (p0, X) , p0, 0)

(b) c is the maximum rate that satisfies both EUN

¡_¯ I (cN) , cN, F ¢ ≥ EUN(L, c, 0) and EUR(IR∗ (p0, X) , p0, 0) ≥ EUR(L, c, 0), and c ≥ p0 (c) EUR ¡_¯ I (¯p) , ¯p, 0¢_{≤ EU}R(IR∗ (p0, X) , p0, 0) ≤ EUR ¡_¯ I (pF) , pF, 0 ¢ (d) EUN ¡_¯ I (cN) , cN, F ¢

≥ EUN(I, p0, F ) where I satisfies EUR(IR∗ (p0, X) , p0, 0) = EUN(I, pF, F )

(e) EUN

¡_¯

I (cN) , cN, F

¢

≥ EUN(I, ¯p, F ) for all I ≤ ¯I (¯p) that satisfy EUR(I, ¯p, 0) ≥

EUR(I_R∗ (p0, X) , p0, 0)

Proof.

1. Figure 7 illustrates the equilibrium. Condition 1b represents the property that the indifference

curve of type R individuals through contract R crosses the locus of contracts ∆N(I, c) = 0

above the line PF. Contract N is then the best contract for type N individuals among the

set of contracts on PF that are not preferred by type R individuals over contract R. Contract

X = (L, c) is the contract with highest net coverage that is not preferred by either type over

their respective equilibrium contract. The condition c ≥ p0 assures that contract (L, p0) does

not attract type N individuals.

2. Figure 8 illustrates this equilibrium. Condition 2a defines contract N . Condition 2c represents the property that the indifference curve of type R individuals through contract R crosses the

locus of contracts ∆N(I, c) = 0 below the line PF but above the line ¯P. Conditions 2d and 2e

assure that type N individuals do neither prefer contract N0 nor prefer any pooling contract

The key factor that allows for separating equilibria with advantageous selection is the fact that type R individuals prefer partial coverage at a fair rate. Type N individuals can separate themselves from type R individuals with more insurance coverage since they value insurance coverage relatively more at the fair rate. Both equilibrium 1 and equilibrium 2 in the above proposition have interesting features.

In equilibrium 1, the presence of type R individuals in the market does not cause any

neg-ative externality on type N individuals. The equilibrium contracts N = ¡I (p¯ F) , pF

¢

and R =

(I_R∗ (p0, X) , p0) are identical to the equilibrium contract under hidden action if there were only one

type of customers in the market. Equilibrium 1 is in fact the only equilibrium with that feature. In equilibrium 2, insurance companies make strictly positive expected profits with contract N while they break even with contract R. However, this is true only under pure separation and also due to the fact that we do not allow for cross-subsidies between types. This implies that there exist semi-separating equilibria under the conditions outlined in equilibrium 2 in which a certain fraction of type R individuals choose contract N . The maximum fraction of those types is determined by the break-even condition of insurance companies for contract N .

3.2.2 Adverse selection

In this section, we characterize the separating equilibrium that predicts a positive relationship between insurance coverage and risk type, i.e. adverse selection.

Proposition 4 Suppose that the cost of investing in self-protection, F , is high enough such that

∆R(I, c) < 0 for all I and c with pF ≤ c ≤ p0. Then the three contracts N = (IN, pF), R =

(I_R∗ (p0, X) , p0), and X = (L, c) constitute a separating equilibrium with adverse selection if and

only if

(b) c is the maximum rate that satisfies both EUN(IN, pF, F ) ≥ EUN(L, c, 0) and EUR(IR∗ (p0, X) , p0, 0) ≥ EUR(L, c, 0), and c ≥ p0 (c) EUR(I_R∗ (p0, X) , p0, 0) ≤ EUR¡I (p¯ F) , pF, 0¢ (d) EUN(IN, p0, F ) ≥ EUN ¡_¯ I (cN) , cN, F ¢ where cN satisfies EUR(I_R∗(p0, X) , p0, 0) = EUR ¡_¯ I (cN) , cN, 0 ¢ (e) EUN ¡_¯ IN, pF, F ¢

≥ EUN(I, ¯p, F ) for all I ≤ ¯I (¯p) that satisfy

EUR(I, ¯p, 0) ≥ EUR(IR∗ (p0, X) , p0, 0)

Proof. Figure 9 illustrates this equilibrium. Condition 1a defines contract N . Condition 1c

precludes equilibrium 1 with advantageous selection in Proposition 3. Conditions 1d and 1e assure

that type N individuals do neither prefer contract N0 nor prefer any pooling contract (I, ¯p) that

would also been taken by type R individuals over contract N .

Under the conditions outlined in the above proposition, the “advantageously selecting”contract N = ¡I (c¯ N) , cN

¢

in Proposition 3 under equilibrium 2 is relatively too expensive such that type N individuals prefer not to self-select into the contract with higher coverage but rather self-select

into the contract N = (IN, pF) which offers partial coverage at their respectively fair rate c = pF.

4

Comparative Statics

In this section, we discuss comparative statics of the model with regard to the types of equilibrium examined in Section 3. In our model, the type of market equilibrium varies with cost of investing in self-protection, F , the intensity of regret of type R individuals, as measured by the convexity of g, and the fraction of type R individuals in the population, λ.

4.1

Cost of investment in self-protection

If the cost of investing in self-protection, F , is extremely high or low both types of individuals optimally do not invest or invest in self-protection. Individuals are therefore heterogeneous only

regarding their preferences but not regarding their risk type. Thus, type N individuals optimally obtain full coverage, whereas type R individuals optimally obtain partial coverage, as shown by Braun and Muermann (2004).

Case 1 For very small (high) levels of F , it is optimal for both type R and type N individuals

to invest (to not invest) in self-protection and the unique equilibrium is a separating equilibrium

in which both types receive the optimal amount of coverage at the rate c = pF (c = p0), i.e. full

coverage for type N and partial coverage for type R individuals.

Suppose that the cost of investing in self-protection is in a range such that we obtain equilibria under which type R individuals do not invest in self-protection but type N individuals do. As the cost F increases, the set of contracts under which it is optimal for type N individuals to invest in

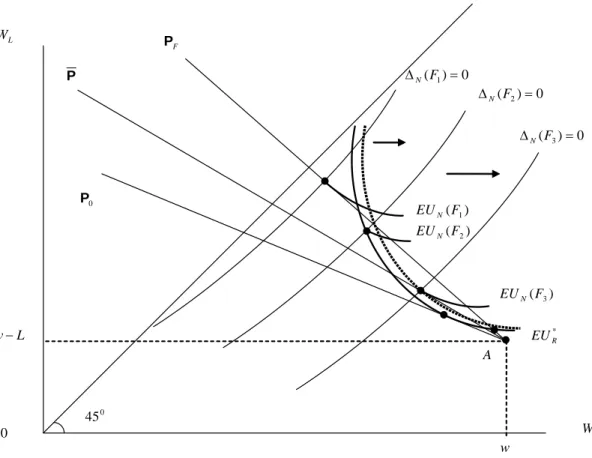
self-protection decreases, i.e. the locus of contracts ∆N(I, c) = 0 shifts down (see Figure 10 with

F1< F2 < F3). We then derive the following comparative statics.

Case 2 Suppose that the cost of investing in self-protection, F , is high enough such that ∆R(I, c) <

0 for all I and c with pF ≤ c ≤ p0.

1. For low levels of F (e.g. F1 in Figure 10), condition 1b in Proposition 3 is satisfied - i.e. type

R indifference curve crosses ∆N(I, p0) = 0 line above the pricing line PF - and a separating

equilibrium with advantageous selection as in Figure 7 is obtained.

2. For medium levels of F (e.g. F2 in Figure 10), condition 2c in Proposition 3 is satisfied

-i.e. type R indifference curve crosses ∆N(I, p0) = 0 line below the pricing line PF - and a

separating equilibrium with advantageous selection as in Figure 8 is obtained.

3. For high levels of F (e.g. F3 in Figure 10), either a separating equilibrium as in Figure 9 or

4.2

Intensity of regret

We measure the intensity of regret by the convexity of the function g. From the slope of type R individuals’ indifference curve (see equation 6) we deduce that the more convex the g function is the steeper the indifference curves of type R individuals are. Furthermore, a higher convexity of

the function g implies a lower level of optimal insurance coverage for type R individuals.2 Figure

11 illustrates the comparative statics with respect to the convexity of g (g3 is more convex than g2

which is more convex than g1 - thus R3< R2 < R1).

Case 3 Suppose that the cost of investing in self-protection, F , is high enough such that ∆R(I, c) <

0 for all I and c with pF ≤ c ≤ p0.

1. For highly convex functions g (e.g. g3 in Figure 11), condition 1b in Proposition 3 is satisfied

- i.e. type R indifference curve crosses ∆N(I, p0) = 0 line above the pricing line PF - and a

separating equilibrium with advantageous selection as in Figure 7 is obtained.

2. For medium levels of convexity of g (e.g. g2 in Figure 11), condition 2c in Proposition 3 is

satisfied - i.e. type R indifference curve crosses ∆N(I, p0) = 0 line below the pricing line PF

- and a separating equilibrium with advantageous selection as in Figure 8 is obtained.

3. For low levels of convexity of g (e.g. g1 in Figure 11), either a separating equilibrium as in

Figure 9 or a pooling equilibrium as in Figure 5 is obtained.

4.3

Fraction of type

R individuals in the population

In Rothschild and Stiglitz (1976), even the separating equilibrium does not exist if the fraction of high risk type individuals in the population is too low. The reason behind this non-existence result is that a pooling contract not only attracts high risk individuals but also low risk individuals as the pooling premium rate is just slightly above the fair premium rate for low risk individuals. The same

2

Alternatively, Braun and Muermann (2004) propose a “regret coefficient” k in the utility function of type R individuals such that uR(W ) = u (W ) − kg (u (Wmax) − u (W )). They show that the higher the regret coefficient k

reasoning applies to the separating equilibrium with adverse selection in Figure 9 if the fraction λ of type R individuals is too low. Then both types of individuals are be better off under a pooling contract. This pooling contract, however, does satisfy condition 2b in Proposition 1, which implies that it cannot be an equilibrium. Thus, as in Rothschild and Stiglitz (1976), there does not exist any equilibrium.

Interestingly, the same result does not hold under the conditions for the existence of a separating equilibrium with advantageous selection.

Lemma 1 The existence of the separating equilibrium with advantageous selection as in Figure 7

does not depend on the level of λ.

Proof. Note that all conditions in 1 of Proposition 3 are independent of λ. Furthermore, for any

level of λ, no pooling contract attracts type N individuals (see Figure 7).

5

Conclusion

Economic models of moral hazard and adverse selection predict a positive correlation between the amount of insurance coverage individuals purchase and their claim frequency. The empirical evi-dence on this prediction is mixed. In some markets, e.g. in the annuity and health insurance market, such positive correlation is confirmed, whereas in other markets, e.g. in the life and long-term care insurance market, the opposite relation holds. In this paper, we propose heterogeneous, hidden de-grees of aversion towards anticipatory regret as a rationale for self-selection in insurance markets. In our equilibrium analysis, we have shown that both pooling and separating equilibria can exist. Furthermore, there exist separating equilibria of both types, advantageous and adverse selection. We have characterized the conditions for each type of equilibrium and examined the comparative statics with respect to the model’s parameter. Understanding the reasons behind advantageous and adverse selection is highly relevant for the design of governmental policies aimed at reducing

populations as the markets for annuities, long-term care insurance, and Medigap insurance become increasingly important for them.

References

[1] Bell, D. E. (1982). “Regret in decision making under uncertainty,” Operations Research 30(5), 961-981

[2] Bleichrodt, H., A. Cillo, and E. Diecidue (2006). “A quantitative measurement of regret the-ory,” working paper.

[3] Braun, M. and A. Muermann (2004). “The impact of regret on the demand for insurance,” Journal of Risk and Insurance 71(4), 737-767

[4] Brown, J. and A. Finkelstein (2004). “Supply or demand: why is the market for long-term care insurance so small?,” working paper

[5] Cawley, J. and T. Philipson (1999). “An empirical examination of information barriers to trade in insurance,” American Economic Review 89(4), 827-846

[6] Cohen, A. and L. Einav (2006). “Estimating risk preferences from deductible choice,” American Economic Review, forthcoming

[7] Crocker, K. and A. Snow (1985). “The efficiency of competitive equilibria in insurance markets with adverse selection,” Journal of Public Economics 26, 207-219

[8] Cutler,D. and R. Zeckhauser (2000). “The anatomy of health insurance” in Handbook of Health Economics ed. by Culyer, A. and J. Newhouse, Elsevier, Amsterdam

[9] de Meza, D. and D. Webb (2001). “Advantageous selection in insurance markets,” RAND Journal of Economics 32(2), 249-262

[10] Fang, H., M. Keane, and D. Silverman (2006). “Sources of advantageous selection: evidence from the Medigap insurance market,” working paper

[11] Filiz, E. and E.Y. Ozbay (2006). “Auctions with anticipated regret: theory and experiment,” American Economic Review forthcoming

[12] Finkelstein, A. and K. McGarry (2006). “Multiple dimensions of private information: evidence from the long-term care insurance market,” American Economic Review 96(4), 938-958 [13] Finkelstein, A. and J. Porteba (2004). “Adverse selection in insurance markets: policyholder

evidence from the U.K. annuity market,” Journal of Political Economy 112(1), 183-208 [14] Gollier, C. and B. Salanié (2006). “Individual decisions under risk, risk sharing, and asset

prices with regret,” Working paper.

[15] Kahneman, D. and A. Tversky (1982). “The psychology of preferences,” Scientific American 246, 167-173

[16] Loomes, G., and R. Sugden (1982). “Regret theory: an alternative theory of rational choice under uncertainty,” Economic Journal 92(368), 805-824

[17] Michenaud, S. and B. Solnik (2006). “Applying regret theory to investment choices: currency hedging decisions,” working paper

[18] Mitchell, O., J. Porteba, M Warshawsky, and J. Brown (1999). “New evidence on the money’s worth of individual annuities,” American Economic Review 89(5), 1299-1318

[19] Miyazaki, H. (1977). “The rate race and internal labour markets,” Bell Journal of Economics 8, 394-418

[20] Muermann, A., O. Mitchell, and J. Volkman (2006). “Regret, portfolio choice, and guarantees in defined contribution schemes,” Insurance: Mathematics and Economics 39(2), 219-229 [21] Muermann, A. and J. Volkman (2006). “Regret, pride, and the disposition effect,” working

paper 06-08 in PARC working paper series

[22] Quiggin, J. (1994). “Regret theory with general choice sets,” Journal of Risk and Uncertainty 8(2), 153-165

[23] Rothschild, M. and J. Stiglitz (1976). “Equilibrium in competitive insurance markets: an essay on the economics of imperfect information,” Quarterly Journal of Economics 90(4), 629-649 [24] Sugden, R. (1993). “An axiomatic foundation of regret,” Journal of Economic Theory 60(1),

159-180

[25] Thaler, R. (1980). “Toward a positive theory of consumer choice,” Journal of Economic Be-havior and Organization 1, 39-60

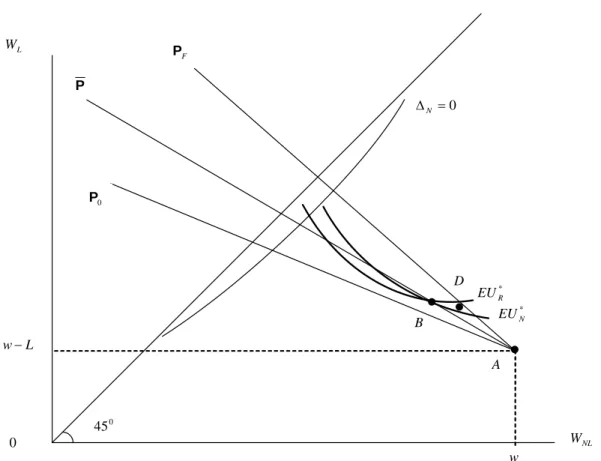
* N EU D B 0 45 F P A L W NL W 0 w L w− * R EU 0 P P 0 = ΔN

Figure 1: No Pooling Equilibrium for I < ˆI: type N individuals invest in self-protection, whereas

type R individuals do not. Indifference curve of type R individuals is flatter at B than that of type N individuals. Contract D attracts type N individuals but not type R individuals.

* N EU D B 0 45 F P A L W NL W 0 w L w− * R EU 0 P P 0 = ΔN

Figure 2: No Pooling Equilibrium for I = ˆI = ¯I: type N individuals invest in self-protection,

whereas R type individuals do not. Indifference curve of type R and type N individuals have the same slope but are more convex at B . Contract D attracts type N individuals but not type R individuals.

* N EU D B 0 45 F P A L W NL W 0 w L w− * R EU 0 P P 0 = ΔN

Figure 3: No Pooling Equilibrium for I = ˆI < ¯I: type N individuals invest in self-protection,

whereas type R individuals do not. Indifference curve of type R and type N individuals have the same slope but are more convex at B . Contract D attracts type N individuals but not type R individuals.

* R EU D B 0 45 F P A L W NL W * N EU 0 0 = ΔN w L w− 0 P P

Figure 4: No Pooling Equilibrium at ˆI < I < ¯I: type N individuals invest in self-protection,

whereas type R individuals do not. Indifference curve of type R individuals is steeper at B than that of type N individuals. Contract D attracts type N individuals but not type R individuals.

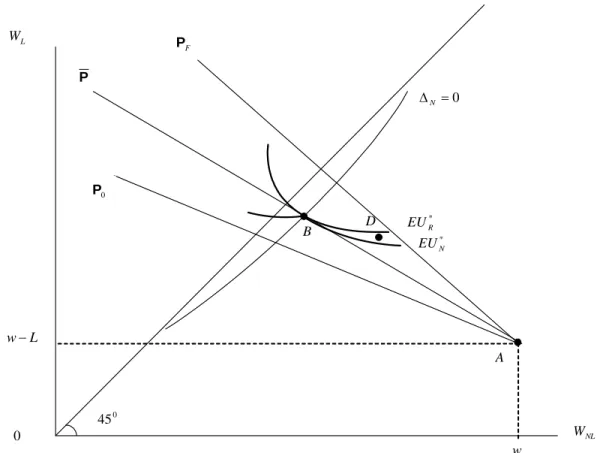
* N EU B 0 45 F P A L W NL W 0 w L w− * R EU 0 P P 0 = ΔN X

Figure 5: Pooling Equilibrium ( ¯I, ¯p): type N individuals are indifferent between investing and not

investing in self-protection under B, type R individuals do not invest in self-protection. Indifference curve of type R individuals is steeper at B than that of type N individuals and type R prefer

contract B over any contract on P0. Note that contract D cannot be offered to attract type N

individuals and induces them to not invest in self-protection and the company offering D would make losses.

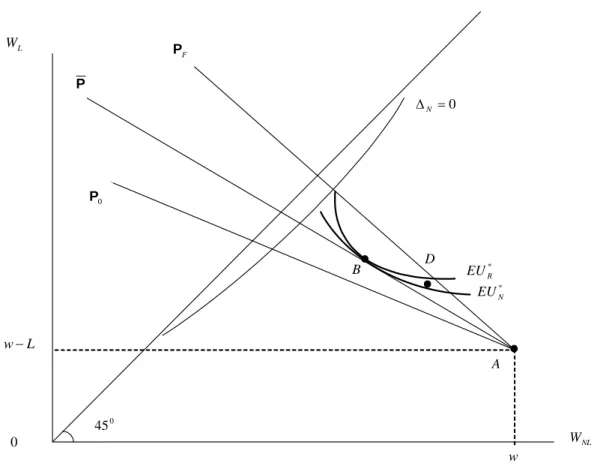
* N EU N 0 45 F P A L W NL W 0 w L w− * R EU 0 P P 0 = ΔN R

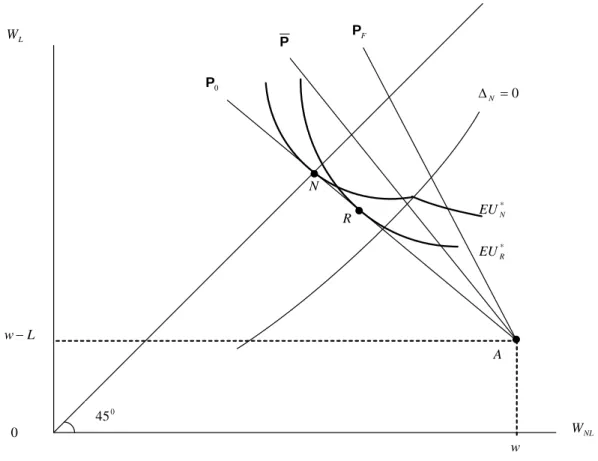
Figure 6: Separating Equilibrium: both types of individuals do not invest in self-protection and receive their respectively optimal amount of insurance coverage.

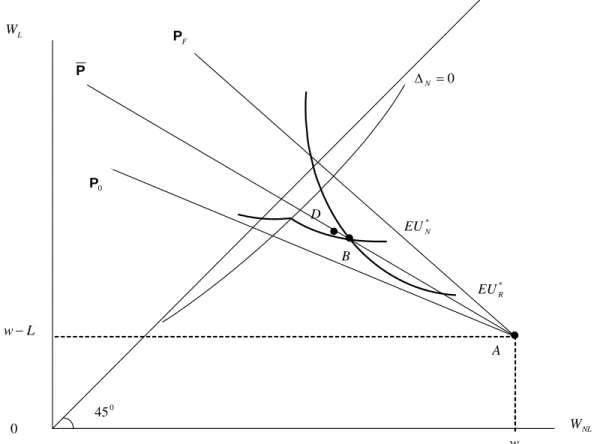
* N EU N 0 45 F P A L W NL W 0 w L w− * R EU 0 P P ΔN =0 R X

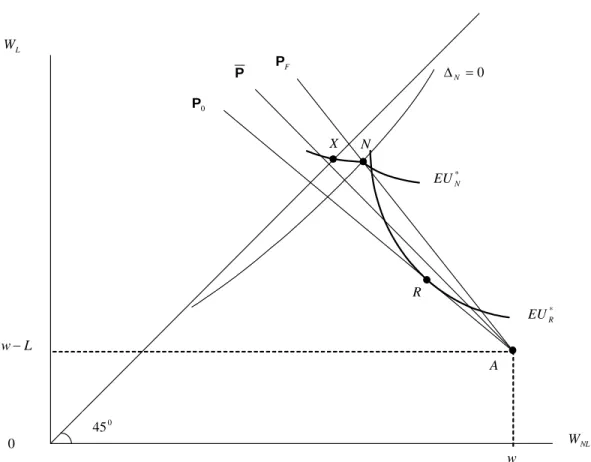
Figure 7: Separating Equilibrium with advantageous selection 1: type N individuals invest in self-protection, whereas type R individuals do not. Type N individuals obtain more insurance coverage than type R individuals.

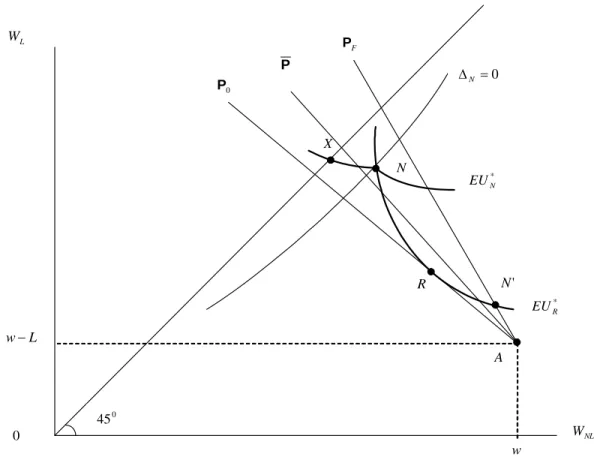
* N EU N 0 45 F P A L W NL W 0 w L w− * R EU 0 P P 0 = ΔN R X ' N

Figure 8: Separating Equilibrium with advantageous selection 2: type N individuals invest in self-protection, whereas type R individuals do not. Type N individuals obtain more insurance coverage than type R individuals.

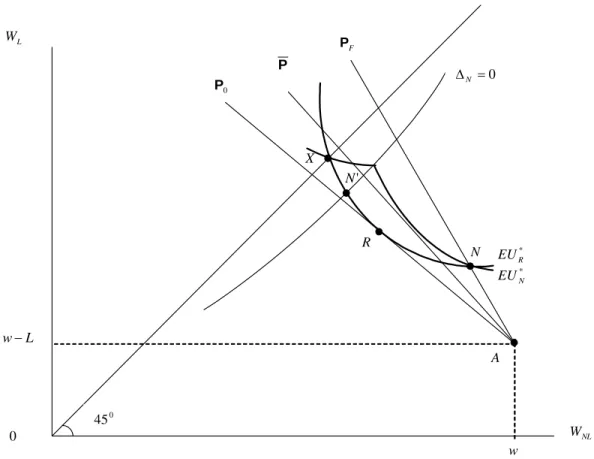
* N EU N 0 45 F P A L W NL W 0 w L w− * R EU 0 P P 0 = ΔN R X ' N

Figure 9: Separating Equilibrium with adverse selection: type N individuals invest in self-protection, whereas type R individuals do not. Type N individuals obtain less insurance coverage than type R individuals.

0 ) ( 1 = Δ FN 0 45 F P A L W NL W ) (F1 EUN 0 w L w− 0 P P * R EU 0 ) ( 2 = Δ FN 0 ) ( 3 = Δ FN ) (F2 EUN ) (F3 EUN

3 R ) ( 2 * g EUR ) ( 3 * g EUR ) ( 1 * g EUR 0 45 F P A L W NL W 0 w L w− 0 P 0 = ΔN P 2 R 1 R

Figure 11: Comparative statics with respect to intensity of regret - g3is more convex than g2 which