PHASE DISTRIBUTION NEAR THE FOCUS IN SYSTEMS OF DIFFERENT FRESNEL NUMBERS

(1)

Yajun Li Vol. 2, No. 10/October 1985/J. Opt. Soc. Am. A 1677

Phase distribution near the focus in systems of different

Fresnel numbers

Yajun Li*

Institute of Electro-Optical Engineering, National Chiao Tung University, 1001 Ta Hsueh Road, Hsinchu, Taiwan 300, China

Received January 31, 1985; accepted June 3, 1985

Three-dimensional phase distribution near the focal plane is demonstrated by cross-section profiles of cophasal surfaces. The phase distribution in the focal plane and the phase anomaly in the focus are discussed in greater de-tail. Numerical results obtained are arranged systematically with Fresnel numbers sampled between 0.5 and 100, a sampling that covers conventional and unconventional cases.

1. INTRODUCTION

Phase distribution near the focus when a converging,

mono-chromatic, spherical wave is diffracted at a circular aperture

on an opaque screen has been treated by many authors after Gouy's discovery in 1890 of the so-called phase anomaly near

the focus.1- The extensive literature related to this subject

is cited in Ref. 3.

Attention is now paid to the same problem, because in a

number of publications

5

-'

2

authors have revealed that, in

principle, many of the classical results are merely special in-stances that are covered by more-general laws. For instance,

classical authors

3

predicted that the cophasal surfaces in the

immediate neighborhood of the focus are nearly plane, while

Gouy' argued that a spherical converging light wave passing

through its focus undergoes a rapid phase change of ir rad. In this paper, it is shown that the cophasal surfaces near the focus

are approximately spherical, that the rapidity of the phase

change along a selected geometrical ray through the focus is

directly proportional to the Fresnel number of the diffracting

aperture, and that therefore Gouy's predictions of phase

anomaly near the focus may describe phenomena in focusing

systems only when their Fresnel numbers are considerably

larger than unity. Moreover, phase distribution in the focal

plane needs to be discussed, because in the focal plane an additional parabolic phase factor has to be taken into account

if some of the assumptions underlying the classical

investi-gations are modified.7

The numerical results obtained in this paper are displayed

systematically by curves and cross-section profiles with the

Fresnel number sampled between 0.5 and 100.

2. EXPRESSIONS OF PHASE DISTRIBUTION

IN THE FOCAL REGION

When a uniform converging spherical wave working at a cir-cular frequency c emerges from a circir-cular aperture in an opaque screen, it is seen that it travels along the z axis toward the geometrical focus at x = y = z = 0 (Fig. 1). By using the

scalar theory of diffraction, it can be predicted that the

be-havior of the diffracted field is determined by the following

parameters: A, amplitude; a, aperture radius; X, wavelength;

and f, focal length. The last three parameters can be

com-bined into the Fresnel number N

= a2/Xf

and the f number

F = f/2a.

In the present investigation, attention is centered on the

phase behavior of the diffraction field near the focus, which

is, apart from a periodic factor exp(-iwt), given by6'7'1 1_'1 2

ON(UN, VN) =

1 uN/2rN

[4F2 UN + VN]

-

a(UN,

VN)

-2

'

(mod 2ir). (2.1)

This is the central equation of this paper. In this equation

UN

= 2rN

zif

1 + zf/

VN =

2irN

rna

1 +

zif

Er = (x 2_{+ y}2 )1/2], (2.2a) (2.2b)

and

S sna=(C2 + S2)1/2' C

COS

a =(C

2

+ S2)1/2

(2.3)

with

C -iS = 2 1JO(VNp) exp - UNP2)PdP. (2.4)

The notation (mod 27r) in Eq. (2.1) means that

ON

is

inde-terminate according to the extension of an additive multiple

of 2zr.

The multivalued function

ON has a branch point at each

zero of the intensity.

3

At all points other than the points of

zero intensity, ON is continuous with respect to (UN,

VN).

In

the special case

of (UN = 0, VN =

0), i.e., at the geometrical

focus (which is not a branch point), we obtain from Eq. (2.1)

that

N(ON

0) = -

2+ mMr,

2

We can then define

(m = 0,1, 2,...). (2.5a)

ON(°, ) =

-as the principal value of ON(O,

0)-(2.5b)

(2)

By substituting these equations into Eqs. (2.3), we obtain

Aperture

plane

Fig. 1. Illustration of the notation.

3. PHASE DISTRIBUTION IN THE FOCAL

PLANE

By putting UN = 0 into Eq. (2.1), the following result is

ob-tained:

ON(O, V) = - V2 - a(0,U) -2'

4r1N 2 (mod 2wr). (3.1)

In this equation the dimensionless parameter

UN,

as defined

by Eq. (2.2b), has been replaced by

r

v = 27rN - . (3.2)

a

Under the condition

UN =

0, Eq. (2.4) yields the following

results:

C = Besinc(M) = 2J

1

(v)/v

and S = 0. (3.3)

sin a = 0

and

cos a = Besinc(u)ABesinc(v)j. (3.4)

From these results, it is clear that the principal value of a(0,

U) in Eq. (3.1) is either 0 or 7r, according to whether the special

wZ function Besinc(v) > 0 or Besinc(v) < 0. These inequalities

are equivalent, respectively, to

fosr<R,

R2p<r<R2p+l,

and

(p = 1,2,3,...).

(3.5b)

Here Rp is the radius of the pth dark ring in the Airy pattern

where the available regions of the following formulas are

di-vided:

'kN(O,

U) = - U2- -r

47rN 2

when inequalities (3.5a) hold, and

kN(O, V) = 1 V2 + r

4rN 2

(mod 27r) (3.6a)

(mod 2r)

(3.6b)

when inequalities (3.5b) hold.

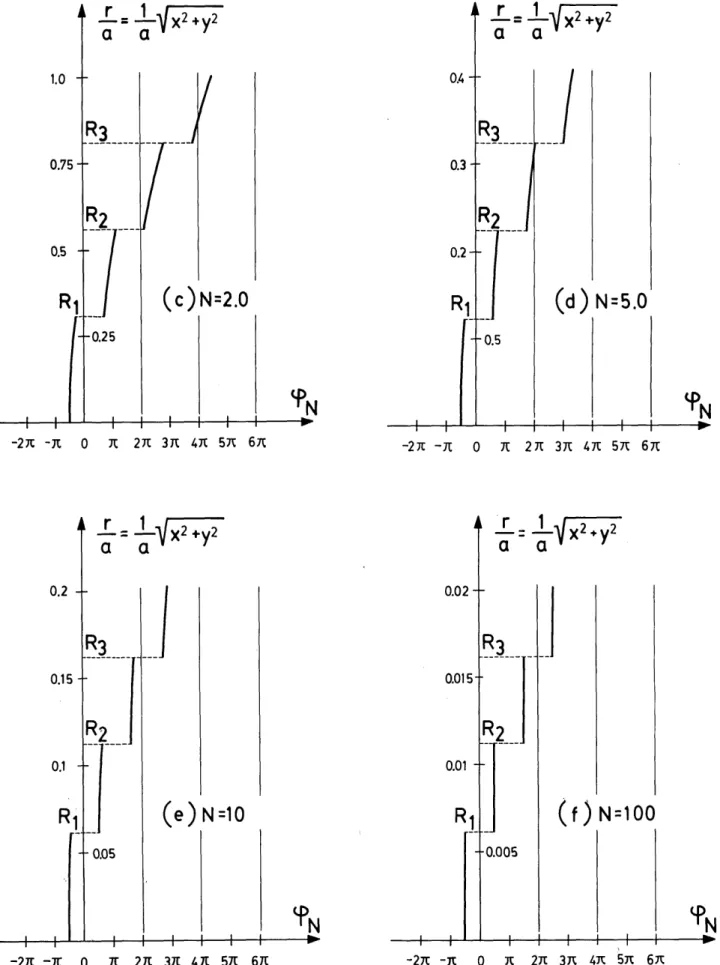
Phase distributions in the focal plane are shown by the

parabolic curves in Figs. 2(a), 2(b), 2(c), 2(d), 2(e), and 2(f) for systems of Fresnel number N = 0.5, 1, 2, 5, 10, 100,

respec-tively. These parabolic curves are cut into segments by the

points of zero intensity at r = Rp, at which the phase

distri-bution undergoes rapid transitions of 7r

rad. In addition, since

calculations in the present study are limited to a region smaller

than the fourth dark ring of the Airy pattern, the v values in

(a) N=O.5

_{(b) N-1.O}

-

i

0

xt

2nt 3it

4x 5Yi 6Jt 7t Bit 9i

I focus _(3-5a)

R2pj < r <

R2p,

r=

**_1VX2*y2**

a

_a

r

= _1VX2+y2

_a

ji

0 ir

27r

37t 4n 57t 6R 77t 87E 9n

(3)

Vol. 2, No. 10/October 1985/J. Opt. Soc. Am. A 1679

a

=

aFX2

+y2

21I

.3

(c)N=2.0

O0 0.3 0.2 -2 -~R 0 it 27C 37t 47C 5it 61t

r=

1 f2yT

a

:3 1

(d ) N =5.0

-2 7 -)i 0 it 27 3it 47i 5i 6ic

a= aVX2+y2

a

N

=10 0.02 0.01

R

r

= -11X2+y2

a

'1----(f ) N=100

-2i t-I 0 t 2At 31 47t 57t 67( -27 -t- 0 i 271 3t 4J 5it 67i

Fig. 2. Phase distribution in the focal plane in systems with different Fresnel numbers N. OR1

,

OR2, and OR3are the radii of the first three

dark rings in the Airy pattern. 1.0 0.75 0.5 0.2 0.15 0.1 Yajun Li

(4)

Eqs. (3.6) range from 0 to 13.32. A consequence of this

limi-tation is that the contribution of the quadratic term on the

right-hand sides of Eqs. (3.6) becomes negligible when the

Fresnel number is much larger than unity. In Fig. 2(f) (N =

100), phase distribution between two adjacent dark rings of

the Airy pattern is practically a constant-a result that may

be regarded as classical and one that has not received much

attention in the classical investigations.

Strictly speaking, a constant phase distribution in any finite

area in the focal plane is unobtainable.

4. THREE-DIMENSIONAL

PHASE

DISTRIBUTION NEAR THE FOCAL PLANE

In order to illustrate the three-dimensional phase distribution

near the focal plane by means of cophasal surfaces, Eq. (2.1)

is treated as a transcendental equation, viz.,

1 4Fv2

+

U2' - UN

1

-

UN/27rN 4FUN +4VN

/2

UN

+ f3(UN, VN) = constant, (4.1)

in which 13(UN, VN) _{can be evaluated in terms of Lommel's U}

functions,' 2i.e.,

sin

l =

_(U12

U

2

Cs /3=

U

1

+ U22)1/2' co (U12 + U22)1/ 2

'

or in terms of Lommel's V functions, i.e.,

(4.2a)

2xT

r= 2

-6 -4 -2

2T r= 2 T

IN=05

1

0

2

4

6 (a)

2xu Z

JN=

10 ]

_

2\

Z

(b)

(5)

s

V

0 cVO-Cos

0 [(V

0-

cos 0)2 + (V

1

+ sin 0)211/2'

V

1

+ sin

0 [(VO

- cos

0)2 +

(V

1

+ sin 0)2]1/2'

0 =-(UN

+-)

(4.2b)

The definitions of Lommel's U and V functions can be found

in Ref. 13.

In this investigation, transcendental Eq. (4.1) was solved

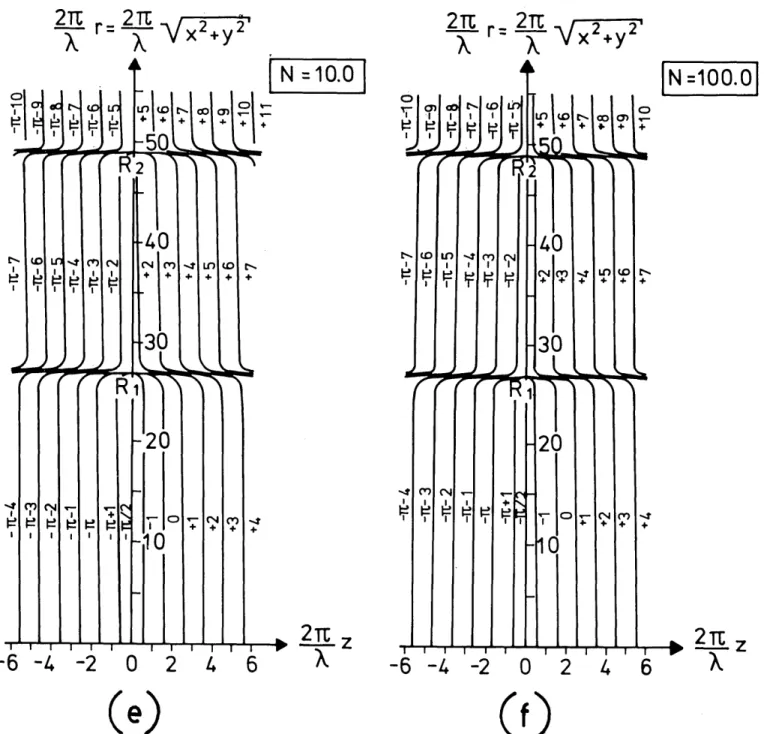
on a computer by employing Lommel's U functions when

I uN/vNI < 1 and Lommel's V function when I UN/VNI > 1. The results obtained are displayed in Figs. 3(a)-3(f) by the profiles

of cophasal surfaces in systems with different Fresnel

num-bers. In these figures, the curves are crowded in the region

near the dark rings of the Airy pattern. In order to avoid

overlapping, curves in those regions are displayed only

sche-matically. Actually, phase structure near the said dark rings

changed much more rapidly than is shown in Figs. 4(a)-4(f).

From these figures, it seems clear that the cophasal surfaces

near the focus are convex to the aperture and nearly

spher-ical.

A further point of interest was a study of the curvature of

cophasal surfaces at the focus. To undertake this, Eq. (2.1)

was transformed into an implicit function with variables r and

z, viz.,

G (z, r; ON) =

0,

(4.3)

where

ON

= constant. From this, the said curvature is

de-termined by

21X

N=5.0

|

_T

-6 -4

-2

0

2

4

6 (c)

N=

2.01 --

_

T Z

-6 -4

-2

0

2

4

6 (d)

(Figure 3 continued overleaf)

Yajun Li

2TE r= 2TE VX_2,_y__2_"

X

t I

(6)

2TU r= 2 T

x

X

-VX~+

y2

A I t--I kz!_I

to

U.,

2 r= 2

X+Y

1 N =10.0

H IWt- o Cn C

Lfl

+ +0N

+ +

--:

n

(

4

v

1§~~~~~~~~~~~~~~~~~

40

*-W U -.tC1)C CN M -S Lf(n t

I

g

g1

+ +

4.44.

30

4 - I)

'10-A

0 I I

-..J A NJ(o1 Lb

II iII

'I- t1n1

to

M "I C

I

-S M N -I -I ill I I I I I I I I - I

--6 -4

-2

O

2

4

6

FRF, 4. toV ,co a

40 N

ItL

4

30

20 1c

C

4+

IN =100.0I

0C I1 WI C1 Im .4

(e)

(f)

Fig. 3. Profiles of cophasal surfaces in the immediate neighborhood of the focal plane in an F/3.5 system with different Fresnel numbers N.

OR₁and OR2are radii of the first and the second dark rings in the Airy pattern.

=GzGr(Gzr + Grz) - (Gr)2

Gzz

- (Gz

)

2

Gr

o (4.4)

(Gz2

+

Gr2)3/ r=O (4)

= - -

K

(4.6)

in which

G,

=G/OzG r = aG/8r, Gzr =

_d

2G/azar,.... After a lengthy derivation, omitted here, the result obtained can be expressed as

f

(1

-

1/16F

2

)

(4.5)

If F

2>>

1, the above relationship is reduced to

K r-

f-1; then

the corresponding radius of curvature

is obtained, a result that indicates that the center of the radius of curvature is in the middle of the aperture. This theoretical outcome, which may be regarded as a fundamental property for focusing systems of any Fresnel numbers, is shown graphically in Fig. 1 by the dashed circular curve. This out-come is also in close agreement with the experimental results obtained in microwave optics, as reported by Farnell (see Figs. 2 and 3 of Ref. 14).

The complete phase distribution near the focal plane can be found by rotating Fig. 3 around the z axis. After this has been done, the curvature circle in this figure becomes a sphere

of radius f.

o

_a

"

(N

I I II I I I I I

-6 -4 -2

0

2

4

6 --

-MWdt-dtv t a . q M N 0 I I cc I V I -Y I

.t

+ 1>1 ^nI

-X z

* 2

TE z

X

(7)

The classical prediction concerning the cophasal surfaces

in the immediate neighborhood of the focus may be considered

as a special case of the present result [expression (4.6)]. This

is because the region in which the classical authors

3

carried

out their calculations was limited by the first several dark rings

in the Airy pattern, which, when the Fresnel number is far

larger than unity, is rather small in comparison with a sphere

of radius f. As a result of the limitation of the region of

ob-servation, it was logical for the classical authors to conclude

that the cophasal surfaces in the immediate neighborhood of

the focus are almost plane.

5. PHASE ANOMALY

In the classical theory of focusing, phase anomaly near the

focus is an important subject that has attracted the attention

of many investigators during the many years past. After

numerous notable investigations, it is now generally accepted

0.5 1.0 Z/f

@-8°718!~

--,,-

I -,,

--'

(edge of the geometrical shadowf _ /2._________ _.________ ____ __

-

N

Z/f

I I I , ,II I I E)=6*

I '1

6 eI§@N

Z/f

0=44° II5N z/f 0=2 0 !N Z/f

I

1 :

I

:,,

, I I,

,I

0=30'

-

---1.0 -0.5 A6N 0.5 1 0 Z/f

(a) N-=0 5

-1.0 -0.5 p5N 0.5 1.0 Z/ f 0= 80 7.8' \

-(edg of th gemer_ a _ haow -1_ 2________ = =

'N z/f 0=6 I I I I I 1 I I I II I I I I 940 --6 N Z/f 6 N Z/f 0=20

I ,

, , |>

|

t6~N

Z / f

-3 01 -1.0 _ *6N 0.5 1.0 Z/f

I

.I.

. . . _

0=0° -0.5 _ _ _ _ _ _ _ _ _ _ _ -_ T 0 -1.0 -0.5 0.5 1.0 Z/f -=80 7.8'

0

(edge of the geometrical shadowf)-/ 2

Z/f

I, I I, L , , I,

~~~~~~~I

I I I I I i I 0=60

O

i6N Z/f , 56N Z/f I ' I I I 1 1 1 1 , I I I I I I I I I 0:20 j L5N Z/f 0-30' _ -1.0 -0.5 6N 0.5 1,0 Z/f

(b) N=1.0

-1.0 -0.5 6N 0.5 1.0 Z/f - 8 7'.8 I I II I

(ldge ot the geometrical shadow) -f12

'5N J Z/f 0=60 5N Z/f 6 N Z/f I, I I I, W

~~~~~~~~~I

I I I I I,, I 0=20 ,N z/f 0=30' _ _ __* _ - --- _

----l.0

-

0.5\ A6N l.0 Z/ f

Q

0 =0

\ \

N

(ax

is)

--if

(C)N=2.0

72_

_--

-(d) N=5.0

(Figure 4 continued overleaf)

-1.0 -0.5 Yajun Li

(8)

-1.0 -0.5 0 0i.5 1.0 Z/f

0=8° 7.8' i ! i i i I I

(edge of the geometrical shadowi \ - -/2

- A aN z/f 9=60 I I I I

,.~~~~

5N

~~Z/f

I @,,,

I

I,- <_X ",,,

i!

I,

,

i.

/

-

-, ---

,,,,

I, I,,,,---

.f

i

~~~~4N

z/f

9=20

- I.xJI Il II ! I A --- - f\_- - I---9=30'

-1.0

-0.5

\ \

\p

0.5 1.0 Z/f

9=0* 1/ _-L~S --- -- -- ---

( f 0

---- a _____ ,

(e) N

=1O

-0.05 -0.025 0.025 0.05 Z/f --- N a &1 Z/ f 9=80 7.8s -. T *

Ldlt2L L" m rica(1 shadow) I7/2

__ * * * 46,

~ ~ ~ ~

---9=60 1

- -1--l

1 §_i_<_

1

i |--- ----e6N Z/f 9:20 o6N

~~~~~~z/f

9)=30O' -0.05 \-0.0 2 5 : 0N 0.025 0.05 Z/f

to consider the phase behavior as the observation point P

moves along a selected geometrical ray through the focus (see

Fig. 1). If 0 is the angle between the axis and the selected

geometrical ray, then we have

N=

2F tan 0.

(5.1)

UN

By inserting the above formula into Eq. (2.1), we obtain

4F2U/2N

(1 UiN 2 cxUN

ON (UN, 0) = 1 F 2 N 1

+ -

tan2

0) (UN 0)

(mod 2ir). (5.2)

In order to determine the linearity in the phase change

de-scribed by Eq. (5.2), we introduce a reference wave

(geomet-rical wave). This wave has a linear phase property as

obser-vations are made in the region of illumination predicted by

geometrical optics and along a ray through the focus, viz.,

D(P)

=exp[-i(UNR

,)

0 < 0 <

tan' (2F), (5.3)

where

0(UN, 0) =

-kR

when UN 1< O

=

+kR

when

UN >O J

Here k = 2-r/X is the wave number, and

R = (Z2

+ r2)1/2 =

_khI-

1 1 4

_UN/2rN

2UNI sec 0

is the distance from point P to the focus 0. The difference

A L

JT _ _ ___ _____

i-807 (edge of the geometricalshadow)

I IT if

A

IT (ax is) - 1-/2

-(f)N100

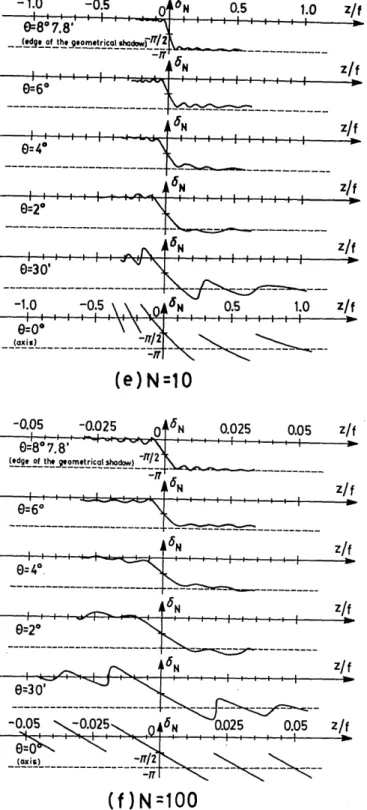
Fig. 4. Phase anomaly along geometrical rays through the focus in an F/3.5 system with different Fresnel numbers N. The angle 0 de-notes the inclination of the ray to the axis.

that -a converging spherical wave undergoes a rapid phase

change of 7r rad in passing through its focus.' This

phe-nomenon is not only observable in focused light fields

2

4 but

also in focused acoustic fields.

In this section of the present study, the classical predictions

concerning phase anomaly near the focus are checked in

sys-tems of different Fresnel numbers. To this end, it is necessary

A

IT

.T

.

0 2 4 6 8 10 12 14

---. I I I . . , . . I I AhI l--1 ie I I I0

-rt--- ---

----0=2°

f-I I6I . , * I I , I I III_30' - 1N

K- , 3 -J 6=0 (axis)

_. ,__ I I |_L --- , _ - - I I -B K Io

0 2 4 6 8 10 12 14

Fig. 5. Difference between phase anomaly

AN

evaluated at the points

z = -0.2f and z = +0.2f in an F/3.5 system. (5.4) (5.5) N N ,,,,-, - , ___ _) 1--11--'

a

I

(9)

Vol. 2, No. 10/October 1985/J. Opt. Soc. Am. A 1685 1 2 3 4 5 6 7 8 9 10 11 12 N 0 (axis) 0.1 0.2 0.3 0.4

N

0.5

(edge of the geometrical shadow)

I Fig. 6. Rapidity of the change of AN in the focus. (5.6)

+U4N

tan

2

01

Further evidence is provided by considering the following

two quantities. First,

A = WN(UN, O)z=-0.2f - N(UN, 0)z=+0.2f, (5.8)

-

a(UN,

0)- '

2

(mod 2r),

(5.7)

is called the phase anomaly along a geometrical ray. In order to compare this result with that given by the classical authors (see, e.g., Fig. 8.47 of Ref. 1), the same f number (i.e., F/3.5)

is now adopted, and the influence of the Fresnel number on

the phase anomaly is observed.

The results obtained from Eq. (5.7) are demonstrated in Fig. 4 for the same Fresnel numbers as those in Figs. 2 and 3. Each curve in Fig. 4 corresponds to a particular geometrical ray through the focus. Phase anomaly near the focus in a N = 100 focusing system [Fig. 4(f)] is essentially the same as the clas-sical result, in which 3

N(UN, 0) (phase anomaly along the axis) is a linear function of the z coordinate, except at the points of zero intensity; for the oblique rays, phase anomaly is an-tisymmetric to the focus and undergoes a rapid but continuous phase change of 7r rad as the rays pass through the focus. These properties, which are notable outcomes of the classical theory of the phase anomaly in the focus, disappear one by one with decreasing values of the Fresnel number N. Figures 4(e)

(N = 10) and 4(d) (N = 5) show that phase anomaly is no

longer antisymmetrical to the focus and that, along the axis

and between two adjacent transitions,

3

N becomes a nonlinear function of the z coordinate. However, the change of aN near

the focus is still r rad. But this property is lost when the

Fresnel number is further decreased. Thus the classical

theory can no longer be used to predict correct results when the Fresnel number is of the order of unity or smaller [see Figs. 4(a), 4(b), and 4(c) for the cases of N = 0.5, 1, 21.

an index number expressing the total amount of the change

of

3

N

between two points on the two sides of the focus; and,

second, a quantity concerning the rapidity of the change of

aN in the focus,'5viz.,

bN'(0

0)

=

MaN

dUN\

7rN

1

dUN

z

-) o = 21

+ 16F

2

(sec 0

-

1)],

0 < tan 0 < (2F)'-. (5.9)

This result indicates that the rapidity of the phase-anomaly

change along a selected geometrical ray is directly proportional

to the Fresnel number of the diffracting aperture.

Under the condition F2>> 1, we have sec 0 - 1 0.5 tan2

0. We then obtain the following expression:

3

N'(O, 0)

= -

-[1

+

8(F tan

0)2],

2

0 < (F tan 0) < 0.5.

(5.10) The quantity A is plotted in Fig. 5 as a function of the

Fresnel number N. From this figure it is seen that the

phase-anomaly change in the focal point and along the edge

of the geometrical shadow attains 7r rad when N> 2, whereas

phase anomaly along the axis attains the same amount of

variation when N 2 5. The rapidity of this variation [Eq.

(5.10)] is demonstrated in Fig. 6, from which it is seen that an appreciably rapid phase change occurs in the focus only when

N > 10. Therefore Gouy's prediction of the anomalous

propagation of phase in the focus, i.e., a converging spherical wave undergoes a rapid 7r rad phase change in passing through its focus, may describe phenomenon in focusing systems only

when their Fresnel numbers are considerably larger than

unity.

0 -10 -20 -30 -40 -50 -60 (89'2.T )

WNUN, a) = ON(UN, a) -(UN, O),

4F21UN [ Yajun Li

(10)

6. CONCLUSIONS

In this paper, phase distribution near the focus is

demon-strated by a series of diagrams. It seems that if these results

are combined with the previous diagrams that show in detail

the structure of the field and the distribution of encircled

energy in the focal region,"1 12a comprehensive knowledge of

the focused field would then be obtained. For this purpose,

the Fresnel numbers in Figs. 2-4 have been arranged in the

same way as those used in the previous investigations.

ACKNOWLEDGMENT

I wish to thank E. Wolf for numerous helpful discussions

concerning the subject matter of the present paper.

* Present address, Institute of Optical Sciences, National

Central University, Chungli, Taiwan 320, China.

REFERENCES

1. M. Born and E. Wolf, Principles of Optics, 6th ed. (Pergamon, Oxford, 1980), Sec. 8.8.

2. A. Rubinowicz, "On the anomalous propagation of phase in the focus," Phys. Rev. 54, 931-936 (1938).

3. E. H. Linfoot and E. Wolf, "Phase distribution near focus in an

aberration-free diffraction image," Proc. Phys. Soc. London 69, 823-832 (1956).

4. R. W. Boyd, "Intuitive explanation of the phase anomaly of fo-cused light beams," J. Opt. Soc. Am. 70, 877-880 (1980). 5. J. J. Stamnes, "Focusing of two-dimensional waves," J. Opt. Soc.

Am. 71, 15-31 (1981).

6. H. J. Erkkila and M. E. Rogers, "Diffracted field in the focal volume of a converging wave," J. Opt. Soc. Am. 71, 904-905 (1981).

7. J. J. Stamnes and B. Spjelkavik, "Focusing of small angular ap-erture in the Debye and Kirchhoff approximations," Opt. Com-mun. 40, 81-85 (1981).

8. E. Wolf and Y. Li, "Conditions for the validity of the Debye in-tegral representation of focused fields," Opt. Commun. 39, 205-210 (1981).

9. Y. Li and E. Wolf, "Focal shifts in diffracted converging spherical waves," Opt. Commun. 39, 211-215 (1981).

10. Y. Li, "Dependence of the focal shift on Fresnel number and f number," J. Opt. Soc. Am. 72, 770-774 (1982).

11. Y. Li, "Encircled energy for systems of different Fresnel num-bers," Optik 64, 207-218 (1983).

12. Y. Li and E. Wolf, "Three-dimensional intensity distribution near the focus in systems of different Fresnel numbers," J. Opt. Soc. Am. A 1, 801-808 (1984).

13. G. W. Watson, A Treatise on the Theory of Bessel Functions, 2nd ed. (Cambridge U. Press, London, 1962), Sec. 16.5.

14. G. W. Farnell, "Measured phase distribution in the image space of a microwave lens," Can. J. Phys. 36, 935-943 (1958). 15. Y. Li, "The anomalous propagation of phase in the focus: a