On multilevel coded MPSK for the Rayleigh fading channel

On

Multilevel Coded MPSK

for

the Rayleigh Fading Channel

Ruey-Yi

Wei

and Mao-Chao Lin

Department of Electrical Engineering, National Taiwan University, ROC

Abstract : We derive a new upperbound on pairwise error probability for MPSK sequences over the Rayleigh fading channel when CSI is not available. This is obtained by adding weight factors in calculating the symbol metrics. Simulation shows that the weight factors which optimize the upperbound are likely t o optimize the error rate too. We also design multilevel coded MPSK schemes which are suitable for the Rayleigh fading channel. These schemes are basically in the form of block coded modulation with interblock memory (BCMIM) [4], which was originally de- signed for additive white Gaussian noise (AWGN) channel. The added weight factors are found to be effective in im- proving the error performances of these BCMIM schemes in case that CSI is not available.

I Introduction

In 1982, Ungerboeck[l] introduced the concept of coded modulation which was originally designed for the additive white Gaussian noise (AWGN) channel. For a coded mod- ulation system applied to the AWGN channel, it is de- sired to maximize its minimum squared Euclidean distance (MSED). In [2], Divsalar and Simon investigate the situ- ation of applying a coded MPSK system to the Rayleigh fading channel. Through the derivation of upperbounds on the pairwise error probability of MPSK sequences, it has been shown that maximizing both minimum symbol dis- tance (MSD) and minimum product distance (MPD) is de- sired regardless of whether channel state information (CSI) is available or not. In this paper, we derive a better upper- bound on the pairwise error probability for the Rayleigh fading channel without CSI by adding weight factors in calculating the symbol metrics. The channel under con- sideration in this paper is the frequency nonselective slow Rayleigh fading channel with perfect phase tracking. We find weight factors which can optimize the upperbound. The new upperbound also shows that maximizing MSD and MPD is desired. Simulation on several examples show that the weight factors which optimize the upperbound are likely to be the best choices in lowering the error rates.

Multilevel coding is a useful method to construct coded modulation systems [3]. The basic idea of multilevel coding is to partition a signal set into several levels and to sep- arately encode each level with a proper component code. We can use either a block code or a convolutional code as the component code in each level. If the component codes

for all the levels are block codes, it is a kind of block coded modulation (BCM).

In

[4],

a kind of multilevel coded modulation called block coded modulation with interblock memory (BCMIM) was designed for the AWGN channel to increase the coding rate without decreasing MSED as compared to the associated multilevel BCM. In this paper, we modify the design of BCMIM for MPSK signals applied to the Rayleigh fading channel such that the coding rate can be increased with- out decreasing MSD and MPD. The error performances of these BCMIM are simulated by computer. When CSI is not available, the error performances of the designed BCMIM schemes are not as good as we expect if conven- tional symbol metrics are used. However, by adding proper weight factors to the symbol metrics, improvement of the error performances can be observed. The optimal choice for the weight factor is a value proportional to the inverse of the level Euclidean distance in each level. In this paper, the coding rate, error performances and decoding complex- ities are provided for some BCM and BCMIM examples so that a fair comparison can be made.

I1

Upperbounds on the Error Rate

for Coded

MPSK

Let x = ( 2 1 , z2,..

.

,

z ~ ) be a transmitted coded MPSK

symbol sequence of length N , where zi is the transmitted symbol at time i. Let r

=

( T ~ , T Z , . . . , ~ N ) be the corre- sponding received sequence, where the ith element, ri, is given by

p i = P j X i f nil

where ni is a zero mean complex Gaussian variable with variance U: and pi is a normalized random variable with Rayleigh distribution.

Consider the case that ideal CSI is available. Given the condition that the fading gain sequence is p = (PI,

. . .

,

PN),

the pairwise error probability of choosing 2 instead of x is (1)

N

~ r { x

-+

2 I p } = P y { C [ m ( r z , z z t p e )

-

m ( r , , ~ * , ~ ) ]

>

01,

(2)

e=1

where m(ri, x i , p i ) is the metric of xi which will be used in

the decoding trellis.

By setting m(ri,zi,pi)

=I

ri - pizi

12,

it

[a]

can be shown that for reasonably large values, the pairwise

error probability of choosing 2 instead of x is bounded by

This upperbound was derived by Divsalar and Simon

[a].

Now we consider the case that CSI is absent, the pair- wise error probability of choosing 2 instead of x given the condition of fading gain sequence p is

N

Pr{x --+ 9

I

p > = P r { C [ m ( r i , xi)

-

m(ri,

2i)l

>

01.

(4)

Traditionally, m(ri, xi) is set to be

1

ri - xi

1’.

We propose to set m(ri, zi) =wi

1

ri -xi

12,

where wi is a weight factor. By applying Chernoff bound to (4), we have

i = l

~ r { x

-+

j7:

I

p>

I

= n e . z p [ - X w i

I

si

-

si

l2

- ~ ~ w i ( p i - I)

E { e s p [ X ( m ( r ; , xi) - m(.ri,

$;))I}.

e”

im

xRe{s;(rci - 2i)*}]

x E { e z p [ - 2 X w ; R e { a ; ( ~ ;

-

2i)*}]}, (5)

where y’ is the complex conjugate of y and Re{y} is the real part of y. Suppose that the

1

zi

I=)

&

1,

it can be shown that

I

xi

-

3i

[’=

2Re{xi(zi

-

ai)’}.

and

E { e x p [ - a X w i R e { n i ( ~ i - ~ i ) * ) I ) = ezp[X2wPai

I

xi--&

1’1.

With da

=I

xi

- Pi

12,

we have

P r { x --+ 2

I

p }

_<

exp[-Xwipid;

+

X2w?vid;]. (6)

{E,

Normalizing the Chernoff parameter (replacing X by A c i ) and substituting

8

for

&

in (6), we have

With the assumption of infinite interleaving, the pair- wise error probability is

P r { x + 9 } =

1”

.

*

.

LW

PrCx + 9

I

P)P(Pl)P(PZ)

. . .P(pN)dpldpZ ’ + ‘ d p N , (8)

where pi and pj are identical and mutually independent

for i

#

j .

With a procedure similar to that used in

[a],

we can have

where

Since erfc z M

9

(1

-

&)

,

we have

where L, is the cardinality of q.

To minimize the righthand side of (lo), we need

for each j E q. It follows from (lo), (1 1) and

To see the effect of the weight factor, we give two simple examples as follows.

Example 1 : Consider two 8PSK sequences, x =

( X I , Q , X ~ ) and 2 = ( 2 1 , & , l i . ~ ) , such that df = 0.586,

dz

=

2, dg = 4. The ratio of optimal weight factors is

w1 : w2 : w3 = -

Upperbounds and simulation results are shown in Fig. 1.

Example 2 : Consider two 16PSK sequences, x =

( q , x 2 , x 3 , z 4 ) and -jz

=

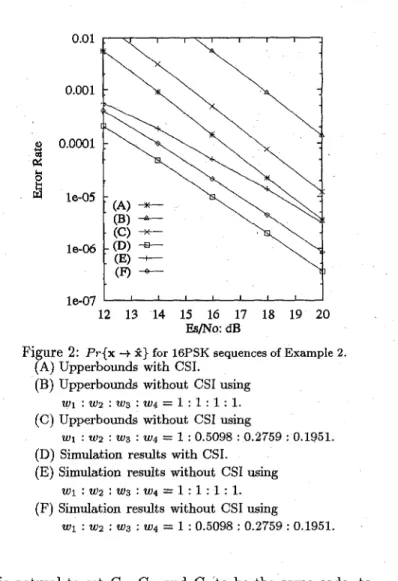
(%1,22,23,24), such that df =

0.152, d? = 0.586, d$ = 2, d: = 4. Upperbounds and simulation results are shown in Fig. 2.

Although to minimize the upperbound of pairwise error probability, we have shown that the best weight factor w j is proportional to the inverse of d j , we are unable to theoret-

ically prove that to minimize the pairwise error probability

P r { x

-+

ji.} also requires that w j be proportional to the inverse of d j

.

However, simulation results indicate that probably setting w j to be proportional to the inverse of dj is the best choice. Hence, we suggest that : “for decoding in the Rayleigh fading channel, the best weight factor at the j-th position may be proportional t o the inverse of the Euclidean distance between the two associated symbols”

.

1 _:

₃

_{1 : -L}

_-

_{1 : 0.5412 : 0.3827.}

4 -

I11

Several Coded

MPSK Systems

for

the

Rayleigh Fading

Chan-

nel

In this section, we will design several coded MPSK systems which are suitable for the Rayleigh fading channel. For the convenience of presentation, we restrict M to be 8.

0.01 0.001 3 e

2

0.0001 E W 1405 (Ej +-

1

-

\ 12 13 14 15 16 17 18 19 20 Es/No: dB

Figure 1: P r { x -+ a} for 8PSK sequences of Example 1.

(A) Upperbounds with CSI.

(B) Upperbounds without CSI using

w 1 : w 2 : w 3 = 1 : 1 : 1 .

(C) Upperbounds without CSI using

~1 : ~2 : ~3 = 1 : 0.5412 : 0.3827.

(D) Simulation results with CSI. (E) Simulation results without CSI

using w1 : w2 : w3 = 1 : 1 : 1.

(F) Simulation results without CSI

using w1 : 202 : w3 = 1 : 0.5412 : 0.3827. 0.011 y I I \ I I I I J 0.001 3 0.0001

2

le05 12 13 14 15 16 17 18 19 20 &/No: dB

Figure 2: P r { x --+ 2 ) for 16PSK sequences of Example 2.

(A) Upperbounds with CSI.

(B) Upperbounds without CSI using

(C) Upperbounds without CSI using

(D) Simulation results with CSI.

(E) Simulation results without CSI using

w 1 : w2 : w3 : w4 = 1 : 1 : 1 : 1.

(F) Simulation results without CSI using

w1 : w2 : w3 : w4 = 1 : 1 : 1 : 1.

~1 : ~2 : ~3 : wq = 1 : 0.5098 : 0.2759 : 0.1951.

~1 : ~2 : ~3 : 204 = 1 : 0.5098 : 0.2759 : 0.1951.

Consider an 8PSK signal constellation as given in [l], in which each signal point is labelled by ( a , b , c), where

a, 6 , and e

E

{0,1}. By successive two-way partitions of 8PSK signal set, the intra-subset squared Euclidean dis- tances are

Si

=

0.586,

S;

=

2 and

S

:

= 4 respectively [l]. Let (ul, b l , el), (a2, b 2 , ea),

. .

be a sequence of transmit-

ted 8PSK signals. A conventional multilevel coding system is designed in such a way that (a1

,

u2,

.

.

.) is a codeword of a binary code C,, ( 6 1 , bar . a . ) is a codeword of a bi-

nary code

cb,

and (cl, c2,

.

..) is a codeword of a binary

code C,. Here,

Ci

is the code used for coding the level i,

i

E { a , 6 , c}. Suppose that Ci is an ( n , ki, di) binary block code with generator matrix

Gi,

where i E { a , 6 , c). Then we have a BCM for which each block consists of n 8PSK signal points and the coding rate is ( k l

+

k2

+

k 3 ) / n bits

per 8PSK signal point. Such a BCM can be easily decoded by a 3-stage decoding, where at the i-th stage of decoding, a trellis for Ci is used.

The important parameters which will affect the error performances of a coded MPSK for the Rayleigh fading channel are MSD, MPD and N ( a , p ) , where N ( a , p ) is

the number of neighbors at a symbol distance of a and at a product distance of

p.

From the upperbounds given in (3) and (12), we see that MSD is the most important parameter for high signal-to-noise ratio (SNR). Hence, it

is natural to set

C,,

cb,

and

C,

to be the same code, to achieve a large MSD.

Example 3 (BCM-1) : Let C, = cb=

C,

be an (8,4,4) binary code. Then, we have a BCM. The coding rate is 12/8 bits per symbol. The parameters MSD, MPD and N(MSD,MPD) are 4, (0.586)* and 224 respectively. Simu- lation results for the Rayleigh fading channel with CSI and without CSI which are obtained from a 3-stage decoding are respectively given in Fig. 4, Fig. 5 and Fig. 6, where in Fig. 4 weight factor is not used and in Fig. 5 optimal weight factors are used. The ratio of optimal weight fac- tors for level a, b and e is w, : wb : w, =1 : 0.5412 : 0.3827. In each stage of the 3-stage decoding, a 4-state trellis for the (8,4,4) binary code is needed.

For BCM-1, the bit error rate (BER) is not satisfactory for high SNR, since the MPD

S

:

is not large enough. One way to increase 6; is to decrease the code rate of C, as given in Example 4.

Example 4 (BCM-2) : Replace C, in BCM-1 by an (8,1,8) code. Then the coding rate is reduced to 9/8 bits per symbol. The parameters MSD, MPD and N(MSD,MPD) are 4, 16 and 224 respectively. Simultion results given in Figures 4, 5 and 6 show the improvement of BER for high SNR. For both BCM-1 and BCM-2, the decoding results without CSI are independent of the weight factors Since

the coding of each level is indepdent of each levels. The BCMIM scheme

[4]

proposed in 1994 is for the AWGN channel. For the Rayleigh fading channel, the de- sign criterion is much different.

Let ( a l , . .

. ,

a,, b l , . . .

,

b,, c1, . .

. ,

e,) represent a block of n 8PSK signal points and (aT,...,u$, br,...,b,f,

c;

,

. .

,

e$) represent the following block. These two adja- cent blocks are combined to be called a superblock. For a B C M , w e h a v e ( a l , . . . , a , ) =Ga.G,, (61,...,bn) = G b . G b

and (el,

. . . ,

e,) =

G,

.G,, where Gi is the generator matrix of the (n, k ; , d ; ) binary block code Ci and i& is a ki-bit message for i E { a , b, e}. For a BCMIM with interblock memory between levels a and b, it is designed such that

( b l , .

' ,

bn, a:, *

' ,

a $ ) = ( E r , 6b) G (13)

where 21.1. is a kr-bit message,

Gbr Gar

'=(

? )

(14)

is the generator matrix of a (2n, k ,

+

k b

+

T ) binary code

c,

Gar and Gbr are both r x n matrices. Also, coding for level c is obtained by (cl,.

. .

,

en)

=

iic

.

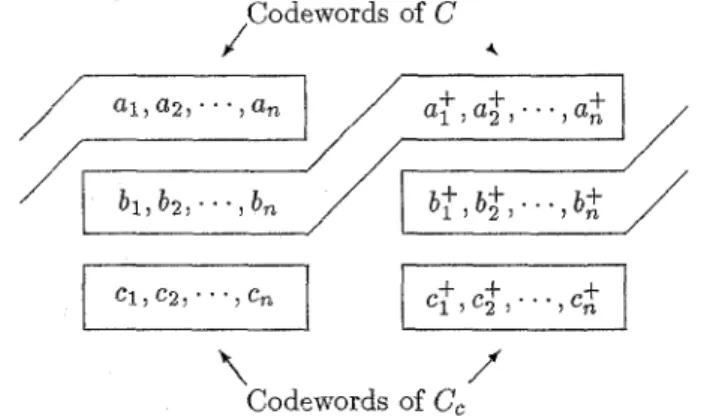
G, The coding configuration is given in Fig. 3.

Codewords of C

J

4

which are encoded into ( b l , ; +

* ,

b,, ci,

.

*

.

,era, a:,

. . .

,

U $ )

and ( b i ,

. . .

,

b,, cl, .

. .

,

L,,

a t

,

. .

+ ) a:') respectively. Con-

sider the following conditions.

(i) Suppose that 6,. = 6;. Then, the MSD and MPD between the associated superblocks are equal to

8~

and A$ respectively.

(ii) Suppose that

er

#

6;. Then, the MSD and MPD between the associated superblocks are

I /

S H r

=

d a u

+

dbb (15) and

A;r =

(SX)daa

( S z ) d b b (16) respectively. In our design, we require either (A)

SH,.

=

SB

and

Agr

>

A$ or (B)

S H ~

>

S H . Note that for high SNR, symbol distance is more important than product distance. Hence, BCMIM and BCM will have almost the same bit error rate

(BER)

at the same

E,,",,

and BCMIM will have lower BER than BCM at the same & / N o which results from the smaller bandwidth required by BCMIM, where

E , is the average energy of each signal point, Eb is the

average energy of each message bit and No is the one-sided

power spectral density of AWGN.

BCMIM for which interblock memory is provided be- tween other levels can be similarly designed.

We will show specific designs of BCMIM for the Rayleigh fading channel in the following examples.

/ .

/ ,

Figure 3: The structure of BCMIM with interblock memory between levels a and 6.

In this way, the coding rate will be (T $- k ,

+

k b

+

k,)/n

bits per 8PSK signal point. If we switch the roles of the '%"and

"2'

symbols in the above coding design, then we have a BCMIM with interblock memory between levels a and e. Of course, we can provide interblock memory be- tween levels b and e in a similar way.

Consider the case that the interblock memory is pro- vided between levels a and b. Let the MSD and

MPD

of the original BCM be b~ and

A;

respec- tively. Let Cii denote the ( n ,

ki

-+

r,d;i) binary block code with generator matrix [GZ,GTIT, i E {a,b,c), where M T is the transpose of a matrix M . Let

( U r , G i , 66, Gc) and

(e;,

Cif',

e;, e,')

be distinct messages

s

!2

0.001 0.0001 .%

ieos

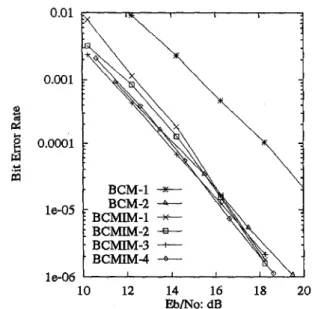
m le-06 BCM-2 -4- BCMIM-1 Jt BCMIM-2

-

BCMIM-3 -t- u - BCMIM-4 -+- 16-07 I I I I 10 12 14 16 18 20 Eb/No: dB

Figure 4: Simulations with CSI.

Example 5 (BCMIM-1) : For this BCMIM, C a , c b , CUU and C b b are (8,1,8), (8,4,4), (8,4,4), (8,4,4) and (8,7,2)

binary codes respectively. The code rate is 12/8 bits per signal point. In the 2-stage decoding, an 8-state trellis for the (16,8,4) binary code C and a 4-state trellis for C, are needed.

Example 6 (BCMIM-2) : For this BCMIM, C,,Cb, C,,

binary codes respectively. The code rate is 12/8 bits per signal point. In the 2-stage decoding, an %state trellis for the (16,8,4) binary code and a 4-state trellis for c b are needed. 0.01 0.001 0

2

0.0001 w .% m l e 0 5 BCM-2 BCMIM-1 -ft BCMIM-2 -8- BCMIM-3 BCMIM-4 -a--- l e 0 6

’

I I I 10 12 14 16 18 20 EbfNo: dB

Figure 5: Simulations without CSI using w a : wb : w c = 1 : 1 :

1. 0.01 0.001 o.oO01 .% l e 0 5 E9 l e 0 6 BCM-1

-

BCM-2

-.I--

BCMIM-1

-

BCMIMP -S- BCMIM-3 -t- BCMIM-4

-

l e 0 7 I I I I 10 12 14 16 18 20 EbfNo: dB

Figure 6: Simulations without CSI using w a : wb : w c = 1 :

0.5412 : 0.3827.

Example 7 (BCMIM-3) : For this BCMIM, Ca,Cb, C,,

binary codes respectively. The code rate is 12/8 bits per signal point. In the 2-stage decoding, an 8-state trellis for the (16,11,4) binary code and a l-state trellis for Ca are needed.

From simulation results shown in Fig. 4, for which per- fect CSI is available, we see that all the three BCMIM have lower BER than the BCM-1 and BCM-2. Among the three BCMIM, BCMIM-2 which provides interblock mem- ory between levels a and c is the best. This can be seen by

c b b and C c c are (8,118)j (8,4,4), (8,4,4), (8,772) and (8,7,2)

more detailedly examining the distance properties of these BCMIM, even though the MSD and MPD of these BCMIM are all identical to the MSD and MPD of BCM-2. In case that U,.

#

U:, we have

SH,.

=

6 and

A;,.

=

(2)2 x (0.586)4

and N ( S H p ,

A;,.)

=

3584 for BCMIM-1; bHr = 6 and

A;,.

=

(4)’ x (0.586)4 and N ( ~ H , . ,

A$,)

= 896 for BCMIM-2;

dHr

=

4 and

A;,.

=

(4)2 x (2)’ and N ( ~ H ~ , A;,.)

=

1792 for BCMIM-3. Since SH,. is more important than A;,. for high SNR, we can expect that BCMIM-2 which also has the smallest N(SH,., A;,.) is the best. Although N ( S H r ,

A:,.) is larger and A;,. is smaller, BCMIM-1 is better than BCMIM-3 for high SNR, which is due to the larger SH,.

From Fig. 5 and Fig. 6, we note that for all the three BCMIM, the usage of weight factors can improve the

BER.

We use BCMIM-2 as an example for explaining the reason. In the first stage of decoding for BCMIM-2, the SED be- tween any two symbols in the first 8 positions is either 4 or 0 and the SED between any two symbols in the last 8

positions is either 0.586 or 0. In decoding this stage, the optimal ratio of weight factors is (1/4)0-5 : (1/0.586)0.5

=

1 : 0.3827. Compared with BCM-2, the coding rate of BCMIM-2 is increased from 9/8 to 12/8, and the error rate is lower. The price is that the decoding complexity for de- coding BCMIM-2 is about twice of that for BCM-2. In the following, we slightly lower the coding rate of BCMIM-2 to more clearly show the advantage of BCMIM over BCM. Example 8 (BCMIM-4) : For this BCMIM, Ca,Cb,

c,,

binary codes respectively. The code rate is 11/8 bits per signal point. In the 2-stage decoding, a 4-state trellis for the (16,7,4) binary code and a $-state trellis for c b are

needed.

The decoding complexity of BCMIM-4 is almost the same as BCM-2. However, the coding rate is higher and the BER is lower.

Caa and Ccc are (8,1,8), (8,4,4), (8,4,4), (8,3,4) and (8,6,2)

References

G. Ungerboeck, “Channel coding with multi- level/phase signals,’’ IEEE Trans. Inform. Theory,

vol. IT-28, no. 1, pp. 55-67, Jan. 1982.

D. Divsalar and M.K. Simon, “The design of trellis coded MPSK for fading channels: Performance crite- ria,” IEEE Trans. Commun., vol. 36, pp. 1004-1012,

Sept.1988.

H. Imai and

S .

Hirakawa, “A new multilevel coding method using error correcting codes,” IEEE Trans.

Inform. Theory, vol.IT 23, pp. 371-376, May.1977. 2 M.C. Lin and S.C. Ma, “A coded modulation scheme with interblock memory,’’ IEEE Trans. Commun.,