Feedback Vertex Sets in Star Graphs

全文

(1)Feedback Vertex Sets in Star Graphs Fu–Hsing Wang1 1 Department. Yue–Li Wang1,∗. Jou–Ming Chang2. of Information Management, National Taiwan University. of Science and Technology, Taipei, Taiwan, Republic of China. 2 Department. of Information Management, National Taipei College of. Business, Taipei, Taiwan, Republic of China.. Abstract. In a graph G = (V, E), a subset F (G) of V (G) is a feedback vertex set if the subgraph induced by V (G) \ F (G) is acyclic. In this paper, we find a lower bound and an upper bound to the size of the feedback vertex set for star graphs.. Keyword: Feedback vertex set, Interconnection network, Star graphs.. ∗. All correspondence should be addressed to Professor Yue–Li Wang, Department of Information Management, National Taiwan University of Science and Technology, 43, Section 4, Kee–Lung Road, Taipei, Taiwan, Republic of China. (Phone: 886–02–27376768, Fax: 886–02–27376777, Email: ylwang@cs.ntust.edu.tw)..

(2) 1. Introduction. Let G = (V, E) be a simple graph, i.e., loopless and without multiple edges, with vertex set V (G) and edge set E(G). A set of vertices F (G) ⊆ V (G) is called a feedback vertex set if the subgraph induced by V (G)\F (G) is acyclic, where V (G)\F (G) = {x|x ∈ V (G) and x 6∈ F (G)}. If the cardinality of F (G), denoted by |F (G)|, is minimum among all possible feedback vertex sets, then we call it a minimum feedback vertex set. The problem of finding a minimum feedback vertex set is NP-hard for general graphs [9]. The approximation ratio of the best known approximation algorithm for this problem is 2 [4]. Besides, most of the work have been devoted to solving the problem for certain classes of graphs. Polynomial time algorithms have been found for some special graphs, e.g., reducible graphs[15], cocomparaibility[10], convex bipartite graphs[10], cyclically reducible graphs[16], and interval graphs[12]. On meshes, toris, butterflies, cube connected cycles and hypercubes, the lower and upper bounds to the size of the feedback vertex set are established and improved recently [5, 7, 13]. The problem has important applications to several fields. For example, we consider the deadlock prevention in operating systems. Once a deadlock has been detected, some strategy is needed to recovery. Usually, a deadlock in a system can be described by using a wait-for graph [14]. In a wait-for graph, each vertex represents a process, and the existence of an edge (i, j) indicates that process i is waiting for process j to release a resource requested by process i. A deadlock exists in a system if and only if the corresponding wait-for graph contains a cycle. One of the best-known approach for solving the deadlock problem can be carried out to abort some deadlocked processes in the wait-for graph. Using graph-theoretic terminology, the strategy is equivalent to finding a (minimum) feedback vertex set for such a system. We consider the problem for a particular interconnection network, namely, star graphs. 1.

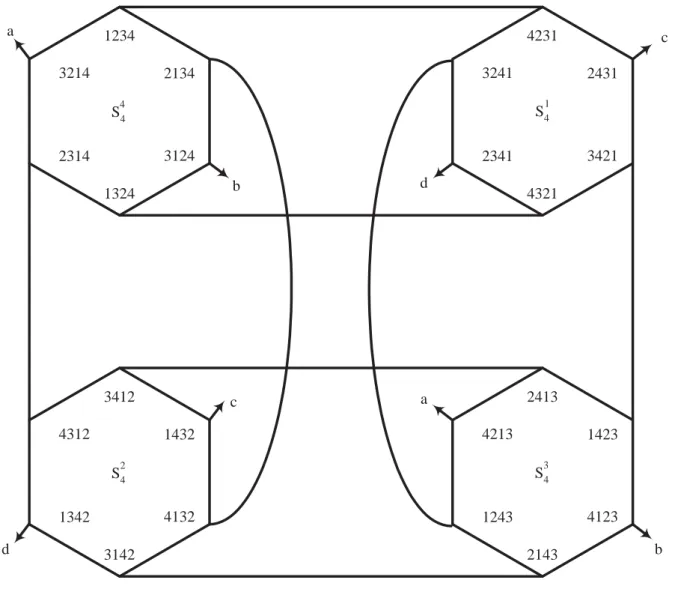
(3) Star graphs were proposed as an attractive alternative to hypercubes with many nice topological properties [1, 2]. Both star graphs and hypercubes provide attractive interconnection scheme for massively parallel systems. Hence characterizations of these architectures have been widely investigated. The star graphs are vertex and edge symmetric, highly regular, strongly hierarchical, and maximally fault-tolerant. Due to the strongly hierarchical structure, a star graph can be defined recursively. Moreover, star graphs have many superior advantages over hypercubes such as smaller degree and diameter. In this paper, we give a lower bound and an upper bound to the size of the minimum feedback vertex for star graphs. The remaining part of this paper is organized as follows. In next section, we present a simple algorithm for finding an upper bound to the size of the minimum feedback vertex on star graphs. In contrast, we also give a lower bound to the problem on regular graphs. Finally, some concluding remarks are given in the last section.. 2. Main Results. The n-dimensional star graph (n-star for short), denoted by Sn , is an undirected graph consisting of n! vertices labeled with distinct permutations [p1 , p2 , . . . , pn ] from the set of symbols N = {1, 2, . . . , n}. Two vertices are connected by an edge if and only if the label of one can be obtained from the label of the other by swapping the first symbol (conventionally, the leftmost) and the ith symbol, where 2 ≤ i ≤ n [1, 2]. Figure 1 depicts S4 which contains 24 vertices, where symbols a, b, c and d indicate the connection through the same symbol. Vertices [1, 2, 3, 4] and [4, 2, 3, 1] are neighbors since their labels differ only in the first and the last positions and swapping these two symbols of one vertex becomes the label of another vertex. Note that an n-star is an edge- and vertex-symmetric regular graph of degree n − 1.. 2.

(4) a. 1234 3214. 4231 3241. 2134. S4 3124. 1324. 3412 4312. b. d. c. a. 4321. 2413 4213. 1423 3. 2. S4. S4. d. 3421. 2341. 1432. 4132. 1342. 2431 1. 4. S4 2314. c. 4123. 1243. 3142. 2143. Figure 1: 4-dimensional star graph S4 .. 3. b.

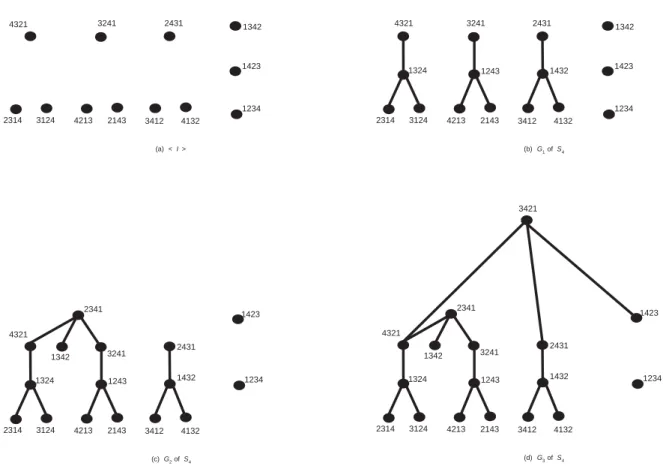
(5) Let [1, 2, . . . , n] denote the identity permutation in Sn . A permutation is odd (resp. even) if it can be turned to the identity permutation through odd (resp. even) number of transitions. Since the star graph is a bipartite graph with equal partite size, half of the vertices are in one partite set [?]. An independent set S of a graph G is a set of vertices such that no two vertices of S are adjacent in G. If the cardinality of S is the maximum among all possible independent sets, the set is called a maximum independent set. Let I be the set of vertices with even permutations, then I is a maximum independent set of Sn , where |I| =. n! . 2. Furthermore, the subgraph induced by I, denoted < I >, has no. cycles in Sn . So V (Sn ) \ I is a trivial feedback vertex set. For i, j ∈ N , let Ni = N \ {i} and Ni,j = N \ {i, i + 1, . . . , j}, where i < j. Define two classes of sets as follows. Φ1 = {[1, p2 , p3 , . . . , pn ] | p2 , p3 , . . . , pn ∈ N1 and pj 6= pk if j 6= k}, and Φi = {[i, p2 , p3 , . . . , pn−i+1 , i − 1, i − 2, . . . , 2, 1] | p2 , p3 , . . . , pn−i+1 ∈ N1,i and pj 6= pk if j 6= k}, for 2 ≤ i ≤ n. It is obvious that Φi , 1 ≤ i ≤ n − 1, are all independents for Sn . Let Gi , 1 ≤ i ≤ n − 1, be the subgraph induced by I. S. Φ1. S. Φ2. S. .... S. Φi . We shall show that V (G) \ V (Gi ), 1 ≤. i ≤ n − 1, is a feedback vertex set and it is smaller than V (Sn ) \ I. The neighborhood N (v) of a vertex v is the set of vertices which are adjacent with v. A vertex v ∈ Gi , 1 ≤ i ≤ n − 1, is called a port vertex of Gi if there exists a vertex u ∈ Φj and j > i such that u ∈ N (v). We use Figure 2 as an example to illustrate the above notation. Figure 2(a) depicts the induced subgraph < I > of S4 . And independent sets Φ1 = {[1, 3, 2, 4], [1, 2, 4, 3], [1, 4, 3, 2]}, Φ2 = {[2, 3, 4, 1]} and Φ3 = {[3, 4, 2, 1]} are sketched in Figure 2(b),(c), and (d), respectively. Consider the induced subgraph G1 of S4 in Figure 2(b). Vertices [4, 3, 2, 1], [3, 2, 4, 1], [2, 4, 3, 1], [1, 3, 4, 2] and [1, 4, 2, 3] are port vertices of G1 , since vertices [4, 3, 2, 1], [1, 3, 4, 2] and [3, 2, 4, 1] are neighbors of the 4.

(6) 3241. 4321. 2431. 4321. 1342. 1423. 3241. 1324. 2431. 1342. 1432. 1243. 1234 2314. 3124. 4213. 2143. 3412. 1423. 1234 2314. 4132. 3124. 4213. 2143. (a) < I >. 3412. 4132. (b) G1 of S4. 3421. 2341. 2341. 1423. 1324. 3124. 2431. 3241. 1342. 2314. 1423. 4321. 4321. 1432. 1243. 4213. 2143. 3412. 1324. 1234. 2314. 4132. 3124. 2431. 3241. 1342. 1432. 1243. 4213. 2143. 3412. 1234. 4132. (d) G3 of S4. (c) G2 of S4. Figure 2: Acyclic subgraph < I >, G1 , G2 , G3 of S4 , respectively in figures (a), (b), (c), and (d).. vertex [2, 3, 4, 1] ∈ Φ2 , and vertices [2, 4, 3, 1] and [1, 4, 2, 3] are neighbors of the vertex [3, 4, 2, 1] ∈ Φ3 . Figure 2(c) illustrates G2 of S4 where vertices [4, 3, 2, 1], [2, 4, 3, 1] and [1, 4, 2, 3] are port vertices of G2 . But the vertices [1, 3, 4, 2] and [3, 2, 4, 1] are not port vertices of G2 , since they are not adjacent with any vertex in Φ3 . Furthermore, Figure 2(d) is a maximum acyclic induced subgraph of S4 . Thus, V (S4 ) \ V (G3 ) is a minimum feedback vertex set. A set D ⊆ V (G) is a dominating set of G if for every vertex u ∈ V (G) \ D there exists a vertex v ∈ D such that u is adjacent to v. In particular, we call D a perfect dominating set if every vertex in V (G) \ D is adjacent to exactly one vertex in D. We call D an independent dominating set if D is also an independent set of G. A dominating set D is. 5.

(7) independent perfect if it is both independent and perfect. In star graphs, Arumugam and Kala [3] showed that Φ1 is not only a minimum independent dominating set, but also a minimum perfect dominating set. That is to say, Φ1 is in fact a minimum independent perfect dominating set.. Lemma 1 G1 is acyclic and each component of G1 has at most one port vertex.. Proof.. Let u, v be two vertices of G1 . Since Φ1 is a minimum independent perfect. dominating set, there is no common vertex between the neighbors of u and v. Since u and v are not adjacent and the neighbors of u and v belong to the independent set I, u and v are in different components of G1 . Since each vertex of I is adjacent with at most one vertex of Φ1 , the component of G1 is either an isolated vertex or a nontrivial tree. Thus, G1 is acyclic. To complete the proof, let T be a component of G1 . We now consider two cases, depending on T is an isolated vertex or a nontrivial tree. Let T be an isolated vertex. It is clear that T is the only possible vertex which is adjacent with some vertex in Φi , i > 1. Thus, the component T has one port vertex if and only if T is a port vertex. Otherwise, T is a nontrivial tree. Let r ∈ Φ1 be the root of T . Since r is a odd permutation vertex, the n − 1 neighbors of r are even permutation vertices of I. Since the first (leftmost) symbol of r is one. Thus, T has exactly one leaf whose last (rightmost) symbol is one. For the other leaves, since both the first and the last symbols are not one, they are adjacent with none of the vertex in Φi , i ≥ 2. So, the vertex in each tree with the last symbol as one is the only possible port vertex. Q. E. D. For each vertex v = [p1 , p2 , . . . , pn ] of Sn , let N Bi (v), 2 ≤ i ≤ n, be the i-th neighbor of v. That is N Bi (v) = [pi , p2 , . . . , pi−1 , p1 , pi+1 , . . . , pn ].. Lemma 2 Each component of Gk , 1 ≤ k ≤ n − 1, has at most one port vertex. 6.

(8) Proof.. We proceed by induction on k. For k = 1, the lemma holds by Lemma 1.. As the inductive hypothesis we assume that each component of Gk , 2 ≤ k ≤ i − 1, has at most one port vertex. We now want to show that the lemma is also true for k = i. Let u, v be two distinct vertices in Φi . Since Φi is an independent set, u and v are not adjacent. Let T be a component of Gi−1 . By hypothesis, T has at most one port vertex. Suppose that T has no port vertex, it is easy to see that T still has no port vertex in Gi . Consequently, we assume that T has exactly one port vertex. Let T (p) be the port vertex of T . If T (p) is not adjacent to any vertex of Φi , then T (p) is still the unique port vertex of T in Gi . Thus, we assume that T (p) is a neighbor of a vertex w ∈ Φi . Let w = [i, p2 , . . . , pn−i+1 , i − 1, i − 2, . . . , 1],w ∈ Φi . To complete the proof, we shall show that there are at most one of the neighbors of w which is a port vertex in Gi . Consider the neighbors N Bj (w), 2 ≤ j ≤ n, of vertex w. Suppose that N Bj (w) is a port vertex in Gi . Then there exists a vertex φ = [i0 , p2 , . . . , pn−i , i, i − 1, . . . , 1] in Gi0 , i0 > i, such that N Bj (w) ∈ N (φ). There are now four cases to consider, depending on the number j. Case 1. 2 ≤ j ≤ n−i. Let N Bj (w) = [pj , p2 , . . . , pj−1 , i, pj+1 , . . . , pn−i+1 , i−1, i−2, . . . , 1]. Compare the positions of symbol i in v ∈ N (φ) and N Bj (w). Since the symbol i of v occurs either in the first or the (n-i+1)-th position, which is different from the position of N Bj (w). Thus, N Bj (w) and φ are not adjacent. It contradicts that N Bj (w) ∈ N (φ). Case 2. n−i+2 ≤ j ≤ n−1. Let N Bj (w) = [pj , p2 , . . . , pn−i+1 , i−1, i−2, . . . , pj−1 , i, pj+1 , . . . , 1]. The proof is similar to Case (1). Case 3. j = n. Let N Bn (w) = [1, p2 , . . . , pn−i+1 , i − 1, i − 2, . . . , 2, i]. Since the symbols in the first and the n-th positions of φ are i0 and 1, respectively. If N Bn (w) ∈ N (φ) then N Bn (w) = N Bn (φ), which implies that i = i0 . It is a contradiction. Case 4. j = n − i + 1. If pn−i+1 = i + 1 then there exists a vertex x ∈ Φi+1 such that N Bn−i+1 (w) and x are adjacent. Thus, N Bn−i+1 (w) is a port vertex of T in Gi . In accordance with the above discussion, N Bj (w) is a port vertex only if j = n − i +. 7.

(9) 1(Case 4). Q. E. D.. Lemma 3 Gi is acyclic, for 1 ≤ i ≤ n.. Proof.. The proof is also by induction on i. For i = 1, the lemma holds by Lemma 1.. Assume the theorem to be true for all Gi , i < n − 1. In Gn−1 , by Lemma 2, since each component of Gi−1 is acyclic and has at most one port vertex, each acyclic component is incident with at most one vertex in Φn−1 . Because Φn−1 is an independent set, the component in Gn−1 is also acyclic, completing the proof. Q. E. D. Theorem 4 |F (Sn )| ≤ 21 [n! − (n − 1)! − (n − 2)! − . . . − 2!] − 1. Proof. By Lemma 3, Gn−1 is acyclic. Thus, V (G) \ V (Gn − 1) is a feedback vertex set. Therefore,. |F (Sn )| ≤ |V (G) \ V (Gn−1 )| = n! − [|I| + |Φ1 | + |Φ2 | + . . . + |Φn−1 |] = n! − [ n!2 +. (n−1)! 2. + ... +. 2! 2. + 1]. = 12 [n! − (n − 1)! − (n − 2)! − . . . − 2!] − 1. Q. E. D. To find the lower bound to the size of the feedback vertex set for star graphs, an analysis based on [7] is given. In [7], Focardi and Luccio state a lower bound related to the number of components of the resulting acyclic subgraph for hypercubes. We now establish an equation, a modification of [7], for calculating the lower bound to the size of the feedback vertex set in r−regular graphs. 8.

(10) Theorem 5 Given an r−regular graph G = (V, E), |F (G)| ≥ |V (G)| −. Proof.. |E(G)|−rc r−2. −c. Let G0 = (V − F (G), E 0 ) be the acyclic induced subgraph of G. Let c be. the number of components in G0 and Ti be the i-th component. The degree of v in Ti is denoted by din (v). For simplicity, let Vi , Ei , Eiin , Eiout denote the number of vertices, edges, internal edges, and external edges of Ti , respectively. Since Ti is a tree, |Vi | = |Eiin | + 1. To count the external edges of Ti , we have |Eiout | = Σv∈Vi (r − din (v)) = r(|Vi |) − Σv∈Vi (din (v)) = r(|Vi |) − 2(|Vi | − 1) = (r − 2)(|Vi |) + 2 = (r − 2)(|Ei | + 1) + 2 = (r − 2)|Ei | + r.. Then, the cardinality of the external edges in G is |E(G) − E 0 (G0 )| = Σci=1 |Eiout | = (r − 2)|E 0 (G0 )| + rc.. Since |E(G)| ≥ |E 0 (G0 )| + |E out | = |E 0 (G0 )| + (r − 2)|E 0 (G0 )| + rc = (r − 1)|E 0 (G0 )| + rc, we have |E 0 (G0 )| ≤. |E(G)|−rc . r−1. The size of the feedback vertex set is |F (G)| = |V (G)| − Σci=1 |Vi | = |V (G)| − Σci=1 |Ei + 1| 9.

(11) = |V (G)| − |E 0 (G0 )| − c.. So, |F (G)| ≥ |V (G)| −. |E(G)|−rc r−1. − c.. Q. E. D. Note that the n-star has n! vertices,. n!(n−1) 2. edges and degree n − 1. The next result. follows.. Corollary 6 |F (Sn )| ≥. (n−3)n!+2 ,n 2(n−2). ≥3. By Theorem 4 and Corollary 6, we get. 13 2. ≤ |F (Sn )| ≤ 7 implying that both the lower. bound and upper bound are tight.. 3. Concluding Remarks. The feedback vertex set problem is oriented from the circuit design. Recently, the related research focused on interconnection networks including meshes, toris, butterflies, and hypercubes are widely studied. Then, new bounds are established one after the other. The star graph is an attractive topologies having many nice properties than the mentioned graphs. In this paper, we set up the upper bound to the size of the feedback vertex set in star graphs by a constructive proof. We also give a formula, a modification of Focardi et al.[7], to show the lower bound of the feedback vertex set in k-regular graphs. Certainly, this bound suits star graphs and is shown to be sharp. However, the feedback vertex set we have found is not the minimum. An interested problem is to explore more precise bounds.. 10.

(12) References [1] S. B. Akers, D. Harel and B. Kirshnamurthy, The Star Graph: An Attractive Alternative to the N -cube, in: Proceedings of the International Conference on Parallel Processing, St. Charles, Illinois, pp. 393–400, 1987. [2] S. B. Akers and B. Kirshnamurthy, A Group-theoretic Model for Symmetric Interconnection Networks, IEEE Transactions on Computers, Vol. 38 (4), pp. 555–565, 1989. [3] S. Arumugam and R. Kala, Domination Parameters of Star Graph, Ars Combinatoria, Vol. 44, pp. 93–96, 1996. [4] V. Bafna, P. Berman, T. Fujito, A 2-approximation algorithm for the undirected feedback vertex set problem, SIAM Journal on Discrete Mathematics , Vol. 12 (3), pp. 289–297, 1999. [5] I. Caragiannis, C. Kaklamanis, and P. Kanellopoulos, New Bounds on the Size of the Minimum Feedback Vertex Set in Meshes and Butterflies, Information Processing Letters, Vol. 83, pp. 275–280, 2002. [6] K. Day and A. Tripathi, A Comparative Study of Topological Properties of Hypercubes and Star Graphs, IEEE Transactions on Parallel and Distributed Systems, Vol. 5, pp. 31–38. [7] R. Focardi, F.L. Luccio, and D. Peleg, Feedback Vertex Set in Hypercubes, Information Processing Letters, Vol. 76 (1-2), pp. 1–5, 2000. [8] P. Festa, P.M. Pardalos, and M.G.C. Resende, Feedback Set Problems, In: Encyclopedia of Optimization, Vol. 2, pp. 94–106, Kluwer Academic Publishers, 2001.. 11.

(13) [9] M.R. Garey and D.S. Johnson, Computers and Intractability: A Guide to the Theory of NP-completeness, Freeman, San Francisco, 1979. [10] J.S. Jwo, S. Lakshmivarahan, and S.K. Dhall, Embedding of Cycles and Grids in Star Graphs , Journal of Circuits Syst. Comput., Vol. 1, pp. 43–74, 1991. [11] Y.D. Liang and M.S. Chang, Minimum Feedback Vertex Set in Cocomparaibility and Convex Bipartite Graphs, Acta Informatica, Vol. 34, pp. 337–346, 1997. [12] M. Livingston and Q. F. Stout, Perfect Dominating Sets, Congressus Numerantium, Vol. 79, pp. 187–203, 1990. [13] C.L. Lu and C.Y. Tang, A Linear-time Algorithm for the Weighted Feedback Vertex Problem on Interval Graphs, Information Processing Letters, Vol. 61 (2), pp. 107–111, 1997. [14] Flaminia L. Luccio, Almost Exact Minimum Feedback Vertex Set in Meshes and Butterflies, Information Processing Letters, Vol. 66, pp. 59–64, 1998. [15] A. Silberschatz, P.B. Galvin, and G. Gagne, Operating Systems Concepts, Sixth Edition, Wiley, 2002. [16] A. Shamir, A Linear Time Algorithm for Finding Minimum Cutsets in Reducible Graphs, SIAM Journal on Computing, Vol. 8 (4), pp. 645–655, 1979. [17] C.Wang, E.L. Lloyd, and M.L. Sofra, Feedback Vertex Sets and Cyclically Reducible Graphs, Journal of the ACM, Vol. 32 (2), pp. 296–313, 1985.. 12.

(14)