A novel approach for robust adaptive beamforming

U4.10

A NOVEL APPROACH FOR ROBUST ADAPTIVE BEAMFORMING

Ju-Hong Lee and Jen-Fu

Wu

Department of Electrical Engineering National Taiwan University

Taipei, Taiwan, R.O.C.

ABSTRACT

This paper concerns the adaptive array beamforming in the presence of steering vector e m r . A robust technique is proposed based on the fact that an optimized steered beam adaptive beamformer possesses the maximum output SINR when the steering vector coincides with the signal phax vector t o iteratively adjust the steering vector t o meet the actual

signal phase vector. The resulting robust adaptive beamformer can provide the optimum performance in the sense of satisfying single-look direction constraint without making any tradeoff between the array performance and robustness Thus the difficulties of u$ing conventional algorithms can be overcome. Several computer simulations are given for illustration.

I. INTRODUCTION

In the literature, it has been found that the performance of a steered beam adaptive array depends heavily on the accuracies of signal and array situations. Basically, optimum adaptive arrays are designed under the assumptions of ideal signal characteristics and exact array configurations. In practical circumstances, however, there exists the problem of mismatch because the real signal characteristics or array geometries differ from the assumed ones. Many reports have mown that the effectiveness of an adaptive array can be destroyed even if a small mismatch arises. The effect due t o the mismatch of steering angle on array performance has been discussed in [ 1-51, Research endeavor has been devoted to this problem

and solution methods have been presented in 16, 71. These methods impox the directional derivative constraints for broadening the main-beam width t o allow direct control of the array sensitivity to the steering angle error. However, a tradeoff between the jamming rejection ability and array tolerance to steering angle error is induced. Moreover, the resulting array degenerates from its optimum even when the steering is correct. Another mismatch is array imperfection. As shown m [5, 81, the array performance is very sensitive even if there exists small imperfection in array geometry. They tackle this problem at the price of reducing the ability of jammer suppression Considering the effect of finite source distance, 1141 has studied the performance of a far-field steering array when the true source distance is finite. It has been shown that the output SNR of a far-field steering array decreases as the ranging mismatch increases.

Recently, many robust techniques have been presented to deal with the problem of mismatch 19-13], However, they still employ additional constraints on the weight vector, such as multiple linear constraints, quadratic inequality constraints, in order to achieve robustness. This leads t o the result that the degrees o f freedom in searching the array optimum weight vector are reduced. Therefore, these robust algorithms inevitably induce the tradeoffs mentioned above.

In this paper, we present a robust technique for adaptive beamforming against steering vector error due to steering angle error, array imperfection, or source ranging mismatch. Based on the fact that the output

SINR

of an optimized steered

2740

CH2673-2/89/OW-2740 $1.00

0

1989 IEEE

beam adaptive beamformer has a maximum if the steering vector coincides with the signal phase vector 121, the approach f m t fmds the optimum weight vector under main-beam constraint for a steering vector b y minimizing the array output power, then searches the correct steering vector in a prescribed class of possible arrival phase vectors of the desired signal to maximize the array output

SINR.

Therefore, unlike existing techniques, the approach does not use additional constraints on the weights for achieving robustness. The resulting robust adaptive beamformer can provide the optimum performance satisfying single-look direction constraint without making tradeoffs between the array performance and robustness. The proposed robust method thus overwmes the difficulties of using existing techniques in combatting steering vector error.

11. A STEERED BEAM ARRAY BEAMFORMER Consider the antenna array with

M

elements shown in Figure 1. The position of the mth array element is designated as (x,,,, y,). A signal source is located at a distance D from

the array center and at an angle @ off broadside. The received signal at the mth array element can be written as

z,(t) = a ( t ) s , + B ( t ) s + n,(t) (1)

where s,,, and s, denote the relative phase shifts of the signal and interference, respectively. o(t) and B(t) are the complex waveforms of the signal and interference, respectively. n,(t) is the white Gaussian noise with mean zero and variance 0:. In the case of fmite source distance, the relative phase shift is approximately given by [ 141

s, = exp(jk(x, sin@

+

ym cose -

(x, cos0 - y, sin@)’/2D)) (2)

In vector form, (1) becomes

Z(t) = o(t) S + P(t)

SI

+ N(t)

( 3)

where 20) = (zl(t), zZ(t),

. .

.

. .

,

z ~ ( t ) Y , N O ) = (nl(t). nz(t), .

. . . .

, nM(t))t, the arrival signal phase vector S

= ( s l , s2,

.

.

. . .

,

S M ) ~ , and

SI

denotes the relative phase shift vector associated with the interference. Under the far-field (i.e., .D = =-) assumption, the steering vector for an array looking

at an angle Tis given as

s d = ( h , l , % , 2 ~ . ~ . ~ . , % , M ) t

with

S d , m = exp (jk

6

,

sinB

+ 7,

cosB)),

m = 1 . 2

, . . . ,

M. (4)

where

(X,,,,

F,)

is the assumed position of the mth array element ,

Let the received signal vector of (3) be fed into an adaptive n ( s d ) = { W I w S d = I } array with Mdimensional weight vector W shown in Figure

2. The output y(t) is given as and

T h u s the output signal-to-interference plus noise ratio (SINR) is of the form

SINR = E(lu(t)Wt Sl’)/E(RNtN(t)l’

+

I P(t) Wt

s,

1’). ₍₇₎

In the ideal steering case, i.e.,

Sr,

= x,, ‘j, = y m , B =

r,

and D =

-, thus

S = sd. The optimum weight vector WO for the adaptive array without constraints is obtained by maximizing (7) [ 151 and given as

WO = KihSd (8)

where p is a constant and R N ~ is the correlation matrix due t o noise and interference. On the other hand, the optimum weight vector for the adaptive array with directional constraint in the signal direction is obtained by minimizing the array output power E(ly(t) 1’) subject to Wt Sd = 1 1151 and given

as

It is shown in [ 171 that e & ) reaches a maximum value when Sd equals the true signal phase vectors S. Moreover, we note from [I71 that in the presence of steering vector error, maximizing the output SINR of (12) is equivalent t o

maximizing the e & ) of (16).

From the above description, we see that the robustness in the design of adaptive array beamformer against steering vector error can be achieved by solving the following optimiza tion problem:

Maximize e(&) Subject to Sd E S,

.

where S , denotes the class of possible arrival phase vectors of the signal. Substituting

(IS)

into (17) yields an equivalent optimization problem:

(18) Maximize { Minimize Wt I(zz W

1

.

S,j E

s,

w

E n ( S d )

Based on the result of (16), the optimization problem of (18) becomes

( 9 )

From (9) and (IO), the optimum weight vector for a steered beam array beamformer is given as

WO = R i i

&:

Sd (11)

in. FORMULATION OF THE ROBUST METHOD In many actual operating situations, the ideal steering assumptions do not hold. From the above description, we can see that any mismatch of the following parameters, namely, the steering angle

8,

array positions (x, , y,), m = 1 , 2 ,

. . .

,

M, and the source distance D, leads to steering vector e m r . As a result, the performance of the adaptive array beamformer suffers deterioration. Furthermore, it is easy to show that the corresponding output SINR is given as

SINR = pj

Si

RI: S St R,:

%/si

Ri\ RNI RA s d (12)

or eauivalently,

IV.

THE ADAFTIVE ALGORITHM

To consider the solution of (20) t o be robust in some sense, we first model the uncertainty class S,. Then an adaptive algorithm is derived for implementing the robust technique.

Define the metric distance of two vectors A and B with dimension M as

I I A - B I I = { (a,-b,)’}”

m = l

where a, and b, are the entries of A and B, respectively. The squared metric distance of the steering vector and signal phase vector is thus given as

where PI

b

E ( l u ( t ) ’ * ) . In [I71 it is shown that the SINR becomes maximum when s d =

s.

.

In the following, we propose a robust technique to over- come the problem o f steering vector error. First, the optimiza- tion problem of soking the optimum weight vector WO can be written as

Next assume that the tolerance ermr of Sd in (22) due t o any

of the three mismatches is 6 . Then (22) can be written as

I 1 Sd

-

s

1 1’ = ( s d

-

S)t (sd

-

s)

<

6 ₍₂₃₎ Since S is an Mdimensional vector and each of its entries is of the form (2), the position of s d is on the hyperplane of radius (MI” centered at the origin as shown in Figure 3. T h e r e

fore, the minimization problem o f (20) becomes

MinimizeE(ly(t)lZ) = Minimize Wt R,, W , Subject t o ~t s d = I.

(13)

Next, define Minimize { S$ R;\ s d }

Subject to I I

&

-

s

I 1’ =

(sd

- S)t ( s d -

s)

<

6 (24) and IQ,,, I = I , m = 1 , 2

, . . . ,

M We u s the Lagrange multiplier h to take into account the inequality constraint. Thuh (24) becomes

Minimize { J(S,, A) = Sb R2z S,

+

((Sd

-

S)t ( s d -

s)

-

8 )

1

Subjectto I Q , ~ I = I , m = l , 2

, . . . ,

M

(25) (25) shows that the minimization problem for satisfying the inequality constraint can be solved using the standard prima& dual method [16] since both the objective function and constraint are quadratic in s d . To satisfy the equality constraints, we can project the solution of s d onto the hyperplane of IQ,,, I = 1, m = 1 , 2 , . .

. . .

,

M at each iteration. Hence, the resulting algorithm for solving (25) can be expressed as

s d ( k + I)=Sd(k)-‘X(k)Vs J ( S d , h ) ’ S d = S d ( k ) %,,,(k+ l)=Sh,,(k+ l ) / l s ~ , , , , ( k + I ) l

S d ( k + l ) = ( S d , i ( k + 1 ) , S d , z ( k + 1 ) , . .

. . . ,

%.M (k + 1))‘ h ( k + l ) = m a x ( O , h ( k ) - P ( ( S d - S ) + ( s d - 9 - 6 ) ) (26) where

v s

J denotes the gradient of J with respect to s d and 0

<

a&)

<

1. The convergence of the algorithm is shown

in [17]. Using the algorithm, we can iteratively adjust the steering vector Sa to approach the signal phase vector S . An adaptive algorithm for solving the optimization problem of (25) with unknown R,, is similar t o (26) except that the inverse of the correlation matrix R,, is estimated as follows a z , ( k + l ) = ( l - q ) ~ , , ( k ) + q Z ( k + l ) Z t ( k + l ) . (27) where q is a smoothing parameter (0 < q

<

I ) and Z(k) is the kth sample vector of the received signal vector Z(t). Using the matrix inversion lemma, we obtain

k2z

(k

+

I ) = kz(k)/( I-q) - q { g z ( k ) Z(i

+

I ) }

t

zt(k + 1 ) i R ; : ( k ) }

/

(1

-

4) { (1

-

9) + q(Zt (k

+

1) k;i(k) Z(k

+

I))

}

. (28) V. SIMULATION EXAMPLES

In this section, several computer simulations are presented for illustration. A linearly periodic array with

M

= 10 was used. The spatially white Gausian noise has power U: = 1.

The signal source has SNR = IO dB. An incoherent interference is at direction angle .9k = 13.9” with the same power as the signal source.

A. Example of Steering Angle Mismatch

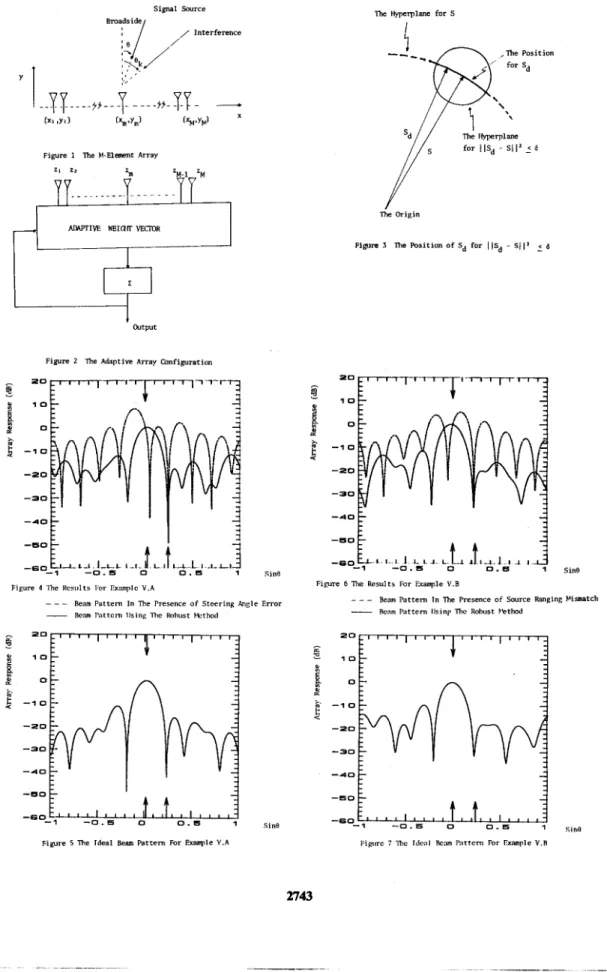
In this case, we a u m e that the array elements are at ideal positions, i.e., xm = mXs/2(A,= wavelength), ym = 0 and the signal is a far-field source with direction angle 0 = 1.1”.

The steering angle is given by B = 0”. Thus the steering angle error is 1.1”. Figure 4 shows the results under the steering angle error and using the proposed robust technique, respectively. The ideal result for this case

( F =

1.1”) is shown in Figure 5. Comparing these results, we note that the robust technique can effectively cure the array performance degrada- tion due to steering angle error. Moreover, the beam pattern using the robust technique is asgood as the ideal beam pattern. B. Example of S g ~ l Ranging Mismatch

In this case, we m u m e that the steering vector error is only due to the fmite source distance. The array elements are at the ideal positions and the steering angle is the same as the signal direction angle, ie.,

8=

0 = 0”. The source ranging D was set to 150 A, for this example. Figure 6 shows the

results under fmite source distance situation and using the robust technique, respectively. The ideal result without mismatch is shown in Figure 7. Agaii, we note from these

results that the proposed robust technique demonstrates its effectiveness in dealing with the degradation effect due to source ranging mismatch and provides a beam pattern as good as that of the ideal case.

REFERENCES

F. Haber, Y. Bar-Ness, and C.C. Yeh, “An Adaptive Interference Canceling Array Utilizing Hybrid Techni- ques”, IEEE Trans. AES, VoL AES19, No. 5, pp. 795-803, Sept. 1983.

R.T. Compton, Jr., “The Effect of Random Steering Vector Errors in the Applebaum Adaptive Array”, IEEE Trans. AES, Vol. AES-18, No. 5, pp. 392-400, Sept. 1982.

R.T. Compton, Jr., “Pointing Accuracy and Dynamic Range in a Steered Beam Adaptive Array”, IEEE Trans. AES, Vol. AES16, No. 3, pp. 280-287, May 1980. L.C. Codara, “Error Analysis of the Optimal Antenna Array Processors”, IEEE Trans. AES, Vol. AES-22, No. 4, pp. 395-409, July 1986.

N.K. Jablon, “Adaptive Beamforming with the Gener- alized Sidelobe Canceller in the Presence o f Array Imper- fections”, IEEE Trans. AP, Vol. A€-34, pp. 996-1012, Aug. 1986.

M.H. Er and A. Cantoni, “Derivative Constraints for Broad-Band Element Space Antenna Array Processors”, IEEE Trans. ASSP, Vol. ASSP-3 1, No. 6, pp. 1378-1393, Dec. 1983.

K.M. Buckley and LJ. Griffths, “An Adaptive Gener- alized Sidelobe Canceller with Derivative Constraints”, IEEE Trans. AP, Vol. AP-34, No. 3, pp. 31 1-319, Mar. 1986.

K. Takao and N. Kikuma, “Tamed Adaptive Antenna Array”, IEEE Trans. AES, Vol. AES-34, No. 2, pp. 388-394, Mar. 1986.

K.M. Ahmed and R.J. Evans, “Robust Signal and Array Processing”, IEE Proc.

Pt.

F, No. 4, pp. 297-302, Aug.

1982.

R.J. Evans and K.M. Ahmed, “Robust Adaptive Array Antennas”, J. Acoust. Soc. Amer., Vol. 71, No. 2, pp. 384394, Feb. 1982.

M.H Er and A. Cantoni, “An Alternative Formulation for An Optimum Beamformer with Robustness Capability”, IEE Proc. Pt. F, No. 6, pp. 447-460, Oct.

1985.

M.H. Er and A. Cantoni, “A New Approach to the Design of Robust Narrow-Band Array Processors”, Proc. of IEEE ICASSP ’86, pp. 2527-2530, Tokyo, Japan, April 1986.

H. Cox, R.M. Zeskind, and M.M. Owen, “Robust Adaptive Beamforming”, IEEE Trans. ASSP, Vol. ASSP- 35, No.

IO,

pp. 1365-1376, Oct. 1987.

C.C. Yeh, Y.J. Hong, and D.R. Ucci, “The Effect of A Finite Distan,ce Source on An Applebaum Array”, IEEE Trans. AP, Vol AP-33, No. 9, pp. 1003-1008, Sept. 1985.

R.A. Monzingo and T.W. Miller, INTRODUCTION TO ADAFTIVE ARRAYS, New York: Wiley, 1980. D. Luenberger, INTRODUCTION TO LINEAR AND NONLINEAR PROGRAMMING, MA: Addison-Wesley, 1973.

Ju-Hong Lee and Jen-Fu Wu, “A Novel Approach for Robust Adaptive Beamforming”, submitted to IEEE Trans. ASSP.

Signal Saurce Emadside,

Figure 1 The #-Elwent Array

L

Figure 2 The Adaptive Array Configuration

The

Y

Origin

FIym 3 The Position of Sd for Is,, - s / 5 6

2 0 1 0 0 2 E o 2 - 1 0

P

-1 0 -20 --2O -30 -30 - 4 0

Figure 4 Ihc IUcsults l'or Pxamplc V . A

_ _ _

Rem Pattern In The Presence of Steering Angle Error

-

lkm Pnttcrn Using The llohust Mcthod

1 - 0 . 6 0 0.6 1

Figure 5 me Ideal Bean Pattern For Exawle V . A Sin8

1 Sine

Figure 6 The Results TOT Example V.B

_ _ _

Beam Pattern In lix Presence of Swrce Ranging Pimatch

-

Ream Pattern I b i n p The Rohwt W t h d

I[,,

, ,

,

,

,

, ,

+ ,

t , ,

,

, ,

, j

1 sihe

0 . 6

1 - 0 . 5 0

-60-

I:igtrc 7 Ihc Ideal l k ~ n Pattern Tor Example V.R

2743