A New Adaptive Linear Multi-Stage Multiuser Detector for DS-CDMA Systems
Chen-Chu Hsu Yumin Lee
Graduate Institute of Comm. Eng. And Dept. of Electrical Eng., National Taiwan University
Taipei 10617, Taiwan
TEL: +886-2-2362658 FAX: +886-2-23683824 E-mail: yuminlee@cc.ee.ntu.edu.tw
Abstract- Conventional linear multi-user detectors (MUD)
such as the decorrelating MUD and MMSE MUD require the inversion of a matrix or solution of a system of linear equations. The high complexity involved makes direct matrix inversion or direct solution of the system of linear equations difficult especially when the number of users is large. In this paper, we propose a new adaptive linear multi-stage MUD that has lower complexity. Parameters of the proposed structure can be optimized offline or updated on the fly according to channel conditions. Simulation results show that the proposed MUD with a few number of stages almost achieves the performance of the linear MMSE MUD.
Ⅰ. INTRODUCTION
Multiple access interference (MAI) is a dominant limiting factor of the capacity of multiuser communication systems based on direct-sequence code division multiple access (DS-CDMA). In a conventional DS-CDMA receiver, detection of the desired user’s signal is performed while treating MAI as thermal noise. Although simple in structure, the conventional receiver fails to realize the full potentials of DS-CDMA because treating MAI as noise loses much information about the structure of MAI. Significant improvement over the conventional receiver can be achieved by viewing MAI as signal rather than thermal noise, and jointly detecting all users’ information symbols. This improved detector is referred to as the multi-user detector (MUD) in the literature[1].
Many MUD structures can be found in the literature for different applications and channel conditions. The linear MUD [1,4] is one of the most suitable choices for downlink or quasi-synchronous uplink DS-CDMA transmission over flat fading channels. In a linear MUD, joint estimation of all users’ transmitted symbols is performed by applying a linear transformation to the received signal. Depending on the optimization criterion for the linear transformation, linear MUD’s can be further classified into the linear decorrelating MUD and linear MMSE MUD. In general, optimization of a linear MUD requires the inversion of a matrix, or equivalently, solution of a system of linear equations. Because of the high complexity involved, direct inversion of the matrix (or direct solution of the system of
linear equations) can be difficult especially when the number of users is large. Therefore computationally efficient linear multi-stage MUD’s have been proposed as alternatives to the direct inversion approach. In [2], for example, a multi-stage linear MUD has been proposed based the successive over-relaxation (SOR) algorithm for solving systems of linear equations[5]. An important real scalar parameter, referred to as the over-relaxation factor, has been introduced in this previously proposed algorithm. By carefully optimizing the over-relaxation factor, the number of stages required can be effectively reduced, thus lowering the computational complexity.
In this paper, we propose a new adaptive multi-stage MUD that is a novel generalization of the previous structure proposed in [2]. Instead of a fixed scalar relaxation factor, the proposed structure uses an adaptive relaxation matrix that can be updated on the fly according to channel conditions. Formulas for adapting the relaxation matrix are also derived in this paper based on the method of steepest descent [5]. Simulation results show that the proposed MUD with a few number of stages almost achieves the performance of linear decorrelating and MMSE MUD’s using direct matrix inversion.
Ⅱ. SYSTEM MODEL
Consider a synchronous DS-CDMA system employing linear MUD in which K≥1 active users transmit their data streams simultaneously over wireless flat-fading channels. The baseband equivalent received signal can be expressed as
∑ ∑
= + − = K k k m k k d mg t mT nt A t r 1 ) ( ) ( ] [ ) ( , (1)where
A
k ,g
k(t
)
, and dk[m] are, respectively, the flat-fading channel gain, signature waveform, and m-th modulation symbol of the k-th user, T is the symbol-period, andn
(t
)
is the additive white Gaussion noise (AWGN) with two-sided power spectral density N0/2. At the receiver,the received signal r(t) is first processed by a bank of K filters matched to gk(t), k = 1,2, …, K. The outputs of the filters are then sampled at the symbol rate. The output samples of the matched filter bank at time m can be expressed as a K ×1 vector given by
y[m] = RAd[m] + n[m], (2) where R is a K×K correlation matrix whose (i,j)-th element is given by
∫
= T i j ij T g t g t dt R 0 *( ) () 1 , (3)A is a K×K diagonal matrix given by
≡ K A A O 1 A , (4)
d[m] is a K×1 symbol vector given by
[ ] [
]
T K m d m d m ≡ 1[ ] L [ ] d , (5)and n[m] is a K×1 vector of filtered Gaussian noise samples. At the receiver, the vector y[m] is processed by a linear MUD to obtain a soft linear estimate x[m] for Ad[m], and the hard decision for d[m] is then obtained by appropriately rotating and slicing x[m]. Mathematically, for linear MUD the soft estimate x[m] satisfies the system of linear equations given by
Lx[m] = y[m], (6) where the K×K matrix L is defined as L= R+N0(AAH)-1 for the linear MMSE MUD and L=R for the linear decorrelating MUD, where “H” denotes Hermitian transposition. Since we only consider the simple case of flat-fading channels due to space limitations, in the remainder of this paper we will omit the time index m whenever it is clear from the context.
Ⅲ. ADAPTIVE SOR MULTI-STAGE LINEAR MULTIUSER DETECTOR
Direct solution of (6) involves the inversion of the K×K
matrix L, which can be difficult when K is large. Computationally efficient multi-stage linear MUD structures have previously been obtained by suitably decomposing L into lower and upper triangular matrices and solving (6) iteratively. In [2], for example, a new multi-stage linear
MUD is derived from the SOR algorithm for solving systems of linear equations[5]. As shown in Fig. 1, this previously proposed structure consists of N cascaded stages, each having a K×1 vector output. The output of the n-th stage, x(n), is related to the output of the previous stage by
[
]
(
)
= ≥ + + − − = − − 0 1 1 1 1 n n n n y y x L )L ( ) L (L x ) ( U D L D ) ( ω ω ω ω,
(7)where
L
D,L
L, andL
U are K×K diagonal, strictly lower triangular, and strictly upper triangular matrices such thatL L L
LD− L − U= , (8) and the relaxation factor ω is a real number chosen by offline simulation. The output of the last stage, x(N), is
processed by the slicer to obtain the hard decisions for the transmitted symbols. Theoretically, N→∞ is required for the multi-stage MUD to be mathematically equivalent to a linear decorrelating or MMSE MUD. In practice, when ω is properly optimized this multi-stage MUD achieves close-to-optimal performance with only a few stages. Using an optimal value for ω is therefore very important for complexity considerations. However, since the optimal value for ω depends on L, it changes in different channel conditions. It is, therefore, desirable to be able to automatically adapt ω according to channel condition.
In this paper, we propose a new multi-stage linear MUD referred to as the adaptive SOR (ASOR) multi-stage MUD. The proposed algorithm includes two novel features: 1) each user uses a different relaxation factor in each stage, and 2) the relaxation factors can be optimized by offline simulation or adaptively (on the fly). As will be shown by simulation, the proposed new algorithm outperforms the approach previously proposed in [2], and approaches the performance of the linear MMSE detector with only a few stages.
The proposed algorithm is as follows. Let the relaxation matrix of the n-th stage at time m be a K×K diagonal matrix
ω ωω
ω(n)[m] whose diagonal elements are denoted as ω 1(n)[m],
ω2(n)[m],…, ωK(n)[m]. The soft output of the n-th stage of the proposed MUD is given by
Stage 1 Stage 2 Stage N
y x(1) x(2) x(N−1) x( N)
[ ]
[ ]
[ ]
[ ]
(
)
= ≥ + + = − − 0 , 1 , ] [ ) 1 ( ) ( 2 ) 1 ( ) ( 1 n m n m m m m n n n n n y y x L Ω x Ω x( ) U , (9)where ΩΩΩΩ1(n)[m] and ΩΩΩΩ2(n)[m] are K×K lower triangular
matrices defined as
[ ]
(
LD ω LL) (
I ω)
LD Ω( ) ( )[ ] 1 ( )[ ] 1n m = − n m K − n m − , (10) and[ ]
(
( )[ ])
1 ( )[ ] ) ( 2 m m m n n n L ω L ω Ω D L − − = . (11)Note that because of its triangular structure, (9) can be easily evaluated using forward substitution. The resulting multi-stage MUD structure is shown in detail for K=2 in Fig. 2.
In the proposed algorithm, the relaxation matrices play the role of the relaxation factor in the conventional SOR algorithm. However, here each user is assigned its own relaxation factor for each stage. In fact, setting
[ ]
m (N )[ ]
m) 1
( , ,ω
ω L to ωIK degenerates the proposed
structure into the receiver previously proposed in [2]. As shown in the Appendix, the relaxation matrices
[ ]
m (N )[ ]
m) 1
( , ,ω
ω L should be chosen to minimize
(
) (
)
{
N H N NH}
K H N K S N E h ( ) ( ) 0 ) ( ) ( tr I −M RAA I −M R + M RM = , (12) where “tr” denotes the trace of a matrix, ES is the symbol energy, and M(N) is obtained by the recursive relation[ ]
[ ]
(
)
= ≥ + + = − − 0 , 1 , ) 1 ( ) ( 2 ) 1 ( ) ( 1 ) ( n n m m K n K n n n n I M L I Ω M Ω M U . (13) ) ( 1 nx
) ( 2 nx
) ( 2t g ) 1 ( 2n+ β ) 1 ( 1 + n β ) ( 1 t g∗ ∫ ) ( 2 2 , 1 xn R − + 1y
1 L/ 1,1 ) ( 1 ) 1 ( 1 n n+ xβ
) ( 2 ) 1 ( 2n+ xn β ) 1 ( 1+ nω
∫
∗() ) / 1 ( L2,2g2t ) ( 1t g ) 1 ( 1n+x
− + 2y
1 L/ 2,2 ) 1 ( 2n+ ω ) 1 ( 2n+ x ) 1 ( 1 1 , 2 2 , 2 ) / 1 ( L R xn+Fig.2 Multistage Structure of the (n+1)-th ASOR stage when K=2, where ) 1 ( ) 1 ( 1 ) 1 ( + + − = + n k n k n k ω ω
β . Lj,j =1 for the linear decorrelating MUD and
2 0 , | | 1 j j j A N
L = + for the linear MMSE MUD..
Unfortunately there is no closed-form formula for the optimal relaxation matrices, therefore the relaxation matrices should be optimized by offline simulation. However, as mentioned earlier, it is sometimes desirable to be able to optimize the relaxation matrices on the fly. In this case joint adaptation of these matrices is possible by using the method of steepest descent [5]. Specifically, let W[m] be a
KN×1 vector defined as
[
]
T N K N K K m m m m m m m ] [ , ], [ , ], [ , ], [ ], [ , ], [ ] [ ) ( ) ( 1 ) 2 ( ) 2 ( 1 ) 1 ( ) 1 ( 1 ω ω ω ω ω ω L L L L L = W.
(14)The vector W[m] can be updated once every symbol-period according to h m m+1]= [ ]−α∇ [ W W , (15)
where the positive constant α is the adaptation step-size and ∇h is the gradient of h with respect to W[m]. Details of the adaptation are given in the Appendix.
Ⅳ. SIMULATION RESULTS
The performance of the proposed scheme is evaluated by computer simulation for uplink wireless communication channels. The total number of users is set to K = 10. Information bits from each user are modulated using binary phase-shift keying (BPSK) and spread using short scrambling sequences with spreading gain 32 as defined in [6]. Users are assumed to be synchronous in the simulations. The wireless channels between the users and the receiver are modeled as uncorrelated flat Rayleigh fading channels corrupted by AWGN. In other words, the channel gains Ak, k = 1…10, are independent zero-mean circularly symmetric complex Gaussian random variables with unity variance. The channel gain matrix A is assumed to be constant within bursts of 1000 symbols, and uncorrelated from burst to burst.
At the receiver, the received signal is processed by a bank of matched filters and sampled at the symbol-rate to obtain the vectors y[m] as described previously. Each vector y[m] is then processed using the proposed adaptive SOR multi-stage MUD with N = 1 stage or N = 2 stages. Moreover, we set L= R+N0(AAH)-1 in the simulations, where N0/2 is the two-sided power spectral density of the AWGN
as mentioned previously. A total of six cases are simulated for the proposed multi-stage MUD. Two cases are for N = 1: 1) ωωωω(1) = ω
1(1)IK, i.e., the relaxation matrix is constraint to have equal diagonal entries; and 2) ωωωω(1) is unconstrained
other than being diagonal. The remaining four cases are for N = 2: 3) ωωωω(1) = ωωωω(2) = ω
1(1)IK , i.e., the relaxation matrices for the two stages are constraint to be the same with equal
diagonal entries; 4) ωωωω(1) = ω
1(1)IK and ωωωω(2) = ω1(2)IK where ω1(1) and ω1(2) can be different, i.e., the relaxation matrices
for the two stages can be different, but each is constraint to have equal diagonal entries; 5) ωωωω(1) = ωωωω(2), i.e., the relaxation
matrices are constraint to be the same but each can have different diagonal entries; and finally 6) ωωωω(1) and ωωωω(2) have no
constraint other than being diagonal matrices. Note that cases 1 and 3 correspond to the receiver structure previously proposed in [2]. Furthermore, performance of the conventional single-user receiver and the MMSE linear MUD are also simulated as baselines for comparison.
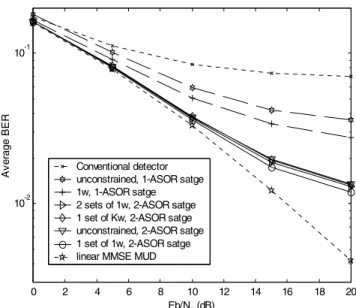
The average bit error rate (BER) performance of the simulated cases are shown in Figs. 3 and 4 as functions of Eb/N0, where Eb is the transmitted energy per user bit. Perfect channel estimation is assumed in this Figure. For N=1, curves labeled as “1w” and “unconstrained” represent cases 1 and 2, respectively. Moreover, for N=2, “1 set of 1w,” “2 sets of 1w,” “1 set of Kw,” and “unconstrained” represent performance of the simulated cases 3, 4, 5, and 6, respectively. In Fig. 3, the relaxation matrices are fixed at the optimal values for the case in which A = IK and Eb/N0 =
10 dB. It can be seen from this figure that for N=1, the performance of the proposed multi-stage MUD is significantly better than the conventional single-user detector, but is significantly worse than the linear MMSE MUD. On the other hand, with two stages the proposed MUD is roughly 4.5dB away from the linear MMSE MUD. It can also be seen that for both N = 1 and N = 2 the best performance is obtained by using only one relaxation parameter. In Fig. 4, the relaxation matrices are adaptively optimized by updating once every symbol period using (15). By comparing Figs. 3 and 4, it can be seen that significant performance gain is achievable by appropriately optimizing the relaxation matrices. In particular, the performance of the proposed multi-stage MUD with two stages is close to that of the linear MMSE MUD. One can also see that with proper optimization, the best performance is achieved by having unconstrained relaxation matrices. Furthermore, here we see that significant performance gain results when the relaxation matrices are allowed to have different diagonal entries. This is because allowing the relaxation matrices to have different diagonal entries provides the flexibility that is necessary for achieving good performance in a multi-user channel. Finally, we also note that it is not as important to use different relaxation matrices for different stages. In fact, cases 5 and 6 achieve almost the same performance and are only approximately 2dB away from the linear MMSE MUD at high Eb/N0.
The sensitivity of the proposed MUD to channel estimation error is also investigated at 10 dB Eb/N0. Here
we assume that the channel gains Ak and noise power spectral density N0 are obtained from the received signal
using some estimation algorithm, and the resulting
0 2 4 6 8 10 12 14 16 18 20 10-2 10-1 Eb/N 0 (dB) A v erage B E R Conventional detector unconstrained, 1-ASOR satge 1w, 1-ASOR satge 2 sets of 1w, 2-ASOR satge 1 set of Kw, 2-ASOR satge unconstrained, 2-ASOR satge 1 set of 1w, 2-ASOR satge linear MMSE MUD
Fig. 3 Average BER of the conventional detector, ASOR MUD, and MMSE MUD. The relaxation matrices in the ASOR MUD are assigned offline.
0 2 4 6 8 10 12 14 16 18 20 10-2 10-1 Eb/N0 (dB) A v erage B E R Conventional detector 1w, 1-ASOR satge unconstrained, 1-ASOR satge 1 set of 1w, 2-ASOR satge 2 sets of 1w, 2-ASOR satge 1 set of Kw, 2-ASOR satge unconstrained, 2-ASOR satge linear MMSE detector
Fig.4 Average BER of the conventional detector, ASOR MUD, and MMSE MUD. The relaxation matrices in the ASOR MUD are adaptively
optimized by the method of steepest descent.
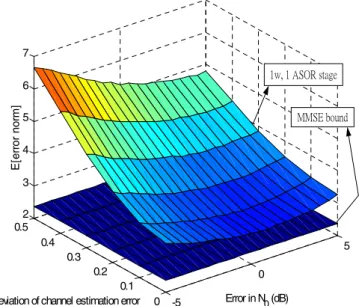
performance of the proposed MUD using a relaxation matrix that minimizes (12) is shown in Fig. 5 for N=1 with a constant-diagonal-entry relaxation matrix (i.e., case 1). The three dimensional plot in Fig. 5 illustrates the sum of all users’ mean-square error (MSE) measured at the output of the proposed MUD as a function of the mean-square channel estimation error and relative estimation error of N0 in dB.
Here the channel estimation error is defined as the difference between the estimated and actual channel gains, and are modeled as complex zero-mean circularly symmetric
Gaussian random variables that are independent and identically distributed from user to user and symbol to symbol. On the other hand, the relative estimation error of N0 is defined as the ratio of the estimated and actual values
of N0. In Fig. 5, the bottom plane corresponds to the output
MSE achieved by a linear MMSE MUD with perfect channel and N0 estimations. As expected, the output MSE
of the proposed MUD increases with the error in channel and N0 estimation. However, it is interesting to note that
the proposed MUD is more sensitive to channel estimation error than error in estimating N0. This is because the
proposed receiver takes the inverse of these estimated channel gains.
Ⅴ. CONCLUSION
Linear multiuser detectors in general require the inversion of a matrix or the solution of a system of linear equations. One way for reducing the complexity of linear multiuser detectors is to make use of multi-stage structure derived from algorithms for solving linear equations. In this paper, we propose a linear multi-stage MUD receiver based on adaptive successive over-relaxation. In contrast to previously proposed linear multi-stage MUD, the proposed structure makes use of over relaxation matrices that can be optimized offline or adaptively updated on the fly. Simulation results show that the proposed MUD outperforms the previously proposed method and achieves a performance that is close to linear MMSE MUD.
REFERENCES
[1] S. Moshavi, “Multi-user Detection for DS-CDMA Communications,” IEEE Commum. Mag., pp. 124-136, Oct. 1996.
[2] Yue-heng Li, Ming Chen, Wang hai-feng, and Shi-xin Chen, “Linear Multiuser Receiver Using Novel Iterative Algorithm for DS/CDMA Systems,” IEEE Vehicular Technology Conference 2000-spring, May 15-18, 2000, Tokyo, Japan, pp. 76-80.
[3] Yue-heng Li, Ming Chen, Wang hai-feng, and Shi-xin Chen, “Decision Feedback Partial Parallel Interference Cancellation For DS-CDMA,” MILCOM 2000. 21st Century Military Communications Conference Proceedings , Volume: 1 , 2000, Page(s): 579 -582 vol.2.
[4] Sergio Verdu, Multiuser Detection, Cambridge University Press, 1998, pp.234-298.
[5] Burden Faires, Numerical Analysis 6th, Brooks/Cole Publishing Company Press, 1997, pp. 443-457.
[6] 3G TS 25.213 V4.1.0 “3rd Generation Partnership Project; Technical
Specification Group Radio Access Network; Spreading and modulation (FDD) (Release 4)”, 2001-06.
APPENDIX: DERIVATION OF THE OPTIMAL RELAXATION MATRICES
It can be seen from (9), (10), and (11) that y
M
x(N) = ( N) , (A.1)
where M(N) satisfies the recursive relation
-5 0 5 0 0.1 0.2 0.3 0.4 0.5 2 3 4 5 6 7 Error in N0 (dB) Deviation of channel estimation error
E [er ro r no rm ] 1w, 1 ASOR stage MMSE bound
Fig. 5 Total MSE of the ASOR multi-stage MUD (case 1) as a function of the channel estimation error and relative estimation error of N0.
[ ]
[ ]
(
)
= ≥ + + = − − 0 , 1 , ) 1 ( ) ( 2 ) 1 ( ) ( 1 ) ( n n m m K n K n n n n I M L I Ω M Ω M U . (A.2) where ΩΩΩΩ1[m] and ΩΩΩΩ2[m] are defined in (10) and (11). Notethat M(N) is inherently a matrix function of W, defined as
T N K N K K
,
,
,
,
,
,
,
]
,
,
[
ω
1(1)L
ω
(1)ω
1(2)L
ω
(2)L
ω
1( )L
ω
( )=
W
. (A.3)We want to find W such that
− =E M(N)y Ad2 h , (A.4)
is minimized. Assuming that
= = K H K S H E E E 0 dn I dd ] [ ] [ , (A.5) where ES is the symbol energy, from (2) we have