排程技術對正交分頻多工多天線系統涵蓋範圍影響之研究

國 立 交 通 大 學

電信工程學系

碩 士 論 文

排程技術對正交分頻多工多天線系統涵蓋範

圍影響之研究

On The Coverage Performance of OFDM-Based

Spatial Multiplexing Systems With

Multi-User Scheduling

研究生：邱正偉

指導教授：王蒞君 博士

排程技術對正交分頻多工多天線系統涵蓋範圍影響之研究

On The Coverage Performance of OFDM-based Spatial Multiplexing Systems

With Multi-User Scheduling

研 究 生：邱正偉 Student：Cheng-Wei Chiu

指導教授：王蒞君 Advisor：Li-Chun Wang

國 立 交 通 大 學

電 信 工 程 學 系

碩 士 論 文

Submitted to Department of Communication Engineering College of Electrical and Computer Engineering

National Chiao Tung University in partial Fulfillment of the Requirements

for the Degree of Master

in

Communication Engineering September 2006

Hsinchu, Taiwan, Republic of China

排程技術對正交分頻多工多天線系統涵蓋範圍影響之研究

學生：邱正偉

指導教授：王蒞君

國立交通大學

電信工程學系碩士班

摘

要

這 篇 論 文 主 要 在 研 究 如 何 在 以 正 交 分 頻 多 工 多 天 線 系 統 (OFDM-Based

Spatial Multiplexing Systems)下有效的分配子通道(Subchannel)以增加可靠涵蓋範

圍(Coverage)，首先討論單一使用者的情況，我們推出在頻率選擇通道環境中之

正交分頻多工多天線系統下的連結中斷機率(Link Outage Probability)之數學表示

式，為了能從連結中斷機率來求得可靠涵蓋範圍的數學表示式，我們另外推出了

另一個連結中斷機率的近似數學表示式。從我們的模擬分析結果中，證明了所推

出的連結中斷機率與可靠涵蓋範圍之數學模型是非常精確的，此外我們也呈現了

傳 送 與 接 收 天 線 之 個 數 、 頻 率 選 擇 多 樣 性 之 程 度 (Degree of Frequency

Selectivity)、以及路徑衰減因子(Pass Loss Exponent)是如何的在正交分頻多工多

天線系統下影響連結中斷機率與可靠涵蓋範圍。

在多重使用者的環境下，我們首先把用於單一傳送接收天線正交分頻多工系

統(SISO OFDM)下的公平性導向子通道分配演算法(FOSA)拓展至多重傳送接收

天線正交分頻多工系統(MIMO OFDM)中，接著提出了簡易且可以增加更多可靠

涵蓋範圍之涵蓋可靠度導向子通道演算法(COSA)。既然 COSA 可以在與 FOSA

差不多公平性下同時增大更多可靠涵蓋範圍，我們把重心放在 SOSA 演算法上，

並且利用順序統計學(Order statistics)以及 Glivenko- Cantelli 定理推導出在使用

COSA 演算法下之連結可靠機率與可靠涵蓋範圍的數學表示式。模擬結果中證明

了在使用 COSA 演算法時我們所推出的可靠涵蓋範圍之數學模型是非常精確

的，此外我們也呈現了整體傳送功率、傳送與接收天線之個數、使用者數量、以

及路徑衰減因子是如何的在各種不同演算法下影響頻率選擇通道環境下之可靠

涵蓋範圍，同時我們也解釋了各種影響因子的物理現象。

Summary

In this thesis we investigate how to efficiently assign the subchannels to enhance the coverage performance of orthogonal frequency division multiplexing (OFDM)-based spatial multiplexing systems. For the single user case, we present an analyt-ical formula that can evaluate the link outage probability for spatial multiplexing multi-input multi-output (MIMO)-OFDM system. We also provide another simpli-fied approximation of the exact link outage probability that can apply to calculated the cell coverage associated a certain link outage probability. From our numerical results, we validate the accuracy of the analytical model and approximation method by simulation. We also present some results to illustrate how and to what extend the number of antennas, frequency selectivity order, and the pass loss exponent affect the link outage and the cell coverage for the spatial multiplexing MIMO-OFDM system. In multi-user case, we first extend the fairness-oriented subcarriers assignment algorithm (FOSA) from SISO OFDM to MIMO OFDM. Next we propose another low-complexity coverage-oriented subcarriers assignment algorithm (COSA) which can achieve larger cell coverage of OFDM-based spatial multiplexing systems than FOSA. Since COSA can achieve almost the same fairness performance as FOSA and have larger cell coverage than FOSA, we focus on COSA and derive an analytical expression form for link outage probability and cell coverage reliability by means of order statistics and Glivenko- Cantelli Theorem. From our numerical results, we vali-date the accuracy of the analytical model and approximation method by simulations. We also present some results to illustrate how the total transmit power, the number of antennas, the number of users and pass loss exponents affect the cell coverage reliabil-ity under various subcarriers assignment algorithms for the spatial multiplexing-based MIMO-OFDM system. Explanations for this physical phenomenon are also included.

vi

Acknowledgments

I would like to thank Dr. Li-Chun Wang who gives me many valuable suggestions in the research during these two years. Without his help, I would not finish this work.

Summary . . . . v

Acknowledgements . . . . vi

List of Figures . . . . x

1. Introduction . . . . 2

1.1 Problems and Solutions . . . 3

1.1.1 Analysis for Coverage Performance for OFDM-Based Spatial Multiplexing Systems . . . 4

1.1.2 Coverage Enhancement for Spatial-Multiplexing-Based MIMO OFDM Systems by Joint Multiuser Scheduling and Subcarriers Assignment . . . 4

1.2 Thesis Outline . . . 5

2. Background . . . . 7

2.1 Scalable OFDMA Physical Layer in IEEE 802.16 WirelessMAN . . . 7

2.2 Scheduling in OFDMA Systems . . . 9

2.3 Scheduling in MU-MIMO Systems . . . 10

2.4 Scheduling in Multi-user MIMO-OFDM Systems . . . 11

2.5 Some Definitions of Performance Metrics . . . 11

2.5.1 Fairness performance . . . 12

viii

2.5.3 Cell Coverage Reliability . . . 13

3. Analysis for Coverage Performance for OFDM-based Spatial Multiplexing Sys-tems . . . . 14

3.1 Introduction . . . 14

3.2 System model . . . 17

3.3 Definitions . . . 18

3.3.1 Link Outage Probability . . . 18

3.3.2 Cell Coverage Reliability . . . 20

3.4 Link Outage Analysis . . . 20

3.5 Cell Coverage Performance . . . 22

3.5.1 Approximation of link outage probability . . . 23

3.5.2 Cell Coverage Reliability . . . 24

3.6 Numerical Results . . . 25

4. Coverage Enhancement for Spatial-Multiplexing-Based MIMO OFDM Sys-tems by Joint Multiuser Scheduling and Subcarriers Assignment . . . . 31

4.1 Introduction . . . 32

4.2 System model . . . 34

4.3 Definitions . . . 36

4.3.1 Link Outage Probability . . . 36

4.3.2 Cell Coverage Reliability . . . 37

4.4 Subcarriers assignment algorithms . . . 37

4.4.1 Fairness-Oriented Subcarriers Assignment (FOSA) . . . 39

4.4.2 Coverage-Oriented Subcarriers Assignment (COSA) . . . 40

4.5 Fairness Performance . . . 41

4.6 Link Outage by COSA . . . 41

4.7 Cell Coverage by COSA . . . 44

5. Concluding Remarks . . . . 48

5.1 Link Outage and Coverage Analysis for OFDM-based Spatial Multi-plexing Systems . . . 49

5.2 Coverage Enhancement for Spatial-Multiplexing-Based MIMO OFDM Systems by Joint Multiuser Scheduling and Subcarriers Assignment . 49 5.3 Suggestion for Future Work . . . 50

Bibliography . . . . 51

Appendices . . . . 55

6. APPENDIX A . . . . 55

7. APPENDIX B . . . . 58

List of Figures

3.1 OFDM-based Spatial Multiplexing Systems. . . 18 3.2 The Eigenvalues in Each Subchannel. . . 19 3.3 The Eigenvalues in Selective Fading Channel. . . 20 3.4 Link outage probability v.s. transmit power Ptfor different values of N

when M = 3, noise power= −103dBm, µ = 3, r = 1km and γth = 2dB. 25

3.5 Link outage probability v.s. transmit power Pt for different values of

M when N = 128, noise power= −103dBm, µ = 3, r = 1km and γth= 2dB. . . 26

3.6 Link outage probability v.s. transmit power Pt for different values of

µ when M = 3, N = 128, noise power= −103dBm, r = 1km and γth= 2dB. . . 27

3.7 Cell coverage radius v.s. transmit power Pt for different values of M

when N = 128, noise power= −103dBm, µ = 3, Pout = 0.1 and

γth= 2dB. . . 28

3.8 Cell coverage radius v.s. transmit power Pt for different N when M =

3, noise power= −103dBm, µ = 3, Pout = 0.1 and γth = 2dB. . . 29

3.9 Cell coverage power v.s. transmit powerPtfor different values of µ while

M=3, N = 128, noise power= −103dBm, Pout= 0.1 and γth= 2dB. . 30

4.1 Architecture for scheduling in multiplexing-based MIMO-OFDM sys-tems. Assume that N = 2, NT = 4, and M = 2 . . . . 34

4.2 Illustration for MIMO OFDM subcarriers assignment. Assume that

N = 4, K = 2 . . . 35

4.3 Fairness-oriented subcarriers assignment (FOSA) . . . 38

4.4 Coverage-oriented subcarriers assignment (COSA) . . . 39

4.5 Fairness performance comparison for K = 5 and M = 3 . . . . 40

4.6 Cell coverage v.s. users for different Pt while N = 32, M = 3, noise power= −103 dBm, µ = 3, Pout = 0.1 and γth = 2dB . . . 45

4.7 Cell coverage v.s. users for different M while Pt = 1W, N = 32, noise power= −103 dBm, µ = 3, Pout = 0.1 and γth = 2dB. . . 46

4.8 Cell coverage v.s. users for different µ while Pt = 1W, M = 3, N = 32, noise power= −103 dBm, Pout = 0.1 and γth= 2dB. . . 47

Introduction

Orthogonal Frequency Division Multiplexing (OFDM) has become a popular modula-tion technique for transmission of broadband signals. OFDM can convert a frequency selective fading channel into a parallel collection of frequency flat fading sub-channels and thus can overcome inter-symbol interference (ISI).

Multi-input multi-output (MIMO) antenna techniques can provide spatial mul-tiplexing gain and diversity gain to increase spectrum efficiency and link reliability, respectively. Combining MIMO with OFDM (MIMO-OFDM) becomes an attractive air-interface solution for the next generation high speed wireless systems. A great deal of research works have been devoted to the area of combining MIMO with OFDM systems. This system combines the advantages of both techniques in providing si-multaneously increased data rate and eliminating the effects of delay spread.

Generally, there are three categories of MIMO-OFDM techniques. One is Spatial Diversity Coding for OFDM which realizes spatial diversity gain in MIMO-OFDM systems. Another is Space-Time-Frequency Coded MIMO-MIMO-OFDM and the data must be suitably spread across space and frequency in order to extract full spa-tial as well as frequency diversity. What we focus on in this paper is the last category of technique called Spatial Multiplexing for MIMO-OFDM. Because the objective of spatial multiplexing in conjunction with MIMO-OFDM is to maximize spatial rate by transmitting independent data streams over different antennas, the high link outage probability and small cell coverage reliability are apparent disadvantages with regard to the space-time-frequency coded MIMO-OFDM. Fortunately, we can use the multi-user and frequency diversity to improve the reduced link quality and cell coverage of

3 the diversity-deficient multiplexing system. Frequency diversity inherently exists in OFDMA systems, while multiuser diversity can be achieved by adopting scheduling algorithms. Although both diversity gains can enhance the system cell coverage, the challenging issue is how to select a scheduling algorithm that can achieve high cell coverage reliability and maintain the fairness performance among users simultane-ously.

1.1

Problems and Solutions

The objective of this thesis is to efficiently assign the subcarriers in order to enhance the coverage reliability of OFDM-based spatial multiplexing systems in a multiuser environment. We investigate the MIMO-OFDM system from another resource alloca-tion viewpoint, i.e, scheduling algorithms. Motivated by the increasing popularity of OFDM and MIMO, how to use the multiuser and frequency diversity simultaneously to improve the coverage reliability of the diversity-deficient multiplexing system is an essential issue. Because the total available transmit power is split uniformly across transmit antennas in the OFDM-based spatial multiplexing systems, increasing the number of transmit antennas leads to a smaller signal-to-noise ratio (SNR) per degree of freedom. In a multiuser wireless system, different users may have different channel responses in a time varying wireless channel. Thus, a channel may be viewed as a bad channel, but may be viewed as a good channel by other users. Consequently, if the system can first pick a user with the best channel quality among a group of users to serve in each subchannel (made up of neighboring subcarriers), then the low link outage and small cell coverage can be improved significantly. Besides, we want to derive an analytical closed form expression for link outage and cell coverage by using the subcarriers assignment algorithm, and show how the total transmit power, the number of antennas, the number of users and pass loss exponents could affect the cell

coverage under this subcarriers assignment algorithm over frequency-selective fading channels.

1.1.1

Analysis for Coverage Performance for OFDM-Based

Spatial Multiplexing Systems

Combining multi-input multi-output (MIMO) antenna techniques with orthogonal frequency division multiplexing (OFDM) modulation (MIMO-OFDM) becomes an attractive air-interface solution for the next generation high speed wireless systems. Nevertheless, because the total available transmit power is split uniformly across transmit antennas in MIMO-OFDM systems, increasing the number of transmit an-tennas leads to a smaller signal-to-noise ratio (SNR) per degree of freedom. Thus the coverage performance of this kind of MIMO-OFDM system becomes an essential issue. In this these by means of order statistics and Glivenko- Cantelli theorem, we develop an analytical expressions for the link outage probability and cell coverage re-liability of OFDM-based spatial multiplexing systems in a frequency selective fading channel, respectively.

1.1.2

Coverage Enhancement for

Spatial-Multiplexing-Based MIMO OFDM Systems

by Joint Multiuser Scheduling and Subcarriers

Assignment

To improve the coverage reliability of the diversity-deficient spatial-multiplexing-based MIMO system, we suggest exploiting the multiuser diversity from schedul-ing techniques and frequency diversity from OFDM subcarrier assignment in the

5 frequency selective fading simultaneously. For this purpose, an efficient and low-complexity sub-carriers assignment scheme combined with multi-user scheduling and is proposed in this paper. By means of the analytical techniques of the order statistics and Glivenko- Cantelli theorem, we develop an analytical expression for the link out-age probability and cell coverout-age reliability. Our results show that the proposed joint multi-user scheduling and sub-carriers assignment scheme can significantly improve the reliability of the spatial multiplexing gain of MIMO-OFDM systems. Moreover, we show that the proposed scheme not only can improve the cell coverage performance of the spatial-multiplexing based MIMO-OFDM systems, but successfully preserve the multiusers’ fairness performance.

1.2

Thesis Outline

The research of this thesis investigates how to efficiently assign the subcarriers in order to enhance the coverage reliability for OFDM-based spatial multiplexing sys-tems. We first focus on the analysis of the link outage probability which could be used as an indicator of the system performance. Because it is hard to analyze the link outage probability in OFDM-based spatial multiplexing systems, there are no closed form expressions in the literature. We evaluate analytical expressions for the link outage probability, and provide another simple approximation of link outage proba-bility to further derive the cell coverage of OFDM-based spatial multiplexing systems over frequency-selective fading channels. Furthermore, we focus on the assignment of each resource dimension to only one user to avoid the complexity and the assignment requires only limited amount of feedback. Besides, we assume frequency selective qua-sistatic channels where channels do not vary within a block of transmission. We first extend the suboptimal subcarriers assigning algorithm from SISO OFDM to MIMO

OFDM systems, and we call it fairness-oriented subcarriers assignment (FOSA) in this thesis. Besides, we propose a low-complexity coverage-oriented subcarriers as-signment algorithm (COSA) which can achieve larger cell coverage than FOSA for OFDM-based spatial multiplexing systems. Furthermore, we derive an approximately analytical expression for link outage and cell coverage by using COSA, and show how the total transmit power, number of antennas, number of users and the pass loss exponent could affect the cell coverage under this subcarriers assignment algorithm over frequency-selective fading channels.

The remaining chapters of this thesis are organized as follows. Chapter 2 intro-duces the background of the scalable OFDMA physical layer in IEEE 802.16 wireless metropolitan area network (WMAN). Furthermore, we discuss the scheduling scheme in multi-user MIMO systems and subchannel allocation approaches in the OFDMA systems. The definition of fairness performance, link outage probability, and cell coverage reliability are also included. Chapter 3 provides an analytical expression of the link outage probility, and provide another simple analytical closed form ap-proximation of the link outage probability to further derive the cell coverage of the OFDM-based spatial multiplexing systems over frequency-selective fading channels. Chapter 4 proposes a low-complexity coverage-oriented subcarriers assignment algo-rithm (COSA) which can efficiently assign the subchannels in order to enhance the coverage reliability for OFDM-based spatial multiplexing systems. At last, Chapter 5 gives the concluding remarks and suggestions for future work.

Chapter 2

Background

In this chapter, we introduce the background of the scalable OFDMA physical layer in IEEE 802.16 wireless metropolitan area network (WMAN), the concept of scheduling techniques, and some definitions of the performance metric about the thesis.

2.1

Scalable OFDMA Physical Layer in IEEE

802.16 WirelessMAN

The IEEE 802.16 WirelessMAN [1] specifies the standards of air interface and medium access control (MAC) protocols for fixed, portable, and mobile broadband wireless access systems. The standard includes requirements for high data rate line of sight (LOS) operation in the 10-66 GHz range for fixed wireless networks as well as require-ments for non line of sight (NLOS) fixed, portable, and mobile systems operating in sub 11 GHz licensed and licensed exempt bands. In a NLOS environment, WMAN in the IEEE 802.16a specification is recommended to operate in a multicarrier modula-tion mode. Each OFDMA symbol consists of various types of subcarriers, including data, pilot and null. The number of the total subcarriers is 2048, which is equal to the fast Fourier transform (FFT) size.

Because of its superior performance in multipath fading wireless channels, or-thogonal frequency division multiplexing (OFDM) signaling is recommended in Wire-lessMAN OFDMA Physical layer modes of the 802.16 standard for operation in sub 11 GHz NLOS applications. The OFDM technology has been recommended in other

wireless standards such as digital video broadcasting (DVB) and wireless local area networking (WLAN), and it has been successfully implemented in the compliant so-lutions.

IEEE 802.16 specifies two flavors of OFDM systems: one is OFDM, and the other OFDMA. The first aims at less challenging applications, quite short distance, eventually indoors. It employs fast Fourier transform (FFT) size 256, and all carriers are transmitted at once. The downstream data is time-division multiplexed (TDM). The upstream time frame is time-division multiple access (TDMA).

In OFDMA the higher FFT space (2048 and 4096 carriers) is divided into sub-channels. They are used in downstream for separating the data into logical streams. Those streams employ different modulation, coding, and amplitude to address sub-scribers with different channel characteristics. In upstream the subchannels are used for multiple access. The subscribers are assigned on subchannels through Media Ac-cess Protocol (MAP).

Unlike many other OFDM-based systems such as WLAN, the 802.16 standard supports variable bandwidth between 1.25 and 20 MHz for NLOS operations. This feature, along with the requirement for support of combined fixed and mobile usage models, makes the need for a scalable design of OFDM signaling inevitable. The con-cept of scalable OFDMA is introduced to the IEEE 802.16 WirelessMAN OFDMA mode by the 802.16 Task Group e (TGe) and has been the subject of many contribu-tions to the standards committee. Other features such as AMC subchannels, Hybrid Automatic Repeat Request (H-ARQ), high-efficiency Uplink (UL) subchannel struc-tures, multiple-input-multiple-output (MIMO) diversity, enhanced advanced antenna system (AAS), and coverage enhanceing safety channels were introduced simultane-ously to enhance coverage and capacity of mobile systems while providing the tools to trade off mobility with capacity.

9

2.2

Scheduling in OFDMA Systems

Successful deployment of wireless voice communication system promises a bright fu-ture for wireless high data rate services such as the internet access or multimedia applications. In order to provide high data rate services, orthogonal frequency divi-sion multiplexing access (OFDMA) is being considered as a viable candidate because of its ability to overcome multipath fading.

If the channel is static and is perfectly known to the transmitter and its receiver, water-filling with adaptive modulation is known to be optimal. Water-filling also applies if the channel is slowly fading as in fixed wireless systems of if the channel estimation and feedback can be performed in a short time span. Because the technique of adaptive loading has been hardly included in actual implementation due to the time varying nature of wireless channels, it starts to receive more attention as the spectral efficiency and the low complexity become more important.

However, the water-filling solution can only be used for single-user systems or multiuser systems with fixed resource assignment. For example, in Time Division Multiple Access (TDMA) or Frequency Division Multiple Access (FDMA) systems with non-adaptive fixed resource allocation, an independent dimension such as time slot or frequency band is assigned to each user regardless of channel response. Here each user effectively becomes a single user who is independent of all other users. In this case, the water-filling solution can be used for each user to maximize its throughput. However, the maximized rate is far below the rate that can be achieved by adaptive resource allocation, and a set of users suffers from poor channel gains of assigned dimensions. If we assign a dimension to users whose channel gains are good for it, larger throughput can be achieved.

The characterization of information theoretic channel capacity for a multiuser system is a complex optimization problem. In order to achieve the channel

capac-ity, highly complex coding and decoding such as maximum likelihood detection or multiuser detection with successive decoding is needed. [2] focused on exclusive as-signment of each resource dimension to only one user to avoid the complexity and the error propagation problems. That is to say, it allows only one user to occupy a dimension related to a specific frequency at a specific time.

2.3

Scheduling in MU-MIMO Systems

In multi-user MIMO (MU-MIMO) systems, all users are coordinated for commu-nications by using scheduling algorithms and considering quality of service (QoS) requirements of each user. When multiple antennas are used on the transmitter and receiver side, the scheduling algorithm is significant in determining the system ca-pacity in a multi-user MIMO environment, where different transmit antennas can be assigned for data transmissions of specific users, simultaneously. When the instanta-neous knowledge of the received signal-to-noise ratio (SNR) is exploited to schedule a user, we can extract the multi-user diversity. As more transmit and receive antennas are used and more users are considered in cellular networks, scheduling algorithms become more important in complicated system environment.

In a multiuser MIMO system over flat fading channels, multiuser diversity can be exploited to improve downlink capacity. [3] proposed a fair scheduling scheme called strongest-weakest-normalized-subchannel-first (SWNSF) which can significantly in-crease the coverage of the multiuser MIMO system while further improving system capacity. Furthermore, this scheduling algorithm requires only scalar feedback, be-cause each user only needs to send back a scalar value to inform the channel condition without considering the number of transmit and receive antennas.

11

2.4

Scheduling in Multi-user MIMO-OFDM

Systems

In principle, OFDM and MIMO can be integrated to offer the benefits in terms of both simplicity and high performance. MIMO OFDM is a special case of the general multiuser multicarrier MIMO system. Such is indeed an active topic within the IEEE 802.16/20 standardization bodies. In [4], it extend the study on OFDMA/SISO to multiuser multicarrier MIMO systems. Also, [4] proved that OFDMA/MIMO is the optimal (in terms of total capacity) downlink scheme under the independent decoding constraint.

However, unlike OFDMA/SISO where the optimal solution can be found with linear complexity (with respect to the number of users and number of the subcarriers), the OFDMA/MIMO problem has no explicit solution due to the tangled effects of subcarrier allocation and power loading. To sum up, in order to obtain the optimal subcarrier allocation and the optimal power loading, and exhaustive search needs to be performed, and the cost of exhaustive search is exponentially increased with respect to the number of subcarriers and is polynomially increased with respect to the number of users.

2.5

Some Definitions of Performance Metrics

2.5.1

Fairness performance

We first define a fairness index F in the multiuser systems as follows

F = Ã 1 K K X i=1 Ti !2 1 K K X i=1 Ti2 = Ã K X i=1 Ti !2 K K X i=1 Ti2 , (2.1)

where Ti is the number of times the subchannels allocated to ith user. For F = 1, it

is the fairest condition between users, and it is not fair as F ¿ 1.

2.5.2

Link outage probability

To begin with, we first define the link outage probability which reflects how reliable a system can support the corresponding link quality. For a single-input single-output (SISO) system in a flat fading channel, link outage is usually defined as the probability that the received SNR is less than a predetermined value γth, i.e. Pout = Pr{γ < γth}

[5]. The link outage for the spatial multiplexing MIMO system in a flat fading channel is defined as the event when the receive SNR of any substream is less than γth [6] [3].

When all the degrees of freedom in the spatial domain of a MIMO system are used for the transmission of parallel and independent data streams to exploit the spatial multiplexing gain, the data stream with the lowest SNR in the MIMO system will dominate the link reliability performance especially when the high-percentile link reliability, such as 90% or even higher, is concerned.

The OFDM-based spatial multiplexing system in a frequency selective fading channel can be viewed as the sum of flat fading MIMO channels. As discussed before, the high-percentile link reliability performance of each MIMO flat-fading channel is dominated by the weakest substream. Considering the average weakest eigen-mode over a series of N’s MIMO flat-fading subchannels, we define the link outage

13 probability of the spatial-multiplexing-based MIMO OFDM system for user k as follows: Pk out = Pr à 1 N N X n=1 γk,n,M ≤ γth ! , (2.2)

where γk,n,M represents the receive SNRs of the weakest substream corresponding to

the kth user in subchannel n for n = 1, . . . , N .

2.5.3

Cell Coverage Reliability

With Pk

out being the link outage probability for user k, we define the cell coverage

for all the users in a cell is the farthest distance at which the link quality suffices for maintaining a required receive SNR γth with cell coverage reliability (1 − Poutk ). Our

focus is on the farthest user in the boundary of the cell coverage. In other words, if the farthest user maintains the link quality, the other (K − 1) users will maintains it too.

Analysis for Coverage Performance for

OFDM-based Spatial Multiplexing

Systems

Combining multi-input multi-output (MIMO) antenna techniques with orthogonal frequency division multiplexing (OFDM) modulation (MIMO-OFDM) becomes an attractive air-interface solution for the next generation high speed wireless systems. Nevertheless, because the total available transmit power is split uniformly across transmit antennas in MIMO-OFDM systems, increasing the number of transmit an-tennas leads to a smaller signal-to-noise ratio (SNR) per degree of freedom. Thus the coverage performance of this kind of MIMO-OFDM system becomes an essential issue. In this chapter by means of order statistics and Glivenko- Cantelli theorem, we develop an analytical expressions for the link outage probability and cell coverage re-liability of OFDM-based spatial multiplexing systems in a frequency selective fading channel, respectively.

3.1

Introduction

Orthogonal frequency division multiplexing (OFDM) modulation has become a pop-ular modulation technique for transmission of broadband signals. OFDM can convert a frequency selective fading channel into a parallel collection of frequency flat

fad-15 ing sub-channels and thus can overcome inter-symbol interference (ISI) [7] [8]. In the meanwhile, multi-input multi-output (MIMO) antenna techniques can provide spatial multiplexing gain and diversity gain to increase spectrum efficiency and link reliabil-ity, respectively [9] [10] [11] [12]. Combining MIMO with OFDM (MIMO-OFDM) becomes an attractive air-interface solution for the next generation high speed wireless systems.

Generally, there are three categories of MIMO-OFDM techniques.

• The first aims to realize spatial diversity and frequency diversity gain without the need for channel state information (CSI) at the transmitter. In the first category, the results in [13] proposed a transmit diversity scheme in a frequency selective fading channel. A space-time code across space and frequency (rather than time) was shown in [14] to yield spatial diversity. In [15, 16], a low-density parity-check (LDPC)-based space time code was proposed to exploit both spatial diversity and selective fading diversity for MIMO-OFDM system in correlated. [17] presented the space-frequency code that can achieve full diversity in space and frequency for MIMO-OFDM systems, where neither transmitter and receiver has perfect CSI. [18] investigated the performance of space-frequency coded MIMO OFDM as a function of Riciean K-factor, angle spread, antenna spacing and power delay profile. In [19], a code design framework for achieving full rate and full diversity in MIMO frequency-selected fading channels was proposed.

• The main goal of the second class of MIMO-OFDM techniques is to increase ca-pacity by exploiting multiplexing gain in the spatial domain, i.e., transmitting independent data streams across antennas and tones. The V-BLAST system sug-gested in [11] is a well-known layered approach to achieve spatial multiplexing gain in multi-antenna systems. [20] showed that a MIMO delay spread channel can provide both higher diversity gain and multiplexing gain than MIMO

flat-fading channels. However, increasing the number of transmit antennas results in a smaller signal-to-noise ratio (SNR) per degree of freedom because the total available transmit power is split uniformly across transmit antennas. This leads to link outage or coverage issue of the spatial multiplexing MIMO system. This issue has been investigated originally in [6] and a multiuser scheduling solution to ad-dress this issue in MIMO flat-fading channels was proposed in [3]. Nevertheless, the coverage performance for spatial-multiplexing-based MIMO-OFDM systems in frequency-selective fading channels has not been widely discussed so far. • The third type of MIMO-OFDM technique is to decompose the channel

coeffi-cient matrix by singular value decomposition (SVD) and construct pre-filter and post-filters at the transmitter and the receiver to achieve the capacity [21]. This technique requires perfect CSI available at both the transmitter and receiver.

In this chapter, we focus on the second type of MIMO-OFDM systems and aim to derive the closed form expressions for link outage and cell coverage cell cover-age of the OFDM-based spatial multiplexing systems over frequency-selective fading channels. The rest of this chapter is organized as follows. In Section II, we describe the system model. In Section III, we define the link outage for MIMO-OFDM sys-tems. In Section IV, we derive the exact analytical expression form of link outage of MIMO-OFDM systems, and provide an approximation analytical form of link out-age of MIMO-OFDM systems in Section V. In Section VI, we discuss the coverout-age performance of MIMO system. In Section VII, we show numerical results and give concluding remarks in Section VIII.

17

3.2

System model

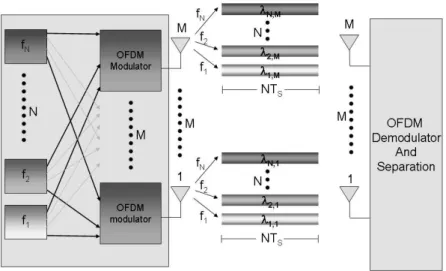
We consider a point-to-point MIMO system with M transmit antennas and M receive antennas. In the meanwhile, we adopt OFDM modulation with total NT sub-carriers

and let a group of adjacent NT/N subcarriers form a subchannel. The total bandwidth

of each subchannel is assumed to be smaller than the channel coherent bandwidth. Figure 3.1 shows the considered structure of the OFDM-based spatial multiplexing systems, where MN independent data streams are multiplexed in M transmit an-tennas and N subchannels. The transmit power is uniformly split to M transmit antennas. It is assumed that the length of the cyclic prefix (CP) in the OFDM sys-tem is greater than the length of the discrete-time baseband channel impulse response so that the frequency-selective fading channel indeed decouples into a set of parallel frequency-flat fading channels [22]. With xnand yn denoting the M × 1 transmit and

receive signal vectors, respectively, we can write yn =

√

gnHnxn+ nn , (3.1)

where n is the sub-channel index and Hnrepresents the M ×M MIMO channel matrix

of the nth subchannel and each entry of Hn is an i.i.d. circular-symmetric complex

Gaussian variable [18]. Represent nn the M × 1 spatially white noise vector with

E[nnn∗n] = σ2nI where (·)∗ is the transpose conjugate operation. At last gn depicts

the large-scale behavior of the channel gain. For a user at a distance of r from the base station, gn can be written as [23]

10 log₁₀(gn) = −10µ log10(r) + g0 [dB] , (3.2)

where µ is the path loss exponent and g0 is a constant subject to certain path loss

Fig. 3.1: OFDM-based Spatial Multiplexing Systems.

3.3

Definitions

3.3.1

Link Outage Probability

To begin with, we first define the link outage probability which reflects how reliable a system can support the corresponding link quality. For a single-input single-output (SISO) system in flat fading channel, link outage is usually defined as the probability that the received SNR is less than a predetermined value γth, i.e. Pout = Pr{γ < γth}

[5]. The link outage for the spatial multiplexing MIMO system in a flat fading channel is defined as the event when the receive SNR of any substream is less than γth [6] [3].

When all the degrees of freedom in the spatial domain of a MIMO system are used for the transmission of parallel and independent data streams to exploit the spatial multiplexing gain, the data stream with the lowest SNR in the MIMO system will dominate the link reliability performance especially when the link reliability likely of high percentile, such as 90% or even higher, is concerned.

19

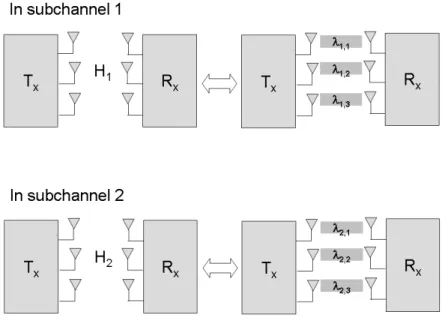
Fig. 3.2: The Eigenvalues in Each Subchannel.

The OFDM-based spatial multiplexing system in a frequency selective fading channel can be viewed as the sum of flat fading MIMO channels as shown in Fig. 3.2. As discussed before, the high-percentile link reliability performance of each MIMO flat-fading channel is dominated by the weakest substream. Referring to Fig. 3.3 and considering the average weakest eigen-mode over a series of N’s MIMO flat-fading subchannels, we define the link outage probability of the spatial-multiplexing-based MIMO OFDM system as follows:

Pout = Pr à 1 N N X n=1 γn,M ≤ γth ! , (3.3)

where γn,M represents the receive SNR of the weakest substream in subchannel n for

Fig. 3.3: The Eigenvalues in Selective Fading Channel.

3.3.2

Cell Coverage Reliability

With Pout being the link outage probability, we define (1−Pout) to be the cell coverage

reliability for its corresponding cell radius associated with the required SNR. That is, for a user at the cell radius with cell coverage reliability (1 − Pout), the probability

of the received SNR being higher than the required threshold γth is no less than

(1 − Pout).

3.4

Link Outage Analysis

To begin with, we first analyze the received SNR of the weakest substream (denoted by γn,M) at the n-th MIMO flat-fading subchannel. With {λn,i}Mi=1 representing the

eigenvalues of the Wishart matrix HnH∗n, we can express γn,M as

21 where ρn is the average receive SNR at the n-th subchannel and is equal to

ρn = Ptgn Nσ2 n = Pt 10 (g0/10) N2 _σ2 n rµ . (3.5)

Arrange {λn,i}Mi=1 in the decreasing order so that λn,1 ≥ λn,2 ≥ ... ≥ λn,M ≥ 0.

Ac-cording to [3] [24], the probability density function (PDF) of the minimum eigenvalue λn,M is exponentially distributed with parameter M as follows

fλn,M(λ) = Me

−M λ _{, λ ≥ 0; (3.6)}

and its cumulative distribution function (CDF) can be written as Fλn,M(λ) =

Z _λ

0

fλn,M(x)dx

= 1 − e−M λ_{, λ ≥ 0. (3.7)}

By applying the singular value decomposition (SVD) method, it can be shown that the MIMO-OFDM channel (Hn) is equivalent to MN parallel substreams, each of

which has effective output SNR γn,i= ρnλn,i/M at the receive antenna. Notice that

γn,M is also an exponentially distributed random variable of which CDF is written

Fγn,M(γ) = 1 − e

−M 2γ_{ρn , γ ≥ 0. (3.8)}

For the i.i.d. exponentially distributed random variables {γn,M}Nn=1, the sum

of exponentially distributed random variable Ω = 1 N

P_N

n=1γn,M becomes the Erlang

distributed random variable. Thus, the PDF of Ω is fΩ(x) = N(M2 ρn) N_(Nx)N −1_e−M 2N ρn x Γ(N) , x > 0 (3.9) and its CDF is FΩ(x) = Z _x 0 fΩ(x)dx = 1 − e−M 2Nρn x N −1_X j=0 (M2_N ρn x) j j! , x > 0 (3.10)

Thus, for a given threshold γth > 0, the link outage probability of the OFDM-based

spatial multiplexing systems can be expressed as Pout = Pr à 1 N N X n=1 γn,M ≤ γth ! = Pr(Ω ≤ γth) = FΩ(γth) = 1 − e−M 2Nρn γth N −1_X j=0 ³ M2_N ρn γth ´_j j! . (3.11)

By substituting (4.5) into (4.11), the link outage can be represented as Pout = 1 − e−X N −1 X j=0 Xj j! , (3.12) where X = M 2 _N2 _σ2 n γth rµ Pt 10(g0/10) . (3.13)

In (4.12), Pout is a function of given parameters {M, N, Pt, σn2, µ, r, γth}. The cell

radius r is defined as the farthest distance at which the link quality suffices for main-taining a required receive SNR γth with the probability no less than (1 − Pout). The

objective is to derive an analytical closed-form expression for the cell radius r to be a function composed of given parameters {M, N, Pt, σn2, µ, γth} and the required Pout

(usually 0.1). Because of complexity, it is not easy to derive an analytical closed-form expression for the cell radius r directly from (4.12).

3.5

Cell Coverage Performance

In this section we first provide another simple approximation to closed-form expression of the link outage (4.12) to facilitate the derivation of the closed-form expression of the

23 cell coverage r associated with link outage probability of spatial-multiplexing-based MIMO-OFDM systems. Then we present an method to calculate the cell coverage reliability of MIMO-OFDM systems.

3.5.1

Approximation of link outage probability

Considering the order statistics of a N random variables {γn}Nn=1, we reorder them

and obtain {γ(1) < γ(2) < ... < γ(N )}. Then γ(i) is called the ith order statistic. It is

assumed that γ(ω) is the value most close to _N1

P_N

n=1γn. Then the link outage can be

rewritten as Pout = Pr à 1 N N X n=1 γn≤ γth ! ' Pr(γ(ω) ≤ γth) , (3.14)

where w ' 0.63N ' Nω (see the details in Appendix A), and Nω is an approximation

integer value of ω. By doing so, link outage probability can be transformed to another form – the probability that at least Nω of the γn are less than or equal to γth. By

applying the theories of order statistics, we obtain Pout ' Pr(γ(Nω) ≤ γth) = F(Nω)(γth) = N X i=Nω CN i Fi(γth) [1 − F (γth)]N −i = IF (γth)(Nω , N − Nω+ 1) = I[1−e−X_](N_ω , N − N_ω+ 1) (3.15)

where X is a function of (M, N, µ, r) defined in (4.13) and Ip(a, b) = R_p 0 ta−1(1 − t)b−1dt R₁ 0 ta−1(1 − t)b−1dt For a > 0, b > 0 and 0 ≤ p ≤ 1 (3.16) is the incomplete beta function. Now we have another closed-form approximation for the approximate link outage probability. From (4.15), we will derive the closed-form expression for the cell radius associated with link outage probability of MIMO-OFDM system, which will be discussed in the next section.

3.5.2

Cell Coverage Reliability

To derive cell coverage r from (4.15), we first introduce the inverse incomplete Beta function which is shown as follows

z = Iw(a, b) ⇒ w = Iw−1(a, b) . (3.17)

By substituting (4.13) and (7.1) into (4.15), the cell coverage is given by r ' "µ Pt Nσ2 n ¶ à 10g010 M2_γ th ! · log à 1 1 − I−1 Pout(Nω , N − Nω+ 1) !#1 µ . (3.18)

Note that (7.2 ) can be viewed as an analytical closed form approximation for the cell radius for OFDM-based spatial multiplexing systems over frequency selective fading channels. It is a function composed of given parameters {M, N, Pt, σn2, µ, γth} and the

25 0 5 10 15 10−3 10−2 10−1 100 Transmit power P t (dBW) Link outage N=8 N=32 N=128

Approximately analytical result Analytical result

Simulation result

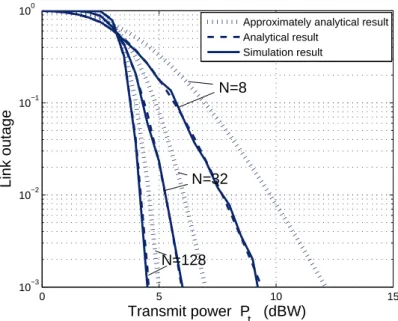
Fig. 3.4: Link outage probability v.s. transmit power Pt for different values of N when

M = 3, noise power= −103dBm, µ = 3, r = 1km and γ_th= 2dB.

3.6

Numerical Results

In this section, we present numerical results to illustrate how the number of antennas, number of subchannels (the order of frequency selectivity), and the pass loss exponent could affect the link outage and cell coverage in OFDM-based spatial multiplexing systems. We first assume a predetermined value γth = 2dB, noise power = −103dBm,

g0 = −32, and r = 1km. Figure 3.4 shows the simulative, analytical, and the

approx-imate link outage with various order of frequency selectivity in the case of M = 3. The performance metric shown in the x−axis is the transmit power Ptin dB domain.

We can see that the link outage reduces as Ptincreases. Furthermore, the link outage

probability will reduce more quickly when the number of subchannels increases. We can also see that the analytical value is very close to the simulation result, and the

0 5 10 15 10−3 10−2 10−1 100 Transmit power P t (dBW) Link outage M=2 M=3 M=4 M=5

Approximately analytical result Analytical result

Simulation result

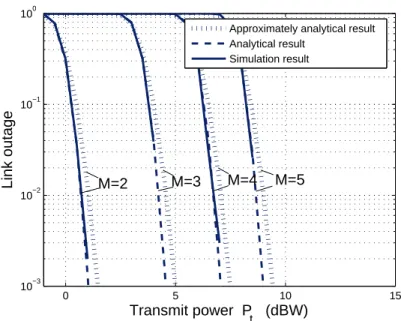
Fig. 3.5: Link outage probability v.s. transmit power Pt for different values of M when

N = 128, noise power= −103dBm, µ = 3, r = 1km and γth = 2dB.

approximately value especially when the number of subchannels is large.

Figure 3.5 shows the link outage performances with various numbers of transmit and receive antennas for N = 128. One can see that when for the case M = 2, Pt increases, the link outage would first reduce. It indicates that the link outage

probability become higher as the number of antennas increases. Thus it is hard to maintain M times of capacity for a large number of M.

Figure 3.6 shows the link outage performances with different pass loss exponents. The link outage probability is high for a large pass loss exponent .

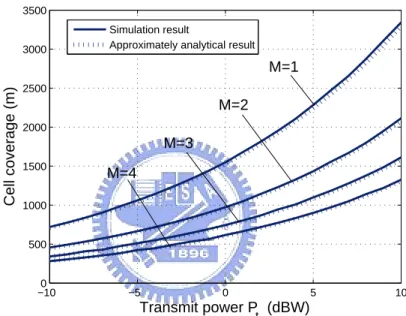
Figure 3.7 shows the cell coverage with different numbers of antennas in the case of N = 128 and µ = 2. We can see that the cell coverage increases as Pt increases,

and it will increase more quickly with fewer antennas. That is, it indicates that the coverage area is easier to maintain M times of capacity when M is small.

27 0 5 10 15 10−3 10−2 10−1 100 Transmit power P t (dBW) Link outage µ=2.9 µ=3 µ=3.1 µ=3.2

Approximately analytical result Analytical result

Simulation result

Fig. 3.6: Link outage probability v.s. transmit power Pt for different values of µ when

M = 3, N = 128, noise power= −103dBm, r = 1km and γ_th= 2dB.

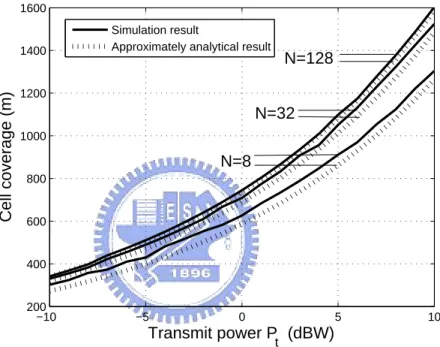
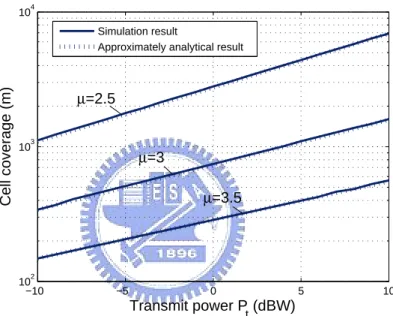
Figure 3.8 shows the cell coverage with various frequency selectivity orders when M = 3 and µ = 2. It shows that the cell coverage is slightly larger in the high-frequency selectivity than in the low high-frequency-selectivity. Figure 3.9 shows the cell coverage with various pass loss exponents in the case of M = 3 and N = 128. Notice that µ = 2 is for free space, and µ = 3.5 ∼ 4 is for two-path model of an urban radio channel. We can see that the cell coverage would increase more quickly for µ = 2.

−100 −5 0 5 10 500 1000 1500 2000 2500 3000 3500 Transmit power P t (dBW) Cell coverage (m) M=1 M=2 M=4 M=3 Simulation result

Approximately analytical result

Fig. 3.7: Cell coverage radius v.s. transmit power P_t for different values of M when N = 128, noise power= −103dBm, µ = 3, Pout = 0.1 and γth= 2dB.

29 −10 −5 0 5 10 200 400 600 800 1000 1200 1400 1600 Transmit power P t (dBW) Cell coverage (m) N=128 N=32 N=8 Simulation result

Approximately analytical result

Fig. 3.8: Cell coverage radius v.s. transmit power Pt for different N when M = 3, noise

−10 −5 0 5 10 102 103 104 Transmit power P_t (dBW) Cell coverage (m) µ=2.5 µ=3 µ=3.5 Simulation result

Approximately analytical result

Fig. 3.9: Cell coverage power v.s. transmit powerPt for different values of µ while M =3,

Chapter 4

Coverage Enhancement for

Spatial-Multiplexing-Based MIMO

OFDM Systems by Joint Multiuser

Scheduling and Subcarriers Assignment

Thanks to the orthogonal frequency multiplexing (OFDM) modulation to overcome the inter-symbol-interference in the frequency-selective fading channel and the multi-input multi-output (MIMO) antenna techniques to deliver high multiplexing capacity gain, MIMO-OFDM has become an attraction option for the next-generation high-speed wireless systems. Due to the fact that the multiplexing gain and diversity gain in the spatial domain are difficult to be maximized simultaneously and that the to-tal transmit power is split over the multiple antenna, the spatial-multiplexing-based MIMO system faces a coverage reliability issue. To improve the coverage reliability of the diversity-deficient spatial-multiplexing-based MIMO system, we suggest exploit-ing the multiuser diversity from schedulexploit-ing techniques and frequency diversity from OFDM subcarrier assignment in the frequency selective fading simultaneously. For this purpose, an efficient and low-complexity sub-carriers assignment scheme com-bined with multi-user scheduling and is proposed in this chapter. By means of the analytical techniques of the order statistics and Glivenko- Cantelli theorem, we de-velop an analytical expression for the link outage probability and cell coverage relia-bility. Our results show that the proposed joint multi-user scheduling and sub-carriers assignment scheme can significantly improve the reliability of the spatial multiplexing

gain of MIMO-OFDM systems. Moreover, we show that the proposed scheme not only can improve the cell coverage performance of the spatial-multiplexing based MIMO-OFDM systems, but successfully preserve the multiusers’ fairness performance.

4.1

Introduction

Orthogonal Frequency Division Multiplexing (OFDM) can convert a frequency se-lective fading channel into a parallel collection of frequency flat fading sub-channels and thus can overcome inter-symbol interference (ISI) [7] [8]. In the meanwhile, multi-input multi-output (MIMO) antenna techniques can provide spatial multiplex-ing gain and diversity gain to increase spectrum efficiency and link reliability, respec-tively [9] [10] [11] [12]. Combining MIMO with OFDM (MIMO-OFDM) becomes an attractive air-interface solution for the next generation high speed wireless systems. The MIMO-OFDM system combines the advantages of both techniques in providing simultaneously increased data rate and elimination of the effects of delay spread.

Spatial-multiplexing based OFDM is one of the categories of MIMO-OFDM techniques. The main goal of spatial-multiplexing based MIMO-MIMO-OFDM tech-nique is to increase capacity by exploiting multiplexing gain in the spatial domain, i.e., transmitting independent data streams across antennas and tones. However, increasing the number of transmit antennas results in a smaller signal-to-noise ra-tio (SNR) per degree of freedom because the total available transmit power is split uniformly across transmit antennas. This leads to link outage or coverage issue of the spatial multiplexing MIMO system. This issue has been investigated originally in [6] and a multiuser scheduling solution to address this issue in MIMO flat-fading channels was proposed in [3].

33 exploited to improve downlink capacity. [3] proposed a fair scheduling scheme called strongest-weakest-normalized-subchannel-first (SWNSF) which requires only limited amount of feedback and can significantly increase the coverage of the multiuser MIMO system while further improving system capacity. In a multiuser orthogonal frequency division multiplexing (OFDM) system over frequency selective fading channels, [2] described an optimal subcarriers allocation algorithm and proposes a low-complexity suboptimal adaptive subcarriers allocation algorithm which performs almost as well as the optimal solution. In a multiuser MIMO OFDM system over frequency selec-tive fading channels, [4] derived the optimal subcarrier allocation criterion and the optimal power loading criterion for downlink MIMO OFDM systems. [25] applied an optimization algorithm to obtain a joint subcarrier and power allocation scheme based on MIMO OFDM combined with dirty paper coding (DPC) when fully instantaneous channel state information (CSI) is available.

In this chapter we focus on the assignment of each resource dimension to only one user to avoid the complexity and the assignment requires only limited amount of feedback. Besides, we assume frequency selective quasistatic channels where chan-nels do not vary within a block of transmission. We first extend the suboptimal subcarriers assigning algorithm proposed in [2] from SISO OFDM to MIMO OFDM systems, and we call it fairness-oriented subcarriers assignment (FOSA) in this chap-ter. Besides, we propose a low-complexity coverage-oriented subcarriers assignment algorithm (COSA) which can achieve larger cell coverage than FOSA for spatial-multiplexing based MIMO-OFDM systems. Furthermore, we derive an approximately analytical closed form expression for link outage and cell coverage by using COSA, and show how the total transmit power, number of antennas, number of users and the pass loss exponent could affect the cell coverage under this subcarriers assignment algorithm over frequency-selective fading channels.

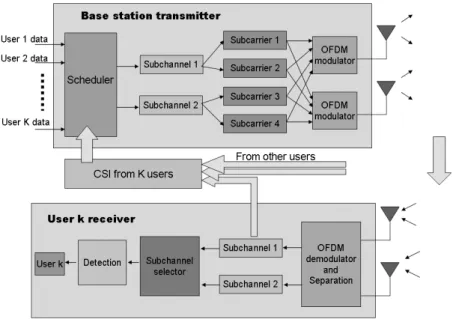
Fig. 4.1: Architecture for scheduling in multiplexing-based MIMO-OFDM systems. Assume

that N = 2, N_T = 4, and M = 2

4.2

System model

We consider K users in a MIMO system with M transmit antennas in base station, and M receive antennas at each mobile. We adopt OFDM modulation with total NT subcarriers and let a group of adjacent NT/N subcarriers form a subchannel.

The total bandwidth of each subchannel is assumed to be smaller than the coherent bandwidth of the channel. Fig. 4.1 shows the considered structure of the spatial-multiplexing based MIMO-OFDM systems. The resource scheduling algorithms are carried out at the base station. In order to keep the scheduling complexity low, we divide the NT subcarriers into N groups which are made up of NT/N neighboring

subcarriers and are the minimum resource units to be allocated. Fig. 4.2 shows an illustration for MIMO-OFDM subchannel assignment where H(k,n) _{represents the flat}

35

Fig. 4.2: Illustration for MIMO OFDM subcarriers assignment. Assume that N = 4, K = 2

subchannel. In the spatial-multiplexing based MIMO-OFDM systems, M transmit antennas and N OFDM sub-channels construct the transmitted symbol vector by multiplexing MN independent data streams. The transmit power is uniformly split to M transmit antennas. It is assumed that the length of the cyclic prefix (CP) in the OFDM system is greater than the length of the discrete-time baseband channel impulse response so that the frequency-selective fading channel indeed decouples into a set of parallel frequency-flat fading channels [22]. With xk,n and yk,n denoting the

M × 1 transmit and receive signal vectors for the user k, respectively, we can write

yk,n =√gk· H(k,n)· xk,n+ nk,n, (4.1)

where n is the sub-channel index while index k represents a specific user. H(k,n)

represents the flat and independent fading M × M channel matrix corresponding to the kth user of the nth subchannel and each entry of H(k,n) is an i.i.d.

circular-symmetric complex Gaussian variable [4] [18]. Represent nk,n the M × 1 spatially

white noise vector with E[nk,n· n∗k,n] = σ2k,nI, where (·)∗ is the transpose conjugate

operation. While H(k,n) _{captures the channel fading characteristics, g}

k depicts the

large-scale behavior of the channel gain. For a user k at a distance of rk from the

base station, gk can be written as [23].

where µ is the path loss exponent and g0 is a constant subject to certain path loss

models.

4.3

Definitions

4.3.1

Link Outage Probability

Define the link outage probability reflect to what extend a system can reliably support the corresponding link quality. For a single-input single-output (SISO) system in flat fading channel, link outage is usually defined as the probability that the received SNR is less than a predetermined value γth, i.e. Pout = Pr{γ < γth} [5]. The link outage for

the spatial multiplexing MIMO system in a flat fading channel is defined as the event when the receive SNR of any substream is less than γth [6] [3]. When all the degrees

of freedom in the spatial domain of a MIMO system are used for the transmission of parallel and independent data streams to exploit the spatial multiplexing gain, the data stream with the lowest SNR in the MIMO system will dominate the link reliability performance especially when the link reliability likely of high percentile, such as 90% or even higher, is concerned.

The spatial-multiplexing based MIMO-OFDM systems in a frequency selective fading channel can be viewed as the sum of flat fading MIMO channels. As discussed before, the high-percentile link reliability performance of each MIMO flat-fading chan-nel is dominated by the weakest substream. Considering the average weakest eigen-mode over a series of N’s MIMO flat-fading subchannels, we define the link outage probability of the spatial-multiplexing-based MIMO OFDM system for user k as fol-lows: P_outk = Pr à 1 N N X n=1 γk,n,M ≤ γth ! , (4.3)

37 the kth user in subchannel n for n = 1, . . . , N .

4.3.2

Cell Coverage Reliability

With Pk

out being the link outage probability for user k, we define the cell coverage

for all the users in a cell is the farthest distance at which the link quality suffices for maintaining a required receive SNR γth with cell coverage reliability (1 − Poutk ). What

we focus on is the farthest user in the boundary of the cell coverage. In other words, if the farthest user maintains the link quality, the other (K − 1) users will maintains it too.

4.4

Subcarriers assignment algorithms

If the channel is static and is perfectly known to the transmitter and the receiver, joint power and subcarrier allocation is known to be optimal for MIMO OFDM systems [4]. However, solving the optimization problems could be very complex to implementation. In [2], the authors show that the total system performance will be close to optimum as long as the energy is poured only into subchannels with good channel gains. They also bring up a concept that a flat transmit power spectral density (PSD) would hardly reduce the system performance if each subchannel is assigned to a user whose channel gain is good for it. Therefore, the authors propose a suboptimal subcarriers assigning algorithm for single-input single-output (SISO) OFDM systems and its complexity is almost negligible compared with the complexity of finding optimal allocation by solving a joint power and subcarrier optimization equation.

In this section, we present two suboptimal subcarriers assignment algorithms for spatial-multiplexing based MIMO-OFDM systems. At first, we show an extended suboptimal subcarriers assignment algorithm – FOSA based on the work in [2]. Then

Fig. 4.3: Fairness-oriented subcarriers assignment (FOSA)

we propose a low-complexity but performance-enhanced COSA algorithm.

In the following subcarriers assignment algorithms, equal amount of power is allocated to each subchannel. Define A = {1, 2, . . . , N}, B = {1, 2, . . . , K}, and Rk

as the subchannel index set and the allocated weakest subchannel metric for kth user

in the following two flow charts, respectively. Notice that λk,n = λmin(H(k,n)· H(k,n)∗)

39

Fig. 4.4: Coverage-oriented subcarriers assignment (COSA)

4.4.1

Fairness-Oriented Subcarriers Assignment (FOSA)

The authors in [2] proposed a suboptimal subcarriers assignment for SISO OFDM systems. Based on the designed principles, we extend the algorithm to a MIMO OFDM system and denote as FOSA in the chapter. The main advantage of FOSA is the negligible complexity compared with the optimal allocation. Furthermore, FOSA can ensure all the mobile users to receive at almost the same times of subchannels, and it can achieve good fairness performance at the same time. Figure 4.3 shows the flow chart of the FOSA algorithm.

1 2 3 4 5 6 7 8 9 10 0.8 0.82 0.84 0.86 0.88 0.9 0.92 0.94 0.96 0.98 1 Time index Fairness index N=64 N=32 N=16 FOSA COSA

Fig. 4.5: Fairness performance comparison for K = 5 and M = 3

4.4.2

Coverage-Oriented Subcarriers Assignment (COSA)

We provide an low-complexity coverage-oriented subcarriers assignment algorithm (COSA) shown in Fig. 4.4. In the following sections, we will show COSA achieve larger cell coverage than FOSA for spatial-multiplexing based MIMO-OFDM systems by applying multiuser diversity. Furthermore, we will show that COSA can achieve almost the same fairness performance as FOSA when the number of subchannels is large.

41

4.5

Fairness Performance

We first define a fairness index F in the multiuser systems as follows

F = Ã 1 K K X i=1 Ti !2 1 K K X i=1 Ti2 = Ã _K X i=1 Ti !2 K K X i=1 Ti2 , (4.4)

where Ti is the number of times the subchannels allocated to ith user. For F = 1, it

is the fairest condition between users, and it is not fair as F ¿ 1. Fig. 4.5 shows the fairness performance comparison for FOSA and COSA, and we can see that COSA achieves almost the same fairness performance as FOSA when the number of subchan-nels is large. Since COSA can achieve almost the same fairness performance, and it can further achieve larger cell coverage than FOSA (we’ll show it in numerical results), we focus on COSA and derive an approximately analytical closed form expression for link outage and cell coverage by using this subcarriers assignment algorithm.

4.6

Link Outage by COSA

To begin with, we first analyze the received SNR of the weakest substream (denoted by γk,n,M) at the nth subchannel for user k. With {λk,n,i}Mi=1representing the eigenvalues

of the Wishart matrix H(k,n)_H(k,n)∗

, we can express γk,n,M as

γk,n,i= ρk,nλk,n,i/M, (4.5)

where ρk,n is the average receive SNR at the nth subchannel and is equal to

ρk,n = Ptgk Nσ2 k,n = Pt 10 (g0/10) N2 _σ2 k,n rkµ (4.6)

Arrange {λk,n,i}Mi=1 in the decreasing order so that λk,n,1 ≥ λk,n,2 ≥ ... ≥ λk,n,M ≥ 0.

According to [3] [24], the marginal probability density function (PDF) of the minimum eigenvalue λk,n,M is exponentially distributed with parameter M.

fλk,n,M(λ) = Me

−M λ _{, λ ≥ 0. (4.7)}

The marginal cumulative distribution function (CDF) of it can be written as Fλk,n,M(λ) =

Z _λ

0

fλk,n,M(x)dx

= 1 − e−M λ_{, λ ≥ 0. (4.8)}

By applying the singular value decomposition (SVD) to H(k,n)_{, we know that an}

open-loop MIMO-OFDM channel is enhanced by forming MN parallel subchannels, each of which has effective output SNR γk,n,i = ρk,nλk,n,i/M at the receive antenna. Notice

that γk,n,M is also an exponentially distributed random variable with the following

marginal CDF

Fγk,n,M(γ) = 1 − e

−M 2γ_ρk,n

, γ ≥ 0. (4.9)

For brevity, we omit the index of M and use γk,nto replace γk,n,M. In (4.9), {γk,1, ...γk,N}

are identically and independently exponential distributed random variables with marginal CDF Fγk,n(γ) = 1 − e

−M 2γ_ρk,n

. By using COSA, any user k competes for services with other (K − 1) users at each time slot for each subchannel n. Assume that the select user at each time slot for each subchannel n is k∗_{. The CDF of γ}

k∗_,n is given by Fγk∗,n(γ) = Pr n max k (γk,n) < γ o = [Fγk,n(γ)] K_{. (4.10)}

Considering the order statistic and a given sample of N variables {γk∗_,1, ...γ_k∗_,N}, we can reorder them so that {γk∗_,(1) < γ_k∗_,(2) < ... < γ_k∗_{,(N )}}. Then γ_k∗_,(i) is called the

43

1 N

P_N

n=1γk∗,n. The link outage can be rewritten as

Pout = Pr à 1 N N X n=1 γk∗_,n ≤ γ_th ! ' Pr(γk∗_,(ω)≤ γ_th), (4.11) where w ' Nω(N, K) = N · à 1 − exp à 1 B(K, 1) K−1_X i=0 CK−1 i (−1)K−i 1 (K − i)2 !!K . (4.12) We’ll show the details in Appendix B, and Nω(N, K) is an approximation integer

value of ω. In (4.12), link outage is transformed to another form of probability which means at least Nω(N, K) of the γk∗_,n are less than or equal to γ_th. By applying the theories of order statistics, we obtain

Pout ' Pr(γk∗_,(Nω(N,K))≤ γ_th) = Fk∗_,(Nω(N,K))(γ_th) = N X i=Nω(N,K) C_iN[Fk∗_,n(γ_th)]i[1 − F_k∗_,n(γ_th)]N −i = IFk∗,n(γth)(Nω(N, K) , N − Nω(N, K) + 1) = I(Fk,n(γth))K(Nω(N, K) , N − Nω(N, K) + 1) = I_[1−e−X(M,N,µ,r)]K(Nω(N, K) , N − Nω(N, K) + 1) , (4.13)

where X(M, N, µ, r) = M 2 _N2 _σ2 n γth rµ Pt 10(g0/10) , γth> 0 (4.14) and Ip(a, b) = R_p 0 ta−1(1 − t)b−1dt R₁ 0 ta−1(1 − t)b−1dt F or a > 0, b > 0 and 0 ≤ p ≤ 1 (4.15)

is the incomplete beta function. Now we have analytical closed form approximation for the link outage. We will show how we can derive the cell coverage from this approximate link outage formula in the next section.

4.7

Cell Coverage by COSA

We can define that the cell coverage for all the users in a single cell is the farthest distance at which the link quality suffices for maintaining a required receive SNR γth

with the probability no less than (1 − Pk

out). We focus on the farthest user in the

boundary of the cell coverage. In other words, if the farthest user maintains the link quality, the other (K − 1) users will maintains it too. In order to derive r (or rk for

the farthest user) from (4.15), we first introduce the inverse incomplete Beta function which is shown as follow

z = Iw(a, b) ⇒ w = Iw−1(a, b). (4.16)

By substituting (4.14) and (4.16) into (4.13), we can obtain the cell coverage as

r ' "µ Pt N σ2 n ¶ à 10g010 M2_γth ! · log à 1 1 − (I_P−1_out(Nω(N, K), N − Nω(N, K) + 1)) 1 K !#1 µ (4.17)