Modeling PCS Networks Under General Call
Holding Time and Cell Residence Time Distributions
Yuguang Fang,
Student Member, IEEE,Imrich Chlamtac,
Fellow, IEEE,and Yi-Bing Lin
Abstract—In a personal communication service (PCS) network, the call completion probability and the effective call holding times for both complete and incomplete calls are central parameters in the network cost/performance evaluation. These quantities will depend on the distributions of call holding times and cell residence times. The classical assumptions made in the past that call holding times and cell residence times are exponentially dis-tributed are not appropriate for the emerging PCS networks. This paper presents some systematic results on the probability of call completion and the effective call holding time distributions for complete and incomplete calls with general cell residence times and call holding times distributed with various distributions such as Gamma, Erlang, hyperexponential, hyper-Erlang, and other staged distributions. These results provide a set of alternatives for PCS network modeling, which can be chosen to accommodate the measured data from PCS field trials. The application of these results in billing rate planning is also discussed.
Index Terms—Billing rate planning, call blocking, call holding time, call termination, cell residence, handoff, PCS.
I. INTRODUCTION
T
HE emerging personal communications services (PCS) technologies have captured considerable attention in aca-demic research as well as commercial deployment. A PCS network can support a wide host of services when users are in motion [2], [13], [20], [21] and can serve a large number of customers by using spectrally efficient cellular systems [13], [21]. In a PCS system, customers can make a phone call as in wired telephony or make a connection to retrieve information messages such as email or stock information or even make a connection to surf the internet.For billing and general performance tuning purposes, the probability of a call completion and effective call holding times need to be analyzed. To this end, the distributions of call holding times and cell residence times need to be evaluated. As a result of the new applications in the PCS networks the classical assumptions on exponential call holding times and cell residence times may not be appropriate for modeling the new emerging integrated services in these systems. Field Manuscript received December 1996; revised July 1997; approved by IEEE/ACM TRANSACTIONS ON NETWORKING Editor S. Krishnan. The work of Y. Fang and I. Chlamtac was supported in part by the U.S. Army Research Office under Contract DAAH04-96-1-0308. The work of Y.-B. Lin was supported in part by the National Science Council in Taiwan under Contract NSC-87-2213-E-009-014.
Y. Fang and I. Chlamtac are with the Erik Jonsson School of Engineering and Computer Science, The University of Texas at Dallas, Richardson, TX 75083-0688 USA.
Y.-B. Lin is with the Department of Computer Sciences and Information Engineering, National Chiao Tung University, Hsinchu, Taiwan, R.O.C.
Publisher Item Identifier S 1063-6692(97)08936-X.
data for call holding times collected in office buildings and residence areas in Taiwan show that the call holding times cannot be modeled by exponential distribution, while Gamma and lognormal distributions provide good (second-order) ap-proximations to the experimental data. Not only does call holding time distribution vary with the new applications, also, the time a customer spends in a cell (the cell residence time) will depend on the mobility of the customer, the geographic situation, and the handoff scheme used, and therefore needs to be modeled as a random variable of general distribution.
In order to facilitate our presentation of the modeling of call holding times and cell residence times, we briefly review the call connection process first. In a PCS system, the service area is populated with base stations with the radio coverage of each base station defining a cell, each with its assigned set of customers. When a new call is originated by a customer in a cell, one of the channels assigned to the base station is used for the communication between the mobile portable and the base station if a channel is available (a survey on channel allocation schemes can be found in [10]). If all channels are in use while a new call (or handoff call) is being attempted, the call will be blocked and cleared from the system. If a call can be assigned a channel, it will keep it until the call is completed or until the mobile moves out of the cell. When the mobile moves into a new cell while its call is active, a new channel needs to be acquired in the new cell using a “handoff procedure.” During the handoff, if no channel is available for the “old” call the call will be forced to terminate before its completion [13].
The duration of the requested call connection is referred to as the call holding time. When the call is connected, the call may be completed after several successful handoffs, or may be incomplete due to a failed handoff. We shall call the duration of an incomplete call the effective call holding time of an incomplete call and the duration of a call connection of a complete call the effective call holding time of a complete call. To evaluate the performance of a PCS network with ap-propriate rating programs such as flat-rate program [1], the effective call holding times, as well as the probability of a call completion, are required. From call completion probability, we can also easily find the call dropping probability, another important design parameter [4]. These quantities depend on the distributions of call holding times and cell residence times as well as the new call blocking probability and handoff call blocking probability. Thus, the new call and handoff call blocking probabilities can be regarded as inputs to the model. Two main approaches to modeling call holding times and cell residence times can be identified in the literature. One 1063–6692/97$10.00 1997 IEEE
uses the assumption of geographic cell (hexagonal) shapes and the assumption of the constant mobiles’ speeds, random distances, or uniformly distributed directions to determine the distribution of cell residence times and call holding times [8], [18], [26]. This approach faces a difficulty when applied to existing cellular systems since, in reality, cell shapes are often highly irregular, the speeds of mobiles or distances covered by the mobiles are highly random (considering highly populated area), and the directions of mobiles may vary in random fashion. It becomes, therefore, very hard with this model to characterize analytically the cell residence times using these modeling assumptions.
The second approach treats the cell residence times and call holding times directly, using information measured from the PCS field trials. Distribution models such as exponen-tial distribution, lognormal distribution have been used to approximate the distributions of call holding times and cell residence times using data from field tests (see [5], [16], [17] and references therein). It is well known that exponential distribution can be used for one-parameter approximation of the measured data while Gamma distribution can be used for two-parameter approximation [9]. It is also known [11] that mixed Erlang distribution (hyper-Erlang distribution in this paper) can be used to approximate any specific nonlattice distributions. Hence, the application of these distributions to model the call holding times and cell residence times in the emerging PCS networks appears to be more practical when field data are available.
In the traditional wired-line telephone models, the call hold-ing times are usually assumed to be exponentially distributed, which has been shown to be a reasonable approximation for measured data. This assumption has been used in past PCS network analysis for reasons of tractability [6], [8], [26], [27]. When call holding times are exponentially distributed, Lin et al. [16], [17], Rappaport et al. [8], [22], [23], Yum and Yeung [27], and Tekinay and Jabbari [25] studied the performance of channel assignment strategies and obtained analytical results for forced termination probability and new call blocking proba-bility. Under the same assumption regarding call holding times and general cell residence time distribution, Lin and Chlamtac [15] obtained formulas for call completion probability and the expected effective call holding times. When call holding times are Erlang distributed and cell residence times have a general nonlattice distributions, Fang, Chlamtac, and Lin [5] obtained easily computable formulas for the call completion probability and expected effective call holding times of a complete or an incomplete call.
As emerging PCS networks are poised to provide various new services they are expected to attract more users while changing the users’ calling habits. Therefore, as pointed out earlier, the call holding times are not expected to be distributed with respect to the exponential (Erlang) distribution. More general distributions for call holding times are, therefore, needed to model these networks. In this paper, we propose a general model that assumes that the cell residence times have general nonlattice distribution and the call holding times are distributed with general distributions such as Gamma, hyper-exponential, and hyper-Erlang distributions. While the
advantages of such distributions are clear in that they reflect the emerging services, applying these distributions to obtain analytical results is a nontrivial task. This paper shows how to accommodate general call holding time distributions in previously proposed analytic models [5], [15]. The following general assumptions will be used in this paper:
• the call arrivals form a Poisson process;
• the cell residence times are independent identically dis-tributed (iid) with nonlattice distribution;
• the call holding times are independent identically dis-tributed (iid) with nonlattice distribution.
Based on these assumptions, we obtain general formulas for the call completion probability (hence, the call dropping probability) and the distribution (its Laplace transforms) of the effective call holding times of both the complete and incom-plete calls from which expected effective call holding times can be obtained. We derive computable formulas for the cases when call holding times are distributed according to Gamma, staged exponential or Erlang, hyperexponential, and hyper-Erlang distributions. Billing rate plans using the expected call holding times for a complete call and an incomplete call are also proposed and discussed briefly. The analysis of the call completion probabilities and effective call holding times can provide the necessary guideline for network performance eval-uation tuning and importantly designing billing rate schemes in the future PCS networks [1].
II. CALL COMPLETION PROBABILITY
In this section, we study the call completion probability. Our previous work [5], [15] obtained formulas for the call completion probability for a PCS network with a general cell residence time distribution and Erlang (exponential) call holding time distribution. Here, we give further results for cases when the call holding times have other distributions. New technique is developed for the case where the residue theorem is not applicable.
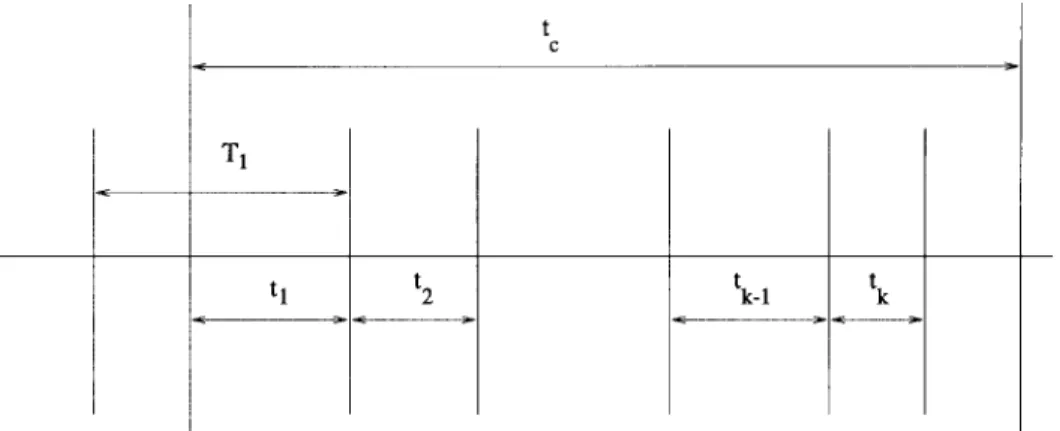
We first consider the effective call holding time for an incomplete call. Fig. 1 illustrates the timing diagram for the call holding time, is the time that the portable resides at cell 1, and is the residence time at cell
According to our assumptions, are iid. Let
have nonlattice density function with the mean and be the Laplace transform of (we will use to denote the Laplace transform following the tradition [12]). Suppose that a call for the portable occurs when the portable is in cell 1. Let be the interval between the time instant when the call arrives and when the portable moves out of cell 1. Let and be the density function and the Laplace transform of distribution, respectively. From the renewal theory [12], is the residual life of the cell residence time of the portable in cell 1, so we have
(1) (2)
Let be the effective holding time and
Fig. 1. The timing diagram for a forced terminated call at kth handoff. Since are independent, it is easy to derive
(3) Let be the probability that a new call attempt is blocked (i.e., the call is never connected), be the probability that a call is completed (i.e., the call is connected and completed), and be the forced termination probability or the probability that no radio channel is available when a handoff call arrives. Then the call dropping probability or the call incompletion probability (i.e., the call is connected but is eventually forced
to terminate) is which is given by
(4) where is the density function of the call holding times. In [5], we have obtained
(5) Since has no poles in the right half complex plane,
Let denote the set of poles of
in the right half complex plane (i.e., is
the set of poles of in the left half plane). In [5], we have obtained the call completion probability for the case when the call holding times are Erlang distribution. Next, we study other cases when the call holding times have other distributions.
Assume that the call holding times are Gamma distributed with the following density function:
(6) where is the shape parameter and is the scale parameter. This density has the following Laplace transform:
(7) Substituting (7) into (5), we obtain
(8) In order to evaluate this integral, we need the following lemma.
Lemma 1: Let and is analytic on
Re Re denotes the real part) with
as in denotes the
integral part of for any positive real number). Then, we have
(9)
where when
Proof: The proof is given in the Appendix. Now, we are ready to give an expression for Let
(10)
Note that is analytic on and on
Taking this into consideration in (8) and using Lemma 1, we have
from which we obtain the following theorem.
Theorem 1: For a PCS network with Gamma distributed calling holding times, the probability of a call completion is given by
(11) Remark: When is a positive integer, the Gamma distri-bution becomes Erlang distridistri-bution. In this case
(12) From (11) and (12), we obtain the same result obtained from the residue theorem in [5].
If the call holding time has such a distribution that its Laplace transform has no branch points but has possible isolated poles, then from the residue theorem we can obtain [5].
Theorem 2: If the Laplace transform of the call holding time distribution only has isolated poles in the left half of the complex plane, then the probability of a call completion is given by
Res
(13) where Res denotes the residue at the pole In particular, when is rational function, then (13) is valid. We have obtained the formula for the case that the call holding times are Erlang distributed [5]. It is well known [12] that the Erlang distribution can be obtained by a series of independent identically distributed random variables. By serial-parallel stages, a large number of general distributions can be obtained from exponential distributed random variables [12]. It is easy to observe that when is a rational function, then Theorem 2 can be easily applied to find The distributions obtained by the method of stages belong to this class. We will discuss some of the important cases next.
Let the call holding times be distributed according to the -stage exponential distribution (the generalized Erlang
distribution) with parameters (which are
distinct) whose Laplace transform is [12]
(14) A random variable with this distribution is in fact the summa-tion of exponentially distributed random variables with the parameters From this, we have the following. Corollary 1: For a PCS network with -stage exponential distribution of distinct positive parameters
the probability of a call completion is
(15)
Proof: From Theorem 2, we obtain
Res
This completes the proof.
Assume now that the call holding times are distributed ac-cording to the -stage Erlang distribution with distinct
param-eters and positive integers ,
which has the following Laplace transform:
(16) This distribution can be obtained from the sum of inde-pendent Erlang distributed random variables with parameters
For this case, we have the following:
Corollary 2: For a PCS network with -stage Erlang dis-tributed call holding times, we have
(17) Equation (17) is specific for serial stages. For -stage paral-lel exponential distribution (the hyperexponential distribution)
with the parameters and with the following Laplace transform [12]:
(18)
Corollary 3: For a PCS network with hyperexponential distributed call holding times, we have
(19) More general cases can be obtained from serial-parallel stages. One important case [12] is the hyper-Erlang distribution with the following density function:
(20) with the following Laplace transform:
(21)
This distribution is obtained from parallel Erlang distributed random variables. It is shown [11] that the hyper-Erlang distri-butions can approximate any general (nonlattice) distribution. Corollary 4: For a PCS network with hyper-Erlang dis-tributed call holding times, we have
(22) One general and interesting case obtained by the method of stages is the distribution with Laplace transform
A similar result for the probability of a call completion can be derived, details are left to the reader. For the method of stages, the interested reader is referred to [12]. For the computation of needed in the above, a recursive algorithm is constructed in [5].
III. EXPECTEDEFFECTIVECALL HOLDING TIMES In the preceding section we discussed the probability for a call to complete. To fully characterize the performance of a PCS network it is necessary to also know the expected elapsed times for the complete and the incomplete calls (their so-called effective call holding times), respectively. In [5], we have presented results for the effective call holding times of complete and incomplete calls, in particular for the case when the call holding times are Erlang distributed. This section provides new results for other cases of interest.
We first consider the effective call holding time of an incomplete call. As in [5], the density function for the effective
call holding time of an incomplete call that is forced to terminate is given by
(23)
where denotes the probability of a call to
be incomplete and is computed in the previous section. In the first equation, the term under the summation is the density that the call is forced to terminate after handoffs.
We want to find the Laplace transform of from which the expected value can be easily obtained. As in [5], from (17) we can obtain
(24) Since
is a removable singular point [14] of the integrand of (24). Thus, the poles of the integrand in the right half-complex
plane is those of i.e., Let
(25) Assume that the call holding times are Gamma distributed as in (6) and (7). Taking (7) into (24), choosing to be greater than the real part of and using Lemma 1, we have
Using the well-known formula
(27)
we obtain the following theorem.
Theorem 3: For a PCS network with Gamma call holding times, the Laplace transform of the density function of the effective call holding times of an incomplete call is given by
(28)
The expected effective call holding time of an incomplete call is given by
(29)
Here, when and the
limit will be taken for when
is an integer).
Proof: Since from
(26) we have
from which we complete the proof.
Remark: When is an integer, the Gamma distribution becomes the Erlang distribution, the above result will reduce to our previous result [5].
If does not have any branch points in the right half complex plane, then the residue theorem can be used to obtain certain computable results. In fact, from (24) we have the following general result [5].
Theorem 4: If only has isolated poles in the left half of the complex plane, then
Res (30)
In particular, when is rational function, then (30) is valid.
If the call holding times are -stage exponentially dis-tributed, we have the following result.
Corollary 5: For a PCS network with call holding times -stage exponentially distributed with Laplace transform as in (14), then
(31)
and the expected effective call holding time of an incomplete call is given by
(32) Proof: By taking (14) into (30), we obtain
Res
This proves (31). Equation (32) can be obtained by This completes the proof.
For -staged Erlang distributed call holding times, we have the following result.
Corollary 6: For a PCS network with call holding times distributed according to -stage Erlang distribution as in (16), we have
and the expected effective call holding time of an incomplete call is given by
(34) Proof: Taking (16) into (30), we have
Res
This proves (33). Equation (34) can be proved by For hyperexponentially distributed call holding times we have the following.
Corollary 7: For a PCS network with hyperexponentially distributed call holding times (as in (18)), we have
(35)
and the expected effective call holding time of an incomplete call is given by
(36)
Proof: Taking (18) into (30), we obtain Res
from which the proof can be easily completed.
For the hyper-Erlang distributed call holding times, we have the following.
Corollary 8: For a PCS network with hyper-Erlang call holding times, we have
(37) and the expected effective call holding time of an incomplete call is given by
(38) Proof: Taking (21) into (30), we have
Res
from which the corollary can be proved.
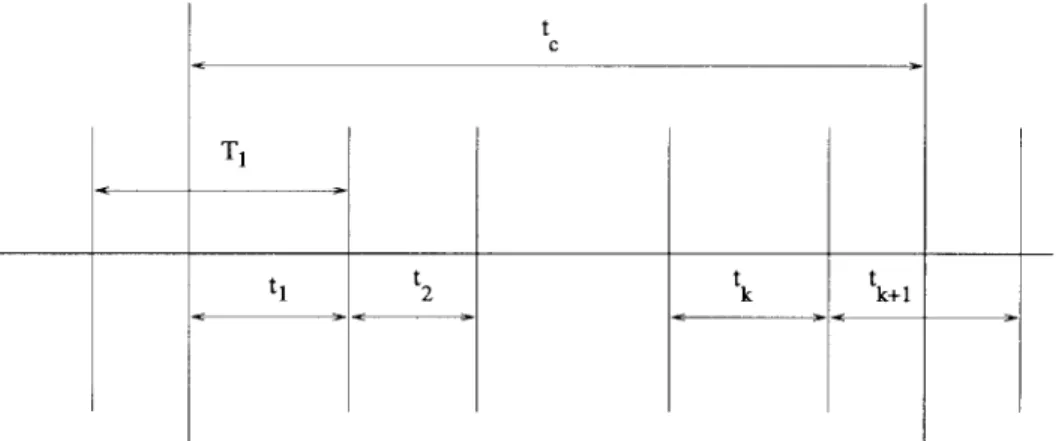
Next, we study the expected effective holding time for a complete call. The timing diagram is shown in Fig. 2 in which the call is completed when the portable is in cell As before, represents the effective call holding time for a complete call.
If while if
Let ; then we have
For (39)
For
(40) Using a simple conditional probability argument, we can obtain the density function of the effective call holding time of a complete call is given by
(41) where
(42)
Fig. 2. The timing diagram for the effective call times of a complete call; the call completes after k handoffs. corresponds to (39) and corresponds to (40),
where is the probability of nonblocking,
is the probability of no-forced termination. Equation (42) can
be derived from , where
denotes the probability that the call is completed in cell and the effective call holding time is not exceeding Rigorous derivation can be obtained following a similar argument in [16].
The Laplace transforms and of and
respectively, are [5] (44) (45) Let (46) (47) Assume that the call holding times are Gamma distributed with the Laplace transform (7). Then, from Lemma 1 we have the Laplace transform of the density function of the effective call holding time of a complete call
from which we obtain the following theorem.
Theorem 5: For a PCS network with Gamma distributed call holding times, we have
(48) and the expected effective call holding time of a complete call is given by
(49)
Remark: When is a positive integer, then Theorem 5 reduces to the result for the case when the call holding times are Erlang distributed [5].
When does not have any branch points and has only finite isolated poles, an application of the residue theorem to (44) and (45) leads to the following result [5].
Theorem 6: For a PCS network, the Laplace transform of the density function of the effective call holding time of a complete call is given by
Res
Res (50)
If the call holding times are -stage exponentially dis-tributed, then we have the following.
Corollary 8: For a PCS network with the -stage exponen-tial call holding times [see (14)], the Laplace transform of the
effective call holding time of a complete call is given by
(51)
and the expected effective call holding time of a complete call is given by
(52)
Proof: This and the following few results can be proved as those for the effective call holding times of an incomplete call and are left to the readers.
If the call holding times are -stage Erlang distributed, then we obtain the following result.
Corollary 9: For a PCS network with call holding times distributed according to the -stage Erlang distribution (16), then
(53) and the expected effective call holding time of a complete call is given by
(54)
If the call holding times are hyperexponentially distributed, then the following result can be obtained.
Corollary 10: For a PCS network with call holding times distributed according to hyperexponential distribution, then
(55)
and the expected effective call holding time of a complete call is given by
(56)
Finally, for the call holding times are hyper-Erlang dis-tributed, we have the following.
Corollary 11: For a PCS network with call holding times distributed according to hyper-Erlang distribution as in (20), we have
(57) and the expected effective call holding time of a complete call is given by
(58)
IV. BILLING RATE PLANNING
In previous section, we derived analytical expressions for expected call holding times for both complete and incomplete calls. From these two quantities, we can easily compute the expected call holding time, i.e., the expected time of service usage for any call (either complete or incomplete). The objective of this section, is to demonstrate the usefulness of the effective call holding times not only for the performance evaluation of the system, but also for effective service charging planning.
Customers may have different calling habits in different places at different times, creating the need for service providers to determine the best rate plan. Based on customer’s usage, service providers may try to adaptively change their charging plans to provide the customer with an optimal rate. For a service provider this may serve to gain customer satisfaction and stay competitive.
As PCS networks are targeted to provide integrated services, one can stipulate that it is not fair to charge the users for the incomplete calls the same rate as for complete calls. For example, in the FTP application, if the portable is forced to terminate, the file needs to be retransferred. It may be more reasonable for this loss to be shared by the customer and the service provider. On the other hand, it may be considered unfair for service providers to charge the same rate for short and long incomplete calls. The possibility to differentiate between service quality and charge accordingly is also in the marketing interest of the PCS providers. Such differentiation is not possible without solutions for the effective call holding times unavailable in the past. Thus, cellular rating systems did not differentiate between complete call and an incomplete calls
using the same rate for the air time, which can be determined by the effective call holding time. Given our results above, it becomes possible to distinguish between the air times for complete calls and incomplete calls so that different rating systems can be developed.
One may contend that it would be difficult to distinguish the “true” forced termination from the false one. The user may purposely terminate the connection, claiming a forced termination. This issue does not exist in the current PCS systems. A service provider only provides services within the service area. In this area, the service provider is responsible for the support of handoffs. The service provider is not responsible for signal disconnection when the portable moves out of the service area. Forced termination can be easily detected when handoff fails due to the channels being assigned by the base stations.
In the following, we briefly discuss a few possible service charging (rating) systems for PCS network services.
A. Flat-Rate Planning
The simplest rate planning is the flat-rate plan, which applies a flat rate to all calls (either complete or incomplete). This rate is easy to implement and easy for customers to understand; the determining factor for the charging rate is the expected effective call holding time
where and Noticing
that we have In wireline
networks, where there is no forced termination the flat-rate planning is reasonable. Obviously, when the call dropping probability is sufficiently small (this is the case when either call traffic is light and mobility is comparably low or the number of channels is sufficient to support all incoming calls), flat rate planning is useful.
B. Partial Flat-Rate Planning
Due to the increase of the number of users and the mobility of users, cell traffic will tend to increase. Hence, the effective call holding times for incomplete calls may be significant. In this case, one should consider using different rates for complete calls and incomplete calls. Let and denote the rates for an incomplete call and a complete call, respectively. Then the average cost per call is given
(59) Clearly, From previous section, we know that the expected effective call holding time for an incomplete call is longer than the expected effective call holding time for a complete call. Hence, from (59), we observe that slightly increasing the rate and decreasing the rate does not change the cost significantly. However, it is important to ob-serve that customers are usually sensitive to call interruption, and insensitive to the new call blocking. Thus, using discounts for interrupted calls is a desirable policy, while these discounts can be compensated by increasing the rate for complete calls, to which the customers are less sensitive.
C. Nonlinear Charging Planning
In this case, the charges for complete calls and incomplete calls are nonlinear functions of the effective holding times for complete calls and incomplete calls. The cost per call may be expressed as
(60) where and are nonlinear functions. By choosing these two functions, we can have different rate planning. It is
obvious if we choose and is a
convex function, then we have
which implies that the rating scheme using and sepa-rately can generate more revenues than a rate scheme which uses the single parameter The convexity of implies that we encourage medium length of calls, and discourage very short calls and very long calls by applying a higher rate to those calls (observing the shape of convex functions). Another practical example is to choose the function to be
while may choose linear function. In this example, we
may choose the parameter and such that
These choices reflect the fact that the setup proce-dure is more expensive, while the longer calls are discouraged in order to accommodate more users.
V. ILLUSTRATIVE EXAMPLES
This section presents some illustrative examples to show how results obtained in this paper can be used to evaluate the performance of PCS networks. We use following scenarios.
1) The cell residence times are iid according to the Gamma distribution with parameter and with different
values (change of mobility);
2) The call holding times are iid according to the following distributions:
• exponential distribution with parameter ; • Gamma distribution with parameters ; • -stage exponential distribution with parameters
and ;
• hyper-exponential distribution with parameters
and ;
• hyper-Erlang distribution with parameters
and .
3) The mobility is changing from 0 to 25.
4) and typically values for current
Fig. 3. Call completion probability for different call holding time distribu-tions.
Fig. 4. Call completion probability; localized piece of Fig. 3.
In our examples, the considered distributions have the same expected values (for exponential and Gamma distributions, their expectations are for -stage exponential distribution its expectation is for hyper-exponential and hyper-Erlang distributions their expectations are
The choice of parameters above is to guarantee that the average call holding times with different distributions are all the same for comparisons, which are equal to
minutes, a value commonly used in the wired telephony trials [13].
Figs. 3 and 4 show the call completion probability for different call holding time distributions in the above scenarios (the marking in Fig. 4 is used for curve reading). The following can be observed.
• With low user mobility, the call holding time distributions do not have significant impact on the call completion probability (hence, the call dropping probability); with high user mobility, the call holding time distributions do have significant impact on the call completion probability.
Fig. 5. Expected effective call holding time for an incomplete call.
Fig. 6. Expected effective call holding time for a complete call.
• The call completion probability is always decreasing as the mobility increases, which is consistent with our intuition that the higher the mobility, the more the hand-offs; hence, the higher the chance that the call will be incomplete or the smaller the call completion probability. These results are very important to the PCS network designers. If the network is designed for low mobility, then the call holding time distributions can be ignored. If high mobility is expected in the PCS system, further analysis of the call holding time distributions are required.
Figs. 5 and 6 show the expected effective call holding times for a complete call and an incomplete call, respectively. The vertical axis shows the normalized effective call holding times by the the average call holding time when there is no new call blocking and no handoff call blocking (the ideal case). Although the type of the call holding time distributions does not significantly affect the call completion probability for low user mobility, it does greatly affect the effective call holding times for a complete call and an incomplete call. This is why we should consider the effective call holding times in
evaluating the performance of PCS networks. From these two figures, we have the following observations.
• The expected effective call holding times (for either a complete call or an incomplete call) are always decreasing as mobility increases as expected intuitively.
• For the expected effective call holding time of a complete call, the dependency on the type of call holding time distributions increases as the mobility increases, however, it is just the opposite for the expected effective call holding time of an incomplete call.
• The expected effective call holding time of a complete call is smaller than the absolute expected call holding time (the ideal case when there is no blocking and no forced termination), i.e., while the expected effective call holding time of an incomplete call can be larger than the absolute expected call holding time for ideal case, for example, for hyper-exponentially distributed call holding times for low mobility. This seems to be counter-intuitive. One can give the following explanation, however: an incomplete call most likely goes through many handoffs; hence, only “long” calls to be dropped, therefore, the completion of “short” calls and dropping of “long” calls display the above phenomenon. The phenomenon that the expected effective call holding time for an incomplete call tends to be longer than the expected call holding time was not shown up in our previous study [5]. In fact, for the case when call holding times are exponentially distributed, we have shown [5] analytically that the expected effective call holding times for both a complete call and an incomplete call are shorter than those of the ideal case.
VI. CONCLUSIONS
Previous performance studies of PCS channel allocation as-sumed that the call holding times are exponentially distributed. While this assumption is justified for existing cellular systems, future PCS systems will provide new types of services that will affect the calling behavior of the users. Thus, a more general distribution is desirable to model the call holding times. In this paper, we use a general distribution to model the call holding times and derive general formulas for the call completion probability (hence, call dropping probability) and the expected effective call holding times of both complete and incomplete calls. For Gamma, (staged) Erlang, hyperexponential and hyper-Erlang call holding time distributions, we obtain easy-to-compute formulas to compute these quantities. These results can be expected to become significant in evaluating and tuning PCS network performance and help in designing new billing rate programs for these networks.
APPENDIX
Proof of Lemma 1: If is not an integer, then is a branch point of the integrand [14]. Let us cut the complex plane on the real axis from right to the as shown in Fig. 7, where
and In the domain enclosed by the
contour
the function is analytic, hence, from the residue theorem [14] we have
from which we obtain
(61)
Since we have
On the line while on
From (61), by letting we obtain
letting
Fig. 7. The integration contour and branching cut.
REFERENCES [1] Bellcore, private communications, 1995.
[2] D. C. Cox, “Wireless personal communications: What is it?,” IEEE Personal Comm. Mag., pp. 20–35, Apr. 1995.
[3] ETSI, Digital European telecommunications services and facilities re-quirements specification, Tech. Rep. ETSI DI/RES 3002, Eur. Telecom-mun. Standards Inst., 1991.
[4] D. E. Everitt, “Traffic engineering of the radio interface for cellu-lar mobile networks,” Proc. IEEE, vol. 82, no. 9, pp. 1371–1382, 1994.
[5] Y. Fang, I. Chlamtac, and Y. B. Lin, “Call performance of a PCS network,” IEEE J. Select. Areas Commun., to be published.
[6] R. A. Guerin, “Channel occupancy time distribution in a cellular radio system,” IEEE Trans. Veh. Technol., vol. 35, pp. 89–99, Aug. 1987. [7] N. A. J. Hastings and J. B. Peacock, Statistical Distributions. New
York: Wiley, 1975.
[8] D. Hong and S. S. Rappaport, “Traffic model and performance analysis for cellular mobile radio telephone systems with prioritized and non-prioritized handoff procedures,” IEEE Trans. Veh. Technol., vol. 35, pp. 77–92, Aug. 1986.
[9] N. L. Johnson, Continuous Univariate Distributions. New York: Wiley, 1970, vol. 1.
[10] I. Katzela and M. Naghshineh, “Channel assignment schemes for cellular mobile telecommunication systems: A comprehensive survey,” IEEE Personal Commun., vol. 3, no. 3, pp. 10–31, June 1996.
[11] F. P. Kelly, Reversibility and Stochastic Networks. New York: Wiley, 1979.
[12] L. Kleinrock, Queueing Systems: Theory. New York Wiley, 1975, vol. 1.
[13] W. C. Y. Lee, Mobile Cellular Telecommunications: Analog and Digital Systems, 2nd ed. New York: McGraw-Hill, 1995.
[14] W. R. LePage, Complex Variables and the Laplace Transform for Engineers. New York: Dover, 1980.
[15] Y. B. Lin and I. Chlamtac, “Effective call holding times for a PCS network,” submitted for publication; also available from http://liny.csie.nctu.edu.tw/.
[16] Y. B. Lin, S. Mohan, and A. Noerpel, “Queueing priority channel assignment strategies for handoff and initial access for a PCS network,” IEEE Trans. Veh. Technol., vol. 43, pp. 704–712, Aug. 1994. [17] Y. B. Lin, A. Noerpel, and D. Harasty, “The subrating channel
assign-ment strategy for PCS handoffs,” IEEE Trans. Veh. Technol., vol. 45, Feb. 1996.
[18] S. Nanda, “Teletraffic models for urban and suburban microcells: Cell sizes and handoff rates,” IEEE Trans. Veh. Technol., vol. 42, pp. 673–682, Nov. 1993.
[19] A. R. Noerpel, Y. B. Lin, and H. Sherry, “PACS: Personal access communications system—A tutorial,” IEEE Personal Commun., vol. 3, no. 3, pp. 32–43, June 1996.
[20] J. E. Padgett, C. G. Gunther, and T. Hattori, “Overview of wireless personal communications,” IEEE Commun. Mag., pp. 28–41, Jan. 1995. [21] K. Pahlavan and A. H. Levesque, Wireless Information Networks. New
York: Wiley, 1995.
[22] S. S. Rappaport, “Blocking, handoff, and traffic performance for cellular communication systems with mixed platforms,” Proc. Inst. Elect. Eng., vol. 140, pt. I, no. 5, pp. 389–401, 1993.
[23] S. S. Rappaport and C. Purzynski, “Prioritized resource assignment for mobile cellular communication systems with mixed services and platform types,” IEEE Trans. Veh. Technol., vol. 45, pp. 443–458, Aug. 1996.
[24] R. Steedman, “The common air interface MPT 1375,” in Cordless Telecommunications in Europe, W. H. W. Tuttlebee, Ed. New York: Springer-Verlag, 1990.
[25] S. Tekinay and B. Jabbari, “A measurement-based prioritization scheme for handovers in mobile cellular networks,” IEEE J. Select. Areas Commun., vol. 10, no. 8, pp. 1343–1350, 1992.
[26] W. C. Wong, “Packet reservation multiple access in a metropolitan microcellular radio environment,” IEEE J. Select. Areas Commun., vol. 11, no. 6, pp. 918–925, 1993.
[27] T.-S. P. Yum and K. L. Yeung, “Blocking and handoff performance analysis of directed retry in cellular mobile systems,” IEEE Trans. Veh. Technol., vol. 44, pp. 645–650, Aug. 1995.
Yuguang Fang (S’92–M’94–S’96) received the
B.S. and M.S. degrees in mathematics from Qufu Normal University, Shandong, The People’s Re-public of China, in 1984 and 1987, respectively, the Ph.D. degree in Systems and Control Engineering from Case Western Reserve University, Cleveland, OH, in January 1994, and the Ph.D degree in electrical and computer engineering from Boston University, Boston, MA, in May 1997. Currently, he is a Visiting Assistant Professor in Erik Josson School of Engineering and Computer Science at the University of Texas at Dallas.
From 1987 to 1988, he held research and teaching positions in both the Mathematics Department and the Institute of Automation at Qufu Normal University. From 1989 to 1993, he was a Teaching and Research Assistant in the Department of Systems, Control, and Industrial Engineering at Case Western Reserve University, where he became a Research Associate from January 1994 to May 1994. He held a Postdoctoral Research Associate in the Department of Electrical and Computer Engineering at Boston University from 1994 to 1995. From 1995 to 1997, he was a Resaerch Assistant in the Department of Electrical and Computer Engineering. His research interests include wireless networks and mobile communications, personal communications services (PCS), stochastic and adaptive systems, hybrid systems in integrated communications and controls, robust stability and control, nonlinear dynamical systems, and neural networks.
Imrich Chlamtac (M’86–SM’86–F’93/ACM F’96) received the Ph.D. degree
in computer science from the University of Minnesota (1979), and the B.Sc. and M.Sc. degrees in mathematics awarded with the Highest Distinction.
He currently holds the Distinguished Chair in Telecommunications at the University of Texas at Dallas. He is also President of Boston Communications Networks, a company dealing with research and development of wireless systems and high-speed networks. He is the author of more than 200 papers in refereed journals and conferences, multiple book chapters, and coauthor of Local Networks (Lexington Books, 1981).
Dr. Chlamtac is the founding Editor in Chief of the ACM-URSI-Baltzer Wireless Networks (WINET) and the ACM-Baltzer Mobile Networking and Nomadic Applications (NOMAD) journals, and served on the editorial board of IEEE TRANSACTIONS ONCOMMUNICATIONSand several other journals. He served as the General Chair of several ACM and IEEE conferences and workshops and is the founder of ACM/IEEE MobiCom. He is an IEEE Fellow and an ACM Fellow, and in the past was a Fulbright Scholar and an IEEE, Northern Telecom, and BNR Distinguished Lecturer.
Yi-Bing Lin received the B.S.E.E. degree from
National Cheng Kung University in 1983, and the Ph.D. degree in computer science from the Univer-sity of Washington in 1990.
From 1990 to 1995, he was with the Applied Research Area at Bell Communications Research (Bellcore), Morristown, NJ. In 1995, he was ap-pointed as a Professor of Department of Computer Science and Information Engineering (CSIE), Na-tional Chiao Tung University (NCTU). In 1996, he was appointed as Deputy Director of Microelectron-ics and Information Systems Research Center, NCTU. Since 1997, he has been elected as Chairman of CSIE, NCTU. His current research interests include design and analysis of personal communications services network, mobile computing, distributed simulation, and performance modeling.
Dr. Lin is a subject area editor of the Journal of Parallel and Distributed Computing, an associate editor of the International Journal of Computer Simulation, an associate editor of IEEE NETWORKS, an associate editor of SIMULATION magazine, an area editor of ACM Mobile Computing and Communication Review, a columnist of ACM Simulation Digest, a member of the editorial boards of International Journal of Communications Systems, ACM/Baltzer Wireless Networks, and Computer Simulation Modeling and Analysis, Program Chair for the 8th Workshop on Distributed and Parallel Simulation, General Chair for the 9th Workshop on Distributed and Parallel Simulation. Program Chair for the 2nd International Mobile Computing Conference, the publicity chair of ACM Sigmobile, Guest Editor for the ACM/Baltzer MONET special issue on Personal Communications, and Guest Editor for IEEE TRANSACTIONS ON COMPUTERS special issue on Mobile Computing.