Constructing a fuzzy model from wavelet transforms

Constructing a Fuzzy Model from Wavelet Transforms

Chum-Kai Lin and Sheng-De Wang

EE Building, Room 441, Department of Electrical Engineering, National Taiwan University, 1 Roosevelt Rd., Sec. 4

Taipei 106, Taiwan

An approach using wavelet transforms to construct a fuzzy model is proposed. This paper shows that a fuzzy inference system with some minor restrictions and modifications can function as a discrete wavelet transform. In the proposed fuzzy inference system, each fuzzy rule is analogous to a wavelet basis function multiplied by a coefficient. Due to the functional equivalence between wavelet transforms and fuzzy inference systems, the fuzzy inference system can share the advantages of wavelet transforms.

1. Introduction

Wavelet theory has advantages over Fourier transforms in analyzing physical situations where the signal contains discontinuities and high frequency components. Wavelets have successfully applied to many fields including image processing, subband coding, acoustics, radar and mathematics applications [8].

Control engineers often face the problems of controlling and modeling systems which are so complex and nonlinear as very difficult to obtain. Fuzzy models have provided a good solution to overcome this problem. However, fuzzy systems require formal synthesis techniques that guarantee the global stability and acceptable performance [3]. In this paper, we hope to show that fuzzy models with some restrictions and modifications can be functionally equivalent to discrete wavelet transforms. Therefore, the fuzzy models can not only offer a framework for combining linguistic information and numerical data in a unified fashion but also take advantages of the rigorous approximation theory of wavelet basis function

expmgiong. SO far as w e know, this is the first article tu discuss the relationship

between fuzzy models and wavelet transforms. Hence, both the application domain of wavelet transforms and the performance of fuzzy models can be promoted.

In order to benefit from the discrete wavelet transform, we modify the general fuzzy models, the Takagi-Sugeno’s model [ 11 and fuzzy basis function expansions [3], such that each fuzzy rule can be viewed as a wavelet basis function multiplied by a real coefficient. The firing strength of the proposed fuzzy model is the fuzzy basis function and the THEN part of each fuzzy rule is a function of premise variables. Furthermore, we use multiple fuzzy rule bases to achieve multiresolution learning. A denser fuzzy rule base would correspond to a higher resolution wavelet h c t i o n , which is suitable to model a given dense data range.

multidimensional wavelet frames. The architecture of a fuzzy model which is functionally equivalent to the discrete wavelet transform is presented in section 3. Section 4 then concludes the paper.

2. Discrete Wavelet Trnsforms

Given a function y E L2( R" )

,

consider the sequence functions {Y,,~} generated by dilating and translating mother wavelet function

y

in the following form

y,,,(x)= detD:/2y(Djx-A,k), (2.1)

where j = [ j l a - . jnIr E T , k~Zn,thedilationmatrix 0, =diag(a'i,..-,a'-), the translation matrix A k = diag(b,,...,b,), a>l, a E R , b = (b,,...,b,) ER"

.

Conditions on y , a and b to guarantee that a multiscaling wavelet frame for

L 2 ( R " ) has been obtained and are given in [ll]. In other words, to construct a multidimensional wavelet function is to find a wavelet function that satisfies the sufficient conditions. Thus, let the multidimensional wavelet functions be the generalizations of one-dimensional wavelet functions, i.e.,

That is, applying one-dimensional wavelet transform separately in each of n orthogonal directions, we have

where @ ; ( m i ) is the Fourier transform of y j ( x j ) , which must satisfy the admissibility condition

For a given function y (x, ) with adequate decay at infinite, (2.4) is equivalent that each

v , ( x i )

has zero mean (jv,(x,)dy, = 0 ) [lo]. In this paper, the sequence functions {y,,,} are a set of wavelet basis functions to constitute a frame for a class

of functions

f

E L 2 ( R " ) to be approximated; i.e., there exist two constants A>O and B<w, such that

Then, due to the dual frame property, the function f E L ' ( R " ) can be approximated by

where the dual frame has the relation @ J , k = A-'y/

,

,

in the tight frame case (A=B>l) and the coefficients c,+ =< f ,

pJ,k

>

.

Therefore, f can be reconstructed by the expansion of {v/ ,,,} exactly.

A family of wavelets including the Battle-Lemarie wavelets, Meyer wavelets, the Haar wavelets with compact support are constructed by Daubechies [ 6 ] . In this paper, the mother wavelets are of the form

w ,

(x, ) = g(x, ) e - a ~ x : / Z , (2.7)

where g ( x i ) is a h c t i o n satisfmg

I

= 0

.

If the function g ( x i ) is a i (1 -six,*) then

v i

( x i ) is the so called 'Mexican Hat' mother wavelet function. Substituting the 'Mexican Hat' mother wavelet function into (2.1) and (2.2) yields

Equation (2.8) illustrates a way to constitute a set of wavelet basis functions with multiresolution to form a multiscaling frame.

3. Functional Equivalence Between Wavelet Transforms and Fuzzy Models

The fuzzy model proposed by Takagi and Sugeno, which is described by fuzzy IF- THEN rules, is of the following form:

-

-

Rule m: IF

x,

is A,, and

...

and

x,

is Amn THEN y = dm0

+

d , l ~ I + ~ ~ . + d , , ~ , ,(3.1)

-

-where A,,

,

A,,

,

...

and

A,"

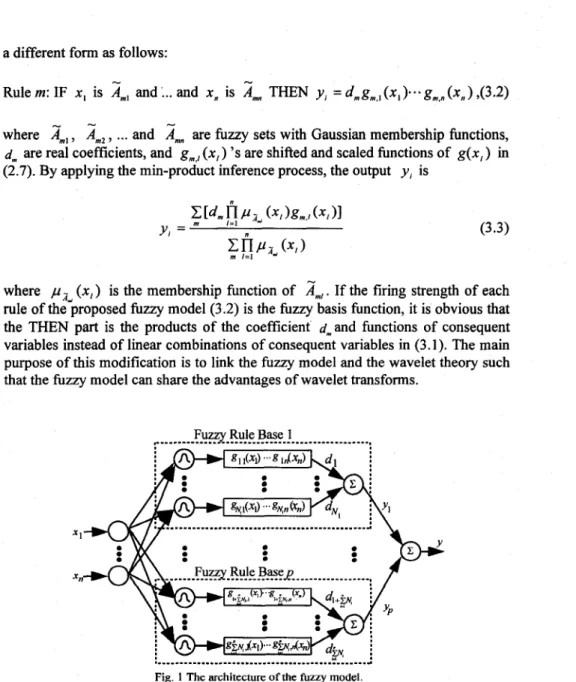
are fuzzy sets, y is the output, and x = [x, x,IT is the input state vector. The THEN part of Takagi-Sugeno's fuzzy model is a linear combination of premise variables to represent local linear input-output relationship of nonlinear systems. A fuzzy model proposed in this paper as shown in Fig. 1 has

a different form as follows:

-

-

Rulem: IF x, is A,,,, and:.. and x, is A,,," THEN yi =d,gm,,(x,)...g,,"(x,),(3.2) where

J,,,,

,

I,,,

...

and

Zn,"

are

fuzzy

sets with Gaussian membership functions,

d, are real coefficients, and gm,, (x,) 's are shifted and scaled functions of g(x,) in (2.7). By applying the min-product inference process, the output y i is

where p Z d (x,) is the membership function of

z,,,,

.

If the firing strength of each rule of the proposed fuzzy model (3.2) is the fuzzy basis function, it is obvious that the THEN part is the products of the coefficient d,and functions of consequent variables instead of linear combinations of consequent variables in (3.1). The main purpose of this modification is to link the

fuzzy

model and the wavelet theory such that the fuzzy model can share the advantages of wavelet transforms.

0

t

Fig. 1 The architecture of the fuzzy model.

Besides the modification of THEN part of fuzzy rules, the fuzzy rule base is implemented by multiple

fuzzy

rule bases corresponding to the multiresolution wavelet functions. A sparse fuzzy rule base is analogous to the low resolution

wavelet basis function. For obtaining accurate approximation, more than one fuzzy rule base is required. Furthermore, assume the centers of membership functions of linguistic terms are equally spaced. For a given resolution j = [ j , a - . j,]' , the

centers of fuzzy basis functions are located in lattice points in

R".

Denoting a sequence of basis vectors for the lattice as {.21,....2,,>, the lattice points can be represented by

where a"b, is the sampling space in i-th dimension. Form the view point of geometry, each lattice point is a fuzzy basis function

4

j,k :

where Wj = diug{a, l(u")';..,a, l ( u ' - ) ' > . Hence, the output of each fuzzy rule base is of the form:

where

v ~ , ~

= g l , k , l ( x l ) - * - g l , k , n ( x " ) $ ~ , ~ and dj,k are real coefficients. For example, it is analogous to 'Mexican Hat' wavelet basis functions, (2.8), by taking the form gl,k,,(x,) = ~ - " a , [ l - a , ( u - ~ ' x , - b , k , ) ' ] . Applying the proposed fuzzy model to approximate function

f,

we have

Therefore, it is easily to show the equivalent functional behavior of the multiresolution wavelet transform and the proposed fuzzy model.

The update law for tuning coefficients, dJ,k

,

in (3.7) can use existing methods such as LMS, Kalman filter algorithms, and the back-propagation law. The fuzzy model may consist of two parts: one is rules extracted from experts and the other is

the rules learned from numerical data as described above.

This paper presents a fuzzy model with some modifications which can function equivalently to discrete wavelet transforms. Therefore, not only the experts’ knowledge but also the numerical data can be used to train the fuzzy model. Furthermore, the pivotal concept of multiple fuzzy rule bases derived from multiresolution wavelets improves the approximation accuracy. One of our future work is to apply the proposed fuzzy model to the function approximation, system identification and control.

References

T. Takagi and M. Sugeno, Fuzzy identification of systems and its applications to modeling and control, IEEE Trans. Systems Man Cybernet. 15 (1985) 116- 132.

M. Sugeno and K. Tanaka, Successive identification of a fuzzy model and its application to prediction of a complex system, IEEE Trans. Systems Man Cybernt. 42 (1991) 315-334.

L. X. Wang, Stable adaptive fuzzy control of nonlinear systems, IEEE Trans.

Fuzzy Systems 1 (1993) 146-155.

J.-S.

R.

Jang and C.-T. Sun, Functional equivalence between radial basis function networks and fuzzy inference systems, IEEE Trans. Neural Networks 4 (1993) 156-158.

B.

R. Bakshi and G. Stephanopoulos, Wave-net: A multiresolution, hierarchical neural network with localized learning, AZCHE

J.

39 (1993) 57- 81.

I. Daubechies, Orthonormal bases of compactly supported wavelets, Comm. in Pure and Applied Math. 41 (1988) 909-996.

I. Daubechies, The wavelet transform, time-frequency localization and signal analysis, IEEE Trans. Informat. Theory 36 (1 990) 96 1

-

1005.

S. G. Mallat, A theory for multiresolution signal decomposition: The wavelet representation, IEEE Trans. Patt. Anal. Mach. Intell. 11 (1989) 674-693. Q. Zhang and A. Benveniste, Wavelet networks, IEEE Trans. Neural Networks 3 (1992) 889-898.

Y. C. Pati and P. S. Krishnaprasad, Analysis and synthesis of feedforward neural networks using discrete affine wavelet transformations, ZEEE Trans. Neural Networks 4 (1993) 73-85.

T. Kugarajah and Q. Zhang, Multidimensional wavelet frames, IEEE Trans. Neural Networks 6 (1 995) 1552- 1556.