On-line Computation for the Euclidean P-Median Problems
全文
(2) to optimize the total cost at individual steps, the main overall strategy is to avoid outrageously unacceptable solutions at any step for all possible given data. One frequently-used measure for the overall performance of on-line algorithms is a quantity called competitive ratio. Roughly, it is defined as an upper bound on the ratio of the optimal solution for current step over the non-on-line optimal solution for all the steps up to and including the current step. Several related on-line problems have been studied in the literature. In the on-line assignment problem [1], the number and locations of the facilities are known in advance and the demand points appear one after another in steps. The problem is to assign each demand point to an appropriate facility immediately in a manner that will balance the load on the facilities. It has been proved that the general greedy algorithm has the best possible competitive ratio that can be achieved by any deterministic on-line algorithm. Another related on-line k-server problem [13] is to plan the motion of k mobile facilities such that the total distance moved by the facilities (the facilities must move to the demand point for providing the service) is minimized. Also, the demand points appear one after another and the service must be provided immediately. In this paper, an algorithm is proposed for solving the on-line version of the Euclidean pmedian problem. To the best of our knowledge, this is the first on-line algorithm for this problem. Our algorithm has a competitive ratio 2n. In general, a competitive ratio of O(n) cannot be considered as a good result. However, at this state of the arts, the best results of most of the on-line algorithms for many other problems are at this order of performance. For example, the best possible competitive ratio for the on-line directed Steiner tree problem is n [17]. Furthermore, in this paper, we will show that a greedy algorithm cannot even achieve a finite competitive ratio for this problem.. Formal Presentation of Problems: The locations of a given a set D of n demand points with weights {ω1,…, ωn} are fixed in the Euclidean plane. The locations of a set of p facilities, where p < n, are to be determined. The off-line and on-line Euclidean k-median problems (k ≤ p) can be formally described as follows: Problem OFF-LINE(k, D): Determine simultaneously the locations of the k facilities and allocate each of the demand points to one and only one of these k facilities in such a n way such that the total cost opt(k) = ∑ j =1 ω j l kj is minimum, where l kj is the Euclidean distance between ω j and its nearest facility. Problem ON-LINE(k, D): At step k, assume that problem ON-LINE(k - 1, D) has been solved. Determine the location of a new facility k and reallocate some of the demand points to facility k so that c(k) is minimum, n where c(k) = ∑ j =1ω j l kj and l kj is the Euclidean distance between ω j and its nearest facility. Notations (In the following, index k is for step, i is for facility and j is for demand point): ωj:. the weight of demand point j. When there is no confusion, we also refer ω j as demand point j.. l je :. fixed distance between demand point j and demand point e. Note that lej = l je .. opt(k): optimal solution value of OFF-LINE(k, D). oik :. location of facility i in the optimal solution for OFF-LINE(k, D).. l kj :. distance between demand point j and its closest facility in the optimal solution for OFF-LINE(k, D)..
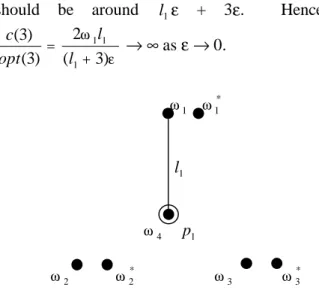
(3) Gik :. nik :. the group of demand points allocated to facility i in the optimal solution for OFFLINE(k, D). the number of demand points in group Gik .. opt( Gik ): cost of group Gik based on the optimal solution for OFF-LINE(k, D). Note that opt(k) = opt( G1k )+opt( G2k )+…+ opt( Gkk ). c(k):. total cost for ON-LINE(k, D), i.e., c(k) = n ∑ j =1ω j l kj .. c( ω j ): cost of ω j based on the solution for ONLINE(k, D), i.e., the weighted distance between ω j and its closest facility in the solution for ON-LINE(k, D). Note that c( ω j ) ≤ ω j lij for any i. c(X): cost of the set of demand points X based on the solution for ON-LINE(k, D), i.e., ∑ω ∈X c(ω j ) . j. 2 ON-LINE ALGORITHMS To show that our algorithm is non-trivial, let us first solve ON-LINE(k, D) by adopting a greedy strategy widely used for solving many other problems). The main idea of a greedy algorithm is to reduce as much as possible the sum of weighted distances at each step from of the previous step. Algorithm GREEDY for solving problem ON-LINE(k, D) Input:. A set D of n demand points and k - 1 facilities which have been located already. Output: The location of the new facility k and the reallocation of demand points. Method: Locate the new facility k and reallocate the n demand points in such a manner that c(k) is minimized. (Note: Any method (e.g., Drezner [7]) achieving this goal can be used.). Definition 1 The competitive ratio ρ of an online algorithm is an upper bound on the ratio between the on-line solution value and the optimal off-line solution value over all steps and for all possible weights and distributions of the demand points. That is, for any weights and distribution of the demand points and 1 ≤ k ≤ p, c(k ) ≤ρ .. For many other on-line problems [1, 8, 9, 10, 15, 17], a greedy algorithm has the best possible competitive ratio. For ON-LINE(p, D), however, the following observation and example confirm that this is indeed not the case.. opt(k ). Observation: Algorithm GREEDY for solving ON-LINE(p, D) has no finite competitive ratio.. We emphasize the fact that the bound spreads over all steps of the solution process. The following lemma was proved in [6] and will be used later in this paper.. Example: Figure 1 illustrates our observation. Consider 7 demand points whose weights satisfy: ω 1 = ω 1* = ω 2 = ω 2* = ω 3 = ω 3* >> ω 4 =ε. The. Lemma 1 Let {( G1k , o1k ),…, ( Gkk , okk )} be the optimal solution for OFF-LINE(k, D), where D = G1k ∪ ... ∪ Gkk and the demand points in Gik are assigned to the facility located at oik for i = 1,…, k. For any k′ , where 1 ≤ k ′ ≤ k, let D′ be the union of any k′ of the k groups. That is, without loss of generality, D ′ = G1k ∪ ... ∪ Gkk′ . Then, {( G1k , o1k ),…, ( Gkk′ , okk′ )} is an optimal solution for OFF-LINE(k', D').. distance between ω 1 and ω 1* , ω 2 and ω 2* and ω 3 and ω 3* are all ε. : ω 1 , ω 2 , ω 3 are at the vertices of an equilateral triangle and ω 4 is at its center. Obviously, Algorithm GREEDY will locate facility 1 at ω 4 since this is the optimal location for OFF-LINE(l, D). Then, no matter where the facilities are located in the next two steps, the total cost c(3) at step 3 is at least 2 ω 1l1 . However, the optimal solution for OFFLINE(3, D) is to locate the 3 facilities at the three vertices separately and the optimal value.
(4) should be around l1 ε + 3ε. 2ω 1l1 c(3) = → ∞ as ε → 0. opt (3) (l1 + 3)ε. Hence,. *. ω1. ω1. l1. ω4. p1. *. ω2. ω2. *. ω3. ω3. Figure 1. For explaining Observation.. The above example shows that, if we place a facility with the aim of minimizing the sum of the weighted distances of the demand points at a certain step, we run the risk of providing a very bad result at some future steps. The main strategy of on-line algorithms is to avoid such a possibility. Our algorithm Algorithm MWD follows a similar strategy. The main idea is, at each step, to locate the new facility at a demand point which has the biggest weighted distance to its closest existing facility. Computationally, Algorithm MWD is relatively simple. The difficulty lies in proving that it has a finite performance ratio as stated in the Theorem 2. o l11 l 1j ω1. l1 j ω. j. Figure 2. For proving Theorem 2 in the case p=1.. Algorithm MWD (Maximum Weighted Distance) for problem ON-LINE(p, D) Input: A set D of fixed demand points with weights { ω 1 ,...,ω n }. Output: The locations of k facilities and the allocation of the n demand points. Method: 1. For k = 1, locate the first facility at the demand point with maximum weight, say ω 1 . Allocate all demand points to this facility. 2. For 1 < k ≤ p, without loss of generality, suppose the first k - 1 facilities are located at the demand points ω 1 ,...,ω k −1 when solving ON-LINE(i, D), i = 1, 2,..., k - 1. (a) For j = k,..., n, let d( ω j ) be the weighted distance between ω j and its closest facility located at one of the points in the set {ω 1 ,...,ω i − 1 }, i.e., d( ω j ) = ω j ⋅ min 1≤ e≤ k −1 (l je ) . (b) Locate the new facility k at the demand point ω j whose d( ω j ) is maximum over k ≤ j ≤ n. Without loss of generality, let this demand point be ω k . (c) Reallocate those demand points to ω k if ω k is the facility closest to them. Theorem 2 Let c(k) be the solution value obtained by Algorithm MWD for ON-LINE(k, D) and opt(k) be the optimal solution value for c(k ) OFF-LINE(k, D). Then, ≤ 2n for 1 ≤ k ≤ opt (k ) p and any possible weights and distribution of the demand points. Proof. We will apply mathematical induction on p. Figure 2 illustrates the case p = 1. Without loss of generality, let o be the optimal location of the facility for OFF-LINE(l, D) and ω 1 be the demand point with maximum weight. Algorithm MWD locates the first facility at ω 1 . The solution value c(1) is.
(5) n. n. c(1) =. ∑ (ω j ⋅ l1 j ) ≤ ∑ ω j (l. 1 1. j= 2. +l. 1 j. for OFF-LINE(k-1, D′). That is,. ). j= 2. =. n. ≤. (∑ ω l ) + (n − 2) 1 j j. 1 ω1 1. 2) l ≤ 2n ⋅ opt (1). cases: | Gkk ∩Ψ| = 1 and | Gkk ∩Ψ| ≥ 2. Case 1, where | Gkk ∩ Ψ| = 1: Consider the new p-median problem over the set D′ of demand points, where D′ = D\ Gkk = G1k G2k ∪ ... ∪ Gkk− 1 . Let c′(k - 1) be the solution value obtained by Algorithm MWD for ONLINE(k - 1, D′) and opt'(k - 1) be the optimal solution value for OFF-LINE(k – 1, D′). Then, since Theorem 2 is true for p = k - 1, we have ∪. c′(k - 1) ≤ 2( n − n kk ) ⋅ opt′(k - 1). (2). ωe. l ke ωk. l kh. l jh. l jk ω. ∑ i 1 opt(G ) . This is the same as =. opt′(k - 1) = opt(k) – opt( Gkk ). 1 ω1 1. Assume that Theorem 2 is true for p = k - 1. That is, Theorem 2 is true for any problem with at most k - 1 facilities and any weights and distribution and number of demand points. We shall prove Theorem 2 for p = k. Let Ψ = { ω 1 ,...,ω k − 1 ,ω k } be the sequence of demand points where the first k facilities are located in the first k steps. Without loss of generality, let k ω k ∈ Gk . Theorem 2 will be proved in two. ωh. =. k i. (1). l. j=1. = opt (1) + ( n −. k−1. k −1. k ∑ i 1 opt′(Gi ). l kk. (3). Since Gkk ∩Ψ = { ω k }, ω k is the only element in Ψ removed together with Gkk . Next, we are going to show that Ψ′ = Ψ\{ ω k } ={ ω 1 ,…, ω k − 1 } is the sequence of locations obtained by Algorithm M for the first k - 1 facilities for ONLINE(k - 1, D′). According to Algorithm MWD, since ω 1 is maximum over D and D′ ⊂ D, ω 1 is also maximum over D′. That is, the first facility will be located at ω 1 when solving ON-LINE(k –1, D′). Again, according to Algorithm MWD, the second facility will also be located at a demand point with maximum weighted distance to ω 1 over D′. Since ω 2 has the maximum weighted distance to ω 1 over D (note that the second facility for ON-LINE(k, D) is located at ω 2 ) and D′ ⊂ D, obviously the second facility for ON-LINE(k - 1, D′) will also be located at ω 2 . By similar argument, we can prove that, for ON-LINE(k - 1, D′), Algorithm MWD locates the facilities at the sequence Ψ′. Next, we consider the total allocation cost for the demand points in D′ for two cases. In the first case, Ψ′ is the locations of the first k-1 facilities for ON-LINE(k - 1, D′) with total cost c′(k - 1). In the second case, Ψ is the locations for the first k facilities for ON-LINE(k, D′) (the total cost is denoted as c(k, D')). Since Ψ contains one more facility than Ψ′ for allocation purpose, we have c(k, D') ≤ c’(k - 1). This is the same as. j. l kj. k −1. okk. k ∑ c(Gi ) ≤ c ′(k − 1). (4). i =1. Case where | Gkk ∩ Ψ| = 1 Figure 3.a. Illustration of Theorem 2 when p = k. By Lemma 1, if {( G1k , o1k ),…, ( Gkk , okk )} is an optimal solution for OFF-LINE(k, D), then {( G1k , o1k ),…,( Gkk− 1 , okk− 1 )} is an optimal solution. By Inequalities 2, 3 and 4, we have k−1. k k k ∑ c(Gi ) ≤ 2(n − nk )(opt(k ) − opt(Gk )) i =1. (5).
(6) Next, we try to prove c(Gkk ) ≤ 2n kk opt (G kk ) .. Case where G kk ∩ Ψ ≥ 2 :. According to Algorithm MWD, we have. Without loss of generality, let Gkk ∩ Ψ = {ω g ,...,. ω. l ≤ ω k l ke. (6). j jh. ω. k. } , where g < k. Since there are k groups, at. least one of the groups, say G kf , does not contain any element of Ψ, i.e., G kf ∩ Ψ = φ .. where l ke = min i≤ k −1 l ki and l jh = min i ≤ k −1 l ji. ωh. Consider those ω j ∈ Gkk . (Note that ω k ∈ G kk ).. l jh ω. k k. c(ω j ) ≤ ω j l jk ≤ ω j (l + l ) ≤ω. l kd. l + ω j l kk ≤ opt (G kk ). l kj. If ω k ≤ ω j , we consider c( ω j ) for two subcases.. ≤ω. ≤. 2ω k (l kj. ≤. 2 opt (G kk ). +. l. k ke. ≤ω. l. k kh. l kk ) ≤ 2ω j l kj. ≤. 2ω k l jk. +. 2ω k l kk. lkk o kf. l jh ≤ l jk , we have. l kh ≤ l jk + l jh ≤ 2l jk . By Inequality 6, we get c (ω j ) ≤ ω j l jh. l gk. ωk. j. ω. g. (7). k j j. In the subcase where. d. l gd. If ω j ≤ ω k , then (Figure 3.a) k j. ω. l gk okk. Case where | Gkk ∩ Ψ| ≥2 Figure 3.b. Illustration of Theorem 2 when p = k. (8). By Inequality 2, Lemma 1 and similar argument as with Inequality 5, we have k. In the subcase where l jk ≤ l jh , we have l kh ≤ 2l jh . By Inequality 6, we have ω. l ≤ ω k l kh and ω j ≤ 2ω k .. 2n kf opt (Gkk ) . In Figure 3, let l jh = min i< k l ji ,. For similar reasons as with Inequality 7, we have c(ω j ) ≤ 2opt (G ) . By Inequalities 7, 8 and 9, we have c(Gkk ) =. ∑. i = 1,i ≠ f. Next, we try to prove the inequality c (G kf ) ≤. j jh. k k. k k k ∑ c(Gi ) ≤ 2(n − n f )(opt(k ) − opt(G f )). (9). l ke = min i< k l ki and l kd = min i< g l ki . Obviously, d < g. Consider those ω j ∈ G kf . In case ω k ≤ ω g , we have c(ω j ) = ω i l jh ≤ ω k l ke ≤ ω k l kg k. k ω j ∈ Gk. ≤ ω k (l k +. c(ω j ) ≤ 2n kk opt (Gkk ) .. Adding this to Inequality 5, we have c(k ) ≤ 2n ⋅ opt (k ) .. ≤. l gk ) ≤ ω k l kk + ω g l gk. (10). opt (G kk ). In case ω g ≤ ω k , we consider c (ω j ) for two subcases. In the subcase where l kg ≤ l kd , since ω k l kd ≤ ω ω k ≤ 2ω. g. l. g gd. .. and By. ωk ω. g. similar. =. l gd l kd. ≤. 2 , we have. argument. as. for. Inequality 10, we have c(ω j ) ≤ 2opt (Gkk ) . In.
(7) the subcase where l kd ≤ l kg , we have l gd ≤ 2l kg . Hence, by Algorithm MWD, we get. [5]. c(ω j ) = ω j l jh ≤ ω k l ke ≤ ω k l kd ≤ ω g l gd ≤. 2ω g l kg ≤ 2ω g (l kk + l kg ). ≤ 2ω. [6]. k g k. l + 2ω g l gk ≤ 2opt (Gkk ). For similar reasons as in the case G kk ∩ Ψ = 1 ,. [7]. we get c(k ) ≤ 2n ⋅ opt (k ) . 3. Conclusion and Future Research We have proposed an on-line algorithm with competitive ration 2n for solving the p-medium problem where the facilities are provided one after another and the demand points are fixed. Though, as far as we know, it is the only available on-line algorithm for solving this problem and the competitive ratio is at the same order as the on-line algorithms for many other problems, we believe that it can be further improved. There is the need for further research for several cases, such as the case where new facilities can be added and existing facilities can be deleted, the case where the demand points can be increased or decreased at various steps, etc. Acknowledgement - We would like to thank Dr. Xiaotie Deng for useful discussion. Research supported financially by Research Grants Council of Hong Kong under Grant RGC CityU 1133/99E.. [8]. [9]. [10]. [11]. [12]. [13]. [14]. REFERENCES [1]. [2]. [3] [4]. Y. Azar, J. Naor and R. Rom, The competitiveness of on-line assignments, Journal of Algorithms 10, 221-237, 1995. I.Bongartz, P.H. Calamai and A.R. Conn, A projection method for lp norm locationallocation problems. Mathematical Programming 66, 283-312, 1994. L. Cooper, Location-allocation problems. Operations Research 11, 331-343, 1963. R. Chen, Solution of minisum and minimax location-allocation problems with. [15]. [16]. [17]. Euclidean distances. Naval Research Logistic 30, 449-459, 1983. P. Crescenzi and V. Kann, A compendium of NP optimization problems, Manuscript 1995. Z. Dai and T.Y. Cheung, A new heuristic approach for the Euclidean p-median problem. Journal of the Operational Research Society 48, 950-960, 1997. Z. Drezner, On the conditional p-median problem, Computer and Operations Research 22, 525-530, 1995. J.A. Garay, I.S. Gopal, S. Kutten, Y. Mansour and M. Yung, Efficient on-line call control algorithms, Journal of Algorithms, 23, 180-194, 1997. M. Imase and B. M. Waxman, Dynamic Steiner tree problems, SIAM Journal on Discrete Mathematics 3, 369-384, 1991. B. Kalyaiiasundaram and K. Pruhs, On-line weighted matching, Journal of Algorithms 14, 478-488, 1993. R. F. Love and H. Juel, Properties and solution methods for large locationallocation problems. Journal of Operational Research Society 33, 443-452, 1982. C. Liu, R. Kao and A. Wang, Solving location-allocation problems with rectilinear distances by simulated annealing. Journal of the Operational Research Society 45, 1304-1315, 1994. M. S. Manasse, L. A. McGeoch and D.D. Sleator, Competitive algorithms for server problems, Journal of Algorithms 11, 208230, 1990. F. Maffioli and G. Righini, An annealing approach to multi-facility location problems in Euclidean space. Location Science 2, 205-222, 1994. R. Motwani, V. Saraswat and E. Torng, On-line scheduling with look ahead: multipass assembly lines, Technical Report of Stanford University, 1997. K. E. Rosing, An optimal method for solving the (generalized) multi-weber problem. European Journal of Operational Research 58, 414-426, 1992. J. Westbrook and D. Yan, Linear bounds for on-line Steiner problems, Information Processing Letters 55, 59-63, 1995..
(8)
數據
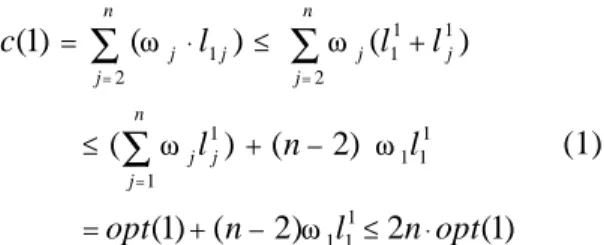

相關文件
In this paper, we have shown that how to construct complementarity functions for the circular cone complementarity problem, and have proposed four classes of merit func- tions for
In section 4, based on the cases of circular cone eigenvalue optimization problems, we study the corresponding properties of the solutions for p-order cone eigenvalue
Monopolies in synchronous distributed systems (Peleg 1998; Peleg
Corollary 13.3. For, if C is simple and lies in D, the function f is analytic at each point interior to and on C; so we apply the Cauchy-Goursat theorem directly. On the other hand,
Corollary 13.3. For, if C is simple and lies in D, the function f is analytic at each point interior to and on C; so we apply the Cauchy-Goursat theorem directly. On the other hand,
Optim. Humes, The symmetric eigenvalue complementarity problem, Math. Rohn, An algorithm for solving the absolute value equation, Eletron. Seeger and Torki, On eigenvalues induced by
We have also discussed the quadratic Jacobi–Davidson method combined with a nonequivalence deflation technique for slightly damped gyroscopic systems based on a computation of
questions and we are dedicated to are dedicated to are dedicated to are dedicated to future research and development to bring you the future research and development to bring you the