Distributed algorithms for the quickest path problem

North-Holland PARCO 683

Short communication

Distributed algorithms for the quickest

path problem

Yung-Chen Hung and Gen-Huey Chen

Department of Computer Science and Information Engineering, National Taiwan University, Taipei, Taiwan Received 26 March 1991

Revised 30 January 1992

Abstract

Hung, Y.-C. and G.-H. Chen, Distributed algorithms for the quickest path problem, Parallel Computing 18 (1992) 823-834.

Let N = ( V , A, C, L) be a network with node set V, arc set A, positive arc capacity function C, and nonnegative arc lead time function L. The quickest path problem is to find paths in N to transmit a given amount of data such that the transmission time is minimized. In this paper, distributed algorithms are developed for the quickest path problem in an asynchronous communication network. For the one-source quickest path problem, we present three algorithms that require O(rn 2) messages and O(rn 2) time, O(rmn) messages and O(rn) time, and O(rm T M log w) messages and O(rn T M log w) time for any E, 0 <E < 1, respectively, where m -- I A I, n = I Vh r is the number of distinct capacity values of N, and w is the maximal arc weight of N. For the all-pairs quickest path problem, we present an algorithm that requires O(mn) messages and O(m) time.

Keywords. Asynchronous networks; distributed algorithms; quickest path problem.

1. Introduction

An asynchronous network

is a point-to-point (store-and-forward) communication network composed of processors and bidirectional non-interfering communication links. Each proces- sor can be uniquely identified. Local memory is provided for each processor, but no common memory is shared between processors. Hence, processors can communicate with each other only by exchanging messages over the communication links. Each processor processes mes- sages received from its neighbours, performs local computation, and sends messages to its neighbours, all in negligible time. Messages can be transmitted independently in both directions on a communication link and arrive after an unpredictable but finite delay, without Correspondence to: Professor Gen-Huey Chen, Department of Computer Science and Information Engineering, National Taiwan University, Taipei, Taiwan.

0167-8191/92/$05.00 © 1992 - Elsevier Science Publishers B.V. All rights reserved ..

824 Y.-C. Hung, G.-H. Chen

error and in

FIFO (First-In-First-Out)

order. When a message is received by a processor, it is

inserted into a queue that is maintained by the processor to store unprocessed messages. We assume that each message is of fixed length.

When a distributed algorithm is executed in an asynchronous network, some processors may be nominated to perform special roles and to execute special routines for this purpose. Nevertheless, it is assumed that at the start of the algorithm, each processor holds a copy of the entire code.

The performance of distributed algorithms can be measured according to two standards: message complexity and time ct~.mplexity. (In some distributed algorithms, e.g. [3,7], only the message complexity is considered in performance analysis, since in an asynchronous dis- tributed environment the number of messages transmitted is significantly more important

than the number of computation steps performed.) The

message complexity

of a distributed

algorithm is the total number of messages transmitted during its execution. The

::.me

complexity

is the number of 'time units' taken by the algorithm, assuming that the D~'opagation delay of any communication link is at most one unit of time. Since processors in an asynchronous network are far apart, the processing time for each message at a processor is small, in comparison with the message transmission time, and thus is negligible. In this paper, like most distributed algorithms, we only consider the message transmission time.

Let N = (V, A, C, L) be a network with node set V, arc set A, positive arc capacity

function C, and nonnegative arc lead time function L. The

quickest path problem,

which was

originally proposed by Chen and Chin [5], is to find the quickest paths to transmit data in N.

The quickest path problem is a variant of the shortest path problem. The

one-source quickest

path problem (1_ QSP

for short) is to find the quickest paths between one node and all other

nodes. The

all-pairs quickest path problem (A _QSP

for short) is to find the quickest paths

between every pair of nodes. Some centralized (single processor) algorithms have been proposed for the quickest path problem. For the I_QSP, Chen and Chin [5] have presented

an O(m2+

mn

log n) time algorithm, where n and m are the numbers of nodes a n d arcs,

respectively, in N. For the A_QSP, Hung and Chen [8] have prese~fted an O(mn 2) time algorithm.

In this paper, distributed algorithms are presented for the quickest path problem in asynchronous networks. For the I_QSP, we present three algorithms that require O(rn 2)

messages and O(rn 2) time,

O(rmn)

messages and

O(rn)

time, and O(rm' +" log w) messages

and

O(rn I +"

log w) time for any ~, 0 < ¢ < 1, respectively, where r is the number of distinct capacity values of N and w is the maximal arc weight. For the A_QSP, we present an

algorithm that requires

O(mn)

messages and O(m) time.

The rest of this paper is organized as follows. In the next section, we introduce some notations and definitions that are used throughout this paper. The distributed algorithms for the 1_ QSP and the A_ QSP are presented in Section 3 and Section 4, respectively. In Section 5, we conclude this paper with some final remarks.

2. Notations and definitions

Let Nffi (V, A, C, L) be a network, where IVlffin, I A l = m , and G = ( V , A ) is an

undirected graph without self loops and without multiple arcs. Also, let

C(u,

v ) > 0 and

L(u, v)>_ 0

denote the capacity and the lead time, respectively, of an arc (u, v ) c A . More

specifically,

C(u, v)

denotes the maximal amount of data that can be transmitted through arc

(u, v) per unit time, and

L(u, v)

denotes the lead time required to send data through arc

(u, v). Hence, if cr units of data are required to be transmitted through arc (u, v), the

For example, suppose

C(u,

v) = 2 and

L(u,

v) = 3. If 8 units of data are required to be sent from node u to node v, no data reach node tJ during the first 3 time units. Then, at each of subsequent time units, 2 units of data reach node v until the transmission ends. Hence, the total transmission time is 3 + 8 / 2 = 7 time units.

The following notations are used throughout this paper.

L(P)

is the lead time of a path P = (u l, u 2 , . . . , Uk), which is defined as k - 1

L( P) -- E L(u,,

u,+,).

i = 1

C(P)

is the capacity of a path

P = (u l, u2,..., uk),

which is defined as

C(P)

= min

C(ui, ui+l).

l <i <<.k-1

T(P, or)

is the total transmission time to send or units of data through a path P. Clearly,

T(P, or) =L(p) +or/C(P).

QP(s, t, or)

is the quickest path to send t,- units of data between node s and node t in N, which is defined as the path P satisfying

T ( P , or) = min{T(Pi,

or)IVP~= (uil,ui2, .... Uik)

in N,

where s =

Uil

and t - llik } .

SP(s, t)

is the shortest lead time path between node s and node t in N, which is defined as the path P satisfying

L ( p ) = m i n { L ( P i ) I V P i =

(uil, Ui2,'..,U,k)

in N,

where s =

uil

and t =

Uik } .

N(c i)

is a subnetwork of N containing only those arcs with capacities larger than or equal to ci (without loss of generality, we assume that the distinct capacity values of N are c I > c 2 > . . . > c,). That is,

N(c i)

= (V,

A i, C,

L), where (u, v) ~ A i if

and only if (u, v) c A and

C(u, v) >_ c~.

SPi(s, t)

is the shortest lead time path between node s and node t in

N(ci).

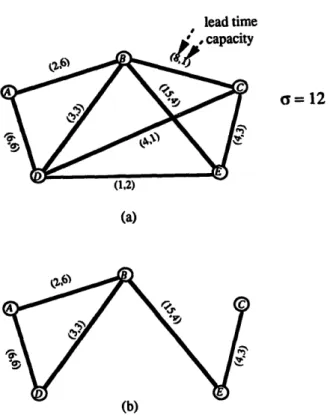
As an illustrative example, let us consider the network N of

Fig. l(a),

where o r - 12 and

each arc is associated with a pair of values: the lead time and the capacity. The path

Pt = ( D , E, C) has

L(PI)=L(D, E)+ L(E,

C ) = 5,

C(Pt)=min{C(D,

E),

C(E,

C)} = 2,

and

T(P 1,

12) =

L(PI) + 12/C(P~)=

5 + 6 = 11. The other paths between node D and node

C are P 2 = ( D , C), P s = ( D , B, C), P 4 = ( D , B, E, C), P s = ( D , A, B, C), P6 =

(D, A, B, E, C), and P7 = (O, E, B, C). The quickest path between i,.,.,.~e D and node C is

QP(D, C,

1 2 ) = Pl, since

T(P l,

1 2 ) = min{T(Pl, 12),

T(P2,

1 2 ) , . . . , T ( P 7, 12)} = min{11, 16, 23, 26, 28, 31, 36} = 11. The shortest i~ad time path between node D and node C is

SP(D,

C ) = P 2, since

L(PE)=min{L(Ps), L(P2),...,L(P7)}

= min{5, 4, 11, 22, 16, 27, 24}

= 4. The distinct capacity values of N are c~ = 6, c 2 = 4, c 3 = 3, c 4 = 2, and c s = 1.

Figure

l(b)

shows the subnetwork N(c s) of N.

The most important concept of the quickest path problem is that the selection of the quickest paths depends not only on the characteristics of the network but also on the amount of data to be transmitted. Taking these two factors into consideration will make the problem more reasonable. For example, when a certain amount of data are required to be transmitted between two nodes in a communication network, the baud rates of the transmission media between these two nodes can be treated as the capacities, and the lengths of different paths

826 E-C Hung, G.-H. Chen (a) lead time q 6 = 1 2 (b)

Fig. 1. Example of (a) a network N, (b) a subnetwork N(3).

between them can be treated as the lead times. For this example, if the amoun~ of data is huge, the paths with larger capacities are preferred. On the other hand, if the am,,~unt of data is quite small, the paths with smaller lead times are preferred. Thus, including t!f,e amount of data into the selection of the quickest paths is practically significant.

In the next two sections, the network N is embedded in an asyncl zaous network in the sense that there is a 1-1 correspondence between the nodes of N and the processors of the asynchronous network, and between the arcs of N and the communication links of the asynchronous network. At the beginning of our distributed algorithms, each processor known only the identities of its neighbours, and the capacities and lead times of its incident arcs. When the algorithms terminate, a routing table for traversing the quickest paths is established within each processor.

3. Distributed algorithms for 1 _QSP

In this section, we first show that the quickest path problem can be solved by applying shortest path algorithms.

Theorem 1.

L(QP(s, t, or)) + or/C(QP(s, t, or))ffi minlsi~_,{L(SPi(s , t)) + or/C(SPi(s ,

t))},

where r is the number of distinct capacity values of N.

Proof. By definition,

L(SPi(s, t)) + or/C(SPi(s , t))>L(QP(s, t, or))+ or/C(QP(s,

t, or)), for i ~ {1, 2,...,r}. This theorem is proved by the fact that

QP(s, t,

or)=

SPj(s, t),

where j {1, 2 , . . . , r } and

C(QP(s, t,

or))=cj. []

Based on Theorem 1, the I _ Q S P can be solved by first finding all SP~(s, t) and then

determining the minimum of L(SP,(s, t))+ or/C(SP~(s, t)), i - 1, 2 , . . . , r , which can be done

by executing any existing one-source shortest path distributed algorithm. (Surely, some modifications are necessary. However, the extra messages and time are negligible.) The complexity of the I _ Q S P distributed algorithm depends on the complexity of the adopted one-source shortest path distributed algorithm. Therefore, we have the following theorem.

Theorem 2. The I_QSP can be solved with O(rM) messages and O(rT) time in an asyn- chronous network N, where M and T stand for the message complexity and the time complexity, respectively, of the adopted one-source shortest path distributed algorithm.

Since the one-source shortest path distributed algorithms proposed by Awerbuch [2],

Frederickson [6], and Lakshmanan et al. [9] can find each Sl'~(s, t) and determine the values

L(SPi(s, t)) and C(SPi(s, t)) using O(m l+~ log w),

O(n2),

O(mn) messages in O(n l-" log w),

O(n2), O(n)

time, respectively, we have the following corollary.

Corollary 1. The I_QSP can be solved in an asynchronous network N using

O(rn 2)

messages in

O(rn 2) time, or using O(rmn) messages in O(rn) time, or using O(rm l+~ log w) messages in

O(m I +~ log w) time for any E, 0 < ~ < 1, where r, n, m, and w are the number of distinct

capacity values, the number of nodes, the number of arcs, and the maximal arc weight in N, respectively.

if more efficient one-source shortest path distributed algorithm is adopted, the result of the paper is improved.

According to Theorem 1, we can also solve the A _ Q S P by repeating the one-source

shortest path distributed algorithm nr times. However, this will result in a very high message

complexity and time complexity. In the following section, we present a distributed algorithm

for the A _ Q S P that requires only O(mn) messages and O(m) time.

4. A distributed algorithm for A _QSP

Since the amount of data to be transmitted is an important factor for the selection of the

quickest paths, it is desirable to find the quickest paths for all possible values of or. Let (0, o0)

be the range of or. If or is very small, then the shortest lead time path is the quickest path. When or increases, the shortest lead time path may no longer be the quickest path, and another path may become the new quickest path. Thus, we can divide the range of or into intervals such tha, the quickest path remains unchanged during each interval of or.

In our algorithm, an n × n x r matrix ML. is provided in each node v to keep some information about the shortest lead time paths and intervals of or. More specifically, the entry

M~.(s, t, i), l < s < n , l _ < t _ < n , l < i < r , records four values: M,,(s, t, i).LT,

M,,(s, t, i).NEXT, My(s, t, i).LEFT and M~,(s, t, i).RIGHT. The value Mv(s,t, i).LT repre-

sents the lead time of SPi(s, t). The value M~.(s, t, i).NEXT represents the next node of v

along S/'t(s, t). If S,~(s, t) does not go through node v, then M,,(s, t, i).NEXT is empty.

When the value of or falls into the interval (M~.(s, t, i).LEFT, M~.(s, t, i).RIGHT), SP,(s, t)

is the quickest path from node s to node t.

The algorithm consists of two stages. The first stage, referred to as heap construction stage,

constructs a spanning tree of the network N, and then constructs a heap from the spanning

tree according to the capacities of arcs. A heap is a tree, in which the value associated with

828 Y.-C. Hung, G.-H. Chen

heap is called a tree arc if it belongs to the heap, and a nontree arc otherwise. The root node

of the spanning tree is assigned as the algorithm leader. In the second stage, which is referred

to as broadcasting stage, the root node broadcasts all the arcs of N (including their end

nodes, capacities, and lead times) over the tree, one by one and in a nonincreasing order of their capacities. Whenever a node v receives one such message, it must update the values

M,.(s, t, i).LT, M,,(s, t, i).NEXT, M,,(s, t, i).LEFT and My(s, t, i).RIGHT. The updating of

the matrix M v is discussed later in this section.

In the algorithm, each arc may be in one of the two statuses: enable and disable. Initially,

all arcs are in status enable. During the execution of the algorithm, each node v must

determine the largest capacity arc among those enabled arcs whose one or two end nodes are in the subtree of v, and then, as a reply to the request of the. parent of v, the selected arc is

sent out and its status is changed to disable.

Next, we give a summary of the main messages used in the algorithm. To simplify the description of the algorithm, various acknowledgement messages will not be described. init

The message is broadcast over the spanning tree. The broadcasting starts from the root

node and propagates toward leaf nodes. When a nonleaf node receives an init message

from its parent, it forwards the message to its children. echo(x, y, L( x, y ), C( x, y ))

When a nonroot node v receives an init message, it must return a message

echo(x, y, L(x, y), C(x, y)) to its parent, where (x, y) is the largest capacity arc among

those enabled arcs whose one or two end nodes are in the subtree of v. arc(u, v, L(u, v), C(u, v))

The root node broadcasts the message arc(u, v, L(u, v), C(u, v)) for each arc (u, v) in N

over the spanning tree. These arc messages are broadcast in a nonincreasing order of

C(u,v)s. Whenever a node w receives an arc message, it must update the matrix M w.

The following is a formal description of the algorithm.

Algorithm A _QSP:

Stage 1: / • Heap constructiutt stage , / (1) Construct a spanning tree of N:

(2) The status of each arc is set to enable.

(3) The root node executes the following.

(3.1) Send an init message to each of its children.

(3.2) Wait for echo messages that are returned from its children.

(4) Upon receiving an init message, a nonleaf node executes the following.

(4.1) Send an init message to each of its children.

(4.2) Wait for echo messages that are returned from its children.

(4.3) Select the largest capacity arc (assuming (x, y)) among the arcs contained in the

returned echo messages, the arcs connecting the node with its children, and the

enabled nontree arcs that are incident to the node.

(4.4) Return the message echo(x, y, L(x, y), C(x, y)) to its parent.

(4.5) If (x, y) is a nontree arc or connects the node with one of its children, then the

status of (x, y) is changed to disable.

(4.6) Otherwise, send an init message to its child from which the node received the

(5) Upon receiving an

init

message, a leaf node executes the following.

(5.1) Select the largest capacity arc (assuming (x, y)) among those enabled nontree arcs that are incident to the node.

(5.2) If no such arc exists, then return the message

echo(O,

0, o0, 0) to its parent.

(5.3) Otherwise, return the message

echo(x, y, L(x,

y),

C(x,

y)) to its parent, and

change the status of (x, y) to

disable.

Stage 2: / •

Broadcasting stage • /

(1) The root node (assuming q) executes the following.

repeat

(1.1) Select the largest capacity arc (assuming (u, v)) among the arcs contained in the

returned

echo

messages and the enabled arcs that are iacident to the root node.

(1.2) If (u, v ) - ( O , 0), then terminate the algorithm (by broadcasting a termination message), and exit the loop.

(1.3) Otherwise, send the message

arc(u, v, L(u, v), C(u, v))

to each of its children.

(1.4) If (u, v) is incident to the root node, then change the status of (u, v) to

disable.

(1.5) Otherwise, send an

init

message to the child from which the root node received

the message

echo(u, v, l(u, v), C(u, v)),

and wait for a reply.

(1.6) Update

Mq(s, t, i).LT, Mq(s, t, i).NEXT, Mq(s, t, i).LEFT

and

Mq(s, t, i).

RIGHT,

where 1 < s < n, 1 < t < n, and

C(u, v) = c i.

forever

(2) Upon receiving a message

arc(u, v, L(u, v), C(u,

v)), a node (assume w) executes the

following.

(2.1) Send the

arc

message to each of its children.

(2.2) Update

Mw(s, t, i).LT, M~(s, t, i).NEXT, M~(s, t, i).LEFT

and

Mw(s, t, i).

RIGHT,

where 1 _< s _< n, 1 _< t _< n, and

C(u, v) = ci.

(3) Upon receiving an

init

message, a node executes the following.

(3.1) Maintain the heap and return an

echo

message to its parent (as we have

described in .eps 4 and 5 of Stage 1).

In order to construct a heap from the spanning tree, the root node broadcasts an

init

message over the tree. Initially, let the status of each arc be

enable.

When a nonleaf node

receives an

init

message from its parent, it forwards the message to its children. Thus, the

init

message is propagated toward leaf nodes. When a leaf node x receives an

init

message, it

returns a message

echo(x, y, L(x,

y),

C(x,

y)) to its parent, where (x, y) is the largest

capacity arc among those enabled nontree arcs that are incident to x. Then the status of

(x, y) is set to

disable

(node x will inform node y of this change). After a nonleaf node has

received all the

echo

messages that are returned from its children, it selects the largest

capacity arc (assuming (x, y)) among the arcs contained in the returned

echo

messages, the

arcs connecting the node with its children, and the enabled nontree arcs that are incident to

the nonleaf node. Then, the nonleaf node returns the message

echo(x, y, L(x,

y),

C(x,

y))

to its parent. If the arc (x, y) is a nontree arc or connects the nonleaf node with one of its

children, then its status is changed to

disable.

The heap construction stage terminates when

the root node has received all the

echo

messages returned from its children. Note that in the

above execution, each node returns to its parent the largest capacity arc that it holds. After this, the heap property may be violated. So, in order to maintain the heap, the node has to

require its one child to send the

echo

message again (see step 4.6 in Stage 1).

The message and time complexities of the heap construction stage are analyzed as follows. The distributed algorithm proposed by Awerbach [1], which requires O(m + n log n) mes- sages and O(n) message transmission time, can be used to find a spanning tree of N. There

830 Y.-C. Hung, G.-H. Chen

are at most two init and echo messages transmitted via each tree arc. Thus, the total number

of messages transmitted are O(m + n log n), where n and m are the numbers of nodes and

arcs in N, respectively. The time required to transmit the init and echo messages is

proportional to the depth of the tree. Thus, the total message transmission time is O(n). In the broadcasting stage, the root node repeatedly selects the largest capacity arc

(assuming (u, v)) among the arcs contained in the returned echo messages and the enabled

arcs that are incident to the root node, and then broadcasts the message arc(u, v, L(u, v),

C(u, v , over the tree. These ""

arc

messages are broadcast in a nonincreasing order of

C(u,

v)s. In the meantime, whenever a node w receives an

arc

message, the matrix M w must be updated. Also, the heap property must be maintained, as discussed in the heap construc-

tion stage. The total n u m b e r of messages transmitted is

O(mn).

Since the

arc

messages m a y

be sent from the root node in m consecutive time steps (the heap maintenance is performed simultaneously), the total message transmission time is O(m).

Now, the remaining problem is h o w to update the matrix M ~ for each node w whenever it

receives an

arc

message. At first, the network N is regarded as empty (containing no arcs).

Since n e w paths m a y be generated from a node s to another node t w h e n an arc (u, v) is

added to N, the quickest path from s to t m a y be altered. Thus, whenever a node w receives

a message

arc(u, v, L(u,

v),

C(u,

v)), it must update the values

M~(s, t, i).LT,

Mw(s, t, i).NEXT, M~(s, t, j).LEFT

and

M~(s, t, i).RIGHT

for evei3' pair of nodes s and t,

where

C(u, v)= ci

is assumed.

Although m a n y n e w paths from node s to node t m a y be generated after adding an arc (u, v) to N, only two paths are needed to be considered. O n e contains the shortest lead time path from s to u (without passing the arc (u, v)), the arc (u, v), and the shortest lead time path from t, to t (without passing (u, v)), and the other contains the shortest lead time path from s to v (without passing (u, v)), the arc (u, v), and the shortest lead time path from u to

t (without passing (u, v)). Initially, let

M~(s, t, O).LT

= o0 and

Mw(s, t, O).NEXT

be empty.

T h e updating of

Mw(s, t, i).LT

and

M~(s, t, i).NEXT

is shown below as the procedure

ComputeSP(u k, v

k, L(u~,

vk),

C(u k, vk)).

Without loss of generality, w e assume that the arcs

of N are broadcast in the sequence of (ut, v~), (u s,

v2),...,(Um,

Vm), where

C(ut, v~)>

C(u,, v2) > "'" > C(u~, vm).

ComputeSP(uk, vk, L(uk, vk), C(uk, vk));

/ . Assume C(uk_l,

Uk-I)-'Cj

and C(uk, vk)=c~. * /

4 5 6 7 8 9 10 11 12 13 14 15 16 for each s ¢ V for each t E V begin T I ~- Mw(s, u k, j ) . L T + L(u k, v k) + Mw(vk, t, j ) . L T ; T 2 ~ Mw(s, v k, j ) . L T + L(u k, v k) + M~(uk, t, j ) . L T ; M~(s, t, i ) . L T , - min{Tl, T 2, M~(s, t, j).LT}; if T I = M~(s, t, i ) . L T then if w - u k then Mw(s, t, i ) . N E X T ,-- v k

else if M~(s, u k, i ) . N E X T is not empty

then M,,(s, t, i).NEXT ~ M~(s, u k, j ) . N E X T

else if M~(vk, t, j ) . N E X T is not empty

then M~(s, t, i ) . N E X T ~- Mw(v k, t, j ) . N E X T

else let M~(s, t, i ) . N E X T be empty;

if T 2 - M ~ { s , t, i).LT and T l # T 2

then if w = v k then M~(s, t, i ). N E X T ,-- u k

else if M~(s, v k, j ) . N E X T is not empty

T(S~(s,O, o)

M v (s,t.3)J.T

M v (s,t,4)LT

I I

~minimai transmission time

. . . | Mv(s~2)ZT ! ! ! ! I ! ! ! W~ (s.z, 5)17 , , I I I I ~v (S,I,6)LT | a ! I ' 0 5 2 5 ! Fig. 2. T h e m i n i m a l t r a n s m i s s i o n time is t h e l o w e r p o r t i o n o f SP~(s, t), i = 1 . . . 6. 17 18 19

else if M ~ ( u k , t ,

j).NEXT

is not empty

then

M~(s, t, i).NEXT ~

M~(uk,

t, j ) . N E X T

else let

M~(s, t, i).NEXT

be empty;

end.

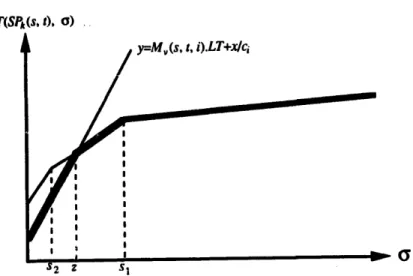
The intervals of or, which is the amount of data to be transmitted, are determined as

follows. Since each

SP~(s, t), 1 < i < r,

has the shortest lead time among those paths from s to

t whose capacities are larger than or equal to c~, the transmission time of each path from s to

t with capacity equal to ci is greater than or equal to the transmission time of

SP~(s, t)

for all

values of or. Thus, only the paths

SP{~(s, t), SPe(s, t),...,SPr(s, t)

are necessary to be

considered in constructing intervals of or for a pair of nodes s and t.

Clearly, the transmission time of each

SP~(s, t)

is a function of or. That is,

y - M~(s, t, i ) . L T + x/c~,

where y -

T(SPi(s, t), or)

and x = or. It is easy to see that the minimal transmission time for

each value of cr can be determined as min{Mw(s,

t, i).LT + x / c i l i -

! , . . . , r}. Equivalently,

the lower portion of these r lines y ffi

Mw(s, t, i).Lt +x/ci, i ffi 1,..., r,

denotes the minimal

transmission time for all values of or (see

Fig. 2),

and the intersection points (sin and s2 in

Fig.

2) along the lower portion separate the intervals.

The intersection points can be found by adding the lines y ffiM~(s,

t , i ) . L T + x / c ~ ,

i = 1 , . . . , r , to the plane, one by one and in increasing sequence of i. The line y =

Mw(s, t, 1).LT + x / c t

is first added to the plane. Then, let us consider the situation of adding

a line y =

Mw(s, t, i ) . L T + x / c i , 1 < i < r,

to the plane. The newly added line intersects the

curreut lower portion at one point z (siace the slopes of the lines are positive and increasing in their order), which can be determiaed by scanning the lower portion from left to right. The

point z is then stored as a new intersection point, and the intersection points (s2 in

Fig. 3)

on

the left of z are discarded.

The values

M~(s, t, i).LEFT

and

M~(s, t, i).RIGHT, i= l , . . . , r ,

are determined as

follows. Initially, set

M~(s, t, I).LEFT= 0

and

M~(s, t, 1).RIGHT

= oo. For each newly

generated intersection point z of two lines y =

M~(s, t, i ) . L T + x / c ~

and y =

Mw(s, t, j ) . L T

+ x / c i,

where j < i, set

Mw(s, t, i).RIGHT ffi M,(s, t, j).LEFT = z,

and

Mw(s, t, k ) . L E F T

=M~(s, t, k).RIGHT=oo,

for

j < k < i .

In the following, the procedure

Computelnt

832 E-C. Hung, G.-H. Chen T(S6(s, t). o) ,. y=Mv(s, t, i).LT+Mq I I I I I I I

',

, I I ! I I ! i I ! I I ! _! ! -- 5 2 z 51 v

Fig. 3. After a line y ffi M,.(s, t, i ) . L T + x / c ~ is added to the plane, a new intersection point z is generated and the intersection point s2 is discarded.

(C(uk, v,)) shows the necessary changes of the intervals of ~r whenever a node w receives an

arc message in the broadcasting stage.

Computelnt(C(uk, vk));

/ • Assume C(uk, Vk) ffi Ci. * / 1 if i > 1 then 2 for each s ~ V 3 for each t ~ V begin 4 j ~ i - I; 5 While (Mw(s, t, i).LT + Mw(s, t, j ) . L E F T / c i > M~(s, t, j ) . L T +Mw(s, t, j ) . L E F T / c s) or M~(s, t, j ) . L E F T = oo begin 6 Mw(s, t, j + 1).LEFT *-- oo; 7 M~(s, t, j + 1).RIGHT *-- o~; 8 y ~ j - 1 end; 9 z ~ (Mw(s, t, j ) . L T - M~(s, t, i ) . L T ) * c i * cS/(c s - ci); 10 M,(s, t, j ) . L E F T *-- z; 11 M~(s, t, i).RIGHT *- z; 12 Mw(s, t, i).LEFT *- 0; end.

Theorem 3. The A _ Q S P can be solved in an asynchronous network using O(mn) messages, in O( m ) time.

It is easy to see that the matrix M w can serve as a routing table for node w. W h e n e v e r node w receives an amount or of O~ta that are required to be transmitted from a node s to a n o t h e r node t, it knows how to route the data so as to minimize the total transmission time

M~,(s, t, i ) . R ! G H T ) such that M,v(s , t, i ) . L E F T < o < Mw(s , t, i).RIGHT. Then, it deter-

mines Mw(s, t, i ) . N E X T as the next node to route the data, since the arc

(w, M~(s, t, i ) . N E X T ) belongs to the quickest path from s to t.

5. Concluding remarks

The quickest path problem is a variant of the shortest path problem. Unlike the shortest paths, the selection of the quickest paths depends on not only the characteristics of the network but also the amount of data to be transmitted. In this paper, we have proposed distributed algorithms for the quickest path problem. For the I_QSP, three algorithms are proposed, which require O(rn 2) messages and O(m 2) time, O(rmn) messages and O(rn) time. and O(rm ~+~ log w) messages and O(rn m+~ log w) time for any ~, 0 < ~ < 1, respectively, where m, n, r, and w are the number of arcs, the number of nodes, the number of distinct

capacity values, and the maximal arc weight, respectively, in the network N. For the A_ Q S P ,

a distributed algorithm, which requires O(mn) messages and O(m) time, is proposed. The quickest path problem has not been solved before in distributed environments.

It is known that for any graph problem, it is always possible to obtain a trivial distributed solution by broadcasting all topological information to all processors, and then solve the problem sequentially in each processor. Using the trivial approach, the quickest path problem can be solved in four main stages: constructing a spanning tree of N, broadcasting all topological information o f N, sorting the arcs of N nonincreasingly according to their capacities, and computing the quickest paths. The most difficult problem in the trivial approach is how to broadcast in a simple and efficient fashion.

Essentially, the proposed A_QSP algorithm is a refinement of the trivial approach. The use of the heap makes the broadcasting simpler and more rhythmical. The main advantages gained due to the use of the heap are as follows. First, the proposed A_QSP algorithm becomes very simple and can be easily implemented. Only three main types of messages are needed; the init and arc messages are sent downwards, and the echo message is sent upwards. Secondly, the arcs are broadcast in a nonincreasing order of their capacities. Thus, the sorting becomes unnecessary. Thirdly, since the arcs are broadcast in a sorted sequence, the message transmission can be overlapped with the message processing (computing the quickest paths). Thus, more parallelism is obtained. Also, note that the proposed approach for computing the quickest paths fully utilizes the advantages of a sorted sequence of arcs.

Finally, since maintaining the heap will cause the arcs with greater capacities moved upwards, the induced cost is made up by the gainings due to data moving. Moreover, the maintenance of the heap is overlapped with the data broadcasting.

Acknowledgement

The authors are pleased t o thank the anonymous referees for their valuable suggestions

and comments. They have improved the paper a lot and made the paper more readable. Also, thanks are due to Professor Jau,Hsiung Hu~ng, who has spent much time in reading this paper very carefully and providing many helpful comments.

References

[1] B. Awerbuch, Optimal distributed algorithm for minimum weight spanning tree, counting, leader election and

834 E-C. Hung, G..H. Chen

[2] B. Awerbuch, Distributed shortest paths algorithms, Proc. 21st STOC (1989) 490-500.

[3] B. Aw¢:'~,h and R. Gallager, A n~v distributed algorithm to find breadth first search trees, IEEE Tra,i~: l~form. Theory 33 (3) (May 1987) 315-322.

[4] L.D. Bodin, B.L. Golden, A.A. Assad and M.O. Ball, Routing and scheduling of vehicles and crews: the state of the art, Comput. Operat. Res. 10 (1982) 63-211.

[5] Y.L. Chen and Y.H. Chin, The quickest path problem, Comput. Operat. Res. 17 (1989) 153-161.

[6] G.N. Frederickson, A distributed shortest path algorithm for a planar network, Inform. and Comput. 86 (1990) 140-159.

[7] M.L. Fredman and R.E. Tarjan, Fibonacci heaps and their uses in improved netv,'ork optimization algorithms, .J'. ACM 34 (1987) 596-615.

[8] Y.C. Hung and G.H. Chen, On the quickest path problem, Lecture Notes in Comput. Sci. 497 (May 1991) 44-46. [9] K.B. Lakshmanan, K. Thulasiraman and M.A. Comeau, An efficient distributed protocol for finding shortest