Embed a Longest Path between Arbitrary Two Vertices of a
Faulty Star Graph
by
Sun-Yuan Hsieh, Gen-Huey Chen
Department of Computer Science and Information Engineering, National Taiwan University, Taipei, TAIWAN
and
Chin-Wen Ho
Department of Computer Science and Information Engineering, National Central University, Chung-Li, TAIWAN
Abstract
The star graph Sn has been recognized as an attractive alternative to the hypercube. Since S1, S2,
and S3 have trivial structures, we focus our attention on Sn with n≥4 in this paper. Let Fv denote
the set of faulty vertices in Sn. We show that when |Fv|≤n−5, Sn with n≥6 can embed a fault−free path of length n!-2|Fv|−2 (n!-2|Fv|−1, respectively) between arbitrary two vertices of even (odd, respectively) distance. Since Sn is bipartite with two partite sets of equal size, the embedded path is the longest in the worst case. Besides, we also show that when |Fv|=n−4 or n−3, Sn with n≥4 can embed a fault−free path of length at least n!-4|Fv|−10 (n!-4|Fv|−9, respectively) between arbitrary two vertices of even (odd, respectively) distance. Since Sn is regular of degree n-1, |Fv|=n−3 is maximum in the worst case in order to embed a longest fault−free path between arbitrary two vertices of Sn.
Index Terms: Bipartite graph, Cayley graph, fault-tolerant embedding, graph−theoretic interconnection network, hamiltonian path, longest path, star graph
Correspondence Address: Professor Gen-Huey Chen
Department of Computer Science and Information Engineering, National Taiwan University, Taipei, TAIWAN 10764
e-mail: ghchen@csie.ntu.edu.tw Fax: (886)-(2)-3628167
1 Introduction
One crucial step on designing a large-scale multiprocessor system is to determine the topology of the interconnection network (network, for short). In recent decades, a lot of networks have been proposed. The interested readers may refer to [4, 18] for extensive references. Among them, the star graph [1], which belongs to the class of Cayley graphs [2], has been recognized as an attractive alternative to the hypercube. It possesses many nice topological properties such as recursiveness, symmetry, maximal fault tolerance, sublogarithmic degree and diameter, and strong resilience, which are all desirable when we are designing the interconnection topology for a parallel and distributed system. Besides, the star graph can embed rings [26], meshes [28], trees [3], and hypercubes [24]. Efficient communication algorithms for shortest-path routing [1], multiple-path routing [12], multicasting [16], broadcasting [32], gossiping [5], and scattering [16] have been proposed. Efficient algorithms for sorting [23], merging [26], selection [25], prefix sums [26], ranking [31], Fourier transform [15], and computational geometry [27] have also been designed.
Since processor and/or link faults may happen when a network is put in use, it is practically meaningful to consider faulty networks. The problems of diameter [29], routing [14, 35], multicasting [22], broadcasting [34], gossiping [13], embedding [11, 30, 36], and fault-tolerant graphs [6−9, 20] have been solved on a variety of faulty networks. This paper is concerned with the problem of fault−tolerant embedding. Throughout this paper, we use network and graph, processor and vertex, and link and edge, interchangeably.
Previously the problem of fault−tolerant embedding on a faulty star graph has been studied in [17, 21, 33]. Let Fv and Fe denote the sets of faulty vertices and faulty edges, respectively. In [21], Latifi and Bagherzadeh showed that an n-dimensional star graph with faulty vertices can embed a fault−free ring and a fault−free path of each length n!-m! if all faulty vertices belong to an m-dimensional star graph and m≤n is minimal. In [33], Tseng, Chang, and Sheu showed that an n-dimensional star graph with |Fe|≤n-3 faulty edges can embed a fault−free longest ring of length n!, and an n-dimensional star graph with |Fv|≤n-3 faulty vertices can embed a fault−free ring of length at least n!-4|Fv|, where n≥4. In [17], the authors showed that an n-dimensional star graph with |Fe|≤n-4 faulty edges can embed a longest fault−free path of length n!−2 (n!−1, respectively)
between arbitrary two vertices of even (odd, respectively) distance, where n≥6. The situation of |Fe|=n-3 is also discussed in [17].
In this paper, we show that an n-dimensional star graph with |Fv|≤n−5 faulty vertices can embed a fault−free path of length n!-2|Fv|−2 (n!-2|Fv|−1, respectively) between arbitrary two vertices of even (odd, respectively) distance, where n≥6. Since the star graph is bipartite with two partite sets of equal size [19], the embedded path is the longest in the worst case. We also show that when |Fv|=n−4 or n−3, an n-dimensional star graph can embed a fault−free path of length at least n!-4|Fv|−10 (n!-4|Fv|−9, respectively) between arbitrary two vertices of even (odd, respectively) distance, where n≥4.
The rest of this paper is organized as follows. In the next section, the star graph is reviewed and some basic operations are defined. In Section 3, a longest fault−free path is embedded between arbitrary two vertices of an n−dimensional star graph with |Fv|≤n−5 vertex faults. The situations of |Fv|=n−4 and n−3 are treated in Section 4. Finally, some concluding remarks are given in Section 5.
2 Preliminaries
In this section, some necessary definitions, notations, and prerequisite results are introduced. First, the n-dimensional star graph, denoted by Sn, is defined as follows.
Definition 1. The vertex set of Sn is denoted by {a1 a2...an | a1a2...an is a permutation of {1, 2, ...,
n}}. Vertex adjacency is defined as follows: a1a2...anis adjacent to aia2...ai-1a1ai+1...an for all 2≤i≤n.
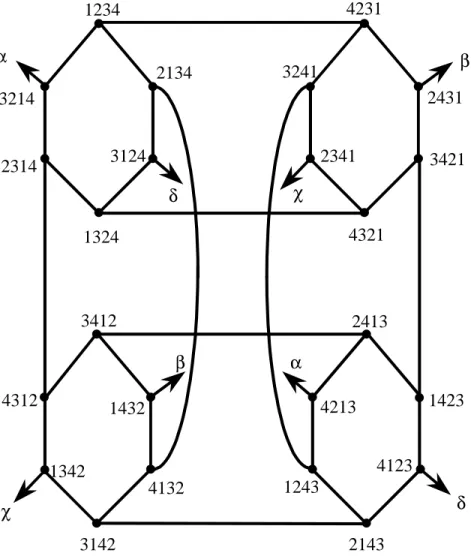
The vertices of Sn are n! permutations of {1, 2, ..., n}, and there is an edge between two vertices of Sn if and only if they can be obtained from each other by swapping the leftmost number with one of the other n-1 numbers. The structure of S4 is depicted in Figure 1 for
illustration. For convenience we refer to the position of ai in a1a2...anas the ith dimension, and
(a1a2...an, aia2...ai-1a1ai+1...an) as the ith-dimensional edge. It is easy to see that Sn is regular of
degree n-1. Since S1 is a vertex, S2 is an edge, and S3 is a cycle of length 6, we focus our attention
There are embedded Sr’scontained in Sn, where 1≤r≤n. An embedded Srcan be conveniently represented by <s1s2...sn>r, where s1=∗, si∈{∗, 1, 2, ..., n} for all 2≤i≤n, and exactly r of s1, s2, ..., sn
are ∗ (∗ denotes a “don’t care” symbol). For example, <∗∗∗3>3, which represents an embedded S3
in S4, contains six nodes 1243, 1423, 2143, 2413, 4123, and 4213. In terms of graph, <∗∗∗3>3 is a
subgraph of S4 induced by {1243, 1423, 2143, 2413, 4123, 4213}. When r=n, <s1s2...sn>n
represents Sn. Two basic operations on Sn are defined as follows.
Definition 2. An i-partition on <s1s2...sn>r partitions <s1s2...sn>r into r embedded Sr-1’s,
denoted by <s1s2...si-1qsi+1...sn>r-1, where 2≤i≤n, si=∗, and q∈{1, 2, ..., n}-{s1, s2, …, sn}.
For example, executing a 3-partition on <∗∗∗15>3 produces three embedded S2’s, i.e.,
<∗∗215>2, <∗∗315>2, and <∗∗415>2.
Definition 3. An (i1, i2, ..., im)-partition on <s1s2...sn>r performs an i1-partition, an i2
-partition, ..., an im--partition, sequentially, on <s1s2...sn>r, where 1≤m≤r−1 and i1i2…im is a
permutation of m numbers from {2, 3, ..., n}. After executing an (i1, i2, ..., im)-partition, <s1s2...sn>r
is partitioned into r(r-1)⋅⋅⋅(r-m+1) embedded Sr-m’s.
For example, when a (3, 2)-partition is applied to <∗∗∗15>3, a 3-partition is first executed on
<∗∗∗15>3 to produce three embedded S2’s, i.e., <∗∗215>2, <∗∗315>2, and <∗∗415>2. Then, a
2-partition is executed on each S2 to produce six embedded S1’s, i.e., <∗3215>1, <∗4215>1,
<∗2315>1, <∗4315>1, <∗2415>1, and <∗3415>1.
Two embedded Sr’s <s1s2...sn>r and <t1t2...tn>r are said to be adjacent if sj≠∗, tj≠∗, and sj≠tj for some 2≤j≤n, and si=ti for all 1≤i≤n and i≠j. The position j is denoted by dif(<s1s2...sn>r, <t1t2...tn>r).
For example, <∗∗23>2 is adjacent to <∗∗13>2, and dif(<∗∗23>2, <∗∗13>2)=3.
Definition 4. Let A1, A2, ..., An(n-1)⋅⋅⋅(r+1) represent those embedded Sr’s that are obtained by
executing an (i1, i2, ..., in-r)-partition on Sn, where 1≤r≤n-1. They form an r-path, denoted by Pr=[A1,
A2, ..., An(n-1)⋅⋅⋅(r+1)], if Ai is adjacent to Ai+1 for all 1≤i≤n(n-1)⋅⋅⋅(r+1)-1. Each vertex of Pr, i.e., Ai, is
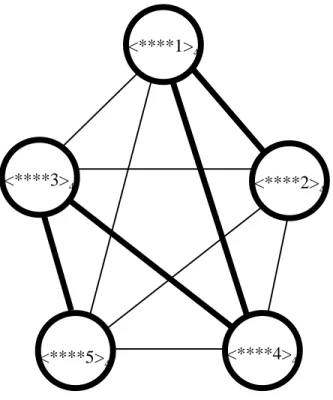
For example, Figure 2 shows a P4 in S5. The vertices of the P4 are <∗∗∗∗2>4, <∗∗∗∗1>4,
<∗∗∗∗4>4, <∗∗∗∗3>4, and <∗∗∗∗5>4, sequentially, which are all 4-vertices. The edges of the P4 are
(<∗∗∗∗2>4, <∗∗∗∗1>4), (<∗∗∗∗1>4, <∗∗∗∗4>4), (<∗∗∗∗4>4, <∗∗∗∗3>4), and (<∗∗∗∗3>4, <∗∗∗∗5>4),
which are all 4-edges. We note that an r-vertex is an embedded Sr and an r-edge comprises (r-1)! edges of Sn.
Definition 5. An i-partition on a Pr=[A1, A2, ..., An(n-1)⋅⋅⋅(r+1)] performs an i-partition on A1, A2, ...,
An(n-1)⋅⋅⋅(r+1), respectively, where 2≤i≤n and 1<r≤n-1. An i-partition on a Pr is abbreviated to a
partition on a Pr if the position i is “don’t care”.
After executing an i-partition on a Pr=[A1, A2, ..., An(n-1)⋅⋅⋅(r+1)], each Aj is partitioned into r
(r-1)-vertices, where 1≤j≤n(n-1)⋅⋅⋅(r+1). Since every two of the r vertices are joined with an (r-1)-edge, each Aj can be viewed as a complete graph of r (r-1)-vertices. Throughout this paper, we use Krr−1 to denote the complete graph. We note that each vertex of Krr−1 is an (r-1)-vertex and each edge of Krr−1 is an (r-1)-edge.
Suppose Aj=<s1...si-1sisi+1...sk-1xsk+1...sn>r and Aj+1=<s1...si-1sisi+1...sk-1ysk+1...sn>r are two neighboring
r-vertices in a Pr, where 1<r≤n-1, x≠y, and si=∗ (without loss of generality, we assume i<k). After executing an i-partition, they each are partitioned into r (r-1)-vertices, and the r-edge between them is split into r-1 (r-1)-edges connecting r-1 pairs of (r-1)-vertices that belong to them, respectively. The other pair of (r-1)-vertices that are not adjacent are <s1...si-1ysi+1...sk-1xsk+1...sn>r-1 and <s1...si-1xsi+1...sk-1ysk+1...sn>r-1.
The authors have shown the following lemma in [17].
Lemma 1.[17] Suppose E=<e1e2...en>r, F=<f1f2...fn>r, and G=<g1g2...gn>r are arbitrary three
consecutive r-vertices in a Pr, where 1<r≤n-1. If edif(E,F)≠gdif(F,G), then after executing a partition on the Pr, each (r-1)-vertex of F is connected to E or G.
In this paper, we consider Sn with faulty vertices. An r-vertex is faulty if it contains one or more faulty vertices, and an r−path is faulty if one or more of its r−vertices are faulty, where 1≤r≤n. Tseng, Chang, and Sheu have shown the following lemma in [33].
Lemma 2.[33] Suppose |Fv|≤n-3. There exists a sequence b1, b2, ..., bn-4 of positions so that
after executing an (b1, b2, ..., bn-4)-partition on Sn, each resulting 4-vertex contains at most one
faulty vertex.
The positions b1, b2, ..., bn-4 in Lemma 2 can be easily determined as follows. We let b1 be a
position where at least two faulty vertices differ. For example, if Fv={123456, 123654}, b1 may
be set to 4 or 6. A b1-partition is then executed on Sn to produce n (n-1)-vertices, and Fv is
partitioned so that two faulty vertices fall into the same subset if and only if they belong to the same (n-1)-vertex. The position b2 can be determined similarly. We simply let b2 be a position
where at least two faulty vertices in some subset differ. A b2-partition is then executed on the n
(n-1)-vertices to produce n(n-1) (n-2)-vertices, and every non-empty subset of Fv is further partitioned accordingly. The process is repeated until every non-empty subset contains one faulty vertex, when the remaining positions are determined arbitrarily.
Lemma 3. Suppose u=u1u2...un and v=v1v2...vn are arbitrary two distinct vertices of Sn and
|Fv|≤n-5. There exists a sequence a1, a2, ..., an-4 of positions so that ua1≠va1 and after executing an (a1, a2, ..., an-4)-partition on Sn, each resulting 4-vertex contains at most one vertex in {u, v}∪Fv.
Proof. We let a1=j, where uj≠vj and j≠1. The other positions a2, a3, ..., an-4 can be determined
similar to b2, b3, ..., bn-4 in Lemma 2. Q.E.D.
Lemma 4. Suppose |Fv|=1. There is a fault-free path of maximal length 4!-3 between arbitrary
two adjacent fault-free vertices of S4.
Proof. Suppose that f=f1f2f3f4 is the faulty vertex and u, v are arbitrary two adjacent fault-free
vertices of S4. Since the star graph is edge symmetric [2], we assume u=u1u2u3u4=1234 and
v=v1v2v3v4=3214 without loss of generality. We have f2≠u2=v2 or f4≠u4=v4, for otherwise f=u or f=v,
which is a contradiction. We further assume f4≠u4=v4=4. If f2≠u2=v2, the discussion is similar.
After executing a 4-partition on S4, both u and v belong to <∗∗∗4>3 and f belongs to <∗∗∗1>3 or
<∗∗∗2>3 or <∗∗∗3>3.
(u=1234, 2134, 3124, 1324, 4321, 3421, 2431, 4231, 3241, 1243, 2143, 4123, 1423, 2413, 3412, 1432, 4132, 3142, 1342, 4312, 2314, 3214=v) if f=2341; (u=1234, 4231, 3241, 2341, 4321, 3421, 1423, 2413, 4213, 1243, 2143, 3142, 1342, 4312, 3412, 1432, 4132, 2134, 3124, 1324, 2314, 3214=v) if f=2431; (u=1234, 4231, 2431, 3421, 4321, 2341, 1342, 4312, 3412, 1432, 4132, 3142, 2143, 1243, 4213, 2413, 1423, 4123, 3124, 1324, 2314, 3214=v) if f=3241; (u=1234, 2134, 3124, 4123, 1423, 2413, 4213, 1243, 2143, 3142, 1342, 4312, 3412, 1432, 2431, 4231, 3241, 2341, 4321, 1324, 2314, 3214=v) if f=3421; (u=1234, 2134, 4132, 3142, 1342, 4312, 3412, 1432, 2431, 3421, 4321, 2431, 3241, 1243, 4213, 2413, 1423, 4123, 3124, 1324, 2314, 3214=v) if f=4231; (u=1234, 2134, 3124, 4123, 2143, 1243, 4213, 2413, 1423, 3421, 2431, 4231, 3241, 2341, 1342, 3142, 4132, 1432, 3412, 4312, 2314, 3214=v) if f=2341.
If f∈<∗∗∗2>3 or <∗∗∗3>3, a fault-free u-v path of length 4!-3 can be obtained similarly. Since
the star graph is bipartite, the u-v path is the longest in the worst case. Q.E.D.
The purpose of this paper is to determine longest fault-free paths in Sn. In the rest of this paper, we use u and v to denote the beginning and ending vertices of a fault-free path, respectively. An r-vertex is called the beginning r-r-vertex (ending r-r-vertex, respectively) if it contains u (v, respectively). A path in a graph G is said to be a hamiltonian path if it contains every vertex of G exactly once [10].
3 Embed a longest fault-free u
−−−−
v path onto S
nwith |F
v|
≤≤≤≤
n-5 faulty vertices
In this section, assuming |Fv|≤n-5, we show that Sn can embed a fault-free u-v path of length n!-2|Fv|-2 if dist(u, v) is even, and of length n!-2|Fv|-1 if dist(u, v) is odd, where dist(u, v) denotes the distance between u and v. Since Sn is bipartite with two partite sets of equal size, the embedded path is the longest in the worst case. Throughout this section, we suppose that n≥6 and a1, a2, ...,
an-4 are a sequence of positions satisfying Lemma 3.
conditions.
(Cond. 1) A1 and An(n-1)⋅⋅⋅6 are the beginning and ending 5-vertices, respectively.
(Cond. 2) One of A1, A2, ..., An(n-1)⋅⋅⋅6 contains at most two faulty vertices, and the others each
contain at most one faulty vertex.
(Cond. 3) For every three consecutive 5-vertices in the P5, say B=<b1b2...bn>5, C=<c1c2...cn>5, and
D=<d1d2...dn>5, bdif(B,C)≠ddif(C,D) holds.
Lemma 5. A good P5 can be obtained by executing an (a1, a2, ..., an-5)-partition on Sn.
Proof. Suppose u=u1u2...un and v=v1v2...vn. We first construct a P6 in Sn. If n=6, Sn is itself a P6
with only one 6-vertex. If n>6, a P6 can be obtained by executing an (a1, a2, ..., an-6)-partition on Sn
as follows. Initially, an a1-partition is applied to Sn, and so a Knn−1 results. Since ua1≠va1, u and v
belong to two different (n-1)-vertices. A Pn-1 whose first and last (n-1)-vertices are the beginning and ending (n-1)-vertices, respectively, can be constructed. For j=2, 3, ..., n-6, a Pn-j whose first and last (n-j)-vertices are the beginning and ending (n-j)-vertices, respectively, can be generated from a Pn-j+1 as explained below.
Suppose Pn-j+1=[An-j+1,1, An-j+1,2, ..., An-j+1,n(n-1)⋅⋅⋅(n-j+2)], where An-j+1,1 is the beginning (n-j+1)-vertex
and An-j+1,n(n-1)⋅⋅⋅(n-j+2) is the ending (n-j+1)-vertex. After executing an aj-partition on the Pn-j+1, each An-j+1,k forms a Kn jn j− +− 1, where 1≤k≤n(n-1)⋅⋅⋅(n-j+2). Since each An-j+1,k contains at least seven (n-j)-vertices, there are two distinct (n-j)-vertices in An-j+1,k, say Xk and Yk, so that X1 is the beginning
(n-j)-vertex, Yn(n-1)⋅⋅⋅(n-j+2) is the ending (n-j)-vertex, and for 2≤j≤n(n-1)⋅⋅⋅(n-j+2)-1, Xj and Yj are
adjacent to Yj-1 and Xj+1, respectively. Since there is a hamiltonian Xk-Yk path in each Kn jn j− +− 1 formed by An-j+1,k, a desired Pn-j can be generated if all hamiltonian paths are interleaved with (n-j)-edges (Y1, X2), (Y2, X3), ..., (Yn(n-1)⋅⋅⋅(n-j+2)-1, Xn(n-1)⋅⋅⋅(n-j+2)). When j=n-6, a P6=[A6,1, A6,2, ..., A6,n(n-1)⋅⋅⋅7] is
obtained, where A6,1 is the beginning 6−vertex and A6,n(n-1)⋅⋅⋅7 is the ending 6−vertex. In the rest of
this paper, Xk and Yk thus specified are referred to as the entry (n-j)-vertex and the exit (n-j)-vertex of An-j+1,k, respectively.
We continue to generate a good P5 from the P6 as follows. If n=6, a P5 whose first and last
5−vertices are the beginning and ending 5−vertices, respectively, can be generated in S6 after an
an-5-partition is executed on the P6, where 1≤r≤n(n-1)⋅⋅⋅7. Let Xr≠Yr denote the entry and exit
5-vertices of each A6,r, respectively. It is easy to establish a hamiltonian X1-Y1 path in the K6
5
formed by A6,1 whose last two 5-vertices are connected to A6,2, a hamiltonian Xn(n-1)⋅⋅⋅7-Yn(n-1)⋅⋅⋅7 path in
the K65 formed by A6,n(n-1)⋅⋅⋅7 whose first two 5-vertices are connected to A6,n(n-1)⋅⋅⋅7-1, and for 2≤j≤
n(n-1)⋅⋅⋅7-1 a hamiltonian Xj-Yj path in the K65 formed by each A6,j whose first and last two 5-vertices
are connected to A6,j-1 and A6,j+1, respectively. All hamiltonian paths interleaved with 5-edges (Y1,
X2), (Y2, X3), ..., (Yn(n-1)⋅⋅⋅7-1, Xn(n-1)⋅⋅⋅7) form a P5.
Next we show the P5 good. Clearly, (Cond. 1) holds. (Cond. 2) holds as a consequence of
Lemma 3 because a1, a2, ..., an-4 satisfy Lemma 3 and the P5 results from executing an (a1, a2, ...,
an-5)-partition on Sn. (Cond. 3) holds because the first two 5−vertices and the last two 5−vertices in each hamiltonian Xi-Yi path are connected to Ai−1 (if existing) and Ai+1 (if existing), respectively,
where 1≤i≤n(n-1)⋅⋅⋅7. The reason is explained as follows. Suppose B=<b1b2...bn>5, C=<c1c2...cn>5,
and D=<d1d2...dn>5 are arbitrary three consecutive 5-vertices in the P5, and let p=dif(B, C) and
q=dif(C, D). If B=Yi for some 1≤i≤n(n-1)⋅⋅⋅7-1, then C=Xi+1 and D is the second 5-vertex in the hamiltonian Xi+1-Yi+1 path, which imply p≠q=an-5 and D is connected to A6,i. Suppose A6,i=<s1...sq-1sq
sq+1...sp-1xsp+1...sn>6 and A6,i+1=<s1...sq-1sqsq+1...sp-1ysp+1...sn>6, where sq=∗, bp=x≠y=dp, and q<p is
assumed. Recall that the pair of 5-vertices in A6,i and A6,i+1 that are not adjacent are <s1 ...sq-1ysq+1...sp-1xsp+1...sn>6 and <s1...sq-1xsq+1...sp-1ysp+1...sn>6. Since D is connected to A6,i, dq≠x=bp holds.
If D=Xj for some 2≤j≤n(n-1)⋅⋅⋅7, then bp≠dq can be shown similarly. Otherwise, if B, C, and D belong to the same 6-vertex, then bp≠dq holds because p=q=an-5. Q.E.D.
Lemma 6. The beginning 5−vertex and the ending 5-vertex of a good P5 that was obtained
according to Lemma 5 each contain at most one faulty vertex.
Proof. Since the good P5 results from executing an (a1, a2, ..., an-5)-partition on Sn, it contains at least min{n-4, |Fv|+2} 5−vertices that each contain at least one vertex in {u, v}∪Fv. If the beginning 5-vertex (or the ending 5−vertex) contains two faulty vertices, then Fv should contain n-5 faulty vertices. This means that there are at most n-5 5−vertices in the P5 that each contain at
The following lemma can be shown similarly.
Lemma 7. Both the beginning 5−vertex and the ending 5−vertex of a good P5 that was
obtained according to Lemma 5 are not faulty.
Definition 7. A P4=[A1, A2, ..., An(n-1)⋅⋅⋅5] in Sn is said to be good if it satisfies the following five
conditions.
(Cond. 1) A1 and An(n-1)⋅⋅⋅5 are the beginning and ending 4-vertices, respectively.
(Cond. 2) A1, A2, An(n-1)⋅⋅⋅5-1, and An(n-1)⋅⋅⋅5 are fault-free, and the other 4-vertices each contain at most
one faulty vertex.
(Cond. 3) For every three consecutive 4-vertices in the P4, say E=<e1e2...en>4, F=<f1f2...fn>4, and
G=<g1g2...gn>4, edif(E,F)≠gdif(F,G) holds.
(Cond. 4) Both every two consecutive 4-vertices in the P4 are not faulty.
(Cond. 5) After executing a k-partition on the P4 for some 2≤k≤n, the beginning and ending
3-vertices (in A1 and An(n-1)⋅⋅⋅5, respectively) are not connected to A2 and An(n-1)⋅⋅⋅5−1, respectively.
Lemma 8. A good P4 can be obtained by executing an (a1, a2, ..., an-4)-partition on Sn.
Proof. Suppose u=u1u2...un and v=v1v2...vn. According to Lemma 5, a good P5=[A1, A2, ..., An(n-1)⋅⋅⋅6] can be obtained by executing an (a1, a2, ..., an-5)-partition on Sn. An an-4-partition is then
applied to the P5, and so each Ai forms a K54, where 1≤i≤n(n-1)⋅⋅⋅6. By Lemma 7 both A1 and An(n-1)⋅⋅⋅6 are not faulty. A good P4 can be obtained according to the following three cases.
Case 1. A1 is faulty. Three 4-vertices X1=<x1x2...xn>4, T, and Q are first selected from A1 so that X1
is the beginning 4-vertex, T is not connected to A2, and Q is faulty. By Lemma 6 Q is unique, and
by Lemma 3 X1 is fault-free. Also select W=<w1w2...wn>4∉{X1, Q} from A1 with wan−4=uk for
some k ∈{2, 3, ..., n}-{a1, a2, ..., an-4}. A hamiltonian path in the K5
4
formed by A1 can be
established as (X1, W, Q, M1, Y1) if T∈{X1, Q, W}, and (X1, W, T, Q, Y1) if T∉{X1, Q, W}, where
M1 and Y1 denote the other 4-vertices of A1. Since there are four 4−vertices of A1 that are
A hamiltonian path in the K54 formed by An(n-1)⋅⋅⋅6 can be established as follows. By Lemma 7
An(n-1)⋅⋅⋅6 is fault-free. Let Yn(n-1)⋅⋅⋅6 be the ending 4-vertex, C be the 4−vertex of An(n-1)⋅⋅⋅6 that is not
connected to An(n-1)⋅⋅⋅6-1, D=<d1d2...dn>4 be the 4−vertex of An(n-1)⋅⋅⋅6 with dan−4=vk (here k is identical
with that appearing in wa
n−4=uk above), and Xn(n-1)⋅⋅⋅6 ∉{C, D, Yn(n-1)⋅⋅⋅6} be a 4−vertex of An(n-1)⋅⋅⋅6. If
Yn(n-1)⋅⋅⋅6=C or (Yn(n-1)⋅⋅⋅6≠C and C=D), a hamiltonian path in the K54 formed by An(n-1)⋅⋅⋅6 can be
established as P[Xn(n-1)⋅⋅⋅6, D]+(D, Yn(n-1)⋅⋅⋅6), where P[Xn(n-1)⋅⋅⋅6, D] denotes an Xn(n-1)⋅⋅⋅6-D path passing
all the vertices of the K54 but Yn(n-1)⋅⋅⋅6 exactly once. If Yn(n-1)⋅⋅⋅6≠C and C≠D, a hamiltonian path in
the K54 formed by An(n-1)⋅⋅⋅6 can be established as P[Xn(n-1)⋅⋅⋅6, C]+(C, D)+(D, Yn(n-1)⋅⋅⋅6), where P[Xn(n-1)⋅⋅⋅6,
C] denotes an Xn(n-1)⋅⋅⋅6-C path passing all the vertices of the K54 but D and Yn(n-1)⋅⋅⋅6 exactly once.
Then, for 2≤j≤n(n-1)⋅⋅⋅6-1, we determine the entry and exit 4-vertices of Aj, denoted by Xj and Yj, respectively, so that both Yj-1 and Xj are not faulty and both Yn(n-1)⋅⋅⋅6−1 and Xn(n-1)⋅⋅⋅6 are not faulty.
Since four 4−vertices of Aj are connected to Aj-1 and four 4−vertices of Aj are connected to Aj+1, there exists a hamiltonian Xj-Yj path in the K54 formed by Aj whose first two and last two 4-vertices are connected to Aj-1 and Aj+1, respectively.
In the above, Xi and Yi are the entry and exit 4−vertices of Ai, respectively, where 1≤i≤ n(n-1)⋅⋅⋅6. All hamiltonian paths interleaved with 4-edges (Y1, X2), (Y2, X3), ..., (Yn(n-1)⋅⋅⋅6-1, Xn(n-1)⋅⋅⋅6)
constitute a P4.
Case 2. An(n-1)⋅⋅⋅6 is faulty. A P4 can be constructed similar to Case 1.
Case 3. Both A1 and An(n-1)⋅⋅⋅6 are fault-free. We first suppose that there is a 5-vertex, say Ar, in the
P5 that contains two faulty vertices. By Lemma 6 r≠1 and r≠n(n-1)⋅⋅⋅6. By Lemma 1 each
4−vertex of Ar is connected to Ar-1 or Ar+1. Let B≠F be the two 4-vertices of Ar that are not connected to Ar-1 and Ar+1, respectively. Since a1, a2, ..., an-4 are a sequence of positions satisfying
Lemma 3, the two faulty vertices belong to two different 4-vertices of Ar, denoted by S and T. If S is connected to both Ar-1 and Ar+1 and T is connected to both Ar-1 and Ar+1, a hamiltonian path in the K54 formed by Ar can be established as (F, S, M1, T, B), where M1 denotes the other 4-vertex of Ar.
If S is connected to both Ar-1 and Ar+1 and T is connected to one of Ar−1 and Ar+1, a hamiltonian
(F, S, M1, T, M2), if T is connected to Ar+1, where M1 and M2 denote the other two 4-vertices of Ar.
If S is connected to one of Ar-1 and Ar+1 and T is connected to both Ar−1 and Ar+1, a hamiltonian path in the K54 formed by Ar can be established similarly.
If S is connected to only Ar−1 (Ar+1, respectively) and T is connected to only Ar+1 (Ar−1,
respectively), a hamiltonian path in the K54 formed by Ar can be established as (M1, S, M2, T, M3)
((M1, T, M2, S, M3), respectively), where M1, M2, and M3 denote the other three 4-vertices of Ar. It is impossible that both S and T are connected to only Ar−1 or only Ar+1.
We note that the first and last 4-vertices in each hamiltonian path above are the entry and exit 4-vertices of Ar, respectively. Besides, the first two and last two 4-vertices are connected to Ar-1 and Ar+1, respectively.
Hamiltonian paths in the other K54's can be established as follows. Let X1 and Yn(n-1)⋅⋅⋅6 be the
beginning and ending 4-vertices, respectively, and select W=<w1w2...wn>4 and D=<d1d2...dn>4 from
A1 and An(n-1)⋅⋅⋅6, respectively, with wan−4=ul and dan−4=vl for some l∈{2, 3, ..., n}-{a1, a2, ..., an-4}.
A hamiltonian path in the K54 formed by A1 can be established as (X1, W, M1, M2, M3), where M1,
M2, and M3 denote the other three 4−vertices of A1 and both M2 and M3 are connected to A2. A
hamiltonian path in the K54 formed by An(n-1)⋅⋅⋅6 can be established as (M1, M2, M3, D, Yn(n-1)⋅⋅⋅6),
where M1, M2, and M3 denote the other three 4−vertices of An(n-1)⋅⋅⋅6 and both M1 and M2 are
connected to An(n-1)⋅⋅⋅6−1. Let Xt and Yt denote the entry and exit 4−vertices of At, respectively, where
2≤t≤n(n-1)⋅⋅⋅6 and t≠r. A hamiltonian Xt−Yt path in the K54 formed by At can be established similar to the hamiltonian Xj−Yj path in Case 1.
Clearly, all hamiltonian paths above interleaved with proper 4-edges constitute a P4. On the
other hand, if every 5−vertex in the P5 contains at most one faulty vertex, hamiltonian paths in the
K54's formed by A1 and An(n-1)⋅⋅⋅6 can be established all the same as the above. Moreover, for
2≤j≤n(n-1)⋅⋅⋅6−1, a hamiltonian path in the K54 formed by each Aj can be established similar to the hamiltonian Xj−Yj path in Case 1. A P4 can be obtained similarly.
Next, we show the P4 good. Clearly, (Cond. 1) holds. (Cond. 2) holds as a consequence of our
construction and an (a1, a2, ..., an-4)-partition on Sn. Recall that we have shown in the proof of
hamiltonian Xi-Yi path are connected to Ai−1 (if existing) and Ai+1 (if existing), respectively, where
1≤i≤n(n-1)⋅⋅⋅7. Here, our construction assures that the first two and the last two 4−vertices in each hamiltonian Xi−Yi path are connected to Ai-1 (if existing) and Ai+1 (if existing), respectively, where 1≤i≤n(n-1)⋅⋅⋅6. Hence, (Cond. 3) holds with arguments similar to the proof of Lemma 5. (Cond. 4) holds as a consequence of our construction. (Cond. 5) holds for the reasons as follows. Suppose W=<w1w2...wn>4 and D=<d1d2...dn>4 are the neighboring 4−vertices of the beginning and ending
4−vertices in the P4, respectively. According to our construction, wan−4=uz and dan−4=vz for some
z∈{2, 3, ..., n}-{a1, a2, ..., an-4}. Let H=<h1h2...hn>3 be the beginning 3−vertex after executing a
z-partition on the P4. Since hz=uz= wan−4≠han−4 and ht=wt for t ∈{1, 2, ..., n}-{z, an-4}, H is not
adjacent to any of the 3−vertices of W (i.e., H is not connected to W). Similarly, the ending 3-vertex is not connected to D. This completes the proof. Q.E.D.
We note that S3 forms a ring of length six. The following two lemmas were shown in [33].
Lemma 9.[33] Suppose E and F are two adjacent 3-vertices in Sn, and let (c0, c1, ..., c5) denote
the ring formed by E. The vertices of E that are connected to F are cj and c(j+3) mod 6 for some 0≤j≤5. Lemma 10.[33] Suppose E=<e1e2...en>3, F=<f1f2...fn>3, and G=<g1g2...gn>3 are three 3-vertices
in Sn, and F is adjacent to both E and G. If edif(E,F)≠gdif(F,G), the two vertices of F that are connected to E are disjoint from the two vertices of F that are connected to G.
Suppose [A1, A2, ..., An(n-1)⋅⋅⋅5] is a good P4 obtained by executing an (a1, a2, ..., an-4)-partition on
Sn. In the following, we generate a fault-free u-v path by sequentially constructing fault-free paths in A1, A2, ..., An(n-1)⋅⋅⋅5. A k-partition is first executed on the P4, where k satisfies (Cond. 5) of
Definition 7. Hence, the beginning and ending 3-vertices are not connected to A2 and An(n-1)⋅⋅⋅5−1,
respectively.
In order to generate a fault-free u-v path,two 3−vertices in each Ai, denoted by αi and βi, need to be determined first,where 1≤i≤n(n-1)⋅⋅⋅5. We let α1 and βn(n−1)⋅⋅⋅5 be the beginning and ending
3-vertices, respectively, and for each faulty Aj, let αj=βj=Q, and βj−1 and αj+1 be the 3−vertices of Aj−1
and Aj+1, respectively, that are adjacent to Q, where 2≤j≤n(n-1)⋅⋅⋅5−1 and Q is a fault-free 3-vertex of Aj that is connected to both Aj-1 and Aj+1. We note that both Aj-1 and Aj+1 are fault-free. Since
there are two 3-vertices of Aj that are connected to both Aj-1 and Aj+1, Q surely exists. Then, for every two consecutive fault-free 3−vertices, say At and At+1, βt and αt+1 are determined as two adjacent 3-vertices that belong to At and At+1, respectively. The following lemma shows a property concerning αi and βi.
Lemma 11. If αi=βi, then bdif
i i
(β−1,α)≠adif(α αi, i+1), where βi−1=<b1b2...bn>3 and αi+1=<a1a2...an>3.
Proof. Suppose conversely αi=βi and bdif
i i
(β−1,α)= adif(α αi, i+1). If dif(βi−1, αi)=dif(αi, αi+1), then
βi−1=αi+1, which is a contradiction. Hence, dif(βi−1, αi)≠dif(αi, αi+1). We note that dif(βi−1,
αi)=dif(Ai−1, Ai) and dif(αi, αi+1)=dif(Ai, Ai+1). Recall that a k−partition was applied to the P4, where
k satisfies (Cond. 5) of Definition 7. Without loss of generality, we assume dif(Ai−1, Ai)=p< dif(Ai,
Ai+1)=q<k, and let Ai−1=<s1s2...sp−1rsp+1...sq−1t'sq+1…sn>4, Ai=<s1s2...sp−1r'sp+1…sq−1t'sq+1…sn>4, and
Ai+1=<s1s2...sp−1r'sp+1...sq−1tsq+1…sn>4, where r≠r', t≠t', and sk=∗. Hence,
βi−1=<b1b2...bn>3=<s1s2...sp−1rsp+1...sq−1t'sq+1…sk−1msk+1…sn>4,
αi=<s1s2...sp−1r'sp+1...sq−1t'sq+1…sk−1msk+1…sn>3, and
αi+1=<a1a2...an>3=<s1s2...sp−1r'sp+1...sq−1tsq+1…sk−1msk+1…sn>3, where m ∈{1, 2, …, n, ∗}−{r, r', t,
t'}−{si | 1≤i≤n and i∉{p, q, k}}. Since r= bdif
i i
(β−1,α)= adif(α αi, i+1)=t, the 3−vertex
<s1s2...sp−1r'sp+1...sq−1t'sq+1…sk−1rsk+1…sn>3 of Ai is not connected to either of Ai−1 and Ai+1. This is a
contradiction because each 3−vertex of Ai should be connected to Ai−1 or Ai+1 according to Lemma
1. Q.E.D.
A fault-free path in A1 is constructed as follows. Assume u=u1u2...un, and let Q1=<q1q2...qn>3
∉{α1, β1} be a 3-vertex of A1 with qk≠u1. Since α1 is the beginning 3−vertex, which is not
connected to A2, we have α1≠β1. A fault-free hamiltonian α1−β1 path in the
3 4
K formed by A1 can
be established as (α1, Q1, M1, β1), where M1 is the other 3-vertex of A1.
Suppose E=<e1e2...en>3, F=<f1f2...fn>3, and G=<g1g2...gn>3 are arbitrary three consecutive
3−vertices in (α1, Q1, M1, β1, α2). Recall that we have shown in the proof of lemma 5 that (Cond.
3) of Definition 6 holds if the first two and the last two 5−vertices in each hamiltonian Xi-Yi path are connected to Ai−1 (if existing) and Ai+1 (if existing), respectively, where 1≤i≤n(n-1)⋅⋅⋅7. Since
note that u is not adjacent to any vertex of Q1 because qk≠u1 and each edge between α1 and Q1 is a
k−dimensional edge. Since A1 and A2 are fault-free, Lemmas 9 and 10 assure that there are distinct
fault-free vertices x1,b∈α1, c,d∈Q1, e,f∈M1, and g,y1 ∈β1 so that every two consecutive vertices
in {x1, b, c, d, e, f, g, y1, x2} are adjacent, where x1=u and x2 is a fault-free vertex of α2. It is easy to
see that there are fault-free hamiltonian x1-b, c-d, e-f, and g-y1 paths in α1, Q1, M1, and β1,
respectively. These fault-free hamiltonian paths interleaved with edges (b, c), (d, e), and (f, g) constitute a fault-free hamiltonian x1-y1 path in A1.
We then construct fault-free paths in A2, A3, …, An(n-1)⋅⋅⋅5-1, sequentially. Suppose a fault-free
xj-1-yj-1 path in Aj-1 has been obtained and yj-1 is adjacent to xj, which is a fault-free vertex of αj, where 2≤j≤n(n-1)⋅⋅⋅5-1. A fault-free xj-yj path in Aj is constructed as follows, where yj is a fault-free vertex of βj. If αj=βj, by Lemma 11 bdif
j j
(β−1,α )≠adif(α αj, j+1) holds, where βj−1=<b1b2…bn>3 and
αj+1=<a1a2…an>3 are assumed. Since αj=βj is fault−free, Lemmas 9 and 10 assure that yj can be
determined so that it is adjacent to both xj and a fault-free vertex of αj+1. If Aj is fault-free, it is not difficult to generate a fault-free hamiltonian xj-yj path in Aj. If Aj is faulty, by Lemma 4 there is a fault-free xj-yj path of maximal length 4!-3 in Aj.
On the other hand, if αj≠βj, two 3-vertices Qj and Lj of Aj are first determined so that Qj≠βj is not connected to Aj+1 and Lj≠αj is not connected to Aj-1. Since Aj is fault-free, a fault-free hamiltonian αj−βj path in the
3 4
K formed by Aj can be established as (αj, M1, M2, βj) if Qj=αj and
Lj=βj, (αj, Qj, M2, βj) if Qj≠αj and Lj=βj, (αj, M1, Lj, βj) if Qj=αj and Lj≠βj, and (αj, Qj, Lj, βj) if Qj≠αj and Lj≠βj, where M1 and M2 are the other 3-vertices of Aj. Without loss of generality, we assume
that (αj, Qj, Lj, βj) is established. The discussions for other possibilities are all similar. Suppose E=<e1e2...en>3, F=<f1f2...fn>3, and G=<g1g2...gn>3 are arbitrary three consecutive 3−vertices in (βj−1,
αj, Qj, Lj, βj, αj+1). Then edif(E,F)≠gdif(F,G) holds as before. A fault-free hamiltonian xj-yj path can be generated from (αj, Qj, Lj, βj), which is similar to the situation of A1.
Thus far we have constructed fault-free paths in A1, A2, …, An(n-1)⋅⋅⋅5-1, and consequently there is
a u−yn(n-1)⋅⋅⋅5-1 path of length n!−2|Fv|−25. We continue to construct a fault-free path in An(n-1)⋅⋅⋅5 as
follows. Assume v=v1v2...vn. Let D=<d1d2...dn>3∉{αn(n−1)⋅⋅⋅5, βn(n−1)⋅⋅⋅5} be a 3-vertex of An(n-1)⋅⋅⋅5 with
dk≠v1. Since βn(n−1)⋅⋅⋅5 is the ending 3−vertex, which is not connected to An(n-1)⋅⋅⋅5−1, we have αn(n−1)⋅⋅⋅5≠
βn(n−1)⋅⋅⋅5. A fault-free hamiltonian αn(n−1)⋅⋅⋅5-βn(n−1)⋅⋅⋅5 path in the
3 4
established as (αn(n−1)⋅⋅⋅5, M1, D, βn(n−1)⋅⋅⋅5), where M1 is the other 3-vertex of An(n-1)⋅⋅⋅5.
Suppose E=<e1e2...en>3, F=<f1f2...fn>3, and G=<g1g2...gn>3 are arbitrary three consecutive
3−vertices in (βn(n−1)⋅⋅⋅5−1, αn(n−1)⋅⋅⋅5, M1, D, βn(n−1)⋅⋅⋅5). Then edif(E,F)≠gdif(F,G) holds as before. We note that v is not adjacent to any vertex of D because dk≠v1 and each edge between D and βn(n−1)⋅⋅⋅5 is a
k−dimensional edge. Since An(n-1)⋅⋅⋅5−1 and An(n-1)⋅⋅⋅5 are fault-free, Lemmas 9 and 10 assure that there
are distinct fault-free vertices xn(n-1)⋅⋅⋅5, r ∈αn(n−1)⋅⋅⋅5, s, t ∈M1, and w, z∈D so that every two
consecutive vertices in {xn(n-1)⋅⋅⋅5, r, s, t, w, z, f} are adjacent, where xn(n-1)⋅⋅⋅5 is the fault-free vertex of
αn(n−1)⋅⋅⋅5 that is adjacent to yn(n-1)⋅⋅⋅5-1 and f is a fault-free vertex of βn(n−1)⋅⋅⋅5.
Let (c0, c1, c2, c3, c4, c5) represent the ring formed by βn(n−1)⋅⋅⋅5, where c0=v is assumed. We let
yn(n-1)⋅⋅⋅5=v=c0. Since v is not connected to D, by Lemma 9 f∉{c0, c3}. If dist(u, v) is even, every u−v
path has even length, because Sn is bipartite. Since f=c1 or c5 causes a u-v path of length n!−2|Fv|−1,
which is a contradiction, we have f=c2 or c4. A fault-free xn(n-1)⋅⋅⋅5-yn(n-1)⋅⋅⋅5 path of length 22 can be
generated in An(n-1)⋅⋅⋅5 accordingly. Similarly, if dist(u, v) is odd, then f=c1 or c5, and a fault-free
hamiltonian xn(n-1)⋅⋅⋅5-yn(n-1)⋅⋅⋅5 path of length 23 can be generated in An(n-1)⋅⋅⋅5.
The fault-free x1−y1, x2−y2, …, xn(n-1)⋅⋅⋅5−yn(n-1)⋅⋅⋅5 paths that we have generated in A1, A2, ..., An(n-1)⋅⋅⋅5,
respectively, interleaved with edges (y1, x2), (y2, x3), …, (yn(n-1)⋅⋅⋅5-1, xn(n-1)⋅⋅⋅5) form a fault-free u−v
path in the P4. The path has length n!-2|Fv|-2 if dist(u, v) is even, and n!-2|Fv|-1 if dist(u, v) is odd.
Hence we have the following lemma.
Lemma 12. A fault-free u-v path can be generated in a good P4 that was obtained by executing
an (a1, a2, ..., an-4)-partition on Sn. The path has length n!-2|Fv|-2 if dist(u, v) is even, and n!-2|Fv|-1
if dist(u, v) is odd.
Since Sn is bipartite with two partite sets of equal size, a u−v path in Sn has length at most n! -2|Fv|-2 if dist(u, v) is even, and at most n!-2|Fv|-1 if dist(u, v) is odd, both in the worst case. As a consequence of Lemma 12, the following theorem summaries the main result of this section.
Theorem 1. Sn with |Fv|≤n-5 faulty vertices can embed a fault-free u−v path of length n!
-2|Fv|-2 if dist(u, v) is even, and n!--2|Fv|-2|Fv|-1 if dist(u, v) is odd, where n≥6 and u, v are arbitrary two vertices of Sn. The path is the longest in the worst case.
4 Embed a fault-free u
−−−−
v path onto S
nwith |F
v|=n-4 or n
−−−−
3 faulty vertices
We have assumed |Fv|≤n-5 in the preceding section. The situation of |Fv|=n-4 or n−3 is discussed in this section. Since Sn is regular of degree n−1, |Fv|=n-3 is maximum in the worst case in order to embed a longest fault−free path between any two vertices of Sn.
Suppose u=u1u2...un, v=v1v2...vn, and b1, b2, ..., bn-4 are a sequence of positions satisfying Lemma
2. There exist a sequence of positions, denoted by p1, p2, …, pn-3, so that up1≠vp1 and after
executing a (p1, p2, …, pn-3)-partition on Sn, each resulting 3−vertex contains at most one faulty vertex. The positions p1, p2, …, pn-3 can be determined as follows. If ubj ≠vbj for some 1≤j≤n−4,
let p1=bj, {p2, p3, …, pn-4}={b1, b2, …, bn-4}−{bj}, and pn-3 ∈{2, 3, …, n}−{b1, b2, …, bn-4}.
Otherwise, if ub
j = vbj for all 1≤j≤n−4, let p1∈{2, 3, …, n}−{b1, b2, …, bn-4} with up1≠vp1, and
{p2, p3, …, pn-3}={b1, b2, …, bn-4}.
Definition 8. A P4=[A1, A2, ..., An(n-1)⋅⋅⋅5] in Sn is said to be partially good if it satisfies the
following five conditions.
(Cond. 1) A1 and An(n-1)⋅⋅⋅5 are the beginning and ending 4-vertices, respectively.
(Cond. 2) One of A1, A2, ..., An(n-1)⋅⋅⋅5 contains at most two faulty vertices, and the others each
contain at most one faulty vertex.
(Cond. 3) For every three consecutive 4-vertices in the P4, say E=<e1e2...en>4, F=<f1f2...fn>4, and
G=<g1g2...gn>4, edif(E,F)≠gdif(F,G) holds.
(Cond. 4) If Ak contains two faulty vertices, both Ak−1 and Ak+1 are not faulty, where 2≤k≤n(n−1)⋅⋅⋅
5−1.
(Cond. 5) After executing a pn-3-partition on the P4, the beginning and ending 3-vertices (in A1 and
An(n-1)⋅⋅⋅5, respectively) are not connected to A2 and An(n-1)⋅⋅⋅5−1, respectively.
Lemma 13. A partially good P4 can be obtained by executing a (p1, p2, ..., pn-4)-partition on Sn.
Proof. Without loss of generality, we assume |Fv|=n−3. A P5=[A1, A2, ..., An(n-1)⋅⋅⋅6] can be
is not difficult to check that (Cond. 1) and (Cond. 3) of Definition 6 hold. Since there are at least n−5 faulty 5−vertices in the P5, a faulty 5−vertex may contain at most three faulty vertices.
In the rest of the proof, we show that a partially good P4 can be generated in the P5. We
consider the situation that a faulty 5−vertex, say Ar, contains three faulty vertices and the other faulty 5−vertices each contain one faulty vertex. Other situations can be treated similarly. A pn-4-partition is first applied to the P5, and so each Ai forms a K5
4
, where 1≤i≤n(n-1)⋅⋅⋅6. Since there are at least n−4 faulty 4−vertices after executing a (p1, p2, ..., pn-4)−partition on Sn, at most one
faulty 4−vertex contains two faulty vertices. The following three cases are discussed, where u=u1u2...un and v=v1v2...vn are assumed.
Case 1. r=1. Let X1 be the beginning 4-vertex, T be the 4−vertex of A1 that is not connected to A2,
W=<w1w2...wn>4≠X1 be the 4−vertex of A1 with wpn−4= upn−3, and Y1 ∉{T, W, X1} be a 4−vertex of
A1 that is adjacent to a fault-free 4−vertex of A2. A hamiltonian path in the K54 formed by A1 can
be established as (X1, W, M1, M2, Y1) if T∈{X1, W}, and (X1, W, T, M1, Y1) if T∉{X1, W}, where M1
and M2 are the other 4-vertices of A1.
A hamiltonian path in the K54 formed by An(n-1)⋅⋅⋅6 can be established similar to the hamiltonian
Xn(n-1)⋅⋅⋅6−Yn(n-1)⋅⋅⋅6 path that was constructed in Case 1 of the proof of Lemma 8. What needs to be
changed is to substitute dpn−4= vpn−3 for dan−4= vk. For 2≤j≤n(n-1)⋅⋅⋅6-1, the hamiltonian Xj−Yj
path that was constructed in Case 1 of the proof of Lemma 8 can serve as a hamiltonian path in the K54 formed by Aj.
All hamiltonian paths above interleaved with proper 4-edges constitute a P4.
Case 2. r=n(n-1)⋅⋅⋅6. A P4 can be constructed similar to Case 1.
Case 3. 2≤r≤n(n-1)⋅⋅⋅6−1. There are two or three faulty 4−vertices in Ar. First we suppose that two 4−vertices of Ar are faulty. Since the P5 satisfies (Cond. 3) of Definition 6, by Lemma 1 each
4−vertex of Ar is connected to Ar−1 or Ar+1. Let B≠F be the two 4-vertices of Ar that are not
connected to Ar-1 and Ar+1, respectively, and S ∉{B, F} be a fault-free 4−vertex of Ar. A hamiltonian path in the K54 formed by Ar can be established as (F, S, M1, M2, B) if F contains two
faulty vertices, (F, M1, M2, S, B) if B contains two faulty vertices, and (F, M1, M2, M3, B) otherwise,
where M1, M2, and M3 are the other 4-vertices of Ar. On the other hand, if three 4−vertices of Ar are
faulty, it is easy to establish a hamiltonian path in the K54 formed by Ar so that the first two and the last two 4−vertices are connected to Ar−1 and Ar+1, respectively.
Hamiltonian paths in the K54's formed by A1 and An(n-1)⋅⋅⋅6 can be established similar to Case 3
of the proof of Lemma 8. What needs to be changed is to substitute wp
n−4= upn−3and dpn−4= vpn−3
for wa
n−4=ul and dan−4=vl, respectively. For 2≤j≤n(n-1)⋅⋅⋅6-1 and j≠r, there is a hamiltonian Xj−Yj
path in the K54 formed by Aj whose first two and last two 4−vertices are connected to Aj−1 and Aj+1,
respectively, where Xj and Yj are the entry and the exit 4−vertices of Aj, respectively.
All hamiltonian paths above interleaved with proper 4-edges constitute a partially good P4 for
the reasons as follows. Clearly, (Cond. 1) and (Cond. 2) hold. Since the first two and the last two 4-vertices in the hamiltonian path for the K54 formed by each Ai are connected to Ai-1(if existing) and Ai+1 (if existing), respectively, where 1≤i≤n(n-1)⋅⋅⋅6, (Cond. 3) holds with arguments similar to the proof of Lemma 5. (Cond. 4) holds as a consequence of our construction. (Cond. 5) holds with arguments similar to the proof of Lemma 8. Q.E.D.
Definition 9. A P3=[A1, A2, ..., An(n-1)⋅⋅⋅4] in Sn is said to be partially good if it satisfies the
following four conditions.
(Cond. 1) A1 and An(n-1)⋅⋅⋅4 are the beginning and ending 3-vertices, respectively.
(Cond. 2) Each 3−vertex contains at most one faulty vertex.
(Cond. 3) Both every two consecutive 3−vertices in the P3 are not faulty.
(Cond. 4) For every three consecutive 3-vertices in the P3, say E=<e1e2...en>3, F=<f1f2...fn>3, and
G=<g1g2...gn>3, edif(E,F)≠gdif(F,G) holds.
Lemma 14. A partially good P3 can be obtained by executing a (p1, p2, ..., pn-3)-partition on Sn.
Proof. Without loss of generality, we assume |Fv|=n−3. By Lemma 13 a partially good P4=[A1,
A2, ..., An(n-1)⋅⋅⋅5] can be obtained by executing a (p1, p2, ..., pn-4)-partition on Sn. A pn-3−partition is
then executed on the P4, and so each Ai forms a K4 3
, where 1≤i≤n(n-1)⋅⋅⋅5. We note that after executing a (p1, p2, ..., pn-3)-partition on Sn, each resulting 3−vertex contains at most one faulty
vertex. When n=4, a partially good P3 can be derived easily. In the rest of the proof, we assume
n≥5 and construct a partially good P3 from the P4.
We first suppose that A1 contains two faulty vertices and An(n-1)⋅⋅⋅5 contains one faulty vertex. If
An(n-1)⋅⋅⋅5 contains two faulty vertices, or A1 and An(n-1)⋅⋅⋅5 each contain one faulty vertex, or only one
of them is faulty, the discussion is similar. Let X1 denote the beginning 3−vertex (in A1), and Q≠L
denote the two faulty 3−vertices of A1. Since the P4 is partially good, X1 is not connected to A2.
Hence, if X1 ∉{Q, L}, both Q and L are connected to A2. Moreover, Q or L is adjacent to a
fault-free 3−vertex of A2. A hamiltonian path in the K4 3
formed by A1 can be established as (X1, Q, M1,
L) if L is adjacent to a fault-free 3−vertex of A2, and (X1, L, M1, Q) if L is adjacent to a faulty
3−vertex of A2, where M1 is the other 3−vertex of A1. If X1 ∈{Q, L}, a hamiltonian path in the K4 3
formed by A1 can be established as (X1, M1, L, M2) if X1=Q, and (X1, M1, Q, M2) if X1=L, where M1
and M2 are the other 3−vertices of A1.
For 2≤j≤n(n-1)⋅⋅⋅5, a hamiltonian path in the K43 formed by Aj can be established as follows. The entry and exit 3-vertices of Aj, denoted by Xj and Yj, respectively, are first determined so that Yn(n-1)⋅⋅⋅5 is the ending 3−vertex and both Yj-1 and Xj are not faulty. Since three 3−vertices of Aj are
connected to Aj-1 and three 3−vertices of Aj are connected to Aj+1, there is a hamiltonian Xj-Yj path in the K4
3
formed by Aj whose first two and last two 3-vertices are connected to Aj-1 and Aj+1, respectively.
All hamiltonian paths above interleaved with proper 3-edges constitute a P3. Next we consider
the other situation that both A1 and An(n-1)⋅⋅⋅5 are fault-free. We first suppose that there is a 4−vertex,
say Ar, containing two faulty vertices, where 2≤r≤n(n-1)⋅⋅⋅5−1. Hence, Ar-1 or Ar+1 is fault-free. Let J≠K be the two faulty 3−vertices of Ar. A hamiltonian path in the K4
3
formed by Ar can be established according to the following three cases.
Case 1. J is connected to both Ar-1 and Ar+1 and K is connected to both Ar-1 and Ar+1. We assume without loss of generality that J is adjacent to a fault-free 3−vertex of Ar-1 and K is adjacent to a fault-free 3−vertex of Ar+1. Let M1 and M2 be the other two 3−vertices of Ar. Since the P4 is
partially good, by Lemma 1 M1 and M2 each are connected to Ar-1 or Ar+1. We further assume that
M1 and M2 are not connected to Ar-1 and Ar+1, respectively. A hamiltonian path in the K4 3
by Ar can be established as (J, M2, M1, K).
Case 2. J is connected to both Ar-1 and Ar+1 and K is connected to one of Ar−1 and Ar+1. Without loss
of generality, we assume that K is connected to Ar+1. Let I denote the 3−vertex of Ar that is not connected to Ar+1. A hamiltonian path in the K54 formed by Ar can be established as (I, J, M1, K) if
K is connected to a fault-free 3−vertex of Ar+1, and (J, I, K, M1) if K is connected to a faulty
3−vertex of Ar+1, where M1 is the other 3−vertex of Ar+1.
Case 3. J is connected to only Ar−1 and K is connected to only Ar+1. Since Ar-1 or Ar+1 is
fault-free, J is adjacent to a fault-free 3−vertex of Ar−1 or K is adjacent to a fault-free 3−vertex of Ar+1. A
hamiltonian path in the K54 formed by Ar can be established as (M1, J, M2, K) if J is adjacent to a
faulty 3−vertex of Ar−1, (J, M1, K, M2) if K is adjacent to a faulty 3−vertex of Ar+1, and (J, M1, M2, K)
otherwise, where M1 and M2 are the other 3-vertices of Ar. We note that the first two and the last two 3−vertices in the hamiltonian path are connected to Ar−1 and Ar+1, respectively. Moreover, both
the first 3−vertex and the 3−vertex of Ar−1 that is adjacent to it are not faulty, and both the last
3−vertex and the 3−vertex of Ar+1 that is adjacent to it are not faulty. For 1≤j≤n(n-1)⋅⋅⋅5 and j≠r, a hamiltonian path in the K4
3
formed by Aj can be established as follows. The entry and exit 3-vertices of Aj, denoted by Xj and Yj, respectively, are first determined so that X1 is the beginning 3−vertex, Yn(n-1)⋅⋅⋅5 is the ending 3−vertex, and both Yk-1 and Xk are not
faulty, where 2≤k≤n(n-1)⋅⋅⋅5 and k≠r. Since three 3−vertices of Aj are connected to Aj-1 and three 3−vertices of Aj are connected to Aj+1, there exists a hamiltonian Xj-Yj path in the K43 formed by Aj whose first two and last two 3-vertices are connected to Aj-1 and Aj+1, respectively.
All hamiltonian paths above interleaved with proper 3-edges constitute a P3. On the other
hand, if each 4−vertex contains at most one faulty vertex, a P3 can be constructed more easily.
The P3 constructed above is partially good for the reasons as follows. Clearly, (Cond. 1) and
(Cond. 2) hold. (Cond. 3) holds as a consequence of our construction. Since the first two and the last two 3-vertices in the hamiltonian path for the K4
3
formed by each Ai are connected to Ai-1(if existing) and Ai+1 (if existing), respectively, where 1≤i≤n(n-1)⋅⋅⋅5, (Cond. 4) holds with arguments similar to the proof of Lemma 5. Q.E.D.
Lemma 15. A fault-free u-v path can be generated in a partially good P3 whose length is at least n!-4|Fv|-10 if dist(u, v) is even, and at least n!-4|Fv|-9 if dist(u, v) is odd.
Proof. Suppose a partially good P3=[A1, A2, ..., An(n-1)⋅⋅⋅4] is obtained by executing a (p1, p2, ...,
pn-3)-partition on Sn according to Lemma 14. Let (qi,0, qi,1, ..., qi,5) denote the ring formed by Ai, where 1≤i≤n(n-1)⋅⋅⋅4. In order to generate a fault-free u-v path, we need to construct fault-free paths in A1, A2, ..., An(n-1)⋅⋅⋅4 sequentially. According to Lemma 9, we assume without loss of
generality that q1,0 and q1,3 are adjacent to two vertices r and s of A2, respectively. If u=q1,0, a
fault-free path in A1 can be constructed according to the following three cases.
Case 1. A1 is fault-free and A2 is faulty. If s is fault-free, either of (q1,0(=u), q1,1, q1,2, q1,3) and
(q1,0(=u), q1,5, q1,4, q1,3) is constructed. If s is faulty, a single vertex q1,0(=u) is constructed.
Case 2. A1is faulty and A2 is fault-free. If q1,1 or q1,2 is faulty, (q1,0(=u), q1,5, q1,4, q1,3) is constructed.
If q1,4 or q1,5 is faulty, (q1,0(=u), q1,1, q1,2, q1,3) is constructed. If q1,3 is faulty, a single vertex q1,0(=u)
is constructed.
Case 3. Both A1 and A2 are fault-free. Either of (q1,0(=u), q1,1, q1,2, q1,3) and (q1,0(=u), q1,5, q1,4, q1,3) is
constructed.
The discussion is similar if u=q1,3. If u ∈{q1,1, q1,2, q1,4, q1,5}, a fault-free path in A1 can be
constructed according to the following three cases.
Case 1. A1 is fault-free and A2 is faulty. If u=q1,1, a fault-free hamiltonian u−q1,0 path in A1 is
constructed if r is fault-free, and (q1,1(=u), q1,0, q1,5, q1,4, q1,3) is constructed if r is faulty. If u=q1,2 or
q1,4 or q1,5, a fault-free path in A1 can be constructed similarly.
Case 2. A1 is faulty and A2 is fault-free. If u=q1,1, (q1,1(=u), q1,0, q1,5, q1,4, q1,3) is constructed if q1,2 is
faulty, (q1,1(=u), q1,0) is constructed if q1,3 is faulty, and (q1,1(=u), q1,2, q1,3) is constructed if q1,0 or
q1,4 or q1,5 is faulty. If u=q1,2 or q1,4 or q1,5, a fault-free path in A1 can be constructed similarly.
constructed. If u=q1,2 or q1,4, a fault-free hamiltonian u−q1,3 path in A1 is constructed.
For 2≤j≤n(n-1)⋅⋅⋅4−1, a fault-free path in Aj can be constructed as follows. Suppose yj−1 is the
last vertex of the fault-free path constructed in Aj-1, and the vertex of Aj that is adjacent to yj−1 is
fault−free. Without loss of generality, we assume that qj,0 is the vertex of Aj that is adjacent to yj−1.
According to Lemma 10, we further assume that qj,1 and qj,4 are adjacent to two vertices g and h of Aj+1, respectively. A fault-free path in Aj can be constructed according to the following three cases.
Case 1. Aj is fault-free and Aj+1 is faulty. If g is fault-free, a fault-free hamiltonian qj,0−qj,1 path in A1 is constructed. If g is faulty, (qj,0 , qj,1, qj,2, qj,3, qj,4) is constructed.
Case 2. Aj is faulty and Aj+1 is fault-free. If qj,5 is faulty, (qj,0 , qj,1, qj,2, qj,3, qj,4) is constructed. If qj,4 is faulty, (qj,0, qj,1) is constructed. If qj,1 or qj,2 or qj,3 is faulty, (qj,0 , qj,5, qj,4) is constructed.
Case 3. Both Aj and Aj+1 are fault-free. A fault-free hamiltonian qj,0−qj,1 path in Aj is constructed. The discussion is similar if both qj,2 and qj,5 are connected to Aj+1. We continue to construct a fault-free path in An(n-1)⋅⋅⋅4 as follows. Suppose yn(n-1)⋅⋅⋅4−1 is the last vertex of the fault-free path
constructed in An(n-1)⋅⋅⋅4-1. Without loss of generality, we assume that qn(n-1)⋅⋅⋅4,0 is the vertex of An(n-1)⋅⋅⋅4
that is adjacent to yn(n-1)⋅⋅⋅4−1. We note that qn(n-1)⋅⋅⋅4,0 is fault-free. If v=qn(n-1)⋅⋅⋅4,1, a fault-free
hamiltonian qn(n-1)⋅⋅⋅4,0−v path in An(n-1)⋅⋅⋅4 is constructed if An(n-1)⋅⋅⋅4 is fault-free, and (qn(n-1)⋅⋅⋅4,0, qn(n-1)⋅⋅⋅4,1(=v)) is constructed if An(n-1)⋅⋅⋅4 is faulty. If v=qn(n-1)⋅⋅⋅4,2, (qn(n-1)⋅⋅⋅4,0, qn(n-1)⋅⋅⋅4,5, qn(n-1)⋅⋅⋅4,4, qn(n-1)⋅⋅⋅4,3, qn(n-1)⋅⋅⋅4,2) is constructed if An(n-1)⋅⋅⋅4 is fault-free or qn(n-1)⋅⋅⋅4,1 is faulty, and (qn(n-1)⋅⋅⋅4,0, qn(n-1)⋅⋅⋅4,1, qn(n-1)⋅⋅⋅4,2) is
constructed if qn(n-1)⋅⋅⋅4,3 or qn(n-1)⋅⋅⋅4,4 or qn(n-1)⋅⋅⋅4,5 is faulty. If v=qn(n-1)⋅⋅⋅4,3, either of (qn(n-1)⋅⋅⋅4,0, qn(n-1)⋅⋅⋅4,1, qn(n-1)⋅⋅⋅4,2, qn(n-1)⋅⋅⋅4,3) and (qn(n-1)⋅⋅⋅4,0, qn(n-1)⋅⋅⋅4,5, qn(n-1)⋅⋅⋅4,4, qn(n-1)⋅⋅⋅4,3) is constructed if An(n-1)⋅⋅⋅4 is fault-free, (qn(n-1)⋅⋅⋅4,0, qn(n-1)⋅⋅⋅4,1, qn(n-1)⋅⋅⋅4,2, qn(n-1)⋅⋅⋅4,3) is constructed if qn(n-1)⋅⋅⋅4,4 or qn(n-1)⋅⋅⋅4,5 is faulty, and (qn(n-1)⋅⋅⋅4,0, qn(n-1)⋅⋅⋅4,5,
qn(n-1)⋅⋅⋅4,4, qn(n-1)⋅⋅⋅4,3) is constructed if qn(n-1)⋅⋅⋅4,1 or qn(n-1)⋅⋅⋅4,2 is faulty. If v=qn(n-1)⋅⋅⋅4,4 or qn(n-1)⋅⋅⋅4,5, the
discussion is similar to v= qn(n-1)⋅⋅⋅4,1 or qn(n-1)⋅⋅⋅4,2, respectively. If v=qn(n-1)⋅⋅⋅4,0, a single vertex v is
constructed.
Thus far we have constructed fault-free paths in A1, A2, …, An(n-1)⋅⋅⋅4. These paths interleaved
with proper edges constitute a fault-free u−v path. The u−v path has minimum length when A1 is
A1, three vertices of A2, and five vertices of An(n-1)⋅⋅⋅4 are excluded from the u−v path and each faulty
Aj may cause at most four vertices excluded from the u−v path, where 2≤j≤n(n-1)⋅⋅⋅4−1, the possibly minimum length is equal to n!−4|Fv|−10. Since Sn is bipartite, the u−v path has length at least n!-4|Fv|-10 if dist(u, v) is even, and at least n!-4|Fv|-9 if dist(u, v) is odd. Q.E.D.
According to Lemmas 14 and 15, we have the following theorem.
Theorem 2. Sn with |Fv|=n-4 or n−3 faulty vertices can embed a fault-free u−v path of length at
least n!-4|Fv|-10 if dist(u, v) is even, and at least n!-4|Fv|-9 if dist(u, v) is odd, where n≥4 and u, v are arbitrary two vertices of Sn.
5 Concluding remarks
In this paper, we have shown that when |Fv|≤n−5, Sn with n≥6 can embed a fault-free path of length n!-2|Fv|−2 (n!-2|Fv|−1, respectively) between arbitrary two vertices of even (odd, respectively) distance. Since Sn is bipartite with two partite sets of equal size, the embedded path is the longest in the worst case. When the two end vertices of the embedded path are adjacent, a fault-free ring of length n!-2|Fv| is obtained, which improves Tseng et al's work [33]. In [33], only a fault−free ring of length n!-4|Fv| can be obtained, where |Fv|≤n−3 is assumed. Instead, our method can obtain multiple fault−free rings of each length n!-2|Fv|.
We also showed that when |Fv|=n−4 or n−3, Sn with n≥4 can embed a fault-free path of length at least n!-4|Fv|−10 (n!-4|Fv|−9, respectively) between arbitrary two vertices of even (odd, respectively) distance. It is still unknown whether or not the embedded path is the longest in the worst case. Since Sn is regular of degree n-1, |Fv|=n−3 is maximum in the worst case in order to embed a longest fault-free path between arbitrary two vertices of Sn.
When |Fv|=0, our result implies that Sn contains a path of length n!-1 between arbitrary two vertices of odd distance. This provides an alternative proof for hamiltonian Sn. Originally, the hamiltonicity of Sn was discussed in [19].