ARTICLE NO.CS975147
Sedimentation Velocity and Potential in a Dilute Suspension
of Charged Composite Spheres
Huan J. Keh1
and Yung C. Liu
Department of Chemical Engineering, National Taiwan University, Taipei 106-17, Taiwan, Republic of China Received May 27, 1997; accepted August 19, 1997
past, due to their wide applications in the areas of chemical, The sedimentation of a charged composite particle composed biomedical, and environmental engineering and science. of a solid core and a surrounding porous shell in an electrolyte
This problem is more complex than that of uncharged colloi-solution is analytically studied. In the solvent-permeable and
ion-dal particles because the electric double layer surrounding penetrable porous surface layer of the particle, idealized
hydrody-each particle is distorted by the fluid flow around the particle. namic frictional segments with fixed charges are assumed to
dis-The deformation of the double layer resulting from the fluid tribute at a uniform density. The equations which govern the ionic
motion is usually referred to as the relaxation effect and concentration distributions, the electric potential profile, and the
gives rise to an induced electric field. The sedimentation fluid flow field inside and outside the surface layer of a charged
potential, which arises in a suspension of settling charged composite particle migrating in an unbounded solution are
linear-ized assuming that the system is only slightly distorted from equi- particles, was first reported by Dorn in 1878, and this phe-librium. Using a perturbation method, these linearized equations nomenon is often known by his name ( 1, 2 ) . The sedimenta-are solved for a composite sphere with the charge densities of the tion potential gradient ( which is of the order 1 – 10 V /m ) rigid core surface and of the surface layer as the small perturbation not only alters the velocity and pressure distributions in the parameters. An analytical expression for the settling velocity of
fluid due to its action on the electrolyte ions but also retards the composite sphere in closed form is obtained from a balance
the settling of the particles by an electrophoretic effect. among its gravitational, electrostatic, and hydrodynamic forces.
An important contribution to the sedimentation theory of a The result demonstrates that the presence of the fixed charges in
nonconducting spherical particle with arbitrary double layer the composite sphere slows down its settling velocity relative to
thickness was made by Booth ( 1 ) . He solved a set of electro-that of an uncharged one. A closed-form formula for the
sedimen-kinetic differential equations using a perturbation method to tation potential in a dilute suspension of identical charged
compos-obtain formulas for the sedimentation velocity and sedimen-ite spheres is also derived by using the requirement of zero net
electric current. The Onsager reciprocal relation is found to be tation potential expressed as power series in the zeta poten-satisfied between sedimentation and electrophoresis. It is shown tial ( z ) of the particle up to O ( z2
) and O ( z ) , respectively. that spherically-symmetric ‘‘neutral’’ composite particles ( bearing Using a unit cell model with the condition of zero net electric no net charge ) can undergo electrophoresis, induce sedimentation current, Levine et al. ( 3 ) derived analytical expressions of potential, and experience a smaller settling velocity relative to
the sedimentation velocity and potential in a suspension of corresponding uncharged particles. The direction of the
electro-identical charged spheres with small surface potential as phoretic velocity or the induced potential gradient is determined
functions of the fractional volume concentration of the parti-by the fixed charges in the porous surface layers of the particles.
cles. In the limiting case of a single particle their result In the limiting cases, the analytical solutions describing the
sedi-somewhat differs from that obtained by Booth, which is not mentation velocity and sedimentation potential ( or electrophoretic
subject to the constraint of zero net current. Numerical re-mobility ) for charged composite spheres reduce to those for
sults relieving the restriction of low surface potential in charged solid spheres and for charged porous spheres. q 1997
Academic Press Booth’s analysis were reported by Stigter ( 4 ) using a
modi-Key Words: composite particles; porous surface layer ; sedimen- fication of the theory of electrophoresis by Wiersema et al.
tation velocity; sedimentation potential; electrophoresis. ( 5 ) . It was found that the Onsager reciprocal relation be-tween the sedimentation potential and the electrophoretic mobility derived by de Groot et al. ( 6 ) is satisfied within 1. INTRODUCTION good computational accuracy. Taking the double layer dis-tortion from equilibrium as a small perturbation, Ohshima et The motions of charged colloidal particles in an electrolyte al. ( 7 ) obtained general expressions and presented numerical solution have received quite an amount of attention in the results for the sedimentation velocity and potential of charged spheres over a broad range of zeta potential and
1
To whom correspondence should be addressed. double layer thickness. Other than cases of spherical
cles, the effect of the deformation of the ion cloud sur- velocity and potential of composite particles have not yet been theoretically investigated.
rounding a charged circular cylinder on the sedimentation
velocity of the particle has also been investigated semianalyt- In this paper, the sedimentation in a dilute suspension of charged composite particles is studied. The densities of the ically ( 8, 9 ) .
The surface of a colloidal particle is generally not hard fixed charges and the hydrodynamic frictional segments are assumed to be uniform throughout the porous surface layer and smooth as assumed in many theoretical models. For
instance, surface layers are purposely formed by adsorbing of each particle, but no assumption is made as to the thick-nesses of the double layer and of the surface layer relative polymers to make the suspended particles stable against
flocculation ( 10 ) . Even the surfaces of model colloids such to the dimension of the particle. In the next section, we present the fundamental electrokinetic equations and bound-as silica and polystyrene latices are ‘‘hairy’’ with a gel-like
polymeric layer extending from the bulk material inside the ary conditions which govern the electrolyte ion distributions, the electrostatic potential profile, and the fluid flow field particle ( 11 ) . In particular, the surface of a biological cell
is not a hard smooth wall, but rather is a permeable rough inside and outside the surface layer of a composite particle migrating in an unbounded solution. These basic equations surface with various appendages ranging from protein
mole-cules on the order of nanometers to cilia on the order of are linearized assuming that the ion concentrations, the elec-tric potential, and the fluid pressure have only a slight devia-microns ( 12 ) . Such particles can be modeled as a composite
particle having a central solid core and an outer porous shell tion from equilibrium due to the motion of the particle. In Section 3, the axisymmetric motion of a charged composite ( 13 ) . The creeping flow of an incompressible Newtonian
fluid past a composite sphere was solved by Masliyah et al. sphere in an unbounded solution of a symmetric electrolyte is considered. Using the Debye – Hu¨ckel approximation, we ( 14 ) using the Brinkman equation for the flow field inside
the fluid-permeable surface layer and the Stokes equations first get the solution of the equilibrium electric potential and ion concentration distributions. Then, the linearized electro-for the flow field external to the particle. An analytical electro-
for-mula for the drag force experienced by the particle was kinetic equations are transformed into a set of differential equations by a perturbation method with the fixed charge derived as a function of the radius of the solid core, the
thickness of the porous shell, and the permeability of the densities of the porous surface layer and of the rigid core surface as the small perturbation parameters. The perturbed shell. They also measured the settling velocities of a solid
sphere with attached threads and found that theoretical pre- ion concentration, electric potential, fluid velocity, and pres-sure profiles are determined by solving this set of differential dictions for the composite sphere are in excellent agreement
with the experimental results. Employing the free-surface equations subject to the appropriate boundary conditions. A closed-form expression for the settling velocity of the cell model for the creeping flow relative to an assemblage
of identical composite spheres, Prasad et al. ( 15 ) later ob- charged composite sphere is obtained from a balance among its gravitational, electrostatic and hydrodynamic forces in tained an analytical solution for the dependence of the
aver-age drag force of this assemblaver-age on the volume fraction of Section 4. In Section 5, the average electric current density in a dilute suspension of identical charged composite spheres the particles.
Most of the past theoretical studies on the electrophoresis is derived, and an explicit formula for the sedimentation potential is resulted from letting the net current in the suspen-of a colloidal particle covered by a charged porous surface
layer ( 12, 16 – 20 ) were performed with the assumption that sion be zero. The Onsager relation between sedimentation and electrophoresis is found to be satisfied for the composite the local radii of curvature of the particle are much larger
than the thicknesses of the electric double layer and of the spheres. Finally, analytical expressions in some limiting cases and typical numerical results of the sedimentation ve-porous surface layer ( i.e., the particle surface is planar and
the applied electric field is parallel to it ) . Experimental re- locity and potential for charged composite spheres are pre-sented in Section 6.
sults of the electrophoretic mobility of charged composite particles are also available for human erythrocytes ( 21 ) , rat
lymphocytes ( 22 ) , and latex particles coated with poly ( N- 2. BASIC ELECTROKINETIC EQUATIONS FOR THE isopropylacrylamide ) hydrogel layers ( 23 ) . Based on a for- MOTION OF A CHARGED COMPOSITE PARTICLE mula derived from the theory of a planar particle surface,
these experimental results could be used to calculate the In this section we consider the relative motion of a charged composite particle of arbitrary shape in an unbounded liquid fixed charge density and the hydrodynamic resistance
param-eter of the porous surface layer. Recently, a general expres- solution containing M ionic species. The definition of a charged composite particle is a charged rigid particle core sion for the electrophoretic mobility of a spherical composite
particle was derived by Ohshima ( 24 ) , neglecting the relax- covered by a surface layer of charged porous substance or adsorbed polyelectrolytes in equilibrium with the sur-ation effect of the double layer. It has been found that the
electrophoretic mobility of a charged composite sphere can rounding electrolyte solution. The porous surface layer is treated as a solvent-permeable and ion-penetrable homoge-be quite different from that of a ‘‘bare’’ rigid sphere.
distribute at a uniform density. Conservation of all species,
Ç2
cÅ 04p
e [ re /h ( x ) Q ] . [ 6 ]
which do not react with one another, in the steady state requires that
Here, Q is the fixed charge density inside the surface layer ;
Ç rJmÅ0, m Å1, 2, . . . , M , [1] eÅ4pe0er, where eris the relative permittivity of the
electro-lyte solution which is assumed to be the same inside and outside the surface layer and e0is the permittivity of a vac-where Jm( x ) is the number flux of species m at position x .
uum. Note that the space charge density in the surface layer If the solution is dilute, the flux can be given by
is the sum of the densities of the mobile ions and the fixed charges.
The boundary conditions at the surface of the nonconduct-Jm Ånmu0Dm
S
Çnm/zmenm
kT
Çc
D
, [ 2 ]ing rigid particle core are
where nm( x ) and zmare the concentration ( number density ) uÅ0 , [ 7a ]
distribution and the valence of species m , respectively; Dm
nrJm Å0, [ 7b ]
is the diffusion coefficient of species m which is assumed to be constant both inside and outside the surface layer ;
u ( x ) is the fluid velocity field relative to the particle; c( x ) is nrÇc Å 04p
e s, [ 7c ]
the electric potential distribution; e is the elementary electric charge; k is Boltzmann’s constant; T is the absolute
tempera-ture. The first term on the right-hand side of Eq. [ 2 ] repre- where n is the unit normal outward from the boundary sur-sents the convection of the ionic species by the fluid and the face, s is the surface charge density of the ‘‘bare’’ particle second term denotes the diffusion and electrically induced core. In Eq. [ 7a ] , we have assumed that the shear plane migration of the species. coincides with the surface of the rigid core. Equations [ 7b ] We assume that the Reynolds number of the fluid motion and [ 7c ] state that no ions can penetrate into the rigid core, is very small, so the inertial effect on the fluid momentum and the Gauss condition holds at the surface of the rigid balance can be neglected. The fluid flow is governed by a core.
combination of the Stokes and Brinkman equations modified The conditions far from the particle are with the electrostatic effect,
ur 0U , [ 8a ] hÇ2 u0h ( x ) f u Å Çp0rg/ reÇc, [ 3 ] nmr n`m, [ 8b ] Ç ruÅ0, [ 4 ] cr 0. [ 8c ]
where h and r are the viscosity and density, respectively,
Here, U is the translational velocity of the particle, n`mis the
of the fluid; f is the friction coefficient inside the surface
constant bulk concentration of type m ions, and the electric layer of the composite particle per unit volume of the fluid;
potential in the bulk solution is set equal to zero. Equations p ( x ) is the fluid pressure distribution, g is the acceleration
[ 2 ] , [ 3 ] , and [ 8a ] take a reference frame that the composite of gravity, and re( x ) is the space charge density resulting
particle is at rest and the velocity of the fluid at infinity is from the mobile ionic species and can be written as
the particle velocity in the opposite direction.
The boundary conditions at the surface of the composite
re Å
∑
M mÅ1
zmenm. [ 5 ] particle ( the boundary between the surface layer and the
external solution, S{) are In Eq. [ 3 ] , h ( x ) is a unit step function which equals unity
uÉS/ ÅuÉS0, [ 9a ]
if x is inside the surface layer and which equals zero if x is
nrsÉS/ ÅnrsÉS0, [ 9b ]
outside the composite particle; r, h, f , and g are assumed to be constant. Note that f can be expressed as 6phaSNS,
nmÉS/ ÅnmÉS0, [ 9c ] where NS and aS are the number density and the Stokes
JmÉS/ ÅJmÉS0, [ 9d ] radius, respectively, of the frictional segments in the surface
layer.
cÉS/ ÅcÉS0, [ 9e ]
The local electric potential c and the charge density re
Here, s( x ) is the sum of the hydrodynamic stress sH ( x ) 0Å Çp( eq ) 0 rg0 e 4pÇ 2 c( eq )Ç c( eq ) 0h ( x ) QÇc( eq ) , and the Maxwell stress sE
( x ) of the fluid given by
[14 ] sH Å 0pI/h[Çu/(Çu )T ] [10a ] Ç2c( eq )Å 0 4p e [
∑
M mÅ1 zmen( eq )m /h ( x ) Q ] . [15 ] andIntegration of Eq. [13 ] shows that n( eq )
m is related to c ( eq ) sE Å e 4p( EE 0 1 2E 2
I) , [10b ] by the Boltzmann distribution,
n( eq )
m Ån`mexp
S
0zme c( eq )
kT
D
. [16 ]where I is the unit dyadic, E ( x )Å 0Çc is the electric field,
and E Å ÉEÉ. Equations [ 9a ] and [ 9b ] are the continuity
requirement of the fluid velocity and stress tensor at the
A governing equation for c( eq )
is obtained by the substitution particle surface. Equations [ 9c ] and [ 9d ] state that the
con-of Eq. [16 ] into Eq. [15 ] . centration and flux of species m must be continuous.
Equa-Substituting Eq. [12 ] into Eqs. [1] , [ 3 ] , and [ 6 ] , using tions [ 9e ] and [ 9f ] indicate that the potential and electric
Eqs. [13 ] – [15 ] , and neglecting the products of the small field are also continuous. The continuity of the electric field
quantities u , dnm, and dc, one obtains
results from the assumption that the relative permittivity of the solution takes the same value both inside and outside the surface layer of the composite particle. From Eqs. [ 9b ] ,
urÇn( eq )m 0DmÇr
F
Çdnm/zmekT ( n ( eq )
m Çdc
[ 9f ] , and [10b ] , one obtains that both the Maxwell stress and the hydrodynamic stress must be continuous at the particle
/dnmÇc( eq ))
G
Å0, mÅ1, 2, . . . , M , [17 ]surface, viz., condition [ 9b ] can be replaced by
nrsHÉS/ ÅnrsHÉS0. [11] Ç2 u0h ( x ) l2 uÅ 1 hÇdp 0 e 4ph( Ç2 c( eq )Ç dc
Because the governing equations are coupled nonlinear
partial differential equations, it is a formidable task to find / Ç2
dcÇc( eq ) ) 01
hh ( x ) QÇdc, [18 ]
a general solution of them. Therefore, we shall assume that the Peclet number is sufficiently small so that the system is
Ç2 dcÅ 0 4p e
∑
M mÅ1 zmednm, [19 ]only slightly distorted from the equilibrium state where the particle and fluid are at rest and replace these nonlinear equations by approximate linear equations. One can write
where lÅ( f / h )1 / 2
. Note that the reciprocal of the parameter
l is the shielding length characterizing the extent of flow
pÅp( eq )
/dp , [12a ]
penetration inside the surface layer of the composite particle. The conditions for dnmand dc that resulted from Eqs. [ 7 ]
nmÅn ( eq ) m /dnm, [12b ] and [ 8 ] are cÅc( eq ) /dc, [12c ]
nrÇdnmand nrÇdc at the rigid core surface
where p( eq )
( x ) , n( eq )
m ( x ) , and c
( eq )
( x ) are the equilibrium
of the composite particle are zero, [ 20 ] distributions of pressure, concentration of species m , and
electric potential, respectively, and dp ( x ) , dnm( x ) , and dn
m and dc at infinity must be zero. [ 21]
dc( x ) are the small perturbations to the equilibrium state.
The quantities p( eq ) , n( eq )
m , and c
( eq )
must also satisfy the
Equations [ 9c ] – [ 9f ] yield the following boundary above-mentioned governing equations and boundary
condi-tions at the surface of the composite particle: tions under the equilibrium state. Thus, the fundamental Eqs.
[1] , [ 3 ] , and [ 6 ] lead to the following equations at uÅ0 :
dnmÉS/ ÅdnmÉS0, [ 22a ] ÇdnmÉS/ Å Çdn mÉS0, [ 22b ] Ç r
S
Çn( eq ) m / zmen ( eq ) m kT Çc( eq )D
Å0, mÅ1, 2, . . . , M , dcÉS/ ÅdcÉS0, [ 22c ] ÇdcÉS/ Å ÇdcÉS0. [ 22d ] [13 ]dc( eq ) dr
Z
r År0 Å 04ps e , [ 25a ] c( eq ) Ér Åa/Å c( eq )Ér Åa0, [ 25b ] dc( eq ) drZ
r Åa/ Å dc ( eq ) drZ
r Åa0 , [ 25c ] c( eq )É rr`r0. [ 25d ]The solution to Eq. [ 23 ] satisfying Eq. [ 25 ] is
c( eq ) Åceq01( r ) sV /ceq10( r ) QU/ O ( sV 3 , sV2 QU, sVQU2 , QU3 ) , [ 26 ] where
FIG. 1. Geometrical sketch for the sedimentation of a composite sphere.
sV Å4pzes
ekkT [ 27a ]
The fluid velocity u is a small perturbed quantity, and the boundary conditions for u have been given by Eqs. [ 7a ] ,
[ 8a ] , [ 9a ] , and [11] . and
3. SOLUTION FOR THE MOTION OF A CHARGED
QUÅ4pzeQ ek2
kT , [ 27b ]
COMPOSITE SPHERE IN SYMMETRIC ELECTROLYTES
We now consider the axisymmetric motion of a charged
which are the nondimensional charge densities of the rigid composite sphere of radius a immersed into an unbounded
core surface and of the surface layer, respectively, of the solution of a symmetrically charged, binary electrolyte with
composite particle, and a constant bulk concentration n` ( M Å 2, z/ Å 0z0Å z ,
n`/Ån`0Ån`, where subscripts/and0refer to the cation
and anion, respectively ) . As illustrated in Fig. 1, the com- ceq01( r ) Å
kT ze
S
kr0 1/kr0D
r0 r e 0 k( r 0r0) ; [ 28a ] posite particle has a porous surface layer of constantthick-ness d so that the radius of the rigid core is r0 Å a 0 d .
ceq10( r ) Å kT ze
H
10S
1/ 1 kaD
e0 kd 1/kr0 The translational velocity of the particle UÅUez, where ezis the unit vector in the axial direction. The origin of the spherical coordinate system ( r , u, f ) is taken at the center
of the particle. 1[ kr0cosh ( kr0kr
0)/sinh ( kr0kr0) ] a r
J
, We first seek the solution of c( eq )for a charged composite sphere. Substituting the Boltzmann distribution, Eq. [16 ] ,
if r0 õrõa , [ 28b ] into Poisson’s equation [15 ] for a symmetric electrolyte, one
obtains the equilibrium Poisson – Boltzmann equation,
ceq10( r ) Å kT ze
H
10S
1/ 1 kaD
e0 kd 1/kr0 [ kr0cosh ( kd ) Ç2 c( eq )ÅkT ze k 2 sinhS
ze c ( eq ) kTD
0h ( r ) 4pQ e . [ 23 ] /sinh ( kd ) ]J
a r e 0 k( r 0a ) , if rúa . [ 28c ] Here, h ( r ) equals unity if r0õrõa and is zero if rúa ;Note that c( eq )
and n( eq )
{ depend on r only due to spherical
k is the Debye – Hu¨ckel parameter defined by
symmetry and that the function ceq01( r ) takes the same form
both in the regions r0õrõa and rúa . Expression [ 26 ] for c( eq )
as a power series in the fixed charge densities of
k Å
S
8pz 2 e2 n` ekTD
1 / 2 . [ 24 ]the composite sphere up to O ( sV, QV ) is the equilibrium
solu-tion for the linearized Poisson – Boltzmann equasolu-tion that is valid for small values of the electric potential ( the Debye – The boundary conditions for c( eq )
resulted from Eqs. [ 7c ] ,
Q of the composite particle must be small enough for the
dpÅh
a
H
U00FP 00( r )/U01FP 00( r ) sV /U10FP 00( r ) QU potential to remain small. Note that, the contribution fromthe effects of O ( sV2
, sVQU, QV2
) to c( eq )
in Eq. [ 26 ] disappears
/
F
U02FP 00( r ) /U00FP 02( r )only for the case of symmetric electrolytes.
To solve the small quantities dn{, u , dp , and dc in terms
of the particle velocity U when the parameters sV and QV are
/aek
2
4ph U00ceq01( r ) Fc01( r )
G
sV 2 small, these variables can be written as perturbationexpan-sions in powers of sV and QV ,
/
F
U11FP 00( r ) /U00FP 11( r ) / aek2 4ph U00 dn{Ån00{/ n01{sV /n10{QU/n02{sV2 1( ceq01( r ) Fc10( r ) /ceq10( r ) Fc01( r ) )G
sVQU /n11{sVQU/n20{QU2 / rrr, [ 29a ] uÅu00/u01sV /u10QU /u02sV 2 /F
U20FP 00( r ) /U00FP 20( r ) /u11sVQU/u20QU2/ rrr, [ 29b ] /aek 2 4ph U00ceq10( r ) Fc10( r )G
QU 2J
cos u, [ 30c ] dpÅp00/p01sV /p10QU /p02sV2 /p11sVQU/ p20QU2 / rrr, [ 29c ] dc ÅU00[ Fc01( r ) sV /Fc10( r ) QU ]cos u, [ 31] dc Åc00/c01sV /c10QU /c02sV 2 dm{ÅU00[ F01{( r ) sV /F10{( r ) QU]cos u. [ 32 ] /c11sVQU /c20QU 2 / rrr, [ 29d ]Here, dm{is defined as a linear combination of dn{and dc
UÅU00/U01sV /U10QU/U02sV2
based on the concept of the electrochemical potential ( 7 ) ,
/U11sVQU /U20QU 2/ rrr
, [ 29e ]
dm{Å
kT
zen` dn{{dc, [ 33 ] where the functions nij{, uij, pij, cij, and Uijare independent
of sV and QV . Both n00{ and c00must equal zero due to not
and Fijr( r ) , Fiju( r ) , FPij( r ) , Fcij( r ) , and Fij{( r ) with i and
imposing the concentration gradient and electric field.
j equal to 0, 1, and 2 are functions of r given by Eqs. [ A4 ] , Substituting the expansions given by Eq. [ 29 ] and c( eq )
[ A19 ] , [ A20 ] , and [ A26 ] in the Appendix. and n( eq )
{ given by Eqs. [ 26 ] and [16 ] into the governing
equations [17 ] – [19 ] and boundary conditions [ 7a ] , [ 8a ] ,
4. SEDIMENTATION VELOCITY OF A CHARGED [ 9a ] , [11] , [ 20 ] , [ 21] , and [ 22 ] , and equating like powers
COMPOSITE SPHERE of sV and QV on both sides of the respective equations, we
obtain a set of linear differential equations and boundary
The total force exerted on a charged composite sphere of conditions for each set of the functions nij{, uij, pij, and cij
radius a settling in an electrolyte solution can be expressed with i and j equal to 0, 1, 2, . . . . These perturbation
equa-as tions and their solutions are presented in the Appendix, and the results for the r and u components of u , dp ( to the orders of sV2
, sVQU , and QV2
) , dc, and dm{( to the orders of sV and Ftotal ÅFg/Fe /Fh. [ 34 ] QV ) can be written as
Here, Fgis the gravitational force ( and buoyant force ) , Fe is the electric force, and Fhis the hydrodynamic drag force urÅ{ U00F00r( r )/U01F00r( r ) sV /U10F00r( r ) QU acting on the particle.
The gravitational force is given by
/[ U02F00r( r )/U00F02r( r ) ] sV2 /[ U11F00r( r ) /U00F11r( r ) ] sVQU/[ U20F00r( r ) F g ÅVt[ gp( rp0 r )/gc( rc 0r ) ] gez, [ 35 ] /U00F20r( r ) ] QU2 } cos u, [ 30a ]
where Vtis the dry volume of the composite particle, rpand uuÅ{ U00F00u( r )/U01F00u( r ) sV /U10F00u( r ) QU
rc are, respectively, the true densities of the surface layer
/[ U02F00u( r )/U00F02u( r ) ] sV2
/[ U11F00u( r ) and the rigid core of the composite particle, gp and gc are the dry volume fractions of the surface layer and the rigid
/U00F11u( r ) ] sVQU /[ U20F00u( r )
core, respectively, and gezÅg is the gravitational
accelera-tion.
/U00F20u( r ) ] QU2
The electric force acting on the charged composite sphere where is given by G02( r ) Åe( ka ) 2 24phr [ F01/( r ) 0F010( r ) ] dceq01 dr , [ 41a ] Fe Å
*
r Åa sE rn dS . [ 36 ] G11( r ) Åe( ka ) 2 24phrH
[ F10/( r )0F100( r ) ] dceq01 dr Using the divergence theorem, the above equation can bewritten as /[ F01/( r ) 0F010( r ) ] dceq10 dr
J
, [ 41b ] FeÅ 0*
VA ÇrsE d V/*
SA sE rn dS , [ 37 ] G20( r ) Åe( ka ) 2 24phr [ F10/( r ) 0F100( r ) ] dceq10 dr . [ 41c ] where SAis an arbitrary close surface surrounding thecom-posite particle and VA is the volume between the particle
In Eq. [ 41] , functions ceq01( r ) and ceq10( r ) have been given
surface and SA. Since the electric potential is screened by
by Eq. [ 28 ] , and F01{( r ) and F10{( r ) are defined by Eq. the ions around the particle and decays exponentially, one
[ A19 ] in the Appendix. can choose SA to be a spherical surface with sufficiently
The hydrodynamic drag force acting on the composite large radius so that the second term on the right-hand side
sphere is given by of Eq. [ 37 ] is negligibly small. Thus, the electric force can
be represented by the integral over the fluid volume outside
the composite sphere. Substitution of the Maxwell stress F hÅ
*
r Åa
{0dpI /h[Çu/(Çu )T
] }rn dS . [ 42 ]
given by Eq. [10b ] into Eq. [ 37 ] with this arrangement produces
Substitution of Eq. [ 30 ] into the above equation results in Fe Å 0
e
4p
*
r úaÇcÇ2
cdV . [ 38 ]
FhÅ 0
H
4phaC006( U00/U01sV /U10QU ) Due to the net electric force acting on the particle at the /F
4pha ( C006U02/C026U00) equilibrium state is zero, the leading order of the electricforce is given by /e( ka ) 2 3 U00ceq01( a ) Fc01( a )
G
sV 2 Fe Å 0 e 4p*
r úa (ÇdcÇ2 c( eq ) / Çc( eq )Ç2 dc ) d V . [ 39 ]/
F
4pha ( C006U11/C116U00)/e( ka )2 3 Substituting Eqs. [ 26 ] and [ 31] into Eq. [ 39 ] , one has
1U00( ceq01( a ) Fc10( a ) /ceq10( a ) Fc01( a ) )
G
sVQU FeÅHF
e( ka )2
3 ceq01( a ) Fc01( a ) /
F
4pha ( C006U20/C206U00)/4pha
*
` aS
r aD
3 G02( r ) drG
U00sV2 /e( ka ) 2 3 U00ceq10( a ) Fc10( a )G
QU 2 /F
e( ka ) 2 3 ( ceq01( a ) Fc01( a )/ceq10( a ) Fc01( a ) ) /O ( sV3, sV2QU , sVQU 2, QU 3)J
ez, [ 43 ] /4pha*
` aS
r aD
3G11( r ) dr
G
U00sVQU where coefficients C006, C026, C116, and C206 are given byEqs. [ A6f ] and [ A27f ] .
At the steady state, the total force acting on the settling
/
F
e( ka )2
3 ceq10( a ) Fc10( a ) particle is zero. Using this constraint after the substitution of Eqs. [ 35 ] , [ 40 ] , and [ 43 ] for a symmetric electrolyte into Eq. [ 34 ] , one obtains
/4pha
*
` aS
r aD
3 G20( r ) drG
U00QU 2 /O ( sV3 , sV2 QU, sVQU2 , QU3 )J
ez, [ 40 ] U00Å Vt[ gp( rp0r ) /gc( rc 0r ) ] g 4phaC006 , [ 44a ]U01Å0, [ 44b ] ESEDÅ 0 1 V
*
V Çcd xÅ 0 1 V*
V Çdcd x , [ 47 ] U10Å0, [ 44c ]where we have used Eq. [12c ] and the fact that the volume U02Å U00 C006
F
0C026/*
` aS
r aD
3 G02( r ) drG
, [ 44d ]average of the gradient of the equilibrium electric potential is zero. In order to calculate ESED, we use the requirement that there exists no net current in the suspension. That is, U11Å U00 C006
F
0C116/*
` aS
r aD
3 G11( r ) drG
, [ 44e ]the volume-average current density,
»i… Å 1 V
*
V i d x , [ 48 ] U20Å U00 C006F
0C206/*
` aS
r aD
3 G20( r ) drG
. [ 44f ]must be zero. In Eq. [ 48 ] , i ( x ) is the current density distri-Here, U00is the sedimentation velocity of an uncharged
com-bution. The mathematical analysis given below is similar to posite sphere, which was obtained by Masliyah et al. ( 14 ) ,
that developed by O’Brien ( 25 ) and Ohshima et al. ( 7 ) . and C006is a function of parameters la and r0/ a only. The
The current density i can be written as definite integrals in the closed-form Eqs. [ 44d ] , [ 44e ] , and
[ 44f ] as well as in coefficients C026, C116, and C206can be
performed numerically using Eqs. [ A27f ] and [ 41] . i Å
∑
MmÅ1
zmeJm. [ 49 ]
From Eqs. [ 29e ] and [ 44 ] , the settling velocity of the composite sphere can be expressed as
Substituting Eqs. [ 2 ] , [12 ] , and [16 ] into the above equation U ÅU00[10( ka )2
H1sV2
0( ka )3
H2sVQU and neglecting products of the small perturbation quantities, one has 0( ka )4 H3QU2 /O ( sV3 , sV2 QU, sVQU2 , QU3 ) ] , [ 45 ]
where the dimensionless coefficients iÅu
∑
MmÅ1 zmen ( eq ) m 0
∑
M mÅ1 zmeDm H1Å 0 U02 ( ka )2 U00, [ 46a ] 1F
Çdnm/zme kT ( n ( eq ) m Çdc/dnmÇc ( eq )G
. [ 50 ] H2Å 0 U11 ( ka )3U00, [ 46b ] Far from any particle ( beyond the double layer ) , n( eq )
m r
n`m, Çc
( eq )r
0 , and Eq. [ 50 ] becomes H3Å 0 U20 ( ka )4 U00, [ 46c ] ir 0
∑
M mÅ1 zmeDmS
Çdnm/ zmen`m kT ÇdcD
. [ 51] and their numerical results calculated by using Eqs. [ 44a ] ,[ 44d ] , [ 44e ] , and [ 44f ] will be presented in Section 6. Note
By adding and subtracting the current density given by the that ( ka )2s
V2, ( ka )3
sVQU, and (ka)4 QU 2
are independent of k
above equation in the integrand of Eq. [ 48 ] , one obtains or n`. For a given electrolyte solution, coefficients H1, H2,
and H3are functions of parameters ka , la , and r0/ a only.
»i… Å 0
∑
M mÅ1 zmeDm V*
VS
Çdnm/zmen ` m kT ÇdcD
d x5. SEDIMENTATION POTENTIAL IN A SUSPENSION OF CHARGED COMPOSITE SPHERES
/ 1 V
*
VF
i/∑
M mÅ1 zmeDmS
Çdnm/ zmen`m kT ÇdcDG
d x . We now consider the steady-state sedimentation of a dilutesuspension of identical charged composite spheres of radius
[ 52 ] a in a solution containing M ionic species. The electric fields
around the individual particles collectively give a
sedimenta-tion field ESED in the suspension. It is assumed that the Note that the magnitude of i and Dm can be taken as zero
inside the dielectric rigid core of each composite sphere. suspension is statistically homogeneous, and all effects of
its boundaries are ignored. ESEDis then uniform in the sus- In a statistically homogenous suspension with constant bulk ionic concentrations, the volume average of Çdnm is
pension and can be regarded as the average of the gradient
of electric potential over a sufficiently large volume V of zero. According to the definition of Eq. [ 47 ] the first term on the right-hand side of Eq. [ 52 ] can be written as the suspension to contain many particles. Namely,
Substituting Eqs. [ A19 ] and [ 44a ] into the above equation 0
∑
M mÅ1 zmeDm V*
VS
Çdnm/zmen ` m kT ÇdcD
d xÅL`ESED.and making relevant calculations, we obtain the sedimenta-tion potential field in a dilute suspension of identical charged [ 53 ] composite spheres, Here, ESEDÅ 0w[ gp( rp0r )/gc( rc 0r ) ] mE L` g . [ 58 ] L`Å
∑
M mÅ1 z2 me 2 n`mDm kT , [ 54 ]Here, wÅNVt/V is the true volume fraction of the composite
particles and mEis the electrophoretic mobility of a charged which is the electric conductivity of the electrolyte solution
composite sphere of radius a at low electric potential, in the absence of the particles. The integral in the second
term on the right-hand side of Eq. [ 52 ] can be calculated by first considering for a single particle as if the others were m
E ÅHs as h /HQ a2 Q h /O ( sV 3 , sV2 QU, sVQU2 , QU3 ) , [ 59 ] absent and then multiplying the result by the particle number
N in V, since the integrand vanishes beyond the double layers
surrounding the particles and the suspension is assumed to where the dimensionless coefficients Hs and HQ have the
be dilute. Also, the volume integral can be transformed into following closed forms: a surface integral over a spherical boundary of infinite radius
containing the single particle at its center. Thus, the second
HsÅ kze 6a2 C006kT
*
` r0 ( 2r3 /r3 0) F00r( r ) dceq01 dr dr , [ 60a ] term becomes N V*
rr`F
nrir /∑
M mÅ1 zmeDmS
dnm / zmen`m kT dcD
nG
dS HQÅ ze 6a3 C006kT*
` r0 ( 2r3 /r3 0) F00r( r ) dceq10 dr dr . [ 60b ] Å 0 N V∑
M mÅ1 zmeDm*
rr`F
rS
Çdnm /zmen ` m kT ÇdcD
In Eq. [ 60 ] , functions ceq01( r ) and ceq10( r ) are given by
Eq. [ 28 ] and F00r( r ) is defined by Eqs. [ A4a ] and [ A4d ] . Again, the contribution from the second-order effects of the
1n0
S
dnm/zmen`m
kT dc
D
nG
dS , [ 55 ] fixed charge densities of the composite spheres to ESEDandmEin Eqs. [ 57 ] and [ 59 ] vanishes only for symmetric elec-trolytes. The numerical results of coefficients Hs and HQ
where r is the position vector relative to the particle center.
calculated from Eq. [ 60 ] will be presented in Section 6. For To obtain Eq. [ 55 ] , the requirement of the conservation of
a specific electrolyte solution, these coefficients are functions electric charge (ÇriÅ0 ) and Eq. [ 51] have been used.
of parameters ka , la , and r0/ a only. It is understood that For a symmetric electrolyte with the absolute value of
the result given by Eqs. [ 58 ] – [ 60 ] is only valid with the valence z , the average current density is obtained by the
requirements that w!1 and kaw01 / 3@
1. substitution of Eqs. [ 33 ] , [ 53 ] , and [ 55 ] into Eq. [ 52 ] ,
Equation [ 58 ] is an Onsager reciprocal relation connect-ing the sedimentation potential with the electrophoretic
mo-»i… ÅL`ESED 0z
2 e2
n`N kTV
*
rr`[ D/( rÇdm/rn0dm/n ) bility ( correct to order w ) derived by de Groot et al. ( 6 )
on the basis of irreversible thermodynamics. For a dilute
0 D0( rÇdm0rn0dm0n ) ] dS . [ 56 ] suspension of impermeable rigid spheres, this relation has
also been demonstrated by Ohshima et al. ( 7 ) . For the situa-Substituting Eq. [ 32 ] into Eq. [ 56 ] and using the require- tion of combined sedimentation and electrophoresis in a di-ment that»i… Å0 , one has lute suspension of colloidal particles, the average electric
current density »i… and mass flux »j… can be expressed in
terms of the Onsager transport coefficients b11, b12, b21, and ESEDÅlim rr` 4pr2 z2 e2 n`NU00 3kTVL`
HF
D/S
r dF01/ dr 0F01/D
b22as 0D0S
r dF010 dr 0 F010DG
sV /F
D/S
r dF10/ dr »i… Åb11E/b12g , [ 61a ] »j… Åb21E /b22g , [ 61b ] 0F10/D
0D0S
r dF100 dr 0 F100DG
QU with /O ( sV3 , sV2 QU, sVQU2 , QU3 )J
ez. [ 57 ] b11ÅL, [ 62a ]between the surface potential and the surface charge density b12Åb21Åw[ gp( rp0r )/ gc( rc0 r ) ] mE, [ 62b ]
of the rigid sphere at equilibrium: b22Åw[ gp( rp0 r )/gc( rc 0r ) ] U g , [ 62c ] sÅe( ka /1 ) 4pa c ( eq ) ( a ) . [ 66 ] where L is the electric conductivity of the suspension. For
charged composite spheres in a symmetric electrolyte, LÅ
Substituting the above equation into Eqs. [ 63b ] and [ 63c ] ,
L` / O ( sV, QV ) with L` Å ( D/ / D0) z2e2n`/ kT , mE is
these degenerated results are the same as those of a rigid given by Eq. [ 59 ] to the second orders of sV and QV , and U
sphere with a low surface potential ( 7 ) . Note that, for the can be evaluated using Eq. [ 45 ] to the second order.
two extreme cases kar0 and kar `, Eq. [ 63b ] precisely reduces to UÅU00and the sedimentation velocity limits to 6. RESULTS AND DISCUSSION
the Stokes velocity. Also, Eq. [ 63c ] together with Eq. [ 66 ] leads to mEÅe c( eq )( a ) / 6ph as kar 0 ( the Hu¨ckel limit )
In this section, we first consider several limiting cases of and mE Å e c( eq )
( a ) / 4ph as ka r ` ( the Smoluchowski the expressions [ 45 ] and [ 59 ] for the sedimentation velocity limit ) .
and electrophoretic mobility ( or sedimentation potential ) , When the composite particle is a homogeneous porous respectively, of charged composite spheres. The correctness sphere, one has r0Å0, d Åa , gpÅ1, gc Å0, and sÅ0. of these expressions may be confirmed by examining some In this limiting case, Eqs. [ 44a ] , [ 45 ] , and [ 59 ] become of these limiting cases for which analytical solutions are
already known. Numerical results of the general cases are
then presented. U00ÅVt( rp0r ) g
6pha
F
2 ( la )3cosh ( la )/3a1( la ) 2 ( la )2a
1( la )
G
, [ 67a ] When there is no permeable layer on the surface of therigid particle core, one has dÅ0, r0Åa , gpÅ0, gc Å1,
UÅU00/ U00QU 2 3 ( la )2 a1( la )
H
3a1( la )*
a 0S
r aD
3 G20( r ) dr Q Å 0, and l Å 0. Equations [ 44a ] , [ 45 ] , and [ 59 ] thenreduce to /6
*
a 0 a1( lr ) G20( r ) dr/[ 2 ( la )3 cosh ( la ) U00ÅVt( rc0r ) g 6pha , [ 63a ] /3a1( la ) ]*
` aS
r aD
3 G20( r ) dr03 ( la )2 a1( la ) U ÅU00F
10 esV 2 96phS
1 D/ / 1 D0DS
kT zeD
2 1*
` aS
r aD
2 G20( r ) dr/[ ( l2 a2 /6 ) a1( la ) 1S
ka ka /1D
2 U1( ka , 1 )/ O ( sV3 )G
, [ 63b ] 02 ( la )2 sinh ( la ) ]*
` a G20( r ) drJ
/O ( QU3 ) , [ 67b ] mEÅ as hS
1 ka /1D
U2( ka , 1 )/O ( sV 3 ) , [ 63c ] mEÅ Q hl2H
1/ 1 3S
l kD
2S
1/e02k a 010e 02k a kaD
where U1and U2 are functions defined by
/13
S
l2 l2 0k2DS
1/ 1 kaD
U1( x , y )Å y3 e2 x [ 5 E6( x )03 E4( x ) ]2 08 ex [ E5( x )0E3( x ) ]/e2 x [ 7 E8( 2 x ) 1FS
l kD
2 ka ( 1/e02k a)01/e02k a la coth ( la )0103 E4( 2 x ) 04 E3( 2 x ) ] , [ 64a ]
U2( x , y )Å2 3/ 1 3y 3 0 y3 ex [ 5 E7( x )02 E5( x ) ] , [ 64b ] 01/e02k a
GJ
/O ( QU 3 ) , [ 67c ] andwhere functions G20( r ) and a1( x ) are defined by Eqs. [ 41c ] and [ A5a ] . Equations [ 67b ] and [ 67c ] are identical to the formulas for the sedimentation velocity ( 27 ) and the electro-En( x ) Å
*
`
1
t0ne0xtdt . [ 65 ]
phoretic mobility ( 24, 27, 28 ) , respectively, of a charged porous sphere derived previously.
When l r ` ( very high segment density in the surface Equation [ 63a ] is the result of Stokes law. From Eq. [ 26 ]
motion inside the surface layer is infinitely large. For this Eq. [ 41] and functions ceq01( r ) and ceq10( r ) are given by
limiting case, Eqs. [ 44a ] , [ 45 ] , and [ 59 ] become Eq. [ 28 ] .
To use the general expressions [ 44a ] , [ 45 ] , and [ 59 ] for the sedimentation velocity and electrophoretic mobility and U00ÅVt[ gp( rp0r )/gc( rc0r ) ] g
6pha , [ 68a ] their simplified formulas [ 63 ] , [ 67 ] , [ 68 ] , and [ 70 ] in the limiting cases, the parameters ka , la , r0/ a , sV, and QV of the colloidal system have to be determined. Experimental data UÅU00
H
10 e 96phS
1 D/ / 1 D0D
[ c( eq ) ( a ) ]2for the surface layers of human erythrocytes ( 21 ) and rat lymphocytes ( 22 ) in electrolyte solutions indicated that the shielding length 1 / l has values about 3 nm and that the
1U1
S
ka , r0 aD
/O ( sV 3 , sV2 QU, sVQU2 , QU3)
J
, [ 68b ] magnitude of Q ranges from quite low to about 1.61 106 C /m3, depending on the pH value and ionic strength of the electrolyte solution. For some temperature-sensitive poly (
N-mEÅ e c( eq ) ( a ) 4ph U2
S
ka , r0 aD
/O ( sV 3 , sV2 QU, sVQU2 , QU3) . isopropylacrylamide ) hydrogel layers on latex particles in salt solutions ( 23 ) , values of 1 / l were found to be about 1 – 50 nm and the magnitude of Q could be as high as 8.7 [ 68c ]
1106 C /m3
. As to the surface charge density, experimental study for the adsorption of poly ( vinyl alcohol ) onto AgI Note that in this case the mobile ions can still penetrate the
reported that the value of s changes from 0 to00.035 C / surface layer and the fixed charges are distributed not only
m2
upon increasing the pAg from 5.6 to 11, while experi-at the rigid core surface but also in the surface layer of the
mental data for a positively charged polystyrene latex used composite particle. Thus, the equilibrium potential
distribu-as the adsorbent for the polyelectrolyte poly ( acrylic acid ) tion c( eq )
( r ) , which is given by Eq. [ 26 ] , and the results
showed that s can have a value as high as 0.16 C /m2 ( 26 ) . for the sedimentation velocity and sedimentation potential
It is widely understood that the Debye length 1 / k is in the ( or electrophoretic mobility ) are generally different from
range from angstroms to about a micron, depending on the those in the case of the true nonporous spheres of radius a .
ionic strength of the solution. For a composite particle with When lr0 ( very low segment density ) , the surface layer
sÅ211003
C /m2
and QÅ21106 C /m3
in an aqueous of the composite particle does not exert any resistance to
solution of a univalent electrolyte with 1 / kÅ1009m, one the fluid motion. Then, the function F00r( r ) in Eq. [ 30a ] for
obtains the dimensionless charge densities sV É 0.1 and QV
the r component of the fluid velocity reduces to
É0.1.
According to Eqs. [ 45 ] and [ 46 ] , the sedimentation veloc-ity of a charged composite sphere in a given electrolyte F00r( r ) Å 012
S
r0 rD
3 /32S
r0r
D
01, [ 69 ] solution can be calculated to the second orders s2, sQ , and Q2
. The corrections for the effects of the fixed distributed and Eqs. [ 44a ] , [ 45 ] , and [ 59 ] become charges to U start from s2
, sQ , and Q2
, instead of s and Q . The reason is that these effects are due to the interaction between the particle charges and the local induced sedimen-U00ÅVt[ gp( rp 0r )/gc( rc 0r ) ] g
6phr0 , [ 70a ] tation field; both are of orders s and Q , and thus the correc-tions are of orders s2
, sQ , and Q2
. Figures 2 – 5 show plots of numerical results for the dimensionless coefficients H1, UÅ U00
H
10 2a 3r0*
` r0S
r aD
3 F00r( r ) [ G02( r ) sV2H2, and H3in Eq. [ 46 ] as functions of parameters r0/ a , ka , and la for the sedimentation velocity of a charged composite
/G11( r ) sVQU /G20( r ) QU 2 ] dr
sphere in an aqueous solution of KCl at room temperature. The values ek2 T2 / 4phD/z2e2 Å 0.263 and ek2T2/ /O ( sV3 , sV2 QU, sVQU2 , QU3 )
J
, [ 70b ]4phD0z2e2Å0.254 ( 29 ) are used in the calculations. It is
found from the numerical results that H1, H2, and H3 are
mEÅ ze 9r0hkT
*
` r0 ( 2r3 /r30) F00r( r ) always positive values and satisfy the relation H22°4H1H3. With this relation of inequality, Eq. [ 45 ] illustrates that the presence of the particle charges would reduce the magnitude
1
S
ks dceq01dr /Q dceq10
dr
D
dr of the sedimentation velocity.Figure 2 illustrates that, for a specified value of the
/O ( sV3 , sV2
QU, sVQU2 , QU3
) . [ 70c ] shielding ratio la for a charged composite sphere with r0/ a
Å0.5, the effects of the particle charges on the sedimentation velocity are maximal at ka equal to about 0.2 – 0.6 and fade Here, functions G02( r ) , G11( r ) , and G20( r ) are defined by
FIG. 2. Plot of the dimensionless coefficients H1, H2, and H3in Eq. [ 45 ] for a sedimenting composite sphere of r0/ aÅ0.5 versus ka at fixed values
of la .
out when the value of ka is getting small or large. The reason a . When la r `, the resistance to the fluid motion inside the surface layer of the composite particle is infinitely large for this behavior is obvious. The limit ka r 0 means that
the effect of the presence of the counterions around the and the velocity profile in the surface layer disappears. The ions can still penetrate the surface layer and the equilibrium charged particle is negligible ( viz. the particle is not affected
by the electrostatic interaction with the surrounding counteri- potential distribution c( eq )
is the same as Eq. [ 26 ] . There-fore, for given values of ka and r0/ a with lar `, H1, H2, ons in the hydrodynamic behavior ) , while the limit kar `
indicates that the total charge density is zero everywhere and H3approach constant values as shown in Fig. 3 and in Eq. [ 68b ] . When lar 0, the surface layer does not exert and the total electric force on the particle vanishes. Both
limits result in H1 ÅH2 Å H3Å 0 ( as they are calculated resistance to the fluid motion, and H1, H2, and H3for given values of ka and r0/ a approach another constant values in from Eqs. [ 46 ] and [ 44d,e, f ] ) and the same sedimentation
velocity as that of an uncharged composite particle, regard- Fig. 3 given by Eq. [ 70b ] . Note that these dimensionless coefficients are very sensitive functions of la over the range less of the values of la and r0/ a . Note that the locations of
the maxima in H1, H2, and H3 shift to smaller ka as la of la equal to 1 – 10.
In Figs. 4 and 5, the coefficients H1, H2, and H3are plotted increases.
Figures 2 – 4 also show that H1, H2, and H3increase mono- as functions of the parameter r0/ a for given values of ka and la . It can be seen in Figs. 4a and 5a that H1 is a tonically with decreasing la for given values of ka and r0/
FIG. 3. Plot of the coefficients H1, H2, and H3in Eq. [ 45 ] for a sedimenting composite sphere of r0/ aÅ0.5 versus la at fixed values of ka .
monotonic increasing function of r0/ a for fixed values of ka values of la and r0/ a and are also monotonic decreasing functions of la for fixed values of ka and r0/ a . When ka and la . In the special case of r0/ aÅ0, the composite particle
degenerates to a homogeneous porous sphere and H1 must is small (©5 ) , Hsand HQhave the same order of magnitude;
however, when ka is large (™20 ) , the magnitude of Hsis
be equal to zero. Obviously, H1is independent of la in the
special case of r0/ a Å 1 in which the composite particle much smaller than that of HQ. Figure 6 illustrates that Hs
is proportional to ( ka )01
and HQis independent of ka when
reduces to a rigid sphere with no surface layer. Conversely,
as illustrated in Figs. 4c and 5c, H3decreases monotonically ka@1, consistent with the predictions obtained by assuming the particle surface is planar ( 19 ) , and that both Hsand HQ
with increasing r0/ a and vanishes when r0/ a Å 1. On the
other hand, H2equals zero in both limiting cases of r0/ aÅ are not sensitive functions of ka when ka ! 1, similar to the relevant results for charged solid spheres ( 7 ) and charged 0 and r0/ aÅ1 and there exists a maximal value of H2 for
given values of ka and la , as shown in Figs. 4b and 5b. porous spheres ( 27 ) . Figure 7 indicates that both Hs and
HQ are independent of la when la @ 1 or la ! 1, in
The dimensionless coefficients Hsand HQfor the
sedimen-tation potential or electrophoretic mobility in the KCl solu- accordance with Eqs. [ 68c ] and [ 70c ] . The value of Hsfor
large la for case of kaÅ100 is very small and cannot be tion calculated from Eq. [ 60 ] are plotted as functions of
parameters ka , la , and r0/ a in Figs. 6 – 9. It can be seen shown in the range of the logarithmic plot of Fig. 7a. As exhibited in Figs. 8a and 9a, Hsis a monotonic increasing
that these dimensionless coefficients, which are always
FIG. 4. Plot of the coefficients H1, H2, and H3in Eq. [ 45 ] for a sedimenting composite sphere with kaÅ1 versus r0/ a at fixed values of la .
case of r0/ a Å0, Hsmust equal nothing. However, as can
be seen in Figs. 8b and 9b, HQdecreases monotonically with mEÅHm
a2 Q
h /O ( QU
3
) , [ 71b ]
increasing r0/ a for given values of ka and la and equals zero when r0/ aÅ1.
Theoretical studies ( 30, 31 ) have predicted that a nonuni- where formly charged but ‘‘neutral’’ impermeable sphere ( with
zero area-averaged zeta potential ) can translate in electric
H0 ÅH301 3
FS
a r0D
2 0S
r0 aDG
H2 fields. It would be of interest to know whether compositespheres with zero net charge ( 4pr2
0s / ( 4p / 3 ) ( a 3
0
r3
0) QÅ0 ) can undergo electrophoresis or produce
sedimen-/19
FS
a r0D
2 0S
r0 aDG
2 H1, [ 72a ] tation potential, and be retarded by this potential gradientduring the sedimentation. For such spherically-symmetric ‘‘neutral’’ composite particles ( with sV Å 0( ka / 3 ) [ ( a / r0)2
HmÅ HQ0 1 3
FS
a r0D
2 0S
r0 aDG
Hs. [ 72b ]0( r0/ a ) ] QV ), Eqs. [45] and [59] become
U ÅU00[10( ka )4
H0QU2/ O ( QU3
dimen-FIG. 5. Plot of the coefficients H1, H2, and H3in Eq. [ 45 ] for a sedimenting composite sphere with laÅ10 versus r0/ a at fixed values of ka .
sionless coefficient H0 for the sedimentation velocity of a or the induced potential gradient is decided by the fixed charges in the porous surface layers ( rather than the surface composite sphere in the KCl solution as functions of
parame-ters ka , la , and r0/ a . It can be seen that H0is positive and charges of the rigid cores ) of the particles. Similar to the coefficient HQshown in Figs. 6b and 8b, Hmdecreases
mono-the presence of mono-the fixed-charge distribution in mono-the ‘‘neutral’’
particle would reduce its settling velocity. The tendency of tonically with the increase of la for given values of ka and r0/ a . However, Hmis not necessarily a monotonic function
the dependence of H0 on ka , la , and r0/ a is quite similar
to that of the coefficient H3presented in Figs. 2c – 5c, except of either ka ( as la is large or r0/ a is small ) or r0/ a ( as la is small or ka is large ) . The trend of the dependence of Hm
that the values of H0 are about two orders of magnitude
smaller and its maxima for fixed values of la and r0/ a occur on ka and r0/ a is quite different from that of HQpresented
in Figs. 6b – 9b. When ka is large (™10 ) , the coefficients at values of ka about an order of magnitude larger.
The dimensionless coefficient Hm for the electrophoretic Hmand HQhave the same order of magnitude, but when ka
is as small as 0.1, the values of Hm are about three orders
mobility or sedimentation potential associated with
compos-ite spheres in the KCl solution is drawn as a function of of magnitude smaller than the values of HQ.
parameters ka , la , and r0/ a in Fig. 11. It can be seen that
7. CONCLUDING REMARKS Hm is always positive so that the ‘‘neutral’’ composite
spheres can experience electrophoresis or generate sedimen- The steady-state electrokinetic phenomena of charged composite particles under the action of gravity in an un-tation potential. The direction of the electrophoretic velocity
leads to an explicit formula, Eq. [ 45 ] , for the settling veloc-ity of the charged composite sphere. The corrections for the effects of the fixed distributed charges to the settling velocity begin at the second order ( s2
, sQ , and Q2
) . Numerical results indicate that these effects have a maximum at a finite value of ka ( equal to about 0.2 – 0.6 as r0/ a Å 0.5 ) and disappear when ka approaches zero and infinite. The analyti-cal expression for the average electric current density in a dilute suspension of identical composite spheres is given by Eq. [ 56 ] . The explicit formula, Eq. [ 58 ] , for the sedimenta-tion potential is derived from Eq. [ 56 ] by letting the net current in the suspension be zero. The Onsager reciprocal relation is satisfied between the sedimentation potential and the electrophoretic mobility. It is also found that the first-order dimensionless coefficients ( Hsand HQ) for the
sedi-FIG. 6. Plot of the dimensionless coefficients Hsand HQin Eq. [ 59 ]
for a dilute suspension of identical composite spheres of r0/ aÅ0.5 versus
ka at fixed values of la .
bounded electrolyte solution are analyzed in this work. The surface layer of each composite particle is treated as a sol-vent-permeable and ion-penetrable shell in which fixed-charged groups and frictional segments are distributed at uniform densities. Solving the linearized continuity equa-tions of ions, Poisson – Boltzmann equation, and combined modified Stokes / Brinkman flow equations applicable to the system of an isolated composite sphere by a regular perturba-tion method, we have obtained the ion concentraperturba-tion distri-butions, the electric potential profile, and the fluid flow field. Since the electric potential distribution differs from the equi-librium values, an electric force acting on the charged
com-posite particle is induced. The total force exerted on the FIG. 7. Plot of the coefficients H
sand HQin Eq. [ 59 ] for a dilute
particle is the sum of the gravitational, electric, and hydrody- suspension of identical composite spheres of r0/ aÅ0.5 versus la at fixed
values of ka . namic forces, and the requirement that the total force is zero
the Debye – Hu¨ckel approximation has been generally stud-ied ( 32 ) , and similarly the electroosmotic flow rate and the streaming potential were shown to satisfy the Onsager reciprocity principle whether the capillary wall adsorbs a surface charge layer or not. Hence, different electrokinetic processes could reflect the same intrinsic phenomena, and measurements of one type of process can be used to check those of another. For instance, one can first measure the sedimentation potential in a dilute suspension of particles and then predict the electrophoretic mobility of the particles in the same system without any other measurements.
Additionally, Eqs. [ 45 ] and [ 58 ] with Eqs. [ 44 ] and [ 59 ] are obtained on the basis of the Debye – Hu¨ckel approxima-tion for the equilibrium potential distribuapproxima-tion around a com-posite sphere. A similar formula for the sedimentation
veloc-FIG. 8. Plot of the coefficients Hsand HQin Eq. [ 59 ] for a dilute
suspension of identical composite spheres with kaÅ1 versus r0/ a at fixed
values of la .
mentation potential or electrophoretic mobility are mono-tonic decreasing functions of ka for constant values of la and r0/ a and that they are also monotonic decreasing func-tions of la for fixed values of ka and r0/ a . Expressions [ 45 ] and [ 58 ] for the sedimentation velocity and sedimentation potential ( or electrophoretic mobility ) in a dilute suspension of charged composite spheres reduce to the corresponding formulas for the charged solid spheres and the charged po-rous spheres, respectively, in the limiting cases of r0/ aÅ1 and r0/ aÅ0.
It is worth repeating that the Onsager relation between sedimentation and electrophoresis holds not only for
imper-meable charged particles but also for porous or composite FIG. 9. Plot of the coefficients H
sand HQin Eq. [ 59 ] for a dilute
ones. Another electrokinetic phenomenon in a circular capil- suspension of identical composite spheres with laÅ10 versus r0/ a at fixed
values of ka . lary with the solution-permeable surface charge layer under
FIG. 10. Plot of the dimensionless coefficient H0in Eq. [ 71a ] for a sedimenting composite sphere with zero net charge versus parameters ka , la ,
and r0/ a .
ity of an impermeable rigid sphere with low z potential was potential allowing the use of arbitrary distributions of fixed charge and fluid drag components in the composite particle shown to give an excellent approximation for the case of
reasonably high z potential ( with an error less than 0.1% and compare it with the approximate solution. for ze / kT°2 in a KCl solution ) ( 7 ) . Therefore, our results
might be used tentatively for the situation of reasonably high APPENDIX electric potentials. On the other hand, the decay of the
den-sity distributions of frictional segments ( 33 ) and fixed The Perturbation Equations and Solutions for the Motion charges ( 20 ) in the surface layer of the composite particle of a Charged Composite Sphere
with the distance from the rigid core surface has not been in Symmetric Electrolytes considered in our calculations. In order to see whether our
After the perturbation expansions given by Eq. [ 29 ] and theory can be reasonably extended to the higher values of
the equilibrium distributions given by Eqs. [ 26 ] and [16 ] electric potential or to the nonuniform density distributions
are substituted into Eqs. [ 7a ] , [ 8a ] , [ 9a ] , [11] , and [17 ] – of frictional segments and fixed charges, we propose to
ob-tain a numerical solution of the electrokinetic differential [ 22 ] , and after like powers of sV and QV are equated on both
sides of the respective equations, a set of differential equa-equations with no assumption on the magnitude of electric
FIG. 11. Plot of the dimensionless coefficient Hmin Eq. [ 71b ] for a dilute suspension of identical composite spheres with zero net charge versus
parameters ka , la , and r0/ a .
tions and boundary conditions for each set of the functions
u00Ér Åa/ Åu00Ér Åa0, [ A2b ]
nij{, uij, pij, and cij with i and j equal to 0, 1, and 2 can be
obtained. nrsH00Ér Åa/ ÅnrsH00Ér Åa0, [ A2c ]
u00Érr`r 0U00ez. [ A2d ]
Zeroth-Order Perturbations
Collecting the zeroth-order terms in the procedure of this The solution for the r and u components of the velocity u00 regular perturbation gives and the pressure p00satisfying the above equations is
u00r ÅU00F00r( r ) cos u, [ A3a ]
Ç2
u000h ( r ) l2u00Å 1
h
Çp00, [ A1a ]
u00u ÅU00F00u( r ) sin u, [ A3b ]
Çru00Å0 ; [ A1b ]
p00Åh
aU00FP 00( r ) cos u, [ A3c ] u00Ér År0Å 0 , [ A2a ]

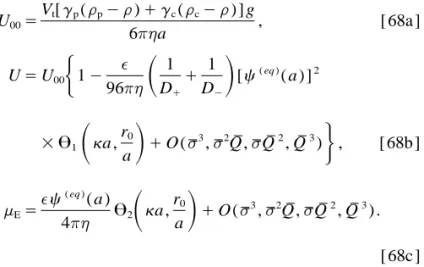
![FIG. 2. Plot of the dimensionless coefficients H 1 , H 2 , and H 3 in Eq. [ 45 ] for a sedimenting composite sphere of r 0 / a Å 0.5 versus ka at fixed values of la .](https://thumb-ap.123doks.com/thumbv2/9libinfo/8868672.247144/12.918.68.852.36.746/plot-dimensionless-coefficients-sedimenting-composite-sphere-versus-values.webp)
![FIG. 3. Plot of the coefficients H 1 , H 2 , and H 3 in Eq. [ 45 ] for a sedimenting composite sphere of r 0 / a Å 0.5 versus la at fixed values of ka .](https://thumb-ap.123doks.com/thumbv2/9libinfo/8868672.247144/13.918.73.852.47.744/plot-coefficients-sedimenting-composite-sphere-versus-fixed-values.webp)
![FIG. 4. Plot of the coefficients H 1 , H 2 , and H 3 in Eq. [ 45 ] for a sedimenting composite sphere with ka Å 1 versus r 0 / a at fixed values of la .](https://thumb-ap.123doks.com/thumbv2/9libinfo/8868672.247144/14.918.72.848.39.749/plot-coefficients-sedimenting-composite-sphere-versus-fixed-values.webp)
![FIG. 5. Plot of the coefficients H 1 , H 2 , and H 3 in Eq. [ 45 ] for a sedimenting composite sphere with la Å 10 versus r 0 / a at fixed values of ka .](https://thumb-ap.123doks.com/thumbv2/9libinfo/8868672.247144/15.918.83.847.47.746/plot-coefficients-sedimenting-composite-sphere-versus-fixed-values.webp)
![FIG. 6. Plot of the dimensionless coefficients H s and H Q in Eq. [ 59 ] for a dilute suspension of identical composite spheres of r 0 / a Å 0.5 versus ka at fixed values of la .](https://thumb-ap.123doks.com/thumbv2/9libinfo/8868672.247144/16.918.48.437.44.747/dimensionless-coefficients-suspension-identical-composite-spheres-versus-values.webp)
![FIG. 8. Plot of the coefficients H s and H Q in Eq. [ 59 ] for a dilute suspension of identical composite spheres with ka Å 1 versus r 0 / a at fixed values of la .](https://thumb-ap.123doks.com/thumbv2/9libinfo/8868672.247144/17.918.54.442.49.754/coefficients-dilute-suspension-identical-composite-spheres-versus-values.webp)
![FIG. 10. Plot of the dimensionless coefficient H 0 in Eq. [ 71a ] for a sedimenting composite sphere with zero net charge versus parameters ka , la , and r 0 / a .](https://thumb-ap.123doks.com/thumbv2/9libinfo/8868672.247144/18.918.56.865.59.774/dimensionless-coefficient-sedimenting-composite-sphere-charge-versus-parameters.webp)
![FIG. 11. Plot of the dimensionless coefficient H m in Eq. [ 71b ] for a dilute suspension of identical composite spheres with zero net charge versus parameters ka , la , and r 0 / a .](https://thumb-ap.123doks.com/thumbv2/9libinfo/8868672.247144/19.918.63.854.55.774/dimensionless-coefficient-suspension-identical-composite-spheres-versus-parameters.webp)