A new dual-type method used in solving optimal power flow problems

(1)

IEEE Transactions on Power Systems, Vol. 12, No. 4, November 1997

A

New Dual-type Method Used

in Solving Optimal Power Flow Problems

Ch’i-Hsin Lin

Shin-Yeu Lin, Member, IEEE

Department

of

Control Engineering

National Chiao Tung University

Hsinchu, TAIWAN

Abstruct-In the framework of SQP method for OPF problems, we propose a new dual-type method for solving the Q P subproblems induced in the SQP method. Our method achieves some attractive features; it is computationally efficient and numerically stable. The computational formulae of our niet,hod are simple, concise and easy to be programmed. We have tested our method for OPF problems on several power systems including a 2500-bus system.

I. INTRODUCTION

Numerous numerical techniques [1]-[lo] have been developed for solving optimal power flow (OPF) problems. These methods are hased on various mathematical programming techniques such as successive linear programming (SLP) method [1]-131, successive quadratic programming (SQP) method [4]-[6], Lagrangian Newton method [7]-[9] or the newly developed interior point (IP) method [lo]. Each of the above methods has its special features and advantages. Observing the SQP method which pos- sesses a quadratic convergence rate, however, the reduced Hessian is dense. The innovative Lagrangian Newton method [7], [8] successfully exploits the sparsity structure of the system; however, efforts are needed to cope with the difficulties of itlciit ifying the binding inequality constraints and the possibility of singular Hessian matrix as pointed out by Moiiticclli and Liu in [9], and they provided remedied strategies to overcome those pitfalls. Nonethe-

PE-549-PWRS-0-01-1997 A paper recommended and approved by the IEEE Power System Engineering Committee of the IEEE Power Engineering Society for publication in the IEEE Transactions on Power System. Manuscript submitted August 1, 1995; made available for printing January 16, 1997.

less, the method in [9] as well as the method in [7] and require sophisticated software programming skill.

In this paper, we use the framework of SQP method and propose a new dual-type method t o solve the QP subproblems. Our method intends to achieve the following features: (i) good convergence rate, (ii) no need to iden- tify the binding constraints, (iii) computational efficiency, (iv) easy programming and (v) numerical stability.

In the framework of SQP method, our method will inherit the advantage of fast convergence as demonstrated in Section V. Features (ii)-(iv) will be achieved by the proposed dual-type method as explained in Section 111. To address feature (v), we provide a mathematical proof for the convergence of the proposed dual-type method in the Appendix.

11. STATEMENT OF THE OPTIMAL POWER FLOW PROBLEM

Throughout this paper, if not specifically explained, we assume the following notations:

e ,

f:

state variables represent the real and imaginary part of the complex voltage.

u: control variables including real and reactive power generation, PG and Q G , transformer tap ratio, switching

capacitor banks,..

. ,

etc..

x : (u, e , f ) denotes the vector of all variables.

F ( z ) : objective function which can be total generation g(x): real and reactive power mismatch.

h(e,

f):

functional inequality constraints such as secu-

V : vector of voltage magnitude,

E

V ,

v:

upper and lower limits of voltage magnitude. a, 3: upper and lower limits of control variables u , such

h , b:

upper and lower limits of functional inequality %, t : iteration index.

a ( % ) ,

p(t)

: step-size.

diag[o] : a diagonal matrix formed by the diagonal terms of the matrix 0 .

A(.) : the increment of the vector cost, pollution cost,, system losses,.

.

,etc.

rity constraints on line flows for specified lines.

d m .

as PG,

L L ,

Q G ,

qGl

etc..

constraints.

(2)

P ( z ) : penalty function for the violations of constraints. w 1 penalty coefficient.

X : the Lagrange multiplier vector.

4(X)

: the dual function of the Q P subproblem.

4"(X)

: unconstrained dual function.

s2 : the set formed by the inequality constraints of the y, 7 , crp, u~ : positive real numbers.

QP subproblems.

TP,TD : E (0, 1).

The OPF problem can be stated as follows:

Remark 1 For the purpose of explanation, we d o not in-

clude the functional inepualzty constraints,

<

h ( e ,

f)

<

h,

in (l), however, this will be treated afterwards.

111. SOLUTION METHOD

A . The S Q P Method

the OPF problem given in (1):

The SQP method uses the following iterations to solve

x(k

+

1) = z ( k )

+

a ( k ) A x ( k ) (2) where a ( k ) is a step-size, and Ax(k) is the solution of the following Q P subproblem:

in which the diagonal matrix H is defined by d Z F ( x ( k ) ) 1

H diag[ _{8 x 2}

I

+

5'7'

(4) where I is an identity matrix, and 7 is a small positive real number but enough t o make H positive definite. termination rule, a cubic fit or quadratic fit method [14] is popular especially for the unconstrained Lagrangian for- mulation in the Lagrangian Newton method [7]. However, in the SQP method, while reducing the value of objective function F ( z ) , we should prevent z ( k

+

1) being too far away from the nonlinear constraints in (1). Therefore, we employ Armijo's rule [ 111, which considers the penalty

Step-srre d e t e r ? n t n a t r o n Concerning the s t e p s & de-

of violating constraints, for the determination of step-size

a ( k ) as follows:

Let 0

<

r p

<

1, u p

>

0, then a ( k ) is set t o be r?(')op

where m ( k ) , the power of T P , is the smallest nonnegative

integer m such that the following inequality holds

F ( x ( L )

+

~ p c ~ p A ~ ( k ) )

+

w P ( z ( k )

+

$ u p A z ( k ) )

2

~ ( z ( l e ) )

+

W P ( + ) ) - : r p p ~ x T ( i l . ) ~ ~ x ( k ) (5)

where the penalty function P ( x ) represents the penalty for the violations on the constraints and is defined by

w is a weighting penalty coefficient, and y E (0,

3).

Al- though Armijo's rule seems inefficient, in most of our test results, the inequality test (5) is passed for m = 0 most of the times. Convergence of the SQP method (2) with a ( k ) determined according to (5) has been shown in [ll].

Treaimenl of dascrete control varaables. In the Q P sub-

problem (3), we treat all the incremental variables Ax as continuous variables. However, the updated formula (2) may make the updated discrete control variables not hav- ing the exact discrete values. To remedy this pitfall, we apply an approximation rule for the update of discrete control variables as follows:

Let U d be the subvector of u denote the discrete control

variables, such as switching capacitor banks, transformer tap ratio, ..., etc., then the continuous-value A u d ( k ) is the

increment of u d ( k ) obtained from solving (3). The ap-

proximation rule for the update of u d ( k

+

1) is

W ( k

+

1) = L U d ( k )

+

& ( k ) A U d ( k ) l , ₍₇₎

where

\(.)I

denote the closest discrete-value to the value of (.). Then u d ( k + l ) obtained froin (7) will be the closest discrete-value of U d to the value of u d ( k )

+

a ( k ) A u d ( k ) .

Cominent 1 When there exzsl znteger varaables an a non- lanear programmang problem, the computataon as very an- volved. Therefore, heurastac methods are developed to handle znteger varzables an most of practacal applacataon problems such a s the approxamataon rule presented here. Though our heurastac rule works well an our problem as s h o w n z n S e c t z o n V, t h e r e z s n o g u a r a n t e e t h a t thzs r u l e wall obtaan satasfactory solutaons an general nonlznear pro- grammang problems coizszstzng of anteger varaables. B. The Proposed Dual-type Method.

Since in (3), all variables Ax are continuous variables,

the objective function is strictly convex, and the constraints are linear, we can solve the dual problem of (3)

(3)

1669 instead of solving (3) directly provided that the solutioii

of (3) exists. This is well-known Duality Theory [14]. The dual problem of the QP subproblem (3) is

max $(A) _x (8)

where the dual function

in which the set R denotes the set of inequality coii- straints in (3) such that

s1=

{ A z l E

5

V ( k )

+

V A e

+

W A f

5 V ,

g

5

u ( k )

+

Au

5

U } .

The proposed dual-type method uses the following iterations to solve (8):

8.f

where

p(t)

is a step-size, and AX(t) is obta.ined from solving the linear equations

in which b

>

0, I is an identity matrix and the unconstrained dual function $u is defined by deleting the primal- variable constraints A.c E R in

4(X)

shown in (9) such that

The first derivative matrix

given in [14] as f o l l o ~ s :

and the approximate Hessian can be computed based on the formula

where AX in (13) is the solution of 4(X(t)) for a given X(t), that is the constrained minimization problem 011 the RHS

of (9) with X = A(!). We will present the method using Projection Theory to solve AX later.

Since

B

+

aZ$" x t is a t least negative semidefinite,

ax2 -

SI

is negative definite. This ensures that

AX(t) = [ # - 6 1 ] - ' w a2$* x t is an ascent direction to

maximize $(A). However, to guarantee the updated point X ( t

+

1) will increase the value of q5(X), we develop an Armijo's rule to determine the step-size

p(t)

as follows:

Let p(t)

=

T - ; [ ~ ) C T D , where

0 <

TD

<

1,

U D

>

0, and m ( t ) is the smallest nonnegative integer m such that

$ ( ~ ( t ) + 6 ? ~ D A ~ ( t ) )

2

$ ( X ( t > ) +

2

6 T D m a D IlAX(t)ll; . (15)

A sketch of the mathematical proof for the justification of (15) and the convergence of (10) is given in the Appendix.

Reinark 2 Sance the objectave functaon

$(A)

an (8) as

contanuous and quadratac, at as practacally suatable t o use a

cubac

fit

or quadratac fit method to determane the step-saze p ( t ) . On account of gavzng a ragorous mathemalacal proof, we prefer t o use Armajo's rule here.

Ayplacabalaty of sparse matrax technaque. The non- zero elements of the fixed-dimension, constant matrix

- 6 1 have the same ax2

structure as the bus admittance matrix of the power net- work. Therefore, we may employ a sparse matrax tech- naque to solve linear equations (11).

However, to set up in (ll), we need to compute AX first as shown in (13).

Applacabilaty of Projectaon Theory. AX is the solution of the constrained minimization problem on the RHS of (9) with X = X(t) which can be solved in two phases using Projection Theory.

Phase 1. Obtain the solution AP of $ u ( A ( t ) ) for a given A(t), that is the unconstrained minimization problem on the RHS of (12) with X = X(t).

Phase 2: Project Ai? onto the constraint set 0, and the resulting projection is AX.

The validity of this two-phase method is justified based on Projection Theory in [12] and is shown in Theorem 1 and Theorem 2 in the Appendix. 111 the following, we

will describe the detailed computational formulae of this two- phase met hod.

From (12), the solution of the unconstrained minimization problem Ai? which is (AGj AZ, Af"), can be analyti- cally derived by

in (14) as well as

Since

H

is a diagonal positive definite matrix, no extra effort is needed to compute H-' in (16).

The inequality constraints for (Ae, A f ) and Au are decoupled, and these inequality constraints are also decoupled for different buses; thus, the projection can be treated separately for each individual bus. T he projection of Ail onto the set R is trivial and can be computed in the following: Let AUa be the projection of AGi onto the subset ( A u i ( 3

5

ui(k)

+

Aua

5

Ui}, then

Ui

-

u i ( k ) ,

Ai&, otherwise.

if ua(k)

+

Ai&

>

Ui,

(4)

Though the projection of (Ai?, A?) onto the set R is more complicated, by simple geometric$ calculation, we can obtain the following: Let ( A & , A f i ) be the pro-

of

a.

Let 7 1 = [V,Je,(k)’+ f,(k)’

-

(e,(k)’

+

f 2 ( k ) 2 ) 1 ,

7 2 = [V-de,(k)2

+

f z ( k ) 2

-

(e,(k)’

+

fZ(k)’)], and 7 3 =

f,(k)AE, - e,(k)Afi then

( e z ( k ) r l $- f Z ( k ) 7 3 ) / ( e ? ( k )

+

f?(’))

A 4 = (ez(k)72

+

f a ( k h ) / ( e ; ( t )

+

f ? ( k ) ) (18) if e , ( k ) A E ,

+

fz(k)Afz

>

TI, if e , ( k ) A &

+

fz(k)Afz

<

~ 2 , A & , otherwise,

I

Afa, otherwise. (fz(k)TI - e Z ( k ) T 3 ) / ( e ? ( l c _ >

+

f?(‘)),

if e,(k)A&

+

fz(k)Afz

>

TI,

if e,(k)AE,

+

fz(k)Afz

<

n,

( f ~ ( ~ ) ~ 2 - e z ( k ) r 3 ) / ( e ? ( l c _ >

+

f?(’)>,

₍₁₉₎

1

A f z =

Remark 3 T h e reason that we do not use polar coorda-

nate for bus voltage as the projectaon of phase angle onto the range ( - 2 7 r , 27r) wall lose valadaty.

C. Summary o f the Overall Method.

Our method for solving O P F problem (1) is using the SQP method (2) where Ax(k) is the solution of the QP subproblem ( 3 ) . The proposed iterative dual-type method

uses (10) t o solve ( S ) , the dual problem of the QP subproblem, instead of solving ( 3 ) directly The AA(t) in (10) is obtained from solving (11) using sparse matrix technique, in which the A 2 needed to set up can be computed using the simple two-phase method. Consequently, the iterative dual-type method converges to optimal solution

A * , and the solution A? of the constrained minimization

problem on the RHS of (9) with X = A* is Ax(k), the solution of ( 3 ) .

D. T h e Advantageous Features of the Proposed Dual-type Method.

In the following, we will describe how the proposed dual- type method achieves the four attractive features (ii)-(v) we claimed in Section 1.

In the dual function (9), we put the set of inequality constraints R as the domain of primal variables Ax so that we can apply the Projection Theory to circumvent the need of identifying the blnding inequality constraints. This address feature (ii).

All the computational requirements of our method for solving OPF problems almost lie in solving the linear equations (11) and the calculations of AX in (16)-(19) Equations (16)-(19) are as simple as they show. The approximate Hessian matrix

EC.P!QU

b x 2 - SI is a sparse con-

stant matrix; then the optimal ordering for the setup of

and guess

I

by (13) and (14)

w

for A W ) P ( 0 by (15) and update Determine and update

-a+

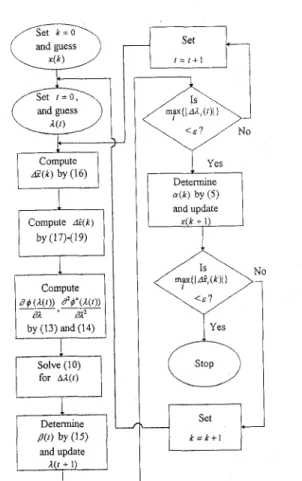
k = k + l

Figure 1: flow chart of our method for solving OP F problems.

memory locations for non-zero elements and fill-ins need only be done once. Therefore, the computational efficiency of our method can be expected. This address feature (iii).

Fig. 1 shows the flow chart of our method. Since all the computational formulae of our method are simple and concise, easy to be programmed is a natural result. This address feature (iv).

Convergence of the SQP method with step-size a ( k )

determined according to (5) has been shown in [ll]. Con- vergence of the proposed dual-type method for solving the dual problem of Q P subproblem is shown in the Appen- dix. These rigorous mathematical justifications address feature (v).

E. The Incluszon of Functzonal Inequalaty Constraints.

constraints on line flows

For the nonlinear inequality constraints such as security

we can convert them into equality constraints by using surplus variable vector z such that

(5)

30-bus 57-bus 118-bus 244-bus 2500-bus Then (21) has the same form of constraints as in (1). Al-

though the inclusion of equality constraints in (21) will increase the dimension of

+,

in our application, the sparsity is still retained; thus the sparse matrix technique can still apply. Consequently, the five attractive features of our method are still valid.

Comment 2 If there are too many functional inequality

constraints, the increase in the dimension of approximate

Hessian matrix and t h e number of surplus variables will cause extra computational complexity even through the f i v e attractive features still exist. However, the functional in- eqllality constraints in OPF problems are mostly the line

flow constraints on specific transmission lines which are generally not too many. Therefore, our approach is suit- able f o r the problena considered i n this paper.

3 2 4 u

x

t

IV. SOME REMARKS

41 86 179 445 3152

A . Remark on Our Method

There are many dual-type methods in the literature; for example, the dual LP method [2], the Lagrangian re- laxation method [14], and the interior point method of primal-dual approa.ch [lo],

...,

etc.. The proposed method for solving the dual problem of QP subproblem is also a dual-type method but differs from all the existing methods. Our method has similarity with the Lagrange relax- ation method. However, in the dual function we defined in (9), we put the set of inequality constraints,

a,

as the domain of the primal variables instead of using Lagrange multiplier p t o associate with the inequality constraints in Lagrangian re1axat)iori approaches. This trick enables our method t o have a constant sparse approximate Hessian matrix and apply Projection Theory t80 deal with the difficulties encountered by binding inequality constraints. Consequently, the four attractive features can be achieved as described in Section 1II.D.

B. Remark on the Objective Function of OPF

Observing froin t,he objective function of (3), if the considered OPF problem is an economic dispatch control problem, the SQP method (2) is a Newton-type method. However, if the criterion is to minimize the system losses, the SQP method (2) is a Jacobi-type method. The Jacobi- type method associated with our dual-type method for solving the O P F problems is still very computationally efficient as we will demonstrate by numerical examples in next sect ion.

C. Remark o n N o Feasible Solution

It is possible that the QP subproblem (3) does not have any feasible solution. If so, the objective value of the dual problem (8) will be unbounded. This is owing to the magnitude of some components of AA(t) increase as iteration t increases; in other words, the magnitude of some coinponent,s of

e

do not decrpase as t increases as can be observed from (11). Investigating fur-

84

x

t

29 54 46 124

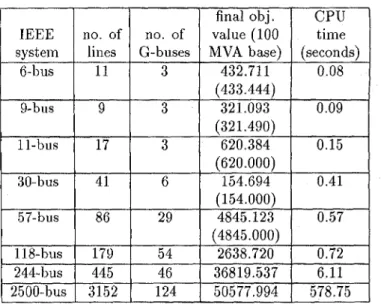
Table I: The final objective value and

CPU

time consumption of the tested O P F problems with economic criterion in Case (i). (154.000) 4845.123 0.57 (4845.000) 2638.720 0.72 36819.537 6.11 50577.994 578.75

I

IEEE

1

no. of 432.711 (433.444) 321.093 (32 1.490) 620.384

I

(620.000)

I

6

I

154.694

I

0.41

ther, we found from (13) and (16) that components of

IAZ

-

APJ with irreducible magnitude should be the ma- jor factor causing the above problem. This implies that if we push all the primal variables 2 to satisfy the inequality

constraints in Q , the objective value of (8) will be unbounded. To remedy this infeasible situation, we may re- lease the constraints with larger magnitude of IAZ

-

APJ

or I h ( z ( k ) + A Z ) - h ( z ( k ) + A f ) l when maxi lAAa(t)I does not decrease. In fact, the above reasoning is similar to the way of handling infeasible solution in [8].

V. TEST RESULTS

We tested our method for three cases of OPF problems on several power systems using a Spark-10 workstation.

Case (i): We consider the O P F with economic criterion with fixed transformer tap ratio, without switching capacitor banks, and no security constraints on line fiows. We use total generation cost

xi

a,Pi,+biPc,+cs as the objec-

tive fuiict,ion of the OPF problem. Th e coefficients ai,

bi,

and c, of the generation cost curve are various for different generation buses. The parameters we select are as follows: E = 10-3, w

=

100, = U p = I, TD

=

Tp

=

0.9,

6

= 11 = 1.0, and y = 0.1. We have tested the OPF problems in this case on eight systems. All computer runs begin from a flat start with initial voltages being e, = 1.0 and fa

=

0.0 for all buses i's. Table I shows the final objective value and the CPU times consumption of each OPF problem in Case (i).

We use IMSL subroutines to verify our solution by running the same problems with same initial guesses. IMSL

subt.out;nes nlonlinoai programming LOO^ implemented by the well-known Han-Powell algorithm [14]. The

(6)

(I

4.6 ---r- .- . k=3 k-4

,.

k=5 k=6 n ₀ 3 6 I I 1 5 '2 2 5 3 3 5 4 4 5 5 5 5 6 6 5

CPU time (seconds)

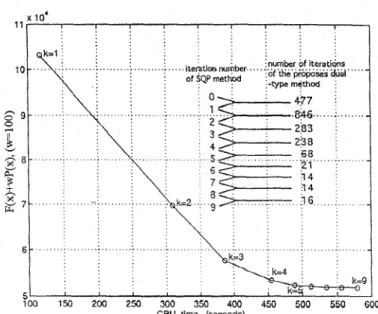
Figure 2(a): Th e detailed progression of our method for solving the O P F problem on IEEE 224-bus system.

final objective values inside the parenthesis listed in Ta- ble I are obtained by IMSL subroutines. The verification cannot continue for systems with more than 60 buses, because IMSL subroutines can not execute due to the large memory requirement. We observed that our method is 30 times faster than IMSL subroutine in the case of modified 57-bus system and experienced an exponential growth of speed-up ratio as system size increases.

To appreciate more about our method, we show in Figs. 2(a) and 2(b) the detailed progression of our method when solving the O P F problems on IEEE 244-bus and IEEE 2500-bus systems. Each circle in the figures represents one iteration of the SQP method. Thus, from Figs. 2(a) and 2(b), we see that our method inherit a good convergence rate of the SQP method. The CPU time consumed in between circles represents the CPU time consumed by the proposed dual-type method for solving (3) completely. We also indicate in Figs. 2(a) and 2(b) the number of iterations of the dual-type method used in each iteration of SQP method. Because of the flat start, the proposed dual-type method takes more iterations to solve (3) in the first few iterations of SQP method. We also observe that the number of iterations used in the dual-type method for solving (3) is linearly proportional with system size, and a reasonably good solution is already obtained in about one half O r two-thirds Of the total CPU Lime listed in Table I

As indicated in Table I, we can obtain the solution of the systems with size in the order of hundred buses, within 10 seconds. In fact, for the 2500-bus system, we are actu- ally obtain a solution of a nonlinear programming problem with 5248 variables, 5000 equality constraints, and 2748 inequality constraints in 580 seconds. This shows the computational efficiency of our method, and the numerical

Figure 2(b): The detailed progression of our method for solving the OPF problem on IEEE 2500-bus system. Table 11: The final objective value and CPU time consumption of the tested OPF problems with system losses criterion in Case liil.

l---

system

no. of no. of object

lines G-buses value time

i

base) (lOOMVA (seconds) 11 3 9.99 0.07 9 3 0.37 0.20 179 54 13.35 0.67 445 I 46 I 37.82 I 5.57 3152

I

124

1

461.50

1

441.23 stability is manifested by the successful test results on the large complex 2500-bus system running from a flat start. Case (ii): The setup of this case is the same as Case (i) except for using the system losses criterion. We let the total active system losses

X I

Pi

be the objective function, where

PI

denote the active loss of transmission line 1. From a flat start, the final objective value and CPU time

consumpC;on E, the OPD prohlerm on eight systems are

listed in Table 11. Comparing with the CPU time in Table

I , we see that the computational efficiency are about the

same. These results show that the Jacobi-type method associated with the proposed dual-type method are still very efficient in solving OP F problems with system losses criterion.

(7)

1673

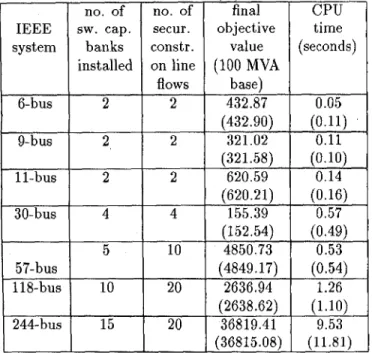
no. of secur. constr. on line

Table 111:

The final objective value and

CPU

time consumption of the tested OPF problems with economic criterion, consisting of switch capacitor banks and security

final CPU objective time value (seconds)

(100

MVA

- constraints on line

Ac

no. of system banks

i

installed 1 l-bus 30-bus 57-bus 118-bus 10 620.59

1

(620.21) (0.16) 4

1

155.39 0.57 4850.73 (2638.62) (1.10) 36819.41 (36815.08) (11.81) performances of the approximation rule (7) for the update of discrete control variables and the way we handle functional inequality constraints described in Section 1II.E. We consider the O P F problem with economic criterion as in Case (i) but installing several switching capacitor banks and assuming security constraints of line flows on several specified lines in each tested system as indicated in Table 111. With the approximation rule (7) and security constraints, the corresponding final objective value and CPU time consumption for the tested OPF problems on eight systems are shown in Table 111. We also test all the OPF problems by assuming the installed switching capacitor banks are continuous variables. The corresponding final objective values shown inside the parenthesis are also listed in Table 111; they are almost the same as the objective values obtained with approximation rule. This implies that the approximation rule for the update of discrete control variables is qualified for application. Furthermore, at the presence of the security constraints on line flows, the CPU time are only slightly larger than those listed in Ta- ble I. This indicates that our way of handling functional inequality constraints are suitable.

Remark 4 O u r machine is small and out of memory

when tested the 2500-bus system with 30 switching capac- itor banks and 50 security constraints.

VI.

CONCLUSION

The proposed dual-type method for solvim the QP

subproblems in the framework of SQP method is a new

method in OPF literature and also a new dual-type method in nonlinear programming methodologies. This method is general, theoretically sound, and computationally efficient. The exploitation of the sparsity structure of power system network and capability of coping with difficulties encountered by inequality constraints make this method attractive for applications on other power system optimization problems.

VII. APPENDIX

The Specaal Structnre of H .

According to [13], almost all the cost criteria can be

formulated as a functions of real power generation. Thus, the diagonal terms of the diagonal positive definite matrix H in (4) corresponding to e and

f

have the same values as +q.

Theorem 1 The solution A2 of the constrained mana-

mazatzon problem on the

RHS

of (9) can be solved an two phases:

Phase

I:

Compute A? = - H - ' [ W

+

-A]

which as (16).

Phase 2: Project A2 onto fll the resultang projectaon as

A?.

Proof: Since the square terms of Ax contains a scaling matrix H, the basic idea of this proof is using a coordinate transformation to transform the minimization problem into a projection problem as follows.

Neglecting constant terms XTg(z(k))and letting Ay = H f A x , where the diagonal positive definite matrix

H i

is defined by

H f

H i

= W , we can rewrite the constrained

minimization problem on the RHS of (9) as

( 2 2 )

Since the constraints H - a A y E C2 is equivalent t o Ay E H f Q , where Hffl is defined as { H i A x l A x E R}. Thus, we can rewrite (22) as

(23) The minimization problem in (23) is simply a projection problem of projecting AC = H - * [ W

+

*A]

onto the set H t Q . Let Ay be the projection of ACl then

A2 = H - + A y . In fact, the above projection process is

-A]) onto the set C2 and the projection is A i as we stated in the two-phase procedures of this Theorem. In the following, we will prove this claim. The set R are decou-

pled for ,-=1= kJi44ug+l bus i, and bhe simple bounded inequality constraints (such as the constraints for real power equivalent to project AZ(= ~ - f ~ i j =

H -

1 [ a F ( z ( k ) ) T

+

(8)

I , hz(u,(k)+ Ai$) I hz(u,(k) + AG,) u, ( k ) + A;,

\

u , ( k ) + AG, h,,’ I I L l ’ ,-’ I I--

Figure 3: (hj?j is the j t h diagonal element of

Hh)

and reactive power generations) tii

5

u z ( k )

+

Ail,

5

fi, are decoupled from the constraints on voltage magnitude

z z - g ( k ) 5

v A e , + v A f z

5 G - - x ( k ) .

Since

H*

is diagonal, and the diagonal terms of

H;

corresponding to e, and

f,

are the same as L q i , Fig. 3 and Fig.

4

geo- metrically show the equivalence of projecting Ai5 onto the set s2 and A$ onto the set H + Q using coordinate transformation. This proves our c l a i m . 0

4

Remark 5 I n general, i f H does not posses special struc- ture, more complacated formula are needed to obtain

AZ

and

AX,

however, the simplicity o f the two-phase proce- dures still hold.

Theorem 2 The AX obtained f r o m (i7)-(i9) is the pro- jectaon of A2 onto the set s2,

Proof The result is trivial by inspection from Fig. 3

and Fig. 4.0

Theorem 3 T h e dual-type method (10) wrth

p(t)

deter- maned accordang to (15) is an ascent method.

Proof First, we can rewrite (8) as min[-+(X)]. From

(14), -[v2$”(X(t))

-

S I ] is positive definite. Using De-

cent Lemma in [12] and by simple calculations, we can set

p ( t ) = T $ ~ ) u ~ , where m ( t ) is the smallest nonnegative

integer m that the following inequality holds

which is (15). We then have

This shows that (10) is an ascent method as long as IlAX(t)ll

#

0. In fact, the condition IlAX(t)ll = 0 implies = 0 which is the necessary condition when

d(X)

achieves its maximum. Thus, (10) is an ascent method to maximize

d(X).

Combining Theorem 3 with the two-phase method shown in Theorems 1 and 2, and also by Duality The- ory [14], we have the following theorem which is the main theoretical result of the proposed dual-type m e t h o d . 0

V , d e , + V 4 = L $ ( Y , - V , ) [ELI

N,

’

a , g,

‘

A

&

LEGEND

-

ye =

5 ,

_{V L}= -, EL Equation ofaLine

CTM Coordinate Transformation Matnx LARV Linearized Adrmssible Range for Voltage

Figure 4: ((Aye,, A y f t ) is the transformed coordinate of

( A e z A f t ) ) .

Theorem 4 The dual-type method (10) converges to a p a n t A* such that = 0 and maxzmzze +(A) Fur- thermore, Aijl the solutzon of the constraaned mrnzmaza- taon problem on the RHS of (9) wath X = A x l equals Ax(k), the optamal solutron of (3).

Proof the proof can be similarly developed from the proof of Proposition 2.1 of Section 3.2.2 in [ 1 2 l . o

VIII. ACKNOWLEDGMENT

The authors wish to thank Professor Yu-Chi Wu for several helpful discussions on the setup of numerical tests. Professor Wu and his colleagues have done excellent research work in [lo].

(9)

ClI’I-HSIN LIN was born in Taiwan,

ROC,

on Aug. 29, 1965. He received the

B.S.

degree in electrical engineering from Feng Chia University, Taiwan, the M.S. degree in electrical engineering from National Tsing Hua Univer- sity, Taiwan, and Ph.D degree in control engineering from Chiao Tung University, Taiwan, in 1989, 1991, and 1996, respectively. He is currently serving as an officier in the army,

SIIIN-YEU LIN was born in Taiwan, ROC. He received the R.S. degree in electronics engineering from National Chiao Tung University, the M.S. degree in electrical engineering from University of Texas at El Paso and the D. Sc. degree i n systems science and mathematics from Washing- ton University in St. Louis, Missouri, in 1975, 1979, and 1983, respectively.

From 1984 to 1985, he was with Washington University working first as a Research Associate and then a Visiting Assistant Professor. From 1985 to

1986,

he was with GTE Laboratory working as a Senior MTS. He joined the De- part meal of Control Engineering at National Chiao Tung University in 1987 and has been a Professor since 1992. His major research interests are Large-Scale Power Sys- tems, Optimization Theory and Applications, and Dis- tributed and Parallel Computations.

This research work is supported in part, by National Sci- ence Couiicil in Taiwan under grant #NSC83-0404-E009- 115.

References

[l] B. Stott, 3 . L. Marinho, and 0. Alsac, “Review of linear programming applied t o power system reschedul- ing,” pp.142154, P I C A 1979.

[a]

B. Stott and J . L . Marinho, “Linear Programming for

Power-System Network Security Applica.tions,” IEEE Trans. on Po.wer Apparatus a n d Systenis, vol.PAS-98, no.3, pp.837-848, May/June 1979.

[3] B. Scott, 0. Alsac, and A. Monticelli, “Secu- rity analysis and optimization,” Proc. IEEE. vo1.75,

no.12, pp.1623-1664, Dec. 1987.

141 T. C. Giras and S. N. Talukdar, ‘(Quasi-Newton method for optimal power flows,” Infernaiioiial Jour- nal of Electrical Power &’ Energy Systems, ~01.3, no.2, [5] S. N. Talukdar and T . C. Giras, “A fast and robust

varhble metric method for optilllull1 power flows,”

I E E E Trans. O I L PAS, vol.101, no.2,pp.415-420, 1982 [6] R. C. Burchett, H. H. Happ, and D. 1%. Vierath, “Quadratically convergent optimal power flow,” I E E E T r a m on Power Apparatus awd Syslenis,

vol.PAS-103, no.11, pp.3267-3275, Nov. 1985. [7] D. I. Sun, B. Ashley, B. Brewer, A . Hughcs, and

W . F. Tinney, “Optimal power flow by Newton a,p- proach,” I E E E Trans. on Power Apparaius and Sys- tems, vol.PAS-103, no.10, pp.2864-2880, Oct. 1984.

[8]

D. I.

Sun, T. I. Hu, G. S. Lin, C. J . Lin, and C. M. Chen, “Experiences with implementing optimal power flow for reactive scheduling in the Tai- wan power system,” I E E E Trails. 011. Power Systems,

vo1.3, no.3, Aug. 1988.

[9] A. Monticelli a.nd W. E. Liu, “Adaptive movement penalty method for the Newton optimal power flow,”

I E E E Trans. o n Power System., pp.334-340, 1992.

[lo]

Y.

C. Wu, A . S. Debs and R. E. Marsten,

“A

di- rect non1inea.r predictor-corrector primal-dual interior point algorithm for optimal power flows,” I E E E

Trans. on Power System, pp.876-883, May. 1994.

[11] D. P. Bertsekas, “Constrained optimiza.tion and La- grange multiplier methods,” Academic Press, 1982.

[12] D. P. Bertsekas and .J. N. Tsitsiklis, “Parallel and distributed coniputatioii: numerical niet~liods,’l

Prentice-Hall Eiiylewood Cliffs, NJ, 1989.

[13] A. S., Debs, “Modern power s y s t e m cont,rol and op-

eration,” Iiluwer Academic Publishers, 1988.

[ 141 D. Luenberger

,

“Linear a.nd nonlinear programming, 2nd ed,” Addison- Wesley Reading, MA, 1984.

BIOGRAPHY