Combinations of Collocation and Finite-Element Methods for Poisson's Equation

(1)

ELSEVIER

An Intemational Journal Available online at www.sciencedirect.com

c o m p u t e r s

&

.o,..~. C~o,..~T.

mathematics

with applications Computers and Mathematics with Applications 51 (2006) 1831-1853

www.elsevier .com/locate/camwa

C o m b i n a t i o n s of

C o l l o c a t i o n a n d

F i n i t e - E l e m e n t M e t h o d s

for P o i s s o n ' s E q u a t i o n

H S I N - Y U N H U A N D Z I - C A I L I * D e p a r t m e n t of Applied M a t h e m a t i c s D e p a r t m e n t of C o m p u t e r Science and Engineering

National Sun Yat-sen University Kaohsiung, Taiwan 80424

National Center for Theoretical Sciences, Taiwan zcli@mat h. nsysu, edu. tw

(Received June 2004; revised and accepted October 2005)

Abstract--In this paper, we provide a framework of combinations of collocation method (CM) with the finite-element method (FEM). The key idea is to link the Galerkin method to the least squares method which is then approximated by integration approximation, and led to the CM. T h e new important uniformly Vh0-elliptic inequality is proved. Interestingly, the integration approximation plays a role only in satisfying the uniformly Vh0-elliptic inequality. For the combinations of the finite- element and collocation methods (FEM-CM), the optimal convergence rates can be achieved. The advantage of the CM is to formulate easily linear algebraic equations, where the associated matrices are positive definite but nonsymmetric. We may also solve the algebraic equations of FEM and the collocation equations directly by the least squares method, thus, to greatly improve numerical stability. Numerical experiments are also carried for Poisson's problem to support the analysis. Note that the analysis in this paper is distinct from the existing literature, and it covers a large class of the CM using various admissible functions, such as the radial basis functions, the Sinc functions, etc. (~) 2006 Elsevier Ltd. All rights reserved.

K e y w o r d s - - C o l l o c a t i o n method, Least squares method, Poisson's equation, Finite.element method, Combined method.

1. I N T R O D U C T I O N Since t h e f i n i t e - e l e m e n t m e t h o d ( F E M ) t o d a y is t h e m o s t i m p o r t a n t m e t h o d a m o n g all n u m e r i c a l a p p r o a c h e s , o w i n g t o w i d e a p p l i c a t i o n s a n d d e e p t h e o r e t i c a l a n a l y s i s , we e m p l o y t h e FEM t h e o r y in [1,2], t o d e v e l o p t h e t h e o r e t i c a l f r a m e w o r k of t h e c o l l o c a t i o n m e t h o d s ( C M ) . I f t h e a d m i s s i b l e f u n c t i o n s a r e c h o s e n t o b e a n a l y t i c a l f u n c t i o n s , e.g., t r i g o n o m e t r i c or o t h e r o r t h o g o n a l f u n c t i o n s , we m a y e n f o r c e t h e m t o s a t i s f y e x a c t l y t h e p a r t i a l d i f f e r e n t i a l e q u a t i o n s (PDEs) a t c e r t a i n collo- c a t i o n n o d e s , b y l e t t i n g t h e r e s i d u a l s t o b e zero. T h i s l e a d s t o t h e c o l l o c a t i o n m e t h o d . Since t h e

*Author to whom all correspondence should be addressed.

We thank Professor N. Yan for her valuable suggestions and comments on this paper.

(2)

1832 H.-Y. Hu AND Z.-C. LI

PDEs and the boundary conditions are copied straightforwardly into the collocation equations, the methods of the paper cover a large class of the collocation method, e.g., those using radial basis functions, the Sinc functions, etc.

The CM is described in a number of books, [3-8]. Here, we also mention several important studies of CM. Bernardi et al. [9] provided a coupling finite-element method and spectral method with two kinds of matching conditions on interface. Shen [10-12] gave a series of research study on spectral-Galerkin methods for elliptic equations. Haidvogel [13] applied double Chebyshev polynomials to Poisson's equation. Yin [14] used the Sinc-collocation method to singular Poisson- like problems. Other reports on CM are given by Arnold and Wendland [15], Canuto et al. [16], Pathria and Karniadakis [17], and Sneddon [18].

In this paper, we follow the ideas in [6], and provide the combination of the finite-element and collocation methods (FEM-CM). The advantages of this combination are threefold,

(1) flexibility of applications to different geometric shapes and different elliptic equations, (2) simplicity of computer programming by mimicking the PDEs and the boundary conditions, (3) varieties of CM using particular solutions, orthogonal polynomials, radial basis functions,

the Sinc functions, etc.

Moreover, optimal error bounds are derived, mainly based on the uniformly V~-elliptic inequalities, which are also proved in Sections 4 and 5. Note that the analysis of the CM in this paper is distinct from the existing literature of CM.

This paper is organized as follows. In the next section, the combinations of FEM-CM are described, and in Section 3, linear algebraic equations are formulated, and the solution methods are provided. In Sections 4, the important uniformly Vh0-elliptic inequality is derived, and in Section 5, the CM involves approximation integrals, and error bounds are derived. In the last section, numerical experiments including a singularity problem are carried out to support the analysis made.

2. C O M B I N A T I O N S

O F F E M S

Consider Poisson's equation with the Dirichlet condition,

- - A u = - \ O x 2 + Oy2. ] = f ( x , y ) , in S, (2.1)

u[r = 0, on F, (2.2)

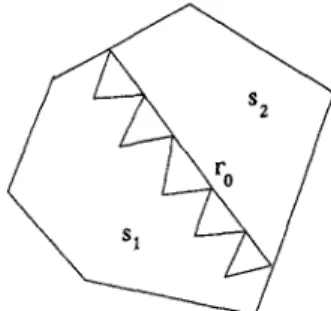
where S is a polygon, and F is its boundary. Let S be divided by F0 into two disjoint subregions, $1 and $2 (see Figure 1): S = $1 U $2 U F0 and Sx N $2 = 0. On the interior boundary r0, there exist the interior continuity conditions,

u + = u - , u + = u ~ , o n F 0 , (2.3)

Ou U+

where u~ = b-~, = u on F0 U $2 and u - = u on F0 U $1. Assume that the solution u in $2 is smoother than u in $1. We choose the finite-element method in $1 and least squares method in $2, whose discrete forms lead to the CM (see Section 3). Let $1 be partitioned into small triangles: ~ i j , i.e., Sx = LAij/kij. Denote hij the boundary length o f / k i j . T h e / ~ i j are said to be

(3)

Collocation and Finite-Element Methods 1833 quasiuniform if h / m i n { h i j } <_ C, where h = max{hij}, and C is a constant independent of h. Then, the admissible functions may be expressed by

{ ~)-- = V k, in S 1,

, = L (2.4)

v + : ~ d ~ i , inS2,

i = l

where ~i are unknown coefficients, and Vk are piecewise k-order Lagrange polynomials in $1. Assume that @i E C2($2 U 0S2) so that v + e C2($2 U 0S2). Therefore, we may evaluate (2.1) directly,

+ = 0, for Q, s 2 , (2.5)

at certain collocation nodes Qi E $2. Note that v in (2.4) is not continuous on the interior boundary F0. Hence, to satisfy (2.3) we have the interior collocation equations,

v + (Qi) = v - (Qi), for Pi e F0, (2.6)

v + (Qi) = v~ (Q~), for Pi E F0. (2.7)

Equations (2.5)-(2.7) axe straightforwardly and easy to be formulated. In this paper, we choose the total number of collocation nodes (e.g., Pi) to be larger (or much larger) than the number of unknown coefficients di. Hence, we may seek the solutions of the entire CM by the least squares method (LSM) in [19], see Remark 2.1 below.

oo

We assume that the solution expansion: u = ~-~i=1 ai@i in $2 where ai are the true coefficients. Denote

L

UL = E a i ~ , in $2. (2.8)

i = l

Then, u = UL + RL, and the remainder,

oo

RL--- E aiqYi" (2.9)

i=L+l

Assume that (2.8) converges exponentially which implies

a i ~ i

IRLI = ~=L+I = 0 ( e - e L ) , in $2, (2.10)

where ~ > 0 and L > 1.

Denote by V ° the finite-dimensional collections of (2.4) satisfying vlr -- 0, where we simply assume ~ilos2nr = O. If such a condition does not hold, the corresponding collocation equations on 0S2 n F are also needed, and the arguments can be provided similarly. The combination of the FEM-CM is designed to seek the approximate solution uh E V ° such that

a (Uh, V) --- f ( v ) , Yv e V ° , (2.11)

where

a(u,.)=/f s

₁

wvv+

_o ₂

(2.12)

(4)

" o~ o4 o~ and n is the unit outward normal to 0S2.

where V u = ux-( + uuj, uz = ~-~, Uy = -~, un = ~-~ ,

h is the maximal boundary length of/~ij or Oij in $1, and Pc > 0 is chosen to be suitably large but still independent of h.

Denote the the space

H* = { v , v c L2(S), v C H I ($1), v C H1($2), Av E L2($2), and vlr = 0}, (2.14) accompanied with the norm

ii]vlll=(l]v[l~,s,+p~[ivli~,s~+p ~

HAV[lo,s

,2

Pc ii

112 Ii

i i / 2 \1/2

. (2.15) \

where HVlll,S, and l[vHl,s2 are the Sobolev norms. Obviously, V~ c H*. For the true solution u to (2.1), we have a(u - Uh,V) = O, V v • V ° . By means of a traditional argument in [1,20], we have the following theorem easily.

THEOREM 2.1. Suppose that there exist two inequalities,

a(u,v) _< cIIMII × Illvllt,

v,., • v ° , (2.16)

a ( v , v ) >_ Col[Ivlll 2, Vv • v ° , (2.17)

where Co > 0 and C are two constants independent of h and L. Then, the solution o f combina- tion (2.11) has the error bound,

Ill~-~hlll = c

inf

Illu-~lll.

(2.18)

v ~ V o

The proof for (2.17) is important but complicated, and is deferred to Section 4. Choose an auxiliary function,

l U I,

in S 1,

UI,L =

L

(2.19)

aiffYi, in $2,

i = 1

where ul is the piecewise k-order Lagrange interpolant of the true solution u, and ai are the true coefficients. Then, u = ~L=I a~ff~ + RL in $2. By means of the auxiliary function (2.19), we obtain the following corollary easily.

COROLLARY 2.1. L e t all conditions in T h e o r e m 2.1 hold. Suppose t h a t

u • H k + l ( S 1 ) and u • Hk+l(Fo). (2.20)

Then, there exists the error bound,

[[lu- uhl[I- C {hklulk+l,s, +

IIRLII2,s~

k

(2.21)

1 IlRLllo,ro + II(RL).ll0,ro) }

+V~

( hk+l/2 lulk+l,ro

+ ~

Also suppose that the number L of v + in (2.4) is chosen such that

IlaLII2,s~ = O (hk),

IIRLIIo,ro = 0

(h k+1/2)

(2.22)

II

(RLL

IIo,ro = O (hk).

Then, there exists the optimal convergence rate,

II1~- ~hlll = o (h~).

(2.23)

REMARK 2.1. The combination (2.11) is nothing new (cf., [6]), except the proof of (2.17) is challenging. Our goal is the CM used in $2, which can be obtained from (2.11) involving approximation integration. Hence, the combination of Pdtz-Galerkin-FEM is a basis for the study in this paper, but more justification will be provided below.

(5)

Collocation and Finite-Element Methods 1835

3. L I N E A R A L G E B R A I C E Q U A T I O N S

OF C O M B I N A T I O N OF F E M A N D C M

Let ~ s 2 and f r o denote the approximations

ffs2

and f r o by some integration rules, respectively. The combination of FEM-CM of (2.11) involving integration approximation is given by the following. To seek the approximation solution Uh E V ° such that

(~h, v)

=

/ @),

Vv e V °,

(3.1)

where

+-cPc/ ~o @+- ~-)(v+- v-)+ Pc/.~o

@+ - < ) (v+ - < ) '

Equation (3.1) can be described equivalently,

a*(Z~h,V) = fl(v),

Vv E V2,

(3.2) (3.3)

(3.4)

where s1 Fo S1 J F o fl(V) : i S

IV.

S1 In $2, we choose the integration rules,

(3.5) (3.6) A

i j

g2 = E

c~jg2(Qij),

Q~j E

s:,

(3.7)

$2

ij

J g2

Qj e

F0, (3.8) Fo j

where aij and aj are positive weights. In fact, we may formulate the collocation equations at Qij E $2, and

Qj E

F0 directly. The collocation equations at Qis, and Qj are given by

(Av + -t- f ) (Qij) --- 0, Qij e $2, (3.9)

(v + - v - ) (Qj) = o, Qj E Fo, (3.10)

(v + - v~-) (Qj) -- 0, Qj E Fo. (3.11)

By introducing suitable weight functions, we rewrite the equations (3.9)-(3.11) as

(Av + + f) (Q,j) = 0,

Qo e 82,

(3.12)

~

(v + - v - ) (Qj) = 0, Qj e F0, (3.13)

(6)

where a O are positive weights, and Qj are the interior element nodes of F0. We give some rules of integration with explicit weights a j and aij in (3.12). First, choose the trapezoidal rule,

A

f g2 = Q~Q2 (g2 (Q1) + g2 (Q2)) = 5 (as (Q~) + H g2 (Q2)) "

QxQ2 2 (3.15)

The weights aj = H / 2 or H when Qj is at a corner of OS or not. Let $2 be a rectangular subdomain of S, and be divided into uniformly difference grids with the meshspacing H, where Qij denote the collocation nodes (i, j). Hence, the weights aij in (3.12) have the following values,

H , (i,j) • $2, 1 2

aij = -~ H , ( i , j ) • 0S2 excluding corners of 0S2, (3.16) H , ( i , j ) • corners o f 0S2.

We may choose more efficient rules, such as the Legendre-Gauss rule with two boundary nodes fixed in [7,21],

n

/ ~ g2(x) dx = E wjg2(xj)' (3.17)

1 j = l

where xj is the j t h zero of P,,(x), and P,,(x) are the Legendre polynomials defined by (-1) '~ d n [( n]

P , ~ ( x ) - - 2nnl dx,~ 1 - x 2) , n > l . (3.18) The weights are given by

2

(3.19)

wj

(1 - zj) [P- (xA]

Then when choosing the collocation nodes Q~j = (xi, yj), the weights in (3.12) are obtained as

oqj = wiwj, (i, j) • $2. (3.20)

Let f = g2 and f • C2'~[-1, 1], then the remainder of (3.17) is given by

22"+1 [n[] a f2n

E ( S ) = f = g 2 , - 1 < ~ < 1 . (3.21)

Let g in [-1, 1] be polynomials of order L. Then, f ( = g2) is polynomials of order 2L. Choose n = L + 1, then the derivatives f2,,(~) = f(2L+2) _~ 0 and E ( f ) - O. Therefore, when $2 is a rectangle, the functions v + in S~ are chosen to be polynomials of order L. Functions Av + are polynomials of order L - 2. The Legendre-Gauss rule with n = L - 1 in (3.7) and (3.20) offers

h

no errors for f f s 2 ( Av+)2' i.e., A

Now, let us establish the linear algebraic equations of combination (3.4) of FEM-CM. First, consider the entire FEM in St only,

(7)

Collocation and Finite-Element Methods 1837 where

al(u,v)=//

VuVv+ f u,~v ,

fl(V)=

ff fv.

(3.24)

S 1 1~0 S 1

We obtain the linear algebraic equations,

A1~I = b*l, (3.25)

where

Xl

is a vector consisting of vii only, and m a t r i x A1 is n o n s y m m e t r i c . Next, equations (3.12)-(3.14) in $2 U F0 are denoted by

A2Z2 = b2, (3.26)

where x2 is a vector consisting of 5i, v U and v0j, and v0j and "vii are the unknowns on the two b o u n d a r y layer nodes in St close to F0 if the linear F E M is used. Denote by M1 the n u m b e r of all collocation nodes in $2 and 0S2, and by N1 the n u m b e r of vii and v0y. M a t r i x A2 E R Mlx(L+NI). Therefore, we can see

lzTATA

_{2 ~ 2 ~ 2} Z _{2 -} A T b2:~2 ₊c'

Pc Pc

_'.

(3.27)

Combining (3.25) and (3.27) yields explicitly 1

AZ" = b, (3.28)

A = A1 + A T A 2 , b' = b'l + ATb*2, (3.29)

where ~ is a vector consisting of the coefficients 5i and vii in $1 LA F0. Denote b y N t h e n u m b e r of nodes on $1 U r 0 , t h e n the vector ~ in (3.28) has N + L dimensions. T h e m a t r i x A is nonsymmetric, b u t positive definite, based on T h e o r e m 5.1 given later.

Let us briefly address the solution m e t h o d s for (3.28). W h e n Pc is chosen large enough, m a t r i x A E R (L+N)x(L+N) in (3.28) is positive definite, n o n s y m m e t r i c and sparse when N >> L. W h e n L + N is not huge, we m a y choose the Gaussian elimination w i t h o u t pivoting to solve (3.28), see [19].

Also, since 5(u - Uh, v) = 0, Vv E V~, we obtain the following theorem. THEOREM 3.1. Suppose that there exist two inequalities,

a(~,v) ~ c[llulll x I]lvlll,

a(v,v) ~

co[llvlll 2,

Vv E V ° , (3.30)

Yv e Vff, (3.31)

where Co > 0 and C are two constants independent of h and L. Then, the solution of combina- tion (3.1) has the error bound,

]l]U-~h]Jl < C inf IIlu-vJ]].

- - vEVh

(3.32) Moreover, the optimal convergence rate (2.23) holds i f the conditions (2.20) and (2.22) are satis-

fied.

lIn (3.29), (3.34), and (3.40), the dimensions of matrices may not be consistent, where the equality means that the matrices of less dimensions should expand by filling up more zero entices.

(8)

1838 H.-Y. Hu AND Z.-C. L1

The proof of inequality (3.31) is deferred to Section 5.

REMARK 3.1. Note that equation (3.28), called Method I, presents exactly combination (3.4). There arises a question. Since (3.28) results from (3.25) and (3.26), should we solve (3.25) and (3.26) directly (i.e., together) by the least squares method? The following arguments give a positive justification.

METHOD I. We rewrite (3.28) and (3.29) as

i.e.,

Aft = b, (3.33)

A H T + A~A2ff = b~ + A~-b2. M E T H O D II. T H E LEAST SQUARES M E T H O D DIRECTLY. Solve

A l : Z = b~, A 2 x = g , (3.34) (3.35) by where I ( £ ) = m i n I ( z - ) , (3.36)

I(z-) = II AI~' -

b~ll 2 + HA2z'- b2112,

and rl II is the Euclidean norm.

(3.37)

PROPOSITION 3.1.

with the relative error bound,

IJx- g[---~[ < Cond. (A "~ jlr~] < Cond. (A) (i +

IIA2[I)

e (3.38)

Ilgll - ' J 6 - 6 '

where the error of Method II is

e = ( A I ~ - ~ 2 +

A2:~-b2

2) 1/2 , Cond. (A) denotes the condition number of A :

/ m x(ATA)

Cond. (A) = W~min

and Amax(ATA) and Amax(ATA) are the maxima/and minimal eigenvalues of A T A , respec-

tively.

PROOF. Denote I(£) = s 2, we then obtain (3.36)

A I ~ - b~ <_ e, A 2 2 - b2 _< s. (3.39)

Consider the remainder of (3.34) when £ replaces ~7:

7 v -= A f - 6 = A I : ~ - b~ q- A - ] - 2 A 2 ; ~ - AT2b~. (3.40) We have from (3.39)

Let ~ and ~7 be the solutions from (3.35) and (3.33) respectively, then ~ .~ g

(3.41)

IIr-'ll ~ A1~-b~ +I[A2[I A2~-b~ ~ (I+IIA2II)E.

Moreover, we have from equations (3.33) and (3.40)

(9)

Collocation and Finite-Element Methods 1839

Since lJ~TJl >- lJb[l/JJAJl from (3.33), the desired result (3.38) is obtained by following [19,21]. Since ~ is very small, the solution ~ of Method II is the solution ff of Method I approximately.

This completes the proof of Proposition 3.1. |

4. U N I F O R M V ~ - E L L I P T I C I N E Q U A L I T Y

The key analysis of combinations (2.11) and (3.1) is to prove the uniform V°-elliptic inequalities (2.17) and (3.31), since the proof for (2.16) and (3.30) is much simpler. We shall prove (2.17) in this section and then (3.31) in the next section.

First, we consider a(v, v) without the term fro v ~ v - . Define the norms

ilvllE ( 2 Pc 2 )1/2

= Ivlx,sl +

Pc

II~vllo~,s2 +

W

I1"+ -'-IIo,ro + Pc IIv: - <l12o,ro

, ( 4 . 1 ) and

IIv+

- v - l l e , r o =

11,3 ÷ -.-I1,,~o,

(4.2)

where g = 0,1/2, and ,3 + is the piecewise k-order polynomial interpolant of v + in $2. Then, we have the following lamina.

LEMMA 4.1. Suppose that there exists a positive constant u(> 0) such that

I1.÷11,,~o _<

CL'"

IIv÷llo,ro ,

e

=

1,2,..

(4.3)

Then, there exists the bound for v E V °,

C Cha/2L2V

II .+

-

~- 111/2,~o <- ~

II ~÷ - ~- IIo,~o +

I1~÷111,s2 •

(4.4)

PROOF. We have from triangle inequalities,

II v+ -"- 111/2,.o -<

II "+ -

"- IIl/~,ro + II ,3+

- " + l l ~ / 2 , r o ,

(4.5)

I I v + -

v-lloxo -< II .÷ - . - llo,ro + II ,3+ - ~÷llo,ro •

Then from the inverse inequality for pieeewise polynomials, there exists the bound,

II "+

- . - IIl/=,ro -< II "+ - . - IIx/=,ro +

P+

- "+ II~/~,ro

C

<_ ~ l l v + - v-IIO,ro + 11,3 + -

v+ll,/=o

(4.6)

C C

<- ~ II "°+ - v- IIo,r.o + ~ II ,3+ - v + Iio,,-o + 11,3

+

- v+ll,./~,,.o •

Moreover, from (4.3) we have

h-'/' 11,3 + - v+ IIo,ro + II ,3+ - "+111/~,~o -<

ch~/~

I1"+ II,,ro

(47)

<_

ch~/=L="

Ik+llo,~o <_

ch~/'L~"

I1~+11,,~

Combining (4.6) and (4.7) yields the desired result (4.4). This completes the proof of Lem-

(10)

LEMMA 4.2. T h e r e exist t h e bounds for v E V.h °,

IIv+lll,s2 < C(IfAv+ll_l,s2 +

ll~+ilv~,os~},

(4.8)

IIv+ll_l/~,ro < C{llAv+ll_~,s ~ + II~+llv~,os~},

(4.9)

where C is a constant independent of h and L.

PROOF. We cite t h e b o u n d from [2, pp. 189-192],

m - - 1 2

II~ll~s,~m(~)

-< C{llA~ll~-~m(~) + ~ IIBk~ll~.-.~-v~(on)},

(4.10)

k = 0

where s < 2m, a n d m is a positive integer. T h e n o t a t i o n s are: A u = Au, Bou = u, B l u = u,~,

g0 = 0 and gl = 1. T h e n o r m on t h e l e f t - h a n d side in (4.10) is defined in [2, p. 183],

r - - 1 2

llull/~.,~(r~) = llull~.(~) + Z~

Dku,~ H'-k-t/2(Ofl) ' 2

(4.11)

k = 0

where r is a positive integer, s is an integer, and D k -- ~ is t h e k t h n o r m a l derivatives. In (4.10), choosing s = 1, m = 1 and ~ = $2, we o b t a i n

2 U 2

ll~ll~,,~(s~)

-< C{llA,,ll~s-,(s,) + II

IIH.~(OS~)},

(4.12)

where the n o r m is given in (4.12) w i t h s = 1, r = 2, a n d ~2 = $2,

2 _- u 2 2 (4.13)

C o m b i n i n g (4.10) a n d (4.13) gives t h e following b o u n d ,

2 2 2

ll~ll~,s~

+

llullv~,os~

+

llu,~ll~-w~,os~ <- C{IIA~II2-1,s~

+

llullv~,os~}.

(4.14)

T h e desired results (4.8) a n d (4.9) are o b t a i n e d d i r e c t l y from (4.14). T h i s c o m p l e t e s t h e p r o o f of

L e m m a 4.2. 1

LEMMA 4.3. Let (4.3) and the [ollowing bound hold,

h3/2L2~ = o(1). (4.15)

Then, for v 6 V~ there exists the bound,

ll.+ll,,s~ < c llv-llv~,,.o + ~ II v+ - v-llo,,.o + ll,"v+llo,s2

,

(4.16)

where C is a constant independent of h and L.

PROOF. F r o m L e m m a 4.1, we have

II~+llv~,~o -< IIv- IIl/~,~o + II .÷

-

v-IIv~ ~o

C Ch3/2L2~ (4.17)

-< IIv-IIv~,ro + ~ II v+ - v-IIo,ro +

IIv+ll,,~: •

F r o m L e m m a 4.2 a n d (4.17)

V +

IIv+ll,,~:-<c{ll

IIv~,,,o+llAv+ll_~,~:}

{ 1 h3/2L2 . } (4.18)

(11)

This leads to

c

{

1 }

IIv+111,.%, < 1

- C A a l 2 L 2~'

II~-II,,=,~o + ~ II ~+ -'-'-Ilo,=o + I1"'~+11o.=,., •

(4.19)

The desired result (4.16) follows from Ch3/2L 2~ < 1/2 by assumption (4.15). This completes the

proof of Lemma 4.3. |

LEMMA 4.4. Let F A $I ¢ 0, (4.3) and

(4.15)

hold, there exists an inequality

Colil',-,lll-< II~ilE,

w • v °,

(4.20)

where II1~111

a~d II~IIE are

denned in (2.15) and (4.1) respectively, and Co > 0 has a

lower

bound

independent of h and L.

PROOF. By the contradiction, we can find a sequence {vt} C H* such that

II1~111

= 1, ilv~llE --* 0, as o__, oo. (4.21)

First, IlvellE -* 0 implies that for large ~, Iv[ll,s, _< 1 and v [ I s , nr = 0, and then

I[v2[ll,Sl

is bounded. Based on the Kandrosov or Rellich theorem [1], there exists a subsequence {v[ } in L 2 ( S 0 (also written as {v~-}) such that v[ ~ v - 6 L2(S1). Then, ~ - 6 H I ( S I ) , since

I~-Ix,s,

are bounded due to tv~ll,s~ < 1. Moreover, LlvdlE - ~ 0 g i v e s I ~ [ I x , s , - * 0 as e --* ~ . Since

Hi(S1) is complete, we conclude that

I~-Ix,s,

= lim~_~¢¢ lv~ Ii,s~ = 0. Hence ~ - is a constant, and ~ - = 0 in 5'1 due to ~-Is~nr = 0.

From the trace theorem [1],

llv;lll;,,ro <- C I1";111,~,,

IIv/111/2,ro is also bounded, and

(4.22)

lim IIv~-II1,,~ro = 11"~-11,,,2,~o = O.

I4.23~

Next, consider the sequence v + in $2. We have from Lemma 4.3,

V + V +

II, II,.;.~,,-o -< c II ~ II,,s,

{ 1 } (4.24)

<

c

IIv;ll,.,,~,~o + ~ II-o~ -,i-IIo.~o + I1."~:11o,~,,

.

We conclude t h a t IIV~-]I1/2,Fo is bounded, and that l i m t _ ~ IIv+H1/2,ro = 0 from (4.24), (4.23) and IlvtllE ~ 0. Based on Lemma 4.2,

~ + V +

il, I1,,~, ~ c {ll,",vtll_,.,~, + li ~

111/2,os~}

(4.2s)

(12)

Hence [Iv~+ill,s2 is also bounded from liveliE --* 0, and then lime-~oo flY+ill,S2 ---- 0. B y repeating the above arguments, there exists also a subsequence v~- to converge 9 + E H I ( $ 2 ) . Moreover, we have [[~+[[1,s2 = lime-+oo [ [ V t l ] I , S 2 = 0, alia then 9 + _= 0 in $2. Hence, ~ = 0 in the entire S and I1[~1[[ = 0. This contradicts the assumption [[1~[[[ = lime--+oo [[[veii[ = 1 in (4.21), and completes

the proof of L e m m a 4.4. |

Now, we give the main theorem.

THEOREM 4.1. Let F rq 0S1 ~ 9, (4.3) and (4.15) hold, and Pc be chosen to be suitably large but still independent of h. Then, the uniformly V ° - e11iptic inequality holds,

c01plvJll 2 < a@,~), w ~ y ° , (4.26)

where Co > 0 is a constant independent of h and L.

PROOF. From L e m m a 4.4, we obtain the bound,

a(v,v) > []vi[~- [ v ~ v - > Clillvil[ 2 - [ vnv

JF o J['o

,)

c~ NvNl,s, +Pcllvll~,s, +PcllAvll2o,s2 +

liv ÷

--

**-v IIo,ro+Pollv~*-vZllo,ro**

(4.27)

- - i F Vn ?3 ' o

where C1 > 0 has a lower bound independent of h and L. Next, we have

f~o

~ v - <_

tlv~ll-~12,i'ollv-IIv2,ro.

(4.28)

Moreover, there exist the bounds for v E V, ° ,

IIv- II,/~,ro -< c II.-II,,~,,

(4.29)

v +

I1<11-~.,~o -< II ~ I1-~/~,~o + I1~: - < 11-,/2,=o

(4.30)

_< c {11.+11~,~2 + Ila.+llo,s: + IIv: - < Ito,ro},

where we have used the bound from L e m m a 4.2,

v +

II'+ll-~/~,ro-<C{llAv+ll-,,~:+ll

11112,os,}

_< c {llA.+llo,~: + I1~+11,,~:}.

Since Cab < ca 2 + (C214e)b 2 for any e > 0, we obtain from (4.29) and (4.30)

Lo vZ-v - _< c IIv-IIl,~, (11,+111,~: +

II,',v÷llo,~: + IIv+ - <llo,ro}

Cl

2 C 2

)2

_7_ iiv-ii,,~ + ~c_T (llv+lll,~ + ila.+llo,~2 + i1.+ _ <llo,r °

_ (4.31) _<

_ 2

<-- ~61N v - II 1,$12 q- ~3C 2 . .~livTli21,Sz"~-NAvTIl~,S2"~t-li'U+n--Vnilo'F°)' where C1 is given in (4.27). Combining (4.27) and (4.31) gives

C1 2

a (v,.) > -7-Ilvlll,s,

2

_ 2

Pc

_ 5

+ c,s'~-3c2"/(llvll,,~: + IIA,ilo~: +llv. + -.° IIo,ro)+C'~ II v+ -v IIo,ro

_{2C1 )}

(4.32)

> -~lll~lll 2,

provided t h a t C1P¢ - (3C2/2C1) >_ (1/2)C1P~. This leads to Pc >_ 3(C2/C~), which is suitably large but still independent of h and L. T h e n the uniformly Vh°-elliptie inequality (4.26) holds

(13)

5. U N I F O R M v O - E L L I P T I C I N E Q U A L I T Y I N V O L V I N G I N T E G R A T I O N A P P R O X I M A T I O N

In this section, w e prove the uniformly V°-elliptic inequality, (3.31). Choose the integration rule,

= = llvll0,ro, (5.1)

J r o ro

where 0 is the k-order interpolant of v. First, w e give a few lemmas. LEMMA 5.1. L e t (4.3) and

ilvtlil,ro -< cL2~ IIv+lll,S~,

v~ c

v2

(5.2)

hold, where v ( > 0) is a positive constant. There exist the bounds for v C V ° ,

,iv + - v-tio,ro >__ air + - v-lio,ro - C h 2 L 2~" laY+ilLs2, (5.3) iiv + - v~-I{o,ro >_ [Iv + - v ; i l o , r ° - C h L 2v lay+HI,s2, (5.4) where C is a constant independent o f h and L.

PROOF. We have

[Iv + - v-ilo,ro < IIv + - v-[to,ro + ]10 + - v+ilo,ro , (5.5) and from (4.3)

[[0+ - v+JJo,ro _< C h 2 [v+J2,r ° < C h 2 L 2" [[V[]o,ro < C h 2 L 2~ ] ] V H I , S 2 . (5.6)

T h e n combining (5.5) and (5.6) gives the first desired b o u n d (5.3),

] ] v + - v-[[o,ro >_ [Jr + - v - [ [ o , r o - C h 2 n 2~ []v[ll,s . (5.7) Similarly, we obtain from (5.2)

il ~+ - < L , r o > - l i < - < L , ~ o - l i < - ~:I[o ~o

>

live+ - v; I]o,ro - c h IFv.ll,,~o

(5.8)

>- ][v+

-

v; [[o,ro

-

ChL2"

II~[I,,s~ •

This is the second desired b o u n d (5.4), and completes L e m m a 5.1. I LEMMA 5.2. Let a11 conditions in L e m m a 5.1 hold. Then,

2 1 _ 2 C h 4 L 4 , + 2

- - v ][o,ro '

][ v + v-{Io,ro >-

~11 ~+

-

I1~ II~,s=

(5.9)

t l ~ - <ll:,ro >- ~

~,~ IIo,ro

-Ch~L~

I1~+11~,~

(5.10)

where C is a constant i n d e p e n d e n t o f h and L. PROOF. Denote x = I{v + - v-llo,ro ,

y = II ~+ - v - IIo,ro,

z = llv+lll,s~,

(5.11) w " : C h 2 L 2v.

(14)

1844 H.-Y. Hu AND Z.-C. LI Equation (5.3) is written simply as x >_ y - w z >_ O. We have

x 2 > (y _ wz)2 --_ y2 _ 2wyz ÷ w2z 2. (5.121 Since 2wyz <<_ y2/2 Jr 2w2z 2, we obtain

x 2 > y 2 + 2 w 2 z 2 + w 2 z 2 - - - w 2 z 2. (5.131

- 2

This is the desired result (5.9) by noting (5.111. The proof for (5.101 is similar, and this completes the proof of Lemma 5.2.

Second, let us consider integration approximation for

ffs:

t, where t -- t(x, y) = ( A u - t - f ) (Av -t- f ) . Let $2 be divided into small triangles Aij and small rectangles K]ij,

Denote by ~ the piecewise r-order interpolant of t on $2, i.e.,

~ = p~(x,y) = ~ a~,~x'y j,

(x,y) •/x~j,

(5.15)

i+j=o or

~ = Q~(x,y) = ~ ai,jxiy j, (x,y) • K],j, (5.16)

i,j=O

where ai,j are the coefficients. Then, the integration rule in (3.7) can be viewed as

Z~jg2(P~j) = f ] g~

ij $2

s: (5.17/

= i f s 5

~3 ij

The partition in (5.141 is regular if max~j(H~j/p~y) <_ C, where H~j is the maximal boundary length of Aij and [3ij, Pij is the diameter of the incircle of Aij and Klij, and C is constant independent of H ( = maxij Hij). The partition (5.141 is quasiuniform if H / m i n i j Hij <_ C. Then we have the following lemma from the Bramble-I-Iilbert lemma [1].

LEMMA 5.3. Let partition (5.141 be regular and quasiuniform. Then, the isltegratiosl rule (5.171 has the error bound,

77 /is

- s2t = (t < C H r+l Itl.+l,s ~ , (5.181

(15)

C o l l o c a t i o n a n d F i n i t e - E l e m e n t M e t h o d s 1845

The integration rule on Aij can be found in Strang and Fix [20], and the rule on [3ij can be formulated by the tensor product of the rule in one dimension, such as the Newton-Cotes rule or the Gaussian rule. The Legendre-Gauss rule given in (3.17)-(3.20) is just one of Gaussian rules with two boundary nodes fixed. For the Newton-Cotes rule, we m a y choose the uniform integration nodes. When r = 1 and 2, the popular trapezoidal and Simpson's rules are given. When v + in $2 are polynomials of order L and choose r = 2L, the exact integration holds,

ff

=

ff,

=

(5.19)

Below, we consider the approximate integration

by the rule with integration orders r < 2L - 1. We have the following lemma.

LEMMA 5.4. Let v + in $2 be polynomials of order L, and the rule (5.17) with order r < 2L - 1 be used for ffs=(Au + f ) ( A v + f). Also assume

II +ll,,s= _

CL('-')"

II +ll,,s=,

e_> 1,

v °,

(5.21)

where u > 0 is a constant independent of L. Then, there exists the bound,

-

Ilvlh,s2,

(5.22)

2 $2

where H is the meshspacing of uniform integration nodes in $2, and C is a constant independent of H and L.

PROOF. For the rule of order r < 2L - 1, we have from L e m m a 5.3 and (5.21),

<- CH'+I I (Av)2 ~+1,s2

r + l

< CHr+l ~

tAvl,,s2

I~vlr+l_,,s~

i = 0

r + l (5.23)

<-

OH"+1 ~

Ilvlli+=,s= II~llr+3-,,s=

i = O r + l < C H r+l i = 0 ( L (i+l)V Hvlll,s2) ( L (r+2-0V Ilv[ll,s2) < cgr+ln(r+a)v 2 IIv[l],s~ •

(16)

1 8 4 6 H . - Y . H u A N D Z.-C. LI

THEOREM 5.1. Let (5.2) and all conditions of Theorem 4.1 and Lemma 5.4 hold. Suppose

hL 2v = o(1), (5.24)

HL (l+2/(r+1))v = o(1). (5.25)

Then the uniformly V°-elliptic inequality (3.31) holds.

PROOF. From Lemmas 5.2 and 5.4 and Theorem 4.1, we have

~(.,v)= ii~

Ivv-I'+

/

<~,-+

P. ff (~.+)'

1

o

J J

$2

+

_-~-IIo,~o

_{+ P~II.= +}

_{- <}

IIo,~o

iS ivv-? + [ ~,z,,- + Pc//(~,,+)~

_S] _J_Fo _{J J $2}

+ P<ll'+2h - v-II~,Fo + ~ IIv+ - vzll~,ro

- CPc (h3L 4v + h2L 4v) _{[Iv[[1,s~ -}2 _CHr+IL(~+3)~_[[v[[~,s~ (5.26) 1

C{Pc(h3L4V h2i4v)Hr+lL(r+3)v}

2 >_ -~a (v, v) - + +

Itvlll,s:

Co {pc (haL4~, H~+,L(~+a). }

__

-7-111viii:

-

c

+

h2L 4v) 4-

Ilvll~,s:

- --2 [[v[[l'sl + 1 - 2 ~ 0 Pc (haL 4~ + h2n 4~) + g r+ln(~+3)~ [[v[[~,s 2

+ ~c H~v,0~ s~ + ~llv+-v-IlLo + vollv:- <llL0/oj

-> -~IIIvlIIL

provided that

°

c

(h3L4 + h L4 )+

_<

(5.27)

which is satisfied by (5.24) and (5.25). This completes the proof of Theorem 5.1. When there is no approximation for ffs2Au+Av+, we have the following corollary.

COROLLARY 5.1. Let (5.2) and all conditions of Theorem 4.1 hold. Also let the integration (5.19) in $2 be exact. Suppose

hL 2v -- o(1). (5.28)

Then, the uniformly V ~ - elliptic inequality (3.31) holds.

Corollary 5.1 holds for the case that v + in $2 are polynomials of order L ( > k), and that the Legendre-Gauss rule in (3.17) with n = L - 1 is used for ffs2 A2v+" Next, let us consider a special case: The functions v + in 5:2 are chosen to be the particular solutions satisfying --Av + = f in $2 exactly. The combination of FEM-CM in (3.4) is given by

(17)

C o l l o c a t i o n a n d F i n i t e - E l e m e n t M e t h o d s 1847 where

a*(u,v)=ff ww+f

S1 J P o (5.30)

f l ( v ) = / /

fv.

(5.31) $1

Note that the term,

Pelf&

(Av) 2, disappears in computation. Obviously, Corollary 5.1 is valid for Motz's problem discussed in Section 6.2.

REMARK 5.1. Different integration rules for

ffs2 (Au + f)(Av + f)

do not influence upon errors of the solutions by combinations of FEM-CM, but guarantee the uniformly Vh°-elliptic inequality (3.31), as long as H is chosen so small to satisfy (5.25), e.g., as long as the number of collocation nodes Pij in quasiuniform distribution is large enough. This conclusion is a great distinctive feature from that in the conventional analysis of FEMs.

REMARK 5.2. For Theorems 4.1 and 5.1, three inverse inequalities, equations (4.3), (5.2), and (5.21), are needed for a polygon $2. For polynomials v + of order L, equation (4.3) holds for

= 2 in [6]. The proof of (5.2) and (5.21) is given in [22].

REMARK 5.3. Equations (3.12)-(3.14) represent the generalized collocation equations using other admissible functions, such as radial basis functions, the Sinc functions, etc. The analysis of this paper holds provided that the inverse inequalities (4.3), (5.2), and (5.21) are satisfied. In fact, these inequalities can be proved for radial basis functions, the Sinc functions, etc. Details of analysis and numerical examples appear in [23].

6. N U M E R I C A L E X P E R I M E N T S

6 . 1 . P o i s s o n ' s P r o b l e m

Consider Poisson's equation,

- A u = 27r 2 sin (Trx) cos (Try), in S,

(6.1)

where S --- { ( x , y ) l - 1 < x < 1, 0 < y < 1}, with the following Dirichlet conditions:

u=O

o n x = + l A 0 < y < _ l ,

u = - s i n ( T r x ) o n y = l A - - l < x < l , (6.2) u=sin(Trx) o n y = 0 A - - l < x < 1.

The exact solution is

u(x,

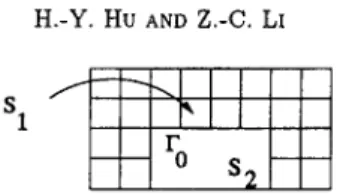
y) = sin(Trx) cos(Try). Divide S by F0 into S1 and $2. The subdomain $1 again is split into uniform regular triangular elements:

$1 -- UqAij,

shown in Figure 2. The admissible functions are chosen as

V-- = Vl, in S1,

V - ~ L

v +

Y~ di~Ti

(2x - 1) T3 (2y - 1), in $2,

i,j=O

(18)

s , \ \ \ s2

\ \ \ \

\ \ \ \ r o

\ \ \ \

Figure 2. Partition of a rectangular solution domain with M =- 4, where M denotes the numbers of partitions along the y-direction in $1.

Table 1. The error norms and condition numbers by combination of FEM-CM using the Legendre-Gauss points as collocation nodes.

M, L, Nd 4, 3, 2 8, 5, 4 16, 7, 6 I1~ -- ~fi IIo,sl 4.06(--2) 1.15(--2) 2.92(--3)

Ilu - ~fi IIl,51 5.87(-1) 2.53(-1) 1.26(-1)

ll~ - '~L llo,s= 4.17(--2) 1.29(--3) 2.05(--4)

Hu - ULHt,s2 1.42(-1) 5.83(-3) 9.67(-4) [[¢+ - ~-[[O,ro 1.92(-2) 1.80(-3) 4.83(-4)

Cond. (A) 8.59(4) 1 . 6 3 ( 6 ) 1.22(7)

Table 2. The error norms and condition numbers by combination of FEM-CM using the trapezoidal points as collocation nodes.

M, L, Nd 4, 3, 4 8, 5, 6 16, 7, 8 I[ u - U h [10,S1 6.92(-2) 1.15(-2) 2.92(--3) Ilu - ~ Ih,sl 7.88(-1) 2.53(-1) 1.26(-1) [[u - uL[]O,S 2 1.64(--2) 4.27(--4) 2.23(--4) H u -- ULIIl,S2 1.09(-1) 4.24(-3) 1.04(-3) II~ + - ~-II0,ro 2.71(-2) 2.81(-3) 5.12(-4) Cond. (A) 8.59(4) 1 . 5 4 ( 6 ) 1.16(7)

where Vl is t h e piecewise linear functions on $1, d~j are u n k n o w n coefficients t o be d e t e r m i n e d , a n d Ti(x) are t h e C h e b y s h e v polynomials, Tk (x) = cos(k c o s - 1 (x)).

We choose t h e L e g e n d r e - G a u s s and t h e t r a p e z o i d a l rules in Section 3 for f f s 2 (Av+)2" Hence, t h e o p t i m a l convergence r a t e O ( h ) in H 1 n o r m s is o b t a i n e d b a s e d on t h e analysis made. Since v + do n o t satisfy t h e b o u n d a r y conditions on O S 2 N F , t h e a d d i t i o n a l c o l l o c a t i o n equations, v + ( P i ) = 0

where Pi E 0 5 2 n F, are also needed. A f t e r t r i a l c o m p u t a t i o n , choose Pc = 50. L e t h = l / M ,

where M d e n o t e s t h e n u m b e r of p a r t i t i o n s along t h e y - d i r e c t i o n in $1 in F i g u r e 2.

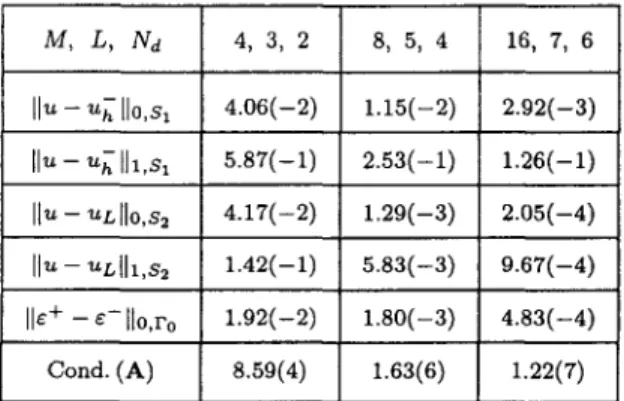
We choose M e t h o d I in Section 3, and t h e error norms are listed in T a b l e s 1 a n d 2, where N d

denotes t h e n u m b e r of collocation nodes along one d i r e c t i o n in $2 in F i g u r e 2, 6 - = u - Uh a n d 6 + = u - U L . T h e following a s y m p t o t i c r e l a t i o n s are observed from T a b l e s 1 a n d 2,

- u h ll 0,sl = O ( h 2 ) , - hIIl,sl = O ( h ) , (6.4)

[]u - ULIIO,S, = 0 ( h 3 ) , [[u - UL[[1,S2 --- 0 ( h 3 ) , (6.5)

116 + - E-H0,ro ---- O(h2), C o n d . ( A ) = O ( h - 3 ) . (6.6) E q u a t i o n s (6.4),(6.5) indicate t h a t t h e n u m e r i c a l solutions have t h e o p t i m a l convergence r a t e

(19)

Collocation and Finite-Element Methods

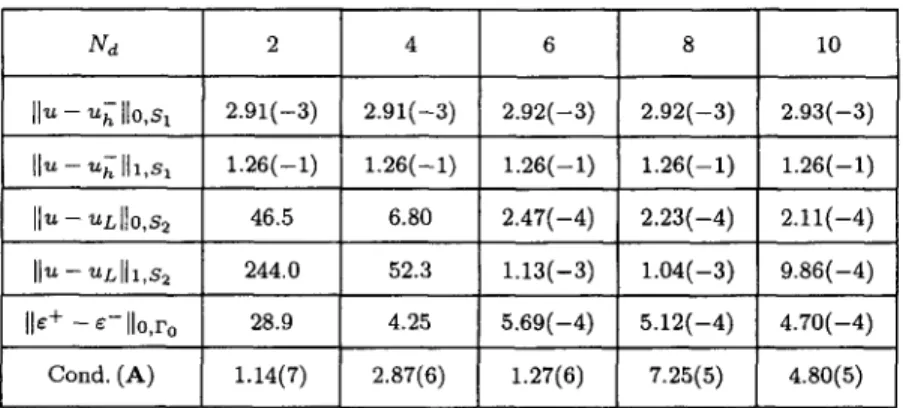
Table 3. The error norms and condition numbers by combination of FEM-CM using the trapezoidal rule with M = 16 and L = 7.

Nd 2 4 6 8 10 I]u - Uh ][O,S 1 2.91(--3) 2.91(--3) 2.92(--3) 2.92(--3) 2.93(--3) I[~ - **~ Ih,s~ 1.26(-1) 1.26(-1) 1.26(-1) 1.26(-1) 1.26(-1) I1'* - ~ L II0,82 46.5 6.80 2.47(-4) 2.23(-4) 2.11(-4) IN - ULlh,s2 244.0 52.3 1.13(-3) 1.04(-3) 9.86(-4) D + - ~-IIo,ro 28.9 4.25 5.69(-4) 5.12(-4) 4.70(-4) Cond. (A) 1.14(7) 2.87(6) 1.27(6) 7.25(5) 4.80(5) Table 4. The error norms and condition numbers by combination of FEM-CM using the Newton-Cotes rules with different orders on M = 16, L = 7, and Nd = 7.

Order r = l r = 2 r = 4 r = 8 [Ju - u h [[0,81 2.91(-3) 2.91(-3) 2.92(-3) 2.92(--3) I[U--Uh[[l,s 1 1.26(--1) 1.26(--1) 1.26(--1) 1.26(--1) Ilu - ~L IIo,s= 1.93(--4) 2.00(--4) 1.99(--4) 1.97(-4) l{** - ~,LHI,s~ 1.05(-3) 1.03(-3) 1.03(-3) 1.12(-3) lie + - ¢-[[0,ro 6.64(-4) 7.03(-4) 6.97(-4) 6.72(-4) 6.59(5) 7.69(5) 8.22(5) 2.86(6) Cond. (A) 1849 of t h e s o l u t i o n s of c o m b i n a t i o n s of F E M - C M , as l o n g as t h e n u m b e r o f c o l l o c a t i o n e q u a t i o n s in q u a s i u n i f o r m d i s t r i b u t i o n is l a r g e e n o u g h . I n T a b l e 3, we c h o o s e M = 16 a n d L = 7, b u t c h a n g e t h e n u m b e r Nd u s e d in t h e t r a p e z o i d a l rule in $2. F r o m T a b l e 3, we c a n see t h a t g o o d s o l u t i o n s c a n b e o b t a i n e d w h e n Nd > 6; t h i s f a c t p e r f e c t l y verifies t h e c o n c l u s i o n s in T h e o r e m 5.1. I n T a b l e 4, w e c h o o s e M = 16, L = 7, a n d Nd = 7, b u t use t h e N e w t o n - C o t e s r u l e w i t h difference o r d e r r. W h e n r = 1, t h e N e w t o n - C o t e s r u l e is j u s t t h e t r a p e z o i d a l rule. F r o m T a b l e s 1, 2, a n d 4, we c a n see t h a t t h e d i f f e r e n t i n t e g r a t i o n rules u s e d in $2 do n o t i n f l u e n c e t h e o p t i m a l c o n v e r g e n c e r a t e , e i t h e r . 6.2. M o t z ' s P r o b l e m C o n s i d e r M o t z ' s p r o b l e m , in S, (6.7) < y < 1}, w i t h t h e m i x e d t y p e of D i r i c h l e t - N e u m a n n o n x = - - l A 0 < y _ < 1, 0 2 u 0 2 u zxu = + 3 7 = o, w h e r e S = { ( x , y ) l - 1 < x < 1, 0 c o n d i t i o n s , ux = O,

(6.8)

u = 500, on x = 1 A 0 _ < y < 1, u y = 0 , o n y = l A - - l < x < l , u = 0 , o n y = 0 A - - 1 _< x < 0, Uy----O, o n y - - - - 0 A 0 < x _ < l .

(20)

' " F0 S 2

Figure 3. Partition of Motz's problem with M = 4.

The origin (0, 0) is a singular point, since the solution behaviour u = O ( r 1/2) as r --* 0 due to the intersection of the Dirichlet and Neumann conditions. Divide S by F0 into $1 and $2, where $2 = { ( x , y ) l - 1/2 < x < 1/2, 0 < y < 1/2}. The subdomain $1 is again split into uniform square elements Dij with the the boundary length h, shown in Figure 3.

The admissible functions are chosen as

{ v- ~--vl'

( 2 )

V ~-

L

V + --- ~ / ) ~ r £ + 1 / 2 c 0 s ~ + O, t=O

(6.9)

where vl is the piecewise bilinear functions in $1,/)~ are unknown coefficients to be determined, and (r, 0) are the polar coordinates with origin (0, 0).

Since the particular solutions r ~+1/2 cos(l + 1/2)0 satisfy (6.7) in $2 and the boundary conditions,

u = 0 , o n y = 0 A - - l _ < x < 0 ,

(6.1o)

u y = 0 , o n y = 0 A 0 < x < _ l , (6.11)

the collocation equations (3.9)-(3.11) are reduced to

(v+ - . - ) (Qj) = 0, (.~+ - , ; ) (Qj) = 0, Q, e r0.

(6.12)

Then, the collocation equations with weights on F0 are given by

Qj E F0, (6.13) where Pc is a penalty constant. In computation, we choose Pc = 50.

We choose Method II, where (3.26) represents (6.13). We adopt the trapezoidal and the Simpson's rules for integrals, ( P c / h ) fro(U + - u - ) ( v + - v - ) and Pc fr0(U + - u ~ ) ( v + - v Z ) . The error norms and the condition numbers are listed in Tables 5 and 7, where M denotes the number of partitions along the y-direction in $1 in Figure 3, and L denotes the term number of the expansion (6.9) in $2. Cond. denotes the condition numbers of the over-determined system (3.35). The following asymptotic relations are observed from Tables 5 and 7,

Ilu - u h l l l , s l + Jl~ - ~LlJl,s2 = O ( h ) ,

, , u , - uhr,,,s, + IJ - LH,,s2 = o

II

**-*- IIo,,-o = o (h=),**

O<a<<l,

Cond. = O ( h - l ) .

(6.14)

(6.15)

(6.16)

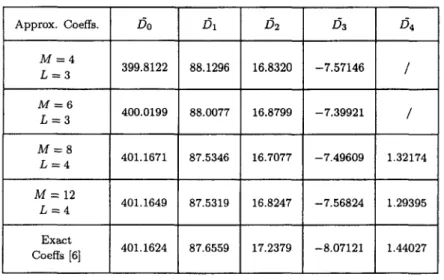
We can see t h a t equations (6.14) and (6.15) coincide with the optimal convergence rates. The approximate coefficients are given in Tables 6 and 8. When M = 12 and L = 4, the approximate

(21)

Collocation and Finite-Element Methods

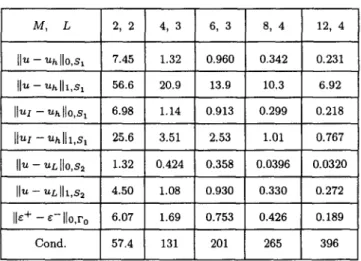
Table 5. The error norms and condition numbers for Motz's problem by combination of FEM-CM using the trapezoidal rule for f r o

M, L 2, 2 4, 3 6, 3 8, 4 12, 4 l]u - Uh I10,$1 7.45 1.32 0.960 0.342 0.231 flu -- uull1,,¢ I 56.6 20.9 13.9 10.3 6.92 IluI - uhHo,sl 6.98 1.14 0.913 0.299 0.218 Ilui - Uhlll,S 1 25.6 3.51 2.53 1.01 0.767 H'a - - U L []0,$2 1.32 0.424 0.358 0.0396 0.0320 HU -- ULI]I,S 2 4.50 1.08 0.930 0.330 0.272 II e+ -- ~-- H0,ro 6.07 1.69 0.753 0.426 0.189 Cond. 57.4 131 201 265 396 1851

Table 6. The approximate and exact coefficients for the Motz's problem by combination of FEM-CM using the trapezoidal rule for fro"

Approx. Coeffs. Do M = 2 397.6500 L = 2 M = 4 399.8047 L = 3 M = 6 400.0200 L = 3 M = 8 401.1672 L = 4 401.1649 M = 1 2 L = 4 Exact Coeffs [6] 401.1624 /Jl 91.0576 88.1314 88.0077 87.5345 87.5318 16.1292 / / 16.8330 --7.57220 / 16.8798 -7.39917 / 16.7077 -7.49616 1.32179 16.8247 --7.56824 1.29397 17.2379 --8.07121 1.44027 87.6559 v a l u e of Do is 401.1649, a n d t h e r e l a t i v e e r r o r is g i v e n b y I/)0 - D01 = 401.1649 - 401.1624 ID01 401.1624 = 6.2 x 10 - 6 . N o t e t h a t s u c h a n a c c u r a c y is h i g h e r t h a n t h a t g i v e n in [6], w h e r e t h e r e l a t i v e e r r o r of Do is a b o u t 10 - 4 w h e n M = 12. F r o m T a b l e s 5 - 8 , we c a n see t h a t t h e t r a p e z o i d a l a n d t h e S i m p s o n ' s rules p r o v i d e a l m o s t t h e s a m e r e s u l t s , t o i n d i c a t e a g a i n t h a t d i f f e r e n t i n t e g r a t i o n rules for t h e i n t e g r a l s , ( P c ~ h ) f r o (u+ -

u - ) ( v + - v - ) a n d Pc fro(U + - u ~ ) ( v + - v ~ ) , d o n o t i n f l u e n c e u p o n t h e c o n v e r g e n c e r a t e s of t h e n u m e r i c a l s o l u t i o n s if t h e i n t e g r a t i o n n o d e s (i.e., t h e c o l l o c a t i o n n o d e s ) a r e l a r g e e n o u g h . O b v i o u s l y , t h e c o n d i t i o n n u m b e r s g i v e n in T a b l e s 5 a n d 7 a r e s i g n i f i c a n t l y s m a l l e r t h a n t h o s e in T a b l e s 1 a n d 2. H e n c e , M e t h o d I I (i.e., t h e l e a s t s q u a r e s m e t h o d in (3.36)) is also r e c o m m e n d e d for t h e c o m b i n a t i o n s of t h e c o l l o c a t i o n m e t h o d s d u e t o b e t t e r n u m e r i c a l s t a b i l i t y .

(22)

Table 7. The error norms and condition numbers for Motz's problem by combination of FEM-CM using the Simpson's rule for fro"

M, L 4, 3 6, 3 8, 4 12, 4 Ilu - uh Ito,sl 1.32 0.960 0.342 0.231 HU -- UhII1,S 1 20.9 13.9 10.3 6.92 HUl -- UhllO,Sl 1.14 0.913 0.299 0.218 IluI -- Uhlll,Sl 3.51 2.53 1.01 0.767 Ilu -- UL tlo,s2 0.422 0.358 0.0396 0.0320 Ilu - UL[]I,S 2 1.07 0.930 0.330 0.272 He + -- e-H0,ro 1.69 0.753 0.426 0.189 Cond. 165 263 350 527

Table 8. The approximate and exact coefficients for the Motz's problem by combination of FEM-CM using the Simpson's rule for fro"

Approx. Coeffs. /90 /91 M = 4 399.8122 88.1296 L = 3 M----6 400.0199 88.0077 L = 3 M = 8 401.1671 87.5346 L = 4 M = 12 401.1649 87.5319 L = 4 401.1624 87.6559 Exact Coeffs [6]

/92

/93

16.8320 -7.57146 16.8799 -7.39921 16.7077 -7.49609 16.8247 -7.56824 17.2379 -8.07121

/:i4

1.32174 1.29395 1.44027

F I N A L

R E M A R K S

To close t h i s p a p e r , let us m a k e a few r e m a r k s .

1. T h i s p a p e r p r o v i d e s a t h e o r e t i c a l f r a m e w o r k of c o m b i n a t i o n s of C M s w i t h o t h e r m e t h o d s . T h e b a s i c i d e a is to i n t e r p r e t C M as a special F E M , i.e., t h e L S M i n v o l v i n g i n t e g r a t i o n a p p r o x i m a t i o n . E q u a t i o n s (3.9)-(3.11) i n C M are s t r a i g h t f o r w a r d l y , a n d easily i n c o r p o - r a t e d i n t o t h e c o m b i n e d m e t h o d s , see (3.25) a n d (3.26). T h e c o m b i n a t i o n of C M in t h i s p a p e r is also a n i m p o r t a n t d e v e l o p m e n t from Li

[6].

2. T h e key a n a l y s i s for c o m b i n a t i o n s of C M is to prove t h e n e w u n i f o r m V ° - elliptic in- e q u a l i t i e s (2.17) a n d (3.31). T h e n o n t r i v i a l proofs i n S e c t i o n 3 are n e w a n d i n t r i g u i n g , w h i c h consists of t w o steps:

Step I for t h e s i m p l e o n e (4.20) w i t h o u t fro vn v ;

S t e p II for T h e o r e m 4.1. N o t e t h a t b o t h (2.6) a n d (2.7) a r e r e q u i r e d i n c o m b i n a t i o n s (2.11) b e c a u s e t h e i n t e g r a l P c f f s 2 A u A v worked as if for t h e b i h a r m o n i c e q u a t i o n i n $2 in t h e t r a d i t i o n a l F E M s , see [1], w h e r e t h e e s s e n t i a l c o n t i n u i t y c o n d i t i o n s u + -- u - a n d u + = u ~ s h o u l d he i m p o s e d o n t h e i n t e r i o r b o u n d a r y Fo.

(23)

3. In algorithms, the integration approximation leads the LSM to the collocation method. In error analysis, the integration approximation plays a role only for satisfying the uniformly V ~ - elliptic inequality, but not for improving accuracy of the solutions. The algorithms and the analysis in this paper are distinctive from the existing literature in CM.

4. In $2, Poisson's equation and the interior and exterior boundary conditions are copied straightforwardly into the collocation equations. This simple approach covers a large class of the CM using various admissible functions, such as particular solutions, orthogonal polynomials, the radial basis functions, the Sinc functions, see [23].

5. The numerical experiments are carried out to verify the theoretical analysis made. Also Methods I and II in Section 3 are proven to be effective in computation.

R E F E R E N C E S

1. P.G. Ciarlet, Basic error estimates for elliptic problems, In Finite Element Methods (Part I), (Edited by P.G. Ciarlet and J.L. Lions), p. 17-352, North-Holland, (1991).

2. J.T. Oden and J.N. Reddy, An Introduction to the Mathematical Theory of Finite Elements, John Wiley and Sons, New York, (1976).

3. C. Bernardi and Y. Maday, Spectral methods in techniques of scientific computing (Part 2), In Handbook of

Numerical Analysis, Volume V, (Edited by P.G. Ciarlet and J.L. Lions), Elsevier Science, (1997).

4. C. Canuto, M.Y. Hussalni, A. Quarteroni and T.A. Zang, Spectral Methods in Fluid Dynamics, Springer- Verlag, New York, (1987).

5. D. Gottlieb and S.A. Orszag, Numerical Analysis of Spectral Methods: Theory and Applications, SIAM, Philadelphia, PA, (1977).

6. Z.C. Li, Combined Methods for Elliptic Equations with Singularities, Interfaces and Infinities, Chapters 7-9, 11, 15, Kluwer Academic Publishers, Boston, MA, (1998).

7. A. Quarteroni and A. Valli, Numerical Approximation of Partial Differential Equation, Springer-Verlag, Berlin, (1994).

8. B. Mercier, Numerical Analysis of Spectral Method, Springer-Verlag, Berlin, (1989).

9. C. Bernardi, N. Debit and Y. Maday, Coupling finite element and spectral methods: First result, Math.

Comp. 54, 21-39, (1990).

10. J. Shen, Efficient Spectral-Galerkin method I. Direct solvers of second- and fourth-order equations using Legendre polynomials, SIAM. J. Sci. Comput. 14, 1489-1505, (1994).

11. J. Shen, Efficient Spectral-Galerkin method II. Direct solvers of second- and fourth-order equations using Chebyshev polynomials, SIAM. J. Sci. Comput. 15, 74-87, (1995).

12. J. Shen, Efficient Spectral-Galerkin method III. polar and cylindrical geometries, SIAM. J. Sci. Comput. 18, 1583-1604, (1997).

13. D.B. Haidvogel, The accurate solution of Poisson's equation by expansion in Chebyshev polynomials, J. Corn-

put. Phys. 30, 167-180, (1979).

14. G. Yin, Sinc-Collocation method with orthogonalization for singular Poisson-like problems, Math. Comp. 62 (205), 21-40, (1994).

15. D.N. Arnold and W.L. Wendland, On the asymptotic convergence of collocation method, Math. Comp. 41 (164), 349-381, (1983).

16. C. Canuto, S.I. Hariharan and L. Lustman, Spectral methods for exterior elliptic problems, Namer Math. 46, 505-520, (1985).

17. D. Pathria and G.E. Karniadakis, Spectral element methods for Elliptic problems in nonsmooth domains,

J. Comput. Phys. 122, 83-95, (1995).

18. C.E. Sneddon, Second-order spectral differentiation matrices, S I A M J. Numer. Anal. 33, 2468-2487, (1996). 19. G.H. Colub and C.F. Loan, Matrix Computations, Second Edition, Chapters 3, 4, 12, The Johns Hopkins

University Press, Baltimore, MD, (1989).

20. C. Strang and C.J. Fix, An Analysis of the Finite Element Method, Prentice-Hall, (1973). 21. K.E. Atkison, An Introduction to Numerical Analysis, John Wiley and Sons 264, (1989).

22. H.Y. Hu, and Z.C. Li, Collocation methods for Poisson's equation, Computer Methods in Applied Mechanics

and Engineering (to appear).

23. H.Y. Hu, Z.C. Li and A.H.C. Cheng, Radial basis collocation method for elliptic boundary value problem,